Over the past few years, scientific research has focused on developing materials with improved properties to meet specific practical requirements. Later, scientists derived metamaterials (MMs), and discovered that these materials possess properties that do not exist in nature1. The scientific community recognizes MMs as synthetic constructs that derive the remarkable functionality from various unique structural arrangement, rather than their elemental composition. As a result, they can display exceptional electromagnetic properties that are not typically observed in organic materials2. These characteristics include a negative refractive index3 inverse Doppler effects4 and perfect imaging5. These properties have sparked interest in utilizing MMs in various applications, such as absorbers6,7,8 filters9,10 Ultra-sensitive sensing devices11 and electromagnetic (EM) cloaking12. The movement of electromagnetic (EM) waves through a material depends on two factors: (i) electric permittivity (ε) and (ii) magnetic permeability (µ). The polarity of both ε and µ dictate the specific characteristics of EM transmission13,14. Materials are classified based on their EM response. Double Positive (DPM) with positive ε and µ, Epsilon Negative (ENM) or negative µ with opposite signs for ε and µ, and Double Negative (DNM) with negative ε and µ, where waves travel oppositely15,16.

Metamaterial absorber (MMAs) is type of MMs and can be used to achieve absorption of EM waves for many applications in energy harvesting. These materials are also employed to minimize electromagnetic interference (EMI) and improve isolation between devices. The principle of absorption focuses on impedance matching through the use of a dielectric layer. The surface impedance of the layer should be aligned with the free space impedance (377 Ω). In the context of this phenomenon, the reflection coefficient is reduced to zero, resulting in maximum absorption17. Moreover, MMAs provide a solution to surpass the thickness restrictions of conventional quarter-wavelength devices18,19. The thickness of a MMA can be approximately 25 times smaller than that necessary for functional layers at their resonance wavelength, resulting in significantly reduced dimensions relative to their conventional counterparts20.

The demand for the applications of Internet of Things (IoT) is increasing, causing lower frequency bands to become saturated. These bands, which are primarily used by existing IoT systems operating below 3 GHz, are facing insufficiency. To address this issue, there is a need to shift to millimetre wave (mm Wave) bands that provide wider unused bandwidth. By utilizing this available spectrum, it is possible to enable a 1000-fold capacity increase for 5G networks compared to current LTE-A technologies21. This poses an opportunity to utilize mm Wave bands for absorption. Presently, research on mm Wave absorbers is primarily focused on developing lightweight and flexible solutions using MMs. These solutions aim to improve absorption properties and adapt to various shapes and structures. Considering that previous studies have concentrated on creating single band absorbers with the right materials and structural features to enhance their absorption capabilities. Multiband MMs designs offer a potentially more compact and lightweight solution compared to conventional single-band absorbers, making them appealing for integration into next-generation electronic devices22.

Single-band MMA are promising in research for their capability to achieve highly targeted absorption at specific frequencies within the electromagnetic spectrum. Recent research has developed a unit cell for a terahertz (THz) MMA that allows light to pass through while remaining unaffected by polarization. This absorber, constructed from Indium oxide doped with indium-tin-oxide (ITO) resistive films, demonstrates remarkable adoption efficiency, reaching a peak of 94.1% at a frequency of 120.8 GHz. The limitation of this work is the dependence on the material’s properties of ITO films. This could potentially limit scalability or future advancements in achieving even higher absorption efficiencies23. A bilayer single-band MMAs unit cell is designed to achieve an absorptivity of 70% at 1.3 terahertz. This design highlighted the difficulty in suppressing higher-order absorption modes. The presence of higher-order modes presented a significant challenge for single-band MMAs designed to achieve ultra-narrowband absorption characteristics24. Previous studies have been conducted on single-band MMA that utilize cut wire and square ring (CW-SR) geometries. These studies have primarily focused on achieving nearly ideal impedance matching along with a high absorption rate of 99.50% at a specific frequency of 4.70 GHz in the microwave range. A drawback is the trade-off between multi-band functionality and fabrication complexity, as achieving specific multi-band responses requires complicated and costly designs25. Researchers demonstrated an ultra-thin MMAs on a flexible substrate for mm Wave frequencies. These absorbers targeted specific bands within the 77–110 GHz range, achieving peak absorption exceeding 90% for single bands. The study also highlighted a key challenge in designing such absorbers, achieving a balance between the desired operating frequency and the level of absorption26.

Multi-band MMA have gained interest because of their capability to control and absorb electromagnetic waves at multiple specific frequencies, allowing for a broad spectrum of practical uses. Multi-band absorbers play an essential role in a variety of applications that require absorption across multiple frequencies. This capability is particularly important in areas like EMI shielding, where a wide range of frequencies often need to be suppressed. The ability to target multiple frequencies simultaneously is essential for achieving compact designs. This compactness is highly valuable in applications where dimensions and weight are key considerations, particularly in next-generation wireless communication devices27,28. Researchers achieved triple-band absorption by utilizing a closed ring square shaped resonator fabricated on an FR-4 substrate. The closed-ring resonator exhibited absorption peaks of 94.98%, 87.10%, and 94.06% in the three bands, all of which were below 95%29. A square-shaped resonator designed showed impressive results, achieving over 99% absorption across multiple frequency bands. However, the downside is the extreme complexity of the meta-atom structure used in the design30. A new design for a triple-band absorber is introduced, utilizing a composite of T-shaped and square like meta-atoms. While this design achieved near-perfect absorption (99%) for one band, it fell short for the other two bands, reaching only 95% and 97% absorption. Additionally, the complexity of the meta-atom design itself remained a challenge31. Researchers developed a sophisticated material with the capability to absorb electromagnetic waves at three specific frequencies: 91.6%, 99.6%, and 99.8%32. Despite achieving acceptable outcomes, these designs are still subject to modifications in terms of complexity, material properties, and size, particularly in the mm Wave band.

A narrowband dual-band absorber, with square and split-ring resonators, achieved over 99% absorption at 1.55 GHz and 3.3 GHz, ideal for GNSS and 5G. The drawbacks included reliance on simulations and potential challenges with scalability and fabrication33. A narrow penta-band metamaterial absorber achieved over 90% absorption at 2.7 GHz, 6.5 GHz, 9.4 GHz, 13.3 GHz, and 15.5 GHz, with polarization insensitivity and broad angle tolerance. Its constraint is reliance on specific frequency peaks, limiting broader range applicability34. An E-shaped fractal-based absorber provides wideband absorption in the 20–30 GHz range, exhibiting polarization insensitivity and robustness in both TE and TM modes. Although it enhances capacitance across various frequencies, its average absorptivity is approximately 80%, achieving near-perfect levels only at certain frequencies35. A single-layer triangular broadband metamaterial absorber with lumped resistances achieved over 90% absorption; however, its performance is influenced by nonlinear changes in geometrical thickness36.

The primary objective of this research is to design and analyse a triple-band MMA with an exceptional absorption capacity at 28 GHz, 33 GHz, and 38 GHz, which are crucial frequencies for futuristic 5G applications and satellite communication. This work employs a single, widely available FR-4 substrate to avoid the complexity and multilayer design structures typically used in such applications. The resonator of the proposed MMA encloses a circular ring with two elliptical resonator and metallic strip using a low-profile dielectric material of single layer. For the purpose of obtaining the high absorption peaks at the frequency of operations, the geometrical dimensions are optimised using parametric optimisation. The performance of this structure in terms of absorption can be demonstrated by analysing its surface current distributions, electric field patterns, and input impedance. Under normal incidence, the suggested MMA exhibits three absorption peaks at 28 GHz, 33 GHz, and 38 GHz, achieving high absorption rates of 99%, 98%, and 99% respectively. The findings highlight the potential use of the suggested structure in 5G communication, beamforming, and MIMO (multi-input and multi-output) antenna systems absorption for satellite communications.

The remaining article is divided into several sub sections. Section II provides an overview of the unit cell structure’s configuration and analyses the results of the metasurface cell configuration. Section III provides the results obtained through simulations using CST Microwave Studio version 2022. Section IV presents the actual measurements obtained through experimentation and Finally, Section V concludes the paper.

Triple band absorber

Metasurface unit cell structure design

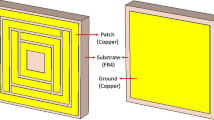
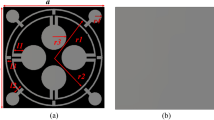
The unit cell geometry of proposed design as well as dimensions are presented in Fig. 1(a). The proposed unit cell is printed on low profile FR-4 substrate material having dimensions 5.8 × 5.8 mm2 (Ls x Ws), with relative permittivity [ϵs = 4.3(1 + 0.02) i], 0.025 loss tangent, and thickness of 1.6 mm. The infinitely repeating metasurface on the xy-plane is designed to interact with electromagnetic waves arriving perpendicularly (z-direction). This unit cell is the fundamental pattern that repeats to create the entire metasurface. The initial design parameters are based on the equivalent circuit components of RLC. Subsequently, parameter-based optimization is employed to regulate the impedance alignment at the target frequencies for absorption. The distinct geometries of each element are anticipated to generate unique absorption peaks in the material’s response. The composed meta-atom comprises three layers placed on top of each other.

The bottom layer consists of a metallic copper layer with a conductivity of σ = 5.8 × 10^7 S/m. The top layer of the meta-atom features a composite resonator, which includes an oval-shaped copper patch surrounded by a circular cross-section copper patch. Both the bottom and top metallic layers have a thickness of mt = 0.035 mm, which is significantly greater than the skin depth, thereby facilitating transmission through the metasurface. The proposed design draws inspiration from the work presented in37 it begins with a focus on a single-band absorber in the initial stage and then optimizes the design for triple-band performance. This approach formed the basis for developing the triple-band absorber discussed in this study. The final unit cell and design stages are shown in Fig. 1. The specifications of the proposed unit cell are depicted in Table 1.

Fig. 1
figure 1

(a) Proposed single unit cell (b) Design evaluation.

Full size image
Table 1 Design considerations for the proposed MMA unit cell.
Full size table

Frequency domain unit cell analysis

The metasurface unit cell is simulated using CST Microwave Studio Suite 2022, employing the Frequency Domain Solver (FDS). In order to understand the behaviour of the suggested unit cell a simulation setup is displayed in Fig. 2.

Fig. 2
figure 2

Computational model for the proposed metasurface unit cell.

Full size image

The simulation configuration is featured with the single unit cell situated across the waveguide port 1 aligned along the positive z-axis. This port is facilitated for the excitation of the unit cell with electromagnetic waves during the simulation process. In the unit cell, the simulated design zmin is directed towards the ground plane, which is set to zero and open in the z-direction. In this analysis, boundary conditions are applied for the unit cell in the x-y directions, while open space boundary conditions are used along the z-direction. To evaluate and identify the execution and electromagnetic properties of the proposed design, the scattering characteristics are investigated, specifically reflection coefficient (S11).

The structure evaluation of unit cell design is presented in Fig. 1(b). In stage − 1, unit cell is composed of a circular ring resonator of width w1 which gives a reflection coefficient of −25 dB at 28.5 GHz with single band reflection coefficient and absorption as shown in Fig. 3(a). In stage − 2, an elliptical resonator of width c is introduced in the canter of circular ring coupling the inner part of ring at both ends. This step makes the resonator dual-band, operating at 28 GHz and 33 GHz with a reflection coefficient of −15 dB and − 43 dB with a 97%, 98% absorption, respectively. For further enhancement, the introduced elliptical resonator is mounted at an angle of 900 as demonstrated in stage-3. This step enhanced the band performance from dual-band to triple band as well as absorption with a resonance of 28 GHz, 32.8 GHz, 38 GHz with a reflection coefficient of −13 dB, −10.5 dB and − 32 dB correspondingly. For further enhancement and to make the absorption maximum at 33 GHz, a metallic strip is introduced in between the resonator as shown in stage − 4. In Stage-4, the metallic strip introduced capacitive coupling between the other elliptical rings therefore in this stage, MSA unit cell performs a tri-band resonance at 28 GHz, 33 GHz and 38 GHz with reflection coefficient of −21 dB, −18 dB, −33dB and an absorption of 99%,98%, and 99% respectively.

Fig. 3
figure 3

(a) The simulated reflection curves of the suggested absorber with three distinct bands. (b) Predicted absorption behaviour of the simulated structures.

Full size image

The absorption capability of the unit cell denoted by A(ω) in mathematical term formulated as38.

$$\:\text{A}\left(\text{w}\right)=1-\text{T}\left(\text{w}\right)-\text{R}\left(\text{w}\right)$$
(1)
$$\:\text{A}\left(\text{w}\right)=1-\:{\left|{\text{S}}_{21}\left(\text{w}\right)\right|}^{2}-\:{\left|{\text{S}}_{11}\left(\text{w}\right)\right|}^{2}\:$$
(2)

whereas,

$$\:{\left|{\text{S}}_{11}\left(\text{w}\right)\right|}^{2}\:=\:{\left|{\text{S}}_{{11}_{\text{x}\text{x}}}\left(\text{w}\right)\right|}^{2}+\:{\left|{\text{S}}_{{11}_{\text{y}\text{x}}}\left(\text{w}\right)\right|}^{2}$$
(3)

The indices xx and yx individually represent the co-polar and cross-polar parts. The continuous metal ground plane in our proposed design exhibits perfect wave impedance, resulting in a null forward transmission coefficient \(\:\left({\text{S}}_{21}=0\right)\).Thus, the absorption features become solely governed by the reflection properties

$$\:\text{A}\left(\text{w}\right)=1-\:{\left|{\text{S}}_{11}\left(\text{w}\right)\right|}^{2}\:$$
(4)

An understanding of the design of the absorber can be improved by applying the impedance alignment theorem. When the effective impedance (Ze) of the metasurface absorber (MSA) matches the ambient impedance (Z0 = 377 Ω in air), reflection coefficient (Γ(ω) ≈ 0) from the designed metasurface is minimized. The effective impedance of the metasurface can be assessed by examining its reflection (R) and transmission (T) coefficients. in the following manner39.

$$\:{\text{Z}}_{\text{e}}=\:\sqrt{\frac{{\left(1+\text{R}\right)}^{2}-{\text{T}}^{2}}{{\left(1-\text{R}\right)}^{2}-{\text{T}}^{2}}}$$
(5)

whereas,

\(\:\left|{\text{R}}^{2}\right|=\:\left\{\begin{array}{c}{\left|{\text{R}}_{\text{x}\text{x}}\right|}^{2}+\:{\left|{\text{R}}_{\text{y}\text{x}}\right|}^{2}\\\:{\left|{\text{R}}_{\text{x}\text{y}}\right|}^{2}+{\left|{\text{R}}_{\text{y}\text{y}}\right|}^{2}\end{array}\right.\) for x and y polarized waves

The absorption of unit cell is shown in Fig. 3(b). The efficiency of the proposed absorber is assessed based on peak absorption at resonant frequencies, which indicates its optimal performance. This widely accepted method demonstrates maximum energy absorption at critical frequencies40. The efficiency values are summarized in Table 2, substantiating the characterization of the structure as highly efficient at 28 GHz. 33 GHz and 38 GHz.

Table 2 Simulated efficiency of proposed design at desired frequencies.
Full size table

The impedance results in Fig. 4 illustrate that the real part of the impedance remains mostly positive within the frequency domain of 24 GHz to 40 GHz. It begins at 2000 Ω at 24 GHz and gradually increases to approximately 8000 Ω at 40 GHz. On the other hand, the imaginary part of the impedance is mostly negative. It starts at −2000 Ω at 24 GHz and decreases (becomes more negative) to about − 8000 Ω. The real and imaginary impedance at 28 GHz, 33 GHz, and 38 GHz are given in Table 3.

Fig. 4
figure 4

Analysis of the normalized input impedance for the tri-band MMA.

Full size image
Table 3 Real and imaginary components of the MMA impedance at resonant frequencies.
Full size table

The absorber’s input impedance (Zin) depends on its relative material properties, specifically the relative dielectric constant (εr) and relative magnetic permeability (µr). These properties, measured in the frequency domain, tell us exactly how a material will respond to electromagnetic radiation. The selection of the appropriate material for electromagnetic applications depends on how its complex permittivity (ε) and permeability (µ) change with frequency. Scientists rely on S-parameter measurements to determine these important properties. The Drude model41 serves as a tool for understanding how materials respond to electric fields by explaining permittivity. Conversely, the Lorentz model42 fulfills a similar function by explaining permeability and how materials react to magnetic fields. Drude and Lorentz’s models offer a helpful starting point but rely on assumptions. To bypass these, techniques like free-space method43 Nicolson-Ross-Weir (NRW) technique44 and NIST iterative nonlinear fitting technique directly extract permittivity and permeability providing a more robust way to characterize material behaviour. In this study, we utilize the NRW technique under conditions where the transmission coefficient (S21) is negligible because of significant attenuation through the lossy FR-4 substrate. Previous research45,46 supports that this situation allows for a reflection-only formulation of the NRW method. This approach facilitates the extraction of effective permittivity and permeability for electrically thick or high-loss structures. This method is selected for its straightforward implementation in retrieving the effective permittivity (εr) and permeability (µr) given as

$$\:{{\varepsilon}}_{\text{r}\text{M}}=\:\frac{2}{\sqrt{\frac{{\upomega\:}}{\text{c}}}\:\times\:\text{L}}\:\times\:\:\frac{1-\:\left(\text{T}+\text{R}\right)}{1+\left(\text{T}+\text{R}\right)}$$
(6)

and

$$\:{{\upmu}}_{\text{r}\text{M}}=\:\frac{2}{\sqrt{\frac{{\upomega\:}}{\text{c}}}\:\times\:\text{L}}\:\times\:\:\frac{1-\:\left(\text{T}-\text{R}\right)}{1+\left(\text{T}-\text{R}\right)}\:$$
(7)

Where, c represents the speed of light, and L denotes the thickness of the substrate.

The electromagnetic properties of the simulated material are characterized by extracting its complex permittivity (ϵ = ϵ′ − jϵ″) and permeability (µ = µ′ − jµ″) over the 24–40 GHz frequency range based on the simulated S11 and S21 parameters. As illustrated in Fig. 5, the real parts of permittivity (ϵ′) and permeability (µ′) remain positive across the entire frequency band, indicating stable energy storage characteristics and favorable impedance matching, which facilitate efficient wave penetration. The imaginary components, ϵ″ and µ″, correspond to dielectric and magnetic losses, respectively. Notably, ϵ″ exhibits higher values at lower frequencies where absorption is strongest, while µ″ displays distinct peaks at 26, 30.5, 35, and 39.5 GHz, confirming the dominant role of magnetic loss in the absorption process. These resonant peaks in µ″ are indicative of enhanced magnetic dissipation, thereby validating a magnetic-loss-driven absorption mechanism within the simulated structure. The aggregated terms for the addition and subtraction of S-parameters can be distinctly illustrated as (T + R) and (T-R) that can be shown in (8) and (9) such that:

$$\:\left(\text{T}+\text{R})=\:{(\text{S}}_{21}+{\text{S}}_{11}\right)$$
(8)
$$\:\left(\text{T}-\text{R})=\:{(\text{S}}_{21}-{\text{S}}_{11}\right)$$
(9)

Figure 5 shows that the real components of permittivity (ϵ′) and permeability (µ′) facilitate impedance matching, while the imaginary components (ϵ″ and µ″) account for dielectric and magnetic losses. At particular resonant frequencies, µ″ surpasses µ′, signifying pronounced magnetic damping and effective energy dissipation. This phenomenon is indicative of low-quality factor absorbers and aligns with previous studies on high-loss metamaterials engineered for near-unity absorption47 thereby affirming the performance of the absorber.

Fig. 5
figure 5

Extracted relative permittivity (ε′) and permeability (µ′) of the Tri-band metasurface unit cell (real - solid, imaginary - dashed).

Full size image

Parametric analysis of unit cell

To determine how different parameters affect the MMA performance, a thorough parametric analysis is carried out, including the length, width, and angle of rotation of the metallic strip, the effect of incidence angleθ, and polarization angle Φ.

Effect of strip length (aL)

Using parametric analysis of the geometrical parameters, the simulation software is able to observe the absorption behaviour of the suggested microwave absorber unit cell. The S11 characteristic and absorptivity are first examined by modifying the length of the metallic strip at the centre that is represented by aL as shown in Fig. 6(a, b). The strip length is adjusted from 2 to 3.5 mm with a step size of 0.5 mm. At a length of 2 mm, an impedance matching with optimum deviation is observed at 28 and 38 GHz while sharp impedance at 33 GHz respectively. Further an increment in the length improved impedance matching and gives enhanced reflection at al = 3 mm achieving a reflected power loss of −21.2 dB, −18dB, and − 28.9 dB at 28.02 GHz, 33 GHz, and 38.048 GHz respectively. The effects of length variation on return loss are shown in Fig. 6(a). The absorptivity of MMA at different lengths of metallic strips. At a strip length of 3 mm, it gives an absorption of 99%, 98%, and 99% at 28 GHz, 33 GHz, and 38 GHz respectively presented in Fig. 6(b).

Fig. 6
figure 6

Simulated results of proposed MMA at the different values of strip length (aL) (a) S-parameters (b) Absorption.

Full size image

Effect of internal strip rotation (aa)

The effect of the rotation of the metallic strip at different angles denoted by the term aa is described in Fig. 7(a, b), in which the strip line rotation gradually increases from 0° to 90° (30° step size). As depicted in Fig. 7(a), at 0° and 30°, a low impedance and a redshift are observed at 28 GHz and 38 GHz, respectively. At 60°, an enhanced impedance matching is noted at 28 GHz and 38 GHz. Further increase in rotation disrupted the impedance matching at the desired frequencies. Figure 7(b) demonstrates the impact of the strip line rotation on the absorptivity of MMA. The results indicate that at 0° and 30°, there is a slight deviation in the absorption peaks. Notably, at aa = 60°, the suggested MMA has absorption of 99%, 98%, and 99% at 28 GHz, 33 GHz, and 38 GHz, respectively. Further increase in rotation produces a redshift in the absorption.

Fig. 7
figure 7

Simulated results of proposed MSA at the different angles for strip rotation (aa) (a) S-parameter (b) Absorption.

Full size image

Effect of polarization angle (TM, TE)

To investigate the insensitivity to polarization of the suggested tri-band MMA, under normal incidence, the rotational direction of electric field (E) and the magnetic field (H) occurs at distinct angles of polarization (TM, TE). The polarization angle (TM) is investigated from 0° to 60° with a 15° step size. Based on the observation of Fig. 8(a), it is evident that the suggested structure of the MMA demonstrates the similar behaviour at lower frequencies while an optimum deviation is noted at higher frequencies. Therefore, the insensitivity to polarization of the suggested MMA design can be attributed to the symmetry of the absorber. Additionally, an analysis is provided of the absorption characteristics exhibited by the proposed tri-band MMA at different incidence angles (TE). The absorption properties associated with various incidence angles of 0°, 15°, 30°, and 45° are illustrated in Fig. 8(b). It can be seen that the MMA is more sensitive to TE polarized incident waves. The MMA exhibits high absorption (> 95%) for TE-polarized waves up to θ = 30°, but a gradual decline occurs at higher angles (e.g., ~ 90% at 38 GHz for θ = 45°). This angular dependence primarily results from the asymmetric interaction between obliquely incident TE waves and the designed MMA unit cell geometry.

Fig. 8
figure 8

Simulated results of proposed MMA at different values of polarization angles (a) Absorption at TM (b) Absorption at TE.

Full size image

Effect of incident angle (θ)

The incident angle (θ) is defined as the angle between the incoming electromagnetic wave and the normal to the surface of the metasurface. To clarify this interaction, a visual representation has been included in Fig. 9.(a). Understanding this angle is crucial for validating the angular stability and practical applicability of the proposed metasurface absorber. MSA demonstrates a significant absorption rate for low frequencies and normal incidence (0 degrees). At approximately 24 GHz, it appears to absorb nearly all incident light. However, as the incidence angle increases, the rate of absorption declines across the entire frequency range as indicated in Fig. 9(b).

Fig. 9
figure 9

(a) Incident angle schematic (b)Absorption response of the MMA under varying incident angles (θ).

Full size image

It has been observed that the surface current densities on the upper surfaces flow in opposite orientation, surrounding the incident magnetic field by creating a circulating current loop shown in Fig. 10. This circulating current generates the magnetic excitation at the frequencies of absorption and also controls the permeability. The primary factor governing the three peak absorption mechanism is the resonant behaviour of the metasurface structure. This occurs when the incident electromagnetic fields interact with the induced currents within the metasurface. The resonance conditions are influenced by the frequency of the incident light and the angle of incidence. The absorption peaks can be explained as the constructive interference of electromagnetic waves within the material, which is amplified by the magnetic excitations produced by the circulating currents. To delve further into the magnetic resonance of the metasurface, the metasurface design must ensure that these resonant conditions are met across the desired frequency range. By incorporating resistive elements of the eight-resistive-arm (ERA) cell48 the absorption bandwidth can be broadened and high performance can be maintained even with varying incidence angles. Additionally, the electric field distribution associated with the upper metallic configuration of the unit cell is excited by the electric field leading to the generation of electric excitation as illustrated. in Fig. 11.

Fig. 10
figure 10

Investigation of surface current patterns in the Tri-band MMA for each resonance peak (a) 28 GHz, (b) 33 GHz, and (c) 38 GHz.

Full size image
Fig. 11
figure 11

Electric field distribution in the Tri-band MMA at the absorption peaks of (a) 28 GHz (b) 33 GHz (c) 38 GHz.

Full size image

Equivalent circuit model

The MSA unit cell can be effectively understood using the equivalent circuit model. The interaction between the incident wave and the absorber’s rings induces electric charges and currents in the conductors, which can be represented by lumped resistor (R), inductor (L), and capacitor (C) components, as shown in Fig. 12(a). The electric and magnetic coupling is realized through a series-shunt RLC circuit, where L1 represents the inductance due to surface currents in the outer ring, C1 denotes the capacitance formed between the outer ring and the two adjacent inner rings, and R1​ corresponds to the intrinsic losses in the absorber, which arise from both the finite conductivity of the metallic elements and the dielectric losses of the FR-4 substrate material. A similar design pattern is applied to the interconnected inner rings, leading to the final RLC circuit model. Additionally, the capacitance between the outer and inner rings is represented by Cg.

Fig. 12
figure 12

Equivalent circuit model of proposed absorber (a) RLC circuit model and (b) comparison of reflection coefficient.

Full size image

Given that the absorber operates at three distinct frequencies, three series RLC circuits are connected in parallel to account for these multiple resonances. The proposed circuit model is simulated in the ADS schematic environment and validated against CST simulation results, as shown in Fig. 12(b). The results indicate that the designed RLC equivalent circuit model aligns with the CST model, demonstrating that the proposed absorber can be comprehended through the designed circuit. The RLC circuit is optimized to achieve accurate correspondence with electromagnetic simulations. The optimized values of RLC components are as follows: R1 = 55.57, R2 = 37.94, R3 = 44.98 (Ω), L1 = 2.58, L2 = 3.55, L3 = 3.38 (nH), C1 = 0.009, C2 = 0.004 pF, C3 = 0.009 (pF), and Cg = 1 pF respectively.

Experimental results and discussion

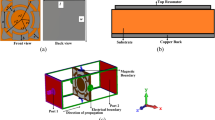
A prototype of the 64 × 64 MSA array structure is fabricated based on the outcomes of the CST simulation. This is accomplished by quantifying the functional response, which is represented in Fig. 13(a, b, c, d). A two-port vector network analyzer (VNA) (model: Agilent N5227A) and two different waveguide ports are included in the measurement equipment configuration as displayed in Fig. 13(b). This equipment is located in the microwave laboratory. The fabricated prototype of array is positioned in the middle of the two waveguide ports, which are linked to the VNA via the probe. To determine the S11 and absorptivity of the proposed structure, we make use of horn antennas that have an operational frequency span of between 24 and 40 GHz and placed above the MSA array at 10 cm. These two horn antennas utilized to precisely determine the reflection coefficient (S11) of the MSA, serving two essential purposes. First, the transmitting horn illuminates the array with a plane wave, while the receiving horn collects both the direct reflection from the MSA and any scattered fields. Second, the antenna-to-array spacing adheres to conventional measurement practices, ensuring that the prototype is positioned within the far-field region of both antennas. This configuration guarantees accurate plane wave incidence and minimizes near-field influence. The S11 is measured by the VNA, which compares the incident and reflected signals; the full ground of the MMA naturally rejects transmission (S21 ≈ 0 on a linear scale).

The far-field distance is calculated using the standard criterion \(\:R=\frac{2{D}^{2}}{{\uplambda\:}}\) where (D) is the horn antenna aperture and \(\:{\uplambda\:}\) is the is the wavelength49. At 24 GHz, with a wavelength of (λ = 12.5 mm) and a WR-28 horn aperture of (D = 2.84 cm), the calculated far-field distance is approximately 12.9 cm. In our setup, the metasurface absorber is positioned 10 cm from each horn. This setup closely approaches the far-field condition and ensures valid plane-wave excitation across the entire operating band of 28–38 GHz.

The simulated and measured reflection coefficient of the suggested array prototype are depicted in Fig. 13(c). It can be shown that simulated and measured results are closely matched despite there being an optimum deviation observed in the peak amplitude of measured values at 28 GHz, 33 GHz, and 38 GHz respectively. The VNA screen displays transmission coefficients at 28 GHz, 33 GHz, and 38 GHz. However, due to the full ground plane in MSA, the transmission is nearly 0 dB, making these results non-contributory to the study’s objectives.

Fig. 13
figure 13

(a) The fabricated prototype of MMA (b) The measurement setup of MMA (c) Simulated and measured S-parameters (reflection) of the proposed Tri-band MMA (d) Comparative analysis of simulated and measured absorption in the Tri-band MMA.

Full size image

The simulated and measured absorption of the suggested array are shown in Fig. 13(d). By using Eq. 2, the absorption performance is determined by applying it to the measured data. The proposed MMA array, with a copper backplane, exhibits remarkable absorption at the resonant frequencies. It can be observed that the suggested array has an absorption of 97%, 95%, and 99.6% at 28 GHz, 33 GHz, and 38 GHz, respectively. It can address the fact that the measured and simulated data are in close arrangement with a minor variance. This tolerance may be attributed to dielectric losses, the coupling impacts of two waveguide ports, and an imperfect laboratory environment resulting in disturbance of measured absorptivity. Furthermore, these influences for such high-frequency applications contributed to absorption displacement. Despite these influences, the 64 × 64 array absorber is capable of achieving exceptional absorptions at the resonances that are sought, which makes it a good candidate for applications related to 5G/6G. The proposed triple band metasurface enabled absorber compared to other works published in literatures in term of unit cell size, number of bands, maximum absorption and fabrication are shown in Table 4.

Table 4 Comparison of proposed work with previous multi band absorbers.
Full size table

The proposed tri-band absorber, resonating at 28 GHz, 33 GHz, and 38 GHz, is ideally suited for millimeter-wave integration in 5G and emerging 6G systems. At 28 GHz and 38 GHz, it effectively suppresses surface waves and reduces electromagnetic interference (EMI) in compact antenna arrays. The 33 GHz band contributes to lowering mutual coupling in MIMO systems, enhancing radiation stability. Its robustness to angular variation and polarization supports conformal applications in intelligent reflecting surfaces (IRS) and vehicular radomes. These features establish its applicability in high-isolation and interference resilient wireless infrastructures55[,56.

Conclusion

The design, performance evaluation and construction of a novel close packed tri-band metasurface absorber (MSA) employing two symmetrical elliptical resonators and a metallic strip with a circular enclosed ring have been given in this study. The suggested design is printed on FR4 substrate with dimensions of 5.8 × 5.8 × 1.5 mm3. The proposed design operates under normal incidence at three frequencies of 28 GHz, 33 GHz, and 38 GHz with peak absorption values of 99%, 98%, and 99%, For design validation, experimental studies have been made in an anechoic chamber. The simulated and measured data show good agreement in absorption peaks. From the measured results, it can be observed that the suggested array has an absorption of 97%, 95%, and 99.6% at 28 GHz, 33 GHz, and 38 GHz correspondingly. Current density on the surface at the frequencies of absorption is used to identify the individual elliptical resonator responsible for absorptions. Regarding the unit cell dimensions, absorptions, and operating bands, we have evaluated the critical parameters and the measurable outcomes of this work with the current multi-band MMA designs that have been published. Thus, the suggested MMA design is considered a good candidate and the most promising solution for 5G/6G applications.