A prototype of secure telephone communication

Abstract

This paper investigates a secure wireline telephone communication system that implements physical layer security (PLS) through artificial noise (AN) injection. The PLS-based telephone system strategically superimposes AN onto transmitted signals to prevent potential eavesdropping attempts along the twisted-pair line while enabling clean signal recovery at legitimate receivers through coordinated AN cancellation. Experimental results demonstrate its effectiveness against wiretapping, with implemented prototype circuits confirming the practical feasibility of our AN-based security approach while maintaining communication quality.

Introduction

Telephone systems have long been used for full-duplex voice or data transmission. Traditionally, cryptographic methods¹ have ensured communication privacy by protecting messages from wiretappers. However, in principle, encrypted messages can still be decrypted through extensive computational efforts. In particular, with the rapid advancement of computing power, the time required to break cryptographic codes for a wiretapper has significantly decreased. This underscores the need to explore alternative methods for the purpose of protecting communication.

Physical layer security (PLS)^2,3,4 provides a fundamentally distinct alternative to cryptographic methods for securing communication. The PLS framework involves two legitimate users (Alice and Bob) and an eavesdropper (Eve). Theoretically, perfect secrecy can be achieved if Eve experiences stronger interference than the legitimate users. Specifically, when Eve’s signal-to-noise ratio (SNR) falls below -1.59 dB⁵, malicious detection becomes infeasible, thereby preventing any meaningful information extraction.

To broaden the applications of PLS, researchers have proposed methods that leverage artificial noise (AN) to degrade Eve’s channel quality over the air interface^6,7,8,9,10. Ideally, legitimate systems must ensure that the AN does not interfere with their own users’ channels. Currently, most AN-based strategies rely on path loss to simultaneously achieve these two objectives. However, these methods fail when Eve is positioned close to the signal source but far from the AN source. In such scenarios, the detected signal can significantly overpower the AN that has traveled a long distance, thereby undermining communication security.

In contrast, the signals of electromagnetic waves in wireline systems experience significantly lower path loss compared to wireless transmission. For example, in a twisted-pair line, signal attenuation typically amounts to just a few decibels per hundred meters. This characteristic equally applies to AN transmission. The minimal power attenuation enables AN to effectively mask communication signals over extended distances, e.g., up to several kilometers, making PLS feasible across entire telephone wireline networks.

Based on these considerations, this paper presents a practical prototype of a secure wireline telephone system. The proposed system employs AN to disrupt Eve’s channels while employing cancellation techniques to maintain a clean reception for legitimate users. Unlike the prior work¹¹, our solution specifically addresses bidirectional secure communication and implements a complete prototype system with two legitimate users and a malicious wiretapper. More importantly, our hardware prototype demonstrates real-world secure bidirectional communication, where the system digitally generates AN, converts it to analog form, and effectively mitigates it at legitimate receivers using a telephone hybrid circuit. Experimental results validate the system’s ability to maintain secure communications, with the AN successfully degrading eavesdropper channels while preserving signal quality for authorized users.

System model

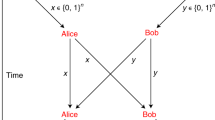
We consider a wireline communication system consisting of two telephone terminals as shown in Fig. 1, where Terminal-A transmits signals to Terminal-B through Alice-1 to Bob-1 using the carrier frequency $f_1$ while Terminal-B transmits signals to Terminal-A through Alice-2 to Bob-2 using another carrier frequency $f_2$. The purpose of using two frequencies, i.e., $f_1$ and $f_2$, is to enable the separation of the bidirectional transmissions by the filters. Then, we describe the PLS model in the presence of a malicious Eve between the two terminals. Since using two filters can separate the bidirectional communication into two independent signal transmissions of the same security issue, we need only to work on the problem of unidirectional transmission of the two, associated with its frequency, and use the result as that of the opposite directional transmission as follows.

Fig. 1

Illustration of the secure wireline telephone system.

Role of artificial noise

In this subsection, we focus on the secure communication problem for unidirectional transmission, as shown in Fig. 1b . In this setup, Terminal-A transmits the signal $s_1$ to Terminal-B through Alice-1 and Bob-1. Meanwhile, the AN $n_1$ is generated by Bob-1 to interfere with Eve’s reception. To ensure secure communication, the AN is suppressed at Bob-1. The power of the signals and AN are assumed to be $P_s$ and $P_n$, respectively. Therefore, the signal intercepted by Eve is a mixture of the transmitted signal and AN. When Eve is positioned at a distance $x$ from Alice, the intercepted signal can be expressed as

$$\begin{aligned} r_\textrm{Eve}(x,t) = \sqrt{\alpha (x)} s_1\left( t-\frac{x}{c}\right) + \sqrt{\alpha (L-x)} n_1\left( t-\frac{L-x}{c}\right) + n_\textrm{Eve}(t), \end{aligned}$$

(1)

where $n_\textrm{Eve}(t)$ represents the thermal noise at Eve, c is the velocity of light, and $\alpha (x)$ is the attenuation factor that describes the decay in signal power as it travels along the wireline.

The signal received by Bob-1, after AN cancellation, can be written as

$$\begin{aligned} r_\textrm{Bob}(t) = \sqrt{\alpha (L)} s_1\left( t-\frac{L}{c}\right) + \beta n_1(t) + n_\textrm{Bob}(t), \end{aligned}$$

(2)

where $\beta$ indicates AN cancellation capability and $n_\textrm{Bob}(t)$ is the thermal noise of Bob. Both thermal noises above are assumed to have a power of $\sigma _n^2$. In (2), a strong cancellation capability ensures that $\beta \ll 1$.

From (1) and (2), it can be observed that, on one hand, we aim for Bob to eliminate the AN, i.e., $\beta = 0$, to achieve optimal signal reception. On the other hand, the power of the AN at Eve’s location should be strong enough to obscure the transmitted signal. This process forms the basis of the proposed PLS model that utilizes AN to enhance communication security.

Secrecy capacity

To ensure communication security, we consider the detection of secret messages across both temporal and spatial dimensions. The maximum energy of the signals potentially intercepted by Eve depends on integrating over the entire symbol duration $T$. Given multiple interceptions, Eve can occasionally synchronize with the symbol, which is the optimal detection scenario.

The transmission delays, $\frac{x}{c}$ and $\frac{L-x}{c}$, are assumed to be negligible because they are significantly shorter than the symbol duration. Without loss of generality, we focus on the first symbol. After combining all the intercepted signals within this interval, we can express the signals intercepted by Eve as

$$\begin{aligned} \hat{r}_\textrm{Eve}^{x} = \frac{1}{T}\int _0^T {r_\textrm{Eve}^{x}(t) \mathop {}\!\textrm{d}t} = \sqrt{\alpha (x)}s_1(0) + \sqrt{\alpha (L - x)} \hat{n}_1 + \hat{n}_\textrm{Eve}, \end{aligned}$$

(3)

where $\hat{n}_1 = \frac{1}{T}\int _0^T{n_1(t)}\mathop {}\!\textrm{d}t$ and $\hat{n}_\textrm{Eve} = \frac{1}{T}\int _0^T{n_\textrm{Eve}(t)}\mathop {}\!\textrm{d}t$. Likewise, the signals Bob receives in the first symbol are expressed as

$$\begin{aligned} \hat{r}_\textrm{Bob} = \frac{1}{T}\int _0^T {r_\textrm{Bob}(t)\mathop {}\! \textrm{d}t} = \sqrt{\alpha (L)}s_1(0) + \sqrt{\beta } \hat{n}_1 + \hat{n}_\textrm{Bob}, \end{aligned}$$

(4)

where $\hat{n}_1= \frac{1}{T}\int _0^T{n_1(t)}\mathop {}\!\textrm{d}t$ and $\hat{n}_\textrm{Bob} = \frac{1}{T}\int _0^T{n_\textrm{Bob}(t)}\mathop {}\!\textrm{d}t$.

From the perspective of colluding eavesdropping, Eve may combine the results of multiple interceptions to maximize the signal-to-interference-plus-noise ratio (SINR). Thus, the SINR of Eve’s interception is calculated as

$$\begin{aligned} \gamma _\textrm{Eve}^{x} = \frac{\alpha (x) \mathbb {E}\left[ \left| s_a(0)\right| ^2\right] }{\alpha (L-x)\mathbb {E}\left[ \left| \hat{n}_b\right| ^2\right] + \sigma _n^2} = \frac{\alpha (x) P_s}{\alpha (L-x) P_n + \sigma _n^2}, \end{aligned}$$

(5)

where $\mathbb {E}[\cdot ]$ denotes the mathematical expectation of a random variable. Clearly, the worst-case scenario for secure communication occurs when Eve’s detection is closest to the signal source and furthest from the noise source, i.e., at $x = 0$. Thus, the maximum SINR at Eve is

$$\begin{aligned} \gamma _\textrm{Eve}^{\max } = \frac{P_s}{\alpha (L) P_n + \sigma _n^2}. \end{aligned}$$

(6)

Correspondingly, Bob’s SINR is given by

$$\begin{aligned} \gamma _\textrm{Bob} = \frac{\alpha (L) P_s}{\beta P_n + \sigma _n^2}. \end{aligned}$$

(7)

The secrecy capacity of our proposed wireline system is then expressed as

$$\begin{aligned} C_s = \left[ \log _2\left( 1 + \gamma _\textrm{Bob} \right) - \log _2\left( 1 + \gamma _\textrm{Eve}^{\max } \right) \right] ^+, \end{aligned}$$

(8)

where $[x]^+$ indicates that $x$ is a non-negative value. The capacity $C_s$ represents the maximum rate at which secure and reliable information can be transmitted from a sender to a receiver in the presence of a wiretapper. For communication security, the system must maintain $\gamma _\textrm{Bob} > \gamma _\textrm{Eve}^{\max }$, which theoretically enables absolute secrecy when using infinitely long codes, thereby establishing the conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} P_n> \frac{1 - \alpha (L)}{\alpha ^2(L) - \beta } \sigma _n^2,\\ \alpha ^2(L) - \beta > 0. \end{array}\right. } \end{aligned}$$

(9)

As can be seen from (9), the AN cancellation capability $\beta$ can be significantly smaller than the wireline’s power attenuation factor $\alpha (L)$. Therefore, the inequality is easily satisfied in practice. It is also important to note that (9) establishes the necessary conditions for ensuring secure transmission in the wireline communication system. Clearly, as the length of the wireline increases, there is a corresponding need for greater AN cancellation capability.

Hardware implementation

Fig. 2

Architecture of the secure telephone system.

The architecture of the proposed system, consisting of Terminal-A and Terminal-B, is shown in Fig. 2a . Terminal-A transmits signal $s_1$ from Alice-1 at frequency $f_1$ to Bob-1 at Terminal-B. To protect $s_1$, the AN generator from Terminal-B transmits the AN $n_1$ at frequency $f_1$. Similarly, Terminal-B transmits signal $s_2$ from Alice-2 at frequency $f_2$ to Bob-2 at Terminal-A, and the AN generator from Terminal-A transmits the AN $n_2$ at frequency $f_2$ to protect $s_2$. For the receivers, Bob-1 and Bob-2, the transmitted signals and the AN are eliminated by the telephone hybrids, while the AN from the opposite direction is reduced by the filters. We note that this design adheres to the interface and signal standards¹², as the signal processor does not alter the data format, and the telephone hybrid circuits are suitable for the telephone interface. The system implements the telephone hybrid circuits using THS6022 and THS6062 chips. All of these ensure the practicality of the proposed system.

As shown in Fig. 2b , the proposed system is implemented via a field-programmable gate array (FPGA) module (i.e., Intel Cyclone V SE FPGA board), analog-to-digital converters (ADCs, i.e., AD9226), digital-to-analog converters (DACs, i.e., AD9767), amplifiers (i.e., AD8065), and filters (i.e., AD8138). Furthermore, the proposed system requires a much higher capability for the AN cancellation compared to traditional telephone hybrids, which are designed primarily for echo cancellation. Therefore, we will explain the circuit design and capability analysis in the following discussions.

Fig. 3

Illustration of the telephone hybrid circuit.

Fig. 4

AN cancellation capability versus parameter $\eta$.

The telephone hybrid circuit including six resistors $Z_i$ ($i=1,2,\cdots ,6$) and an equivalent impedance $Z_0$ is depicted in Fig. 3. From Alice’s perspective, Bob is her load; therefore, $Z_0$ represents the equivalent input impedance of Bob’s circuit, and vice versa. $V_s$ is an equivalent voltage source that generates the transmitted signals. The received signal is denoted by $V_1 - V_2$, and $V_3$ and $V_4$ are the differential voltages on the wireline. To evaluate the AN cancellation capability, we assume that $V_s$ represents the transmitted AN and $V_r = V_1 - V_2$ is the residual AN.

Applying the mesh current method and Kirchhoff’s voltage law to each loop, we obtain the following linear equations in matrix form, i.e., $\textbf{Z}\textbf{I} = \textbf{V}$, with $\textbf{I} = \left[ I_1,I_2,I_3\right] ^T$, $\textbf{V} = \left[ 0,0,-V_s \right] ^T$, and

$$\begin{aligned} \textbf{Z} = \left[ {\begin{array}{*{20}{c}} {{\mathrm{{Z}}_0}\mathrm{{ + }}{\mathrm{{Z}}_1}\mathrm{{ + }}{\mathrm{{Z}}_2}\mathrm{{ + }}{\mathrm{{Z}}_3}}& {\mathrm{{ - }}{\mathrm{{Z}}_0}}& {\mathrm{{ - }}{\mathrm{{Z}}_3}}\\ {\mathrm{{ - }}{\mathrm{{Z}}_0}}& {{\mathrm{{Z}}_0}\mathrm{{ + }}{\mathrm{{Z}}_4}\mathrm{{ + }}{\mathrm{{Z}}_5}\mathrm{{ + }}{\mathrm{{Z}}_6}}& {\mathrm{{ - }}{\mathrm{{Z}}_5}\mathrm{{ - }}{\mathrm{{Z}}_6}}\\ {\mathrm{{ - }}{\mathrm{{Z}}_3}}& {\mathrm{{ - }}{\mathrm{{Z}}_5}\mathrm{{ - }}{\mathrm{{Z}}_6}}& {{\mathrm{{Z}}_3}\mathrm{{ + }}{\mathrm{{Z}}_5}\mathrm{{ + }}{\mathrm{{Z}}_6}} \end{array}} \right] . \end{aligned}$$

(10)

Under Cramer’s rule, the mesh currents can be solved as

$$\begin{aligned} I_i = \frac{\det (\textbf{Z}_i)}{\det (\textbf{Z})},~i = 1,2,3, \end{aligned}$$

(11)

where $\textbf{Z}_i$ denotes the matrix formed by replacing the $i$-th column of $\textbf{Z}$ with $\textbf{V}$, and $\det (\cdot )$ denotes the determinant of a matrix.

Moreover, based on Kirchhoff’s voltage law, the voltages $V_1$ and $V_2$ can be calculated as

$$\begin{aligned} \left\{ { \begin{array}{l} V_1 = V_s + I_1Z_1\\ V_2 = (I_2 - I_3) Z_6 \end{array}. } \right. \end{aligned}$$

(12)

With (11) and (12), the residual AN can be expressed as

$$\begin{aligned} V_r = V_1 - V_2 = V_s \times Z_\chi , \end{aligned}$$

(13)

where $Z_\chi$ is extremely complicated in its expression and difficult to handle. However, in practical applications, the residual AN can be further approximated and simplified. Specifically, the resistance values are designed to satisfy $Z_1,Z_2,Z_5,Z_6\gg Z_3,Z_4$. In this case, the output resistance $Z_0$ approximates to $Z_3+Z_4$, i.e., $Z_0 \approx Z_3+Z_4$. The residual AN can thus be simplified by neglecting the minor terms. As a result, we have

$$\begin{aligned} V_r \approx V_s \left[ {\frac{Z_4Z_5-Z_0Z_6}{(Z_3+Z_4+Z_0)(Z_5+Z_6)}} + {\frac{Z_2Z_3+Z_0Z_2}{(Z_3+Z_4+Z_0)(Z_1+Z_2)}} \right] . \end{aligned}$$

(14)

In practice, the resistance values are carefully designed with $Z_1 = Z_6$, $Z_2 = Z_5$, and $Z_3 = Z_4$. Recalling that $Z_1,Z_2,Z_5,Z_6\gg Z_3,Z_4$, we further assume $Z_3 = Z_4 \buildrel \Delta \over = Z_S$, $Z_2 = Z_5 \buildrel \Delta \over = Z_L$, and $Z_1 = Z_6 \buildrel \Delta \over = \eta Z_L$. With these notations, we obtain $Z_0 \approx Z_3 + Z_4 = 2Z_S$. Finally, the residual AN can be simplified and expressed as

$$\begin{aligned} V_r \approx V_s\left[ \frac{Z_SZ_L-2\eta Z_SZ_L}{4(1+\eta )Z_SZ_L} + \frac{Z_SZ_L+2Z_SZ_L}{4(1+\eta )Z_SZ_L}\right] = \frac{2-\eta }{2+2\eta }V_s = \beta V_s. \end{aligned}$$

(15)

Using the approximation analyzed above and the parameters from (15), we illustrate the residual AN in Fig. 4. It is observed that for maximum AN cancellation capability, the parameter $\eta$ should be set to two.

Performance evaluation

Fig. 5

Frequency response of the proposed system.

Fig. 6

Comparison of SINRs of legitimate and eavesdropping links.

Fig. 7

Secrecy capacity versus the power of AN.

In this section, we carry out simulations and experiments to demonstrate the AN cancellation capability and security performance of the proposed system. We set the signal power $P_s = 0$ dBm, the AN power $P_n = 20$ dBm, and the noise power $\sigma _n^2 = -100$ dBm, with the signal strength attenuating by 2 dB per hundred meters over the wireline¹¹. For the telephone hybrid design, we use resistors with values $Z_3 = Z_4 = 50\;\Omega$, $Z_1 = Z_6 = 2\;\textrm{K}\Omega$, and $Z_2 = Z_5 = 1\;\textrm{K}\Omega$.

First, Fig. 5 shows the measured frequency response of the proposed system for the generated AN. In these measurements, a single-frequency sinusoid ranging from 0 Hz to 4 KHz, used to mimic the AN, is generated by the AN generator. We captured the transmitted AN at position $x = 0$ meters and the residual AN after cancellation by the telephone hybrid. Both the transmitted and residual AN are plotted in the figure. The results demonstrate that the hardware prototype achieves significant AN cancellation, with approximately 26 dB of suppression. This high level of cancellation effectively minimizes the AN, which prevents it from interfering with the desired signals. Importantly, the desired signals are preserved with only negligible degradation and it confirms that signal quality is maintained throughout the process. Furthermore, the frequency response of both the transmitted and residual AN remains remarkably consistent and flat up to 4 KHz. This stability indicates that the system performs reliably across this frequency range without introducing significant distortions or variations. It also highlights the effectiveness of the hardware design in maintaining signal fidelity while providing robust AN cancellation.

Next, Fig. 6 investigates the SINRs of the legitimate and eavesdropping links. In this setup, the communication link from Alice-1 to Bob-1 operates at $f_1 = 500$ Hz, while the reverse link operates at $f_2 = 2$ KHz. The test signals, each lasting one second, are superposed with the AN from Terminal-A and the combined signals are then transmitted through a 100-meter wireline to Terminal-B. For comparison, the theoretical SINRs are calculated using (6) and (7) by assuming $\beta = 26$ dB (measured in Fig. 5). The results show that, in each case, the SINR of the legitimate link is consistently about 20 dB higher than that of Eve’s link, closely matching the theoretical performance of 22 dB. This consistent SINR difference highlights the system’s robust ability to secure the communication channel against eavesdropping. The slight 2 dB degradation from the theoretical value indicates that the system is functioning near maximum levels, effectively balancing performance and security. Notably, this 20 dB advantage is observed across multiple cases, thereby underscoring the stability and reliability of the system performance.

Finally, Fig. 7 illustrates the relationship between secrecy capacity and AN power under a measured AN cancellation capability of 26 dB. The secrecy capacity is computed using (8) for wireline lengths of 100, 200, and 300 meters. From the figure, it is evident that as the wireline length increases, the secrecy capacity decreases. This is due to the greater signal attenuation over longer distances, which reduces the SINR advantage for the legitimate receiver and makes it easier for eavesdroppers to intercept the signal. Moreover, the figure shows that increasing the power of AN significantly enhances the system’s secrecy capacity. This improvement occurs because stronger AN creates more interference for Eve, effectively masking the legitimate signal and making it more difficult for unauthorized parties to extract useful information. As a result, the system’s overall security is bolstered. These findings emphasize the importance of balancing wireline length and AN power to optimize secrecy capacity. In scenarios with longer wireline distances, increasing AN power becomes particularly crucial to maintaining a high level of security in the communication system.

Conclusion

This paper proposed a secure wireline telephone system that uses the AN, in the frame of the PLS model, to contaminate Eves’ channels, where the bidirectional legitimate communications can be free of the AN effects, enabled by the telephone hybrid circuits. We introduced the design principle and formulated the AN cancellation schemes. Our analysis presented the effects of the various system parameters, i.e., AN power and its required cancellation capabilities, in simulation and experimental aspects. The results depicted the conditions for realizing the security of the proposed system.