Introduction

Environmental contamination from toxic dye effluents discharged into natural ecosystems such as rivers, lakes, and seas presents a profound environmental challenge1. Cationic dyes, including methylene blue (MB) and rhodamine B (RhB), are recognized for their high toxicity and carcinogenic potential, exerting deleterious effects on aquatic life and posing substantial health hazards to humans through the consumption of contaminated seafood2. Although various remediation techniques—such as coagulation, nanofiltration, and advanced oxidation processes—have been investigated, these methods often encounter limitations related to high operational costs and the risk of secondary pollution3,4. Conversely, adsorption has gained prominence as a cost-effective and efficient approach for dye remediation, driving extensive research into the development of multifunctional adsorbents to enhance wastewater treatment efficacy.

Within the spectrum of carbon-based and semiconducting nanomaterials, graphitic carbon nitride (g-C3N4) has emerged as a seminal material in the realm of advanced nanotechnology, distinguished by its exceptional structural and electronic characteristics that render it highly suitable for a diverse array of applications, including photocatalysis, energy storage, and environmental remediation5,6. Composed predominantly of layered sheets of carbon and nitrogen atoms, g-C3N4 exhibits notable chemical robustness, tunable band gap energies, and superior thermal stability—attributes that make it an ideal candidate for solar energy harvesting and catalytic applications7. Its intrinsic porosity, coupled with the presence of functional groups, significantly amplifies its adsorption efficiency, positioning g-C3N4 as a pivotal agent in the removal of pollutants such as toxic dyes and heavy metals from effluents8,9. As ongoing research deepens our understanding of this material, it continues to demonstrate vast potential not only in mitigating environmental hazards but also in fostering the development of sustainable technologies and innovative renewable energy solutions.

The physicochemical properties of g-C3N4 are profoundly governed by a constellation of operational parameters, including synthesis temperature, precursor selection, heating rate, annealing duration, and environmental conditions. Elevated synthesis temperatures have been demonstrated to augment the crystallinity of g-C3N4, although this often occurs at the expense of porosity, thereby necessitating meticulous optimization to achieve an optimal balance between structural order and surface accessibility10. The choice of precursors—such as thiourea or melamine—is of paramount importance, as it exerts a direct influence on the resulting material’s structural framework and chemical functionality, which in turn modulates surface area and adsorption efficacy11. Moreover, the heating rate markedly affects particle size distribution and the development of porous architectures, with precise control over thermal ramping facilitating the formation of well-defined and highly efficient pore structures12. In addition, the duration of annealing treatments is critical for the polymerization process and the progression of crystalline phases, further refining the material’s adsorption performance13. Collectively, these operational parameters synergistically determine the suitability and effectiveness of g-C3N4 as an adsorbent across diverse environmental and technological applications.

Recent scientific advancements in the synthesis methodologies of g-C3N4 have markedly enhanced production efficiency, thereby minimizing energy demands and synthesis durations while simultaneously preserving or improving the material’s structural robustness14. A multitude of synthesis approaches—including thermal polymerization, sol-gel techniques, hydrothermal and solvothermal processes, chemical vapor deposition, as well as microwave and ultrasound-assisted methodologies—have been rigorously investigated15. Of particular significance are the progressive refinements observed in direct thermal polymerization, which focus on optimizing reaction parameters, judicious selection of precursors, and the incorporation of functional additives to bolster material properties16,17. These technological innovations not only accelerate the fabrication process but also significantly enhance the functional attributes of g-C3N4, reinforcing its status as a highly versatile material for a broad spectrum of applications, notably within environmental remediation and energy conversion domains9,17.

An extensive corpus of scholarly inquiry has rigorously investigated the synthesis of g-C3N4, meticulously analyzing how variations in thermal conditions, synthesis duration, and precursor selection influence its structural, optical, morphological, and physicochemical properties18. For instance, seminal studies by Thomas et al.19 and Alwin et al.20 employed precursors such as cyanamide, dicyandiamide, and melamine, subjecting them to thermal treatments within the temperature range of 500 °C to 600 °C over a four-hour timeframe, thereby elucidating the intricate correlations between monomeric structure and the resultant morphology and functional characteristics of g-C3N4. Additionally, Hong et al.21 achieved the synthesis of ultrathin g-C3N4 nanosheets (NS) from thiourea, optimizing photocatalytic hydrogen evolution by modulating synthesis temperatures at 540 °C, 560 °C, and 580 °C over similar durations. Parallelly, Sewnet et al.22 introduced a direct synthesis protocol involving the calcination of a urea-thiourea mixture at temperatures spanning 500 °C to 650 °C for three hours in an ambient air atmosphere, aimed at amplifying Rhodamine B degradation efficiency. Furthermore, Hoai et al.23 developed an innovative morphological control strategy for g-C3N4 nanosheets, significantly enhancing their photocatalytic performance through precise manipulation of structural architecture.

This investigation portrayed the novel synthesis of g-C3N4 via a streamlined one-step thermal polymerization process, employing thiourea as the precursor, which is subsequently subjected to annealing at 550 °C for a duration of two hours in an ambient air atmosphere. The strategic incorporation of sulphur heteroatoms derived from thiourea is projected to substantially augment the specific surface area, pore volume, and interconnectivity of the tri-s-triazine frameworks at elevated temperatures, thereby promoting self-condensation and polymerization mechanisms24,25. The resultant material will be extensively characterized using an array of advanced analytical techniques. Following to characterization, adsorption isotherm and kinetic investigations will be conducted, accompanied by comprehensive assessments of the material’s reusability. These evaluations are designed to elucidate the efficiency and operational sustainability of the synthesized g-C3N4 nanosheets in the effective remediation of cationic dyes MB and RhB from aqueous solutions.

Results and discussion

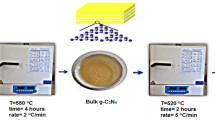
Throughout the thermal polymerization process, thiourea undergoes a phase transition from solid to liquid within the temperature range of 150–160 °C, concomitant with the formation of thioamide functional groups and the release of ammonia (NH3). As the temperature escalates, these thioamide moieties decompose further into carbon disulfide (CS2) and hydrogen sulfide (H2S), thereby contributing to the formation of melamine, a triazine-based intermediate26. Subsequent heating to approximately 315–320 °C triggers additional polymerization via condensation reactions, which release further ammonia and progressively facilitate the removal of sulfur species. With continued thermal input reaching about 520 °C, triazine oligomers condense to form melem, and at approximately 550 °C, the synthesis of poly(heptazine imide) is accomplished. The excess ammonia generated during this thermal progression acts as a pivotal facilitator for condensation reactions critical to establishing the final layered architecture characteristic of g-C3N4. The comprehensive transformation26 pathway of thiourea into g-C3N4 is schematically depicted in Fig. 1.

Fig. 1
figure 1

Schematic illustration of thiourea conversion to g-C3N4 via thermal polymerization.

Full size image

Structural investigation

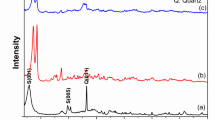
The XRD spectra of the synthesized g-C3N4, as illustrated in Fig. 2a, exhibit distinct diffraction peaks at 2θ values of 12.88° and 27.56°, corresponding to the (100) and (002) crystal planes, respectively. The peak at 12.88° (100) indicates intra-planar stacking of tri-s-triazine moieties, as noted by Kumar et al.27, while the peak at 27.56° (002) is attributed to the graphitic stacking of conjugated triazine units, corroborated by Yu et al.28. A notable shift of the (002) peak toward higher angles from the standard position of 27.4° in g-C3N4 suggests an increase in nitrogen content and changes in interlayer spacing, resulting in a more densely packed framework. These peaks align with JCPDS No. 87–1526, confirming the successful formation of hexagonal g-C3N4. The average crystallite size, calculated from the (100) reflection using the Debye–Scherrer equation, is approximately 4.64 nm. The FT-IR spectrum in Fig. 2b displays a prominent peak at 2174.04 cm−1, indicating terminal cyano groups (C ≡ N) and retained nitrile functionalities28. An absorption band at 1622 cm−1 corresponds to C ≡ N stretching vibrations within heterocyclic frameworks, confirming the integrity of nitrogen-rich heterocycles. Additionally, strong absorption bands at 808 cm−1 and 1316 cm−1 are associated with in-plane bending vibrations of tri-s-triazine rings, confirming the structural organization of these aromatic units29. The broad peak around 3151 cm−1 suggests the presence of uncondensed amino groups or surface-bound N–H groups, indicating incomplete condensation and highlighting reactive sites on the material’s surface27.

Fig. 2
figure 2

(a) XRD, (b) FT-IR, and (c) EDX, and (d) Raman spectra of g-C3N4.

Full size image

The EDX spectrum in Fig. 2c shows a composition of 34.55% carbon (C), 55.33% nitrogen (N), and 6.91% oxygen (O) by weight. The C:N ratio averages 0.72, which is close to the theoretical value of 0.75 for g-C3N4. The presence of trace amounts of hydrogen and oxygen may indicate adsorbed O2 or H2O from amino groups on the sample’s surface. Due to the nanoscale dimensions of the material, the surface is densely terminated with amino groups, enhancing its chemical reactivity and potential interactions for various applications. In Fig. 2d, the Raman spectra display absorption bands within range of 772–1572 cm−1, indicative of layered g-C3N430. Notably, bands at 753, 977, 1120, 1229, and 1319 cm−1 correspond to the stretching vibrations of aromatic C–N heterocyclic structures characteristic of the melem unit31. The peak at 1319 cm−1, known as the D-band, signifies disordered or defective regions within the carbon network, whereas the G-band observed at 1572 cm−1 is related to the in-plane vibrations of sp2-hybridized carbon atoms, highlighting the crystalline structure of g-C3N432.

Figure 3 presents the TGA/DTA analysis of g-C3N4 conducted under a nitrogen atmosphere. Initially, an insignificant weight loss is observed, attributable to the desorption of physically adsorbed moisture. The TGA curve indicates a total weight reduction of approximately 2.5% up to 500 °C, reflecting its robust thermal stability. A pronounced weight decrease occurs between 550 °C and 700 °C, likely corresponding to the oxidation of g-C3N4 into graphite and nitrogen (N2). The exothermic peak centered around 740 °C is plausibly associated with the oxidation of graphite to CO2, further elucidating the material’s thermal decomposition profile and stability at high temperatures.

Fig. 3
figure 3

TGA-DTA curve of g-C3N4.

Full size image

Morphological investigation

The SEM images in Fig. 4a–c reveal the intricate microstructural features of g-C3N4, characterized by a multilayered architecture comprised of disordered nanosheets33. Specifically, Fig. 4a illustrates the stacking arrangement, demonstrating that individual nanosheets consist of aggregated nanoparticles with dimensions spanning from 22 to 100 nm, as depicted in Fig. 4c. This nanoscale heterogeneity is anticipated to augment the material’s surface area and enhance its adsorption capacity, thereby facilitating more efficient interactions with target pollutants.

Fig. 4
figure 4

SEM images of the g-C3N4.

Full size image

The TEM images of g-C3N4 depicted in Fig. 5 illustrate a quintessential sheet-like morphology, with an average interlayer spacing of approximately 0.2 nm corresponding to the (100) and (002) crystallographic planes, thereby affirming the crystalline integrity of the g-C3N4 nanosheets. Figure 5a displays these aggregated nanosheets exhibiting wrinkles and bent edges—features that are likely to diminish surface energy and bolster structural stability34. The measured thickness of the nanosheets varies from 6.9 to 20.88 nm [Fig. 5e–f], underscoring their nanoscale dimensions. Moreover, the observed electron transparency further corroborates their ultrathin nature, a pivotal characteristic that significantly influences their physicochemical behaviour.

Fig. 5
figure 5

TEM images of the g-C3N4.

Full size image

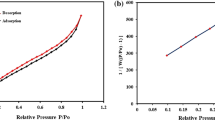
The g-C3N4 sample exhibited a specific surface area of 101.2 m2/g, as depicted in Fig. 6a, signifying a considerable availability of surface sites conducive to molecular interactions. The pore size distribution, derived from BET analysis, indicated an average pore diameter of 7.01 nm [Fig. 6b], while the adsorption isotherms displayed a Type IV classification in accordance with IUPAC standards, characterized by an H1 hysteresis loop suggestive of capillary condensation phenomena35. This hysteresis behaviour reflects a highly ordered porous architecture, which facilitates efficient fluid retention during adsorption processes. Consequently, BET analysis provides vital insights into the surface area, pore size distribution, and overall porosity of the adsorbent material35. A higher specific surface area correlates positively with enhanced adsorption capacity, as it offers an increased number of active sites for interaction with dye molecules. Additionally, the pore size distribution underscores the suitability of g-C3N4 for the diffusion and adsorption of targeted cationic dyes, with optimally sized pores augmenting adsorption efficiency and reinforcing the material’s performance across various applications35,36.

Fig. 6
figure 6

BET analysis of g-C3N4 (a) N2 adsorption–desorption isotherm and (b) Pore-size distribution curve.

Full size image

XPS spectra

The XPS survey spectra of g-C3N4, encompassing the survey Fig. 7a, C1s and N1s core-level spectra, are depicted in Fig. 7. The C1s spectrum, shown in Fig. 7b, features peaks at binding energies of 284.6 eV and 288.1 eV. The peak at 284.6 eV is attributed to carbon atoms involved in C–C bonding, indicative of graphitic or amorphous carbon domains. The peak at 288.1 eV corresponds to carbon atoms covalently bonded to three nitrogen neighbours, characteristic of the triazine rings within g-C3N437. The N1s spectrum, presented in Fig. 7c, can be deconvoluted into two distinct peaks at 398.7 eV and 399.3 eV. The peak at 399.3 eV is associated with nitrogen atoms trigonally bonded to three sp2-hybridized carbon atoms within the C–N framework, while the 398.2 eV peak signifies nitrogen atoms sp2-bonded to two carbon atoms, reflecting the heterocyclic core structure37. Collectively, these XPS findings corroborate the presence of a graphite-like sp2-bonded configuration in g-C3N4, emphasizing its potential electronic and conductive properties38,39. Additionally, the weak O1s peak observed at 532.5 eV indicates the presence of surface hydroxyl groups, corroborating the elemental composition deduced from the EDS spectra.

Fig. 7
figure 7

XPS spectra (a) survey, (b) C1s and (c) N1s spectrum of g-C3N4.

Full size image

Adsorption examination

The adsorption investigations rigorously evaluated the efficacy of g-C3N4 nanosheets as an advanced adsorbent for the removal of cationic dyes, specifically MB and RhB. Critical parameters—including adsorbent dosage, initial dye concentration, and contact time—were systematically optimized to delineate their influence on adsorption performance. Furthermore, comprehensive analyses encompassing adsorption isotherms, kinetic modeling, and reusability assessments were conducted, offering vital insights into the material’s long-term operational stability, efficiency, and overall sustainability for continuous dye remediation in wastewater treatment applications.

To elucidate the impact of adsorbent dosage on the decolorization efficacy of MB and RhB, a series of experiments were systematically performed with dosages spanning from 10 mg to 40 mg. As depicted in Fig. 8a, increasing the dosage from 10 mg to 20 mg significantly enhanced decolorization performance, presumably owing to the augmented availability of active adsorption sites40. However, further escalation to 40 mg yielded only marginal improvements, with approximately 90% of the dyes being adsorbed, indicative of the attainment of adsorption equilibrium. Consequently, an optimal dosage of 20 mg was identified, as higher concentrations resulted in diminishing returns regarding adsorption efficiency, thereby underscoring the importance of optimizing adsorbent loading for maximal performance.

Fig. 8
figure 8

Influence of (a) adsorbent dosage, and (b) initial adsorbate concentration on dye removal performance; (c) decolorization efficiency over contact time; and (d,e) UV–vis spectra of MB and RhB, respectively, obtained at an adsorbent dose of 20 mg, dye concentration of 25 mg/L, and pH 7.5.

Full size image

The influence of adsorbate concentration on the adsorption efficacy was systematically examined by varying dye concentrations from 25 to 100 mg/L, while maintaining a constant adsorbent dosage of 20 mg of g-C3N4 at pH 7.5 over a duration of 150 min. As demonstrated in Fig. 8b, escalating the dye concentration from 25 to 100 mg/L resulted in a noticeable decline in decolorization efficiency, primarily attributable to the limited availability of active adsorption sites on the g-C3N4 surface41. The increased molecular concentration intensifies competition for these active sites, thereby diminishing the adsorption capacity and removal efficiency for both MB and RhB. Accordingly, an initial dye concentration of 25 mg/L was identified as optimal for subsequent studies, as higher concentrations substantially compromised the adsorption performance.

In this adsorbate-adsorbent system—comprising an initial dye concentration of 25 mg/L, 20 mg of g-C3N4, and maintained at pH 7.5—continuous stirring over a 150-min period yielded a progressive enhancement in removal efficiency. As illustrated in Fig. 8c, decolorization for both MB and RhB exceeded 90% by 105 min. The initial rapid decolorization phase can be attributed to the abundance of vacant active sites, facilitating swift adsorption. Beyond this point, only marginal improvements were observed, indicating that the majority of reactive sites on the g-C3N4 surface had become saturated. Ultimately, the process achieved decolorization efficiencies surpassing 99% within 150 min, a result corroborated by the UV–vis spectra presented in Fig. 8d,e.

Adsorption kinetics

To comprehensively elucidate the mechanistic pathways governing the adsorption of MB and RhB on the surface of g-C3N4 nanosheets, four kinetic models were systematically applied: the pseudo-first-order, pseudo-second-order, Weber–Morris intraparticle diffusion, and liquid film diffusion models. These analyses are depicted in Fig. 9, with the corresponding parameter datasets summarized in Table 1. The plotting of log(Qe - Qt) against time (t) yielded the pseudo-first-order rate constants [Fig. 9a], with coefficients of determination (R2) of 0.9345 for MB and 0.9382 for RhB. Nonetheless, the calculated equilibrium adsorption capacities (Qe(exp)) exhibited poor concordance with the experimentally determined values (Qe(cal)), thereby indicating that the pseudo-first-order kinetic model fails to adequately describe the adsorption kinetics of these dyes42.

Fig. 9
figure 9

 Evaluation of adsorption kinetics through (a) pseudo-first-order, (b) pseudo-second-order, (c) Weber–Morris intraparticle diffusion, and (d) liquid film diffusion models, conducted at an adsorbent dosage of 20 mg, dye concentration of 25 mg/L, and pH 7.5.

Full size image

Conversely, the assessment of the pseudo-second-order rate constant was conducted by plotting t/Qt against time (t), which yielded a highly linear relationship characterized by superior coefficients of determination (R2) of 0.9997 for MB and 0.9882 for RhB [Fig. 9b]. This pronounced correlation with the experimental data, alongside the close correspondence between the calculated (Qe(cal)) and experimental (Qe(exp)) adsorption capacities, suggests that the adsorption mechanism is predominantly governed by chemisorption, indicative of stronger adsorbate–adsorbent interactions—specifically between MB and RhB molecules and the g-C3N4 nanosheets43.

The Weber–Morris intraparticle diffusion model, illustrated in Fig. 9c, was utilized to elucidate the adsorption kinetics by plotting Qt against (t1/2) to determine the diffusion rate constant (Kid) from the slope and the intercept (I). A linear correlation indicates the participation of intraparticle diffusion in the adsorption mechanism, with an intercept passing through the origin suggesting that intraparticle diffusion may act as the rate-limiting step44. Conversely, if the line does not intersect the origin, it implies the presence of boundary layer effects, indicating that intraparticle diffusion is not the sole operative mechanism and that other kinetic processes may concurrently influence the adsorption dynamics. The coefficients of determination (R2) for MB and RhB were calculated as 0.9562 and 0.8948, respectively, pointing to the conclusion that the Weber–Morris model alone is insufficient for fully capturing the complexities of dye adsorption kinetics on g-C3N4 nanosheets.

The liquid film diffusion model was subsequently evaluated by plotting βt against time (t), as depicted in Fig. 9d, which resulted in a nonlinear relationship. The coefficients of determination (R2) for MB and RhB were calculated as 0.9349 and 0.9665, respectively, further indicating that this model inadequately captures the complete adsorption kinetics. For MB, the ranking of kinetic model fitting, based on the descending order of R2 values, is as follows: pseudo-second-order (0.9997) > intraparticle diffusion (0.9562) > liquid film (0.9349) ≈ pseudo-first-order (0.9345). Conversely, for RhB, the order is: pseudo-second-order (0.9882) > liquid film (0.9665) > pseudo-first-order (0.9382) > intraparticle diffusion (0.8948)45.

Table 1 Kinetic parameters governing the adsorption dynamics of MB and RhB on the surface of g-C3N4 nanosheets.
Full size table

Adsorption isotherms

Adsorption isotherms furnish vital insights into the mechanisms and capacity of adsorption systems, thereby evaluating the interaction efficacy between g-C3N4 nanosheets and target adsorbates. To thoroughly elucidate these interactions, four isotherm models—Langmuir, Freundlich, Dubinin-Radushkevich (D-R), and Temkin—were employed to fit the experimental data, as illustrated in Fig. 10. The parameters obtained from these models, summarized in Table 2, facilitate a nuanced understanding of the extent to which each model approximates the observed data and reveal underlying adsorption mechanisms. Analysis of Fig. 10; Table 2 indicates that the experimental data is most accurately described by the Freundlich and Dubinin-Radushkevich isotherms, as evidenced by their superior coefficients of determination (R2). Specifically, the Freundlich isotherm exhibits R2 values of 0.9642 for MB and 0.9860 for RhB, indicating a highly accurate fit. Conversely, the Langmuir model yields R2 values of 0.8956 for MB and 0.9820 for RhB, which are comparatively lower, suggesting adsorption predominantly occurs on a heterogeneous surface. Further, the Dubinin-Radushkevich (D-R) isotherm demonstrates excellent correlation, with R2 values of 0.9599 for MB and 0.9958 for RhB; additionally, the computed ε2 values of 0.74184 kJ/mol for MB and 1.0004 kJ/mol for RhB strongly imply that the primary adsorption mechanism involves physical sorption. The Temkin model, with R2 values of 0.8858 for MB and 0.9710 for RhB, shows comparatively limited applicability, indicating it inadequately characterizes the adsorption process under the tested conditions. The model fit hierarchy based on R2 values is as follows: for MB, Freundlich (0.9642) > Dubinin-Radushkevich (0.9599) > Langmuir (0.8956) > Temkin (0.8858); for RhB, Dubinin-Radushkevich (0.9999) > Freundlich (0.9860) ≈ Langmuir (0.9820) > Temkin (0.9710).

Fig. 10
figure 10

 Adsorption isotherms: (a) Langmuir, (b) Freundlich, (c) Dubinin-Radushkevich, and (d) Temkin models describing the adsorption of MB and RhB at an adsorbent dosage of 20 mg, dye concentration of 25 mg/L, and pH 7.5.

Full size image
Table 2 Isotherm parameters characterizing the adsorption of MB and RhB on the surface of g-C3N4 nanosheets.
Full size table

Adsorption mechanism

RhB exhibits superior adsorption efficiency relative to MB, attributable to a confluence of interrelated factors rooted in molecular architecture, dimensional attributes, geometry, and specific intermolecular interactions (Fig. 11)  on the surface of g-C3N4 nanosheets. Primarily, RhB’s more compact molecular configuration, as opposed to the bulkier structure of MB, enables facile penetration into the porous framework of g-C3N4, thereby enhancing accessibility and facilitating a more rapid adsorption process. Additionally, the functional groups present in RhB foster stronger interactions with the nitrogen-rich sites on g-C3N4, resulting in more robust binding affinities46. The diminutive size and favorable geometric arrangement of RhB further contribute to its effective pore occupancy; its smaller molecular dimensions allow for efficient integration into the available pore spaces, whereas the larger dimensions of MB hinder its accommodation within the porous architecture, limiting adsorption capacity47. This optimal spatial fit permits a higher surface coverage of RhB molecules. Moreover, the intrinsic nature of the interactions—such as π–π stacking and hydrogen bonding—between RhB’s aromatic structures and functional groups and the graphitic lattice of g-C3N4 nanosheets substantially enhances adsorption affinity46,47. Conversely, the weaker intermolecular interactions associated with MB lead to comparatively lower adsorption efficiency, underscoring the critical role of molecular interactions in adsorption performance.

Fig. 11
figure 11

Proposed mechanistic pathways the adsorption of MB and RhB onto the surface of g-C3N4 nanosheets.

Full size image

Thermodynamic parameters

The thermodynamic parameters are detailed in Fig. 12; Table 3. The standard Gibbs free energy changes (ΔG°) for MB and RhB are calculated as −0.77878 kJ/mol and − 0.98180 kJ/mol, respectively, indicating that the adsorption processes are spontaneous, with a more pronounced thermodynamic favorability for RhB due to its more negative ΔG°. The positive ΔH° values suggest that the adsorption is an endothermic process, predominantly governed by physisorption mechanisms up to approximately 30 °C. Additionally, the positive ΔS° values reflect an increase in disorder at the solid–liquid interface during adsorption, highlighting the enhanced randomness associated with the adsorption phenomena.

Fig. 12
figure 12

Thermodynamic parameters determined at an adsorbent dosage of 20 mg, dye concentration of 25 mg/L, and pH 7.5.

Full size image
Table 3 Thermodynamic parameters related the adsorption of MB and RhB onto g-C3N4 nanosheets.
Full size table

Reusability

Reusability is a critical parameter for evaluating the economic feasibility and environmental sustainability of an adsorbent. To assess the long-term performance of g-C3N4 nanosheets in the adsorption of MB and RhB dyes, six successive adsorptions–desorption cycles were performed, as illustrated in Fig. 13a. Effective desorption was achieved through two consecutive washing procedures with ethanol prior to each cycle. Notably, even after five cycles, the removal efficiencies for both dyes remained above 80%, underscoring the exceptional reusability of the g-C₃N₄ nanosheets. This resilience affirm the potential of g-C3N4 nanosheets as a durable and cost-efficient adsorbent for industrial wastewater treatment applications. Furthermore, the preservation of all characteristic diffraction peaks of g-C3N4 in the XRD spectra [Fig. 13b] post-reusability testing confirms the material’s structural stability and integrity throughout multiple operational cycles, highlighting its robustness under repeated usage conditions.

Fig. 13
figure 13

(a) Reusability assessment of g-C3N4 nanosheets over six consecutive adsorption cycles, (b) XRD spectra of g-C3N4 nanosheets after six adsorption cycles.

Full size image

Table 4 provides a comparative analysis of the adsorption efficiencies of g-C3N4 nanosheets against other adsorbents documented in the literature for the removal of aqueous MB and RhB dyes. The g-C3N4 nanosheets demonstrate rapid adsorption kinetics, achieving equilibrium within 150 min. Notably, the adsorption capacities are exceptionally high, recorded at 2.251 × 10⁷ mg/g for MB and 9.226 × 10⁷ mg/g for RhB—substantially surpassing the 2.697 × 10⁵ mg/g capacity reported for g-C3N4@ZnO by Khezami et al.48. The enhanced performance can be attributed to the elevated surface area and pore volume of the g-C3N4 nanosheets, which significantly augment their adsorption efficacy for MB and RhB. Consequently, g-C3N4 nanosheets emerge as a highly promising candidate for the removal of diverse organic pollutants from aqueous media.

Table 4 Comparison of MB and RhB adsorption on g-C3N4 nanosheets with reported adsorbents.
Full size table

Materials and methods

Materials

Thiourea (CH4N2S, purity ≥ 99.5%), cationic methylene blue (MB, purity ≥ 95%), and rhodamine B (RhB, purity ≥ 95%) were procured from Merck, Mumbai. All reagents utilized in this study were of analytical grade and were employed without further purification, with distilled water used consistently throughout the experimentation process.

Synthesis of g-C3N4 nanosheets

g-C3N4 nanosheets were synthesized via a one-step thermal polymerization process (Fig. 14), employing thiourea as the precursor. Specifically, 10 g of thiourea were calcined in a silica crucible at 550 °C for a duration of 2 h, utilizing a heating rate of 10 °C/min in an ambient air atmosphere. Following calcination process, the product was allowed to cool to room temperature and subsequently ground into a fine powder. The synthesis was executed under controlled conditions, and the resulting g-C3N4 was subjected to a comprehensive characterization using various analytical techniques to confirm its structural and physicochemical properties.

Fig. 14
figure 14

Schematic of the synthesis of g-C3N4 and its efficient adsorption of MB and RhB from aqueous solutions.

Full size image

Characterization techniques

X-ray diffraction (XRD) analysis was performed using a Bruker AXS D8 Advance diffractometer equipped with Cu Kα radiation (λ = 0.154 nm) over a 2θ range of 20° to 80°. Fourier transform infrared (FT-IR) spectroscopy was conducted on a Bruker IFS 66v spectrophotometer, capturing spectra in the range of 400–4000 cm−1 with a resolution of 4.0 cm−1 using the KBr pellet method. The elemental composition of the samples was examined via energy dispersive spectroscopy (EDS) from Oxford Instruments. Raman spectra were recorded using a Horiba LabRam HR 800 spectrometer at an excitation wavelength of 532.15 nm. Thermogravimetric analysis (TGA) and differential thermal analysis (DTA) were conducted at a heating rate of 10 °C/min in a nitrogen atmosphere. Detailed assessments of surface morphology were achieved through scanning electron microscopy (SEM) and transmission electron microscopy (TEM). Surface area measurements were obtained using the Brunauer–Emmett–Teller (BET) method via nitrogen adsorption/desorption isotherms, utilizing a Micromeritics ASAP 2010 analyzer at liquid nitrogen temperatures. Finally, X-ray photoelectron spectroscopy (XPS) was employed with a monochromatic Al Kα source to investigate the surface chemistry.

Adsorption experiment

Adsorption experiments were performed to optimize several key parameters, including the dosage of the adsorbent (g-C3N4) set at 10, 20, 30, and 40 mg, the initial concentrations of the adsorbates [MB and RhB] at 25, 50, 75, and 100 ppm, and the contact times at 0, 15, 30, 60, 90, 120, and 150 min. In each trial, one parameter was systematically varied while the others were held constant to isolate the effects of each variable. The initial concentrations of MB and RhB were quantified using a UV-Vis spectrophotometer set at wavelengths of 665 nm and 555 nm, respectively. After a manual agitation period of 2 min, the samples were centrifuged, and the remaining dye concentrations were assessed by measuring absorbance. All experiments were carried out in the absence of light irradiation in closed chamber at a controlled room temperature of 25 ± 2 °C, with the pH meticulously maintained at 7.5.

The decolorization efficiency was calculated using Eq. (1).

$$\:\text{D}\text{e}\text{c}\text{o}\text{l}\text{o}\text{r}\text{i}\text{z}\text{a}\text{t}\text{i}\text{o}\text{n}\:\text{E}\text{f}\text{f}\text{i}\text{c}\text{i}\text{e}\text{c}\text{y}\:\left(\text{\%}\right)=\left\{\frac{{\text{A}}_{\text{i}}-{\text{A}}_{\text{f}}}{{\text{A}}_{\text{i}}}\right\}\times\:100$$
(1)

Where Ai denotes the initial absorbance before dye adsorption, and Af indicates the final absorbance after dye adsorption.The adsorption capacity qt (mg g−1) was calculated using the formula provided in Eq. (2)53:

$$\:{\text{q}}_{\text{t}}=\frac{\left({\text{C}}_{\text{o}}-{\text{C}}_{\text{e}}\right)\:\text{V}}{\text{M}}$$
(2)

Where, Co (mgL–1), Ce (mgL–1) are the initial and equilibrium concentrations of the dye, respectively, V is the volume of the dye solution, and M refers to the molar mass of the adsorbent53.

Adsorption isotherm

Quantifying the adsorption process is essential for commercialization. This study employs mathematical models to evaluate interactions between the adsorbent and adsorbate while assessing adsorption capacity. By analyzing experimental concentration data with isotherm models, the present study identifies the most suitable model for the adsorption process. The models used include Langmuir54, Freundlich55, Dubinin–Radushkevich56, and Temkin57. This comprehensive analysis enhances the understanding of adsorption dynamics and helps optimize practical applications.

Langmuir

The Langmuir isotherm54 model represented the relationship between the maximum adsorption capacity (Qmax) and the Langmuir constant (KL), which indicates the affinity of the binding sites, as represented by the linearized Langmuir Eq. (3)54.

$$\:\frac{{\text{C}}_{\text{e}}}{\text{Q}\text{e}}=\frac{1}{{\text{Q}}_{\text{m}\text{a}\text{x}}{\:\text{K}}_{\text{L}}}+\frac{{\text{C}}_{\text{e}}}{{\text{Q}}_{\text{m}\text{a}\text{x}}}$$
(3)

Where Ce denotes the equilibrium concentration (mg/L) of the adsorbate, Qe signifies the amount of adsorbate adsorbed per gram of adsorbent, KL represents the Langmuir constant (dm−3/mole), and Qmax indicates the monolayer Langmuir adsorption capacity (mg/g). Plotting Ce (mg/L) against Qe (mg/g) results in a linear relationship, allowing for the determination of the slope and intercept. The dimensionless separation factor (RL) offers valuable insight into the nature of the adsorption process, indicating whether it is favorable (0 < RL < 1), unfavorable (RL > 1), linear (RL = 1), or irreversible (RL = 0). This relationship is described by Eq. (4).

$$\:{\text{R}}_{\text{L}}=\frac{1}{1+\text{b}\:{\text{C}}_{\text{I}\text{n}}}$$
(4)

Where b represents the Langmuir adsorption equilibrium constant (L/mol) and CIn indicates the initial dye concentration (mol/L).

Freundlich

The Freundlich isotherm55 model represents an empirical equation used to characterize non-ideal adsorption processes associated with heterogeneous adsorption. The equation is expressed in its linear form Eq. (5)55.

$$\:{\text{l}\text{n}\text{q}}_{\text{e}}={\text{l}\text{n}\:\text{K}}_{\text{F}}+\frac{1}{\text{n}}{\:\text{l}\text{n}\:\text{C}}_{\text{e}}$$
(5)

Where KF is a constant that indicates adsorption efficiency, while qe (mg/g) represents the quantity of adsorbate adsorbed per gram of adsorbent. Ce refers to the dye solution concentration at equilibrium. The slope of 1/n, which ranges from 0 to 1, reflects the intensity of adsorption and surface heterogeneity, becoming more pronounced as it approaches zero. A 1/n value of less than 1 suggests conformity to the conventional Langmuir isotherm, whereas a 1/n value greater than 1 signifies cooperative adsorption.

Dubinin–Radushkevich

The Dubinin- Radushkevich model56 calculates the apparent energy of adsorption, as demonstrated by the fundamental Eq. (6) shown below56.

$$\:{\text{l}\text{n}\text{q}}_{\text{e}}={\text{l}\text{n}\:\text{q}}_{\text{D}\text{R}}-{\upbeta\:}\:{{\upepsilon\:}}^{2}$$
(6)

Where β represents the activity coefficient, qDR is the hypothetical inundation capacity, and ε denotes the Polanyi potential, as defined in Eq. (7).

$$\:{\upepsilon\:}=\text{R}\text{T}\:\text{l}\text{n}\left(1+\frac{1}{{\text{C}}_{\text{e}}}\right)$$
(7)

Where T is the temperature and R is the universal gas constant. The value of β allows for the determination of the mean sorption energy, which represents the energy required to transfer one mole of solute from infinity to the surface of an adsorbent. This energy can be calculated using the equation provided in the following Eq. (8).

$$\:{\mathbf{E}}_{\mathbf{S}}=\frac{1}{\sqrt{2\varvec{\upbeta\:}}}$$
(8)

Temkin

The Temkin model57 is employed to analyze the effects of adsorbate-adsorbent interactions on adsorption phenomena. The linear form of the Eq. (9) can be expressed as follows57:

$$\:{\text{Q}}_{\text{e}}={\text{B}\:\text{l}\text{n}\:\text{A}}_{\text{t}}+{\text{B}\:\text{l}\text{n}\:\text{C}}_{\text{e}}$$
(9)
$$\:\text{B}=\frac{\text{R}\text{T}}{{\text{b}}_{\text{t}}}$$
(10)

Where T signifies the temperature, set at 298 K, and B is a constant that correlates with the heat of sorption (expressed in J mol−1). Furthermore, At represents the Temkin equilibrium binding constant (measured in L/g), bt is the Temkin isotherm constant, and R denotes the universal gas constant, which is 8.314 J/mol·K.

Adsorption kinetics

Adsorption kinetics refers to the rate of solute absorption, affecting the time needed for the adsorption process and revealing the underlying mechanism. This is essential for evaluating adsorption efficiency over time. The analysis of adsorption behaviour and rate was conducted using data from linear kinetic experiments and assessed through various models, including pseudo-first-order kinetics58 represented by Eq. (11)58, pseudo-second-order kinetics59 expressed by Eq. (12)59, Weber–Morris intraparticle diffusion60 mathematically described by Eq. (13)60, and liquid film diffusion models61 denoted by Eq. (14)61. All kinetics experiments were conducted at room temperature (25  ± 2 °C) while maintaining a pH of 7.5.

$$\:\text{l}\text{o}\text{g}{\:(\text{Q}}_{\text{e}}-{\text{Q}}_{\text{t}})=\text{l}\text{o}\text{g}{\text{Q}}_{\text{e}}-{\text{K}}_{1}\frac{\text{t}}{2.303}$$
(11)

Where Qt denote the amounts of dye adsorbed per unit mass on the adsorbent at equilibrium and at time t, respectively. K1 represents the pseudo-first order adsorption rate constant.

$$\:\frac{\text{t}}{{\text{Q}}_{\text{t}}}=\frac{1}{{\text{K}}_{2}{\text{Q}}^{2}}+\frac{\text{t}}{\text{Q}\text{e}}$$
(12)

Where K2 (g mg−1 min−1) denotes the pseudo-second-order rate constant. Qe denotes the equilibrium adsorption capacity (mg/g). The values of Qe and K2 can be calculated from the slope (1/Qe) and intercept (1/K2Qe2) of the linear plot of t/Qt versus t.

$$\:{\text{Q}}_{\text{t}}={\text{K}}_{\text{i}\text{d}}{\:\text{t}}_{0.5}+\text{I}$$
(13)

Where Qt refers to the amount of dye adsorbed (mg/g) at time t, I indicate the thickness of the layer, and Kid represents the intra-particle diffusion constant (mg/g min¹/2).

$$\:-\text{ln}\left(1-\text{F}\right)=\:{-\text{k}}_{\text{f}\text{d}}\times\:\text{t}$$
(14)

Here, F represents the fractional equilibrium attainment (F = Qt/Qe), and Kfd (min−1) denotes the film diffusion constant.

Thermodynamics parameters

The adsorption capacity at room temperature (25 ± 2 °C) was assessed to evaluate the thermodynamic parameters62, specifically free energy (ΔG°), enthalpy (ΔH°), and entropy (ΔS°), utilizing the Eq. (15)62.

$$\:{\text{l}\text{n}\:\text{K}}_{\text{c}}=\frac{\varDelta\:{\text{S}}^{\text{o}}}{\text{R}}-\frac{\varDelta\:\text{H}}{\text{R}\text{T}}$$
(15)
$$\:\varDelta\:{\text{G}}^{\text{o}}=-\text{R}\text{T}\:\text{l}\text{n}{\:\text{K}}_{\text{c}}$$
(16)
$$\:{\text{K}}_{\text{c}}=\frac{{\text{C}}_{\text{a}\text{d}\text{s}}}{{\text{C}}_{\text{e}}}$$
(17)

In this context, ΔG° represents the change in free energy (in kJ mol−1), R denotes the universal gas constant (8.314 J mol−1 K−1), T indicates the absolute temperature (oKelvin), and Kc refers to the equilibrium constant. The values for ΔH° and ΔS° can be derived from the Van’t Hoff equation by plotting ln Kc against 1/T, resulting in a straight line where the slope equals (−ΔH°/R) and the intercept equals (ΔS°/R)62.

Conclusions

This study introduces a novel synthesis method for the production of g-C3N4 nanosheets that utilizes a rapid thermal polymerization process with thiourea, followed by a 2-hour annealing in air at 550 °C. The approach not only accelerates the production timeline but also improves the structural and morphological qualities of the g-C3N4 nanosheets, making them highly effective adsorbents for the removal of toxic MB and RhB. Analytical characterization results reveal a hexagonal phase, nitrogen-rich heterocyclic structures, and a porous architecture with a surface area of 101.2 m2/g and an average pore size of 7.01 nm—features that promote efficient dye adsorption. The enhanced performance observed with RhB (99.80%) compared to MB (94.56%) is linked to RhB’s more compact molecular structure and stronger interactions with the surface of g-C3N4 nanosheets. Kinetic and isotherm analyses further indicate that the adsorption process is spontaneous and endothermic, demonstrating the material’s favourable affinity for dye molecules. Additionally, the g-C3N4 nanosheets maintained over 85% adsorption efficiency after five cycles, underscoring its durability and cost-effectiveness for wastewater treatment applications. Overall, these findings demonstrate how our innovative synthesis method produces effective g-C3N4 nanosheets for addressing environmental challenges associated with toxic dyes, supporting advances in sustainable and efficient wastewater treatment technologies.