Sensitivity analysis of digital twin model for energy community PV system

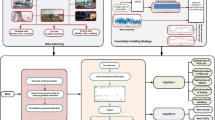
Abstract

The current energy situation in Ukraine is researched, considering the analysis of damages from missile attacks during the war. One of the ways to improve Ukrainian energy security is defined as decentralization of energy resources comprised with digitalization, decarbonization, democratization and deregulation (5D) increasing flexibility of the sector. The objectives are to examine in detail the 5D strategy. Distributed renewable energy sources are defined within the frame of Energy Community (EC) which was developed to adapt to current shortages in Ukrainian centralized grid. The EC digitalization is based on Digital Twin (DT) concept targeting design, monitoring, operational modifications and developing recommendations for the stable and optimal operation of photovoltaic systems. Energy community development and optimization include technical, meteorological, social, financial and environmental factors. Criterion programming was chosen as an effective solution to complex optimization problems. Sensitivity theory application is the basis for simplifying and optimizing the process of EC management. A model energy community ‘shelter city’ was created. The article highlights the problem of PV modules biological corrosion and suggests ways to eliminate it. In cases when biological corrosion cannot be avoided, approaches reducing its harmful effects are proposed to help during the design stage of a PV plant.

Introduction

Exploring aspects related to green transactions through the digitization of renewable energy is new task for the energy community in Ukraine. The “Recovery Plan of Ukraine” emphasizes energy independence and focus on the “green deal” and presents major projects including the construction of smart grids, localization of production of equipment for renewable energy sources and more¹. After the latest attacks, on March 22, 2024, Ukraine turned from an energy surplus country (maximum exports of more than 700 MW) into an energy deficit country with a maximum import capacity of about 1500 MW during peak hours. To understand the current situation in Ukraine’s energy sector, also the IRENA report was analyzed. The infographic of July 31, 2024 on Fig. 1 shows that in wartime between 2022 and 2023 the installed capacity of renewable energy sources remains at the same level according to the Energy Profile of Ukraine presented by IRENA².

Fig. 1

Installed capacity trend in Ukraine.

Currently, 3–3.5 GW installed power is damaged, and the deficit in power grid is near 2 GW in 2024, according to information³. The main problem is that many maneuverable power plants are destroyed or require significant reconstruction. Technical conditions of transformers and substations have been critical in the last 10 years. In this case, increasing installed capacity with instable powerful renewable energy sources is difficult, and can have negative influences on the dynamic stability of the energy system and the power quality. In this case, it can be useful to “swarm electrification model” as presented in paper⁴.

The 5Ds (decarbonization, digitalization, decentralization, democratization, deregulation) strategy deals with 5D Giga Trends and is described in Ref.⁵. It can be implemented in Ukrainian power grids with considering the technical conditions of the post-Soviet Union countries. A chaotical installation of renewable energy sources (RES) produces new challenges for stability and cybersecurity of the power grid but can be solved by improving the old and developing the new approaches of control system for RES. The decentralized decision-making and cybersecurity of the power grid are crucial issues during wartime and can be solved with ideas presented decision in Ref.⁶.

Studies about the dependence on power generation by renewable energy sources on meteorological factors are presented in papers: photovoltaic system⁷, wind power plants⁸ and small hydro-power plants⁹. Considering specific photovoltaic systems, high-level dependence on the meteorological conditions is obligatory to respect during design, operate and control according to the project. Also, for increasing the efficiency of renewable energy sources, speed-on the installation process of new capacity, simplify the process of sharing of the generated green energy and compensation the instability, Ukrainian government in war time allows use of the “cable-pooling” technology. “Cable-pooling” allows the connection of multiple renewable energy installations to a single grid connection point for reducing the costs. Integration of renewable energy sources into power systems (PS) is a trend, impacting various problems in the specific conditions of particular countries. “Cable-pooling” is used in Denmark and Poland¹⁰ already and can be used for RES of energy communities in Ukraine.

Prof. Ihor Blinov, during a presentation at a round table on March 11, 2025, noted that today, the structure of electricity generation capacities in Ukraine is undergoing significant changes due to the destruction of the electricity infrastructure because of hostilities. Additionally, there has been a significant increase in the share of RES in the overall balance. This necessitates the development of distributed energy through the appropriate restructuring of network infrastructure based on modern smart grid technologies and ensuring guaranteed power supply to critical infrastructure facilities.

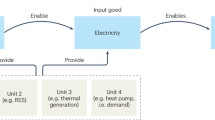
The Cabinet of Ministers of Ukraine (July 18, 2024, No. 713-p) approved the Distributed Generation Development Strategy for the period up to 2035 and approved an operational plan for its implementation in 2024–2026. The main goal of the strategy is to strengthen the resilience of the IPS of Ukraine in the context of ongoing military aggression, eliminate the insufficiency of generating capacities, meet the requirements for ensuring the security of electricity supply to consumers and operational security by creating favorable conditions for the development of distributed generation. The solution to some of the tasks set by the Government of Ukraine in this area is to apply a combined approach, which provides for the allocation of a part of the grid to an isolated (island) mode around a distributed generation (DG), if necessary, and automatic maintenance of the main grid parameters. After analyses references, the main benefits of distributed energy generation (for example, photovoltaic systems) are shown in the flow-chart on Fig. 2.

Fig. 2

Benefits of the distributed generation (DG).

The idea of decentralization for Ukrainian power grid is proposed before war time, namely in Ref.¹¹ proposed developing small distribution systems.

Digital twin of renewable energy sources

Digital transformation helps to decarbonize the energy supply, decrease the reliance on fossil fuels and promote the usage and integration of renewables in PS, while increasing its resilience¹². In this case, usage of Digital Twin concept can help optimize the photovoltaic system for power and heat supply of an energy community. RES can be also used for power and heat supply of a shelter-city. The shelter-city is a community for citizens (refugees), who lost their homes in war-conditions. Building the shelter-cities makes problems in the existing PS and impacts the power quality. For better RES operation and higher reliably, the development of Digital Twin (DT) could be the correct decision. The global DT market size is expected to reach $41.77 billion in 2026¹³.

The implementation, development and adaptation for war or post-war PS condition, the DT in control process of a shelter-city can make the prosumers and consumers more beneficial (Fig. 1). DT of RES can manage their day-to-day operations and optimize performance to increase efficiency and speed up the binding EU target promising that the share of electricity produced from renewables must grow to 50% by 2030. Energy communities start to be more popular in Europe including Czech Republic. From a technical point of view, DT EC can be presented like a smart power grid with RES¹⁴. The CORDIS Results Pack report presents EU-funded projects developing digital solutions (including DT) to build a secure and diversified energy supply, improving RES efficiency and resilience, reducing emissions and providing citizens with innovative energy services¹⁵. Vision 2030 on Market Design and System Operation of ENTSO-E identifies drivers to power system for next 10 years: rise of renewables (green deal), way to electrification, increase of decentralized resources and digitization. The INTERFACE project develops interface between transmission and distribution system operators and their customers to allow seamless RES integration and efficient use^16,17. The FLEXIGRID project shows solutions that will protect the security and reliability of the electricity grid as it incorporates growing amounts of RES¹⁸.

TwinERGY project introduced a first-of-a-kind DT framework that will incorporate the required intelligence to optimize energy demand and usage and the RES responses. TwinERGY provides further ideas and catalyzes collaborative advancements in research, innovation, and regulatory and market issues around Demand Response, RES Integration, and Consumer Engagement¹⁹. Furthermore, these DTs will provide a basis for new market structures allowing wider use of distributed RES²⁰. The creation of a DT consists of three steps: development of a digital model, adaptation of the digital shadow and, finally, approbation of the digital twin²¹. The DT is successfully implemented for RES projects²² and can be classified as shown on Fig. 3.

Fig. 3

Usage DT for RES.

DT is then used to support the processes of design, development, monitoring and targeting interoperability between the real and digital representations of any object. The level of correspondence between a real object and its DT is the critical task, as it impacts on the accuracy of the information available through the DT and the reliability of any decision based upon it and requires many additional resources.

Also, the PV industry progresses fast on the path of digital transformation²¹. DT is already in use across the lifecycle of a PV system starting from the design, going through the monitoring all the way to the decommissioning and dismantling²⁰. The current state of the research shows the relevance of the proposed topic and importance of developing new methods and recommendations for control RES with usage of DT. That also helps to optimize the power supply of shelter-city in war and post-war time²¹.

Our team is dealing with criterion programming and DT application for shelter-city since the beginning of Ukrainian war. The authors in Ref.²³ considered the use of digital twins to build integrated photovoltaic systems. They also noted the importance of digital twins for improving the construction industry by addressing its specific challenges, such as complex project management, delays, quality control, safety issues, and environmental impact. These issues are also relevant for the construction of a shelter city with integrated (rooftop) photovoltaic systems.

Aims of the study

The main goal of the research work is to study new ways of RES digitalization with usage of the criterion programming. The DT has been created with the aim of supporting the balance of the power grid, including shelter-city prosumers, energy community and energy cooperatives. The objective is to study and increase the potential and performance of the RES with the usage of innovative DT improved with the criterion programming. Obtained results will be used not just for developing energy communities in Czech Republic and EU but also as the essential contribution of Czech knowledge for the Ukrainian PS reconstruction and modernization after the war will finish.

The purpose of this research is to improve energy efficiency photovoltaic system by creating first stage digital twin and study of the methodology for evaluating quality obtained model.

To achieve the goal, the following tasks were solved:

• To investigate the processes of forming criterion similarity for assessment sensitivity DT model.

• Perform a project of DT of PV system for shelter-city of energy community, with help software PV*SOL premium.

The remainder of this paper is divided as follows: “Methods and methodical procedures” section presents the theoretical background of the work and concentrates on methods and methodological procedures. “Criterion modeling” section shows the research method applied in this study, namely, criterion method. In “Criterion modeling” section, a lot of attention is paid to developing influences variables and explanation of their meaning. Complex optimization tasks are presented in “Criterion modeling” section. Preparation of technical parameters for using the criterion method is presented. “Analysis of known systems of relative units” section highlights the different systems of relevant units and deep explanation of the criteria method. The analyses of criterion method applications are noted in “Analysis of known systems of relative units” section. “DT design of PV system for energy community” section discusses the paper’s results, findings, overall explanation, and technical remarks of design of a PV system DT. Finally, the conclusions of the work are highlighted.

Methods and methodical procedures

Activities and methodology of the study focuses on approaches to increase the flexibility of PS with RES. The implementation of the new DT in PS simulations will allow us to install more renewables without affecting the system stability and increasing the reliability and sustainability of the PS. This task is more complex in the case of PV system and the research will deal with various aspects affecting the lifecycle, efficiency, and power production forecast. Originality and novelty are the way of RES DT development using the criterion programming for analyzing sensitivity of the proposed DT model. The practical significance can be demonstrated in the design of power supply for a shelter-city. The main problem of DT usage is the determination of sensitivity and adequacy in a control task. The criterion method showed great results for decision tasks, sensitivity and adequacy. Authors²⁴ presented a criterion model for optimal control power system and shows the criteria programming practical application to determination of the mode optimal value parameters of a power system. Obtained results are used for the correction of the control influence in the bulk power system for decreasing the energy losses²⁵. The theory of sensitivity is already used for a power system control task and implemented when the necessary assessment influences the input deviation information (current, voltage, power, resistance and so on) on the function optimality (power losses). In power engineering, both these theories are applied for determining the current power mode and to the optimal mode. Authors^26,27 used the sensitivity analyses theory for calculation of best regulatory action of the bulk power system standalone modes. Last few years sensitivity analyses and criterion optimization methods approved for power grids with renewable energy sources. A more detailed description of criterion modeling, as part of the criteria method and similarity theory is presented in the next paragraph. Information about the methods and procedures is described in more detail and links to the sections of the article that show step-by-step the use of the software to create a digital twin of a photovoltaic power plant. Information on the proposed methodology, namely the use of similarity theory in a special case of the criterion method (namely its first part of criterion programming) is described in more detail in “Methods and methodical procedures” section. Methodologies for assessing the sensitivity of the resulting model to external perturbations (to changes the influencing factors) are presented in the paper. The proposed theory of sensitivity analysis with a detailed explanation of different systems of relative units is described in “Analysis of known systems of relative units” section. For practical creation of Digital Twin in proposed case-study the PV*SOL premium software is used. The Digital Twin is presented through a Digital View. PV*SOL premium is the standard industrial photovoltaic design software, which helps to design and simulate modern PV systems. The 3D visualization of a PV system by PV*SOL premium is increasing the design and presentation efficiency²¹. More information about the creation of the DT by PV*SOL premium is presented in Sect. 5.

Criterion modeling

The tasks of the energy community with optimal control have some features. The main issue is manifested at the levels of mathematical model formulation, calculation and presentation of the initial result in the form of optimal control law, which uses different systems of relative units and some parameters. This trend is particularly pronounced based on the criterion modeling (CM). Here, with the help of known systems of relative units (SRU), analytical connections are established between the parameters of the process and the parameters of the system elements in which this process takes place.

In general, in criterion models (except for canonical functions) similarity criteria are identified under the condition of information completeness about the object of study (energy community or particular householder) and can be determined by the method of integral analogues only when the coefficients of the output model are known. However, it is often necessary to determine the main characteristics of the system in the presence of a mathematical model, but in the absence of complete information about it. Therefore, it is necessary to apply such SRU, by means of which the similar criteria could be found without knowledge of these constants. This section discusses approaches that expand the capabilities of CM in this direction. Assume that the existing relationships between the parameters of the control process and the parameters of the elements of the system in which this process continues can be represented as^28,29:

$$y\left(x\right)=\sum_{i=1}^{{m}_{1}}{a}_{i}\prod_{j=1}^{n}{x}_{j}^{{\alpha }_{ji}},$$

(1)

where y(x) is some generalized technical and economic indicator. a_i, α_ji are constant coefficients, which are determined by the properties of the system, x_j are variable system parameters and m₁ is the number of members of the objective function of the model.

Variable system parameters are divided into five groups. Classification of the parameters is presented on Fig. 4.

Fig. 4

Classification of the influenced parameters.

Detailed analyses and descriptions of parameters, which characterize the influence of installed PV-system to the power quality of the centralized electric networks and power grid of energy community householders are summarized in Table 1. The first group consist from two sub groups technical parameters (x_{tech_j}), which included: first sub-group are parameters x_{tech_1,} that characterize influence installed PV-system to the power quality of the centralized electric networks and power grid of energy community householders, for example total harmonic distraction (THD), measured in %; x_{tech_2} is power losses in local energy grid (kW); x_{tech_3} is deviation level of voltage on the node from nominal values. SAIDI (x_{tech_SAIDI}), SAIFI (x_{tech_SAIFI}), CAIDI (x_{tech_CAIDI}), CTAIDI (x_{tech_CTAIDI}), CAIFI (x_{tech_CTAIFI}), CELID (x_{tech_CELID}), CEMIn (x_{tech_CEMIn}), MAIFI (x_{tech_MAIFI}), ENS (x_{tech_ENS}) indicators also can be included in this first subgroup, depending on the observed information³⁰. The second subgroup includes technical characteristics of installed PV-system and can be control in the stage design or during operation. Technical parameters of second subgroup are installed capacity of PV-system, configuration, control opportunity (tracker or standalone) (x_{tech_system}); inverter control (x_{tech_inverter}), battery storage system control (x_{tech_BESS}), feed appliances control (x_{tech_app}). The technical parameters of second subgroup are noted in Table 2.

Table 1 Technical parameters of the subgroup A and subgroup B.

Table 2 Meteorological factors (Group 2).

The second group of the indexes contains meteorological factors^7,21, exactly which are available for the assessment and selected technologies of the power and heat supply. In this group, irradiation (global (x_{met_gl}) and diffusion (x_{met_dif})), temperature (x_{met_tem}), humidity (x_{met_hum}), wind speed (x_{met_wind speed}) can be included. In NASA resources, it is possible to find hourly metrological information for chosen location. Proposed in Table 2, the set of metrological parameters should be modified depending on available data for location of installation RES.

The third group indexes are presented in Table 3. Third group indexes consider social factors, for example who will be live in house, lifestyle (x_{soc_st}), saving behavior (x_{soc_bh}), how much time spend at home, online or offline works etc. This is just a proposed set of parameters, which can be modified in cases after discussion with stakeholders of the chosen energy community, depending on the region and cultural context.

Table 3 Social factors (Group 3).

The fourth group of the indexes is influenced by the ecology (more detailed presented in Table 4), and shows, how much CO₂ emissions is reduced due to the developed PV-system for single-family tiny-house or all the energy community (x_{eco_CO2}).

Table 4 Ecological influences (Group 4).

The fifth group of the indexes contains financial indexes, and cover revenue (x_{fin_rev}); point of breakdown (x_{fin_time}); first year investments (x_{fin_inv}); electricity saving bills (x_{fin_el_sav}) and so on (fifth group of the indexes is explained in Table 5).

Table 5 Financial indexes (Group 5).

Complex optimization tasks should be solved for the power and heat supply energy of a community using renewable energy sources. In this task, parameters are compared with different physical meaning, units and measurements, so that some relevant system units should be used for transferring the physical parameters to relative units. To solve such optimization problems, it is necessary to compare the options and to choose the best one according to a certain criterion. Therefore, it should be adapted for this class of tasks. The comparison of options should be carried out with the basic values y_b, x_jb,

${y}_{*} ,{x}_{*}$ are the relevant units and indexes which help to transfer basic value to the current value. Any variant of the object can be expressed through these values:

$$y={y}_{*}\cdot {y}_{b};$$

$${x}_{j}={x}_{*}\cdot {x}_{b}.$$

(2)

Substituting (2) into (1), is obtained

$${y}_{*}\cdot {y}_{b}=\sum_{i=1}^{{m}_{1}}{a}_{i}\prod_{j=1}^{n}{{x}_{j*}^{{\alpha }_{ji}}x}_{jb}^{{\alpha }_{ji}}.$$

The similarity criteria are dimensionless combinations of parameters that are numerically identical for all similar processes and are mathematically defined as the ratio of the current value of the parameter to the base value. Similarity criterion ($\pi$) is obtained after transformations and replacements can be presented in view (3):

$${\pi }_{ib}=\frac{{a}_{i}\prod_{j=1}^{n}{x}_{jb}^{{\alpha }_{ji}}}{{y}_{b}}.$$

(3)

The Eq. (1) in the criterion form can be rewritten in form (4) with take into account (3):

$$y_{*} = \mathop \sum \limits_{{i = 1}}^{{m_{1} }} \pi _{{ib}} \mathop \prod \limits_{{j = 1}}^{n} x_{{j^{*} }}^{{\alpha _{{ji}} }} .$$

(4)

With the help of (4) the problems of proportionality and sensitivity can be solved.

In this case, there is a real possibility of studying the behavior of the posynomial function (1)³¹ around the characteristic point, taken as the basic value, with less information than its analysis in absolute units. From this position, is considered the possibility of writing a mathematical model using different systems of relative units in the criterion form, which under certain conditions can be represented as the law of the optimal control of the power supply of an energy community.

Analysis of known systems of relative units

In the construction of the heuristic system of relevant units (SRU)³², the method of relative units is used to obtain the criterion equation of the process described in (1). As is known from²⁸, the essence of this method is to reduce the equation to a dimensionless form by dividing all its members by one of them. In general, the choice of divisor is arbitrary, but the most informative variables (similarity criteria) are obtained in the case of division by efficiency. This transformation is possible using Fourier’s theorem, according to which all members of the equation describing any physical phenomenon and presented as the sum of homogeneous functions in an absolute system of units must have the same dimension. Thus, in the transition from absolute to relative characteristics, an equation is obtained, which is determined by the relationship between dimensionless parameters is the similarity criteria. For heuristic SRU it is:

$$\sum_{i=1}^{{m}_{1}}{\pi }_{i}=1.$$

(5)

This expression is called the rationing condition because it normalizes the criteria for the similarity of the objective function. It is advisable to use a heuristic system of relative units if the given interval x_j contains the extremum of the objective function, the values of which are taken as the base value y_b, x_jb. To identify the effect of each term of the objective function on the value y, as well as to determine the change in relation to when changing x_j from ${x}_{jb}$ use a heuristic system of relative units. It is also advisable to use polynomials in which m₁ = 1 then π_b = 1.

The criterion dependence (4) will look like

$${y}_{*}=\prod_{j=1}^{n}{x}_{{j}^{*}}^{{\alpha }_{ij}}.$$

(6)

In this case, the objective function has the form of a Cobb–Douglas production function

$$y=A{x}_{1}^{{\alpha }_{1}}\cdot \dots \cdot {x}_{1n}^{{\alpha }_{n}}.$$

(7)

When creating a criterion SRU from a set of basic values distinguish independent and dependent values. As noted in Ref.²⁸, the number of independent basic units and the type of functional connection is determined based on the analysis of similarity indicators that determine the possibility of the existence of a group of similar phenomena.

Expression (4) will be written in the criterion system of relative units

$${y}_{b}=\sum_{i=1}^{{m}_{1}}\prod_{j=1}^{n}{x}_{jb}^{{\alpha }_{ij}}.$$

(8)

On this basis, are also got

$$\sum_{i=1}^{{m}_{1}}{\pi }_{ib}={m}_{1}.$$

(9)

The use of the criterion SRU significantly reduces the complexity of the mathematical apparatus of the study, as well as reduces the number of variables in which the problems of optimal control are considered. The operation of differentiation can serve as an extractive feature of differential SRU, since the search for the extremum of the posynomial. can be formulated based on this operation.

The system of orthonormal equations in this SRU has the form:

$$\left\{\begin{array}{c}\sum_{i=1}^{{m}_{1}}{{\alpha }_{ij\cdot }\pi }_{\mu b}={k}_{j};\\ \sum_{i=1}^{{m}_{1}}{\pi }_{\mu b}=1,\end{array}\right.$$

(10)

where

$${k}_{j}={k}_{j}{\prime}\cdot \frac{{x}_{j}}{{y}_{b}}=\frac{\frac{\partial y}{\partial x}}{\frac{{y}_{b}}{{x}_{jb}}}=\frac{tg\beta }{tg\gamma }.$$

(11)

β is the angle of inclination tangent to the abscissa axis.

γ is the angle of inclination of the beam connecting the origin with the point on the dependence curve (1), which corresponds to the abscissa axis (Fig. 5).

Fig. 5

Graphical interpretation of the coefficient k.

However, if the researcher’s attention is drawn to the behavior of the posynomial in the region of its extremum, it is possible to use a modification of this SRU, in which the coefficients take zero values. Then the system of orthonormal equations of differential SRU is transformed into the form of a system of linear equations (conditions of orthogonality and normalization)²⁸. We show a more detailed derivative system of relative units. The search for the optimal solution can be presented as determining the position of characteristic points on the curves of the process equations, which are due to the location of the planes of orthogonality and normalization in space (motivated by conditions of orthogonality and normalization, respectively). Derivative SRU determines the degree of influence on the displacement of the normalization plane with a change in the normalization coefficient b³¹

$${\sum }_{i=1}^{{m}_{1}}{\pi }_{i}=b.$$

(12)

The introduction determining derivative SRU serves as a kind of addition to the heuristic SRU but introduces a broader concept of similarity criteria when they are normalized to an arbitrary number. The similarity criteria of the modified heuristic system of relative units differ from the criteria of the heuristic system itself and are determined³¹:

$${\pi }_{i}=\frac{{a}_{i}{\prod }_{j=1}^{n}{x}_{j}^{{\alpha }_{ji}}}{{y}_{min}}b.$$

(13)

In this case, the system of relative units is built considering the properties of similarity criteria²⁴, namely: similarity criteria of any phenomenon can be transformed into criteria of another form, obtained by multiplication, division of criteria, exponentiation or multiplication by any constant coefficient b. Using this property, is obtained b π_i = idem for any value π_i = idem. As a result of such a transformation of the basic solution, a set of solutions is considered, which determines the group of similar phenomena for all possible values of the factor b. Such properties are important for the rational construction of similarity criteria in process modeling.

In this case, Eq. (8) is transformed into the form:

$${y}_{*}=\frac{1}{b}{\sum }_{i=1}^{{m}_{1}}{\pi }_{ib}{\prod }_{j=1}^{n}{x}_{j*}^{{\alpha }_{ji}}.$$

(14)

The choice of the value of the normalizing coefficient of the derivative SRU affects the location of the normalization plane in space and can play the role of a means of influencing the pace of development of the management process. Thus, the transient phenomenon due to the introduction of the coefficient b can be reproduced in the simulation at a slow pace, which allows for detailed observation. Otherwise, this approach can accelerate the process of continuing the simulated phenomenon by tens, hundreds, and even thousands of times.

The choice of the coefficient b is subject to virtually no restrictions; for each case, its value is determined by the purpose of the study.

In addition, in optimal control problems it is often necessary to enter different measurement intervals for the same value or to build a separate measurement system for each phenomenon. In this case, the use of derivative SRU can be quite effective. For example, for a synchronous machine, the time is calculated not in seconds, but in fractions of the synchronous speed. Thus, when studying oscillations, it can be used instead entered t: $\tau =t\sqrt{F/{M}_{J}}$ and then $b=1/\sqrt{F/{M}_{J}}$.

Transitive SRU arose when it was necessary to create a transitional mathematical model between the direct and dual task.

To establish the relationship between the variables of the direct and dual problems of CP (criterion programming), is used the fourth statement of the first duality theorem²⁴:

$${a}_{i}{\prod }_{j=1}^{n}{x}_{j}^{{\alpha }_{ji}}={\pi }_{i}\cdot {y}_{min, } i=\stackrel{-}{1,{m}_{1}},$$

(15)

$${a}_{r}{\prod }_{j=1}^{n}{x}_{j}^{{\alpha }_{jr}}=\frac{{\pi }_{r}}{{\sum }_{i={m}_{k}+1}^{{m}_{k+1}}{\pi }_{i}}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}k=\overline{1,\hspace{0.33em}p}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} r=\overline{{m}_{1}+1,\hspace{0.33em}{m}_{p+1}}.$$

(16)

The first part of the equations reflects the connections that take place in the complexes of the members of the objective function of the mathematical model. The second part is the connections in the constraints.

Analysis of these systems allows us to build a transitive SRU. By logarithmizing both parts of these equations, selecting from several similarity criteria dependent and independent criteria and performing some simple transformations, is obtained:

$$\left\{\begin{array}{c}\sum_{j=1}^{n}{\alpha }_{ji}\cdot ln{x}_{j}-ln{y}_{min}=\text{ln}\left(\frac{{\pi }_{i}}{{a}_{i}\cdot {\lambda }_{i}}\right), i=\stackrel{-}{1,m-s};\\ \sum_{j=1}^{n}{\alpha }_{ji}\cdot ln{x}_{j}-ln{y}_{min}-ln{y\pi }_{i}=\text{ln}\left(\frac{l}{{a}_{i}\cdot {\lambda }_{i}}\right), i=\stackrel{-}{m-s+1, m}.\end{array}\right.$$

(17)

where

$${\lambda }_{i}=\left|\begin{array}{c}1\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}i=\overline{1,\hspace{0.33em}{m}_{1}};\\ {\sum }_{j={m}_{k}+1}^{{m}_{k+1}}{\pi }_{j}\hspace{0.33em},\hspace{1em}\hspace{0.33em}\hspace{0.33em}k=\overline{1,p},\hspace{0.33em}\hspace{0.33em} i=\overline{{m}_{1}+1,\hspace{0.33em}m}\hspace{0.33em};\end{array}\right.$$

(18)

is normalized Lagrange multipliers.

s = m–n-1 is the complexity of the task.

Or in matrix form:

$$\left[\widetilde{\alpha }\right]\times \left[h\right]=\left[\widetilde{\pi }\right],$$

(19)

where

$$\left[\widetilde{\alpha }\right]=\left[\begin{array}{ccccccc}{\alpha }_{11}& {\alpha }_{21}& ...& {\alpha }_{n1}& -1& ...& 0\\ {\alpha }_{12}& {\alpha }_{22}& ...& {\alpha }_{n2}& -1& ...& 0\\ ...& ...& ...& ...& ...& ...& ...\\ {\alpha }_{1{m}_{1}}& {\alpha }_{2{m}_{1}}& ...& {\alpha }_{n{m}_{1}}& -1& ...& 0\\ {\alpha }_{1,{m}_{1}+1}& {\alpha }_{2,{m}_{1}+1}& ...& {\alpha }_{n,{m}_{1}+1}& 0& ...& 0\\ ...& ...& ...& ...& ...& ...& ...\\ {\alpha }_{1m}& {\alpha }_{2m}& ...& {\alpha }_{nm}& 0& ...& -1\end{array}\right] ,$$

(20)

$$\left[h\right]=\left[\begin{array}{c}\mathit{ln}{x}_{1}\\ ...\\ \mathit{ln}{x}_{n}\\ \mathit{ln}{y}_{min}\\ \mathit{ln}{\pi }_{m-s+1}\\ ..\\ \mathit{ln}{\pi }_{m}\end{array}\right]; \left[\widetilde{\pi }\right]\left[\begin{array}{c}\mathit{ln}\frac{{\pi }_{1}}{{a}_{1}}\\ ...\\ \mathit{ln}\frac{{\pi }_{{m}_{1}}}{{a}_{{m}_{1}}}\\ ...\\ \mathit{ln}\frac{{\pi }_{m-s}}{{\sum }_{i={m}_{m-s-{m}_{1}}+1}^{{m}_{m-s-{m}_{1}+1}}{\pi }_{i}}\\ ...\\ \mathit{ln}\frac{1}{{\sum }_{i={m}_{p}+1}^{{m}_{p+1}}{\pi }_{i}}\end{array}\right].$$

(21)

Note that the dimension of the matrix $\left[\widetilde{\alpha }\right],$ $k=\stackrel{-}{m-s+1, m}, \left[m\times m\right]$, and its (m-s) column consists of “ − 1” (in the absence of restrictions in the mathematical model) or m₁ “− 1” and “0” (in the presence of restrictions). The column with the highest ordinal number, k, contains one “− 1”. In the case of canonical models, those k columns are missing. From the last system of equations, we obtain the dependences of the variable parameters of the system x_j, j = $\stackrel{-}{1,n}$, independent similarity criteria and the ${\pi }_{t}, t=\overline{m-s+1,m}$ minimum efficiency index y_min on the vector of dependent ${\pi }_{k},\hspace{0.33em}k=\overline{1,m-s} s$ imilarity criteria:

$$\left\{\begin{array}{c}{x}_{j}={\prod }_{i=1}^{m-s}{\left(\frac{{\pi }_{i}}{{a}_{i}}\right)}^{{\beta }_{ji}}{\prod }_{k=1}^{p}{\left(\frac{1}{{\sum }_{i={m}_{k}+1}^{{m}_{k+1}}{\pi }_{i}}\right)}^{{\sum }_{i={m}_{k}+1}^{{m}_{k+1}}{\beta }_{ji}},j=\overline{1,n}; (22)\\ \left(\frac{{\pi }_{t}}{{a}_{t}}\right)={\prod }_{i=1}^{m-s}{\left(\frac{{\pi }_{i}}{{a}_{i}}\right)}^{{\beta }_{ti}},t=\overline{m-s+1,m}); (23)\\ {y}_{min}={\prod }_{i=1}^{m-s}{\left(\frac{{\pi }_{i}}{{a}_{i}}\right)}^{{\beta }_{n+1,i}}{\prod }_{k=1}^{p}{\left(\frac{1}{{\sum }_{i={m}_{k}+1}^{{m}_{k+1}}{\pi }_{i}}\right)}^{{\sum }_{i={m}_{k}+1}^{{m}_{k+1}}{\beta }_{n+1,i}}, (24)\end{array}\right.$$

where β_ji is elements of the inverse matrix $\left[\widetilde{\alpha }\right]$.

Dependencies (22), (24) will be incomplete (do not cover all). To introduce the missing similarity criteria in (24), we resort to the artificial formation of the model of the minimum efficiency indicator:

$${y}_{min}={\prod }_{j=1}^{s}\left({\left(\frac{{\pi }_{m-s+j}}{{a}_{m-s+j}}\right)}^{{c}_{j}}{\left(\frac{{\pi }_{m-s+j}}{{a}_{m-s+j}}\right)}^{-{c}_{j}}\right).$$

(25)

After substitution (23), (24) in (25) is obtained:

$${y}_{min}={\prod }_{i=1}^{m-s}{\left(\frac{{\pi }_{i}}{{a}_{i}}\right)}^{{\beta }_{n+1,i}+{\sum }_{t=m-s+1}^{m}{c}_{t-(m-s)}{\beta }_{ti}}{\prod }_{t=m-s+1}^{m}{\left(\frac{{\pi }_{t}}{{a}_{t}}\right)}^{-{c}_{t-\left(m-s\right)}}.$$

(26)

Based on the condition of the extremum of the functions, the optimal values of the similarity criteria are determined through additional variables C_j, $j=\overline{1,\hspace{0.33em}s}$:

$$\left\{\begin{array}{c}{\pi }_{0i}=-\left({\beta }_{n+1,i}+{\sum }_{t=m-s+1}^{m}{c}_{t-\left(m-s\right)}{\beta }_{ti}\right)\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}i=\overline{1,\hspace{0.33em}m-s}\hspace{0.33em};\\ {\pi }_{0i}={c}_{t-\left(m-s\right)}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}i=\overline{m-s+1,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}m}\hspace{0.33em}.\end{array}\right.$$

(27)

To find the variables C_j, a system s of nonlinear equations of independent similarity criteria is solved from the vector of dependent criteria, which is completely determined by substitution (27) in (23):

$$\frac{{c}_{t-\left(m-s\right)}}{{a}_{t}}={{\prod }_{i=1}^{m-s}\left(\frac{-{\beta }_{n+1,i}-{\sum }_{t=m-s+1}^{m}{c}_{t-\left(m-s\right)}{\beta }_{ti}}{{a}_{i}}\right)}^{{\beta }_{ti}}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}t=\overline{m-s+1,\hspace{0.33em}m}.$$

According to the results of solving this system of equations, using (11), is obtained a complete dependence ${y=f\left(\pi \right)}_{min}$, which determines the dependence $y=f\left(\pi \right)$:

$$y={\sum }_{i=1}^{m}{\pi }_{i}\times {y}_{min}.$$

(28)

The optimal values x_j0 of the parameters are determined directly from (22). If necessary, a complete dependence is built ${x}_{j}=f\left(\pi \right)$ on a similar method. First, a complete model is formed artificially with unknown indicators:

$${x}_{j}\left(\pi \right)={x}_{j}\left(\pi \right){\prod }_{i=1}^{s}\left({\left(\frac{{\pi }_{m-s+i}}{{a}_{m-s+i}}\right)}^{{c}_{ij}}{\left(\frac{{\pi }_{m-s+i}}{{a}_{m-s+i}}\right)}^{-{c}_{ij}}\right),\hspace{0.33em}\hspace{0.33em}j=\overline{1,n}$$

(29)

After substitution (22), (23) in (28) is obtained:

$${x}_{j}={\prod }_{i=1}^{m-s}\begin{array}{c}{\left(\frac{{\pi }_{i}}{{a}_{i}}\right)}^{{\beta }_{ji}+{\sum }_{t=m-s+1}^{m}{c}_{\left[\left(t-\left(m-s\right)\right),j\right]}{\beta }_{ti}}\\ \end{array},$$

$${\prod }_{t=m-s+1}^{m}{\left(\frac{{\pi }_{t}}{{a}_{t}}\right)}^{-{c}_{\left[\left(t-\left(m-s\right)\right),j\right]}},\hspace{0.33em}\hspace{0.33em}j=\overline{1,n}.$$

(30)

However, to find additional variables C_ij, in this case use the substitution of the complete dependence y = f (π) (28) and artificially formed dependences x_i = f (π) (30) in the criterion form of the direct problem CP (4):

$${y}_{*}=\frac{y\left(\pi \right)}{y\left({\pi }_{o}\right)}={\sum }_{i=1}^{{m}_{1}}{\pi }_{io}\times {{\prod }_{j=1}^{n}\left(\frac{{x}_{j}\left(\pi \right)}{{x}_{j}\left({\pi }_{o}\right)}\right)}^{{\alpha }_{ij}}$$

(31)

Equating the exponents with it is obtained the values of C_j that characterize the dependence (30).

Let’s analyze the ${\pi }_{i},\hspace{0.33em}i=\overline{1,{m}_{1}}$ dependence, writing it as follows:

$$y={\sum }_{i=1}^{{m}_{1}}{\pi }_{i}{\prod }_{j=1}^{m}{\left(\frac{{\pi }_{i}}{{a}_{i}}\right)}^{-{\pi }_{io}}{\prod }_{k=1}^{p}{\left({\lambda }_{k}\right)}^{{\lambda }_{ko}}.$$

(32)

Taking the optimal option as the basic and assuming is ${\sum }_{i=1}^{{m}_{1}}{\pi }_{io}=1$ obtained the criterion equation of transitive SRU:

$${y}_{*}={\sum }_{i=1}^{{m}_{1}}{\pi }_{i}{\prod }_{j=1}^{m}{\pi }_{j*}^{-{\pi }_{jo}}{\prod }_{k=1}^{p}{\lambda }_{k*}^{{\lambda }_{ko}}.$$

(33)

Let’s build a model of dependence on the absolute deviation $\Delta$ of the criterion included in the objective function (λ = 1). Optimal value objective function is π:

$${y}_{*}=\left(1+\Delta \right){\left(1+\frac{\Delta }{\pi }\right)}^{-\pi }$$

(34)

Therefore, expression (33) can be considered generalizing for both cases, both for the criteria of the purpose function (λ = 1) and for the criteria of constraints. The analysis of the optimal decision based on the (transitive system of relative units in modeling the influence of similarity criteria in the law of optimal control used obtained results. Values of the dependence (32) have the content of similarity criteria, which allows us to identify the generalized properties of the system. Since the lack of data on constants does not violate the informativeness of the criterion dependence, research in transitive SRU can be conducted in conditions of incomplete information about the model. For canonical tasks, the transitive system of relative units allows us to construct the dependencies, y_* = f (π) , x_* = f (π_*), y = f(π), x = f (π) without many difficulties, without moving from the direct task of to the highlighted dual. When solving problems of high complexity, can be also used transitive SRU. The criterion equation of transitive SRU makes it possible to analyze the sensitivity of the direct problem of CP as a function of dual variables. This gives the law of optimal control in the space of direct and dual variables, allows to highlighted area of optimal solutions—the zone of the insensitivity of specific area, which is adequate to the accuracy and completeness of the source information.

The signomial system of relative units also can be used for interpretation variables and more detailed described Lezniuk and Bevz³², one of the benefits of proposed SRU, a lot of practical example of usage in power engineering optimization tasks with technical limitations (for example, load of energy community, power generation PV-modules, invertor capacity, degradation PV modules, guarantees of some equipment—PV-module 30 years, invertor -15 years, mounting system 10 years and so on). To solve the optimal control task, it is often necessary to calculate polynomial tasks and tasks with no explicitly competing effect on one or more variables. Signaling system of relative units was created. The polynomial (signomial) task can be formulated as follows:

Minimize

$$y\left(x\right)={\sum }_{i=1}^{{m}_{i}}{\varpi }_{i}{a}_{i}{\prod }_{j=1}^{n}{x}_{j}^{{\alpha }_{ji}},$$

(35)

under conditions

$${g}_{k}\left(x\right)={\sum }_{i={m}_{k}+1}^{{m}_{k+1}}{\varpi }_{i}{a}_{i}{\prod }_{j=1}^{n}{x}_{j}^{{\alpha }_{ji}}\le {\Omega }_{k}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}k=\hspace{0.33em}\overline{1,\hspace{0.33em}p}.$$

(36)

The sign functions of the signomial SRU ${\varpi }_{i}$, $i=\overline{1,\hspace{0.33em}m}$, $\Omega$, ${\Omega }_{k}$, $k=\overline{1,\hspace{0.33em}p}$ objectively supplement the rationing conditions formed CP model:

$${\sum }_{i=1}^{{m}_{1}}{\omega }_{i}{\pi }_{i}=\Omega ,$$

(37)

and orthogonality

$${\sum }_{i=1}^{m}{\omega }_{i}{\alpha }_{ji}{\pi }_{i}=0, j=\overline{1,n},$$

(38)

and a dual function

$$d\left(\pi \right)=\Omega {\left[{\prod }_{i=1}^{m}{\left(\frac{{a}_{i}{\lambda }_{i}}{{\pi }_{i}}\right)}^{{\varpi }_{i}{\pi }_{i}}\right]}^{\Omega },$$

(39)

where

λ_i are normalized Lagrange multipliers:

$${\lambda }_{i}=\left|\begin{array}{c}\hspace{0.33em}1,\hspace{1em}\hspace{0.33em}\hspace{0.33em}i=\overline{1,\hspace{0.33em}{m}_{1}}\hspace{0.33em};\\ \hspace{0.33em}{\Omega }_{k}{\sum }_{j={m}_{k}+1}^{{m}_{k+1}}{\omega }_{i}{\pi }_{j}, \hspace{0.33em}\hspace{0.33em}k=\overline{1,\hspace{0.33em}p}\hspace{0.33em},\hspace{1em}\hspace{0.33em}i=\hspace{0.33em}\overline{{m}_{1}+1,\hspace{0.33em}m}\hspace{0.33em}.\end{array}\right.$$

(40)

The following dependences are used function variables of the direct problem:

$${a}_{i}{\prod }_{j=1}^{n}{x}_{j}^{{\alpha }_{ji}}=\Omega {\pi }_{i}{y}_{o}\hspace{0.33em},\hspace{0.33em} \hspace{0.33em}\hspace{0.33em}i=\overline{1,\hspace{0.33em}{m}_{1}};$$

(41)

$${a}_{i}{\prod }_{j=1}^{n}{x}_{j}^{{\alpha }_{ji}}=\frac{{\pi }_{i}}{{\lambda }_{i}}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} i=\overline{{m}_{1}+1,\hspace{0.33em}m}.$$

(42)

The signomial function $\Omega$ SRU should not be perceived constantly. Its value is determined by the condition that the similarity criteria are integral. If this condition is violated, the signomial function $\Omega$ takes the opposite value.

To create criteria models of signomial SRU, the base optimal variant of system should be considered:

$${y}_{o},{x}_{jo},j=\overline{1,\hspace{0.33em}n,}{\pi }_{io},i=\overline{1,\hspace{0.33em}m}.$$

(43)

For this in (43) artificially is imputed signum-function and is made the replacement the variables

$$y={y}_{*}\cdot {y}_{o},{x}_{j}={x}_{j*}\cdot {x}_{jo},j=\overline{1,\hspace{0.33em}n}.$$

(44)

From (44) is determined the optimal values of similarity criteria of the objective function:

$${\pi }_{io}=\frac{{a}_{i}{\prod }_{j=1}^{n}{x}_{j}^{{\alpha }_{ji}}}{\Omega \cdot {y}_{o}}.$$

(45)

Using (46) and transformed accordingly (45), the criterion program of the signomial task is obtained:

$${y}_{*}=\Omega \left({\sum }_{i=1}^{{m}_{1}}{\varpi }_{i}\cdot {\pi }_{io}{\prod }_{j=1}^{n}{x}_{j*}^{{\alpha }_{ji}}\right).$$

(46)

Based on (46), the analysis of the optimal solution for sensitivity is performed in the signomial SRU. When solving canonical tasks in the signal SRU use the conditions of orthogonality and normalization, which correspond to the signal functions ${\varpi }_{i}$, $i=\overline{1,\hspace{0.33em}m}$, $\Omega$. The vector of optimal similarity criteria is determined from linear equations system compiled under these conditions. The maximum value of the dual function, which corresponds to the minimum of the direct problem of the CP, considering constraints is determined from (46). To solve problems of high complexity $s=m-n-1>>0$ in this system of relative units use a special algorithm, which is developed below. Thus, it has improved the general system of relative units that can apply to criterion modeling. Criterion Programming (CP) as an optimization method and as an integral part of similarity theory, Digital Twin is designed to study optimization processes in complex dynamical systems. With the advent of real technical possibilities for optimal control of these systems, this method develops in the direction of creating methods and means for obtaining and generalizing optimality conditions in the form of stable patterns and relationships between optimal values of objects and phenomena for which appropriate Digital Twins are created. Therefore, it is important to study the conditions for determining the optimal similarity criteria, which in the CP task are not only certain dimensionless combinations of parameters, as suggested by similarity theory, but also variables of the dual optimization task²⁴. At an earlier stage, a DT is a 3D shadow object. The paper shows the DT design of a power supply shelter city. A shelter city can be adapted to the energy community because the behavior and lifestyle of its citizens will correspond to the vision and mission of the European energy community.

DT design of PV system for energy community

In Ukraine right now a lot project realized already tiny-houses, shelter-city, but people who last home increasing every day. But they decided just half problem, because power supply, also can be problem after crashed a lot of condensing power plant in Ukraine. For example, projects “Give Housing to a Ukrainian Family” give houses, but don’t help with power independent power supply³³.

After analyses experiences of operation tiny-house, for current project was chosen location for 10 tiny-houses. This location is near a beautiful lake, green and quiet. The nature area is old, but probably work transformer 10/0,4 kV. Little dams are a few meters from location help in future to developed territory. After war, when refuge-families will come back to their region or house, houses possible used for green tourism.

Also, free territory near location, used for agricultural purposes, but can be changed for agrivoltaics³⁴. Analyses metrological conditions for chosen area, allowed propose used PV-system for particular cover energy needs. PV*SOL premium software was used for practical applications of creating sample Digital Shadow of shelter-city³⁵.

The meteorological data refer to a given climate zone, the entire country, precisely to a selected location—Ukraine, Vinnitsya city, near river Rivets. It is possible to use MeteoSyn module, which allows access to climate data for chosen location³⁶.

Firstly, the meteorological conditions were checked and analyzed. For this proposal after few experiments was chosen the Meteonorm 8.2³⁷. Monthly and hourly distribution or global radiation, wind speed and temperature in area, when plan build shelter-city are presented on Fig. 6. Main factors, which influence on the power generations PV system, are irradiation, wind speed and temperature^7,20 for Ukraine conditions. Hofman model for the simulation of diffusion irradiation was used, and Hay and Davies model for the simulation of the irradiation on the inclined place^38,39.

Fig. 6

Meteorological parameters, which influence on the efficiency of PV system generation in chosen area (Rivets, Vinnytsia region, Ukraine): (a) average monthly global radiation; (b) average hourly global radiation; (c) average monthly global temperature; (d) average hourly global temperature; (e) average monthly global wind speed; (f) average hourly global wind speed; (g) detailed hourly irradiation in July and (h) detailed hourly irradiation in January.

The amount of electrical energy generated by RES deal load profile of a typical tiny-house will be used more efficiently in case west–east photovoltaic system, because morning and evening maximum energy consumption will respond to generation by RES. In the case of south orientation PV-system the main value of energy is generated from 11 a.m. up to 15.00 p.m., and during this time consumption is low. South orientation of the PV modules influences badly for energy efficiency roof PV system in tiny-house case. PV-modules are overheated and work with less efficiency, also increasing power losses during charge-recharge battery storage system.

Storing the PV energy generated in early morning and late evening hours requires a large battery storage system, that increases cost of the project. Presented on Figs. 6 and 7 meteorological parameters allowed to decide that west–east PV system for power supply shelter city for obtained location is relevant, because it is more corresponding to load diagram, than South orientation.

Fig. 7

Irradiation and consumption of tiny-house.

This assessment was made from a comparison consumption diagram of tiny-house and power generation PV system diagram in typical summer worker day. East–west orientation of PV system helps cover more power needs by PV system. PV*SOL premium allows uses parameters the daily, weekly, monthly changes during year for the location, but main issue was choosing correct model of PV system and design of power load profile.

The location of the shelter-city building was chosen for sustainability of the project, and conditions for used green energy for power and heat supply. For more precise estimation it is better to choose one day profile and check meteorological factors for each area designed PV-system, for example, if global radiation is not influenced for orientation PV system, than irradiance on to titled surface has deviation depend on orientation. In Fig. 8 shown level of irradiances for east and west oriented PV system for location Rivets, Vinnitsya region in Ukraine.

Fig. 8

Irradiance level for PV system in Rivets, Vinnytsia region in Ukraine.

PV*SOL premium allows two variants for design load, first variant is choosing load profile from library, and second variant is designing own load profile with considering appliances and time usage them. The second variant gives possibility to change energy behavior and develop recommendation for owners of tiny-houses of shelter city. For optimization of the PV system and choosing energy efficiency project few variants are simulated, and best results are presented in Table 6.

Table 6 Production forecast of PV system.

The level of self-sufficiency in the production forecast is the criteria for the PV project choosing. The number of the panels, inclination angle, configuration of strings was changed during optimization. For creating DT of PV system is used PV*SOL premium, which allows made 3D visualization with considering shedding. In available location possible build for comfortable life 10 houses.

For design of a PV system, one typical house was chosen. Main concept of proposed methodology used PV is creating load profile, where a lot of appliances have possibility charging or operating, when PV system produces enough energy (boiler, vacuum cleaner, washing machine). In paper was optimized one householder, and after typical decision share 10 times.

Design of PV system in Ukraine is not easy right now, because it is necessary to consider available PV system equipment (PV-modules, invertors, accumulators) on Ukrainian market⁴⁰. Also, renewable energy projects are supported by grants and fundraising and require some rules, for example it is eligible to buy just EU produced inverter. Used 10–11-year PV panels and inverters are received from EU donors and can be installed for energy community projects after detailed design and calculation.

All available roof-square for PV-system were used, probably all consumption will cover, and power flow feed grid. Few large householders located near and can consume solar energy, other possibility to rebuild old hydropower plants and work in pumping mode. But using this system is very expensive (more than 200 K USD for installation) and requires large investments in the first years.

The shading analyses of every house allows avoid PV-modules, which have shading losses of more than 3 percents. One of the issues is that it is correct to give recommendations for profile electricity load. Vacuum cleaner (1000 W); washing machine (1400 W); dishwasher (1700 W); computer-laptop (150 W); boiler (1500 W); water pump (750 W) and other appliances which are possible to program start time or have accumulator system inside are simulated like dynamic surplus consumption.

Dynamic surplus consumption means that some appliances begin operating when PV-system generates maximum energy and consumes minimum energy from grid. Maximum and minimum power from the grid can be limited through group surplus appliances. In case, when PV system doesn’t give enough power, appliances priority can be planned. Figure 9 presented DT models shelter-city from different points of view and centralized power grid, yellow lines are PV generated energy, green lines are storage system energy.

Fig. 9

DT of tiny house with PV-system from different views.

Graphical interpretation flow-chart energy community are presented in Fig. 9.

Considering current situation in Ukrainian power grid, concept designed project is minimize power feed from grid. In this case, electrical heating is not used, which is typical for such kind tiny-house. Wood or pellet heating system is designed.

Near shelter-city there exist free land, where possible mounted terrestrial photovoltaic power plants are mounted. Beautiful nature, clean air and water, a quiet place of the location can be used in the future like resorts or for green tourism.

Predicting the instantaneous value of the power consumed, supplied by the grid, and charged to the battery is shown in the flowchart in Fig. 10. This makes it possible to independently evaluate the efficiency of the designed photovoltaic system.

Fig. 10

Graphical interpretation flow-chart energy community: blue lines are feeding from grid, yellow lines are feeding from PV system, green lines are feeding from batteries (all values in kWh).

The system efficiency criterion is the ratio of the amount of energy produced by the photovoltaic system to the power required to supply the consumer.The proposed PV system should take into account the minimization of power losses due to increased charging and discharging cycles of the batteries and power consumption from the centralized grid. The Flow-chart diagram (Fig. 10) presents graphical interpretation of distribution power flows.

PV system produces 125,579 kWh, 64,441 kWh from them are consumption of appliances and 2780 kWh from them are consumption of batteries; 58,357 kWh are sent to power grid (can be used power supply village near location). PV generation is shown by yellow lines in Fig. 10. Green lines present energy from battery storage system (2104 kWh). Blue lines show energy from grid (212 kWh) to battery storage system (169 kWh) and load (43 kWh). This flow can be optimized in the future.

One of the important factors is forecasting energy generation and consumption. Figure 11 presents monthly production and consumption of the shelter-city. Tiny-house has two floors, ground floor: 6 m is the width, and 6 m is the depth; 7 m is the width of the attic storey; 3 m is the height; 7 m is width, roof pitch is 45°.

Fig. 11

Monthly production and consumption of tiny-house.

From histogram it is visible that almost all shelter-city consumption is covered from PV-system, because surplus consumption will turn on when PV-system will be generated. Considering forecasting power supply in Ukraine winter 2024–2025 will be difficult energy deficit period, so proposed decision has high level energy independence, but haven’t high comfort standard. Design PV-system consists of 20 areas, 10 oriented to the east, and 10 oriented to the west. This configuration was chosen after analyses profile power consumption. Typical construction of one east and one west area is presented in Fig. 11. For Ukrainian grid, it is typically to have a one-phase 220 V system.

Figure 12 shows 14 modules for the west side while 16 modules are installed in the east side, because shading from the chimney produces power losses. For the optimal configuration, 2 inverters were used for both sides (for example: 7 panels for 1 inverter on west side)—see Fig. 12a, and 8 panels for east side (Fig. 12b). More detail about the project is noted in Table 7. The table presents configuration of one typical PV system project consisting of 30 modules. 16 PV-modules are mounted on east oriented roof and 14 PV-modules are mounted on west oriented roof. The chimney in west oriented roof makes shading and decreases the number of PV modules. The situation on Ukrainian market with inverters and PV-modules is clear. It is possible to buy chosen or equal types on PV-modules or invertors without any problems, but with battery storage systems there can be issues. The project uses 5 units CEL 10kWh 2 kW 1 ph BlueSky GmbH, AC coupled, with nominal output 2 kW and a lithium titanate technology.

Fig. 12

Linear flow-chart east (a) and west (b) areas for roof one house.

Table 7 Module and invertor configuration of typical decision for one tiny-house.

The efficiency of a PV system is sensitive for lot of factors, including temperature, for understanding process degradation and expected issues was simulated temperature on the modules in hours and days horizons during year (Fig. 13).

Fig. 13

Typical dependence module temperature of the West roof location PV system during day and year.

Presented on Fig. 14, dependence helps to create recommendations for operation and maintenance (for example infrared thermography control). Analyses of presented dependence can help correctly plan diagnostic of PV system. In the proposed location, there may be a problem with the efficiency of the photovoltaic system, since there is a small reservoir near the location, created for the operation of a hydroelectric power plant, which is currently not operating. The plants and the big lake in the location are great front point of ecology, air purity, green tourism, but at the same time they create excessive humidity, which is the source and cause of biological corrosion of electrical devices (see Fig. 14). This problem was first encountered during energy efficiency studies of a 20-year-old photovoltaic station, which is located on the roof of an educational building with many ventilation ducts. In Fig. 14a, hard dust is shown, which is very difficult to clean. In Fig. 14b, the earlier stage of dust appearance is shown, and it is possible to clean without damaging the glass. Secondly, this problem was detected at a ground-based photovoltaic station, which was installed on the territory of a previously dried-up lake where fish were bred. That is, in the third year of operation, groundwater began to seep to the surface, and during rainy days and spring tides, this location was over moistened. This was the reason for the appearance of mold and moss on the lower part of the panels, regardless of the rotation (vertical or horizontal). Interestingly, with a vertical arrangement, the gap between the aluminum frame and the generating photovoltaic panels is larger, which temporarily reduces the negative impact of biological corrosion. With horizontal installation of photovoltaic modules, biological corrosion, which in some cases reaches 5–7 cm, significantly affects the amount of electricity generation. Also, biological corrosion can cause excessive heating of individual cells. Figure 14 demonstrates 2 examples of biological corrosion on the sample 20 kWp PV system commissioned during 2004 and consisting of 192 monocrystalline silicon panels Isofoton I-106. The corrosion strongly depends on the exact position of the panel in the array. Two most significant examples are presented to demonstrate the corrosion process.

Fig. 14

Biological corrosion of the electric equipment PV system (on example PV-module).

In this case, it is necessary to make additional research and calculated sensitivity optimization parameters on biological corrosion, if influence more 5% degradation PV-modules in DT model should be corrected depending on the level of biological corrosion.

Discussion

The active popularization of the digitalization of renewable energy sources has led to the rapid introduction of digital twin technology. The creation of digital twins requires the improvement of existing methods for checking the adequacy of the obtained digital twins to physical objects. The theory of similarity has great potential in establishing adequacy. For dynamic processes, such as the generation of electricity by photovoltaic power plants, it is advisable to use the criterion method. From the analysis of literature sources, it is clear that the criterion method is successfully used to optimize control systems for the parameters of electric power system modes. Therefore, the paper shows the possibility of its adaptation to solve the issue of checking the adequacy of the digital twin of a photovoltaic system to a physical object. The criterion method is quite extensive and consists of three main areas: criterion modeling, criterion programming, and criterion sensitivity analysis. The article focuses in more detail on criterion modeling, i.e., describing the methodology for creating a criterion model under the condition of various influential criteria. Digital twins should respond qualitatively and quickly to changes in the physical object, so the criterion analysis of the sensitivity of the obtained mathematical models is also important. Since it is necessary to consider technical, economic, social and other indicators, it is advisable to move from named units to relative ones. The expediency of using systems of relative units for solving problems by the criterion method is shown. The heuristic, criterion and differential systems of relative units are considered. It is established that the comparison of dimensionless quantities is more informative about the essence of phenomena than the analysis of dimensional ones. It is shown that the systems of relative units contain a set of dimensionless coefficients that characterize the object and simplify comparison. Dimensionless parameters help to avoid mistakes in the process of transition from one system of units to another.

We describe and adapt the derivative, transitive, and signal systems of relative units to solve the problem of optimizing the PV system of an energy community. The derivative system of relative units allows to influence the speed of development of the modeled process by introducing a normalizing factor to reproduce the transient phenomenon at a slower pace, and, conversely, to accelerate the duration of long-term processes. The transitive system of relative units establishes a connection between the parameters of direct and binary criterion programming problems and allows for sensitivity analysis in the region of stationary points of the first model, which includes direct and binary variables. The system of signaling relative units allows studying polynomial type problems and problems in which mathematical models do not have an explicitly competing effect. The possibility of using the criterion method for solving optimization problems whose objective function and constraints are nonlinear is considered. It is shown that cumbersome computational procedures can be avoided when solving canonical problems. The behavior of a binary function in an unbounded binary space under orthonormalized conditions and without them is investigated on the basis of the derivative of the system of relative units. The dependence of the maximum of the binary function on the normalization coefficient is revealed. The relationship between the minimum of the direct problem and the maximum of the dual problem when the normalization coefficient changes is established. Based on the transitive system of relative units, an alternative method for solving optimization problems without the traditional transition from a direct criterion programming problem to a dual problem is developed by establishing a relationship between a direct criterion programming problem and dual variables. This method is presented in four generalized cases, which are determined by the type of mathematical model of the problem. The proposed method does not require knowledge of the theory of duality to estimate the dual variables included in the model. Meanwhile, the use of this approach significantly increases the information content of the model parameters.

The creation of a digital twin takes place in several stages, starting with the creation of a digital image, then a digital mirror is created, and only then a digital twin. The article focuses on the first stage, because the physical object does not yet exist. After the shelter city is built and the photovoltaic systems are installed, data will be collected for the digital twin for some time. Much attention is paid to creating an optimal photovoltaic station. The use of PV*SOL premium made it possible to partially automate the process, but no software is able to take into account the multiplier effect, as a rule, the optimization problem is solved by the criterion of maximizing power generation or minimizing power losses. From the options presented in the paper, the photovoltaic system was selected from 300 modules located on the roofs of 20 buildings, at an angle of 45 degrees and east–west orientation.

Also, this project has a wide scope for improvement and optimization. For example, the paper does not clearly solve the problem of heating water for tiny houses, and in the future it is possible to use new technologies, such as a wind heater⁴¹, but this solution requires new research. The next urgent task is that every fifth car in Vinnytsia region is an electric vehicle, so the installation of charging stations for electric vehicles with the possibility of increasing the energy efficiency of photovoltaic power plants should be taken into account in further research⁴².

The study of the latest developments in the field of digital twins and their application for future research allowed us to draw the following conclusions and formulate future directions:

• 1. The use of digital twins can be used to optimize the structure of photovoltaic panels and the materials from which they are made. The study proposed by the authors⁴³ can be partially used to solve the problem of biological corrosion and degradation in future research for the design of PV power plants.

• 2. The use of digital twins can be used for the control system of a photovoltaic power plant to optimize generation, consumption and identification of damage and degradation. The research results proposed by the authors⁴⁴ will be used in the future to develop a system for online monitoring of the technical condition of photovoltaic equipment.

• 3. PV system prediction digital twin can improve efficiency existed PV system. The presented solution in paper⁴⁵ will be interesting apply in design PV system and compare deviation between real data, PV*SOL premium and domain adaptation neural network.

Conclusions

• 1. The optimal condition of the object under study is characterized by certain values of similarity criteria. Moreover, the optimal values of the similarity criteria are in the ratios that determine the conditions of optimality. The latter, summarizing the relationship between the optimal values of the parameters, carries information that can be implemented to optimize the state of the system. Based on the quasi-optimums obtained of the criterion programming problem, an algorithm for determining the optimal values of similarity criteria is used, which are used to create criterion models and sensitivity analysis of the optimal solutions.

• 2. Creating the DT of a power supply system allows easy simulation of different conditions and configuration of the PV-system and appliances. Sensitivity theory can help to clarify the set of influences factors. Criterion method be used for analyzing incomparable parameters (technical, social, meteorological ecology and financial). Activities and methodology of the study are dealing with focus on approaches to increase the flexibility of power system (PS) with RES. Implementation of new DT in PS simulations will allow us to install more renewables without affecting the system stability. This task is more complex in the case of PV system and the research will deal with various aspects affecting the lifecycle, efficiency, and power production forecast. Originality and novelty are the way of RES DT development using neuro-fuzzing modeling and criterion programming. Criterion programming is described in the paper. Practical significance was demonstrated on the design of power supply for shelter-city using PV*SOL premium. Few projects are presented and one with the highest efficiency is chosen.