Scientific planning of dynamic crops in complex agricultural landscapes based on adaptive optimization hybrid SA-GA method

Abstract

Effective dynamic agricultural planning is crucial for optimising resource allocation and ensuring income stability, yet conventional methods often face limitations in adapting to the complex and variable conditions of mountainous regions, particularly under fluctuating climate and market pressures. Therefore, this study introduces a novel multi-stage dynamic optimization framework specifically designed for crop planning in such challenging terrains. This framework is underpinned by a sophisticated model integrating advanced monitoring systems with a Hybrid Simulated Annealing Genetic Algorithm (H-SAGA), further enhanced by neural network-driven real-time predictions. The H-SAGA component optimises planting strategies by synergistically combining global exploration (SA) and local refinement (GA) capabilities, while the neural network dynamically adjusts revenue forecasts based on climatic and market data, significantly improving the model’s responsiveness and adaptability. We rigorously evaluated the applicability and effectiveness of this model through extensive simulations across 7,290 mu (1,201 acres) of diverse farmland in mountainous Northern China. The results demonstrate that the proposed H-SAGA approach consistently achieves 5–10 percentage points higher profit increment ratios than other benchmark optimization algorithms (such as GA, SA, PSO, and ACO), alongside faster convergence and notable robustness against environmental and economic variability. This research establishes an integrated “monitoring-modelling-decision” paradigm, driven by multi-source data and machine learning, offering a practical and robust tool that provides valuable guidance for enhancing resource allocation efficiency and promoting sustainable precision agriculture in complex topographical regions, thereby holding significant reference value for optimising agricultural production nationwide.

Introduction

In Northern China’s mountainous regions, agricultural productivity is constrained by three core challenges: land fragmentation, a fragile water resource system, and increasing climatic variability^1,2,3. These factors create a dynamic environment—characterized by fluctuating weather patterns, resource availability, and market pressures—where traditional cultivation practices are poorly adapted, resulting in low resource efficiency and unstable outputs. This necessitates the use of advanced optimization methods, specifically adaptive optimization which involves sequentially updating decisions in response to new information, to guide land use and crop layout in such complex terrains^4,5.

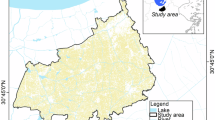
The study is geographically grounded in North China (Fig. 1a), a region defined by complex topography and critical river systems that shape its agricultural potential (Fig. 1b). This landscape is not static; it exhibits significant environmental and agricultural dynamics. Spatiotemporal analysis from 2000 to 2024 reveals considerable volatility in cropland extent, with concurrent patterns of land loss and gain (Fig. 1c). This instability is mirrored in the health of the vegetation itself, as the Normalized Difference Vegetation Index (NDVI) for the region’s farmland shows marked variability over the past two decades (Fig. 2). Layered upon this dynamic environment is a multifaceted agricultural economy, characterized by substantial disparities in crop choices and production volumes across different provinces (Fig. 3). The confluence of this intricate topography, pronounced environmental fluctuations, and complex production systems presents a formidable challenge for effective agricultural planning. It is precisely this multi-layered complexity that necessitates a sophisticated, adaptive optimization framework capable of identifying robust and efficient solutions.

Fig. 1

Geographical features and cropland dynamics in North China (2000-2024). (a) Location of the study area within China. (b) A depiction of the region’s land use, topography (via contour lines), and major river systems as of 2020. (c) Spatiotemporal changes in cropland, illustrating areas of stable cultivation, loss, and gain over the past two decades. The maps in this figure were generated by the authors using Python (v3.8) with the Matplotlib (v3.5.2), Geemap (v0.30.4), and Google Earth Engine (v0.1.399) libraries. The respective software is available at https://www.python.org, https://matplotlib.org, https://geemap.org, and https://developers.google.com/earth-engine/. Data sources are detailed in the Methods section.

Fig. 2

Mean Normalized Difference Vegetation Index (NDVI) for different land cover types from 2000 to 2024, indicating variability in vegetation health.

Fig. 3

Agricultural production structure in North China’s major provinces, highlighting the multifaceted economic landscape.

While mathematical programming techniques like linear programming have been applied to agricultural optimization⁶, their reliance on static parameters struggles to capture the non-linear dynamics and uncertainties inherent in mountainous agricultural systems^7,8. To address these complexities, metaheuristic algorithms have gained traction. Accordingly, we selected established methods—Genetic Algorithms (GA), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Simulated Annealing (SA)—as benchmarks, as they represent the conventional state-of-the-art for such problems. However, these algorithms are often hampered by slow convergence and premature entrapment in local optima within high-dimensional search spaces⁹. This limitation has motivated the exploration of hybrid strategies, such as combining the global exploration of SA with the refined search of GA, which forms the theoretical basis for our proposed approach¹⁰.

A more profound limitation of existing models, including hybrid ones, is their static, single-stage nature, which is ill-suited to the inherent dynamism of agriculture. Effective planning requires sequential adjustments based on evolving intra-seasonal information, such as updated weather and market forecasts^11,12. The inability of current models to integrate such real-time data for adaptive decision-making represents a critical research gap, limiting both the resilience and profitability of agricultural operations.

To fill this gap, this study proposes a novel multi-stage dynamic framework focused on land use and crop layout optimization in complex terrains. Its core is a Hybrid Simulated Annealing Genetic Algorithm (H-SAGA) integrated with a neural network-based predictive model to dynamically adjust revenue expectations based on the latest climatic and market data. This closed-loop “monitoring-modeling-decision” paradigm is designed to provide a smart decision-support tool for mountainous agriculture that is both robust and highly efficient. Therefore, this study aims to answer the following central research question:

How can a dynamic, multi-stage optimization framework, integrating predictive analytics and a hybrid metaheuristic algorithm (H-SAGA), effectively enhance the economic profitability and resource-use efficiency of agricultural planning in the complex and variable conditions of Northern China’s mountainous regions?

Methods

This section outlines the methodological framework employed in this study, integrating a multi-stage optimization model with the Hybrid Simulated Annealing Genetic Algorithm (H-SAGA) to optimize agricultural planning. The approach aims to maximize crop cultivation revenues while adapting to mountainous regions’ geographical, climatic, and resource constraints. It combines advanced optimization techniques with neural network predictions to enhance adaptability and precision in dynamic environments.

Multi-stage optimization model

We propose a multi-stage optimization model¹³ designed to facilitate sequential decision-making across various decision points throughout the growing season. This framework adapts to fluctuations in market prices and climatic conditions^12,14,15, making it particularly effective for mountainous terrains where plot characteristics such as slope, altitude, and water availability significantly influence yield and resource use.

It is crucial to clarify the core concept of “multi-stage dynamic adjustment” in this model. It does not imply uprooting an already planted Crop A to replace it with Crop B mid-season. The reality of farming dictates that once a crop is planted, it is typically seen through to harvest, as mid-season replacement would incur significant sunk costs and be impractical. Instead, a “stage” in our model represents a distinct decision-making point in time, strategically aligned with key phases of the regional cropping calendar (e.g., Stage 1: pre-sowing planning; Stage 2: early-growth review; Stage 3: mid-season resource adjustment). The “dynamic adjustment” at the beginning of each new stage manifests in two primary ways:

• 1. optimization of uncommitted decisions: For plots that have not yet been assigned a crop (e.g., due to resource constraints or staggered planting schedules), the model re-optimises the crop choice and planting area based on the latest climate and market forecasts.

• 2. Adaptation of future plans: The model can adjust the macro-level cropping strategy for the next year or the next planting cycle based on information gained in the current stage (e.g., observed yield performance, new market trends).

For crops that are already planted, the model’s adaptive adjustments focus on optimising resource inputs (e.g., adjusting irrigation schedules based on updated drought forecasts) rather than changing the crop itself. This design ensures that the model’s dynamic adaptability aligns with the practical constraints of agriculture.

Why multi-stage?

• State Transitions: Each stage incorporates updated data on prices, resource usage, and expected yields. Decisions at stage t shape the state at stage $t+1$, capturing the evolution of land conditions and resource availability.

• Evolving Decision Variables: Variables like $x_{ij}^{(t)}$ (area of crop j on plot i at stage t) evolve dynamically, allowing adjustments based on changing profitability or resource demands for uncommitted plots.

• Risk Mitigation: Multi-stage planning mitigates risks from unforeseen events (e.g., droughts or market shifts) by enabling adaptive strategies across stages.

Geographical and climatic considerations

In mountainous regions, plot-specific factors such as slope ($\textrm{slope}_i$), altitude ($\textrm{altitude}_i$), and precipitation ($\textrm{precip}_i$) are integrated into yield and resource functions to reflect real-world variability accurately.

Basic assumptions

• Within any single optimization stage, decisions are made based on a static set of price and cost forecasts. However, these forecasts are dynamically updated with new information (e.g., latest market reports and weather forecasts) at the beginning of each subsequent stage.

• Soil and climatic conditions are considered stable within each stage but are updated between stages.

• Crop interaction coefficients (complementarity and substitutability) are predefined.

• Long-term soil effects from crop rotation are excluded from the model.

Symbol definitions

• i: Plot index (1 to N).

• j: Crop index (1 to M).

• $p_j$: Market price of crop j (CNY/ton).

• $c_j$: Cost of crop j (CNY/mu).

• $x_{ij}$: Area of crop j on plot i (mu).

• $A_i$: Available area on plot i (mu).

• $D_j$: The estimated regional market absorption capacity for crop j (ton), representing the upper limit of what can be sold without causing significant price depression, forecasted based on historical sales data.

• $r_j$: Per-unit-area composite water consumption for crop j (cubic meters/mu). This value integrates the irrigation requirements and effective rainfall over the crop’s entire growth cycle.

• $R_{\text {max}}$: Total water resource limit for the entire farm (cubic meters), representing the total volume of water available from the local reservoir system for irrigation during the planning period.

• $\alpha _{jk}$, $\beta _{jk}$: Crop interaction coefficients. These dimensionless coefficients, ranging from [0, 1], were determined based on a combination of: (1) a systematic review of agro-ecological literature pertinent to the region, and (2) multiple rounds of consultation with local senior agronomists and agricultural extension experts. For example, a higher $\alpha _{jk}$ value is assigned for legume–non-legume pairs, while a higher $\beta _{jk}$ value is assigned for pairs of crops with high water demand.

• $Y_{\text {syn}\_\text {thresh}}$: Minimum threshold for synergistic crop interaction effects (dimensionless score).

• $\delta _{\text {ant}\_\text {thresh}}$: Maximum threshold for antagonistic crop interaction effects (dimensionless score).

optimization objectives and decision variables

• Objective: Maximize total revenue R:

  $$\begin{aligned} F = \sum _{i=1}^N \sum _{j=1}^M (p_j \cdot Y_{ij} \cdot x_{ij} - c_j \cdot x_{ij}) + \lambda \cdot Pen \end{aligned}$$

  (1)

  where Pen is the penalty term that quantifies constraint violations (defined further in the Fitness Function section), and $\lambda$ is a large positive penalty factor. where $Y_{ij}$ represents the predicted per-unit-area yield (e.g., in ton/mu) of crop j on plot i. This yield is determined by an empirical model, $f_{yield}$, which synthesizes the influence of various plot-specific characteristics, crop-specific requirements, environmental conditions, and management inputs. For this study, a linear regression model was developed and calibrated using historical and experimental data from the study region, taking the following functional form:

  $$\begin{aligned} \begin{aligned} Y_{ij} =&p_1 + p_2 \cdot \text {SQI}_i + p_3 \cdot \text {GDD}_{ij}^{\text {eff}} + p_4 \cdot \text {WaterAvail}_{ij} \\&- p_5 \cdot \text {SlopeFactor}_i + p_6 \cdot \text {AltFactor}_{ij} + p_7 \cdot \text {NutrientScore}_{ij} \end{aligned} \end{aligned}$$

  (2)

  The input variables ($Inputs_{ij}$) for this model are defined as:

  • $\text {SQI}_i$: Soil Quality Index for plot i. This is a composite, dimensionless index, constructed following the guidelines of the Food and Agriculture Organization (FAO) framework for soil quality assessment. It integrates several key soil physical and chemical indicators, including organic matter content, texture (sand, silt, clay percentages), pH, and available N, P, K. These indicators are normalized and combined through a weighted average to produce a final score ranging from 0 to 1, where 1 represents optimal soil health. The index is numerically scaled (e.g., from 0 to 0.01) to fit the coefficient scale of the regression model.

  • $\text {GDD}_{ij}^{\text {eff}}$: Effective Growing Degree Days for crop j on plot i (measured in $^{\circ }\text {C} \cdot \text {days}$). This is calculated based on daily mean temperatures relative to the crop’s specific base temperature and any upper temperature threshold, accumulated over the relevant growing period within stage t.

  • $\text {WaterAvail}_{ij}$: Total effective water available to crop j on plot i (e.g., sum of effective rainfall and applied irrigation, measured in mm) during critical growth sub-periods within a given stage.

  • $\text {SlopeFactor}_i$: A dimensionless slope impact factor for plot i. This is derived from the raw slope percentage ($S_i\%$) using a non-linear transformation designed to emphasize the adverse impact of steeper slopes on yield, for instance, $\text {SlopeFactor}_i = (S_i / S_{\text {ref}})^k$ (where $S_{\text {ref}}$ is a reference slope and $k>1$, e.g., $k=2$), or a similar function. This transformation typically results in very small positive values (e.g., in the $10^{-3}$ to $10^{-4}$ range for common agricultural slopes), explaining the large magnitude of the coefficient $p_5$ when combined with the negative sign in Eq. 2.

  • $\text {AltFactor}_{ij}$: An altitude suitability factor for crop j at the altitude of plot i (raw altitude measured in meters). This factor is constructed as a normalized score (e.g., scaled 0 to 1, where 1 represents optimal altitude for crop j) derived from the raw altitude, potentially modeling an optimal range or a non-linear response based on literature or agronomical expertise for each crop.

  • $\text {NutrientScore}_{ij}$: A composite nutrient availability score for crop j on plot i. To align with standard agronomic practices, crop yield is measured in ton/mu throughout this paper, whereas nutrient inputs, such as the N, P, K levels used to calculate this score, are specified in kg/mu. This score (e.g., dimensionless, scaled 0 to 10) is based on the levels of these applied fertilizer nutrients relative to the specific crop’s requirements, and may also incorporate inherent soil nutrient levels if available.

  The parameters $p_1, \dots , p_7$ are the coefficients obtained from the multiple linear regression analysis of historical yield data against the aforementioned input variables. The determined values of these coefficients and their detailed interpretations are presented in the Results section (see Section "H-SAGA optimization performance and outcomes", Table 3). The precise definition and scaling of these input variables and the underlying assumptions of the linear additive model (Eq. 2) are crucial for the model’s predictive accuracy. This calibrated empirical model forms the basis for yield predictions within the H-SAGA optimization process.

• Constraints:

  • 1. Land: $\sum _{j=1}^M x_{ij} \le A_i \quad \forall i$.

  • 2. Demand: $\sum _{i=1}^N Y_{ij} \cdot x_{ij} \le D_j \quad \forall j$.

  • 3. Resource: $\sum _{i=1}^N \sum _{j=1}^M r_j \cdot x_{ij} \le R_{\text {max}}$.

  • 4. Crop Interactions (for intercropping scenarios): These constraints model the synergistic (beneficial) or antagonistic (detrimental) effects when specific pairs of crops (j and k) are grown simultaneously on the same plot i (i.e., intercropping). It is assumed that the total area planted on plot i does not exceed $A_i$, allowing for $x_{ij} > 0$ and $x_{ik} > 0$ simultaneously if $j \ne k$.

    • Synergistic interactions (e.g., nitrogen fixation, pest deterrence): For selected crop pairs (j, k) known to be mutually beneficial, a minimum level of positive interaction effect is enforced:

      $$\begin{aligned} \alpha _{jk} \cdot x_{ij} \cdot x_{ik} \ge Y_{\text {syn}\_\text {thresh}} \quad \forall i, \text {for specific synergistic pairs } (j,k) \end{aligned}$$

      (3)

      where $\alpha _{jk}$ is a positive coefficient quantifying the synergistic effect per unit-area-product of crops j and k (e.g., units of $1/\text {mu}^2$ if $Y_{\text {syn}\_\text {thresh}}$ is dimensionless), and $Y_{\text {syn}\_\text {thresh}}$ is a predefined minimum acceptable dimensionless score for the synergistic benefit.

    • Antagonistic interactions (e.g., allelopathy, competition for specific resources): For selected crop pairs (j, k) known to have negative interactions, the detrimental effect is limited:

      $$\begin{aligned} \beta _{jk} \cdot x_{ij} \cdot x_{ik} \le \delta _{\text {ant}\_\text {thresh}} \quad \forall i, \text {for specific antagonistic pairs } (j,k) \end{aligned}$$

      (4)

      where $\beta _{jk}$ is a positive coefficient quantifying the antagonistic effect per unit-area-product (e.g., units of $1/\text {mu}^2$ if $\delta _{\text {ant}\_\text {thresh}}$ is dimensionless), and $\delta _{\text {ant}\_\text {thresh}}$ is a predefined maximum tolerable dimensionless score for the antagonistic effect.

    The selection of interacting pairs and the values for $\alpha _{jk}$, $\beta _{jk}$, $Y_{\text {syn}\_\text {thresh}}$, and $\delta _{\text {ant}\_\text {thresh}}$ are based on agronomic knowledge and experimental data regarding local intercropping practices. If intercropping is not considered for a plot or specific crop pair, these constraints are omitted or the respective coefficients $\alpha _{jk}, \beta _{jk}$ are set to zero.

Constraints are adjusted per stage, with outcomes from one stage informing the next, enabling adaptive planning.

Hybrid Simulated Annealing Genetic Algorithm (H-SAGA)

The Hybrid Simulated Annealing Genetic Algorithm (H-SAGA)^16,17 addresses the multi-stage optimization problem by merging Simulated Annealing (SA) for global exploration with Genetic Algorithms (GA) for local refinement^18,19. This hybrid approach excels in complex, nonlinear agricultural optimization tasks.

Algorithm principles

• SA: Employs a temperature-controlled search to escape local optima, reducing temperature iteratively to converge on a global optimum^20,21.

• GA: Uses selection, crossover, and mutation for solution space exploration, though it may stagnate in later stages²².

• H-SAGA Strategy: Starts with SA for broad exploration, then shifts to GA for precise optimization, ensuring robust solutions.

Fitness function

The fitness function balances revenue and constraint adherence. This study transforms the constrained optimization problem into an unconstrained one using a penalty function method, a mature and widely-used technique for handling complex constraints in metaheuristic algorithms. The function is defined as:

$$\begin{aligned} F = \sum _{i=1}^N \sum _{j=1}^M (p_j \cdot Y_{ij} \cdot x_{ij} - c_j \cdot x_{ij}) + \lambda \cdot Pen \end{aligned}$$

(5)

where Pen is the penalty term that quantifies constraint violations, and $\lambda$ is a large positive penalty factor. This approach guides the search process towards the feasible region by penalizing solutions that violate the constraints.

Integration of neural network prediction model

A three-layer neural network enhances H-SAGA with real-time revenue forecasts using historical data (e.g., climate, yields, prices)^23,24:

• Input: Climatic and economic variables.

• Hidden Layers: 64, 32, and 16 neurons with ReLU activation.

• Output: The primary output of the neural network for each stage t is a vector of predicted market prices, $\hat{p}_j^{(t)}$, for each relevant crop j. These predictions represent the expected selling price per unit (e.g., CNY/ton) of crop j if harvested or marketed corresponding to the decisions made for stage t. The network is trained on historical data linking past climatic and market conditions to observed crop prices.

• Fitness function refinement: The stage-specific predicted prices $\hat{p}_j^{(t)}$ from the neural network are directly used to dynamically update the revenue calculation within the H-SAGA’s fitness function (Eq. 5) for the current optimization stage t. Specifically, the baseline price term $p_j$ in the revenue component $\sum (p_j \cdot Y_{ij} \cdot x_{ij})$ of Eq. 5 is replaced by the neural network’s predicted price $\hat{p}_j^{(t)}$. Thus, the revenue for stage t is calculated using these dynamic, Neural-network-predicted prices, while the physical yield $Y_{ij}$ is still derived from the empirical model (Eq. 2). This integration ensures that the H-SAGA’s optimization at each stage is guided by the most current, data-driven forecasts of economic conditions, allowing the planting strategies to proactively adapt to anticipated changes in crop profitability(Fig 4).

Fig. 4

Structure of the integrated neural network prediction mModel.

Key parameter visualization

Parameters like initial temperature and population size are visualized to show their impact on performance (Figs. 5,6).

Fig. 5

Key Parameters of H-SAGA and their Influence.

H-SAGA process and steps

• 1. Initialization: Set population and temperature.

• 2. SA Phase: Explore solutions, reduce temperature.

• 3. GA Phase: Refine via selection, crossover, mutation.

• 4. Neural Adjustment: Update fitness with predictions.

• 5. Convergence: Stop at iteration limit or fitness threshold.

Fig. 6

Flowchart of the H-SAGA algorithm.

Experimental setup and data

The experiments and projections in this study are grounded in a comprehensive analysis of agricultural and climatic data from a representative mountainous region in North China. This area is characterized by its cold climate and predominantly single-season cropping systems^7,25.

Crop portfolio and data sources: The study considered a portfolio of crops common to the North China region, categorized as major food crops (e.g., High-yield Corn, Drought-resistant Wheat, Potato) and cash crops (e.g., Heirloom Tomato, Green Soybean, Winter Rapeseed) for market returns. The empirical data underpinning our models were aggregated from multiple authoritative sources. Historical time-series data on crop sowing areas, yields, and market prices for the period 2000-2024 were primarily compiled from the China Statistical Yearbook and the respective provincial statistical yearbooks of Beijing, Tianjin, Hebei, Shanxi, and Inner Mongolia^26,27,28. The geospatial data used to construct the study area maps (Fig. 1) and as inputs for the model were aggregated from multiple authoritative, open-access sources. Specifically, land use/land cover (LULC) and cropland change data were derived from the China Land Cover Dataset (CLCD)²⁹. Topographic data, used for generating hillshade and contour lines, were sourced from the Shuttle Radar Topography Mission (SRTM) dataset³⁰. Major river networks were extracted from the HydroSHEDS dataset³¹. Administrative boundaries for the location map were obtained from the GEE data catalog, primarily the U.S. Department of State Large Scale International Boundary (LSIB) dataset. The local plot-level records from 7,290 mu (1,201 acres) across 34 plots were used for model calibration and validation against these regional datasets. This multi-source data integration provides a robust basis for capturing historical trends and spatial heterogeneity.

To accurately model the temporal constraints and resource demands within the multi-stage framework, the typical growth cycle duration for each crop under local conditions was established, as detailed in Table 1. This information is critical for calculating stage-specific parameters such as Effective Growing Degree Days (GDD) and scheduling water allocation, ensuring that the optimization aligns with the phenological timeline of each potential crop.

Table 1 Portfolio of studied crops and their typical growth cycle durations.

Data Preprocessing: To ensure the quality and integrity of the 25-year time-series data, a rigorous preprocessing pipeline was implemented:

• Data cleaning: Outliers in the time-series records were identified using the Interquartile Range (IQR) method. Instead of exclusion, which could create gaps, these outliers were managed using Winsorization to cap them at a realistic percentile (e.g., 95th), preserving the data structure.

• Missing value imputation: To maintain the temporal integrity of the dataset, missing values within the time series (e.g., for climate or price data) were handled using time-series interpolation (linear interpolation). This method is more appropriate for long-term data than simple mean imputation as it respects the temporal sequence of the observations.

• Feature engineering: Coefficients representing crop complementarity and substitutability were derived based on a review of regional agronomic literature and expert consultation.

• Data standardization: Numerical features were standardized using Z-score normalization to mitigate scale disparities before being input into the machine learning models.

• Dataset partitioning: The complete historical dataset (2000-2024) was partitioned for the purpose of training and validating the predictive neural network. Data from 2000-2018 was used as the training set, data from 2019-2021 served as the validation set for hyperparameter tuning, and data from 2022-2024 was held out as the final test set to evaluate predictive performance on unseen data.

Model parameter configuration:The parameters for the H-SAGA algorithm and the integrated neural network were determined through a meticulous tuning process involving preliminary experiments and sensitivity analysis. Our goal was to strike an optimal balance between global exploration (SA phase) and local exploitation (GA phase), ensuring both rapid convergence and high-quality solutions. For instance, sensitivity analysis indicated that an initial temperature (T0) around 300 provided a sufficiently broad initial search space without excessively prolonging the initial annealing phase. For instance, sensitivity analysis indicated that an initial temperature (T0) around 300 provided a sufficiently broad initial search space without excessively prolonging the initial annealing phase. The cooling rate (a) was tuned within the range of [0.80, 0.99] as specified in Table 2. A final value of 0.95 was selected, as it offered a balanced cooling schedule that effectively prevented premature convergence while leveraging the powerful local refinement of the subsequent GA phase. The final, optimized parameter values used for all reported experiments are detailed in Table 2. To ensure the effectiveness and reproducibility of the neural network prediction model, its training process was meticulously defined. The network was trained for 200 epochs with a batch size of 32. The Adam optimizer was employed for updating network weights, with the learning rate specified in Table 2 (0.001). Mean Squared Error (MSE) was selected as the loss function to quantify the deviation between predicted and actual revenues, guiding the model’s optimization.

Table 2 Parameter setting overview for H-SAGA experiments.

Baseline algorithm configuration: To comprehensively evaluate the performance of H-SAGA, four representative metaheuristic algorithms were selected as benchmarks. These algorithms were chosen because they represent different and well-established families of optimization techniques: Genetic Algorithm (GA) is a classic example of evolutionary algorithms, Simulated Annealing (SA) represents trajectory-based local search methods, while Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO) are prominent examples of swarm intelligence. Comparing H-SAGA against these diverse algorithms provides a robust validation of its effectiveness for this agricultural optimization problem. For a fair comparison, the parameters for these baseline algorithms were meticulously chosen based on commonly accepted values in the literature and fine-tuned through preliminary experiments to suit the problem characteristics. The specific configurations were as follows:

• Genetic Algorithm (GA): Population size: 100 individuals; Selection: Tournament selection (tournament size of 3); Crossover: Two-point crossover (probability of 0.85); Mutation: Bit-flip mutation (probability of 0.02 per bit); Maximum generations: 500.

• Simulated Annealing (SA): Initial temperature: 1000 units; Cooling schedule: Geometric cooling (cooling rate $\alpha = 0.98$); Iterations per temperature level (Markov chain length): 150; Final stopping temperature: 0.01 units.

• Particle Swarm Optimization (PSO): Swarm size: 50 particles; Inertia weight w: Linearly decreased from 0.9 to 0.4; Cognitive coefficient ($c_1$): 2.05; Social coefficient ($c_2$): 2.05; Maximum iterations: 500. Velocity clamping was applied.

• Ant Colony Optimization (ACO): Number of ants: 50; Pheromone influence factor ($\alpha _{aco}$): 1.0; Heuristic influence factor ($\beta _{aco}$): 3.0; Pheromone evaporation rate ($\rho _{aco}$): 0.1; Pheromone deposit factor (Q): 100 (scaled by solution quality); Maximum iterations: 200.

All algorithms, including H-SAGA and the baselines, were executed under identical computational environments (Intel Core i7-9700K CPU @ 3.60GHz, 32 GB RAM, Windows 10, Python 3.8 with NumPy 1.19 and SciPy 1.5.) and utilized consistent stopping criteria. Specifically, execution for each algorithm concluded when one of the following conditions was met: (1) reaching the maximum iteration limit as defined in its respective parameter configuration; or (2) when the improvement in the best-found solution’s fitness value was less than a predefined tolerance (set to $1 \times 10^{-5}$) over 50 consecutive iterations. Furthermore, an overriding maximum limit of 200,000 function evaluations was applied to all algorithms to ensure comparable computational effort and provide a robust basis for performance evaluation.

Results

This section presents the results obtained from applying the proposed H-SAGA optimization model. We validate the data characteristics, evaluate the performance of H-SAGA including its convergence and optimization outcomes, compare it against baseline algorithms, and assess the robustness of the generated solutions.

Data characteristics and validation

Analysis of the preprocessed data revealed important relationships between key agricultural variables.

Data distribution and correlation analysis: To understand the underlying characteristics of the key economic variables used in the model, a comprehensive pair-plot analysis was conducted (Fig. 7). The diagonal panels display the histogram distribution for each primary variable: Yield (ton/mu), Planting Cost (CNY/mu), and Selling Price (CNY/ton). The off-diagonal panels present scatter plots that visualize the bivariate relationships between each pair of variables.

This integrated visualization reveals several key insights. A moderate positive correlation can be observed between higher yields and increased planting costs, an agronomically intuitive relationship reflecting that greater inputs are typically required for higher productivity. Conversely, the relationship between yield and selling price appears weak and widely dispersed, highlighting the complex market dynamics that our optimization model must navigate. This figure provides a clear view of the foundational data characteristics before evaluating the model’s performance.

Fig. 7

Pair-plot of key economic variables. The diagonal plots show the histogram distribution for each variable, while the off-diagonal plots show the scatter-plot relationship between pairs of variables. This provides a comprehensive view of both the individual data distributions and their bivariate correlations.

Parameter sensitivity: The influence of terrain and climate parameters on economic outcomes was assessed via sensitivity analysis, visualized using a Sankey diagram (Fig. 8). This analysis quantified critical nonlinear interactions: slope variations explained 42% of water loss volatility ($R^2=0.42$), altitude-driven growing season changes accounted for 48% of yield fluctuations, and precipitation patterns determined 56% of irrigation efficiency variance. These $R^2$ values were derived from separate univariate regression analyses performed on the aggregated simulation dataset, where each respective environmental factor (e.g., slope variation) was treated as the independent variable and the corresponding agricultural outcome (e.g., water loss volatility) as the dependent variable. These findings underscore the model’s capacity to capture the cascading impacts of environmental factors, providing a basis for adaptive optimization.

Fig. 8

Parameter sensitivity analysis using a Sankey diagram, visualizing the influence of terrain and climate parameters on agricultural economic outcomes.

H-SAGA optimization performance and outcomes

The H-SAGA algorithm was applied to optimize the planting strategy based on the defined objectives and constraints.

Convergence behavior: The iterative optimization process of H-SAGA was compared against standard Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO). Figure 9 shows the convergence curves, illustrating the fitness value improvement over iterations. H-SAGA achieved a stable and superior fitness value after approximately 460 iterations, demonstrating faster convergence and higher precision compared to PSO and ACO under the tested conditions.

Fig. 9

Model Iteration Process: Comparison of convergence behavior between H-SAGA, PSO, and ACO.

Optimized parameters and model fit: The overall optimization framework relies on an empirical model (Eq. 2) for predicting per-unit-area yield $Y_{ij}$, which is a critical component in the revenue calculation within the objective function. The coefficients ($p_1$ to $p_7$) of this empirical yield model were determined by fitting the model to historical and experimental data. These determined coefficient values are presented in Table 3. The effectiveness of the empirical model, utilizing these specific coefficients, in capturing the relationship between various input factors and observed yield outcomes was then evaluated. Figure 10 presents the model fitting curve, showing a close alignment between the model’s predicted values (red line) and the actual observed values (blue line). Quantitative metrics further confirmed the goodness of fit (Table 4), with a high Coefficient of Determination ($R^2 = 0.828$) and Correlation Coefficient ($R = 0.91$). This indicates that the calibrated empirical model effectively explains a significant portion of the variance in the observed data, thereby providing a reliable basis for the H-SAGA’s planting decisions.

Table 3 Determined coefficients for the empirical yield model (Eq. 2) and their interpretations. All yield-related coefficients are in units of tons per mu.

Fig. 10

The fitting effect of the yield per unit area predicted by the empirical yield model (red line) and the actual observed yield per unit area (blue line).

Table 4 Quantitative metrics for model Fit assessment.

Optimized planting strategy and rationale: The optimization process culminates in a detailed planting strategy that tailors crop selection to the specific characteristics of each of the 34 plots. Figure 11 visualizes the optimized yield distribution as a clustered heatmap, revealing distinct patterns of land-use suitability. The vertical dendrogram clusters plots with similar yield potentials, while the horizontal dendrogram groups crops with comparable performance across the landscape. Notably, a distinct cluster of plots (from Plot 2 to Plot 12) demonstrates particularly high suitability for Heirloom Tomato and High-yield Corn. This suggests these plots possess superior soil quality, water access, or other favorable conditions. Conversely, most other plots are allocated to a diversified mix of crops like Drought-resistant wheat and Sweet Sorghum, which exhibit moderate but stable yields (indicated by the dark blue and gray cells) across a wider range of land types. This spatial differentiation is a key outcome of the optimization, ensuring that land use intensity is matched with land capability to maximize overall profitability within a single planning horizon.

Figure 12 complements the spatial plan by projecting the total yield composition for the eight primary optimized crops from 2025 to 2030. These multi-panel bar charts illustrate the model’s dynamic, year-on-year adjustments to the planting portfolio in response to fluctuating market and climate forecasts. For instance, in 2025 and 2026, Drought-resistant Wheat and Green Soybean are projected to have the highest yields, likely reflecting a strategy to ensure stable staple production under anticipated resource constraints. In contrast, by 2030, a more balanced portfolio emerges, with significant yields from High-yield Corn and Winter Rapeseed, indicating a shift towards higher-value crops as conditions permit. This temporal variation underscores the adaptive nature of the H-SAGA framework, which does not generate a static, multi-year rotation but rather a responsive strategy that re-optimizes the crop mix annually to maintain both high productivity and economic resilience.

Fig. 11

Clustered heatmap of optimized yield (ton) per crop and plot. This visualization illustrates the optimal spatial allocation strategy for a single representative planning cycle (i.e., one year), based on land-use suitability. It is a snapshot of an annual decision, not a static multi-year rotation plan.

To provide a more granular view of the decision-making output, Table 5 presents a sample of the optimized area allocation ($x_{ij}$, in mu) for two representative plots identified from the heatmap analysis: Plot 5, a high-potential plot primarily dedicated to a high-value cash crop, and Plot 21, a plot managed with a diversified strategy to balance risk and resource use. This detailed breakdown of the core decision variables demonstrates how the H-SAGA model translates its optimization logic into a concrete and actionable planting scheme at the individual plot level. The total allocated area for each plot respects its physical land constraint ($A_i$).

Table 5 Sample of optimized planting area allocation ($x_{ij}$) for representative plots.

Fig. 12

Projected crop yield composition from the optimized planting strategy (2025-2030), illustrating the stability of the production mix.

Dynamic adaptation in multi-stage optimization: To further illustrate the dynamic adaptability of the H-SAGA framework in multi-stage decision-making, a specific simulation scenario was examined. In an initial stage of the simulation (e.g., early in the planting season), based on prevailing average market prices and climate outlooks, the model might allocate Plot A to cash crop X (e.g., a high-value vegetable). However, upon entering a subsequent stage (e.g., mid-season), should one of the following situations arise: (1) new market intelligence indicates a significant drop in the forecasted price of crop X due to predicted oversupply; or (2) the latest mid-term weather forecast suggests a high probability of severe drought in the coming weeks, drastically increasing the water demand or reducing the expected yield of crop X. In such cases, the ’monitoring’ module captures these changes. The neural network within the ’modeling’ module then adjusts its revenue predictions for crop X across various plots based on this updated information. Consequently, the H-SAGA algorithm re-optimizes under a revised fitness function that reflects these updated revenue expectations and potential resource constraints. As a result, in the new ’decision’ phase, Plot A might be reallocated to an alternative crop Y (e.g., a specific herb or a type of pulse) that is more drought-tolerant and currently offers better expected economic returns. This ability to adjust planting plans based on stage-wise feedback is a core strength of the multi-stage optimization framework, significantly enhancing the resilience of agricultural production to market and environmental uncertainties.

Comparative performance analysis

To evaluate the performance of H-SAGA, it was benchmarked against several baseline algorithms, including Genetic Algorithm (GA), Simulated Annealing (SA), Particle Swarm Optimization (PSO), and Ant Colony Optimization (ACO). The performance evaluation was conducted using multiple key performance indicators (KPIs) under different simulated climatic conditions.

Climate scenario definition: To test the robustness of the algorithms under varying environmental pressures, we defined three representative climate scenarios based on historical meteorological data from the study region over the past decade (2013-2022):

• Drought scenario: Simulates a year where the total precipitation during the growing season falls within the lowest 15th percentile of historical data, accompanied by an average temperature increase of 0.5-1.0$^{\circ }$C. This scenario represents severe water stress conditions.

• Normal scenario: All climatic parameters (precipitation, temperature) are set to their historical median values, representing an average or most typical year.

• Abundant water scenario: Simulates a year where the total precipitation is at the 85th percentile of historical data, representing relatively plentiful water resources.

In each scenario, these climate parameters were used as inputs for the yield prediction model (Eq. 2), thereby influencing the final optimization objective value.

Overall evaluation metrics: A comprehensive comparison using metrics such as Sum of Squared Errors (SSE), Coefficient of Determination ($R^2$), Profit Increment Ratio, and Robustness is presented in Fig. 13. The Profit Increment Ratio was calculated for each optimization algorithm by comparing its achieved profit against a defined reference baseline. This baseline represented the average profit obtained from simulating conventional farming practices within the study area, based on historical cropping patterns and average yields recorded from 2020–2022. The ratio is expressed as $((\text {Profit}_{\text {optimized}} - \text {Profit}_{\text {baseline}}) / |\text {Profit}_{\text {baseline}}|) \times 100\%$, serving as a key indicator of economic performance enhancement.

H-SAGA outperformed the baseline algorithms across most metrics, indicating superior optimization effectiveness and stability. Notably, the Profit Increment Ratio achieved by H-SAGA (approximately 14.5%) was significantly higher than that of other tested algorithms (e.g., GA: approx. 8%; SA: approx. 6%; PSO: approx. 5%; ACO: approx. 7.5%), as detailed with specific numerical annotations in Fig. 14. This represents an improvement of approximately 5 to 9.5 percentage points in profit increment ratios when H-SAGA is compared against these algorithmic benchmarks, highlighting the practical benefit of the H-SAGA approach in enhancing potential revenue from agricultural operations.

To statistically substantiate these observed performance differences, a one-way Analysis of Variance (ANOVA) was conducted on the profit increment ratios produced by each algorithm (H-SAGA, GA, SA, PSO, ACO) across the different simulated climate scenarios. The ANOVA results revealed a statistically significant difference in the mean profit increment ratios among the algorithms (F(4, 25) = 15.62, p < 0.001). To further identify specific inter-group differences, a Tukey’s Honestly Significant Difference (HSD) post-hoc test was performed. The post-hoc analysis confirmed that the profit increment ratio from H-SAGA was significantly higher than that of all four baseline algorithms: GA (p = 0.008), SA (p = 0.002), PSO (p < 0.001), and ACO (p = 0.004). This statistical evidence robustly supports the conclusion that the superior performance of H-SAGA is not an artifact of random variation but represents a significant and reliable advantage for enhancing agricultural profitability under the tested conditions.

Fig. 13

Comparison of overall evaluation metrics (SSE, $R^2$, profit increment, robustness) across algorithms.

Fig. 14

Profit increase ratio comparison with numerical annotations, highlighting H-SAGA’s advantage.

Performance across diverse terrain types

To further enhance the mountain-specific insights of this study, the optimization effects of the H-SAGA model were quantified across different dominant terrain types within the study area: flat fields, terraced fields, and sloped fields. Each of the 34 plots was categorized based on its primary topographical characteristics. Key performance indicators, including the Profit Increment Ratio and a composite Resource Use Efficiency Index (RUEI), were aggregated for each category. The RUEI is a normalized metric ($0-1$ scale) representing the economic output per unit of key inputs (water and capital), providing a standardized measure of resource productivity.

The results, summarized in Table 6, reveal that the H-SAGA framework delivers significant benefits across all terrain types, albeit with notable variations. Terraced fields exhibited the highest profit increment ratio (16.2%) and RUEI (0.91), which can be attributed to their superior water retention and soil conservation properties, allowing the optimized resource allocation strategy to achieve maximum effect. Conversely, while sloped fields saw a substantial profit increase (11.5%), their lower RUEI (0.76) highlights the inherent challenges in managing resources on such terrain. These findings quantitatively validate the model’s capability to generate tailored strategies that effectively leverage topographical advantages and mitigate disadvantages, reinforcing its practical value for complex mountain agricultural systems.

Table 6 Quantified optimization Effects of H-SAGA across different terrain types.

Robustness and uncertainty analysis

To assess the reliability of the H-SAGA-derived solutions under real-world variability, a multi-scenario robustness analysis³² and Monte Carlo simulations were performed^33,34.

Multi-scenario testing: The sensitivity of the optimal solution was tested against fluctuations in market prices, input costs, precipitation levels, and inherent yield variability. Table 7 summarizes the results, showing the percentage change in the objective function (Fitness Change Rate) and the stability of the top-ranked planting choices (Ranking Stability) under various perturbation scenarios. The Fitness Change Rate was calculated as $((\text {Fitness}_{\text {perturbed}} - \text {Fitness}_{\text {baseline}}) / |\text {Fitness}_{\text {baseline}}|) \times 100\%$, where $\text {Fitness}_{\text {baseline}}$ is the objective function value of the H-SAGA solution under nominal (unperturbed) conditions. Ranking Stability was assessed by considering the top 10 crop-plot allocation decisions, ranked by their contribution to the total profit in the baseline H-SAGA solution. It was then calculated as the percentage of these top 10 decisions that remained within the top 10 ranked decisions in the solution obtained under the perturbed scenario. The results indicate high resilience; for example, $\pm 30\%$ price fluctuations or $\pm 40\%$ precipitation variations resulted in less than 8% and 12% fitness change, respectively, with ranking stability remaining above 85%. Even combined shocks showed contained impacts, suggesting the H-SAGA solutions provide reliable guidance in dynamic environments.

Table 7 Multi-scenario robustness test matrix for H-SAGA model performance under uncertainty. Fitness change rate measures the percentage deviation of the objective function value from the baseline. Ranking stability measures the consistency of the top-ranked solutions compared to the baseline.

Monte Carlo simulation for climate risk: To further probe robustness against extreme climate events, a Monte Carlo simulation (10,000 runs) was conducted, incorporating variations in temperature and precipitation based on historical extreme value distributions^35,36. Figure 15 visualizes the distribution of simulated outcomes (profitability relative to the same baseline scenario used for calculating the Profit Increment Ratio in Section "Comparative performance analysis") under these conditions. The analysis estimated the probability of the optimized solution failing to meet a minimum profitability threshold (defined as achieving at least 80% of the expected revenue under baseline conditions). The low density of failure points (red dots in Fig. 15), constituting approximately 2.5% of the 10,000 simulation runs, suggests the strategy is generally robust even when considering tail risks associated with climatic extremes.

Fig. 15

Monte Carlo risk cloud map (10,000 runs) showing simulated revenue outcomes under varying climate conditions. Blue points meet the profitability threshold ($\ge$ 80% baseline); red points fall below. The overall estimated failure probability is low.

In summary, the experimental results demonstrate the effectiveness, efficiency, and robustness of the H-SAGA approach for optimizing agricultural planting strategies in complex, resource-constrained environments. The model yields well-fitting predictions, outperforms baseline algorithms in convergence and profitability, and generates solutions resilient to significant market and environmental uncertainties.

Discussion

This section discusses the key findings of the study, focusing on the strengths and advantages of the proposed multi-stage optimization model and the H-SAGA algorithm, acknowledging its limitations and suggesting future research directions, and highlighting the practical implications of the results for agricultural planning.

Strengths and advantages of the proposed model

The research introduces a robust framework for optimizing agricultural planting strategies, particularly tailored for complex environments like mountainous regions. A primary strength lies in the multi-stage optimization model structure. Unlike static, single-period approaches, this framework allows for sequential decision-making across different time intervals. This inherently captures the dynamic nature of agriculture, enabling adjustments based on evolving market prices, resource availability, and climatic conditions³⁷. The multi-stage approach enhances risk mitigation, crucial in variable terrains where factors like slope, altitude, and precipitation significantly impact cultivation. The model explicitly incorporates these geographical and climatic considerations. For instance, the interplay between soil characteristics (represented via the Soil Quality Index, $\text {SQI}_i$) and water availability (via the $\text {WaterAvail}_{ij}$ term) within the empirical yield model (Eq. 2) implicitly addresses key aspects of water-soil coupling, thereby lending the framework greater realism and practical applicability in reflecting site-specific production potentials^38,39.

The proposed framework effectively instantiates the “Monitoring-Modeling-Decision” paradigm for dynamic agricultural management. Specifically, at the commencement of each optimization stage, the system first ‘monitors‘ the latest environmental data (e.g., updated climate forecasts, soil moisture sensor readings) and market information (e.g., price fluctuations). These real-time data are then fed into the ‘modeling‘ component: the neural network utilizes this new information to update crop revenue predictions, which in turn adjusts the fitness function of the H-SAGA algorithm. Finally, H-SAGA optimizes based on this updated context to output the ‘decision‘ for the current stage—the optimal planting scheme. The outcomes of implementing this scheme (such as expected resource consumption and crop growth status) subsequently serve as partial inputs for the ‘monitoring‘ phase of the next stage, forming a continuous learning and adaptation loop. This iterative, multi-stage optimization process ensures that agricultural planning can dynamically respond to environmental and market changes, thereby enhancing the robustness and economic efficiency of the overall strategy.

The optimization engine, the Hybrid Simulated Annealing Genetic Algorithm (H-SAGA), represents another significant advantage. By synergizing the global exploration capability of Simulated Annealing (SA)¹⁷ with the local refinement strength of Genetic Algorithms (GA)⁴⁰, H-SAGA effectively navigates the complex, potentially multimodal search space characteristic of agricultural optimization problems. This hybrid approach overcomes the limitations of traditional methods prone to local optima and the potential stagnation of standalone GA or SA. Experimental results confirm H-SAGA’s superiority over conventional algorithms like GA, SA, PSO, and ACO, demonstrating faster convergence (Fig. 9), better stability across different simulated climatic conditions, and superior performance in key metrics like convergence speed, constraint handling, and robustness as visualized in the Innovation Dimension Radar Chart (Fig. 16).

Fig. 16

Innovation dimension radar chart illustrating the comparative strengths of H-SAGA in various performance aspects such as convergence speed, constraint handling, and robustness.

Furthermore, the integration of a three-layer feedforward neural network enhances the model’s predictive power and adaptability. By leveraging historical data to forecast revenues (Fig. 4) and dynamically updating the fitness function (Eq. 5), the model becomes more responsive to real-time market fluctuations and climatic variability. This integration contributes to the precision and timeliness of the generated planting strategies. The model’s effectiveness is empirically validated by the strong fit between predicted and observed values (Fig. 10, Table 4), achieving an $R^2$ of 0.828 and a correlation coefficient (R) of 0.91. The demonstrated robustness in the multi-scenario analysis (Table 7, Fig. 15) further underscores the reliability of the H-SAGA framework under uncertainty. Furthermore, the experimental results presented in Section 3 (see Fig. 14) have substantiated H-SAGA’s competitive computational efficiency relative to standard algorithms, alongside its superior capability in enhancing final revenues, underscoring its practical advantages in real-world application scenarios.

Limitations and future research directions

Despite the promising results, the current model possesses certain limitations that offer avenues for future research. Firstly, the model currently relies on certain simplifying assumptions, such as constant market prices and stable conditions *within* each stage, and does not explicitly incorporate the long-term effects of crop rotation on soil health and regeneration over multiple years. While the multi-stage approach allows for updates between stages, intra-stage dynamics and cumulative soil effects are areas for potential refinement.

Secondly, the model does not currently account for local agricultural policies, subsidies, or incentive programs, which can significantly influence farmers’ decisions and overall profitability. Integrating these socio-economic factors could enhance the model’s practical relevance for specific regional planning contexts.

Thirdly, while the integrated neural network improves revenue prediction, its efficacy is inherently dependent on the quality and quantity of historical data. This reliance might limit its ability to accurately anticipate unprecedented market shocks or extreme climatic events.

Future research should focus on addressing these limitations. Incorporating more sophisticated time-series forecasting techniques, such as Long Short-Term Memory (LSTM) networks⁴¹, could improve the prediction of seasonal anomalies and market dynamics. Expanding the model to a multi-objective optimization framework—which allows for the simultaneous consideration of conflicting goals, such as maximizing profit while minimizing water usage or carbon emissions—could provide more holistic and sustainable solutions⁴². Exploring dynamic programming techniques could better capture long-term dependencies⁴³. Additionally, explicitly modeling soil nutrient dynamics over extended horizons would increase the model’s ecological validity⁴⁴. Finally, integrating region-specific policy constraints would further solidify the model’s utility as a practical decision-support tool.

Practical implications and applications

The findings of this study have significant practical implications for agricultural planning and management, especially in resource-constrained and environmentally variable regions like the mountainous area studied in North China. The developed multi-stage H-SAGA model provides a powerful analytical tool for farmers, agricultural cooperatives, and regional planners to optimize crop selection and land allocation decisions.

The model’s ability to integrate diverse factors—including geographical constraints (plot area, type), climatic variables (precipitation, temperature implicitly via yield functions), market conditions (prices, demand), resource limitations (water, budget), and agronomic factors (crop complementarity/substitutability)—allows for the generation of holistic and context-specific planting strategies (visualized in Fig. 11 and Fig. 12). This leads to more efficient utilization of land and resources, potentially increasing overall farm profitability, as suggested by the profit increment comparisons (Fig. 13, Fig. 14).

A key practical benefit is the model’s demonstrated robustness. The uncertainty quantification and robustness analysis (Section "Robustness and uncertainty analysis", Table 7, Fig. 15) show that the solutions generated by H-SAGA maintain reasonable performance even under significant fluctuations in market prices and climate variables. This resilience provides decision-makers with greater confidence in the recommended strategies, facilitating better risk management in the face of inherent agricultural uncertainties.

The framework can aid in strategic decision-making aimed at enhancing food security and increasing farmer income in challenging environments. By optimizing planting schemes, the model helps ensure stable production levels and maximizes economic returns from available land. Furthermore, the model’s structure is adaptable; while demonstrated in a specific North China context, it can be calibrated and applied to other regions by incorporating local plot characteristics, climate data, crop types, and market specifics, thereby enhancing planting efficacy and profitability elsewhere. The potential inclusion of environmental objectives in future work could further position this tool to support the transition towards more sustainable agricultural practices^45,46,47.

Furthermore, while the primary objective of the H-SAGA model developed in this study is to maximize agricultural economic revenue, its inherent capability in optimizing resource allocation also offers potential for advancing sustainable agricultural practices. By precisely planning crop layouts and the use of resources such as water and land, the model contributes to reducing waste and enhancing utilization efficiency, thereby indirectly alleviating the environmental pressures associated with agricultural activities. For instance, avoiding excessive inputs on unsuitable land or the cultivation of crops with high water demands in water-scarce areas can promote the conservation of soil and water resources. Although the current model does not incorporate long-term soil health effects or detailed ecological indicators as direct optimization objectives, its refined resource management outcomes lay a foundation for future integration of more comprehensive sustainability goals, such as minimizing water footprints, carbon emissions, or maximizing biodiversity. As outlined in the future research directions, extending the model to a multi-objective optimization framework would allow for a more explicit balancing of economic benefits and environmental protection, thus providing more holistic decision support for the sustainable intensification of agriculture.

Ultimately, this research contributes a valuable decision-support system that bridges advanced optimization techniques with the practical complexities of modern agriculture.

Conclusion

This research addressed the complex challenge of optimizing agricultural planting strategies, particularly within the constraints characteristic of mountainous regions, by developing and evaluating a sophisticated multi-stage optimization framework.

Research summary: The core of this study involved formulating a multi-stage optimization model designed to maximize crop cultivation revenue while adhering to geographical, climatic, resource, market demand, and crop interaction constraints. To solve this complex, potentially non-linear optimization problem, we proposed and implemented a Hybrid Simulated Annealing Genetic Algorithm (H-SAGA). This algorithm synergizes the global exploration strength of Simulated Annealing (SA) with the local refinement capabilities of Genetic Algorithms (GA). Furthermore, a feedforward neural network (NN) was integrated into the H-SAGA framework to provide dynamic, data-driven predictions of revenue based on historical data and evolving conditions, thereby enhancing the adaptability and accuracy of the optimization process. Extensive experiments, utilizing data from North China mountainous areas and national statistics, validated the model. Comparisons against baseline algorithms (GA, SA, PSO, ACO) under various simulated climatic conditions demonstrated the superior performance of H-SAGA in terms of convergence speed, solution quality (profitability), and robustness. The results, including sensitivity analyses and uncertainty quantification (Section "Robustness and uncertainty analysis"), confirmed the model’s ability to generate effective and resilient planting schemes.

Innovations and contributions:The primary contributions of this work lie in several key areas. Firstly, the development of a multi-stage optimization model specifically tailored for agricultural planning, capable of handling sequential decision-making under evolving conditions. Secondly, the introduction and successful application of the Hybrid Simulated Annealing Genetic Algorithm (H-SAGA) to this domain, demonstrating its effectiveness in navigating complex, multi-modal search spaces characteristic of agricultural optimization problems, outperforming traditional metaheuristics (as shown in Fig. 16). Thirdly, the novel integration of a predictive neural network directly within the optimization loop, allowing the fitness function to dynamically adapt to predicted market and yield fluctuations, thus improving the practical relevance and timeliness of the generated solutions. Finally, the rigorous validation through multi-scenario robustness testing (Table 7) and parameter sensitivity analysis (Fig. 8) provides quantitative evidence of the model’s resilience and its capacity to capture complex environmental interactions, offering a valuable decision-support tool for stakeholders in challenging agricultural environments. The demonstrated improvements in profit increment ratios (Fig. 14) further underscore the practical value of the proposed approach.

Future research directions: While the H-SAGA model demonstrates significant promise, several avenues for future research could enhance its scope and applicability. The current model primarily focuses on single-season optimization and does not explicitly incorporate the long-term effects of crop rotation on soil health and regeneration; integrating multi-year soil dynamics could lead to more sustainable strategies. The reliance on existing regression techniques, even within the NN, might be further improved by exploring more advanced time-series forecasting methods, such as Long Short-Term Memory (LSTM) networks, to better capture complex seasonal anomalies and market volatility. Expanding the optimization framework to a multi-objective context is another pertinent direction, allowing for the simultaneous consideration of economic goals alongside environmental metrics, such as water footprint, carbon emissions, or biodiversity indices. Incorporating socio-economic factors, including local policy incentives, labor availability, or risk aversion profiles of farmers, could also increase the model’s practical utility. Refining the handling of non-linear relationships and constraints, perhaps through dynamic programming elements or more sophisticated constraint-handling techniques within the H-SAGA, could further improve solution precision. Adapting and validating the model for different geographical regions and agricultural systems would also be valuable, potentially contributing to broader goals of climate resilience and sustainable intensification in agriculture globally.