Introduction

In recent years, advances in remote sensing technology have significantly enhanced our ability to monitor surface conditions and changes, thereby supporting environmental conservation and promoting harmonious co-existence between humans and nature. The widespread application of change detection (CD) techniques has proven to be particularly valuable in disaster prevention, mitigation, and relief efforts. These techniques allow for the assessment of disaster impacts through the analysis of changes in monitored areas, providing crucial support for disaster management and prevention strategies. Therefore, the study of change detection using remote sensing images is of paramount importance in current research.

In the initial phase of CD, traditional methodologies are primarily employed, which can be broadly categorized into algebraic methods1, feature-based methods2, and post-classification comparison methods3. Algebraic methods are known for their simplicity and ease of operation, which provide quick response to changes. Feature-based methods involve the selection of multiple image features, followed by their transformation and fusion to achieve change detection. Unlike the aforementioned approaches, post-classification comparison methods not only detect changes within a specific region but also classify these changes.

Although the above-mentioned traditional CD algorithms have significantly contributed to the advancement of CD tasks and demonstrated remarkable performance, the continuous development of artificial intelligence4,5,6 and deep learning has shifted the focus towards employing deep learning techniques for change detection. The powerful feature extraction capabilities of deep neural networks have substantial potential to improve the overall performance of these tasks.

To extract richer deep features and improve the robustness and generalization capabilities of CD networks, numerous researchers have developed deep learning-based CD networks for various tasks, achieving commendable results. However, these methods, whether based on fully convolutional networks, Siamese networks, or GAN-based CD networks, have certain limitations: (1) Fully convolutional networks with symmetric structures7,8,9,10,11,12 employ diverse feature fusion strategies to enhance information extraction. For example, references7,9 utilized simple skip connection mechanisms on intermediate features, while references8,13 applied various attention mechanisms to fuse deep feature maps and change maps. Despite these achievements, the reliance on simplistic fusion methods limits their ability to capture fine-grained changes and may introduce noise; (2) Siamese CD networks based on UNet aim to enhance network performance through various supervision methods. For example, studies14,15,16 employed contrastive learning to supervise the final output. Although these methods achieved satisfactory results, they neglected effective supervision of intermediate features, leading to a loss of valuable information; (3) References17,18,19 demonstrated good network performance by integrating GANs. However, these methods struggle to model the interdependencies among feature pairs, which is crucial for generating more detailed change maps. Therefore, effective extraction and fusion of features at different time points and proper constraint of these features remain significant challenges in CD tasks.

In response to the limitations of previous research, we propose a novel model to monitor regional changes, termed the Siamese Network Based on Information Interaction and Fusion for Change Detection (SNIIF-Net). SNIIF-Net introduces a Feature Information Interaction Module (FIIM), which leverages a spatial attention mechanism to enhance the semantic information of features. Additionally, a Feature Pair Fusion Module (FPFM) is employed to capture semantic relationships between feature pairs. The FPFM fully utilizes spatial information to obtain richer detail and enhance the edge information of images, thereby improving model performance. Furthermore, we developed a Multi-Scale Supervision Method (MSSM) based on contrastive learning to refine feature pairs obtained from multiple decoder stages. Experimental results and ablation analysis on two benchmark datasets demonstrate that these modules enable SNIIF-Net to achieve state-of-the-art performance.

Our primary contributions are fourfold:

  • We propose a Feature Information Interaction Module (FIIM) that enhances the semantic richness of the features. By integrating this module at each stage, our network captures more comprehensive information.

  • Unlike other methods that merely concatenate or perform sub-operations, we employ a Feature Pair Fusion Module (FPFM) to effectively model semantic relationships between feature pairs. This module enhances edge information and fully leverages the spatial details of the input image pairs to obtain richer detail information.

  • We also introduce a Multi-Scale Supervision Method (MSSM) based on contrastive learning to constrain the feature pairs obtained from the multiple decoder stage. This approach allows unchanged pixel pairs to approach each other in feature spaces at multiple scales, while changing pixel pairs move away from each other, resulting in a more refined change map.

  • Extensive experiments are conducted to demonstrate the effectiveness of our proposed SNIIF-Net and its constituent modules.

Related Works

  • Feature Enhancement and Fusion

The integration of deep convolutional networks with feature fusion techniques20,21,22 has significantly improved the accuracy and robustness of remote sensing CD tasks. Effective fusion of multi-scale features is critical for CD. Zhang et al.23 proposed the BiFA network, which utilizes a dual temporal interaction module for channel-level alignment and combines the adaptive difference flow field module to alleviate spatial misregistration issues caused by changes in perspective. However, this method is sensitive to noise and does not fully exploit the hierarchical differences in multi-scale features. To further optimize the interaction efficiency of multi-scale features, Liu et al.24 proposed the ExNet, which aligns feature distributions using dynamic low-pass filters and strengthens frequency domain features through frequency division enhancement modules, significantly improving detection robustness in complex scenes. However, its model training requires complex hyperparameter tuning, limiting its generalization capabilities. Wang et al.25 proposed the MSGFNet, which is based on Siamese EfficientNetB4 to extract dual-temporal features and dynamically weight different scales of boundary detail features through the multi-scale gated fusion module, significantly improving the CD accuracy for small objects. In addition, methods based on attention mechanisms also enhance the feature information. Noman et al.26 further designed the ELGC-Net, which captures global and local context information through a pooling-transpose attention mechanism and deep convolution, enhancing noise robustness with multi-scale pooling, although its complex feature fusion process limits real-time performance. With the introduction of the UNet and residual connections, the representation ability of multi-scale features has been enhanced. Huang et al.27 designed the MFCF-Net, which uses an encoder to extract features of the adjacent layer and combines dense skip connections and cross-attention mechanisms to fuse global spatial information, effectively alleviating false detection caused by changes in lighting, but its performance is limited by the dependence on annotated data in imbalanced sample scenarios. Ren et al.28 designed a DAGMSANet, which aggregates adjacent scale semantic information during the encoder stage and combines spatial and channel attention to suppress background noise during the decoder stage, performing excellently in imbalanced sample scenes, although at a significant computational cost. Although the above methods have achieved good results, they have insufficient utilization of multi-scale semantic information in the decoder stage and rely on simple feature subtraction operations (such as subtraction), which collectively limit further performance improvement.

  • Distance Metric Learning

In change detection tasks, adopting appropriate distance measurement methods to assess feature information is crucial for evaluating the effectiveness of change detection algorithms. Most algorithms rely on Cross-Entropy Loss or content loss to constrain change maps. Distance metric learning is employed to evaluate the algorithm’s performance by assigning larger values to changing pixel pairs and smaller values to unchanged pixel pairs. Reference29 introduces a distance metric learning method based on contrastive learning, with the aim of reducing the emphasis on invariant feature pairs while increasing the focus on changing ones. Similarly, Reference13 proposes a weighted contrastive learning method to train a twin convolutional network that takes advantage of the distance between feature vectors to detect changes between image pairs, leading to improved results. Reference15 presents a threshold-based contrastive loss method to calculate changes between feature pairs, effectively minimizing the distance between invariant pairs and maximizing the distance between changing pairs. All these methods adopt the contrastive learning constraint approach proposed in Reference29 to learn distance measurement for change features, improving the detection accuracy. In our work, we also employ contrastive learning-based measurement methods to constrain change feature pairs at different scales, thereby improving network performance. Although the above methods improve network performance through specific constraint strategies, they did not apply distance metric constraints based on contrastive learning to different scale feature maps generated by the decoder. Therefore, the model still has room for improvement in fully utilizing multi-scale feature information.

Method

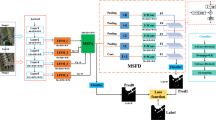
To enhance the use of remote sensing images in monitoring natural disasters and modeling regional changes induced by such events, in this section, we introduce a Siamese Change Detection Network (SNIIF-Net) based on information exchange and fusion. SNIIF-Net is a symmetrically structured network that shares weight parameters and is primarily designed to detect geological and geomorphic changes by analyzing input image pairs. The overall architecture of the proposed SNIIF-Net is illustrated in Fig. 1.

Fig. 1
figure 1

Overall structure of Siamese network based on information interaction and fusion for change detection. The input images \(I_{1}\) and \(I_{2}\) are sourced from the LEVIR-CD dataset30.

Full size image

Overview

As illustrated in Fig. 1, the SNIIF-Net architecture processes a pair of remote sensing images taken at different times, denoted as \(I_{1}\), \(I_{2}\). These images are initially input into a Siamese convolutional neural network (CNN) to extract the features of remote sensing image feature pairs, represented as \(x_{1}\) and \(x_{2}\). Subsequently, the feature pairs are fed into a symmetric encoder-decoder network that utilizes three encoding stages. Each encoding stage employs two convolutional layers (3\(\times\)3 kernels, stride 1) followed by 2\(\times\)2 max pooling (stride 2), reducing spatial dimensions to (h/2, w/2), (h/4, w/4), and (h/8, w/8), where w and h denote the width and height of the feature map, respectively. In the decoding stage, SNIIF-Net refines feature extraction from different scales using the Feature Information Interaction Module (FIIM), which is based on a spatial attention mechanism to enhance the semantic information of the features. To achieve more precise change features, SNIIF-Net employs the Feature Pair Fusion Module (FPFM) to further process the feature pairs. Additionally, SNIIF-Net integrates residual connections to merge features of various scales, thereby mitigating information loss that may occur during decoding. Finally, SNIIF-Net implements contrastive learning to effectively constrain features of different scales in the decoding stage, thereby enhancing the performance of the change detection network.

Feature information interaction module

The use of multiple downsampling operations in the encoding stage of SNIIF-Net inevitably leads to some information loss, which may impact the accuracy of the final change detection. To mitigate the loss of important information, SNIIF-Net incorporates feature information interaction modules (FIIM) in both symmetric networks. The FIIM module draws inspiration from the Position Attention Module (PAM) in DANet31. While both model spatial dependencies via attention maps, FIIM adapts PAM for change detection by (1) independently processing bi-temporal input features, and (2) integrating residual connections to preserve original features. This module leverages attention mechanisms for feature enhancement, mitigates information loss and can refine change region delineation.

Fig. 2
figure 2

The structure figure of feature information interaction module.

Full size image

The network structure of the Feature Information Interaction Module (FIIM) is illustrated in Fig. 2. As depicted, the FIIM module first applies a transpose operation to the input feature f. Here, \(f\in \Re ^{C\times H\times W}\) represents the input feature, where C denotes the number of feature channels, while H and W correspond to the height and width of the feature, respectively. Subsequently, the FIIM multiplies the transposed features (of dimension C\(\times\)H\(\times\)W) by the deformed features in a matrix format, followed by a softmax operation to generate a spatial attention relationship map \(M_{s}\in \Re ^{(H\times W)\times (H\times W)}\). The implementation process can be expressed as the following equation.

$$\begin{aligned} M_s=\frac{\exp (f_i,f_j)}{\sum _{i=1}^N\exp (f_i,f_j)} \end{aligned}$$
(1)

where \(f_{i}\) and \(f_{j}\) denote features at different positions, and N represents the total number of features. This calculation process allows the determination of the degree of correlation between features located at different positions. Specifically, a stronger correlation between two features corresponds to a higher value of \(M_{s}\).

Subsequently, the FIIM module applies the spatial attention relationship map to the transformed features, resulting in features that incorporate spatial correlation information and are processed in a size of C\(\times\)H\(\times\)W. In particular, to mitigate the potential loss of feature information during this process, the FIIM module employs residual connections to merge features containing spatial information with the original input data, thereby enhancing feature extraction. The final output feature \(f_{s}\) of this feature information interaction module can be represented by the following equation:

$$\begin{aligned} f_s=\lambda \sum _{i=1}^NM_sf+f \end{aligned}$$
(2)

where, \(\lambda\) represents the parameter that is automatically optimized by the network. From the above equation, it is evident that the output feature \(f_{s}\) of the feature information interaction module is a weighted sum of the feature information from all positions and the original input feature. Consequently, \(f_{s}\) encompasses rich global contextual information. Furthermore, since the output feature \(f_{s}\) is derived from the spatial attention mechanism, it can adaptively select and aggregate contextual information, model long-term semantic dependencies between features, improve semantic consistency, promote similar semantic features, and ultimately allow SNIIF-Net to more effectively differentiate between changing and unchanged features.

Feature pair fusion module

The effective fusion of bi-temporal features is crucial for change detection tasks utilizing Siamese networks and significantly enhances network performance. Most existing algorithms employ simple subtraction or concatenation methods to refine bi-temporal features. Although these methods can improve the change detection performance to some extent, they often fail to meet high-precision requirements due to spatial position and color shifts in the input images during the feature extraction process. To address this limitation, SNIIF-Net introduces a Feature Pair Fusion Module (FPFM) designed to combine input feature pairs, thus extracting more refined change features. Specifically, the dual-branch design of the FPFM simultaneously captures change magnitude (subtraction branch) and edge consistency (summation branch), with residual connections preserving spatial details. The structure of the FPFM is illustrated in Figure 3.

Fig. 3
figure 3

The structure figure of feature pair fusion module.

Full size image

As illustrated in Fig. 3, the FPFM module comprises two branches (I and II), with branch I serving as the subtraction branch and branch II functioning as the summation branch. The subtraction branch receives two inputs, \(f_{s1}\) and \(f_{s2}\), which are remote sensing image features extracted at different time points and represented as \(f_{s1},f_{s2}\in \Re ^{C\times H\times W}\). Subsequently, three sequential convolution and ReLU operations are performed to further process the input features, utilizing a convolution kernel size of 3\(\times\)3 and a stride of 2. Additionally, to enhance the output features’ information content, the FPFM module employs multiple residual connection operations (red arrows) to fuse the features during the feature extraction stage. For generating fine-change regions, the FPFM module processes the two features by subtracting one from the other. After applying convolution, batch normalization (BN), and ReLU activation, the output feature \(f_{I}\) of branch I is obtained. The above process can be expressed by the following equation.

$$\begin{aligned} f_{I}=F_{1}\left( \left| \left( f_{s 1}^{s u b 1}+f_{s 1}^{s u b 2}+f_{s 1}^{s u b 3}\right) -\left( f_{s 2}^{s u b 1}+f_{s 2}^{s u b 2}+f_{s 2}^{s u b 3}\right) \right| \right) \end{aligned}$$
(3)

where \(F_1\)() represents the operations of convolution, BN and ReLU in the subtraction branch, and \(f_{s i}^{s u b i}\) denotes the features obtained after the i-th convolution and ReLU operations in the subtraction branch, with the input feature \(f_{s i}\).

The summation branch, which runs parallel to branch I, is designed to enhance edge information and mitigate pseudo-change phenomena caused by feature mismatches. Similarly to the subtraction branch, the FPFM module performs a summation operation on the two features after the convolutional layer, resulting in the output feature \(f_{II}\) of the summation branch. The above process can be expressed by the following equation.

$$\begin{aligned} f_{II}=F_{2}((f_{s1}^{sum1}+f_{s1}^{sum2}+f_{s1}^{sum3})+(f_{s2}^{sum1}+f_{s2}^{sum2}+f_{s2}^{sum3})) \end{aligned}$$
(4)

where \(F_2\)() represents the operations of convolution, BN and ReLU in the summation branch, and \(f_{s i}^{s u b i}\) denotes the features obtained after the i-th convolution and ReLU operations in the summation branch, with the input feature \(f_{s i}\).

Finally, the chapter employs vector-wise summation to fuse the output features of the two branches, resulting in the final output \(f_{c}\) of the FPFM module. This feature enables the FPFM fusion module to effectively combine multiple features within each branch, resulting in more refined change features. The primary reasons for this approach are as follows: (1) parallel processing of complementary features (change magnitude + edge consistency), and (2) residual connections that mitigate information loss.

Multi-scale supervision method

As shown in Fig. 1, during the decoder stage, we utilize multi-scale features to model changing regions. Solely employing the FPFM module to capture the change information of feature pairs is insufficient for fine change detection tasks based on pixel segmentation. We define changing regions at the same position in different image pairs as positive samples and unchanged regions at the same position in different image pairs as negative samples. Our objective is to assign distinct distance metrics to different categories to enable effective sample separation. A positive sample should exhibit changes, and we aim for the distance between the changing samples to be maximized. In contrast, negative samples, which remain unchanged, should demonstrate significant similarity, which warrants a very small distance value. This implicit distance measure ensures that the unchanged negative samples are as close as possible while maintaining separation between changing positive samples. Based on this concept, we propose a multi-scale supervision method (MSSM) grounded in contrastive learning to assess the distance between feature pairs across various scales. Specifically, we aim to bring unchanged pixel pairs closer together in feature spaces at multiple scales while simultaneously pushing changing pixel pairs apart.

The input for this module consists of feature pairs \((f_{s1}(i,j),f_{s2}(i,j)\in \mathbb {R}^{C\times H\times W}\), where \(1\le i\le H\) and \(1\le j\le W\). These pairs are processed by the FIIM, with \(f_{s1}(i,j)\) representing the intensity vector at the position (i, j) in the image. We define the distance D between feature pairs using the Euclidean distance, which can be expressed by the following equation:

$$\begin{aligned} D(f_{s1}(i,j)^{m},f_{s2}(i,j)^{m})=\parallel f_{s1}(i,j)^{m}-f_{s2}(i,j)^{m}\parallel _{2},m=1,2 \end{aligned}$$
(5)

where, m denotes the m-th layer feature in the decoder stage, characterized by a feature scale of \(1/2^{4-m}\). The function D(.) represents the distance function that the network must learn. For clarity in subsequent descriptions, we denote the process described in Equation (5) as \(D_{i,j}\).

To enhance the network’s ability to effectively distinguish information in changing regions and accelerate convergence speed, we require that the distance between positive samples exceeds a specified boundary value (\(\theta\)>0). Only when the distance between positive samples is within this range will the changed pixel pairs influence the loss function. This process is represented by the following equation.

$$\begin{aligned} \ell _{_{positive}}=\frac{1}{2}\{max(\theta -D_{_{i,j}})^{2}\} \end{aligned}$$
(6)

For negative samples, we expect the distance between them to be less than a specified boundary value (\(\varepsilon\)>0). Only when the distance between negative samples falls within this range will unchanged pixel pairs influence the loss function. This process can be expressed by the following equation.

$$\begin{aligned} \ell _{negative}=\frac{1}{2}\{max(D_{i,j}-\varepsilon )^{2}\} \end{aligned}$$
(7)

Thus, the loss function of MSSM based on contrastive learning during the decoder stage can be defined as the following equation:

$$\begin{aligned} \ell _{MSSM}=\sum _{m=1}^{M}\sum _{i}^{H}\sum _{j}^{W}\lambda _{1}y_{i,j}^{m}\ell _{positive}^{m}+\lambda _{2}(1-y_{i,j}^{m})\ell _{negative}^{m} \end{aligned}$$
(8)

where, \(y_{i,j}^m\) represents the feature of the true label in the decoder stage layer, which is mapped to the input image pair with dimensions H\(\times\)W. When \(y_{i,j}=0\), it indicates that the corresponding pixel pair has not changed; when \(y_{i,j}=1\), it means that the corresponding pixel pair has changed. The parameters \(\lambda _{1}\) and \(\lambda _{2}\) assign different weights to distinct loss functions, addressing the issue of imbalanced positive and negative samples. Using this calculation method, we can derive more detailed change maps in the feature space by applying the distance between features of varying scales.

Loss functions of SNIIF-Net

To take advantage of additional feature information for improved change detection accuracy, we have designed the following loss functions to constrain SNIIF-Net to specific network architectures:

$$\begin{aligned} \ell _{loss}=\mathcal {\ell }_{change}+\mathcal {\ell }_{MSSM} \end{aligned}$$
(9)

where, \(\ell _{MSSM}\) represents the supervision method of multi-scale contrastive learning, and \(\ell _{change}\) represents the constraint on the final change feature, which can be represented by the following equations:

$$\begin{aligned} \mathcal {\ell }_{change}=\sum _{m=1}^Mloss_m \end{aligned}$$
(10)
$$\begin{aligned} loss=\frac{1}{H\times W}\sum _{h=1,w=1}^{H,W}\ell (softmax(X_{hw}^{change}),Y_{hw}) \end{aligned}$$
(11)

where, \(X_{hw}^{change}\) denotes the change feature at the pixel position (h, w), \(Y_{hw}\) represents the corresponding label and \(\mathcal {\ell }(\cdot )\) indicates the cross-entropy loss function. To enforce the constraint of changing features, we employ a multi-scale training strategy. By applying this constraint to features at various scales during the decoder stage, we can enhance network performance and ultimately extract more detailed change information.

Experiments and results

Datasets

We first performed training and testing on publicly standard datasets, CDD32 and LEVIR-CD30. The CDD dataset is an open and seasonal remote sensing change detection dataset comprising multi-source remote sensing images and 11 pairs of original images. This includes 7 pairs of change images with dimensions of 4725\(\times\)2200 pixels and 4 pairs of change images measuring 1900\(\times\)1000 pixels, with a spatial resolution ranging from 3 to 100 cm. The CDD dataset was processed and divided into a training set of 10,000 samples, a validation set of 3,000 samples, and a testing set of 3,000 samples, each with a pixel size of 256\(\times\)256. The LEVIR-CD dataset consists of image pairs and semantic and change detection labels for buildings captured at the same location in 2012 and 2016, situated in the area affected by a magnitude 6.3 earthquake in Christchurch, New Zealand, in February 2011. The LEVIR-CD dataset includes 637 pairs of high-resolution images (445 pairs for training) with a spatial resolution of 50 cm and a pixel size of 1024\(\times\)1024.

Experimental settings

The experimental hardware environment comprises an Intel\(\textcircled{R}\) \(\hbox {Core}^{TM}\) CPU at 3.50 GHz and an NVIDIA GeForce GTX TITAN X. The operating system is Ubuntu 16.04, and the compilation environment is Python 3.7, with Python 1.7 selected for specific tasks. Regarding experimental details, SNIIF-Net is configured with a parameter value of \(\theta = 1\), \(\varepsilon = 0.1\), weight decay set to 5e-5, an initial learning rate of 1e-4, 2000 epochs, a batch size of 2, and the Adam optimizer for network optimization. We use the F1 score to evaluate network performance.

Comparisons with other methods

To evaluate the effectiveness of SNIIF-Net, we first compare it with several advanced algorithms using the standard CDD dataset. The results of the quantitative comparison are presented in Table 1, while Fig. 4 provides a visual comparison of various algorithms. Among these, FC-EF7 refers to the concatenation of pairs of input bi-temporal images, treating them as different channels of a single image before processing them through the network for feature extraction. The FC-Siam-con7 employs two parallel branches to process the input bi-temporal images, sharing weight parameters between these branches. Subsequently, convolution operations are applied to combine the two output features using a skip connection approach. The FC-siam-diff7 also utilizes a parallel branch structure typical of Siamese networks. However, unlike FC-Siam-con7, it does not directly concatenate the output of the parallel branches; instead, it computes the absolute value difference between the feature maps of the parallel branches before concatenation.

Table 1 Performance comparison with other advanced methods on CDD dataset.
Full size table

Table 1 clearly indicates that: (1) Methods based on UNet and Siamese networks7 often utilize simple structures and skip connection mechanisms to process features, which limits their ability to extract rich semantic information. Furthermore, significant detail is lost during the downsampling process, and ineffective supervision of features during upsampling further affects performance; (2) The \(\text {UNet++\_MSOF}\) network8, which employs deep supervision, first utilizes a fully symmetric convolutional network to extract features from the input image and then introduces a differential discrimination network to detect changes in the output feature pairs. This network also incorporates an attention mechanism to fuse depth features and image difference features at various scales. Although \(\text {UNet++\_MSOF}\) with different numbers of channels (16 and 32, representing the number of output channels) performs better than FC-EF, FC-Siam-conc, and FC-Siam-diff, it still relies on a simple skip connection mechanism to fuse intermediate features, which hampers its ability to capture deep features and effectively reconstruct images. Consequently, the F1 score obtained by \(\text {UNet++\_MSOF}\) is relatively low, at 0.062 (16 channels) and 0.020 (32 channels) below the F1 score of SNIIF-Net; (3) DASNet13, which is based on contrastive learning and a dual attention mechanism, improves network performance through the introduction of contrastive learning methods. However, DASNet only supervises the final output features, lacking constraints on intermediate features. Furthermore, the dual attention mechanism increases the burden of the network to some extent, leading to suboptimal performance, with an F1 score that is 0.044 lower than that of SNIIF-Net; (4) SNUNet-CD16, a Siamese network based on UNet, proposes an integrated channel attention fusion method to process intermediate features, outperforming DASNet. However, its use of simple Focal Loss does not adequately supervise the network, resulting in suboptimal performance; (5) Recent methods34,37,38,40,41,45 have achieved high F1 scores through innovative fusion methods or network structures. However, whether leveraging the global feature extraction capabilities of Transformers, employing feature fusion methods with varying attention mechanisms, or utilizing different design approaches based on UNet, these methods often neglect effective constraints on intermediate features, leading to suboptimal performance.

Fig. 4
figure 4

Visual comparison with some algorithms on CDD dataset. Different colors are employed to enhance clarity: white indicates true positives, black represents true negatives, red denotes false positives, and blue signifies false negatives. The input images \(x_{1}\) and \(x_{2}\) are sourced from the CDD dataset32.

Full size image
Fig. 5
figure 5

Visual comparison with some algorithms on LEVIR-CD dataset. Different colors are employed to enhance clarity: white indicates true positives, black represents true negatives, red denotes false positives, and blue signifies false negatives. The input images \(x_{1}\) and \(x_{2}\) are sourced from the LEVIR-CD dataset30.

Full size image
Table 2 Performance comparison with other advanced methods on LEVIR-CD dataset.
Full size table

In contrast to the aforementioned methods, SNIIF-Net enhances network performance through the innovative design of three modules: the Feature Interaction and Integration Module (FIIM), the Feature Pair Fusion Module (FPFM), and the Multi-Scale Supervision Module (MSSM). This enhancement is primarily attributed to the following factors: (1) the FIIM utilizes attention mechanisms to model contextual information of local features, thus strengthening the interdependence among features and improving the differentiation of change regions; (2) the FPFM effectively leverages spatial and relational information from image pairs to extract more detailed data, enhance edge information, and boost model performance; and (3) the MSSM employs a supervision method based on contrastive learning to effectively constrain intermediate features, enabling the network to generate more refined change maps, which ultimately increases the accuracy of the network.

The visual comparisons presented in Fig. 4 demonstrate that SNIIF-Net outperforms other methods. For example, DASNet lacks effective supervision of intermediate features, which hampers its ability to extract rich semantic information, resulting in coarser change maps and instances of missed detection. In contrast, SNUNet-CD employs a straightforward feature fusion method to generate changing features, inevitably introducing noise that affects the precision of the final change map. In general, SNIIF-Net benefits from contrastive learning-based supervision of intermediate features and incorporates the FIIM and FPFM modules to enhance spatial and semantic relationships. These enhancements improve edge information in the image, making the SNIIF-Net change map more accurate in contour and more closely aligned with the labels, thus more effectively reflecting regional changes compared to those generated by the competing methods.

To further validate the effectiveness of SNIIF-Net, we conducted training and testing on the LEVIR-CD dataset and compared its performance with several algorithms. All experiments used identical settings. Table 2 presents the quantitative comparison results, while Fig. 5 illustrates the visual comparisons of selected algorithms. Similarly to the experimental results obtained from the CDD dataset, SNIIF-Net achieves a better F1 (0.911 vs. 0.910 from M-Swin). The visual results (Fig. 5) show reduced false positives in complex urban areas (e.g., blue pixels in row 2) due to the incorporation of FIIM, FPFM and MSSM.

Ablation study

In this section, we conduct several ablation experiments to evaluate the effectiveness of various components within the SNIIF-Net architecture. The experimental results on the CDD and LEVIR-CD datasets are presented in Table 3, while Figures 6 and 7 illustrate the comparative visualization effects for the two datasets. First, we replace the FIIM module in SNIIF-Net with traditional convolutional operations. Next, we remove the FPFM module using only a simple subtraction operation to process the intermediate features. Finally, we eliminate the MSSM, which is based on contrastive learning, indicating that SNIIF-Net does not employ contrastive learning to supervise the multi-scale output features in the decoder’s intermediate layer.

Table 3 Comparison of different ablations of SNIIF-Net on two datasets.
Full size table

The experimental results of two datasets indicate the following conclusions: (1) In the absence of the Feature Information Integration Module (FIIM), the SNIIF-Net F1 scores decreased by 0.025 and 0.020, respectively. This finding suggests that replacing the FIIM module with traditional convolution results in a loss of critical detail in the intermediate features extracted. In contrast, employing an attention-based approach to feature extraction enhances the richness of feature information and improves network performance. (2) Replacing the Feature Pyramid Fusion Module (FPFM) with a simple subtraction operation leads to spatial and color shifts during feature extraction and introduces significant noise. In contrast, the application of the FPFM module mitigates the drawbacks of simple subtraction methods and enriches feature information, thus improving accuracy. (3) The absence of the Multi-scale Supervision Module (MSSM) results in the most substantial decrease in network performance, as the MSSM effectively supervises multiple intermediate features and enhances overall network performance. This underscores the MSSM’s critical role in generating fine change maps. Furthermore, comparative analysis of the visualization figures reveals that the contours of the change maps obtained using the aforementioned modules are more refined and closer to the actual labels, yielding better results.

Fig. 6
figure 6

Visual comparison of different ablation settings on CDD dataset. Different colors are employed to enhance clarity: white indicates true positives, black represents true negatives, red denotes false positives, and blue signifies false negatives. The input images \(x_{1}\) and \(x_{2}\) are sourced from the CDD dataset32.

Full size image
Fig. 7
figure 7

Visual comparison of different ablation settings on LEVIR-CD dataset. Different colors are employed to enhance clarity: white indicates true positives, black represents true negatives, red denotes false positives, and blue signifies false negatives. The input images \(x_{1}\) and \(x_{2}\) are sourced from the LEVIR-CD dataset30.

Full size image

Finally, we investigate the impact of the Multi-Scale Supervision Module (MSSM) on the performance of SNIIF-Net. The experimental results are presented in Tables 4 and 5, where the values 1/8, 1/4, 1/2, and 1/1 correspond to features on different scales. The data indicate that supervising only a specific scale of features through contrastive learning results in suboptimal network performance. However, utilizing the MSSM to supervise multiple feature layers leads to a gradual improvement in performance. When SNIIF-Net supervises the features across all four scales of the decoder, it achieves the highest F1 score, suggesting that monitoring the features on each scale allows the network to capture more detailed information about the changes, thus enhancing its overall performance.

Table 4 Comparison of the usage of MSSM modules on CDD dataset.
Full size table
Table 5 Comparison of the usage of MSSM modules on LEVIR-CD dataset.
Full size table

Conclusion

To address the limitations of previous change detection methods, including inadequate constraints on intermediate features, insufficient modeling of relationships between bi-temporal features, and overly simplistic fusion techniques. We propose SNIIF-Net to improve the precision of change detection tasks. SNIIF-Net significantly improves the semantic richness of features, enhances edge information in images, and boosts model performance through the design of a feature information interaction module and a feature pair fusion module that utilize a spatial attention mechanism. In addition, a contrastive learning-based supervision method effectively constrains intermediate features, allowing the network to generate more detailed change maps. The effectiveness of SNIIF-Net has been validated through experiments conducted on multiple datasets.

Although our approach achieves significant improvements in feature semantics, edge detail preservation, and overall performance, several limitations warrant acknowledgment. The architectural complexity introduced, notably spatial attention mechanisms, may increase computational demands, potentially hindering real-time deployment scenarios. Future research will prioritize: (1) developing lightweight model variants to enhance deployment efficiency; (2) refining multi-scale change detection mechanisms for improved granularity; and (3) strengthening model robustness against environmental perturbations and sensor variations.