Introduction

The spinal cord provides a pathway for bidirectional communication between the brain and the periphery, enabling motor, sensory and autonomic function. While electrophysiology often focuses on the neuronal soma, recording from nerve tracts has the potential to inform a variety of applications, such as brain-machine interfaces, intraoperative monitoring, and as a modality to characterise injury and disease1.

In current clinical practice intraoperative neuromonitoring (IONM) is used, where electrical connectivity through the spinal cord is monitored during surgeries that manipulate the spine and potentially increase the risk of compromised spinal integrity. IONM is commonly used to monitor tumour removal, scoliosis or spinal decompression surgery2. Sensory networks are assessed by electrically stimulating peripheral nerves and recording the response in the brain, while motor networks are evaluated in reverse by stimulating the brain and recording the response in the periphery. Changes in amplitude and latency are monitored to provide an early warning towards potential damage during manipulation of the spinal cord3. IONM is well established; however, it only assesses a small fraction of the neural circuitry at a given time4 and, whilst IONM allows for the identification of gross changes to spinal cord circuitry, it indirectly records spinal electrical activity through recording from electrodes either in the brain or the periphery. Recently, this technique has advanced with the use of high-density microelectrode arrays directly on the spine, which provides sufficient spatiotemporal resolution to identify the spinal midline5whilst other groups have adapted the technique for use outside of the operating theatre6,7.

While IONM and its derivatives are relatively non-invasive, others have used traditional penetrating electrodes, such as microwire electrode arrays, inspired by or directly using the FDA-approved Utah array to record from the cortical or rubrospinal tracts8 or the dorsal or lateral columns9,10. Spinal tissue, however, is more mobile than the brain, introducing movement artefacts during recordings and increased stress on the implant itself, with reported failure cases including signal degeneration, wire breakage and neural injury1. To reduce tissue trauma and the risk of spinal cord deformation, flexible, non-penetrating designs provide an advantage11,12.

Non-penetrating, spinal cord implants include spinal cord stimulators. Spinal cord stimulation (SCS) has been used to relieve neuropathic pain, and more recently shown to have multi-system effects, such as motor and sensory function improvements13,14,15,16. There is a large volume of research dedicated to understanding the mechanisms of SCS, with groups recording muscle activity in response to SCS17,18 and compound action potentials (CAPs) from the spinal cord directly14,15,19,20,21. CAPs are generated by applying a stimulus in one location and recording the resulting propagated waveform, assessing the neural circuitry between the stimulated and measured location, with the primary application to investigate the method of action of SCS15,16,19. Key properties of recorded CAPs include propagation velocity and amplitude. The propagation velocity is determined by the distance between the stimulating and recording electrode divided by the latency between the applied stimulation pulse and the corresponding CAP19. The propagation velocity of a nerve is primarily determined by axon diameter and myelination, with speeds recorded in the rodent spinal cord between 5 and 50 ms−115,16,22, . Conduction velocity has been used to study the properties of injured tissue, with regenerated axons having a much lower conduction velocity (5 ± 3.4 ms− 1), attributed to chronic demyelination, compared to intact axon segments (19.3 ± 6.8 ms− 1)23.Yang et al. delivered SCS in injured rats and recorded the corresponding CAP at the sciatic nerve. The area under the CAP was larger for animals that responded well to SCS, as determined by withdrawal threshold to a pain stimulus, compared to non-responders16. Parker et al. stimulated and recorded from the spinal cord in sheep, finding that as the distance from the stimulation site increased, the CAP amplitude decreased, and dispersion increased. Dispersion represents the width of the CAP waveform, with the increase occurring due to the contribution of slow-conducting small-diameter fibres19. In an in vitro study in white matter preparations, as stimulation intensity was increased, amplitude increased due to a larger number of stimulated fibres, however, the time delay and subsequent propagation velocity of the CAP decreased due to the recruitment of slower conducting neurons22. There is a relationship between fibre recruitment and the amplitude and propagation velocity of CAPs generated through electrical stimulation.

Due to the shared processing of neural structures, electrical stimulation to induce a targeted response, such as in IONM or CAP experiments, also affects unrelated neural circuitry24. Whilst stimulation has therapeutic benefits, such as in SCS, recordings generated during stimulation do not represent innate electrophysiology. To understand true spinal cord networks and electrophysiology, recordings generated during natural movement are advantageous.

We have previously developed a thin film polyimide bioelectronic implant that can be surgically implanted and maintained beneath the spinal dura mater without any deficits in hindlimb function or change in the shape of the spinal cord12,25. The implant positions two rows of twelve 60 μm sputtered iridium oxide (SIROF) electrodes, one row per hemisphere, along the dorsal surface of the spinal cord. Here, we expand on this work to describe and characterise electrical recordings taken from these electrodes in freely behaving rats. Due to the subdural electrode position, we hypothesise that propagation of electrical activity in the spinal cord is characteristically different in injured animals. We investigate this by developing an algorithm to calculate action potential propagation velocity and compare the properties of neural spikes in spinal cord injured and non-injured rats.

Methods

Experimental overview

The data presented is generated using the bioelectronic implant described in12. The implant is an 8 μm polyimide thin film, with 60 μm diameter sputtered iridium oxide (SIROF) electrodes. The electrodes are positioned in two rows on the subdural surface of the spinal cord, spaced 800 μm apart. The implant is soldered to a PCB which is housed inside a 3D-printed, epoxy-filled backpack, with a 32-channel omnetics connector exposed and providing an interface with the electrophysiology equipment.

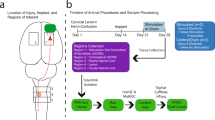
An overview of the study and key data analysis steps is presented in Fig. 1.

Fig. 1
figure 1

Experimental overview of the study. A flexible, polyimide based bioelectronic implant has been developed12comprised of 12 recording electrodes on each arm of the implant. Each recording electrode is 60 μm in diameter and spaced 800 μm apart. The device is surgically implanted with recording electrodes positioned on the subdural, dorsal surface of the T13-L3 spinal segments. In injured animals, a contusion injury is applied at the border of the L1 and L2 segment. Open-field recordings are conducted where the animal is free to explore a large open area. Recordings were conducted and analysed for two-weeks post-implantation. Key analyses include bandpass filtering to isolate neural spikes, identification of propagating spikes ascending and descending in the spinal cord and an analysis of differences in spike properties between injured and non-injured animals.

Full size image

Surgical implantation

Ten 2–3-month-old female Sprague Dawley rats were obtained from the University of Auckland animal facility (VJU SBS). All methods were approved by the University of Auckland Animal Ethics Committee (Approval number: AEC22644) and the New Zealand Animal Welfare Act 1999. Reporting of methods within the manuscript follows the ARRIVE guidelines. Rats were housed together for two weeks in a dedicated colony/behavioural room on a 12:12 light/dark cycle with rat chow and water available ad libitum. During this time, rats were habituated to handling and were introduced to a circular open field (100 cm diameter white wooden floor with 20 cm Perspex walls). They were first placed in the open field in their home-cage groups and allowed to explore for 10 min on two subsequent days. On the third day, they were individually placed in the open field for 5 min each. At the time of surgery, these rats weighed between 230 and 290 g.

The implant and surgical procedure are described in detail in12,25. In summary, animals were anaesthetised with isoflurane before a laminectomy was performed, exposing spinal segments T13, L1, L2, and L3. The two implant arms were guided beneath the dura through small dural incisions at T13 via catheters to sit directly on the pial surface of the spinal cord. The tips of each implant arm exited the dura at L3 and were secured to the T13 spinal process using a suture. Gelfoam was applied over the exposed cord, and muscle and skin layers were sutured. The backpack housing was positioned rostral to the laminectomy in a subcutaneous pocket. The backpack base comprised five splayed feet sutured to an oval surgical mesh, which were secured to deep muscle with non-absorbable suture. At the end of the study, animals were euthanised by lethal injection of sodium pentobarbitone (Pentobarb 300).

Injury and post-operative care

Five of the ten animals received a contusion injury, using an Infinite Horizons impactor with a 2.5 mm diameter tip to deliver an impact of 1.75 N (175 kdyn). The injury was delivered at the border between the L1 and L2 spinal segments after the implant was inserted beneath the dura, with the implant spanning the injury site and electrodes located both rostral and caudal to the injury centre (Fig. 1). All animals received post-op analgesics (Metacam 5 mg/ mL, 0.03 mL per 100 g; buprenorphine 0.3 mg/mL, 0.1 mL per 100 g; bupivicaine injected along incision site 2.5 mg/mL, 0.1 mL per 100 g) and antibiotics (Baytril 25 mg/mL, 0.04 mL per 100 g) for three days. Rats with contusion injuries had their bladders manually expressed by experimenters three times daily (morning, midday, and evening) as needed and continued to receive antibiotics until spontaneous urination was observed for three consecutive days.

Generating electrophysiology recordings

Recordings of spinal cord electrical activity were generated 2–3 times each week, using a Multi-Channel Systems (MCS) MEA2100 with either a small and lightweight µPA32 head stage (2 g) or a wireless W2100-HS32 head stage (3.6 g). The head stages interfaced via an Omnetics plug housed within a protective case on the rat’s back. In each recording session, animals were allowed to roam around an open field for 5 min. Electrophysiology data was sampled at 20 kHz and saved for offline analysis using MCS Experimenter. Data is presented from recording sessions within the first two weeks after the implantation, with the earliest 3 days post-surgery. Although injured animals showed some functional recovery during the evaluation period, their performance remained well below that of uninjured controls (Supplementary Table 1).

Data analysis

Data analysis was carried out using custom-made scripts on MATLAB (2021b).

Identification and extraction of neural spikes

A second-order bandpass infinite impulse response (IIR) filter was applied to the data to isolate the action potential component of the signal between 300 Hz and 3000 Hz26.

After filtering the data, action potential spikes were isolated using threshold-based spike detection. The detection threshold was defined as four times the standard deviation of the baseline noise (σn), where σn was calculated from the two seconds with the lowest absolute mean voltage. When the voltage crossed the detection threshold, a 5 ms segment of the trace was stored, centred at the time of detection, and a 2 ms inter-spike spacing was enforced to ensure spikes did not overlap. Principal Component Analysis (PCA) was used to determine if spikes could be separated into distinct waveforms.

Calculation of propagation velocity

The action potential signal recorded was hypothesised to originate from fibre tracts in white matter. We developed an algorithm to determine the propagation velocity of these spikes. First, spike detection was carried out on all channels along one arm of the implant, with any duplicates removed. Duplicates were defined as spikes with spike centres within 1.5 ms of another spike, indicating more than 30% overlap. For each spike identified, electrical activity was correlated between all pairs of channels. If the Pearson correlation coefficient between a given pair of channels was greater than 0.85, a time delay was determined using cross-correlation, resulting in a matrix of time delays (12 × 12, where there are 12 channels). The top channel was used as a reference channel for propagation. Each time delay was shifted relative to the reference channel (Fig. 2). Each row in the time delay matrix was averaged. A linear model was fitted to a vector of time delays, representing the average delay for each channel, and a distance vector, representing the distance between the electrodes. Finally, delay and distance vectors were used to calculate the propagation velocity of the spike. We define a positive velocity as a spike propagating towards the caudal end of the spine.

Fig. 2
figure 2

Schematic of the propagation algorithm. (a) A representative spike is present on all electrodes, with the middle electrodes (E5, E6 and E7) highlighted to further illustrate the algorithm in panels b-d. (b) Cross-correlation between the waveforms on E5 and E6 (top row), and E6 and E7 (bottom row). Delays of 0, 1 and 2 data points are shown. For the correlation between E6 and E5, a delay of 1 aligns these spikes the best, whereas for E7 relative to E6, a delay of 2 is best. Cross-correlation is carried out between all pairs of electrodes to create a matrix, with the two examples shown in purple and orange. (c) Each column is shifted to align the top channel as the reference, creating a row of zeros. The mean is calculated for each row to determine an average delay between each channel and the reference channel, resulting in a single delay for each electrode. (d) A linear model is fitted between the average time delays calculated in c) and the known distances between the electrodes. The gradient of this linear model represents the velocity of the given spike.

Full size image

Development of a synthetic dataset

A synthetic dataset was developed to explore the algorithm’s limitations in calculating spike velocity, specifically, the influence of noise and the signal-to-noise ratio (SNR).

First, a representative spike waveform for a single channel was calculated by averaging 200 spikes extracted from one channel of one recording. From this representative spike, we generated synthetic spikes, representing velocities between ± 200 ms− 1, by shifting the representative spike in time along the electrode array. To allow shifting of the spike in time, at a resolution greater than that of the original data, the representative spike was upsampled to 200 kHz using a spline interpolation (Matlab 2021b, interp1, spline method). The velocities reported for action potentials in fibre tracts in the rodent spinal cord range from 5 to 50 ms− 115,16,22. Initial testing on our experimental dataset resulted in velocities up to 200 ms− 1, prompting the design of the synthetic dataset to explore higher velocities and better understand the validity of these results. Synthetic spikes with defined propagation velocities were then resampled to 20 kHz to match the experimental data.

To evaluate the influence of noise on the ability to recover the propagation velocity of a synthetic spike accurately, we extracted segments of noise from an experimental data set and added these segments to the synthetic spikes. Noise segments were defined as 5 ms portions of an experimental recording where the voltage remained below 3σn of the baseline, ensuring these are below the threshold used for spike detection. For each spike of a given synthetic velocity, 150 random noise variations were added. SNR was also investigated, with SNR determined as the amplitude of the spike divided by the noise threshold for the specific channel.

We evaluated the ability of the velocity calculation to accurately recover the ground truth from the synthetic data with two measures: bias and spread. Bias was defined as the mean absolute difference between the calculated and ground truth velocities and represents the tendency to over- or under-estimate the ground truth. Spread was defined as the standard deviation of the calculated velocities and represents how susceptible a velocity calculation is to the presence of noise. Lastly, we also calculate the ability of the velocity calculation to at least recover the correct direction of propagation, even if the magnitude of the velocity could not be accurately determined. The direction confidence is defined as the percentage of spikes in the synthetic dataset where the direction of propagation is correctly determined.

From analysis of the synthetic dataset (A synthetic dataset validates the ability to detect propagating spikes) we determined ranges of velocities and spike SNRs where we could accurately calculate the velocity of a spike. Specifically, we define the velocity calculation as accurate if the synthetic velocity could be recovered with a bias of at most 2 ms− 1 and a spread of at most 5 ms− 1. Similarly, we define the region of direction confidence as the range of velocities and spike SNRs where the direction was correctly recovered from the synthetic data set 95% of the time.

Statistics

The spike properties were compared for injured and non-injured animals. There were eight distributions compared: the mean and standard deviations of the ascending and descending velocities and the mean and standard deviations of the ascending and descending amplitudes. For each distribution there were 15 samples, from five non-injured and five injured animals, each with three independent recordings. The normality condition was assessed using the Anderson-Darling test and where the normality assumption was not met for one or both distributions, the non-parametric Wilcoxon rank sum test, equivalent to the Mann-Whitney U-test was used. If both distributions had a normal distribution a two-sample t-test was used. Comparisons between distributions were deemed insignificant when the p-value was > 0.05. Significance was indicated by * (p-value < 0.05), ** (p-value < 0.01) and *** (p-value < 0.001).

Results

Bandpass filtering isolates high-frequency spiking activity

Figure 3 shows the effect of a bandpass filter on the raw data, removing the low-frequency field potential activity and isolating high-frequency activity, representing neural spikes. Notably, spiking activity appears to be similar along the length of the array (Fig. 3a-c).

Spike cutting was carried out to investigate the properties of individual spikes. Figure 3(d) shows a segment of data illustrating the spike detection threshold and the resulting spike events, a subset of which are overlaid in Fig. 3(e). A limitation in the detection algorithm, resulting in a small number of spikes being undetected (Fig. 3e), is the enforced 2 ms inter-spike spacing used to ensure spikes did not overlap.

Fig. 3
figure 3

Bandpass filtering to extract high-frequency activity reveals spiking events across all channels on the implant. (a) An implant schematic highlighting the electrode locations. (b) A 5 s segment of the recording from the rostral (top) electrode before any filtering is applied. (c) A 5 s recording trace from all electrodes along one arm of the implant, filtered with a 300–3000 Hz bandpass filter. (d) A 5 s segment of 300–3000 Hz filtered data, with the threshold used for spike cutting overlayed in red and identified spikes shown in blue. (e) An overlay of 250 identified spikes, with the mean waveform in red. (f–h) Binned scatter plots of pairs of the first three principal components, with colour indicating spike count. i) A histogram of the SNR of all extracted spikes from the representative electrode.

Full size image

All spikes have a similar triphasic shape, with a prominent negative peak. PCA was used to determine if spikes could be separated into distinct clusters. Figure 3(f-h) shows scatter plots of pairs of the first three principal components, explaining 67% of the variation in the identified spikes. There is no clear separation of clusters in these scatterplots, suggesting that the population of spikes have similar properties and cannot be separated further into independent units. Lastly, Fig. 3(i) shows the distribution of SNRs, with 95% of the spikes having an SNR below 7.55.

A synthetic dataset validates the ability to detect propagating spikes

A synthetic dataset was developed to investigate the limitations of the propagation algorithm. We observed that noise in the data significantly influenced the ability to recover the ground truth velocities. In Fig. 4(a-c), the red dots represent the calculated velocities when no noise is added, whilst black represents the calculated velocities when random noise samples are overlaid. Generally, lower velocities were more accurately recovered, and as SNR increases, the ability to recover ground truth velocity increases.

Quantification of the accuracy of calculated velocities, in the presence of noise, was evaluated across a range of SNRs (Fig. 4(d-i)). At each SNR, a range of velocities, from − 200 to + 200 ms− 1 were evaluated and the bias (Fig. 4(d), spread (Fig. 4(e)) and direction confidence (Fig. 4(f)) were determined. The conditions where velocity can be accurately resolved are when bias is less than 2 ms− 1, spread is less than 5ms− 1 and direction confidence is greater than 95%, presented across the range of SNRs and velocities as a set of binary heatmaps (Fig. 4(g-i). Despite a more extensive spread associated with higher velocities, the algorithm can determine the direction of propagation in most cases, particularly at high SNR (Fig. 4(f)), with the direction being accurately resolved (direction confidence > 95%) shown in yellow in Fig. 4(i).

In the subsequent analyses, detected spikes in the experimental data were categorised into those where speed and direction (velocity) could be accurately calculated and those where only direction could be confidently determined.

Fig. 4
figure 4

Validation of velocity calculations using a synthetic dataset. (a–c) Scatter plots illustrate the impact of varying SNR magnitudes on the calculated velocities for each ground truth velocity. Red lines represent the calculated velocity in the absence of any noise. Inserts highlight the relationship at low velocities (− 50 to 50 ms- 1). (d) Heat map of bias, showing the difference between the ground-truth velocity and the mean calculated velocity for each SNR and velocity combination. (e) Heat map of spread, where the spread is defined as the standard deviation of the calculated velocities, providing an indication of precision across different velocity and SNR conditions. (f) Heat map of direction confidence, representing the proportion of spikes for which the direction is correctly determined for each combination of ground truth velocity and SNR. (g) Binary map highlighting the combination of SNR and velocity where the bias condition (bias is less than 2 ms- 1) is met. (h) Binary map highlighting the combination of SNR and velocity where the spread condition (spread is less than 5 ms-1) is met. i) Binary map highlighting the combination of SNR and velocity where the direction condition (direction confidence is greater than 95%) is met.

Full size image

Detected spikes ascend and descend along the spinal cord

Next, the propagation algorithm evaluated a representative experimental data set while considering its accuracy constraints. Examples of propagating spikes are shown in columns in Fig. 5(a), with red and blue indicating positive and negative time delays, respectively. Shading reflects the relative magnitude of the time delay for each spike.

Figure 5(b) shows the distribution of propagation velocities from this representative data set and the subsets for which direction and velocity could be calculated. The distribution of velocities is relatively symmetric at lower velocities (< 50 ms− 1); however, at higher velocities, there is a greater proportion of ascending spikes. These faster velocities cannot be accurately determined due to the high errors outlined in the synthetic dataset (Fig. 4); however, we can be confident in the direction they propagate. For this five-minute recording, there were 51,879 spikes identified, of which we can calculate the velocity of 46.16% (23949), the direction only for 47.96% (24882) and neither speed nor direction for 3.10% (1608) of the spikes. The remaining 2.78% (1440) represent spikes where the velocity was unresolved, either due to no delays identified between channels (1434) or a calculated velocity of 0 (6).

Fig. 5
figure 5

Propagation velocity of identified spikes from a single session. (a) A selection of extracted spike waveforms from one arm of the implant, with each column a representing an individual spike and each row showing the activity on every channel along one arm of the implant. The propagation reference channel is shown in black, with red representing spikes with positive delays and blue with negative delays. The shading represents the relative length of the delay, with darker traces having a more considerable delay with respect to the reference channel. (b) A histogram showing the extracted spikes, with velocity confident spikes (bias < 2ms-1 and error < 5 ms- 1) shown in blue, direction confident spikes (direction confidence > 95%) in black and all spikes in grey.

Full size image

Propagation observed in injured and non-injured animals

The properties of the extracted spikes were investigated between non-injured and injured animals. The number, amplitudes and velocities of spikes are presented for a representative non-injured and injured animal (Fig. 6).

Across all recording days, the injured animal exhibited fewer detected spikes (Fig. 6(a-b)). Moreover, the amplitude of detected spikes was consistently lower in the injured animal compared to the non-injured animal (Fig. 6(c-d)). The non-injured animal exhibited a wider distribution of recorded velocities, and an extended range of high-velocity action potentials compared to the injured animal (Fig. 6(e-f)).

Fig. 6
figure 6

Propagation velocities and properties of spikes over time for a representative non-injured (a, c, e) and injured (b, d, f) animal. (a, b) The number of ascending and descending detected spikes that meet the velocity confident conditions (bias < 2 ms- 1, spread < 5 ms- 1) for the non-injured and injured animals, respectively. (c, d) Distributions of ascending and descending amplitudes for the non-injured and injured animals, respectively. (e,f) Distributions of ascending and descending velocities for the non-injured and injured animals, respectively.

Full size image

Figure 7 summarises recordings from five non-injured and five injured animals, with three recordings for each animal. The mean velocity of ascending and descending spikes for the non-injured group was 12.426 ms− 1 and 11.874 ms− 1, respectively, whilst for the injured group was 10.377 ms− 1 and 10.672 ms− 1. Whilst spikes detected in the injured group had a lower mean velocity, this was not significantly different from the non-injured group. Despite no significant difference in the mean velocities (Fig. 7a), a significant difference was identified in the standard deviations of the velocities (Fig. 7(b)), where the non-injured have a greater standard deviation than the injured animals, due to the larger number of high-velocity spikes detected as shown in Fig. 7(e-f).

Fig. 7
figure 7

Comparisons of spike propagation and properties between injured and non-injured animals. (a) Comparison of mean ascending and descending velocities. (b) Comparison of the standard deviation of ascending and descending velocities. (c) Comparison of mean amplitudes for ascending and descending spikes. (d) Standard deviation of the amplitudes for ascending and descending spikes. For all panels, the boxplots represent the velocities and amplitudes from recordings of five non-injured and five injured animals, with three recordings for each animal. *p-value < 0.05, **p-value < 0.01, ***p-value < 0.001.

Full size image

A significant difference in amplitudes was observed for both ascending and descending spikes (Fig. 7(c)). The mean amplitude of ascending and descending spikes for the non-injured group was 0.072 mV and 0.071 mV, respectively, whilst for the injured group was 0.043 mV for both ascending and descending spikes. Additionally, there was a significant difference in the standard deviation of the amplitudes, with non-injured animals having a greater standard deviation. All p-values for the statistical testing outlined in Fig. 7 are presented in Supplementary Table 2.

Discussion

Recording electrical activity from the spinal cord is an established method for determining the integrity of its neural connections. In this work, we explore using a subdural spinal implant to record innate spinal activity in freely moving animals and characterise differences in non-injured and spinal cord injured animals.

We demonstrate the ability to extract spikes from subdural spinal recordings and hypothesise that these originate from the extracellular action potential waveform from axons in the underlying white-matter fibre tracts of the spinal cord. In isolation, a single, long, non-branching axon produces an extracellular waveform with a triphasic shape that propagates unchanged along the axon27. Figure 3e demonstrates this triphasic waveform and its relatively stable shape along the array. Notably, the shapes of the spike waveforms do not cluster into distinct groups, as would be typical for APs recorded from neuronal soma28,29. The lack of separability is likely due to the simpler underlying geometry of axons in the spinal cord, where the electrodes are only in contact with axons arranged in a cylindrical and uniform arrangement.

Close to the dorsal surface where the implant is located are the dorsal column pathways, containing large and highly myelinated sensory axons30. The corticospinal tract is located deep within the dorsal columns, carrying highly myelinated and fast-propagating axons responsible for motor control. The rubrospinal tract, located in the lateral white matter in rodents, is another efferent tract responsible for transmitting motor information31,32. We record a similar number of ascending and descending spikes in both non-injured and injured animals. Given that the electrodes in our implant sit primarily over sensory tracts, we expected to record ascending signals; however, sensory axons entering the spinal cord from the dorsal roots ascend or descend before entering the grey matter32,33 and could explain the relative symmetry of ascending and descending spikes.

The mean velocities for injured and non-injured animals were not significantly different (Fig. 7(a)). However, the distribution of velocities in the injured groups was less variable, with significantly lower standard deviations of velocity (Fig. 7b) due to higher velocity spikes in the non-injured animals. One explanation for less high-velocity spikes in the injured animal is that the injury causes demyelination, resulting in a reduction in high-velocity spikes34. A second explanation that cannot be ruled out is that the lack of high-velocity spikes for the injured animals is an artefact of the velocities we can accurately calculate, as defined by the synthetic dataset. For our algorithm to accurately calculate the velocity of faster spikes, the spikes require a higher SNR; however, we observed that the amplitude of detected spikes for injured animals was significantly less than that for non-injured animals (Fig. 7(c)).

The first possible explanation for the smaller spike amplitudes observed in the injured animals is that the injury causes damage to axons closer to the spinal cord’s dorsal surface, resulting in recorded signals representing further away axons, with subsequently smaller amplitudes. The second is that the injury results in an increase in inflammatory and glial cells35causing an increase in resistance between the neuron and the electrode, decreasing the amplitude of recorded spikes.

A limitation of this study is that we cannot always accurately determine the velocity of fast-travelling spikes. To improve this, we could increase the span of the implant to allow for recording a greater length of the spinal cord, either by increasing the distance between electrodes or increasing the length of the implant and adding more electrodes. Electrode configurations will also need to be optimised future studies with male rats, larger animal models and human translation. During recording sessions animals were exhibiting range of different behaviours, notably, resting, walking and standing on their hind limbs. The spinal cord is relatively mobile in humans elongating between 2 and 10% during neck flexion36. Future refinements of this work will need to take potential spinal elongation in relation to different behaviours.

The work developed here can aid in understanding the relationship between the electrical signals recorded from the spinal cord and function. The spikes identified are representative of innate functional activity, through being identified during natural, freely moving behaviour rather than in response to artificial stimulation24suggesting that it is possible to monitor the connectivity of the spinal cord, as with IONM, post-operatively. Whilst many groups quantify spiking waveforms using an external stimulation15,19,37 (CAP experiment), we can identify and quantify propagation during natural activity. The next steps are to investigate signals in different frequency bands and how the properties of recorded signals change with activity. We envisage that monitoring of SCI and recovery will be possible with the future development of this work.

Conclusions

We have identified propagating neural spikes recorded from a subdural spinal implant. The distribution of spike velocities suggests clusters of both slow and fast and ascending and descending signals in the spinal cord. In non-injured animals, there were more fast, ascending spikes compared to the injured animals. The spike amplitude in non-injured animals was significantly larger than in injured animals, suggesting changes to the underlying neural architecture or modifications to the tissue’s electrical properties due to post-injury immune responses. A key novelty of this work is the ability to generate recordings while the animal is freely behaving, enabling post-operative monitoring of electrical activity in the spine. The results highlight signals recorded from the spinal cord can identify differences between signalling in non-injured and injured animals.