Multi-head deep Q-learning for continuous beamforming with selective MC-CDMA operation in V2X highway communications

Abstract

This study investigates a large-scale dynamic Vehicle-to-Everything (V2X) communication network, in which multiple Roadside Units (RSUs) are deployed along highways to enable high-speed vehicular links. To ensure robust and adaptive performance under fast-varying conditions, we propose an integrated framework that combines resource block-based MC-CDMA modulation with dynamic beamforming optimized for complex propagation environments. A custom code mapper and resource element (RE) allocator are introduced to support interference-aware transmission and enhance signal robustness in dense deployment scenarios. The MC-CDMA scheme enables extended-range coverage per RSU, outperforming traditional OFDM-based transmission in terms of reliability and scalability. To further optimize performance, a Deep Reinforcement Learning (DRL) model is employed to jointly handle beam tracking and time-varying channel conditions. Specifically, a physics-inspired Deep Q-Learning (DQL) strategy is proposed, using a force-arm-based mechanism to adaptively correct beam misalignment caused by mobility and Doppler effects. Simulation results demonstrate that the proposed system achieves significant improvements in bit error rate (BER), bitrate stability, handover smoothness, and spectral efficiency. When equipped with a large-scale antenna array, the system ensures continuous beam tracking and substantially outperforms conventional RL-based techniques. These results highlight its potential for future 6G-enabled V2X deployments, where scalability, adaptability, and robust link quality are essential.

Introduction

With the rapid deployment of Smart Cities, Central Business Districts (CBDs), and large-scale administrative hubs in developing countries across highways, highways have emerged as strategic, irreplaceable infrastructure, serving as the backbone of modern transportation networks¹. Beyond reducing travel time and enhancing regional connectivity, highways catalyze socio-economic exchanges between urban centers, enabling the development of satellite city models and optimized population/function distribution². Critically, in the context of digitally driven smart cities, modern highways now integrate sensor networks, AI-powered cameras, and electronic tolling systems, forming the foundation for Intelligent Transportation Systems (ITS), a core component of smart urban ecosystems in Transportation 5.0^3,4.

The sixth generation of wireless technology (6G) is envisioned as a network that supports Smart Connectivity^5,6. 6G aims to enable a more intelligent and autonomous communication environment, where IoT devices, autonomous vehicles, and industrial applications can interact efficiently and automatically, with systems that can adapt dynamically to both environmental conditions and connectivity demands, and most importantly, it enables deep integration of artificial intelligence⁷.

To support intelligent communication on highways, all vehicles must be connected via the V2X (Vehicle-to-Everything) protocol, ensuring reliable data sharing between vehicles and Roadside Units (RSUs) under rapidly changing fading channels and heterogeneous wireless conditions⁸. V2X plays a critical role in the context of smart applications and services in urban areas, traffic systems, and mobile environments⁹. V2X enables not only Vehicle-to-Vehicle (V2V) communication, but also communication between vehicles and infrastructure (V2I), vehicles and pedestrians (V2P), and vehicles and networks (V2N)¹⁰. V2X enhances environmental awareness, allowing vehicles to share information about traffic conditions, emergency events, or hazardous situations for early warnings, thereby reducing accident risks. Furthermore, V2X allows vehicles to autonomously adjust their behavior, such as emergency braking, lane changing, or sending alerts to other nearby vehicles in the case of dangerous scenarios¹¹.

Besides, the exponential growth in traffic volume and Connected/Autonomous Vehicles (CAVs) necessitates the optimized deployment and operational management of Roadside Units (RSUs) along these corridors^12,13. These RSUs must deliver low-latency communication and intelligent control services for vehicles via 6G cellular networks, ensuring seamless V2X (Vehicle-to-Everything) integration^14,15. V2X communication plays a pivotal role in enhancing safety, traffic efficiency, and providing support for autonomous vehicles^16,17.

Related works

There have been extensive efforts in the literature on V2X communications, including various modulation schemes and beamforming techniques tailored for V2X systems. Initially, V2X communications were based on Wi-Fi technologies, namely IEEE 802.11p with Dedicated Short-Range Communications (DSRC) operating in the 5.9 GHz band, to enable Vehicular Ad-Hoc Networks (VANETs)¹⁸. In 5G networks, V2X has evolved into cellular-V2X (C-V2X)¹⁹, with further enhancements introduced through Enhanced Vehicle-to-Everything (eV2X), which is based on 5G New Radio (NR)²⁰. However, with the emergence of 6G, V2X communications face new requirements, including integrated artificial intelligence (AI), network intelligence (Network AI), the use of terahertz (THz) frequencies, ultra-reliable communications with a target reliability of 99.99999%, and multi-layer redundant networking. 6G also demands the ability to autonomously switch between heterogeneous networks (e.g., seamlessly transitioning from 6G to satellite networks upon signal loss) and to support multi-tier satellite connectivity involving RSUs, UAVs, and satellites²¹. Given these stringent requirements, the design of modulation schemes that can guarantee high reliability while supporting satellite-based connections has become a critical and urgent issue in the development of next-generation V2X communications.

MC-CDMA

5G-V2X sidelink transmissions typically employ cyclic prefix orthogonal frequency-division multiplexing (CP-OFDM) along with low-density parity-check (LDPC) codes^22,23. This study considers the Multi-Carrier Code Division Multiple Access (MC-CDMA) scheme as a promising alternative, since MC-CDMA combines the advantages of Orthogonal Frequency Division Multiplexing (OFDM) and Code Division Multiple Access (CDMA)^24,25. The multi-carrier modulation effectively mitigates frequency-selective fading, while the spread spectrum characteristics enhance signal robustness against jamming and dynamic environments^26,27. Therefore, MC-CDMA is a strong candidate to support massive access, provide reliable data communication, and improve coverage in scenarios requiring robust connectivity and satellite integration. Several recent studies further highlight the benefits of using MC-CDMA. In²⁸, a novel downlink multicarrier direct-sequence code division multiple access (MC-DS-CDMA) resource allocation scheme was proposed to achieve higher throughput in low Earth orbit (LEO) satellite-ground integrated networks. In²⁹, a multicarrier direct-sequence CDMA scheme was introduced to improve performance with lower energy consumption. In³⁰, serial bicode and serial multicode direct-sequence spread-spectrum techniques were extended to CDMA for efficient synchronization in MEO and LEO systems. In³¹, a codomain detection method for free-space optical communications was developed based on pseudorandom code spread-spectrum modulation, and in³², CDMA signals utilizing analog chirp filters were applied for joint sensing and communication (JSAC) in IoT applications. These studies collectively demonstrate the significant advantages and strong potential of integrating MC-CDMA signaling into next-generation V2X communication systems.

Beamforming management

There are a number of studies where DRL has been applied for beam tracking, beam management, and handover in V2X communications. In³³, a distributed multi-user multi-agent deep Q-learning (DQL) algorithm was proposed for beam tracking to adapt to dynamic environments, where each user is treated as an independent agent. Similarly³⁴, introduced a distributed multi-agent double deep Q-learning algorithm for beamforming, allowing multiple base stations (BSs) to automatically and dynamically adjust their beams to serve multiple highly mobile user equipments (UEs). The work in³⁵ presented a machine learning-based method for optimizing beam pair selection and update timing for a single gNB and a single UE. On the other hand, in mmWave communications, where the high carrier frequency exacerbates the effects of path loss, fading, and Doppler shift³⁶, proposed a collaborative beamforming strategy based on Deep Q-Network (DQN) reinforcement learning to address sidelobe interference in 5G networks. An interesting approach was introduced in³⁷, where an intelligent beam management scheme based on a deep RL algorithm was proposed to balance the trade-off between achievable performance and beam training overhead for high-speed train communications. Furthermore³⁸, proposed a novel DRL-based coordinated beamforming scheme to generate suboptimal beamforming vectors, where multiple base stations jointly serve a single mobile station.

In addition, a V2V resource allocation framework based on double deep Q-network (DDQN) was proposed in³⁹ to intelligently allocate resources and reduce signaling overhead. For vehicle handover management under high mobility conditions^40,41, proposed deep Q-learning-based algorithms. However, there has yet to be a fully integrated algorithm that simultaneously addresses both beam tracking and handover in V2X systems. Moreover, it is observed that reducing the signal synchronization time (i.e., increasing the effective transmission time) could improve the system-wide effective bit rate. To further enhance communication efficiency, lower transmission power, and mitigate interference, mmWave communication systems increasingly adopt MIMO transceiver architectures with large-scale antenna arrays. As a result, the beamwidth becomes extremely narrow, and due to the high-speed mobility of vehicles, stricter and more precise beam management is required.

While model-based methods such as the Kalman Filter have been used in beam tracking⁴², they often underperform in high-mobility, non-linear V2X environments, especially under Rician fading and non-Gaussian dynamics. KF assumes fixed noise covariances and first-order motion models, which often fail in real-world V2X contexts. Likewise, continuous-action DRL methods such as Proximal Policy Optimization (PPO) and Deep Deterministic Policy Gradient (DDPG) require structural adaptation to operate in discrete beam selection environments⁴³.

Motivation and contributions

Motivated by the mentioned research gap, in this paper, we consider a large-scale dynamic V2X network, where multiple RSUs are deployed to serve high speed vehicles on highways. We aim at an effective method based on the integration of a specialized modulation scheme that enhances coverage to maintain UE operation, and a beamforming technique tailored for dynamical and complex environments. The ultimate goal is to improve the total system throughput by optimizing the beamforming process to minimize the number of RSU-by-RSU placements, meanwhile maintaining the robustness of the signal under interference by MC-CDMA modulation mode.

Our research approaches include:

1) Towards the development of a V2X network architecture and a coverage extension mechanism based on a selective MC-CDMA transmission scheme, designed to ensure signal robustness in dynamical, complex propagation environments.

2) Towards a context-aware interference management framework for V2X. Most existing works estimate an achievable sum rate based on signal models where interference is assumed to originate from all transmissions other than the user of interest. In contrast, our study quantitatively models the impact of beam directions to enable optimal beam interference management.

3) Towards a DRL for beam generation, tracking, handover among RSUs and adaptive selection of the MC-CDMA mode.

While conventional approaches focus on the transmission from a single RSU (acting as the base station) to its associated users and design beam management algorithms solely on the RSU side, this paper proposes an efficient DRL framework for V2X communication that jointly optimizes beamforming strategies and transmission mode selection (MC-CDMA vs. OFDM). Our framework is designed to operate effectively in high-mobility, complex highway environments characterized by vehicle density and dynamic fading. To reflect the realistic physical behavior of beam steering, lever-arm dynamics are modeled in the state-space domain, allowing continuous and interpretable beam adaptation. The transmission strategy is selected via a selective MC-CDMA operation mode, which improves robustness under harsh propagation conditions.

Unlike conventional codebook-based methods that rely on exhaustive scanning or fixed beam directions, resulting in scalability issues. Our approach reduces computational overhead and mitigates overfitting through:

• A multi-agent, multi-head neural architecture, where each RSU operates as an independent agent with partial observation.

• Joint training of beamforming and transmission mode policies, enabling adaptive learning without increasing model complexity.

• Selective action spaces to reduce redundant beam search, improving convergence speed and generalization across traffic patterns.

This joint optimization ensures efficient resource allocation, robust connectivity, and practical deployability in edge-enabled intelligent transportation systems.

Our contributions in this paper are summarized as follows:

1) Signal modeling and coverage extension via MC-CDMA transmission: We propose a novel signal model, and a coverage extension mechanism based on a selective MC-CDMA transmission scheme. We formulate the corresponding optimization problem and develop a comprehensive mmWave communication model between RSU and UE, incorporating delay spread, pathloss modeling, and a highway V2X fading channel that accounts for Doppler shifts.

2) Context-aware interference management in V2X: We introduce a context-aware interference management strategy tailored to V2X environments, in which interference is quantitatively modeled to align with AI-based algorithmic decision-making frameworks. This approach enables more efficient and adaptive interference control under realistic V2X scenarios.

3) Beam dynamics and DRL framework: To reflect realistic beam movement, we propose to describe the physical behavior of beamforming via lever-arm dynamics in the state-space domain. Unlike traditional codebook-based beamforming methods, where beam vectors are selected randomly or exhaustively scanned during the initialization phase. Our approach overcomes limitations in complex environments with a large number of users and beam directions.

In this study, we propose an efficient DRL framework that integrates lever-arm beamforming dynamics in the state-space with selective MC-CDMA operation modes for robust and adaptive V2X communication.

4) We demonstrate that our method has fast convergence by extensive simulations. In addition, the proposed method outperforms the conventional methods.

The rest of the paper is organized as follows. Section “Material and Methods” presents network architecture, resource block-based MC-CDMA signal model, interference management and channel model, continous beamforming, optimization problem formulation, and proposed deep reinforcement learning model. Section “Results and Discussion” provides simulation results and performance of the proposed algorithm. Finally, Section “Conclusion” presents concluding remarks, and suggestions for further research of this paper.

Throughout the paper, bold capital letters are denoted for matrices, while lowercase bold letters are for vectors, (.)^T and (.)^H stand for transpose, Hermitian transpose of (.), respectively. Other notations are summarized in Table 1.

Table 1 Summary of notations.

Materials and methods

Network architecture

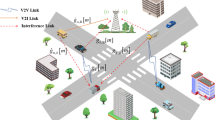
In this work, we consider a V2X mmWave communication system in 6G networks, deployed with multiple Roadside Units (RSUs) positioned along a highway spanning ${L_{total}}$ km, serving a set of connected vehicles equipped with Onboard Units (OBUs). The traffic density is defined as the number of vehicles per unit length of the highway (e.g., vehicles/km), as illustrated in Fig. 1. For simplicity, Fig. 1 only depicts RSU₁ and RSU₂ out of all available ${N_{RSU}}$RSUs. Here, the vehicles are served by beams generated from beamformers designed within the RSUs.

Each RSU is equipped with ${N_{rf}}$ fully connected radio frequency chains. The maximum number of UEs that an RSU can serve simultaneously is U. In this case, we have $U={N_{rf}}$. To steer beams toward the UEs, the RSU employs an analog beamforming architecture with phase shifters. The analog beamformer is equipped with ${N_t}$ transmit antennas. The number of RF chains is typically much smaller than the number of antennas, i.e., ${N_{rf}} \ll {N_t}$.

Regarding the system architecture, since each RSU is equipped with an analog beamformer, it must incorporate a beamformer control mechanism that can: (1) dynamically generate beams on demand, and (2) perform efficient, adaptive beam tracking to maintain connectivity with high-speed and very-high-speed vehicles.

Resource block-based MC-CDMA signal model

The system model with MC-CDMA operation mode and integrated analog beamformer is illustrated in Fig. 2. Let ${{\mathbf{b}}_{i,u}}=\{ {b_{i,u}}(n)\}$ denote the binary input data sequence of u-th UE which is served by i-th RSU at time instant n.

Fig. 1

Overview of Multi-RSU Deployment for Highway V2X Networks.

Fig. 2

Proposed Analog Beamforming and MC-CDMA Operation Scheme for RSU.

Suppose that ${b_{i,u}}(n)$takes values ± 1 with equal probability and bit period T_b. The input data is channel encoded, scrambled to assure that the noise affecting each symbol is independent, then fed through symbol mapper (using modulation schemes such as BPSK, QPSK, QAM…) to create modulated data symbols $\{ {a_{i,u}}\}$. M-ary symbol mapping ${{\mathbf{b}}_{i,u}}(s) \in {\{ 0,1\} ^{q \times 1}} \mapsto {a_{i,u}} \in {{\mathbf{\chi }}_u}$ is implemented as follows. Data is partitioned into segments of length q, each segment includes combination of q bits of data ${{\mathbf{b}}_{i,u}}(s)=[{b_{i,u}}(s),{b_{i,u}}(s+1),...,{b_{i,u}}(s+q)]$, where s denotes s-th symbol with symbol period ${T_s}=q{T_b}$. Each combination chooses one of M available symbols from M-ary alphabet ${{\mathbf{\chi }}_u}=\{ {a_{u,1}},{a_{u,2}},...,{a_{u,M}}\}$, where ${a_{u,m}} \in {\mathbb{C}}$, and $M={2^q}$. Next, the code mapper performs Resource Allocation Schemes with spreading codes as follows. The principle of MC-CDMA modulation is that the MC-CDMA signal of each user is created by a spreading code. Each data symbol is spread over the entire cycle of the spreading code. The entire spreading code cycle is transmitted simultaneously by assigning each chip of the code to a separate OFDM subcarrier.

To ensure practical relevance, we integrate the MC-CDMA modulation with Resource Allocation Schemes in the form of a Resource Grid, following the 5G NR architecture, as illustrated in Fig. 3. The frame structure shown in Fig. 3 follows the 3GPP 5G NR standard. The number of slots per subframe is${2^\mu }$ (i.e. $N_{{slot}}^{{(\mu )}}={2^\mu }$), where µ is subcarrier spacing (SCS) index, µ = 0, 1, …, 4. The slot duration depends on µ. 5G NR supports two frequency ranges FR1 (Sub 6 GHz) and FR2 (millimeter wave range, 24.25 to 52.6 GHz). 5G NR uses flexible SCS derived from basic 15 kHz used in LTE to values of 30, 60, 120 kHz. For SCS of 15 kHz, a subframe has 1 slot of 1 ms duration. The total number of subcarriers is ${N_{total}}={{B{W_{total}}} \mathord{\left/ {\vphantom {{B{W_{total}}} {\Delta f}}} \right. \kern-0pt} {\Delta f}}$, where BW_total represents the total system bandwidth. Suppose that at the i-th RSU, U_i users are allocated a bandwidth part BWP_i, which consists of $N_{c}^{{(i)}}$​ subcarriers, where $N_{c}^{{(i)}}={{BW{P_i}} \mathord{\left/ {\vphantom {{BW{P_i}} {\Delta f}}} \right. \kern-0pt} {\Delta f}}$, starting from the frequency ${f_0}={k_0} \times \Delta f.$​ U_i users transmit $N_{s}^{{(i)}}$​ consecutive OFDM symbols within a subframe, beginning with symbol index s₀​.

Without loss of generality, we consider a typical generalized MC-CDMA system model where the processing gain (i.e. code sequence length) G equals the number of subcarriers $G=N_{c}^{{(i)}}$. The data of the u-th user served by the i-th RSU ${{\mathbf{a}}_{i,u}} \in {{\mathbb{C}}^{N_{s}^{{(i)}} \times 1}}$is ${{\mathbf{a}}_{i,u}}={\left[ {\begin{array}{*{20}{c}} {a_{u}^{{(i)}}(0)}&{a_{u}^{{(i)}}(1)}& \cdots &{a_{u}^{{(i)}}(N_{s}^{{(i)}} - 1)} \end{array}} \right]^T}.$ The user data of all U_i UEs served by the i-th Roadside Unit (RSU) is expressed as a matrix ${{\mathbf{A}}_{i,{U_i}}}={\left[ {\begin{array}{*{20}{c}} {{\mathbf{a}}_{{i,1}}^{T}}&{{\mathbf{a}}_{{i,2}}^{T}}& \cdots &{{\mathbf{a}}_{{i,{U_i}}}^{T}} \end{array}} \right]^T}$.

Fig. 3

Proposed Code Mapping and Resource Element Allocation Framework.

Code mapper and RE mapper for MC-CDMA operation

The Walsh-Hadamard matrix used as spreading codes for Ui users takes the form ${{\mathbf{C}}_{i,{U_i}}}={\left[ {\begin{array}{*{20}{c}} {{{\mathbf{c}}_{i,1}}}&{{{\mathbf{c}}_{i,2}}}& \cdots &{{{\mathbf{c}}_{i,{U_i}}}} \end{array}} \right]^T}$, where each row ${{\mathbf{c}}_{i,u}}={\left[ {\begin{array}{*{20}{c}} {{c_{i,u,0}}}&{{c_{i,u,1}}}& \cdots &{{c_{i,u,N_{c}^{{(i)}} - 1}}} \end{array}} \right]^T} \in {\left\{ {+1, - 1} \right\}^{N_{c}^{{(i)}} \times 1}}$ in the orthogonal Walsh-Hadamard ${{\mathbf{C}}_{i,{U_i}}} \in {\left\{ {+1, - 1} \right\}^{N_{c}^{{(i)}} \times N_{c}^{{(i)}}}}$​ forms an orthogonal code sequence assigned to each user. The IDFT matrix for multicarrier modulation starting from index k₀ is given by.

$${\mathbf{F}}_{{N_{c}^{{(i)}}}}^{{ - 1}}=\frac{1}{{{N_{total}}}}\left[ {\begin{array}{*{20}{c}} {{e^{j\frac{{2\pi {k_0} \cdot 0}}{{{N_{{\text{total}}}}}}}}}&{{e^{j\frac{{2\pi ({k_0}+1) \cdot 0}}{{{N_{{\text{total}}}}}}}}}& \cdots &{{e^{j\frac{{2\pi ({k_0}+N_{c}^{{(i)}} - 1) \cdot 0}}{{{N_{{\text{total}}}}}}}}} \\ {{e^{j\frac{{2\pi {k_0} \cdot 1}}{{{N_{{\text{total}}}}}}}}}&{{e^{j\frac{{2\pi ({k_0}+1) \cdot 1}}{{{N_{{\text{total}}}}}}}}}& \cdots &{{e^{j\frac{{2\pi ({k_0}+N_{c}^{{(i)}} - 1) \cdot 1}}{{{N_{{\text{total}}}}}}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{e^{j\frac{{2\pi {k_0} \cdot (N_{c}^{{(i)}} - 1)}}{{{N_{{\text{total}}}}}}}}}&{{e^{j\frac{{2\pi ({k_0}+1) \cdot (N_{c}^{{(i)}} - 1)}}{{{N_{{\text{total}}}}}}}}}& \cdots &{{e^{j\frac{{2\pi ({k_0}+N_{c}^{{(i)}} - 1) \cdot (N_{c}^{{(i)}} - 1)}}{{{N_{{\text{total}}}}}}}}} \end{array}} \right]$$

(1)

The signal of u-th UE after code mapper and RE mapper, IFFT conversion, ${{\mathbf{s}}_{i,u}} \in {{\mathbb{C}}^{N_{c}^{{(i)}} \times N_{s}^{{(i)}}}}$is

$${{\mathbf{s}}_{i,u}}={\mathbf{F}}_{{N_{c}^{{(i)}}}}^{{ - 1}} \cdot {{\mathbf{c}}_{i,u}} \cdot {\mathbf{a}}_{{i,u}}^{T}$$

(2)

Each sample ${s_{i,u}}(n,k)$ of ${{\mathbf{s}}_{i,u}}$in the time domain $n=1..N_{s}^{{(i)}}$ and frequency $k=1..N_{c}^{{(i)}}$is analog precoded on $N_{t}^{{(i)}}$ antennas, assuming in Uniform Linear Array (ULA) configuration with inter-element spacing d, the precoding vector is given by

$${{\mathbf{w}}_{i,u}}=\frac{1}{{\sqrt {N_{t}^{{(i)}}} }}{\left[ {\begin{array}{*{20}{c}} {\;\;\begin{array}{*{20}{c}} 1&{{e^{j2\pi \frac{d}{\lambda }\sin {\theta _u} \cdot 1}}}&{{e^{j2\pi \frac{d}{\lambda }\sin {\theta _u} \cdot 2}}}& \cdots &{{e^{j2\pi \frac{d}{\lambda }\sin {\theta _u} \cdot (N_{t}^{{(i)}} - 1)}}} \end{array}} \end{array}} \right]^T}$$

(3)

The transmitted signal matrix for the u-th user after analog precoding ${{\mathbf{x}}_{i,u}} \in {{\mathbb{C}}^{{N_t}N_{c}^{{(i)}} \times N_{s}^{{(i)}}}}$ is given by

$${{\mathbf{x}}_{i,u}}=({{\mathbf{w}}_{i,u}} \otimes {{\mathbf{I}}_{N_{c}^{{(i)}}}}) \cdot {\mathbf{F}}_{{N_{c}^{{(i)}}}}^{{ - 1}} \cdot {{\mathbf{c}}_u} \cdot {\mathbf{a}}_{{i,u}}^{T}$$

(4)

The aggregate transmitted signal matrix for all Ui users is expressed as

$${{\mathbf{X}}_{i,{U_i}}}=\sum\limits_{{u=1}}^{{{U_i}}} {{{\mathbf{x}}_{i,u}}}$$

(5)

Assume channel estimation is performed over all $N_{c}^{{(i)}}$subcarriers and $N_{s}^{{(i)}}$ symbols. Denote ${{\mathbf{h}}_{i,u,k}} \in {{\mathbb{C}}^{N_{t}^{{(i)}} \times N_{s}^{{(i)}}}}$ the channel vector between the i-th RSU and u-th user on the k-th subcarrier across all symbols, where $N_{t}^{{(i)}}$ is the number of transmit antennas at the i-th RSU. The channel matrix for the u-th user is ${{\mathbf{H}}_{i,u}} \in {\left[ {\begin{array}{*{20}{c}} {{\mathbf{h}}_{{i,u,1}}^{H}}&{{\mathbf{h}}_{{i,u,2}}^{H}}& \cdots &{{\mathbf{h}}_{{i,u,N_{c}^{{(i)}}}}^{H}} \end{array}} \right]^T} \in {{\mathbb{C}}^{N_{c}^{{(i)}} \times N_{t}^{{(i)}}N_{s}^{{(i)}}}}$. The received signal of u-th user can be written as

$$\begin{gathered} {{\mathbf{Y}}_{i,u}}={{\mathbf{H}}_{i,u}}{{\mathbf{X}}_{i,{U_i}}}+{{\mathbf{n}}_{i,u}} \\ =\underbrace {{{{\mathbf{H}}_{i,u}}{{\mathbf{x}}_{i,u}}}}_{{{\text{Desired}}\,{\text{Signal}}}}+\underbrace {{{{\mathbf{H}}_{i,u}}\sum\limits_{{v=1,v \ne u}}^{{{U_i}}} {{{\mathbf{x}}_{i,v}}} }}_{{{\text{Intra-}}{\text{RSU}}\,{\text{Interference}}}}+\underbrace {{{{\mathbf{H}}_{i,u}}\sum\limits_{{j=1,j \ne i}}^{{{N_{RSU}}}} {\sum\limits_{{v=1}}^{{{U_j}}} {{{\mathbf{x}}_{j,v}}} } }}_{{{\text{Inter-}}{\text{RSU}}\,{\text{Interference}}}}+\underbrace {{{{\mathbf{n}}_{i,u}}}}_{{{\text{Noise}}}} \\ \end{gathered}$$

(6)

where n_i,u is the complex additive white Gaussian noise with zero mean and variance equal to $\sigma _{{i,u}}^{2},$i.e.${{\mathbf{n}}_{i,u}}\sim \mathcal{C}\mathcal{N}(0,\sigma _{{i,u}}^{2}{{\mathbf{I}}_{N_{c}^{{(i)}} \times N_{s}^{{(i)}}}}).$

Interference management and channel model

Path loss and fading model

This study focuses on V2V and V2I communications on highways. To accurately compute the received signal power at the receiver and to implement beam adjustment algorithms that ensure optimal channel quality, it is necessary to account for channel loss. The loss model incorporates both delays spread (DS) and Doppler spread effects. Due to the high and very high mobility of vehicles, the wireless propagation environment varies rapidly with speed⁴⁴. As a result, Doppler effects significantly impact signal transmission. Path loss is calculated based on the Urban Macrocell (UMa) model, defined in 3GPP TR 38.901, which is applicable for coverage distances ranging from 500 m to 5 km⁴⁵.

In this highway V2X fading channel model, the received signals are predominantly line-of-sight (LoS) and follow a Rician distribution, with delay spreads ranging from 20 to 100 nanoseconds and Doppler spreads that can reach up to 1 kHz⁴⁶. In a map-based channel model, the path loss is simplified and expressed using three parameters, A, B, and C, as follows:

$$P{L_{dB}}=A\,{\text{lo}}{{\text{g}}_{10}}\left( {\tfrac{d}{{1{\text{m}}}}} \right)+B\,{\text{lo}}{{\text{g}}_{10}}\left( {\tfrac{f}{{1{\text{GHz}}}}} \right)+C$$

(7)

.

where, d is the distance between the transmitter and receiver (in meters), f_c​ is the carrier frequency (in GHz), A, B, C are model-specific constants determined by the propagation scenario.

The LoS path loss model is

$$P{L_{LOS}}=\left\{ {\begin{array}{*{20}{c}} {P{L_1},}&{10{\text{m}} \leqslant {d_{2{\text{D}}}} \leqslant d_{{BP}}^{\prime },} \\ {P{L_2},}&{d_{{BP}}^{\prime } \leqslant {d_{2{\text{D}}}} \leqslant 5{\text{km,}}} \end{array}} \right.$$

(8)

where

$$\begin{gathered} P{L_1}=22\,{\text{lo}}{{\text{g}}_{10}}\left( {\tfrac{{{d_{3{\text{D}}}}}}{{1{\text{m}}}}} \right)+20\,{\text{lo}}{{\text{g}}_{10}}\left( {\tfrac{{{f_c}}}{{1{\text{GHz}}}}} \right)+28.0 \hfill \\ P{L_2}\,=40\,{\text{lo}}{{\text{g}}_{10}}\left( {\tfrac{{{d_{3{\text{D}}}}}}{{1{\text{m}}}}} \right)+20\,{\text{lo}}{{\text{g}}_{10}}\left( {\tfrac{{{f_c}}}{{1{\text{GHz}}}}} \right)+28.0 - 9\,{\text{lo}}{{\text{g}}_{10}}\left[ {{{\left( {\tfrac{{d_{{{\text{BP}}}}^{\prime }}}{{1{\text{m}}}}} \right)}^2}+{{\left( {\tfrac{{{h_{RSU}} - {h_{{\text{UE}}}}}}{{1{\text{m}}}}} \right)}^2}} \right]. \hfill \\ \end{gathered}$$

(9)

The NLoS path loss model is

$$P{L_{NLOS}}=\hbox{max} (P{L_{LOS}},PL_{{NLOS}}^{\prime })$$

(10)

where

$$PL_{{NLOS}}^{\prime }=13.54+39.08{\log _{10}}(\tfrac{{{d_{3D}}}}{{1m}})+20{\log _{10}}(\tfrac{{{f_c}}}{{1GHz}}) - 0.6({h_{UE}} - 1.5)$$

(11)

and breakpoint (BP) distance $d_{{BP}}^{\prime }$ is given by⁴⁷

$$d_{{BP}}^{\prime }={\alpha _{BP}}\frac{{4h_{{RSU}}^{\prime }h_{{UE}}^{\prime }{f_c}}}{c}$$

(12)

where f_c is the center frequency, c is the speed of light, and α_BP is a breakpoint scaling factor, which is a function of the radio frequency and is introduced as

$${\alpha _{BP}}=0.87{e^{ - \frac{{{\text{lo}}{{\text{g}}_{10}}\left( {\frac{{{f_c}}}{{1{\text{GHz}}}}} \right)}}{{0.65}}}}$$

(13)

and $h_{{RSU}}^{\prime }$ and $h_{{UE}}^{\prime }$ are the effective antenna heights at RSU and UE, respectively. The effective antenna heights $h_{{RSU}}^{\prime }={h_{RSU}} - {h_E}$ and $h_{{UE}}^{\prime }={h_{UE}} - {h_E}$, where h_RSU and h_UE are the actual antenna heights, and h_E is the effective environmental height. For UMa h_E = 1 m.

$${P_{LOS}}(d)=\hbox{min} (\frac{{18}}{d},1)(1 - {e^{ - \frac{d}{{36}}}})+{e^{ - \frac{d}{{36}}}}$$

(14)

Therefore, the probability of non-line-of-sight (NLoS) occurrence is $1 - {P_{LOS}}(d)$.

Delay spread loss

Delay Spread (DS) is a critical parameter in wireless channel modeling, describing the time dispersion between the direct (Line-of-Sight, LoS) signal and the reflected or scattered (Non-Line-of-Sight, NLoS) signal components arriving at the receiver. It is typically quantified by the Root Mean Square (RMS) Delay Spread, which is calculated as follows.

$${\tau _{RMS}}=\sqrt {\frac{{\sum\nolimits_{{i=1}}^{N} {{P_i}{{({t_i} - \bar {t})}^2}} }}{{\sum\nolimits_{{i=1}}^{N} {{P_i}} }}}$$

(15)

where t_i denotes the arrival time of the i-th propagation path, P_i is the power of the i-th path, N is number of paths, and $\bar {t}$is the mean delay of all received paths. The Delay Spread is modeled as a log-normal distribution with mean µ_τ​ and standard deviation σ_τ​, depending on the distance from the RSU to the vehicle as ${\tau _{{\text{DS}}}}\sim \mathcal{N}({\mu _\tau },{\sigma _\tau })$, RMS value of delay spread is ${\tau _{RMS}}\ominus ={10^{\mathcal{N}({\mu _\tau },{\sigma _\tau })}}$seconds, where µ_τ​ is calculated by${\mu _\tau }= - 7.03+0.11{\log _{10}}(d),$ ${\sigma _\tau }=0.18,$and d is the distance between transmitter and receiver (in meters).

Delay spread can impact path loss, as it reflects the degree of signal dispersion caused by reflection, scattering, and diffraction components in the propagation environment. When the delay spread is large, particularly in OFDM-based systems, inter-symbol interference (ISI) may occur, leading to data loss and increased effective attenuation. To account for this, path loss can be adjusted based on the delay spread, using empirical models to estimate the excess path loss (EPL) introduced by time dispersion. The adjusted path loss model that incorporates delay spread can be expressed as:

$$PL(d)=P{L_0}(d)+{k_{DS}}{\log _{10}}({\tau _{RMS}})$$

(16)

where PL₀​(d) is basic Path Loss (LoS or NLoS) at distance d, ${\tau _{RMS}}$is RMS of Delay Spread (ns), and ${k_{DS}}$is the empirical DS coefficient, typically ranges from 5 to 15 dB, depending on the characteristics of the propagation environment. As a result, the average path loss from the RSU to the user is obtained as

$$PL(d)={P_{LOS}}(d) \cdot P{L_{LOS}}+(1 - {P_{LOS}}(d)) \cdot P{L_{NLOS}}+{k_{DS}}{\log _{10}}({\tau _{RMS}})$$

(17)

Highway V2X fading channel model with doppler shift

The received signal follows a Rician distribution, with a delay spread ranging from 20 to 100 ns, and a Doppler spread of up to 1 kHz under practical conditions. Rician K-factor K is defined as the ratio between the power of LoS component to NLoS components as $K={{{P_{LOS}}} \mathord{\left/ {\vphantom {{{P_{LOS}}} {{P_{Scattered}}}}} \right. \kern-0pt} {{P_{Scattered}}}}$. Doppler Frequency is ${f_D}=\tfrac{v}{c}{f_c},$​ where v is velocity of UE (m/s) and f_c, c being the carrier frequency and the light speed, respectively. Accordingly, the channel matrix in a Rician fading channel with delay spread and Doppler shift is defined as follows.

$${\mathbf{H}}(t)=\sqrt {\frac{K}{{K+1}}} {{\mathbf{H}}_{{\text{LoS}}}}(t)+\sqrt {\frac{1}{{K+1}}} \sum\limits_{{l=1}}^{L} {{\alpha _l}} \cdot {e^{j2\pi {f_{D,l}}t}} \cdot {e^{ - j2\pi {f_s}{\tau _l}}}{{\mathbf{a}}_R}({\phi _l}){\mathbf{a}}_{T}^{H}({\theta _l})$$

(18)

where, ${{\mathbf{H}}_{{\text{LoS}}}}(t)={{\mathbf{a}}_R}({\phi _{{\text{LoS}}}}){\mathbf{a}}_{T}^{H}({\theta _{{\text{LoS}}}})$is LoS component of channel matrix, L is number of multipath,${f_{D,l}}=\tfrac{v}{c}{f_c}\cos ({\phi _l})$ is Doppler Shift of l-th path, ${\tau _l}={{{d_l}} \mathord{\left/ {\vphantom {{{d_l}} c}} \right. \kern-0pt} c}$ is delay of l-th path, ${{\mathbf{a}}_T}({\theta _l})=\tfrac{1}{{\sqrt {{N_t}} }}{[1,{e^{ - j\tfrac{{2\pi }}{\lambda }d\sin ({\theta _l})}},...,{e^{ - j\tfrac{{2\pi }}{\lambda }({N_t} - 1)d\sin ({\theta _l})}}]^T}$ is transmit steering vector, ${{\mathbf{a}}_R}({\phi _l})=\tfrac{1}{{\sqrt {{N_r}} }}{[1,{e^{ - j\tfrac{{2\pi }}{\lambda }d\sin ({\phi _l})}},...,{e^{ - j\tfrac{{2\pi }}{\lambda }({N_r} - 1)d\sin ({\phi _l})}}]^T}$ is receive steering vector, and ${N_r}$is number of anten at receiver. In case UE has one antenna, (i.e., ${N_r}=1$), the receive steering vector becomes ${{\mathbf{a}}_R}({\phi _l})=1$.

Interference management in 6G V2X

Interference caused by multiple users sharing the same V2X infrastructure can generally be categorized into two types: co-channel interference and adjacent-channel interference. Similarly, in V2X systems employing beamforming techniques, we define two types of interference: Co-beam interference: occurs when two user equipments (Ues) are located such that their beams may overlap, for example, two vehicles moving in parallel in the same lane or crossing paths at the time of data transmission. Adjacent beam interference occurs when the beams serving different Ues are spatially close but not directly overlapping. The interference modeling is illustrated in Fig. 4.

Interference is classified into two main categories: intra-RSU interference and inter-RSU interference. As shown in Fig. 4, we have two cases. Case a: Obstacle Loss. In V2X systems, when an obstacle (e.g., a vehicle) is located between the Base Station (BS) and the User Equipment (UE), the transmitted signal experiences additional attenuation due to diffraction and absorption caused by the obstructing object.

Fig. 4

Interference characterization for V2X systems on highways.

The obstacle loss model characterizes the signal attenuation resulting from the obstruction of the direct line-of-sight path. This type of loss can be modeled using diffraction loss based on the knife-edge theory. The obstacle loss $P{L_{obs}}$can be calculated using the Fresnel diffraction parameter v, as follows:

$$P{L_{obs}}=10{\log _{10}}\left( {1+{{\left( {\tfrac{v}{2}} \right)}^2}} \right)$$

(19)

The Fresnel diffraction parameter, which quantifies the degree of diffraction by treating the obstacle as a knife-edge, is calculated as

$$v=h\sqrt {\frac{2}{\lambda }\left( {\frac{1}{{{d_1}}}+\frac{1}{{{d_2}}}} \right)}$$

(20)

where d₁ is the distance from the RSU (transmitter) to the obstacle (e.g., a vehicle), d₂​ is the distance from the obstacle to the target vehicle (receiver), h is the effective height of the obstacle relative to the direct line-of-sight path between the RSU and the target vehicle, λ is the wavelength. Finally, the total path loss incorporating obstacle loss is given by

$$P{L_{total}}=PL(d)+P{L_{obs}}$$

(21)

Case b: Inter-RSU interference: The signal received by the bus is a superposition of transmissions from two different RSUs, both aiming at their respective target users. As a result, the interference power is defined as the received power at the target UE from non-serving RSUs transmitting in the direction of the UE on the same subcarrier or frequency resource as the desired signal.

The extended range transmission model using MC-CDMA

Consider the u-th UE in the i-th RSU, denote d_{i, u} is the distance from RSU to UE. Combining large-scale path-loss component PL(d_{i, u}) and small-scale fading channel gain components, the receive power at u-th UE is

$$P_{r}^{{(i,u)}}({d_{i,u}})=G_{t}^{{(i,u)}} \cdot G_{r}^{{(i,u)}} \cdot \left\| {{{\mathbf{H}}_{i,u}}} \right\|_{F}^{2} \cdot {10^{ - \frac{{PL({d_{i,u}})+\alpha _{{i,u}}^{{MC - CDMA}}G_{c}^{{(i)}}}}{{10}}}} \cdot P_{t}^{{(i,u)}}=G_{{total}}^{{(i,u)}} \cdot P_{t}^{{(i,u)}}$$

(22)

where $P_{t}^{{(i,u)}}$is the transmit power of the RSU, $G_{t}^{{(i,u)}}$and $G_{r}^{{(i,u)}}$ are the transmit and receive antenna gains, respectively, H_{i, u} is the channel matrix between the i-th RSU and the u-th UE. The term $\left\| {({{\mathbf{H}}_{i,u}})} \right\|_{F}^{2}$ denotes the squared Frobenius norm of the channel matrix, representing the total power gain across all subcarriers and antenna elements. PL(d_{i, u}) represents the total distance-dependent path loss in decibels (dB). The total path loss PL(d_{i, u}) is typically modeled by$PL({d_{i,u}})=PL_{{ref}}^{{(i,u)}}+10 \cdot \beta _{{ref}}^{{(i,u)}}\log ({d_{i,u}})$, where $PL_{{ref}}^{{(i,u)}}$ is the reference path loss at 1 m, $\beta _{{ref}}^{{(i,u)}}$ is the path loss exponent, and d_{i, u} is the distance between RSU and UE.

The factor $\alpha _{{i,u}}^{{MC - CDMA}}.G_{c}^{{(i)}}$, where $G_{c}^{{(i)}}=10\log (N_{c}^{{(i)}})$, represents the coding gain provided by MC-CDMA (in dB), with $\alpha _{{i,u}}^{{MC - CDMA}}=1$ when CDMA mode is enabled and $\alpha _{{i,u}}^{{MC - CDMA}}=0$ otherwise.

The exponential term ${10^{ - \frac{{PL({d_{i,u}})+\alpha _{{i,u}}^{{MC - CDMA}}G_{c}^{{(i)}}}}{{10}}}}$ converts the total path loss from logarithmic to linear scale.

Fig. 5

MC-CDMA-based extended coverage scheme with code mapping.

The receiver sensitivity $P_{{\hbox{min} }}^{{(i)}}$ (in dBm) of the i-th UE is given by

$$P_{{\hbox{min} }}^{{(i)}}={N_0}+10{\log _{10}}\left( {\frac{{BW{P_i}}}{{{U_i}}}} \right)+NF+SN{R_{\hbox{min} }}$$

(23)

where N₀​ is the one-sided power spectral density of white Gaussian noise (in dBm/Hz), typically − 174 dBm/Hz at 290 K, NF is the receiver’s noise figure (typically 3–7 dB), and SNR_min is the minimum required signal-to-noise ratio to decode the signal reliably, depending on the modulation format (normally from − 3 dB to + 3 dB).

To ensure received signal quality, we must maintain $P_{r}^{{(i,u)}}({d_{i,u}}) \geqslant P_{{\hbox{min} }}^{{(i)}}$. Consequently, as shown in Fig. 5, to ensure that the received signal power exceeds the receiver sensitivity threshold, the path loss must remain below a certain limit, which defines the maximum allowable communication range for a given modulation scheme. When MC-CDMA mode is used, the effective range can be extended due to coding gain.

The maximum enhanced distance ratio, comparing MC-CDMA to a non-coding reference such as OFDM, is approximated as

$${\text{Distance ratio}}=\frac{{d_{{i,u}}^{{(\hbox{max} ,MC - CDMA)}}}}{{d_{{i,u}}^{{(\hbox{max} ,OFDM)}}}}=10{}^{{\frac{{G_{c}^{{(i)}}}}{{10\beta _{{ref}}^{{(i,u)}}}}}}$$

(24)

where $d_{{i,u}}^{{(\hbox{max} ,MC - CDMA)}}$is the maximum coverage distance when using MC-CDMA mode, $d_{{i,u}}^{{(\hbox{max} ,OFDM)}}$is the maximum coverage distance when using OFDM mode, respectively. Equation (24) shows that even moderate coding gains can significantly extend the effective coverage distance, particularly in propagation environments with low path loss exponents (e.g., highway LOS scenarios). However, this extended coverage comes at the cost of reduced effective bit rate, due to the spreading factor applied in MC-CDMA. Specifically, the throughput per user is reduced by a factor of $1/N_{c}^{{(i)}}$ where $N_{c}^{{(i)}}$ is the number of subcarriers and is spreading code length.

Table 2 Estimated coverage distance gain of MC-CDMA over OFDM under various coding gains and path loss exponents.

Fig. 6

Beam pattern model with scan angle discretization and main lobe/interference analysis.

Table 2 illustrates the theoretical ratio of maximum coverage distances for MC-CDMA compared to OFDM/SC-FDMA, under various coding gains and path loss exponents. The results show that even a modest coding gain of 3 dB can yield a ~ 26% coverage improvement under typical V2X highway conditions ($\beta _{{ref}}^{{(i,u)}}$= 3.0), and higher gains can nearly double the range in low-attenuation scenarios.

Beam pattern modeling

Since the RSU is equipped with an antenna array consisting of N_t elements, the transmit and receive signal strength is influenced by the array factor (AF). This factor captures the beamforming gain in a specific direction and is given by

$$AF(\theta )={\left| {\frac{{\sin ({N_t}\pi {d_a}\sin \theta /\lambda )}}{{{N_t}\sin (\pi {d_a}\sin \theta /\lambda )}}} \right|^2}$$

(25)

where ${d_a}$denotes the spacing between adjacent antenna elements, θ is the angle between the transmission/reception direction and the obstacle, and N_t is the number of elements in the transmit antenna array. The antenna gain of the RSU at angle θ is directly influenced by the array factor as ${G_t}=AF(\theta )$.

When the beam of the k-th UE is steered toward an angle θ_k ​, the phase coefficients are selected such that the signals emitted from all antenna elements constructively interfere in the desired direction θ_k. For a Uniform Linear Array (ULA) with element spacing of d/2, the steering vector at angle θ_k is commonly expressed (in 2D notation) as ${{\mathbf{w}}_k}({\theta _k})=\frac{1}{{\sqrt {{N_t}} }}{\left[ {1,{e^{j\frac{{2\pi }}{\lambda }{d_a}\sin ({\theta _k})}},...,{e^{j\frac{{2\pi }}{\lambda }({N_t} - 1){d_a}\sin ({\theta _k})}}} \right]^T}$, where λ is wavelength.

In mmWave V2X communications, the angular resolution of an antenna array with N_t elements is typically estimated based on either the main lobe beamwidth or the number of orthogonal beams that can be formed.

For a Uniform Linear Array (ULA) with N_t antenna elements, if steering vectors are uniformly spaced in the domain of sin(θ_k), then approximately N_t distinct beam directions can be generated, corresponding to N_t spatially resolvable beams. More precisely, the beamwidth (BW) determines the angular coverage of each beam and is approximately given by

$$G(\theta )=\left\{ \begin{gathered} {G_{\hbox{max} }}{\left| {AF(\theta )} \right|^2},\,\,\,\,\,\,\,\,\,\,\,\,\left| \theta \right| \leqslant BW/2, \hfill \\ 0\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| \theta \right|>BW/2. \hfill \\ \end{gathered} \right.$$

(26)

where G_max​ is the maximum gain of the main lobe. The array factor (AF) AF(θ) determines the radiation pattern of the antenna array as a function of the angle θ is written as

$$AF(\theta )=\left| {\sum\limits_{{n=1}}^{{{N_t}}} {{w_n}{e^{j(n - 1)k{d_a}\sin \theta }}} } \right|=\frac{{\sin \left( {\tfrac{{{N_t}\pi \sin \theta }}{2}} \right)}}{{{N_t}\sin \left( {\tfrac{{\pi \sin \theta }}{2}} \right)}}$$

(27)

The main lobe beamwidth, commonly measured at the − 3 dB Half Power Beamwidth (HPBW), characterizes the angular spread of the main lobe of the radiation pattern, as illustrated in Fig. 6.

• Blue region: represents the useful beam directed toward the intended UE.

• Red region: indicates the sidelobes, which may cause interference to other nearby UEs.

The HPBW of a Uniform Linear Array (ULA) can be approximated as follows:

$BW \approx \frac{{2 \cdot 0.886 \cdot \lambda }}{{{N_t} \cdot {d_a}}} \approx \frac{{102}}{{{N_t}}}$ (degrees). (28)

Since beam selection and interference decisions are often based on bit energy, while beamforming is performed based on spatial domain, it is useful to define the beam power density as the ratio between the power allocated to a beam and its angular beamwidth. To evaluate the influence of different beams on system performance, we define the power density ratio between the main lobe and the aggregate sidelobes as follows. The power of the main lobe is

$${P_{main}}=\int_{{mainlobe}} {{{\left| {AF(\theta )} \right|}^2}} d\theta$$

(29)

Total power is

$${P_{total}}=\int\limits_{{ - \pi }}^{\pi } {{{\left| {AF(\theta )} \right|}^2}d\theta }$$

(30)

Then, the main lobe power density is $\eta ={{{P_{main}}} \mathord{\left/ {\vphantom {{{P_{main}}} {BW}}} \right. \kern-0pt} {BW}}$, the side lobes density is $\varsigma ={{({P_{total}} - {P_{main}})} \mathord{\left/ {\vphantom {{({P_{total}} - {P_{main}})} {(2\pi - BW)}}} \right. \kern-0pt} {(2\pi - BW)}}$.

We see that the power density of the main lobe increases proportionally to $N_{t}^{2}$, while the power density of the sidelobes gradually decreases, owing to the improved energy focusing capability as the array size increases. This indicates that the main beam not only carries more energy but also concentrates it within a narrower angular range, whereas sidelobes spread their energy across wider angles.

From a reinforcement learning perspective, the beamspace has been discretized into a finite set of possible beam directions. Each time the receiver successfully aligns with the correct beam, the reward function is incremented (e.g., green level). Conversely, if the selected beam fails to align with the target direction, a penalty (e.g., red level) is applied to the reward function. This reinforcement learning-based framework allows the agent to gradually learn optimal beam selection policies, favoring directions with high signal power concentration (main lobes) and avoiding those dominated by interference (sidelobes).

Optimization problem formulation

Shannon’s theorem defines the channel capacity R as the maximum data rate at which information can be transmitted without error, assuming ideal channel coding. It is given by $R=B \times {\log _2}(1+\gamma )$, where B is channel bandwidth (Hz), $\gamma$represents Signal-to-Interference-plus-Noise Ratio (SINR). Similar to previous studies, in this work, we initially adopt the total sum-rate, calculated using the Shannon capacity formula above, as the performance metric for evaluating the system performance. The signal-to-interference-noise ratio (SINR) of u-th user in i-th RSU is expressed as

$${\gamma _{i,u}}=\frac{{G_{{total}}^{{(i,u)}} \cdot P_{t}^{{(i,u)}}}}{{\sum\limits_{{v=1,v \ne u}}^{{{U_i}}} {G_{{total}}^{{(i,v)}} \cdot P_{t}^{{(i,v)}}} +\sum\limits_{{j=1,j \ne i}}^{{{N_{RSU}}}} {\sum\limits_{{u=1}}^{{{U_j}}} {G_{{total}}^{{(j,u)}} \cdot P_{t}^{{(j,u)}}} +{N_0}\frac{{BW{P_i}}}{{{U_i}}}} }}$$

(31)

As a result, the effective throughput of u-th user of i-th RSU is

$${R_{i,u}}=\frac{1}{{{{(N_{c}^{{(i)}})}^{\alpha _{{i,u}}^{{MC - CDMA}}}}}} \cdot \frac{{BW{P_i}}}{{{U_i}}}{\log _2}(1+{\gamma _{i,u}})$$

(32)

where N₀ is the one-sided power spectral density of white Gaussian noise.

In summary, the total system throughput is expressed as

$${\mathcal{R}_{total}}=\sum\limits_{{i=1}}^{{{N_{RSU}}}} {\sum\limits_{{u=1}}^{{{U_i}}} {{R_{i,u}}} }$$

(33)

We aim to maximize the total system throughput by optimizing the beamforming process and minimizing the number of RSU-by-RSU placements, meanwhile we maintain the robustness of the signal under interference by MC-CDMA modulation mode. We formulate an optimization problem as

$$\begin{gathered} \hbox{max} {\mathcal{R}_{total}} \\ s.t.\,\,{\text{C}}1:\sum\limits_{{u=1}}^{{{U_i}}} {P_{t}^{{(i,u)}}} \leqslant {P_{\hbox{max} }},\forall i \in \{ 1,2,...,{N_{RSU}}\} \\ {\text{C}}2:\,\sum\limits_{{i=1}}^{{{N_{RSU}}}} {d_{{i,u}}^{{(\hbox{max} )}}} \geqslant {L_{total}},\,\,d_{{i,u}}^{{(\hbox{max} )}} \leqslant {d_{\hbox{max} }},\forall u \in \{ 1,2,...,{U_i}\} ,\forall i \in \{ 1,2,...,{N_{RSU}}\} , \\ \end{gathered}$$

(34)

where, C1 is the power constraint: The total transmit power must not exceed a predefined threshold. C2 is deployment and coverage constraint: The inter-RSU distances must satisfy optimal coverage criteria, and ensure the number of RSUs remains within the allowable limit.

Proposed DRL model

In this part, a machine learning-based approach is proposed to support beam generation, reception, and tracking for vehicle handover, reception, and mobility management in highly dynamic V2X environments. The beam synchronization process for tracking the movement of vehicles consists of two stages: the Beam Acquisition Phase and the Beam Tracking Phase.

a) Beam Acquisition Phase: This phase includes two mechanisms: (1) Random acquisition mechanism: When a UE requires a new connection (e.g., during device activation or directional changes), a random beam acquisition process is initiated. This mechanism is analogous to the code acquisition process in CDMA systems, ensuring that the UE is initially allocated a beam with sufficient accuracy to establish a connection and proceed to subsequent tracking procedures for optimal transmission. (2) Continuous acquisition mechanism: Once a UE has been allocated a beam and is moving within the coverage area, the system continuously tracks the UE’s position and dynamically prepares an alternative beam for seamless handover to another RSU if needed. In this phase, an intelligent agent actively learns and handles environmental variations and unexpected scenarios. If transmission errors occur during the tracking process, the system will reset and reinitiate the beam acquisition procedure.

Fig. 7

Physics-inspired arm-force model for adaptive beam tracking.

b) Beam Tracking Phase: In this phase, the UE has already been assigned an appropriate beam, and the system continuously tracks the UE’s position to maintain optimal transmission quality. Two conditions are distinguished: either the link quality is optimal, or the link quality is acceptable, meaning that the SINR remains above a predefined threshold sufficient to satisfy the quality of service (QoS) requirements based on the UE’s current data rate or service demands. If the link quality falls below the required threshold, the system must immediately switch back to the beam acquisition phase or perform a handover to a different RSU. Clearly, in principle, within a beam tracking system, the RSU must steer its beam to continuously follow the OBU (i.e., the moving vehicle).

In practical mmWave systems, beam steering cannot occur instantaneously due to physical constraints such as mechanical inertia, limited control resolution, and signal processing delays. To capture this real-world behavior more accurately, we introduce a lever-arm dynamic model inspired by classical mechanics. This model treats the beam steering process as a second-order rotational system with inertia and friction, similar to a physical arm being rotated by an applied torque. The dynamics are governed by Newton’s second law for rotational motion, allowing us to incorporate angular velocity and control smoothness into the learning process. Figure 7 shows the lever-arm model simulating beam adjustment via mechanical rotation, with Deep Q-Learning (DQL) optimizing beam control.

Considering the -th UE associated with the -th RSU, the beam motion equation based on the lever-arm kinematic model is formulated as follows:

$${I_{i,u}}\frac{{{d^2}{\theta _{i,u}}}}{{d{t^2}}}={F_{i,u}} - {\mu _{i,u}}\frac{{d{\theta _{i,u}}}}{{dt}}$$

(35)

where θ_i,u is the current beam angle, F_i,u is force, µ_i,u represents the frictional force (this parameter ensures that the beam cannot instantly slip away from the acquired angle), and m_i,u denotes the mass of the lever arm, ${I_{i,u}}={m_{i,u}}L_{{_{{i,u}}}}^{2}$ the moment of inertia of the beam arm with length L_i,u. If the applied force F_i,u is sufficiently large, the beam will rotate more quickly. Conversely, if the frictional force µ_i,u ​ is large, the beam will update its direction more slowly. This formulation allows the agent to learn not only the target beam direction but also how smoothly and quickly to steer toward it, ensuring physical feasibility and improving tracking stability under high mobility.

The proposed Deep Q-Learning algorithm based on arm-force dynamics is as follows. The objective is to learn to select the optimal rotational force F and rotation angle θ so that the beam continuously tracks the OBU, minimizing the beam misalignment error, that is, minimizing $\left| {\Delta \theta } \right|=\left| {{\theta _{{\text{beam}}}} - {\theta _{{\text{OBU}}}}} \right|$ while avoiding overshoot.

State space

The state of the agent:$S_{t}^{{(i,u)}}=(\theta _{t}^{{(i,u)}},\omega _{t}^{{(i,u)}},P_{t}^{{(i,u)}},\Delta \theta _{t}^{{(i,u)}},\alpha _{{i,u}}^{{MC - CDMA}})$, where θ_t is current beam angle, ${\omega _t}={{d\theta } \mathord{\left/ {\vphantom {{d\theta } {dt}}} \right. \kern-0pt} {dt}}$ is the current beam rotation speed, P_r is the received signal power​, $\Delta \theta ={\theta _{{\text{beam}}}} - {\theta _{{\text{OBU}}}}$ is the angular misalignment error between the beam direction and the actual OBU direction.​ In high-mobility conditions, full channel state information (CSI) may not be instantaneously available due to Doppler effects and feedback delay. Therefore, the agent operates under partial observability, relying on measurable proxies such as ​$P_{r}^{{(i,u)}}$, $\theta _{t}^{{(i,u)}}$ and $\dot {\theta }_{t}^{{(i,u)}}$. These variables can be estimated locally at the RSU using standard tracking and Doppler pre-estimation modules. To mitigate the effect of outdated observations, the DRL agent is trained with experience replay over time-varying conditions, allowing it to learn robust policies that generalize well despite partial observability and delayed information. This design ensures practical deployability while preserving learning efficiency in dynamic highway scenarios.

Action space

Two sets of actions are implemented to maximize the learning objective:

Beamforming control action set

The agent selects the rotational force F to adjust the beam, with the action set defined as.

A_t = {F_low, F_medium, F_high}. (36)

Under the application of F_low​, the beam rotates slowly with minimal energy consumption, F_medium induces moderate rotation, and F_high results in rapid rotation but risks overshoot. Each time an action is executed with a selected force F, the beam angle is then updated as

$$\theta _{{t+1}}^{{(i,u)}}=\theta _{t}^{{(i,u)}}+\omega _{t}^{{(i,u)}}\Delta t+\frac{1}{2}\frac{{{F_{i,u}} - {\mu _{i,u}}\omega _{t}^{{(i,u)}}}}{{{I_{i,u}}}}{(\Delta t)^2}$$

(37)

and the beam rotation speed is updated as

$$\omega _{{t+1}}^{{(i,u)}}=\omega _{t}^{{(i,u)}}+\frac{{{F_{i,u}} - \mu \omega _{t}^{{(i,u)}}}}{{{I_{i,u}}}}\Delta t$$

(38)

MC-CDMA operation transition mode

${A_t}=\{ OFDM,MC - CDMA\}$.

The ε-greedy strategy $\pi _{{{A_t}}}^{{{S_t}}}$ is implemented to balance exploration and exploitation by using a parameter 0 < ε < 1, as

$${A_t}=\left\{ {\begin{array}{*{20}{c}} {\arg \mathop {\hbox{max} }\limits_{A} Q({S_t},{A_t}),}&{{\text{exploitation}}\,{\text{with probability }}1-\varepsilon {\text{,}}} \\ {{\text{random}}\,{\text{action,}}}&{{\text{exploration with probability }}\varepsilon {\text{.}}} \end{array}} \right.$$

(39)

Reward space (R_t​)

To ensure adaptive learning in dynamic V2X beam management, the agent’s reward at time is defined as a composition of context-sensitive components as

$${R_t}({S_t},{A_t})={R_{{\text{tracking}}}}+{R_{{\text{handover}}}}+{R_{{\text{interference}}}}+{R_{{\text{mode\_switch}}}}.$$

(40)

Each component is selectively activated based on the network condition as follows:

Beam tracking reward

We define the beam tracking reward as a multi-level context-aware term, depending on both the alignment angle and the beam motion smoothness.

$${R_{{\text{tracking}}}}=\left\{ {\begin{array}{*{20}{c}} {+2{r_A},}&{{\text{if beam aligned}}\,{\text{with max RSSI,}}} \\ {+{r_A},}&{{\text{if }}|\Delta \theta | \leqslant {\theta _{{\text{threshold}}}}{\text{ (beam aligned),}}} \\ { - {r_A},}&{{\text{if }}|\Delta \theta |>{\theta _{{\text{threshold}}}}{\text{ (beam misaligned),}}} \\ { - 2{r_A},}&{{\text{if beam rotation is too fast causing overshoot}}{\text{.}}} \end{array}} \right.$$

(41)

The beam tracking reward ${R_{{\text{tracking}}}}=f(\Delta {\theta _t},RSS{I_t},{\dot {\theta }_t})$ is defined based on the instantaneous alignment error, the signal quality (RSSI), and beam rotation dynamics. The reward is maximized when the beam is aligned with the direction yielding the highest received power, moderately positive for general alignment, penalized when misaligned, and strongly penalized if the agent overshoots or rotates too aggressively.

Handover reward

Successfully capturing the vehicle from the initial handover, continuously tracking it, and successfully handing it over to the neighbor RSU.

$${R_{handover}}=\left\{ {\begin{array}{*{20}{c}} {+{r_H},}&{{\text{if~successful~initial~capture,~tracking,~and~final~handover~occur,}}} \\ { - {r_H},}&{{\text{if premature of failed handover detected}}{\text{.}}} \end{array}} \right.$$

(42)

This term rewards seamless vehicle tracking across RSU boundaries and penalizes unstable or frequent handovers.

Interference management reward/penalty overlaps

The reward mechanism is designed to minimize the total number of beams with overlapping directions (i.e., beams targeting the same or similar angles) at each RSU, thereby reducing Multiple Access Interference (MAI). A penalty is applied when two or more beams at the same RSU overlap significantly (angle-wise), indicating high interference as.

$${R_{{\text{interference}}}}= - {r_I} \cdot \sum\limits_{{i \ne j}} {{{\mathbf{1}}_{{\text{overlap(}}i,j)}}} +{r_I} \cdot {{\mathbf{1}}_{{\text{successful\_separation}}}}$$

(43)

A bonus is granted if the agent replaces overlapping beams with distinct, interference-minimized assignments while maintaining SINR for all users.

Transmission mode switching reward

A positive reward is assigned when the received SINR falls below the operational threshold of the OFDM mode, and the system successfully switches to the MC-CDMA mode, ensuring continued communication performance.

$${R_{{\text{mode\_switch}}}}=\left\{ {\begin{array}{*{20}{c}} {+{r_{MC}}}&{{\text{if~}}SINR{_{{\text{OFDM}}}}<threshold~{\text{and~switch~to~MC-CDMA~is~successful,}}} \\ 0&{{\text{otherwise}}.} \end{array}} \right.\,$$

(44)

This encourages the agent to use mode switching as a fallback to sustain link quality under challenging channel conditions.

Algorithm 1

Deep Q-Learning for scan beam tracking and transmission mode.

Algorithm 1

proposes the use of Deep Q-Learning to control the scan beamforming vector and select the appropriate transmission mode for each UE within a distributed RSU system. Each RSU initializes a dedicated DFT beamforming codebook and an individual Q-Network to learn optimal beam control policies based on the observed UE states, including received power level, beam angle error, and connection status. During training, the algorithm iterates over all RSUs and the UEs they serve. Based on the ϵ-greedy strategy, the agent selects an action, either randomly exploring a beamforming vector index from the codebook or exploiting the current Q-Network policy. After executing the selected action, the system updates the beam angle and receives feedback from the environment (e.g., updated received power, angle error, or BER) to compute the reward. Each experience tuple is stored in the replay buffer and used to update the Q-Network. When the received power drops below a predefined threshold, the algorithm triggers a handover procedure, transitioning the UE to the closest RSU. The tracking state and beam angle are re-initialized based on the new RSU. This process repeats until convergence of the learned policy is achieved.

Algorithm 2

Deep Q-Learning for arm-force beam tracking and transmission mode transition.

Algorithm 2

extends Deep Q-Learning by employing a multi-head Q-Network architecture, enabling the agent to simultaneously learn two distinct types of actions: Head 1 controls the beamforming rotational force F, Head 2 governs the supplementary rotation angle or the transmission mode. Each RSU is initialized with a Q-Network containing two output heads, along with an experience replay buffer to store state–action–reward tuples. The initial beam angle and rotation speed are predefined for each UE.

During training, each RSU interacts with the list of UEs it currently serves. At each step, the agent observes the current state, including received power, beam angle deviation, and UE orientation, and selects actions from both heads of the Q-Network based on the ϵ-greedy strategy. The selected actions are then used to update the beam angle, rotation speed, and beamforming vector. The system subsequently transmits the MC-CDMA signal through the wireless channel and receives feedback, which is used to compute the reward. If the received power drops below a predefined threshold, the algorithm initiates a handover procedure, transferring the UE to the adjacent RSU and reinitializing its tracking state and beam alignment relative to the new RSU. The experience tuples collected during interactions are stored in the replay buffer and used to train the Q-Network via gradient descent. This process continues until the learned policy converges. A shared state vector is employed across both heads to ensure coherent decision-making and preserve interdependence between the learned actions.

Results and discussion

Simulation setup

This section provides numerical results for evaluating the proposed DRL framework’s performance in a highly dynamic V2X environment. First, we simulate a vehicular mobility model that combines the Car-Following Model (CFM) with Markov Chains, including lane-changing behavior, to realistically emulate vehicle dynamics and interactions on a highway⁴⁸. Each vehicle is modeled with a maximum speed of 120 km/h, maximum acceleration of 3 m/s², an average length of 4.5 m, and a minimum safe following distance of 3 m. To simulate lane-changing behavior, a lane-change priority factor of 0.2 is applied, along with a lane-keeping probability of 70%, allowing for realistic variations in driver behavior under highway traffic conditions.

The simulation considers the Hanoi–Hai Phong Expressway in Vietnam, which spans approximately 105.5 km in length and has a total roadway width of 33 m, including six traffic lanes and two emergency lanes. The typical vehicle density on this highway ranges from 1000 to 1500 vehicles per hour per lane, representing typical expressway traffic levels.

The channel incorporates both path loss and fading effects. Due to high vehicular speeds, Doppler spread significantly impacts transmission, and delay spread is also considered. Path loss is modeled based on the UMa (Urban Macrocell) scenario from 3GPP TR 38.901, covering distances from 500 m to 5 km.

The fading follows a Rician distribution, reflecting the predominance of line-of-sight (LoS) components in highway V2X scenarios. Typical delay spread ranges from 20 to 100 ns, while Doppler spread may reach up to 1 kHz. Carrier frequency and bandwidth are set to 26.7 GHz and 122.8 MHz, otherwise denoted.

Each vehicle moves along the full length of the road, passing through the coverage areas of multiple RSUs. Accordingly, it must undergo beam tracking and handover at different stages of its trajectory. When a vehicle enters the simulation, the system initializes a corresponding beam to establish the initial connection. The beam is then continuously tracked as the vehicle moves. Once the vehicle exits the coverage range of the current RSU, a handover is triggered to the next RSU. This process is repeated until the vehicle reaches the final RSU at the end of its path.

Detailed parameter settings are listed in Table 3.

Table 3 Simulation parameters. The hyperparameters for learning models is described in Table 4. The simulation platform runs on an environment of python 3.12, a workstation with CPU intel E5-1603 v3 @ 2.80 ghz (Installed RAM 15.8 GB) and GPU Nvidia GTX 1050 Ti (4 GB).

Table 4 Hyperparameters for learning models.

Handover simulation and bitrate analysis

We simulate a highway scenario with ${N_{RSU}}=5$ equally spaced RSUs and U = 10 vehicles, tracking bitrate over a time window of 0 to 500 s under varying carrier frequencies and Rician K-factors. Three spectrum settings are considered: 26.7 GHz/122.8 MHz (n257), 38.5 GHz/400 MHz (n260), and 64.8 GHz/2160 MHz (IEEE 802.11ay), with K = 0, 5, 10 dB. Figure 8 shows the bitrate of UE#0 and handover events between RSUs are highlighted as red segments in the bitrate plots. Results show that lower K-factors and lower frequencies lead to more frequent and severe bitrate fluctuations, due to increased fading and instability in beam alignment under NLoS conditions. In contrast, higher frequencies and stronger LoS propagation yield smoother and more stable transmission performance.

Fig. 8

Bitrate and handover behavior across time steps; (a)–(c): F_c = 26.7 GHz, and BW = 122.8 MHz under Rician K-factors of K = 0, 5, 10 dB; (d)–(f): F_c = 38.5 GHz, BW = 400 MHz, and K = 0, 5, 10 dB; (g)–(i): F_c = 64.8 GHz, BW = 2160 MHz, and K = 0, 5, 10 dB, respectively.

Tracking error simulation

We evaluate the tracking error performance across three different beam control force sets F_list, each tested under Rician K-factors of 0, 5, and 10 dB. The tested force sets are: F_list = [0.005,0.01,0.02]; [0.05,0.1,0.2] and [0.1,0.2,0.3]. Figure 9 shows that larger force values F_list lead to faster convergence in beam tracking, especially under high-K (LoS-dominant) conditions, while smaller forces provide more stable post-convergence behavior with lower fluctuations in tracking error. Specifically, in subplots (a)–(c), smaller F_list values result in slower convergence, requiring approximately 100–160 time steps for beam alignment. But, once converged, they achieve higher steady-state accuracy than their larger-force counterparts.

Simulation results further indicate that the proposed Arm-Force MH-DQN converges more slowly than the standard DQN, reaching its stable regime in roughly 100–160 time steps, yet ultimately attains lower steady-state tracking errors across all tested K-factors. This behavior stems from the multi-head architecture’s ability to jointly learn both beam control force and operational mode, which expands the exploration space and delays convergence but yields improved final tracking precision. While the fixed-offset case represents an idealized scenario without tracking dynamics, Arm-Force MH-DQN approaches this performance in high-K environments and maintains robustness across varying channel conditions. This trade-off highlights the importance of adaptive force tuning: low F_list is preferable for precision and stability, whereas high F_list favors responsiveness in rapidly changing scenarios.

BER simulation

The bit error rate (BER) performance was evaluated using 5 × 10⁶ channel realizations via Monte Carlo simulations. We compared multiple beamforming strategies, including a fixed-offset baseline with a 1-degree misalignment, a standard DQN-based method (serving as the baseline RL algorithm), and the two proposed algorithms (Algorithm 1 and Algorithm 2). We investigate the impact of the number of transmit antennas ${N_t} \in \{ 8,16,32,64\}$ on BER across different algorithms. Additionally, simulations were conducted for various Rician K-factors (0 dB, 5 dB, and 10 dB) to assess the influence of fading. As shown in the Fig. 10, at ${N_t}=8$, the standard DQN algorithm achieves slightly better BER performance, and the fixed-offset scheme with a 1-degree error provides near-equivalent performance. However, as N_t increases, the proposed MH-DQN-based algorithms significantly outperform the baseline methods in terms of BER. The improvement becomes more pronounced in larger antenna array settings, demonstrating the superior interference resilience and tracking accuracy of the proposed learning framework. This robustness is clearly illustrated in the BER plots under varying fading conditions.

Fig. 9

Tracking Error performance versus time steps; (a)–(c): F_list = [0.005, 0.01, 0.02] under Rician K-factors of K = 0, 5, 10 dB; (d)–(f): F_list = [0.05, 0.1, 0.2] with K = 0, 5, 10 dB; (g)–(i): F_list = [0.1, 0.2, 0.3] with K = 0, 5, 10 dB, respectively. In (a)–(c), smaller F_list values result in slower convergence, requiring more time steps to align the beam, but achieve lower steady-state tracking errors once stabilized. In contrast, larger F_list values, as in (g)–(i), converge more quickly but exhibit higher residual error, reflecting a trade-off between responsiveness and final tracking precision.

As observed in Fig. 10, the BER performance of standard DQN and fixed-offset methods degrades notably as the number of transmit antennas N_t increases. This phenomenon is primarily due to the narrowing of the beamwidth with increasing array size, which makes the beamforming system more sensitive to even small angular misalignments. Since conventional DQN and fixed-offset schemes do not adapt their beam control to the current Doppler profile or antenna configuration, they are more prone to beam deviation in high-resolution settings, leading to increased BER.

In contrast, the proposed MH-DQN framework incorporates Doppler-aware dynamic control and joint learning of beam offset adjustment, enabling it to maintain beam alignment accuracy even under narrow beamwidth conditions. This adaptive behavior explains the superior BER performance of MH-DQN when N_tincreases, especially in challenging fading environments.

ASE vs. distance simulation

In this simulation, we set Rician fading $K=10\,{\text{dB}}$, ${N_t}=64$. Figure 11 shows that spectral efficiency (ASE) decreases with distance due to path loss. Figure 11 illustrates that, among strategies, the proposed AF DQN consistently achieves the highest ASE across all distances. MC DQN performs slightly below but remains stable. DQN shows good performance at short range but degrades faster. Fixed offset results in the lowest ASE due to its static beam alignment.

Fig. 10

BER performance versus transmit power; (a)–(c): K = 5 dB, N_t = 8, 16, 64, respectively; (d)–(f): K = 0, 10 dB, N_t = 8, 16, 64; (g): K = 5 dB, N_t = 8, 16 comparision; (h): K = 5 dB, N_t = 8, 32 comparision; (i): K = 5 dB, N_t = 8, 64 comparision.

Fig. 11

Average spectral efficiency performance versus distance.

To assess the convergence stability of the proposed Deep Q-Learning algorithm, we monitored the temporal-difference (TD) loss during training. Figure 12 illustrates the TD loss over 50,000 training steps, using an average moving window of 500 steps. The TD loss shows a rapid decrease during the initial phase, dropping from above 1.6 to below 0.7 within the first 10,000 steps. This initial trend reflects effective learning and fast convergence of the Q-network. Beyond 10,000 steps, the TD loss remains consistently low and stable, fluctuating only slightly around a mean value near 0.6. Importantly, no divergence or sharp increase is observed throughout the remaining training duration, indicating strong stability in the learning process. These results confirm that the multi-head DQN framework not only converges effectively but also maintains stable value estimation across extended training. Such stability is essential for ensuring adaptive beam control under high-mobility V2X scenarios.

Fig. 12

Temporal difference (TD) loss.

Conclusion

This paper investigates the joint optimization of MC-CDMA transmission mode and continuous beamforming for V2X communication in high-mobility highway environments. One of the critical requirements in V2X systems is to ensure signal robustness and stability under complex and dynamic channel conditions. To meet this challenge, we proposed and implemented a Multi-Head Deep Q-Learning (MH-DQN) framework that enables adaptive beam control and mode selection between MC-CDMA and OFDM modulation scheme. The proposed beamforming strategy maintains physical realism while allowing smooth and responsive tracking of fast-moving vehicles, especially when deployed with a large number of transmit antennas. By combining MC-CDMA with large-scale antenna arrays, the system effectively extends communication range, which is particularly beneficial for long-distance V2X scenarios. The use of high-gain antennas and the processing gain from MC-CDMA significantly enhances interference mitigation and connectivity robustness.

This study primarily focused on control-plane-level beam tracking and transmission mode selection. In future work, we aim to extend both the reward structure and the action space to support cross-layer coordination, including joint scheduling, power control, and mobility prediction, potentially within a multi-agent decentralized learning framework. Additionally, we plan to investigate the optimal placement of RSUs under varying traffic densities, as well as the deployment of mobile RSUs (e.g., UAV-mounted infrastructures) to enhance spatial flexibility and dynamic coverage. Finally, we intend to explore synchronized transmission mode-switching mechanisms, particularly under dominant Rician fading conditions, which may further enhance system adaptability and end-to-end communication performance.