Influence of roof cutting depth on stability of gob side entry in thick coal seams with a bulky limestone roof

Abstract

For the gob-side entry retained by roof cutting, the roof pre-splitting depth is directly related to its stability, especially under the condition of fully mechanized mining in 4.5 m thick coal seam underneath 13.7 m thick limestone roof. Due to insufficient investigation, the Yongning coal mine 10202 gob-side entry retained by roof cutting experienced large rock pressure, causing severe prop deformation and sharp reduction in the cross-section of the entry, which greatly affects its reuse. Extensive field measurements were conducted to analyze the severe rock pressure in the 10202 gob-side entry retained. Two typical models of overburden structure after roof pre-splitting were established, and they were used to study the effect of pre-splitting depth on the stability of gob-side entry retained in terms of the roof subsidence and the support resistance, respectively. A numerical investigation of the effect of roof pre-splitting depth on the stress distribution near the gob-side entry retained was carried out. Afterwards, the roof pre-splitting parameters for the 10204 gob-side entry retained were optimized, and they were validated through field experiments. The results indicated that insufficient pre-splitting depth is the main factor causing the severe rock pressure of the 10202 gob-side entry retained. The roof subsidence and support resistance after main roof pre-splitting were reduced by 35.2% and 24.8% compared with immediate roof pre-splitting, respectively. As pre-splitting depth increased, the stress-relaxation area expanded, but the pressure-relief effect weakened beyond 20 m. As the roof pre-splitting depth increased, the weighting interval increased, but the working resistance decreased, which indicates that the goaf is almost densely filled by the collapsed roof and the main roof has no space for subsidence movement. Thus, the rock pressure behaviors of the 10204 gob-side entry retained were milder than that of the 10202 gob-side entry retained.

Introduction

In China, the resource reserves of thick coal seams account for 45% of the proven coal reserves, and the production of thick coal seams accounts for about 50% of the total coal production¹. The rational mining of thick coal seams, especially extra-thick coal seams, is crucial to the stable development of the coal industry. Fully mechanized caving mining has replaced slicing mining technique due to its advantages of low cost, high output, high efficiency and simplicity, and has become the mainstream mining technique for efficient and high-production mining in thick and extra-thick coal seams^2,3,4. In fully mechanized caving mining, a coal pillar with a width of about 30 m is usually left between two adjacent longwall panels, resulting in the roadway being located in the zone of reduced mining pressure, and the width of the remnant coal pillar increases with increasing mining depth⁵. These remnant coal pillars generally cannot be recovered, leading to significant coal resource waste and a reduced coal recovery ratio. In addition, these remnant coal pillars are the main factor causing mine disasters, which increases the stress in the rock strata, raises the risk of rock bursts, and deteriorates the mining environment underneath these remnant coal pillars^6,7,8,9. The rapid development of social economy poses a severe challenge to the demand for coal resources. Therefore, how to improve the coal recovery ratio has become the focus of coal mining technique.

In the 1950s, gob-side entry retained mining technique was first developed in Britain and Germany. For this technique, the original entry along the goaf edges after coal mining is maintained by building a backfilling side-wall, so that it can be reused in the adjacent longwall panel. This coal mining technique can reduce the amount of roadway excavation in adjacent longwall panels, extremely reduce excavation costs, ease constraints on continuous production, improve the coal recovery ratio, and prolong the life of the mine, thereby bringing significant economic and social benefits. There are mainly six types of gob-side entry retained mining, namely dense pillar method, gangue stacking method, masonry wall method, cast-in-place concrete partition wall method, large self-moving filling support method, and roof cutting method^10,11,12,13. The first five types are referred to as traditional gob-side entry retained technique, which is focused on controlling the coordinated movement between the roadside support body and roof subsidence. For traditional gob-side entry retained technique, the roof rock structure is not artificially modified, the process is cumbersome and inefficient. Moreover, roof failures are prone to occur due to incompatibility between the deformation of the roadside support structure and the roof movement^14,15,16. Therefore, the gob-side entry retained by roof cutting mining technique was proposed by Manchao He¹⁰ and was employed under different geo-conditions in China^17,18. The mining technique, which involves gob-side entry retained by roof cutting with no remnant coal pillar, cuts off the load transfer path between the goaf and the gob-side entry before the mining process through roof pre-splitting blasting. When the longwall panel advances, dense single hydraulic props are arranged close to the pre-splitting blasting line in a timely manner to provide roadside gangue support. Under the action of weight and rock pressure, the roof of the goaf automatically collapses along the pre-splitting blasting fracture surface, then the gob-side entry is automatically formed. Moreover, the roadside is sprayed to isolate the gob-side entry from the goaf.

Roof pre-splitting blasting has become a necessary component of coal pillar-free mining technique¹⁹. At present, the gob-side entry retained by roof cutting mining technique has been successfully used in medium-thick and thin coal seams under different mining geological environments. The effect of pre-splitting roof cutting is directly related to the stability of the gob-side entry. However, it has not been studied theoretically and experimentally under the conditions of thick coal seam directly underneath a hard-to-cave limestone immediate roof with a thickness of 13.7 m. The technical difficulties for gob-side entry retained by roof cutting under this mining environment mainly include the following two aspects: (1) The hard-to-cave limestone immediate roof is easy to form a suspended roof in the goaf, and the suspended roof has a long retention time and a large retention space, which will increase the stress of the surrounding rock and support body of the gob-side entry, and cause significant nonlinear deformations, such as roof subsidence, rib spalling, roadside support failure, and floor bulging. Therefore, how to cut the roof to ensure that the hard-to-cave limestone roof is cut off and collapsed smoothly is one of the issues that need to be solved urgently. (2) The fracture of the thick hard-to-cave limestone roof is likely to impact the gob-side entry, resulting in significant damage and deformation to the surrounding rock of the gob-side entry. Under the impact of strong dynamic pressure, the support bodies such as conventional anchor cables often fail to break, shear, etc., which will cause the gob-side entry collapse. It is urgent to develop a new support technique that adapts to the spatial-temporal change of rock pressure in the gob-side entry²⁰.

Yongning coal mine is located in Lvliang city, Shanxi Province, China. The average mining height in 102 district is 4.5 m, and the immediate roof is a 13.7 m thick limestone roof. The 10202 and 10204 longwall panels in this district have been laid out. A barrier pillar with a width of 30 m and a length of 1130 m was originally designed to isolate the effect of mining on one side of the block from the other side. Considering the advantages of gob-side entry retained by roof cutting mining technique, a single barrier coal pillar can recover about 135,000 tons of coal. In order to increase the coal recovery rate and prolong the service life of the mine, the gob-side entry retained by roof cutting mining technique was adopted. Due to insufficient investigation, the rock pressure of the gob-side entry retained is severe, the surrounding rock undergoes significant deformation, and the cross-section of the entry is sharply reduced, which severely affects the high-efficiency production.

This work focuses on the severe rock pressure and large deformation of the Yongning coal mine 10202 gob-side entry retained by roof cutting, the effect of pre-splitting depth on the stability of gob-side entry retained during thick coal seam full-mechanized mining under limestone immediate roof with a thickness of 13.7 m was investigated. Firstly, based on field measurements and theoretical analysis, the main factors causing the severe rock pressure and large deformation of the 10202 gob-side entry were investigated. Secondly, the models of overburden structure after roof pre-splitting were established to study the effect of pre-splitting depth on the stability of gob-side entry retained in terms of roof subsidence and support resistance, respectively. Thirdly, numerical investigation was conducted to assess the influence of roof pre-splitting depth on the stress distribution near the gob-side entry retained was carried out. Finally, the roof pre-splitting parameters for the 10204 gob-side entry retained were optimized, and the effect of roof pre-splitting depth on the stability of gob-side entry retained by roof cutting during full-mechanized mining in a thick coal seam beneath a 13.7 m thick limestone immediate roof was revealed.

There are three main research methods currently being used in related fields: field tests, similar simulation, and numerical simulation. Field tests involve on-site inspections to verify the validity of hypotheses, offering high reliability but presenting challenges due to their difficulty and long timeframes. Similarity simulation experiments can be conducted in a lab setting, providing a relatively simple and quick way to assess the feasibility of research theories. However, they are influenced by human factors, such as difficulties in matching material strength with actual rock properties, which may affect result reliability. Numerical simulations have seen significant advancements recently and are widely adopted in mining due to their efficiency, reliability, and strong presentation capabilities. In recent years, numerical simulations have been widely used to analyze the issues of gob-side entry, and have made many contributions^21,22. Given these considerations, this study employs a combination of numerical simulation, theoretical analysis, and field measurements to strive for more accurate conclusions.

Field practice of 10202 gob-side entry retained

Production geology

Yongning coal mine 10202 longwall panel exploits No. 10 coal seam. The thickness of No. 10 coal seam ranges from 2.46 m to 5.46 m, with an average of 4.5 m. The inclination angle of the coal seam is about 0 ~ 6°, with an average of 2°. There are generally 4 partings in the coal seam, which has a complex structure. No. 10 coal seam is uniform with minimal thickness variation, and the entire area is suitable for mining. The immediate roof is L1 limestone, with a thickness of 12.40–14.42 m and an average thickness of 13.70 m, classified as hard-to-cave rock; the floor consists of mudstone, partially sandy mudstone, classified as soft rock. The lithology of 10202 longwall panel is shown in Fig. 1. The mechanical properties of the overlying strata are listed in Table 1.

Fig. 1

Lithology of the 10202 longwall panel.

Table 1 Mechanical properties of coal and rock mass.

Field gob-side entry retained

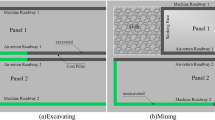
The south of the 10202 longwall panel is the three main entry, the west is the 10204 tailgate, the east is the main return-air roadway, and the north is the solid coal. The length of 10202 longwall panel along the strike is 1075 m, along the dip is 187 m, and the buried depth is 366–411 m. Gob-side entry retained technique is developed in 10202 headgate, where it is maintained along the goaf edges after coal mining, as shown in Fig. 2.

Fig. 2

10202 and 10204 gob-side entries retained mining plan.

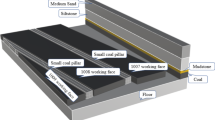
In the field, methods such as shaped charge, constant-resistance-large-deformation cables and shrinkable U-shaped steel block gangue support are applied to maintain the 10202 headgate along the goaf edges. The overall work steps of gob-side entry retained by roof cutting are as follows. (1) Install constant-resistance-large-deformation cables to reinforce the support of 10202 headgate within 150 m in front of the longwall panel, as shown in Fig. 3. (2) Drilling borehole with a spacing of 0.5 m, charging and cut 10202 headgate roof by shaped charge in front of the longwall panel, as shown in Fig. 3. The roof pre-splitting parameters are listed in Table 2. (3) Arrange the dense single hydraulic props and U-shaped steel block gangue point columns along the goaf edges immediately after mining. Then, promptly lay metal wire-mesh on the gob-side of the dense props in time. At the same time, arrange five rows of reinforced single hydraulic props within the 10202 gob-side entry retained. (4) After the rock pressure is stable, remove the third and fifth rows of single hydraulic props near the solid coal side, and determine whether to withdraw the second and fourth rows based on the field measurement. It is expected to retain the first row of single hydraulic props and U-shaped steel block gangue point columns along the goaf edges as permanent support.

Fig. 3

10202 headgate reinforcement support and borehole arrangement.

Table 2 Roof pre-splitting parameters for the 10202 gob-side entry retained.

Rock pressure behaviors

The 10202 gob-side entry retained experiences large rock pressure, causing severe prop and U-shaped steel block gangue point column deformation and sharp reduction in the cross-section of the entry, which greatly affects its reuse. Typical rock pressure behaviors are shown in Fig. 4.

In order to evaluate and improve the gob-side entry retained technique, field measurement of rock pressure is carried out. The monitoring content mainly includes the working resistance of the hydraulic powered supports, the bed separation amount, the roof-to-floor convergence, and the pressure of single hydraulic props.

• (1) Working resistance of the hydraulic powered supports.

The working resistance changes of the No.1 hydraulic powered support on the upper part of the 10202 longwall panel, No. 74 hydraulic powered support on the middle part, and No. 115 hydraulic powered support on the lower part during mining are shown in Fig. 5. The No. 1 hydraulic powered support is close to the 10202 gob-side entry retained. The No.115 hydraulic powered support is close to the 10202 tailgate, and the roof has not been pre-splitting cut.

Under the effect of roof pre-splitting, the behaviors of the first weighting at both ends of the longwall panel are significantly different. Compared with the lower non-roof pre-splitting part of the longwall panel, the first weighting interval of the upper roof pre-splitting part is reduced by 8.0 m, and the peak working resistance during first weighting is reduced by 4.08 MPa. Meanwhile, the periodic weighting interval of the upper roof pre-splitting part is increases by 1.6 m, and the peak working resistance during periodic weighting decreases by 3.85 MPa. Among the upper, middle and lower parts of the longwall panel, the middle part of the longwall panel has the smallest weighting interval and large working resistance during both first and periodic weighting.

Fig. 4

Typical rock pressure behaviors of 10202 gob-side entry retained. (a) Sharp reduction in the section of the entry; (b) Severe prop and U-shaped steel block gangue point column deformation.

Fig. 5

Working resistance of hydraulic powered supports with respect to the advancement distance.

• (2) Bed separation.

Field measurement of the bed separation for the 10202 gob-side entry retained is shown in Fig. 6. Starting 30 m behind the longwall panel, the bed separation starts to increase rapidly. The growth rate of the bed separation starts to slow down at 75 m behind the longwall panel and finally stabilizes at 124.1 mm.

Fig. 6

Bed separation filed measurement.

• (3) Roof-to-floor convergence.

The surrounding rock of the 10202 gob-side entry retained deforms under the effect of the mining-induced stress. By monitoring the deformation of the surrounding rock, the 10202 gob-side entry retained technique can be evaluated and improved. Convergence meters are used to study the roof-to-floor convergence, which are arranged along the goaf edges with an interval of 20 m. The typical measurement results of the roof-to-floor convergence are shown in Fig. 7.

Fig. 7

Roof-to-floor convergence filed measurement.

According to the roof-to-floor convergence rate, the roof-to-floor convergence curve can be divided into three segments. In segment ①, the goaf roof, within 87 m behind the longwall panel, subsides rapidly under the load of overlying strata and its own weight, and the mining-induced stress is transmitted to both sides of the goaf, which forces the roof and floor of the 10202 entry to converge sharply. In segment ②, the goaf roof, within 87–184 m behind the longwall panel, collapsed and swelled, and began to gradually recover bearing capacity, which suppress the rotation and subsidence the main roof. Then, the roof and floor of the 10202 entry converge gently. In segment ③, the roof-to-floor convergence tends to be stable at 184 m behind the longwall panel. After the third and fifth rows of single hydraulic props are removed, the roof-to-floor convergence reaches 1170.9 mm.

• (4) Pressure of single hydraulic props.

Pressure sensors are installed on the single hydraulic props near the roof-to-floor convergence measurement positions with an interval of 20 m. The typical measurement results of the pressure of single hydraulic props are shown in Fig. 8. As the location approaches to the goaf edges, the pressure of the single hydraulic prop increases. The pressure rises rapidly and reaches stable within 20 m behind the longwall panel, and the pressure of the single hydraulic prop near the goaf side of 10202 entry reaches 36.67 MPa, which causes severe prop deformation and damage in the field.

Fig. 8

Pressure of single hydraulic props filed measurement.

Field measurement summary

Based on the field measurements, the reasons for the severe rock pressure in 10202 gob-side entry retained can be summarized as follows.

• (1) Limestone tends to collapse in large blocks with small bulking factor. In the case of insufficient roof pre-splitting depth and small amount of collapsed rock, it is easy to cause the goaf un-dense filling. Then, there is still a large space for the main roof rotation and subsidence, which is the main reason for the similar rock pressure behaviors in the upper and middle part of the 10202 longwall panel after roof pre-splitting and the large rock pressure in 10202 gob-side entry retained.

• (2) The bed separation and roof-to-floor convergence is large, and the position of their peak value is far away from the longwall panel, which indicates that a large area of roof has been disturbed after the mining, and the limestone immediate roof has not collapsed sufficiently.

• (3) The roof pre-splitting depth of 13 m fails to completely cut off the load transfer from the goaf to the 10202 gob-side entry retained. A hinged arch is formed between the thick limestone immediate roof blocks and transfers the load from the goaf to the 10202 gob-side entry, causing deformation of the prop and U-shaped steel block gangue point column deformation, along with a sharp reduction in the cross-section of the entry.

Theoretical analysis of the roof pre-splitting depth effect

According to the field measurements, the thick limestone roof collapses in the form of large blocks with small bulking factor when 13 m roof pre-splitting depth, making the mined-out space difficult to fill densely and providing sufficient subsidence space for the limestone roof. Then, a large load is transferred from the goaf to the surrounding rocks of the 10202 gob-side entry retained during the roof subsidence movement, which causes severe rock pressure behaviors in the 10202 gob-side entry. Therefore, it is important to investigate the roof pre-splitting depth effect to provide a basis for selecting of the roof pre-splitting depth. Based on the field practice, two typical overburden structure models after roof pre-splitting were established and were used to study the effect of pre-splitting depth on the stability of the retained gob-side entry in terms of the roof subsidence and the support resistance, respectively.

Fig. 9

Two typical models of overburden structure after roof pre-splitting.

Model 1- small roof pre-splitting depth

In this model, the roof pre-splitting depth reaches the upper boundary of the immediate roof. The main roof breaks at the solid coal side of the goaf, and the position where the hinged arch forms between the main roof blocks is far away from the retained gob-side entry, as shown in Fig. 9 (a). The roof subsidence and the support resistance of the gob-side entry are determined as follows.

After the overlying strata movement is stable, the subsidence ${{\text{\varvec{\upomega}}}_{\text{2}}}\left( {\text{x}} \right)$ of the main roof suspended above the gob-side entry can be expressed as the following Eq. (1).

$$\begin{array}{*{20}{c}} {{\omega _2}\left( x \right)=\frac{{q{x^2}}}{{4{E_2}h_{2}^{3}}}\left( {{x^2} - 4Lx+6{L^2}} \right) - \frac{{P{x^2}}}{{4{E_2}h_{2}^{3}}}\left( {{x^2} - 6x_{2}^{2}} \right) - \frac{{{q_n}{x^2}}}{{4{E_2}h_{2}^{3}}}\left( {{{\text{x}}^{\text{2}}} - {\text{4}}{{\text{x}}_{\text{2}}}{\text{x+6x}}_{{\text{2}}}^{{\text{2}}}} \right){\text{,}}} \end{array}$$

(1)

where ${\text{q}}$ is the uniform load subjected by the main roof, unit MPa; ${\text{x}}$ is the distance from the broken position of the main roof above the solid coal, unit m; ${{\text{E}}_{\text{2}}}$ is the elastic modulus of the main roof, unit GPa; ${{\text{h}}_{\text{2}}}$ is the thickness of the main roof, unit m; ${{\text{x}}_{\text{2}}}$ is the distance from the broken position of the main roof above the solid coal to the solid coal side of the gob-side entry, unit m; ${\text{L}}$ is the distance between the two broken positions of the main roof above the solid coal and the goaf, unit m; ${\text{P}}$ is the support resistance of the gob-side entry, unit MPa; and ${{\text{q}}_{\text{n}}}$ is the supporting load provided by the solid coal side of the entry to the immediate roof, unit MPa.

The distance ${\text{L}}$ between the two broken positions of the main roof above the solid coal and the goaf is given by Eq. (2).

$$\begin{array}{*{20}{c}} {L={h_2}\sqrt {\frac{{{R_T}}}{{3q}}} {\text{,}}} \end{array}$$

(2)

where ${{\text{R}}_{\text{T}}}$ is the tensile strength of the main roof, unit MPa.

Under the action of the support resistance ${\text{P}}$, the supporting load ${{\text{q}}_{\text{n}}}$ and the overlying strata load ${{\text{q}}_{\text{1}}}$, the roof subsidence ${{\text{\varvec{\upomega}}}_{\text{1}}}\left( {\text{x}} \right)$ of the gob-side entry can be expressed as follows.

$$\begin{array}{*{20}{c}} {{\omega _1}\left( x \right)={\omega _{{q_1}}}\left( x \right) - {\omega _P}\left( x \right) - {\omega _{{q_n}}}\left( x \right),} \end{array}$$

(3)

$$\begin{array}{*{20}{c}} {{\omega _{{q_1}}}\left( x \right)=\frac{{\left( {q+{\gamma _2}{h_2}} \right){x^2}}}{{4{E_1}h_{1}^{3}}}\left[ {{x^2} - 4\left( {{x_1}+a+\frac{{{h_1}\tan \theta }}{2}} \right)x+6{{\left( {{x_1}+a+\frac{{{h_1}\tan \theta }}{2}} \right)}^2}} \right],} \end{array}$$

(4)

$$\begin{array}{*{20}{c}} {{\omega _P}\left( x \right)=\frac{{P{x^2}}}{{4{E_1}h_{1}^{3}}}\left( {{{\text{x}}^{\text{2}}} - {\text{6x}}_{{\text{1}}}^{{\text{2}}}} \right){\text{,}}} \end{array}$$

(5)

$$\begin{array}{*{20}{c}} {{\omega _{{q_n}}}\left( x \right)=\frac{{3{q_n}x_{1}^{4}}}{{4{E_1}h_{1}^{3}}} - \left( {x - {x_1}} \right)\tan \left( {\frac{{{q_n}x_{1}^{3}}}{{{E_1}h_{1}^{3}}}} \right),} \end{array}$$

(6)

where ${{\text{\varvec{\upomega}}}_{{{\text{q}}_{\text{1}}}}}\left( {\text{x}} \right)$ is the immediate roof subsidence under the overlying strata load, unit m; ${{\text{\varvec{\upomega}}}_{\text{P}}}\left( {\text{x}} \right)$ and ${{\text{\varvec{\upomega}}}_{{{\text{q}}_{\text{n}}}}}\left( {\text{x}} \right)$ are the deformation of the immediate roof subsidence restrained by the support resistance ${\text{P}}$ and the supporting load ${{\text{q}}_{\text{n}}}$, respectively, unit m; ${{\text{\varvec{\upgamma}}}_{\text{2}}}$ is the bulk density of the main roof, unit kN/m³; ${{\text{E}}_{\text{1}}}$ is the elastic modulus of the immediate roof, unit GPa; ${{\text{h}}_{\text{1}}}$ is the thickness of the immediate roof, unit m; ${{\text{x}}_{\text{1}}}$ is the distance from the broken position of the immediate roof above the solid coal to the solid coal side of the gob-side entry, unit m; ${\text{a}}$ is the width of the gob-side entry; and ${\text{\varvec{\uptheta}}}$ is the angle of the borehole dip to the goaf.

${{\text{x}}_{\text{1}}}$ and ${{\text{x}}_{\text{2}}}$ can be expressed as follows:

$$\begin{array}{*{20}{c}} {{{\text{x}}_{\text{1}}}{\text{=}}\frac{{{{\text{h}}_{\text{1}}}{\text{\varvec{\uplambda}}}}}{{{\text{2tan}}{{\text{\varvec{\upvarphi}}}_{\text{1}}}}}{\text{ln}}\left( {\frac{{{\text{k\varvec{\upgamma}H+}}\frac{{{{\text{c}}_{\text{1}}}}}{{{\text{tan}}{{\text{\varvec{\upvarphi}}}_{\text{1}}}}}}}{{\frac{{{{\text{c}}_{\text{1}}}}}{{{\text{tan}}{{\text{\varvec{\upvarphi}}}_{\text{1}}}}}}}} \right){\text{,}}} \end{array}$$

(7)

$$\begin{array}{*{20}{c}} {{{\text{x}}_{\text{2}}}{\text{=}}\frac{{{{\text{h}}_{\text{2}}}{\text{\varvec{\uplambda}}}}}{{{\text{2tan}}{{\text{\varvec{\upvarphi}}}_{\text{2}}}}}{\text{ln}}\left( {\frac{{{\text{k\varvec{\upgamma}H+}}\frac{{{{\text{c}}_{\text{2}}}}}{{{\text{tan}}{{\text{\varvec{\upvarphi}}}_{\text{2}}}}}}}{{\frac{{{{\text{c}}_{\text{2}}}}}{{{\text{tan}}{{\text{\varvec{\upvarphi}}}_{\text{2}}}}}}}} \right){\text{,}}} \end{array}$$

(8)

where ${\text{\varvec{\uplambda}}}$ is the coefficient of lateral pressure, ignoring the influence of horizontal stress, the value takes 1; ${{\text{\varvec{\upvarphi}}}_{\text{1}}}$ and ${{\text{\varvec{\upvarphi}}}_{\text{2}}}$ are the angle of internal friction of the immediate roof and the main roof, and they take values of 35.3° and 32.3°, respectively; ${\text{k}}$ is the stress concentration factor, the value takes 2.41 based on the field measurement; ${\text{\varvec{\upgamma}}}$ is the average bulk density of the overlying stratum, the value takes 25.2 kN/m³; ${\text{H}}$ is the buried depth of the gob-side entry, the value takes 397 m; ${{\text{c}}_{\text{1}}}$ and ${{\text{c}}_{\text{2}}}$ are the cohesion of the immediate roof and the main roof, and they take values of 4.13 MPa and 3.20 MPa, respectively.

The uniform load ${\text{q}}$ subjected by the main roof is given by Eq. (9).

$$\begin{array}{*{20}{c}} {{\text{q=}}\frac{{{{\text{E}}_{\text{2}}}{\text{h}}_{{\text{2}}}^{{\text{3}}}\left( {\sum {{\text{\varvec{\upgamma}}}_{\text{i}}}{{\text{h}}_{\text{i}}}} \right)}}{{\sum {{\text{E}}_{\text{i}}}{\text{h}}_{{\text{i}}}^{{\text{3}}}}}{\text{,}}} \end{array}$$

(9)

where ${{\text{E}}_{\text{i}}}$, ${{\text{h}}_{\text{i}}}$, and ${{\text{\varvec{\upgamma}}}_{\text{i}}}$ are the elastic modulus, thickness and bulk density of the ith strata above the main roof, respectively.

When the surrounding rock of the gob-side entry is in a stable state, the immediate roof and the main roof are in close contact, and there is no bed separation between them above the goaf side of the gob-side entry, i.e., ${{\text{\varvec{\upomega}}}_{\text{1}}}\left( {{{\text{x}}_{\text{1}}}{\text{+a}}} \right){\text{=}}{{\text{\varvec{\upomega}}}_{\text{2}}}\left( {{{\text{x}}_{\text{2}}}{\text{+a}}} \right)$. Given that the main roof generally has higher rock strength and bears greater overlying stress, its fracture often induces simultaneous fracturing in the immediate roof, resulting in similar positions for their rotation pivot points (x1 ≈ x2). Therefore, it can be assumed that the broken positions of the main roof and the immediate roof above the solid coal side of the gob-side entry are coincident, i.e., x₁ = x₂, this assumption consistent with observed geological behaviors.

Finally, the roof subsidence ${{\text{\varvec{\upomega}}}_{\text{1}}}\left( {{{\text{x}}_{\text{1}}}{\text{+a}}} \right)$ and the support resistance ${{\text{P}}_{{\text{model\_1}}}}$ of the gob-side entry are given by Eqs. (10) and (11), respectively.

$$\begin{aligned} \omega _{1} \left( {x_{1} + a} \right) & = \omega _{2} \left( {x_{2} + a} \right) = \frac{{\left( {q + \gamma _{2} h_{2} } \right)\left( {x_{2} + a} \right)^{2} }}{{4E_{1} h_{1}^{3} }}\left[ {\left( {x_{2} + a} \right)^{2} - 4\left( {x_{2} + a + \frac{{h_{1} \tan \theta }}{2}} \right)\left( {x_{2} + a} \right)} \right. \\ & \begin{array}{*{20}c} {\left. {\,\;\; + 6\left( {x_{2} + a + \frac{{h_{1} \tan \theta }}{2}} \right)^{2} } \right] - \frac{{P\left( {x_{2} + a} \right)^{2} }}{{4E_{1} h_{1}^{3} }}\left[ {\left( {x_{2} + a} \right)^{2} - 6x_{2}^{2} } \right] - \frac{{3q_{n} x_{2}^{4} }}{{4E_{1} h_{1}^{3} }} + a\tan \left( {\frac{{q_{n} x_{2}^{3} }}{{E_{1} h_{1}^{3} }}} \right),} \\ \end{array} \\ \end{aligned}$$

(10)

$$\begin{aligned} P_{{\bmod el\_1}} & = \left\{ {\frac{{\left( {q + \gamma _{2} h_{2} } \right)}}{{E_{1} h_{1}^{3} }}\left[ {\left( {x_{2} + a} \right)^{2} - 4\left( {x_{2} + a + \frac{{h_{1} \tan \theta }}{2}} \right)\left( {x_{2} + a} \right) + 6\left( {x_{2} + a + \frac{{h_{1} \tan \theta }}{2}} \right)^{2} } \right]} \right. \\ & \;\; - \frac{q}{{E_{2} h_{2}^{3} }}\left[ {\left( {x_{2} + a} \right)^{2} - 4L\left( {x_{2} + a} \right) + 6L^{2} } \right] + \frac{{q_{n} }}{{E_{2} h_{2}^{3} }}\left[ {\left( {x_{2} + a} \right)^{2} - 4\left( {x_{2} + a} \right)x_{2} + 6x_{2}^{2} } \right] \\ & \;\;\;\begin{array}{*{20}c} {\left. { - \frac{{3q_{n} x_{2}^{4} }}{{E_{1} h_{1}^{3} \left( {x_{2} + a} \right)^{2} }} + \frac{{4a}}{{\left( {x_{2} + a} \right)^{2} }}\tan \left( {\frac{{q_{n} x_{2}^{3} }}{{E_{1} h_{1}^{3} }}} \right)} \right\}/\left[ {\left( {a^{2} + 2ax_{2} - 5x_{2}^{2} } \right)\left( {\frac{1}{{E_{1} h_{1}^{3} }} + \frac{1}{{E_{2} h_{2}^{3} }}} \right)} \right],} \\ \end{array} \\ \end{aligned}$$

(11)

Model 2- large roof pre-splitting depth

The roof pre-splitting depth extends to the upper boundary of the main roof in this model as shown in Fig. 9 (b). The main roof is penetrated by pre-splitting cutting, and a hinged arch is formed between the main roof blocks on both sides of the pre-splitting fracture. The roof subsidence and the support resistance of the gob-side entry are mainly controlled by the hinged arch subsidence.

Under the action of the support resistance ${\text{P}}$, the supporting load ${{\text{q}}_{\text{n}}}$ and the overlying strata load ${\text{q}}$., the subsidence ${{\text{\varvec{\upomega}}}_{\text{b}}}\left( {\text{x}} \right)$ of the main roof suspended above the gob-side entry can be expressed as Eq. (12).

$$\begin{aligned} \omega _{b} \left( x \right) & = \frac{{qx^{2} }}{{4E_{2} h_{2}^{3} }}\left\{ {x^{2} - 4\left[ {x_{2} + a + \frac{{\left( {h_{1} + h_{2} } \right)\tan \theta }}{2}} \right]x + 6\left[ {x_{2} + a + \frac{{\left( {h_{1} + h_{2} } \right)\tan \theta }}{2}} \right]^{2} } \right\} \\ & \;\;\;\begin{array}{*{20}c} { - \frac{{Px^{2} }}{{4E_{2} h_{2}^{3} }}\left( {x^{2} - 6x_{2}^{2} } \right) - \frac{{3q_{n} x_{2}^{4} }}{{4E_{2} h_{2}^{3} }} + \left( {x - x_{2} } \right)\tan \left( {\frac{{q_{n} x_{2}^{3} }}{{E_{2} h_{2}^{3} }}} \right),} \\ \end{array} \\ \end{aligned}$$

(12)

And, under the action of the support resistance ${\text{P}}$, the supporting load ${{\text{q}}_{\text{n}}}$ and the overlng strata load ${{\text{q}}_{\text{1}}}$, the roof subsidence ${{\text{\varvec{\upomega}}}_{\text{a}}}\left( {\text{x}} \right)$ of the gob-side entry can be expressed as Eq. (13).

$$\begin{array}{*{20}{c}} {{{\text{\varvec{\upomega}}}_{\text{a}}}\left( {\text{x}} \right){\text{=}}{{\text{\varvec{\upomega}}}_{\text{1}}}\left( {\text{x}} \right){\text{,}}} \end{array}$$

(13)

When the subsidence of the hinged arch reaches a stable state, the immediate roof and the main roof are in close contact, and there is no bed separation between them above the goaf side of the gob-side entry, i.e., ${{\text{\varvec{\upomega}}}_{\text{a}}}\left( {{{\text{x}}_{\text{1}}}{\text{+a}}} \right){\text{=}}{{\text{\varvec{\upomega}}}_{\text{b}}}\left( {{{\text{x}}_{\text{2}}}{\text{+a}}} \right)$. Generally, the breaking of the main roof forces the immediate roof beneath it to subside synchronously. Therefore, it can be assumed that the broken positions of the main roof and the immediate roof above the solid coal side of the gob-side entry are coincident, i.e., ${{\text{x}}_{\text{1}}}{\text{=}}{{\text{x}}_{\text{2}}}$. Then, the roof subsidence ${{\text{\varvec{\upomega}}}_{\text{b}}}\left( {{{\text{x}}_{\text{2}}}{\text{+a}}} \right)$ and the support resistance ${{\text{P}}_{{\text{model\_2}}}}$ of the gob-side entry are given by as Eqs. (14) and (15), respectively.

$$\begin{aligned} \omega _{b} \left( {x_{2} + a} \right) & = \frac{{q\left( {x_{2} + a} \right)^{2} }}{{4E_{2} h_{2}^{3} }}\left\{ {\left( {x_{2} + a} \right)^{2} - 4\left[ {x_{2} + a + \frac{{\left( {h_{1} + h_{2} } \right)\tan \theta }}{2}} \right]\left( {x_{2} + a} \right)} \right. \\ & \left. {\;\;\; + 6\left[ {x_{2} + a + \frac{{\left( {h_{1} + h_{2} } \right)\tan \theta }}{2}} \right]^{2} } \right\} - \frac{{P\left( {x_{2} + a} \right)^{2} }}{{4E_{2} h_{2}^{3} }}\left[ {\left( {x_{2} + a} \right)^{2} - 6x_{2}^{2} } \right] \\ & \;\;\; - \frac{{3q_{n} x_{2}^{4} }}{{4E_{2} h_{2}^{3} }} + a\tan \left( {\frac{{q_{n} x_{2}^{3} }}{{E_{2} h_{2}^{3} }}} \right), \\ \end{aligned}$$

(14)

$$\begin{aligned} P_{{\bmod el\_2}} & = \left\{ {\frac{{\left( {q + \gamma _{2} h_{2} } \right)}}{{E_{1} h_{1}^{3} }}\left[ {\left( {x_{2} + a} \right)^{2} - 4\left( {x_{2} + a + \frac{{h_{1} \tan \theta }}{2}} \right)\left( {x_{2} + a} \right) + 6\left( {x_{2} + a + \frac{{h_{1} \tan \theta }}{2}} \right)^{2} } \right]} \right\} \\ & \;\;\; - \frac{q}{{E_{2} h_{2}^{3} }}\left\{ {\left( {x_{2} + a} \right)^{2} - 4\left[ {x_{2} + a + \frac{{\left( {h_{1} + h_{2} } \right)\tan \theta }}{2}} \right]\left( {x_{2} + a} \right)} \right. \\ & \left. {\;\; + 6\left[ {x_{2} + a + \frac{{\left( {h_{1} + h_{2} } \right)\tan \theta }}{2}} \right]^{2} } \right\} + 3q_{n} x_{2}^{4} \left( {\frac{1}{{E_{2} h_{2}^{3} }} - \frac{1}{{E_{1} h_{1}^{3} }}} \right) \\ & \begin{array}{*{20}c} {\;\; + a\left[ {\tan \left( {\frac{{q_{n} x_{2}^{3} }}{{E_{1} h_{1}^{3} }}} \right) - \left( {\frac{{q_{n} x_{2}^{3} }}{{E_{2} h_{2}^{3} }}} \right)} \right]/\left[ {\left( {a^{2} + 2x_{2} a - 5x_{2}^{2} } \right)\left( {\frac{1}{{E_{2} h_{2}^{3} }} - \frac{1}{{E_{1} h_{1}^{3} }}} \right)} \right],} \\ \end{array} \\ \end{aligned}$$

(15)

Roof pre-splitting depth effect

According to the production geology and filed practice, take ${{\text{h}}_{\text{1}}}{\text{=13}}{\text{.7}}$ m, ${{\text{h}}_{\text{2}}}{\text{=4}}{\text{.9}}$ m, ${\text{a=5}}{\text{.2}}$ m, ${{\text{\varvec{\upgamma}}}_{\text{2}}}{\text{=24}}{\text{.1}}$ kN/m³, ${ {\varvec{\uptheta}=15^\circ }}$; ${{\text{E}}_{\text{1}}}{\text{=40}}{\text{.2}}$ GPa, ${{\text{E}}_{\text{2}}}{\text{=7}}{\text{.1}}$ GPa, ${{\text{q}}_{\text{n}}}{\text{=0}}{\text{.41}}$ MPa, and ${{\text{R}}_{\text{T}}}{\text{=4}}{\text{.18}}$ MPa. It can be obtained that ${\text{L=14}}{\text{.94}}$ m, ${\text{q=0}}{\text{.15}}$ MPa, ${{\text{x}}_{\text{2}}}{\text{=5}}{\text{.62}}$ m.

To verify the effect of pre-splitting the main roof on roof subsidence, substitute them into Eqs. (10) and  (14), it can be obtained that ${{\text{\varvec{\upomega}}}_{\text{2}}}\left( {{{\text{x}}_{\text{2}}}{\text{+a}}} \right){\text{=1}}{\text{.05}}$ m and ${{\text{\varvec{\upomega}}}_{\text{b}}}\left( {{{\text{x}}_{\text{2}}}{\text{+a}}} \right){\text{=0}}{\text{.68}}$ m, in comparison, roof subsidence decreased by 35.2%. Furthermore, it can be obtained that ${{\text{P}}_{\text{1}}}{\text{=1}}{\text{.65}}$ MPa and ${{\text{P}}_{\text{2}}}{\text{=1}}{\text{.24}}$ MPa by Eqs. (11) and  (15). Compared with immediate roof pre-splitting, the support resistance after main roof pre-splitting has decreased by 24.8%.

Numerical investigation of the roof pre-splitting depth effect

Through theoretical analysis, it can be seen that the rock pressure behaviors of the gob-side entry retained mainly depend on the subsidence of the short cantilever beam formed after roof pre-splitting above the entry. The shorter the length of the cantilever, the greater the bending stiffness, the smaller the downward deflection deformation, and the smaller the load transferred to the gob-side entry, all of which are beneficial to the stability of the gob-side entry. The stress field near the gob-side entry will change discontinuously under the influence of roof pre-splitting. The roof pre-splitting depth has an important effect on the stress discontinuity, which directly determines the distribution of the stress-concentration area and the stress-relaxation area in the surrounding rocks of the gob-side entry. In addition, due to the influence of the front and side abutment pressure, the stress distribution becomes more complicated. Therefore, it is important to investigate the influence of the roof pre-splitting depth on the stress distribution near the gob-side entry.

Model configuration

Based on the production geology of the 10202 longwall panel, a 397 × 287 × 173 m³ numerical model was built as shown in Fig. 10. The four perimeter boundaries limited horizontal movement but permitted vertical movement. Conversely, the bottom boundary limited vertical movement but allowed horizontal movement, while a uniform load of 8.5 MPa was applied to the top boundary. The Mohr-Coulomb yield criterion was used to describe the failure of overlying strata. The mechanical behaviors of the coal seam and the collapsed rock blocks in the goaf were simulated by strain softening model and double yield model, respectively. The interface elements were used to describe the interaction between the two sides of the pre-splitting fracture. The model was used to investigate the influences of four roof pre-splitting depths of 10 m, 15 m, 20 m, and 25 m on the stress distribution near the gob-side entry.

Fig. 10

Numerical model(FLCA3D 5.0-demo, https://itascasoftware.com/demo-download/).

Influence of roof pre-splitting depth on the side abutment pressure

In order to obtain the side abutment pressure, a series of measurement lines are arranged in the roof 1 m away from the top of the coal seam along the dip direction of the longwall panel. The side abutment pressure distributions in front of the longwall panel are shown in Fig. 11. The x-coordinate axis represents the distance from the model boundary. The x-coordinate of the gob-side entry is greater than 50 m and smaller than 55 m. It is less than 50 m for the solid coal side of the gob-side entry, and greater than 55 m for the goaf side of the gob-side entry.

Fig. 11

Side abutment pressure distributions in front of the longwall panel.

The surrounding rocks of the gob-side entry within 30 m in front of the longwall panel are affected by the mining-induced disturbance. Stress-concentration areas are formed on both sides of the gob-side entry. The side abutment pressure on the goaf side is greater than that on the solid coal side, and the peak abutment pressures on both sides move deeper. The abutment pressure gradually decreases as it moves away from the longwall panel. As the roof pre-splitting depth increases, the abutment pressure on the goaf side decreases, while the abutment pressure on the solid coal side increases slightly.

Under the condition of 15° dip angle of the borehole to the goaf, hinged arch is difficult to form between the rock blocks after roof pre-splitting, which greatly weakens the ability to transfer the gob-side strata load to the solid coal side. The overlying strata load is mainly borne by the solid coal on the goaf side of the gob-side entry after roof pre-splitting. Thus, the side abutment pressure on the goaf side is greater than that on the solid coal side under the mining-induced disturbance. After roof pre-splitting, a large part of the energy is released due to the reduction of the constraints on the roof. The range of stress-relaxation area increases with the pre-splitting depth, which shows that the abutment pressure decreases with the increase of the pre-splitting depth on the goaf side of the entry. When the pre-splitting depth exceeds 20 m, the pressure-relief effect is weak.

Fig. 12

Side abutment pressure distributions behind the longwall panel.

The side abutment pressure distributions behind the longwall panel are shown in Fig. 12. Generally, the side abutment pressure behind the longwall panel first increases and then decreases as it moves away from the longwall panel, and it decreases with the increase of the roof pre-splitting depth. The roof pre-splitting effect is weak when the pre-splitting depth is greater than 20 m. The mining-induced disturbance range increases with the advancement of the longwall panel, which causes the side abutment pressure to gradually increase. When the distance from the longwall panel exceeds 50 m, the side abutment pressure behind the longwall panel gradually decreases, which indicates that the collapsed rock has filled the goaf densely and borne a part of the strata load in the goaf.

Influence of roof pre-splitting depth on the strike-direction abutment pressure

In order to obtain the strike-direction abutment pressure, a series of measurement lines are arranged on the solid coal side of the gob-side entry along the strike direction of the longwall panel, as shown in Fig. 13. The strike-direction abutment pressure distributions as the longwall panel advances 100 m are shown in Fig. 14. The x-coordinate axis represents the distance from the model boundary in the advancing direction of the longwall panel. The x-coordinate of the solid coal behind the setup entry is less than 30 m, greater than 30 m and less than 130 m for the goaf, and greater than 130 m for the solid coal in front of the longwall panel.

Fig. 13

Arrangement of the measurement lines for the strike-direction abutment pressure.

Fig. 14

Strike-direction abutment pressure distributions on the solid coal side of the gob-side entry.

The strike-direction abutment pressure distributions on the solid coal side of the gob-side entry shown in Fig. 14 indicate that roof pre-splitting can effectively relieve the stress concentration on the solid coal side, but the pressure-relief effect is weak when the roof pre-splitting depth exceeds 20 m. As shown in Fig. 14 (a), the width of the stress-relaxation area on the solid coal side exceeds 2 m regardless of the roof pre-splitting depth, i.e., the failure depth of the solid coal side is greater than 2 m. Since the field bolt length is usually 2.2 m, it is slightly greater than the failure depth of the solid coal side, which is likely to cause the failure and wall-like falling-off of the coal mass on the solid coal side due to the overall pull from the anchorage end of the bolt. It can also be seen from Fig. 14 (b)-(d) that the roof pre-splitting depth mainly affects the stress-concentration area of the solid coal side between 10 and 90 m behind the longwall panel and 5–10 m away from the solid coal side. The coal mass 40 m away from the solid coal side of the gob-side entry, at a deeper depth, is hardly affected by the influence of roof pre-splitting and mining, and it is basically in the in-situ stress state.

Field application

Limestone strata tend to collapse in large blocks with small bulking factor. With an insufficient roof pre-splitting depth of 13 m and a small amount of collapsed rock, the goaf is easily left insufficiently filled. Then, there is still a large space for the main roof rotation and subsidence. Since the limestone immediate roof has not collapsed sufficiently, a hinged arch is formed between the thick limestone immediate roof blocks. This structure transfers the load from the goaf to the 10202 gob-side entry, causing severe deformation in the prop and U-shaped steel block gangue point column, as well as a sharp reduction in the cross-section of the entry. The roof pre-splitting depth of 13 m fails to completely cut off the load transfer from the goaf to the retained 10202 gob-side entry. Insufficient pre-splitting depth is the main factor causing severe rock pressure and large deformation of the 10202 gob-side entry. Theoretical analysis suggests that, following main roof pre-splitting, roof subsidence and support resistance are reduced by 35.2% and 24.8%, respectively, compared with immediate roof pre-splitting. After roof pre-splitting, a large part of the energy is released due to reduced constraints on the roof. The range of stress-relaxation area increases with the increase of the pre-splitting depth, which shows that the abutment pressure decreases with the increase of the pre-splitting depth. When the pre-splitting depth exceeds 20 m, the pressure-relief effect is weak.

Based on the previous analysis, the roof pre-splitting depth for the retained 10204 gob-side entry is finally determined to be 20 m. The clamping action at the borehole bottom becomes increases due to the greater roof pre-splitting depth. In order to ensure that the cracks coalesce after roof pre-splitting, the charge per borehole is adjusted to 11.7 kg, and the line charge density is 0.585 kg/m, which is 0.154 kg/m greater than the 0.431 kg/m used for the 10202 gob-side entry roof cutting borehole. The indirect priming method is adopted. The cartridge is laid inside the cylindrical charge and close to the borehole bottom, and detonator bottom is set toward the borehole collar. The total explosive charge per blast is increased to 117 kg, with ten boreholes detonated simultaneously in each blast.

The roof pre-splitting parameters for the 10204 gob-side entry retained by roof cutting are summarized in Table 3. The roof pre-splitting results are measured using a borescope, as shown in Fig. 15. It is obvious that 2 or 3 radial tensile cracks developed around the borehole and ran through the whole length of the borehole. In addition, blasting fume flowed out from the observation borehole. These phenomena indicate that cracks had coalesced after roof pre-splitting, and good roof cutting results were obtained. In order to evaluate the results of the 10204 gob-side entry retained, field measurement of rock pressure is carried out. The monitoring content mainly includes the working resistance of the hydraulic powered supports, the bed separation, the roof-to-floor convergence, and the pressure on single hydraulic props. Detailed field measurements are summarized in the following subsections. Based on the field measurement, the surrounding rock deformation of the 10204 gob-side entry retained by roof cutting has been effectively controlled.

Table 3 Roof pre-splitting parameters for the 10204 gob-side entry retained.

Fig. 15

Roof pre-splitting results of the 10204 gob-side entry retained by roof cutting.

Field measurement configuration

Along the dip direction of the 10204 longwall panel, a total of 11 pressure sensors are installed to measure the working resistance of the hydraulic powered supports. Pressure sensors are installed at an interval of 15 hydraulic powered supports in the middle part of the longwall panel, and at an interval of 7 hydraulic powered supports at both ends. Convergence meters are used to measure the roof-to-floor convergence and are arranged along the goaf edges with an interval of 20 m. Pressure sensors are installed on the single hydraulic props near the roof-to-floor convergence measurement positions with an interval of 20 m. Bed separation is measured using the differential roof sag meters, which are arranged along the roof pre-splitting edge at an interval of 50 m. The field measurement configuration is shown in Fig. 16.

Fig. 16

Field measurement configuration.

Working resistance of the hydraulic powered supports

Working resistance of the hydraulic powered supports located on the upper, middle and lower parts of the 10204 longwall panel during mining are shown in Fig. 17. The No. 1 hydraulic powered support is close to the 10204 gob-side entry retained. The No. 53 hydraulic powered support is set on the middle part of the 10204 longwall panel. The No. 94 hydraulic powered support is close to the 10204 tailgate, and the roof has not been pre-splitting cut. The rock pressure behaviors of the 10204 and 10202 longwall panels are summarized in Table 4.

Fig. 17

Working resistance of hydraulic powered supports with respect to the advancement distance.

Table 4 Rock pressure behaviors of the 10204 and 10202 Longwall panels.

Compared with 10202 longwall panel, the rock pressure behaviors in the middle and lower parts of the 10204 longwall panel change insignificantly after increasing the roof pre-splitting depth, respectively. However, it has a greater impact on the upper part of the 10204 longwall panel. The first and periodic weighting interval increase by 4 m and 3.4 m, respectively. At the same time, peak working resistances during first weighting and periodic weighting decreases by 7.24 MPa and 7.60 MPa, respectively. Additionally, the average working resistance decreases by 1.81 MPa. Compared with 10202 longwall panel, the weighting interval of the 10204 longwall panel is larger, but the working resistance of the hydraulic powered supports is lower, which indicates that the goaf is densely filled by the collapsed roof and the main roof has no space for subsidence movement. Thus, the rock pressure behaviors of the 10204 longwall panel are milder than those of the 10202 longwall panel.

Bed separation

The field measurement results of the bed separation for the 10204 gob-side entry retained are shown in Fig. 18 (a). Compared with 10202 gob-side entry, the growth rate of the bed separation for 10204 gob-side entry retained decreases and remains stable at 84.3 mm, which is 43.8 mm smaller than that of the 10202 gob-side entry retained.

Fig. 18

Rock pressure behaviors of the 10204 gob-side entry retained.

Roof-to-floor convergence

The roof-to-floor convergence of the 10204 and 10202 gob-side entries retained during mining are shown in Fig. 18 (b). Compared with the 10202 gob-side entry retained, the growth rate of the roof-to-floor convergence for 10204 gob-side entry retained decreases and remains stable at 756.3 mm, which is 416.6 mm smaller than the 10202 gob-side entry retained.

Pressure of single hydraulic props

The pressure of single hydraulic props for the 10204 gob-side entry retained are shown in Fig. 18 (c). In general, the pressure of single hydraulic props decreases after the roof pre-splitting depth is increased. Compared with 10202 gob-side entry retained, the pressure of the single hydraulic prop near the goaf side, the middle and the solid coal side of the 10204 gob-side entry retained are reduced by 1.53 MPa, 1.19 MPa and 1.52 MPa, respectively. At the same time, field observations found that few single hydraulic props experience automatic pressure-relief and severe deformation or breakage.

Discussions

Assumptions and implications

The heterogeneous characteristics of rock are scale-dependent. In laboratory physical tests, rocks generally exhibit heterogeneous properties. For engineering scales, numerous studies indicate that when the research object’s size exceeds the Representative Elementary Volume (REV), its heterogeneous characteristics gradually diminish. In coal rock containing multi-scale structural features including face cleats, butt cleats, and bedding planes, Bieniawski’s^23,24 in-situ strength tests revealed that mechanical properties such as stiffness and strength remain essentially constant when coal rock blocks exceed 1 m³. This suggests that coal rock exhibits homogeneous characteristics beyond this critical scale. Similar size effects and REV principles apply to other rock types - when the study scale surpasses their respective REV dimensions, the material can be considered homogeneous.

This fundamental assumption has been widely adopted in overburden movement and ground pressure studies to facilitate analytical solutions. The validity of homogeneity assumption correlates with actual stratum thickness. It holds reasonably well in thick rock formations, whereas in thinner strata discrepancies emerge between main roof and immediate roof fracture patterns. Specifically, the immediate roof’s rotational pivot shifts deeper into the solid coal compared to the main roof, i.e., the assumption of x1 = x2 in section “Model 2- large roof pre-splitting depth” will be revised to x1 > x2, resulting in amplified subsidence on the goaf side of retained roadways. This phenomenon increases required support resistance for roof control.

Error analysis

In the numerical simulation part, based on the FLAC^3D model, a ± 10% perturbation test was conducted on the pre-splitting depth (D) and the elastic modulus of the rock mass (E). The results show that the sensitivity coefficient of roof subsidence to D is 0.87, while the sensitivity coefficient to E is only 0.12. In the model validation, the average relative error between the simulated values and the measured values at three independent measuring points is 6.8%, which meets the requirements of engineering accuracy.

In addition, to quantify the actual effect of the roof pre-splitting technique and conduct an error analysis, the complete data from six measuring points were collected. The data content is summarized in Table 5. Based on the data in Table 5, a statistical analysis of roof subsidence and support resistance was carried out.

Table 5 Field-measured subsidence and support resistance data.

The measured values of roof subsidence and support resistance at each measuring point all passed the normality test. An independent-samples t-test was used to compare the data differences before and after pre-splitting. The results show that the roof subsidence in the roof cutting area is significantly less than that in the original area (Δ = 387.67 mm, p < 0.001), and the support resistance is also significantly reduced (Δ = 14.82 MPa, p < 0.001). These results indicate that, compared with the original area, the roof cutting technique has a remarkable effect in reducing roof subsidence and support resistance. The results of the t-test are presented in Table 6.

Table 6 t-test results of roof subsidence and support resistance.

Adaptability analysis of roof pre-splitting height

The main idea behind roof pre-splitting and pressure relief lies in accelerating the natural collapse of the roof through artificial means, thereby relieving the pressure generated by the roof’s collapse, this approach aims to reduce stress transmission. The key principle is, under the fragmentation effect, the rock fills sufficiently after collapse, reducing the space for the key layer to rotate downward and subsidence, and minimizing relative movement between key layers.

This study is particularly based on the Yongning 10202 longwall panel for research. According to the geologic columnar profile, the unmined 10# coal seam’s roof consists sequentially of a 13.7-meter limestone layer, a 4.9-meter sandy mudstone layer, and a 0.3-meter 7# coal seam. The first key layer is the 13.7-meter limestone layer, characterized by high rock strength, large block sizes after collapse, and small bulking factor. The challenge under these conditions lies in ensuring the complete cutting and collapse of the limestone to minimize the length of suspended roof and promote the subsidence of follower strata, thereby creating an environment with relatively smaller stresses for the surrounding rock and facilitating stress control of the gob-side entry.

The main idea of the aforementioned roof pre-splitting technology is applicable under any geological conditions. Generally, there exists one or more key rock layers in the roof strata. The determination of which key layer to cut depends on the longwall panel’s mining height. Typically, the roof pre-splitting height should not be less than 2.6 times the mining height, and the bulking factor of collapsed rock is generally 1.3. If the first key layer in the overlying strata is within 2.6 times the mining height²⁵ cutting this first key layer is sufficient, the follower strata will collapse along with it and fill the goaf. When the position of the key layer exceeds 2.6 times the mining height, setting the pre-splitting height to 2.6 times the mining height is adequate to fill the goaf, thereby reducing the movement space of the first key layer.

For the Yongning 10202 longwall panel, with a mining height of 4.5 m, 2.6 times the mining height equals 11.7 m. This value is less than the thickness of the direct roof limestone layer, which is 13.7 m. Given that the thick and hard roof has good integrity, large block sizes, poor collapse properties, tends to form articulated structures, and given that it also serves as the first key layer, the pre-splitting height should be at least greater than 13.7 m to fully penetrate this layer and achieve pressure relief.

Conclusions

In this study, we focus on the 10202 gob-side entry at Yongning Coal Mine, which is characterized by a 4.5-meter-thick coal seam and a 13.7-meter-thick limestone roof. The research employs comprehensive methods including theoretical analysis, numerical simulation, and field applications to analyze the issues related to excessively high rock pressure and cross-sectional deformation in the entry during the full-mechanized mining operations, and discussed the effect of pre-splitting depth on the stability of the gob-side entry. From the results, we can conclude the following:

• 1. Under the conditions of Yongning 10202 longwall panel, the main reasons for the large deformation and severe compression of the gob-side entry are the insufficient pre-splitting depth (13 m), which fails to cut off the load transfer path.

• 2. Through theoretical analysis, under the conditions of Yongning 10202 longwall panel, compared with the immediate roof pre-splitting, the roof subsidence and support resistance after main roof pre-splitting are reduced by 35.2% and 24.8%, respectively.

• 3. After roof pre-splitting, the overlying strata load are mainly beard by the solid coal on the goaf side of the gob-side entry after roof pre-splitting. Thus, the side abutment pressure on the goaf side is greater than it on the solid coal side under the mining-induced disturbance.

• 4. The width of the stress-relaxation zone in the solid coal exceeds 2 m regardless of the roof pre-splitting depth, meaning the failure depth on the solid coal side is greater than 2 m. Since the field bolt length is typically 2.2 m, which slightly surpasses the failure depth, this could potentially lead to the failure and wall-like spalling of the solid coal side by the overall pull from the anchorage end of the bolt.

• 5. With the increased roof pre-splitting depth, the clamping action at the borehole bottom intensifies, necessitating an increase in explosive charge to achieve the required blasting effectiveness.