Visibility graph analysis for educational data: potentials and a case study of predicting at-risk online students

Abstract

This paper introduces visibility graph analysis as a supplementary approach for examining educational time series data, particularly in online learning environments. By converting temporal data into graph representations, we uncover previously hidden patterns and relationships in student interactions, enabling more effective analysis, classification, and prediction of learning outcomes. Through a rigorous case study using the Open University Learning Analytics Dataset, we demonstrate how visibility graph metrics can accurately predict at-risk online students based on their clickstream patterns, achieving classification accuracy exceeding 87% using gradient boosting algorithms. Our novel methodology outperforms several recent deep learning approaches while providing interpretable insights about student behavior through graph-theoretical features such as global efficiency, assortativity coefficient, and betweenness centrality. This research establishes visibility graph analysis as an innovative tool in educational data mining that complements traditional machine learning techniques, opening new avenues for early intervention strategies and personalized learning pathways. However, accurately modeling the problem and selecting the appropriate type of visibility graph for the educational time series data remains dependent on the researcher’s knowledge.

Introduction

Nowadays, E-learning refers to the integration of digital technologies to enhance the instructional process within an educational environment¹. It is facilitated through a diverse array of digital learning platforms and tools, including language learning applications, video conferencing technologies, virtual tutoring systems, online instructional software, and comprehensive learning management systems such as Moodle².

The integration of technology in education has led to a significant increase in the amount of time-series data being generated. Examples of educational time series data include clickstream data, which records students’ digital interactions and activities with learning materials, providing insights into their learning behaviors and preferences³. Sensor data collected through wearable devices measures physiological or behavioral indicators, giving insights into students’ attention levels, emotional states, and physical engagement during learning activities⁴. E-assessment log data captures detailed information about participants’ behaviors and performance during digital assessments, enabling the analysis of strategies, engagement, and areas for improvement⁵. Video analytics data, derived from the analysis of user behavior and interactions within video content, helps to understand students’ viewing habits, identify patterns of engagement, and make informed decisions about instructional design⁶.

These different types of time series data contribute to a comprehensive understanding of the learning process, allowing educators to optimize digital learning experiences, personalize interventions, and improve assessment practices and instructional design. Together, they offer a multifaceted perspective on student learning, facilitating data-driven decision-making and improving educational outcomes. However, effective analytical approaches to extract actionable insights about student learning from educational data remain underdeveloped. Traditional machine learning techniques have been widely applied in educational data mining; but, the increasing complexity of learning environments has led to a growing interest in advanced models such as deep learning. While these models often provide higher predictive accuracy, they are frequently criticized for their lack of interpretability due to their reliance on multiple hidden layers that obscure the decision-making process⁷. Also, the “black box” nature of analytical methods presents a major limitation in educational settings, where transparency and explainability are critical for educators and policymakers³. Moreover, deep learning also suffers from high computational overhead for large datasets and a tendency to overfit when applied to small datasets. As a result, there is an urgent need for interpretable and efficient analytical tools that avoid the complexities associated with deep learning and other machine learning methods.

In this context, visibility graphs have emerged as a supplementary tool, with applications across various disciplines. Originally developed to convert time series data into complex networks⁸.Visibility graphs have proven effective in identifying temporal patterns through the analysis of network topologies. Metrics such as degree distribution and average degree enable the extraction of distinguishing features with high accuracy and effective visualization⁹. Also, the analysis of visibility graphs has been extensively employed in diverse domains, including medicine¹⁰, economics¹¹, image processing¹², water management¹³, industrial processes¹⁴ and other areas to predict future values better, distinguish between normal and abnormal states without using complex methods, and add more efficient analysis with new computational insights¹⁵. However, their application in the educational domain, particularly for analyzing learning-related time series data, remains largely unexplored.

This paper explores the application of the visibility graph algorithm in transforming E-Learning time series data into a graph to analyze the resulting topological properties. We specifically focus on the applications of visibility graphs in three main categories: analysis, classification, and prediction: (1) Analysis to provide a unique perspective for understanding educational time series data, uncovering patterns and relationships that shed light on student learning behaviors and instructional effectiveness; (2) classification to enable the identification of significant events, anomalies, and areas for improvement within the data; and (3) Prediction to allow educators to forecast future values and outcomes based on the temporal dependencies captured in the data. By exploring these applications, this paper highlights how visibility graphs can contribute to a comprehensive understanding of educational time series data and leverage them to inform data-driven decision-making in education. To prove the efficiency of the application, we will present a case study for predicting student success or failure with a visibility graph analysis approach. This innovative approach allows educators to actively identify students who may need additional support, enabling timely and targeted interventions that enhance their learning experience. We will compare and evaluate the performance of the case study with some recent studies as well.

The structure of the research is outlined as follows: Sect. “Background” provides an overview of E-Learning time series data analysis and introduces the concepts of visibility graphs. Section “Visibility graph analysis potentials for educational data” outlines the use of visibility graphs in education based on the three applications of analysis, classification, and prediction. In Sect. Case study: visibility graph analysis for predicting at-risk online students, a detailed case study is presented, focusing on the prediction of at-risk students based on their clickstream data. Finally, Sect. “Results and discussion” concludes the study and provides insights into potential future research directions.

Background

Visibility graph

The concept of the Natural Visibility Graph (NVG), or simply visibility graph, was first introduced by Lacasa et al. in 2008. A visibility graph is a method that converts a time series into a network by treating each data point as a node and connecting nodes if they can “see” each other based on their relative heights, values Fig. 1. Therefore, the point ${t}_{i}$ with value ${y}_{i}$, which corresponds to node ${n}_{i}$ in the graph, is connected to the time point ${t}_{j}$ with value ${y}_{j}$, which corresponds to node ${n}_{j}$ in the graph. The condition for establishing an edge is that if the tops of the vertical bars are visible to one another, even when considering the presence of a middle bar between two graph points, an edge will be drawn under the stipulations outlined in Eq. (1). Consequently, in mathematical language, the condition of constructing an edge between two nodes $\left({t}_{i},{y}_{i}\right)$ and $\left({t}_{j},{y}_{j}\right)$ with the attendance of the middle rod $\left({t}_{n},{y}_{n}\right)$ is to apply Eq. (1)¹⁶.

Fig. 1

(a) (Time series bar graph) time points on the horizontal axis are the nodes of the graph, and the lines connecting the values are the edges of the graph, which are drawn with the condition of being true in relation 1). (b) The visibility graph resulting from the time series.

$${y}_{n}<{y}_{j}+\left({y}_{i}-{y}_{j}\right)\frac{{t}_{j}-{t}_{n}}{{t}_{j}-{t}_{i}}$$

(1)

Although there are other popular types of visibility graphs according to their construction method, such as horizontal visibility graphs (HVG)⁸ or limited penetrable visibility graph (LPVG)¹⁷. HVG is a similar graph representation to NVG, but it connects each point in a time series to all others that can be reached by drawing horizontal lines unobstructed by intermediate points of equal or greater value, whereas a natural visibility graph connects points based on direct line-of-sight visibility over the plotted data without the horizontal constraint. Moreover, LPVG is a variation of NVG that allows connections between points even if there are other points in between, but only up to a certain threshold of penetration, making it more flexible in capturing the underlying structure of the time series. However, in the case study of this research, the natural visibility graph will be used.

Visibility graph analysis

The analysis of visibility graphs shares similarities with complex network analysis, albeit with a distinction that it involves calculating graph parameters derived from time series data. Given the frequent utilization and referencing of complex network parameters in this study, Table 1 presents a brief and easy-to-understand description of the graph properties used. Numerous sources are available for formal equations and precise definitions^18,19,20.

Table 1 One sentence definition for each of the graph properties.

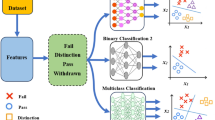
Besides, the analysis of visibility graphs has emerged as a valuable tool for time series analysis across various research domains, yielding significant outcomes in fields such as medicine, biology, economics, geology, water management, image processing, etc. Figure 2 illustrates that visibility graph analysis can be employed for three primary purposes: revealing new insights, distinguishing between two or more states, and predicting new values.

Fig. 2

Visibility graph analysis applications.

Essentially, the notion of revealing new insights implies leveraging the distinct perspective of visibility graphs on time series data resulting from graph analysis properties such as graph density, diameter, centrality, clustering coefficient, average shortest path length, degree distribution, scale-free or small world phenomena, and so on, as described in Table 1. This benefit has the potential to enhance the exploration of novel views and augment the understanding of time series data beyond the limitations of traditional direct analysis. Moreover, such techniques may contribute to the advancement of comprehension of the underlying data within the time series. For instance, the bitcoin price time series data can be modeled in diverse ways using visibility graph analysis techniques, leading to novel insights and a deeper understanding ²¹. There are different examples of finance²², earthquake²³, water¹³, etc.

In distinguishing or diagnosis, time series data can be categorized into two groups: those related to normal states and those related to abnormal states. For example, in the context of diseases, we may encounter time series data related to vital symptoms of both healthy individuals and diseased individuals. Considerably, visibility graph analysis is a useful tool for accurately diagnosing such conditions without relying on complex machine learning algorithms or other sophisticated methods. Improved differentiation and diagnosis between these two categories can lead to better outcomes in different areas, such as medical^24,25, engineering^26,27, etc.

Additionally, visibility graph analysis can aid in predicting future values in time series data, such as weather patterns or disease spread, providing valuable solutions for subsequent steps^28,29. Several recent studies are concentrating directly on improving the prediction accuracy of time series data with visibility graph processing approaches^30,31,32.

Visibility graph analysis potentials for educational data

Visibility graphs offer a unique theoretical framework for analyzing time series data by converting sequential observations into graph structures. This method preserves both local and global properties of a time series, enabling the extraction of complex dynamics such as nonlinearity, fractal characteristics, and scale invariance directly from the graph topology. In such graphs, each observation is represented as a node, while the edges represent a “visibility” criterion—essentially encoding the temporal ordering and intrinsic structure of the data (Eq. 1). This approach not only integrates principles of network science with time series analysis but also provides a more profound understanding of the inherent connectivity and interaction among different time points. Moreover, this transformation circumvents some limitations of traditional methods by offering enhanced computational efficiency, making it an attractive theoretical tool across various domains³³.

Another significant advantage lies in the versatility of visibility graphs, which can be adapted to capture different aspects of time series behavior. Various forms of these graphs—such as horizontal, k-visibility, and image visibility graphs—are available to accommodate different analytical needs, from clustering to prediction. Recent research has demonstrated that these graph-based representations can be pivotal in improving forecasting frameworks and pattern recognition models. By emphasizing the structural properties that are often overlooked in conventional analyses, visibility graphs facilitate a more comprehensive theoretical exploration of data dynamics. This flexibility in mapping and analyzing temporal data empowers researchers to design novel methodologies that are both robust and computationally scalable, as evidenced by emerging studies in the field³⁴.

There are several time series data in the E-Learning systems, Fig. 3, such as clickstream, learning progress, web server log, activity, time spent, assessment, and log-in, which we briefly explain as follows.

• 1. Clickstream data: This type of data tracks the sequence of actions performed by learners, such as clicks on course materials, navigation through online modules, and interaction with learning resources.

• 2. Assessment data: It includes learners’ performance on quizzes, tests, and assignments over time. This data can be used to analyze trends in learning outcomes and identify areas where students may need additional support.

• 3. E-assessment log data: This data refers to the collection of digital records or logs that capture various activities and events occurring during an e-assessment or e-exam. These logs contain detailed information about the interactions and behaviors of participants within the e-assessment system or platform.

• 4. Video analytics: It is the data on which part of a video recording has been watched. Also, data that is collected from students’ interactions with educational videos over time can fall into this category.

• 5. Web server log file: E-Learning applications hosted on web servers store website accesses and actions in text files as log entries, encompassing information such as access time, retrieved URL, client IP address, access time, HTTP status code, and more. These log entries can be treated as time series data and analyzed accordingly³⁵.

• 6. Sensor data: It’s the data type captured through wearable devices that measure physiological or behavioral indicators such as eye movements, heart rate, or motion to understand students’ attention, arousal levels, and physical movements during learning activities³⁶.

Fig. 3

Different forms of time series data in E-Learning systems.

By analyzing these types of time series data, researchers and educators can gain valuable insights into learners’ behaviors, performance, and engagement within the E-Learning environment. Building upon the previous section of this paper, as depicted in Fig. 2, we classify the applications of visibility graphs in the field of E-Learning into three distinct categories: analysis, classification, and prediction.

Analysis

This application seeks to address the question of which valuable indicators may be derived from the visibility graph. Specifically, it aims to identify the salient features of the graph under investigation within the educational domain. Furthermore, it endeavors to determine whether the structure of the extracted graph can be verified or not. For example, by applying community detection algorithms to the extracted visibility graph, various opportunities arise for gaining deeper insights into the time series. Network structures often exhibit inhomogeneous link distributions with communities. In that way, it demonstrates that clusters of nodes are more densely connected internally than externally. Various algorithms have been developed to detect these communities, typically by optimizing a quality measure known as the modularity index (Eq. 2)³⁷.

$$Q=\sum_{i}{({e}_{ii}- {a}_{i})}^{2}$$

(2)

where ${e}_{ii}$ is the fraction of edges in the network between any two nodes in the group i and ${a}_{i}$ is the total fraction of links originating from it and connecting nodes belonging to different ones. This possibility can be effectively applied to identify changes in behavior patterns in user interactions with the E-Learning system. Additionally, anomaly detection within the graph enables the detection of unusual or potentially noisy data points in the time series. Moreover, the exploration of graph motifs facilitates the discovery of predominant patterns in the time series from a different perspective. Some similar applications in different fields are^29,38.

Another instance of gaining from the visibility graph to analyze the educational data is the identification of the extracted graph structure. Graphs arising from human activities typically do not exhibit purely random or regular structures; instead, they often display scale-free or small-world properties, which are commonly observed in various graphs. A scale-free graph is a type of graph where the distribution of connections or links follows a power law (Eq. 3)³⁹, meaning that a few nodes have a disproportionately large number of connections while the majority of nodes have only a few connections. In other words, the graph exhibits a "rich get richer" phenomenon, where highly connected nodes, called hubs, tend to attract more connections over time. Scale-free graphs are characterized by their resilience to random failures but vulnerability to targeted attacks on the most connected nodes. Examples of scale-free graphs include the World Wide Web, social networks, and biological graphs.

$$p\left(k\right)\sim {k}^{-\gamma }$$

(3)

That γ is the power-law tail exponent of the degree distribution, and k is the degree of the graph. The power-law distribution indicates that the graph is a scale-free property³⁹.

On the other hand, a small-world graph is a graph where most nodes can be reached from any other node by a relatively short number of steps or connections. It exhibits both high local clustering (where the node’s neighbors tend to be connected densely to each other) and short average path lengths (the average number of steps it takes to reach any other node in the graph). Small-world graphs are characterized by their efficient information transfer and are commonly found in social graphs, neural graphs, and transportation graphs⁴⁰. When we detect the graph structure figured from the time series data, we may identify the hub node, and important times, or distinguish the dense relations between the neighboring points based on the global graph properties (Eq. 4)⁴¹.

$$L =\alpha + \beta \mathit{ ln}N$$

(4)

where $L$ is the average shortest path length, and $N$ is the number of nodes. Also, if there is a linear relationship between the $L$ and the logarithm $N$, the network is of small-world properties⁴¹.

Moreover, various topological graph parameters aid in comprehending time series data from a graph perspective. These parameters encompass average degree, average shortest path length, graph density, centrality measures, and more¹⁸. For instance, centrality measures help find the important time points in the time series from different viewpoints. Researchers can select and utilize these attributes based on their domain expertise and the specific objectives of employing the visibility graph to enhance data understanding. As an example, betweenness centrality can identify time points that act as bridges between other segments of the time series. Removing such points may split the time series into two or more parts with distinct properties, consequently dividing the corresponding visibility graph into separate components. For a specific timepoint (or node), it can be calculated as the fraction of all shortest paths ($\sigma$) that pass through it. This is represented by the Eq. 5, which $\frac{\sigma (i,j|e)}{\sigma (i,j)}$ denotes the proportion of shortest paths between nodes i and j that traverse node e⁴²:

$$c(e) = \sum\limits_{(i,j)}^{{}} {\frac{\sigma (i,j|e)}{{\sigma (i,j)}}}$$

(5)

Classification

There are several situations for educational data in which the researcher may need to determine the distinction between two or more groups of users or different attributes or levels by a machine learning technique like classification. For example, data related to student performance, such as test scores, grades, attendance records, and demographic information, can be used to classify students into different performance categories (e.g., high achievers, average performers, and struggling students). Moreover, data on various factors associated with student dropouts, such as academic performance, socio-economic background, attendance, and disciplinary records, can be used to classify students into different risk categories (e.g., high risk, moderate risk, and low risk) is another example. Many of these data features are in the time series format and can be converted into a visibility graph. The next scenario is data on students’ course enrollment history, including the subjects they have taken and their grades, that can be used to classify students into different academic tracks or specializations. The last example in this case is Learning Material Recommendation, in which data on students’ preferences, learning history, and assessment results can be used to classify students into different groups for personalized learning material recommendations (e.g., beginner, intermediate, and advanced learners).

Cases with multiple time series can be analyzed by constructing distinct visibility graphs. By employing graph comparison techniques or efficient features, these subjects can be classified with reduced complexity. Similar instances in various domains validate the successful utilization of visibility graphs for classifying between two states, such as distinguishing between healthy and patient categories^24,43,44. As an example from other domains, in a research, human electroencephalogram (EEG) signals are analyzed using a visibility graph algorithm to classify healthy, seizure, and inter-ictal states. EEG data are mapped to VGs, and features such as mean degree and node degree distribution are extracted. Significant differences are observed between healthy and epileptic EEGs, particularly in mean degree and in nodes with degrees five and eight. High classification accuracy is achieved, demonstrating the method’s effectiveness for epilepsy diagnosis⁹. Based on Eqs. (6)¹⁵ and (7)³⁹ the characteristics of the mean degree (MD) and the degree distribution are described.

$$MD= \frac{{K}_{i}}{N}$$

(6)

That ${K}_{i}={\sum }_{j}^{n}{X}_{ij}$, which N is the number of all nodes in the graph. If node i is connected to node j, ${X}_{ij}$ is equals to 1 otherwise 0. So, ${K}_{i}$ is the degree of all n nodes connected to node i in the graph. Also, degree distribution is mathematically described as follows:

$$P\left(k\right)= \frac{{N}_{k}}{n}$$

(7)

where n is the total number of nodes, and N_k is the number of nodes with degree k.

There is a significant number of published articles in this field, to the extent that several recent review papers have also been written on the subject^10,45. In educational data classification, visibility graph application can be employed by first gathering the relevant time series data, transforming it into visibility graphs for each of the two cases, examining the topological structures of the extracted graphs to identify appropriate features, and finally feeding these calculated features into classification algorithms.

Prediction

Another probable application of the visibility graph for educational data is predicting new values for a sample time series. Educational time series data prediction offers several potential applications in the field of learning and E-Learning. These applications include:

• 1. Student performance prediction: By analyzing historical educational time series data, predictive models can be developed to forecast students’ future academic performance. These models can take into account various factors such as past grades, assessment scores, and learning behaviors to provide early indicators of students who may require additional support or intervention.

• 2. Dropout prediction: Educational time series data can be leveraged to predict the likelihood of student dropout. By examining patterns such as declining engagement, decreasing participation, or academic struggles, predictive models can identify students at risk of dropping out and enable proactive interventions to enhance their retention.

• 3. Intervention planning: Educational time series data prediction can help in planning effective interventions for struggling students. By identifying patterns indicative of academic challenges or disengagement, educators can design appropriate interventions, such as providing additional support, personalized feedback, or targeted remedial resources.

• 4. Resource allocation: Predictive models based on educational time series data can aid in optimizing resource allocation in educational institutions. By forecasting student enrollment, course demand, or resource utilization patterns, institutions can make informed decisions regarding faculty allocation, course offerings, infrastructure planning, and budgeting.

• 5. Adaptive learning: Educational time series data prediction can drive adaptive learning systems that dynamically adjust learning content and pathways based on real-time student performance. By continuously monitoring and predicting students’ learning progress, these systems can provide personalized recommendations, adaptive assessments, and tailored feedback to optimize learning outcomes.

These applications demonstrate the potential of educational time series data prediction to enhance educational practices, improve student success rates, and support data-driven decision-making in educational institutions. However, numerous recent scientific papers have extensively explored the application of the visibility graph concept in time series value prediction, some of which are^30,31,32. These studies have demonstrated the superior effectiveness of this approach compared to traditional methods in predicting various types of time series data. Notably, a significant focus has been placed on price and cost prediction due to the considerable significance of these computational domains^46,47. For instance, analyzing the characteristic exponent (λ) of the degree distribution alongside the global clustering coefficient of the network constructed via the Horizontal Visibility Graph method enables a deeper understanding of the underlying dynamics and the degree of predictability inherent in streamflow processes. Additionally, the global clustering coefficient (GC) quantifies the overall clustering tendency of a network, reflecting its structural stability. A GC value approaching 1 indicates a fully connected and highly stable network, whereas a value near 0 suggests complete disconnection. In time series-derived networks, a GC of 1 implies perfect linearity, as every data point is connected to all others²⁸. It is defined in terms of node triplets, sets of three nodes connected by either two or three edges. A triplet is considered closed if all three nodes are mutually connected. The global clustering coefficient $C$ is thus calculated as the ratio of the number of closed triplets to the total number of possible triplets (both open and closed) in the network. This measure can be derived analytically from the network’s adjacency matrix (Eq. 8)⁴⁸.

$$C= \frac{{\sum }_{i,j,k}{{A}_{ij }A}_{jk }{A}_{ki}}{{{\sum }_{i }k}_{i}({k}_{i}-1)}$$

(8)

where ${k}_{i}$ denotes the degree of node i, and if the denominator is null, then C is defined to be 0.

Case study: visibility graph analysis for predicting at-risk online students

Time series data analysis in education

Numerous studies have been conducted in educational data analysis, focusing on leveraging time series data derived from clickstream activities. Clickstream data represents the sequential recording of user clicks within various systems, capturing their interactions at different points in time. As a result, corporations, institutions, and universities have employed clickstream tracking technology to observe and monitor the behavior of individuals visiting their websites. Extensive analysis of clickstream data enables these entities to extract valuable insights into user behavior, including their interests, preferences, engagement patterns, duration of interactions, and potentially overlooked options leading to premature disengagement.

With the emergence of technology and graphs, online learning in higher education has become widespread and a new learning method in all fields. The advantages of this type of learning include reducing the importance of time and location for education, reducing the costs associated with education, and creating learning opportunities for all those who may not be able to attend in-person classes^49,50. However, one concern in this area is the high percentage of failure or dropout rates in such courses. In a study conducted, only 1.5% of enrolled students in online courses were able to complete their courses⁵¹. Therefore, there is a fundamental need to identify and assist students who are at risk so that timely interventions can be made to prevent these conditions⁵². Some factors that help analyze and identify at-risk students include the large volume of data continuously generated and stored in these environments⁵³, as well as various techniques for analyzing this data, which form educational data mining (EDM).

Predicting students’ academic performance and identifying at-risk students is an important research topic in Educational Data Mining (EDM)^54,55. Recently, machine learning techniques have been widely used for this purpose. Many studies examine the interaction data of students with online learning platforms to investigate their performance^56,57. Some studies also use demographic data to examine their model results and measure the predictions against them^56,58. Several studies analyze the data generally, for example, based on past periods, using the entire dataset for examination^55,59, while others analyze data in multiple time intervals to achieve faster results and interventions^60,61.

Studies conducted in the field of online education can be categorized into three groups: predicting student acceptance or rejection^55,56,59,60 Predicting student grades⁶¹, and predicting student at-risk status^62,63. Several studies have explored machine learning and deep learning methods to predict at-risk students. We will briefly review some of these approaches in the following paragraphs.

A recent study based on extracting relational features between the students and a graph convolutional network that utilizes new features extracted from the correlation between the students’ information achieved an accuracy of 87.4% in the classification of students into three classes: “failed”, “at risk”, and “good”⁶⁴. In another study, Aljohani et al. used a deep LSTM (Long Short-Term Memory) model to predict whether students will pass or fail their course. The results were calculated weekly and showed that the accuracy of the proposed model continuously increased with the accumulation of data over weeks, reaching its peak in the final week. Their performance reached 0.9346 for Precision and 0.7579 for Recall⁶⁰.

In a study conducted by Wang et al., predicting student dropout or failure was considered a binary classification problem. Their proposed method uses a CRRNN model (Convolutional Residual Recurrent Neural Network) for prediction. This model utilizes a convolutional neural network to learn features of activity in each period of input matrix data, which represents total clicks. In addition, behavior change patterns throughout periods are preserved using a recurrent neural network. Finally, the final behavior is fed into a fully connected neural network to predict whether the student will complete the course or not⁵⁹. Another study focuses on predicting the performance of at-risk students in five time intervals using six machine learning algorithms and one deep learning technique. The models are designed to classify students into four categories: dropped out, failed, passed, and excellent. The first part of the study uses demographic data only, while the second part combines demographic data with clickstream and assessment scores. Adnan et al. then improve the classification of dropouts and failures by grouping them as “fail” and the other two categories as “pass”. After testing various machine learning algorithms, they use a deep feed-forward neural network (DFFNN) to train a model on three sets of data. They also use a data engineering approach to transform four types of target variables into two (pass/fail). Finally, they divide the period into five time intervals and use random forest analysis to select the best-performing prediction model. This model can assist educators in intervening early in students’ academic progress⁵⁶.

Based on our knowledge, most studies have analyzed clickstream data related to online learning using machine learning and deep learning models⁶⁵. No graph vision has been conducted on this type of data. However, the visibility graph is used to powerfully analyze time series data in other fields. Therefore, a new perspective is to use it for analyzing educational data and introducing it as a helpful topic in EDM. In this section, we are going to transform time series data generated in online learning environments into visibility graphs and use extracted features from the resulting graphs to train models and improve the result accuracy.

Dataset

We utilized the OULA dataset available on Kaggle, (https://www.kaggle.com/datasets/rocki37/open-university-learning-analytics-dataset) preprocessed and curated for direct use. We conducted multiple experiments on two tables from the OULA dataset collection⁵³, one of which is used for learning analytics. What makes this dataset unique is that it includes both demographic data and clickstream data from student interactions in a virtual learning environment (VLE). This allows us to analyze student behavior, which has been demonstrated through its application. The OULA dataset was collected from 32,593 students in a VLE and includes not only demographic and clickstream data but also activity type, course information, and assessment submissions. OULA consists of seven data tables: studentInfo, studentRegistration, studentAssessment, assessments, courses, studentVle, and VLE. The dataset includes 22 courses belonging to seven modules named AAA to GGG. The interactions of students with VLE are displayed as clickstream data, categorized into 20 click activities. The interactions are recorded in the studentVle and VLE tables. The studentVle table contains 10,655,280 rows with column features such as code_module, code_presentation, id_student, id_site, date, and sum_click. These represent the module identification code, presentation identification code, student ID, VLE material identification number, date of interaction registration, and the total number of clicks on the material. Another important table used in our analysis is the studentAssessment table, which contains assessments that students have participated in. This table has 173,912 rows and column features such as id_assessment, id_student, date_submitted, is_banked, and score. These represent the assessment identification number, student ID, submission date indicating the number of days passed since the module presentation, a status flag indicating whether the assessment result has been transferred from a previous presentation, and the score obtained within a range of 0–100.

The proposed model aims to predict whether a student can complete a course or not. Therefore, we will assign a specific label of either “fail” or “pass” to each student. Among all the described tables in OULA, we selected two tables, namely studentVle, and studentAssessment, which represent students’ interaction with online learning platforms and their corresponding assessments, respectively. In the first stage of converting and extracting suitable data for constructing time-series data, we used the studentVle table. This table includes all interactions of students with the targeted online learning platform. Subsequently, we aggregated the total number of clicks per student per day (which may include clicks on a specific module recorded in rows on the same day) to obtain data that specifies the number of clicks on different days. The resulting dataset has three features: student IDs, days with clicks, and the total number of clicks on that day. As shown in Fig. 4, we have presented a summary of the average clicks for all students in the range of days from − 25 to 263.

Fig. 4

Average clicks per day for all students.

Feature selection

By using the studentVle file, we can easily provide inputs for transforming time series data into a visibility graph (VG). At the next stage, a statistical summary is provided for each student, which is briefly outlined in the workflow diagram shown in Fig. 8. We have provided the following features for each student, including the date of their first and last clicks in the course, the average number of clicks per day in the course, pre-final exam scores out of 100, and final exam scores. It should be noted that in the student assessment grade table, there are two types of grades: one is the pre-final exam grade, which is the sum of several evaluations and has a weight of 100 in total, and the other is a final exam grade with a weight of 100. We then placed these features in a new dataset.

After extracting scores from the studentAssessment file for each student and placing them in the new dataset, it was observed that many students did not have final exam scores and were given a score of 0 in that field. Additionally, 596 students had participated in more than one course, such that their pre-final exam scores exceeded 100; to standardize all students’ scores, these students were removed. We then calculated the average number of clicks per day for all students. Ultimately, our number of students became 14,972, and we divided them into two categories: those whose homework grades were below 40 and were rejected (6281 students), and those whose homework grades were above 40 and were accepted (8691 students) (Fig. 5).

Fig. 5

The number of accepted and rejected students according to their homework scores with a threshold of 40.

It should be noted that we have only used the grades of pre-exam assignments as our evaluation criterion, as the exam grades of many students (12,720 individuals) are 0⁶⁶, (Fig. 6). Also, based on this definition of VG, we have drawn a VG for each of the two groups of accepted and rejected students, as well as for each student within them. We extracted all the mentioned features from the research background section for graphs and added them to the other student features in both the accepted and rejected datasets. We then compared the differences in the extracted features between the two groups to determine their importance.

Fig. 6

The number of zero grades in three sections, including assignment grades, exam grades, and both.

While visual inspection of the graph may reveal apparent differences between features for the determination of pass and fail students, statistical methods are required to accurately assess the significance of these features in distinguishing between the two groups. One of the statistical analysis methods is statistical inference, which allows us to decide on a population based on information provided by samples. Statistical tests related to means, such as the T-test, are one type of this method that judges the mean of a population. In this study, we used the two independent sample T-tests to compare the means of two independent populations. Our null hypothesis, for example, for feature GIC, is that the mean GIC scores for accepted (Aµ) and rejected (Bµ) students are equal. Based on samples from both groups, the T-test is conducted with the following assumptions, Eq. 9.

$$\left\{\begin{array}{c}{H}_{0}:{\mu }_{A}={\mu }_{B}\\ {H}_{1}:{\mu }_{A}\ne {\mu }_{B}\end{array}\right.$$

(9)

As we cannot assume equal variances for both populations, the test statistic is written as follows (Eq. 10):

$$T=\frac{{\overline{x}}_{A}-{\overline{x}}_{B}}{\sqrt{\frac{{S}_{A}^{2}}{{n}_{A}}+\frac{{S}_{B}^{2}}{{n}_{B}}}}$$

(10)

${S}_{A}^{2}$ and ${S}_{B}^{2}$ represent the variances of populations A and B, respectively, and this statistic has a t-distribution with the degrees of freedom given below (Eqs. 11).

$$df=\frac{{\left(\frac{{S}_{A}^{2}}{{n}_{A}}+\frac{{S}_{B}^{2}}{{n}_{B}}\right)}^{2}}{\frac{{S}_{A}^{4}}{{n}_{A}^{2}\left({n}_{A}-1\right)}+\frac{{S}_{B}^{4}}{{n}_{B}^{2}\left({n}_{B}-1\right)}}$$

(11)

Based on these considerations, we conducted a two-sample T-test to examine differences in characteristics between the pass and fail groups. As per Table 2, the results of the Clustering Coefficient and Average Degree had high P values, indicating no significant differences in these features between pass and fail groups. Therefore, we removed them from our set of features. Up to this point, our sample sizes for the two groups were not equal, with more passes than fails. To address this issue, we equalized the sample sizes and did not consider the removed student VGs in subsequent analyses. We then merged separate datasets for passes and fails into one dataset with a target class variable called "class," which takes on values of 0 for fails and 1 for passes. To provide greater clarity, we have illustrated the process of selecting the most relevant features in Fig. 7.

Table 2 The obtained P values for the VG features.

Fig. 7

The process of creating the most effective feature set as input to machine learning models.

Case study workflow

To evaluate the predictive performance in identifying at-risk online students using clickstream-derived visibility graph characteristics, the research methodology is systematically structured into five core stages, as illustrated in Fig. 8. These stages include the following components:

• Data preprocessing: Filtering tables and columns, then converting the data into the time series.

• VG generation: Constructing natural visibility graphs from time series.

• Network analysis: Extracting key graph features from visibility graphs.

• Feature analysis: Analyzing features to identify the most effective ones.

• Classification: Applying multiple classifiers to find the best model based on standard evaluation metrics.

Fig. 8

The proposed architecture of the case study.

The process initiates with data collection from the OULA dataset repository, specifically utilizing the studentVLE (virtual learning environment interactions) and studentAssessment (assessment outcomes) files. Subsequently, at the Data preprocessing step, for each student with a unique ID, the relevant features are computed over the period spanning from the student’s initial interaction with the virtual learning environment to their final recorded activity. Subsequently, the sum_click per day for each student is aggregated and transformed into a structured time series format, which facilitates subsequent analysis. This approach represents a novel application in our context and contributes to the methodological framework of our study.

Also, Students with incomplete data are excluded from the analysis. This exclusion criterion encompassed cases where clickstream data or assessment scores were missing (i.e., contained null values). Furthermore, duplicate student IDs are detected and removed to maintain the integrity and reliability of the dataset.

Next, the structured time series is transformed into Natural Visibility Graphs (NVGs), where each student’s sum of clicks are represented as a node, and edges are established based on the natural visibility criterion as defined in Eq. (1). Since NVG effectively preserves the temporal structure and dynamics of time series while enabling graph-theoretic analysis, it yields a simple, connected, undirected, straightforward, and parameter-free graph¹⁵. Therefore, based on these features and capabilities, the VG method is a suitable option for capturing behavioral patterns in student interactions within the online learning environment across multiple days.

Subsequently, a consistent set of structural features is extracted from each visibility graph, including the clustering coefficient, diameter, global efficiency, assortativity coefficient, average shortest path length, average degree, maximum degree, betweenness centrality, and the GIC attribute. These features are computed uniformly for all students to ensure comparability across their visibility graphs. As these features encapsulate various aspects of student interaction patterns, such as network complexity, cohesiveness, and centrality, they are hypothesized to contribute to the prediction of student performance.

A comprehensive analysis of the extracted features will be conducted in the "Results and discussion" Section, employing both statistical methods (two-sample t-tests) and visual representations (box plot visualizations) to identify the most predictive indicators of at-risk students. Furthermore, during this process, two features from the extracted set will be excluded, as the t-test results indicate no statistically significant differences between the pass and fail groups for these features.

Finally, to identify the best-performing classification algorithms for predicting student performance, a range of classification algorithms are employed, including Decision Tree, K-Nearest Neighbors, Random Forest, Naïve Bayes, Gradient Boosting, and Logistic Regression. To ensure robust evaluation and enhance the generalizability of the results, tenfold cross-validation is applied. In this approach, the dataset is randomly partitioned into 10 equally sized subsets; during each iteration, one subset is used as the test set while the remaining nine served as the training data. This process is repeated ten times, and model performance is assessed using the average of the results across all folds. Standard evaluation metrics, Accuracy, Precision, Recall, F1-score, and ROC_AUC, are calculated to measure the effectiveness of each classification algorithm. The detailed experimental results are presented in the following section.

Results and discussion

This section presents and explores the case study research findings from various perspectives. Specifically, we created visibility graphs of pass and fail ones based on their sum clicks per day in the OULA E-Learning system.

The graphs constructed from the dataset’s time series were simple, devoid of self-loops for each node, and bearing no weight or direction for any edge. According to visibility graph principles, the nodes in these graphs represent the timestamped interactions, ranging from − 25 to 263 days. Consequently, each visibility graph comprises 288 nodes. For each user, we have a graph representing their clickstream with 288 nodes, with the number of edges varying depending on the user’s interactions with the online learning system.

After extracting the VGs and examining the relevant characteristics of each student’s VG, we conducted an initial comparison between the pass and fail groups to identify potential differences. To achieve this goal, we visualized box plots for various VG characteristics of both groups (Fig. 9). Subsequently, we assessed the significance of the differences by conducting a two-sample T-test, as depicted in Table 2.

Fig. 9

Box plots for various VG characteristics of both pass and fail groups.

Based on Fig. 9, it is evident that there is a significant difference between the pass and fail groups in terms of Global Efficiency, Assortativity Coefficient, Avg shortest Path Len, Max Degree, and Avg Betweenness. Additionally, the GIC and Diameter features are almost separated in the middle 50% of the boxes and differ between the two groups. However, this is not the case for Clustering Coefficient and Avg Degree, as they are very similar to each other. Therefore, we were able to gain a suitable understanding of the adequacy of our features using this plot. Furthermore, we also utilized a two-sample T-test to support our claim as per Table 3. Figure 9 and the obtained P values are in line with each other regarding the importance of VG features. According to Fig. 9, we found a P value of 0 for 6 out of 9 features, indicating a significant difference in the mean between the pass and fail groups.

Table 3 The results of various machine learning algorithms are evaluated based on different metrics. Significant values are in [bold].

To train and evaluate the performance of machine learning models and to make their results more robust and accurate, we used tenfold cross-validation. This method is essentially used in machine learning to estimate the performance of a machine learning model on unseen data, and its function is to randomly divide the data into 10 equal parts in 10 steps, each time using one of the parts as a test and the remaining parts as training data for the model. Finally, the evaluation result of the models using metrics will be the average of the 10 obtained results.

Accordingly, Table 3 provides the results of various classifiers categorized by different evaluation metrics for model performance. As shown, all algorithms achieved performance levels exceeding 80% across all evaluation metrics, with some algorithms surpassing 90% in both recall and ROC_AUC metrics. These results indicate the effectiveness of features derived from the visibility graph of clickstream time series data in classification tasks. Consequently, among the classifiers evaluated, Gradient Boosting (GB) ranked among the top performers, with high results in accuracy, recall, F1-score, and ROC_AUC.

High failure and dropout rates in distance education were considered as a binary classification problem and are addressed through the development of a two-stage predictive model designed to identify at-risk students based on clickstream data. A recent model utilized a Convolutional Residual Recurrent Neural Network (CRRNN) to capture both short-term learning activities and long-term behavioral patterns. Experimental evaluation conducted on the OULA dataset demonstrated that the model achieves an accuracy of 82.70%, indicating its potential for practical application in educational intervention and student support⁵⁹. Similarly, a graph-based machine learning approach for predicting student performance and identifying at-risk learners was presented. Tabular data was converted into graphs using distance measures, and topological features were extracted to improve predictive accuracy. When tested on an educational dataset, up to 87.4% accuracy and 0.97 AUC were achieved in the classification of students into three classes: “failed”, “at risk”, and “good”. Prediction results were further enhanced by incorporating graph convolutional networks⁶⁴.

Besides, as shown in Table 3, the effectiveness of the proposed VG-based method with a GB classifier demonstrated superior performance across key evaluation metrics, including Accuracy, Recall, F1-score, and ROC_AUC, when applied to structured clickstream data. Unlike, deep learning models such as CRRNN may be more suitable for time-series or sequential data, but can be prone to overfitting and require careful hyperparameter tuning. Also, Graph-based approaches, including Graph Convolutional Networks (GCNs), involve additional preprocessing steps, are sensitive to graph construction choices, and often require substantial labeled data and longer training times, the VG method achieves higher performance while maintaining lower complexity and improved interpretability, suggesting its potential, particularly to deploy in real-world educational systems where interpretability matters. Although both this study and recent deep learning approaches employ the same clickstream data to ensure fairness in predicting at-risk students, they differ notably in their methodological frameworks and classification objectives. As depicted in Fig. 10, the proposed method of this research achieves higher predictive accuracy relative to recent deep learning approaches studied. Nevertheless, further refinement and evaluation across diverse datasets are necessary to more effectively benchmark the approach against state-of-the-art methods.

Fig. 10

Comparing the results with the recent related papers on the OULA dataset.

It is important to know that the performance of visibility graph analysis versus deep learning in classification tasks depends on data characteristics, computational constraints, and problem domain. For example, in a recent research, visibility graph analysis excels over deep learning in scenarios with limited or noisy data and when preserving temporal dynamics is critical, as demonstrated in EEG classification where VG-derived topological features (e.g., clustering coefficients) capture non-linear brain patterns with 100% accuracy in small Alzheimer’s cohorts, while deep learning struggles with overfitting. Conversely, deep learning outperforms visibility graph analysis in large-scale, high-dimensional data due to its hierarchical feature learning, though it remains data-hungry and computationally intensive⁶⁷. Therefore, research in other fields suggests visibility graph analysis can be better for specific tasks like texture classification and biomedical time series, especially where interpretability is key, and particularly in scenarios with limited or noisy data and when preserving temporal dynamics is critical. But it seems likely that deep learning excels in complex image classification and large datasets, due to its ability to learn hierarchical features.

Several studies analyze student activity clickstreams to predict academic success or failure. However, applying a graph perspective to this time series data remains relatively unexplored. Visibility graphs offer a promising method for converting such data into a graph, unlocking the potential of hidden relationships between students. By calculating and extracting graph features, we captured these underlying connections and leveraged their predictive power for student success analysis.

Indeed, clickstream is a type of fine-grained data from which various information can be obtained. However, the main challenge is discovering hidden knowledge in this data. The present study focuses on an innovative method using VG quantitative analysis. Information related to student interaction with VLE is graphed by VG to utilize the knowledge available in time-series data that is not easily understandable. To our knowledge, this study is the first to use VG for analyzing clickstream data related to student interactions with VLE, and as observed, it demonstrated very good performance. Overall, it appears that VG analysis has great potential for future applications in virtual learning data.

Several factors can affect the performance of graph-based clickstream data analysis, offering opportunities to enhance results. Firstly, visibility graph construction isn’t limited to the natural visibility graph. Variants with lower computational complexity or improved noise handling can be explored¹⁰. Secondly, graph purification through weak link removal based on a well-chosen threshold may yield a clearer graph with more robust features. Thirdly, graph properties like scale-free or small-world attributes can influence outcomes, suggesting that clickstream patterns and time series characteristics directly impact classifier success⁴⁰. Finally, incorporating further diverse graph operations and properties, such as community detection, could potentially extract better features for improved at-risk student identification.

Conclusion and future works

This paper explored the potential of visibility graph analysis for extracting insights from educational time series data. We introduced the fundamentals of visibility graphs and discussed their applications in transforming time series data into a graph. Through analysis, classification, and prediction, visibility graphs provide new perspectives for understanding patterns and trends in educational data.

A case study demonstrated the use of visibility graphs in forecasting at-risk students in educational online systems. By converting the clickstream time series into natural visibility graphs, hidden relationships between pass and fail students for predicting student success could be identified through graph analysis parameters like degree distribution. This showcases the ability of visibility graphs to uncover valuable insights from educational data. However, we acknowledge that the applicability of these findings to other educational contexts basically depends on availability of the timeseries format (such as clickstream) in the dataset. The choice of visibility graph variants and parameters, as well as the specific nature of clickstream data in the OULA dataset, may not generalize directly to other datasets without further validation. It highlights the need for additional research to develop standardized procedures and benchmarks for applying visibility graph analysis in diverse educational settings, suggesting that computational challenges and data-specific characteristics could influence outcomes. Future studies should focus on cross-institutional validation by applying the proposed visibility graph methodology to datasets from other universities, K–12 schools, or MOOC platforms. In addition, although predictive models like ours offer valuable potential for the early identification of at-risk students, their application raises important ethical considerations, including concerns related to data privacy, intervention fairness, and the risk of stigmatization. Future research should consider the responsible implementation of these models, necessitating a commitment to transparency, rigorous efforts to mitigate algorithmic bias, and robust measures to safeguard student data.

Nonetheless, this paper highlights the promising potential of visibility graph techniques for education. Visibility graphs open up new possibilities for analyzing learning behaviors, predicting academic performance, planning interventions, and improving instructional design. As educational data continues to grow, visibility graph analysis can provide the analytical capabilities to fully harness its value. Further explorations of visibility graphs for assessing student engagement, dropout prediction, adaptive learning systems, and personalized interventions could be impactful areas for future work. Also, deep learning techniques specifically developed for graph-structured data can be leveraged in future work to further enhance the performance of the proposed model⁶⁸.