Introduction

In the era of information explosion, various technologies have been developed to assist online users in information filtering and decision-making. Among them, recommendation systems (RS)1, as one of the most widely applied decision support systems, have become a core technology for alleviating information overload by mining users’ latent preferences to achieve precise content distribution. Nowadays, recommendation systems have expanded beyond traditional domains such as movies2, music3, news4, and tourism5, penetrating popular fields such as e-commerce6, social networks7, and location-based services8, playing a crucial role in enhancing user experience and increasing platform engagement.

To achieve efficient recommendation, a wide range of recommendation methods have emerged, including collaborative filtering9,10, content-based methods11, and hybrid methods12. In recent years, deep learning-based recommendation methods have attracted widespread attention due to their powerful nonlinear modeling capabilities. These methods utilize neural networks to model the representations of users and items, as well as their complex matching relationships. In particular, recommendation methods based on Graph Neural Network (GNN) provide a new research perspective for recommendation systems. User-item interactions inherently form complex heterogeneous graph structures, containing multi-dimensional information such as user social relationships and item attribute associations. Unlike traditional Euclidean space data, graph data has non-translation invariance and dynamic topological characteristics. GNN aggregate neighborhood information through message-passing mechanisms, effectively modeling these complex relationships, and have become an important representative in deep recommendation methods13. Despite the significant progress made in recommendation systems in recent years, the sparsity of user-item interaction data remains a widespread and persistent challenge. Existing studies have shown that most mainstream recommendation approaches follow a supervised learning paradigm, where training signals primarily rely on users’ historical interactions. However, compared to the vast space of potential interactions, the observed user-item interactions are extremely sparse, which severely limits the ability to learn high-quality embeddings14. This sparsity poses even greater challenges for GNN-based recommendation methods. Current GNN-based approaches suffer from the following major limitations during modeling: (1) sparse supervision signals; (2) noise introduced by graph augmentation; and (3) rigid neighborhood aggregation. However, the interaction data between users and items is extremely sparse, making it difficult to learn high-quality representations. To address the limitations of existing GNN-based recommendation methods, we propose a GNN recommendation algorithm based on multi-scale attention and contrastive learning (GR-MC). This method treats node self-discrimination as a self-supervised task, introduces contrastive learning to provide auxiliary signals for representation learning, combines it with a multi-scale attention embedding propagation mechanism, and designs a graph structure augmentation strategy based on user-focused edge dropout to form a robust overall framework. This effectively alleviates the problem of data sparsity and enhances the model’s generalization and representation capabilities. Specifically, our work mainly includes the following aspects:

  • To enhance the generalization ability of the model while preserving user-item interaction structure information, a strategy based on user-focused edge dropout is introduced in the data augmentation layer. By intentionally reducing the influence of high-degree user nodes, this strategy alleviates the degree bias problem, improves the modeling of user preferences, and reduces the interference of noisy information.

  • A multi-scale attention embedding propagation mechanism is designed, which combines Large Kernel Attention, Multi-scale Mechanism, and Gated Aggregation strategies to effectively enhance the modeling of multi-level collaborative relationships between users and items, thereby improving the accuracy of the embedding representations.

  • Contrastive learning is introduced as an auxiliary training framework for the graph neural network. Through the node self-discrimination task, auxiliary signals are provided. Combined with a dynamic weighting mechanism, this further distinguishes the importance differences among different neighbor nodes while considering their relevance, significantly enhancing the discriminative power of the embeddings and the robustness of the model.

  • Extensive experiments were conducted on five benchmark datasets to evaluate the proposed GR-MC algorithm. The experimental results show that, while balancing computational cost and performance, the algorithm achieves an average improvement of 9.98% in Recall@20 and 14.45% in NDCG@20. Additionally, it demonstrates superior performance in cold-start scenarios, significantly alleviating the issue of data sparsity.

The structure of the paper is arranged as follows: Section 2 reviews related research work; Section 3 defines the problem and provides a detailed description of the model architecture; Section 4 presents the experimental results and discussion;  Section 5 and 6 conclude the paper and discuss future work.

Related work

Data modeling-based recommendation methods

The development of data modeling in recommendation systems has undergone a significant shift from shallow representations to deep learning. Early collaborative filtering algorithms were primarily based on explicit analysis of the user-item interaction matrix. Matrix factorization techniques15, such as Singular Value Decomposition (SVD), mapped the high-dimensional sparse interaction matrix into a low-dimensional latent space, showing significant advantages in the Netflix competition16. Although these methods are computationally efficient, their linear modeling characteristics struggle to capture the nonlinear features of user preferences. Research by Koren et al.15 indicates that the performance of traditional matrix factorization significantly deteriorates when user behavior data exhibits complex temporal dynamics.

Nowadays, machine learning plays an important role in many fields. For example, in the study of unstable motion in frictional processes, statistical methods and machine learning tools are employed to address complex nonlinear problems that are difficult to model with traditional analytical approaches17. These data-driven methods have achieved significant results, which bears similarity to the challenges faced in predicting user behavior in recommendation systems. In the field of recommendation systems, deep learning techniques have been introduced to enhance the expressive capability of models. He et al.18 proposed the NeuMF framework, which innovatively combines matrix factorization and multi-layer perceptrons, using neural networks to learn the nonlinear interaction between users and items. Subsequent research, such as that by Xue et al.19, further discovered that deep neural networks can automatically learn higher-order feature combinations, performing excellently when handling heterogeneous features. Kuang et al.20 found that hybrid deep learning methods, by combining the advantages of multiple deep learning models, can more effectively handle the diversity and complexity in recommendation tasks. However, Cheng et al.21 pointed out that these methods still face the cold-start problem and struggle to effectively utilize the temporal patterns in user behavior sequences.

In recent years, graph representation learning techniques have brought new opportunities to recommendation systems. The DeepWalk algorithm, proposed by Perozzi et al.22, was the first to apply the Skip-gram model from natural language processing to graph-structured data, learning network representations by generating node sequences through random walks. Grover et al.23’s Node2Vec further improved the walking strategy, enabling more flexible exploration of network structures. Research by Tang et al.24 showed that these methods can effectively capture higher-order similarities in user-item graphs, but their unsupervised nature leads to a discrepancy between the learning objective and the recommendation task. This limitation prompted researchers to turn towards end-to-end graph neural network methods.

It is worth noting that with the increasing complexity of recommendation scenarios, multimodal data fusion has become a new research direction. Wei et al.25 explored how to enhance item representations by combining visual features and textual descriptions. Chen et al.26 further demonstrated that graph neural networks integrating spatiotemporal features can more accurately model dynamic user preferences. These advancements have laid a solid foundation for building more powerful recommendation systems, but they also bring new challenges such as computational complexity and model interpretability.

Relationship-enhanced recommendation methods

The development of graph neural networks has driven the rapid evolution of relationship-enhanced techniques in recommendation systems. Early graph neural network-based recommendation models mainly relied on the user-item bipartite graph structure. For instance, PinSage proposed by Ying et al.27 was the first to demonstrate the effectiveness of GNNs in large-scale recommendation systems. Later, Wang et al.28 introduced the NGCF framework, which explicitly models higher-order connectivity through multi-layer graph convolutions, but it suffers from high computational complexity. He et al.29 proposed LightGCN, which significantly improved efficiency by simplifying the message-passing mechanism. Their research showed that removing non-linear transformations and feature transformations can actually lead to better recommendation performance.

Multi-relational modeling is an important approach to improving recommendation performance. Fan et al.30 pioneered GraphRec, which integrates social relationships and user-item interactions, demonstrating the value of cross-graph information propagation. Wang et al.31 introduced KGAT, which further incorporates knowledge graphs and learns relation-specific propagation weights through an attention mechanism. However, Yang et al.32 pointed out that such methods heavily rely on the quality of auxiliary information, and may introduce noise when the data is sparse. To address this, researchers have developed various single-relation enhancement techniques. Wu et al.14 proposed SGL, which enhances model robustness through self-supervised contrastive learning, while Yu et al.33 introduced XSimGCL, which achieves comparable performance by applying linear transformations to the user-item interaction matrix, providing new theoretical support for efficient contrastive learning and revealing the feasibility of extreme simplification.

The attention mechanism plays a key role in relationship enhancement. The Transformer architecture proposed by Vaswani et al.34 has inspired many attention-based recommendation models. In particular, Wang et al.35 introduced DGCF, which differentiates the influence factors of different relations through disentangled representation learning. Despite significant progress, existing methods still have important limitations. Chen et al.36 revealed that most GNN-based recommendation models struggle to balance the importance of local and global information. In addition, Adjeisah et al.37 pointed out that current data augmentation methods generally adopt random strategies, such as random perturbations of nodes or edges, which may damage the structural consistency and semantic integrity of the graph. They further emphasized that future graph data augmentation should be more structure-aware, meaning that the importance of nodes and edges should be reasonably considered during augmentation to avoid damaging critical structures. These findings provide important inspiration for the innovations proposed in this study.

Existing challenges and research opportunities

Current recommendation systems face three key challenges. First, in relation modeling, fixed-pattern neighborhood aggregation27,28 struggles to adapt to the information propagation needs of different scenarios. Experiments by Luo et al.38 show that the diversity of user interests and the heterogeneity of item attributes require a more flexible relation modeling approach. They proposed an adaptive neighborhood-awareness recommendation method (ANGCN), which dynamically adjusts information propagation based on the importance of neighborhoods, effectively enhancing the flexibility and adaptability of recommendation systems. Second, the issue of the universality of data augmentation strategies is becoming increasingly prominent. Ding et al.39, in their survey, pointed out that although data augmentation can improve model robustness in graph learning, existing augmentation strategies often rely on simple random operations (such as perturbations of nodes or edges), which may not be suitable for all tasks. Especially when dealing with sparse graphs or complex tasks, these strategies may damage the original structural information and semantic consistency. Finally, the adaptability of optimization strategies is insufficient. The study by Zamfirache et al.40 shows that by combining reinforcement learning and metaheuristic algorithms, the adaptability of optimization strategies can be improved. Additionally, Li et al.41 demonstrated that fixed-weight multi-task learning can limit the expressive power of models.

In response to these challenges, this paper proposes three innovative directions.

  • First, a multi-scale relation propagation mechanism is introduced, which dynamically models the influence of different-order neighbors on user interests through a hierarchical attention model, aiming to capture finer-grained user behavior patterns.

  • Second, a user-aware graph augmentation strategy with targeted optimization is proposed, which focuses more on the key edge dropout of user nodes during the augmentation process, thereby avoiding excessive loss of core information in user behaviors.

  • Finally, this paper introduces a dynamically weighted contrastive learning strategy, which adaptively adjusts the optimization strength of the main task and auxiliary tasks based on the evolution pattern of representations during training, thereby improving both the training efficiency and recommendation accuracy of the model.

Methodology

In this section, we specifically describe the proposed Graph Neural Network-based recommendation algorithm (GR-MC), which incorporates multi-scale attention and contrastive learning, and explain how it addresses several key issues in existing GNN-based recommendation methods. First, to reduce the interference of irrelevant information, we improved the data augmentation method by adopting an edge dropout strategy that only applies to user nodes. Next, to address the issues of fixed neighborhood aggregation scale and undifferentiated node importance, we designed a Multi-scale Attention Embedding Propagation Layer (MAEP), and enhanced the model’s ability to learn multi-level collaborative representations through a dynamic weighting mechanism. Furthermore, by integrating contrastive learning into the embedding prediction and training layer, we further improved the model’s representational capacity, thereby effectively improving the performance of the recommendation system in cold start and sparse data scenarios.

Problem formulation

The main goal of this paper is to enhance the accuracy of personalized recommendation. To address the limitations of existing GNN-based recommendation methods, such as data sparsity and fixed-scale neighborhood aggregation, we propose the GR-MC algorithm by designing a multi-scale attention embedding propagation layer combined with contrastive learning. This approach strengthens the representation capability of user and item features while effectively capturing the complex relationships and latent structural patterns between users and items. Let the set of users be \(\textrm{U}\), the set of items be \(\textrm{I}\) and the embeddings for users and items are represented as \({e}_{u}\) and \({e}_{i}\). Firstly, the multi-scale attention mechanism is used to weight and fuse these embeddings, resulting in the initial embeddings of users and items as \(e_{u}^{\prime }\) and \(e_{i}^{\prime }\). Subsequently, feature propagation is performed through GCN to obtain the updated embeddings \(e_{u}^{\prime \prime }\) and \(e_{i}^{\prime \prime }\) for users and items. where, \(e_{u}^{\prime \prime }\) and \(e_{i}^{\prime \prime }\) are the final user and item features that integrate neighborhood information under the joint effect of the multi-scale attention mechanism and graph convolutional propagation. Assuming that the interaction relationship between users and items is represented by a sparse adjacency matrix \(A\), and is propagated through multi-layer graph convolution, the following mathematical expression is obtained:

$$\begin{aligned} e_u^{\prime \prime }=F_u\left( A,e_u^{\prime }\right) ,e_i^{\prime \prime }=F_i\left( A,e_i^{\prime }\right) \end{aligned}$$
(1)

where \(F_u\begin{pmatrix}\cdot \end{pmatrix}\)and \(F_i\begin{pmatrix}\cdot \end{pmatrix}\) respectively represent the embedding propagation process of users and items, and the adjacency matrix A is used to propagate and update the embeddings.

Final prediction of user interaction probability with items:

$$\begin{aligned} & Y=g\left( e_u^{\prime \prime },e_i^{\prime \prime }\right) \end{aligned}$$
(2)
$$\begin{aligned} & Y=\sigma \left( e_u^{\prime \prime },e_i^{\prime \prime }\right) \end{aligned}$$
(3)

where \(\text {Y}\) is the predicted interaction probability of the user to the item, \(g\begin{pmatrix}\cdot \end{pmatrix}\) is a \(\textrm{Sigmoid}\) function to calculate the interaction probability through the embedding vector, and \(\mathbf {\sigma }\) is an activation function to map the output value to the probability interval [0, 1].

Overview of GR-MC

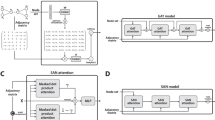
The overview of GR-MC is illustrated in Fi. 1. As shown, GR-MC consists of four key components: (a) Input and Data Augmentation Layer, which enhances the model’s generalization ability by randomly dropping some edges, generating two slightly different subgraphs; (b) Multi-Scale Attention Embedding Propagation Layer, which recursively propagates embeddings from neighboring nodes to update their representations, adopts a multi-scale attention mechanism that aggregates multi-scale features to capture multi-level collaborative relationships between users and items, and utilizes a dynamic weighting strategy to adaptively assign weights, enhancing the modeling of neighbor information and improving recommendation accuracy; (c) Embedding Fusion Layer, which performs weighted fusion of embeddings from different layers in the bipartite graph to generate the final user and item embeddings; (d) Prediction and Training Layer, which predicts the interaction probability between users and items and trains the model parameters, incorporates contrastive learning based on graph structure and embedding augmentation, and minimizes the contrastive loss jointly with the BPR loss to optimize the model. The implementation details of GR-MC are shown in algorithm 1.

Fig. 1
figure 1

Overview of GR-MC.

Full size image
Algorithm 1
figure a

Algorithm Pseudo-code of GR-MC

Full size image

Input and data augmentation layer

The input of the GR-MC model consists of discrete user and item IDs, and a user-item bipartite graph is constructed based on historical interaction data. Specifically, users and items are modeled as two types of nodes in the graph, with edges established based on their interaction records, thereby forming a sparse adjacency matrix. This matrix serves as the foundational structure for message propagation and representation learning in graph neural networks, carrying key structural signals in collaborative filtering. However, conventional data augmentation methods used in computer vision (CV)42 and natural language processing (NLP)43 tasks (such as geometric transformations or blurring) are not applicable to graph-based recommendation systems. The reasons are as follows: (1) user and item features are inherently discrete, such as one-hot encoded IDs and categorical variables, which cannot be directly transformed using operations from image or text domains; (2) Unlike CV and NLP tasks, where data instances are treated in isolation, in recommendation systems, users and items are interconnected and dependent. Therefore, graph recommendation tasks require specifically designed data augmentation strategies. This paper performs data augmentation by leveraging the collaborative filtering signals embedded in the user-item bipartite graph, using an edge dropout strategy.This method randomly drops a portion of the edges in the graph to generate two subgraphs with structural perturbations, aiming to improve the robustness of node embeddings. The formal definition is as follows:

$$\begin{aligned} S_1\left( G\right) =\left( V,M_1\odot \varepsilon \right) ,S_2\left( G\right) =\left( V,M_2\odot \varepsilon \right) \end{aligned}$$
(4)

where \(M_1,M_2\in \begin{Bmatrix}0,1\end{Bmatrix}^{\begin{vmatrix}\varepsilon \end{vmatrix}}\) is a mask vector over the edge set, controlling which edges are retained for message propagation. The two subgraphs, perturbed with different structures, guide the model to learn embedding representations that are stable to structural changes, effectively mitigating noise and abnormal interactions.It is important to note that user behaviors are dynamic, while item semantic properties are relatively stable (e.g., book genres or movie styles). Existing studies often apply perturbations to both user and item nodes, which may introduce redundant noise and degrade final performance. To address this, we propose a user-focused edge dropout strategy that randomly removes a portion of edges between users and items, thereby promoting the generalization of user representations and enhancing the modeling of user preferences.

After this augmentation step, we design an embedding initialization strategy to provide a foundation for subsequent propagation and optimization. The embedding layer aims to generate low-dimensional embedding vectors for users and items to capture their latent feature representations. We adopt a widely-used embedding modeling approach44, assuming that each user and each item is associated with an embedding vector. To ensure favorable convergence properties of the initial parameters, all embeddings are initialized using Xavier uniform distribution. Let \({E}_{u}\) and \({E}_{i}\) denote the initial embeddings for users and items, respectively. The embedding matrices are defined as:

$$\begin{aligned} E_{initial}\in \left\{ E_u,E_i\right\} \end{aligned}$$
(5)

Where, \({E}_{initial}\) encompasses the initial user embeddings \(E_u=\left\{ e_u^1,e_u^2\cdots ,e_u^m\right\}\) and the initial item embeddings \(E_i=\left\{ e_i^1,e_i^2\cdots ,e_i^n\right\}\). Specifically, \(e_{u}^{m}\) denotes the m-th initial embedding of user u, and \(e_{i}^{n}\) denotes the n-th initial embedding of item i. These embedding vectors are stored in a unified embedding dictionary and serve as the input to the graph neural network propagation. In conjunction with the edge dropout strategy, we perform contrastive learning on the two augmented views \(S_1\left( G\right)\) and \(S_2\left( G\right)\). Let \(z_{u_1}\) and \(z_{u_2}\) denote the two augmented views of a node u, and let U represent the set of all user nodes. For the same node u, its two augmented views \(z_{u_1}\) and \(z_{u_2}\)are treated as a positive sample pair. For different nodes u and v, even if they are augmented to generate different views \(z_{u_1}\) and \(z_{v_2}\), they are considered as a negative sample pair:

$$\begin{aligned} & \left\{ \left( z_{u_1},z_{u_2}\right) |u_1,u_2\in U\right\} \end{aligned}$$
(6)
$$\begin{aligned} & \left\{ \left( z_{u_1},z_{\nu _2}\right) |u_1,\nu _2\in U,u_1\ne \nu _2\right\} \end{aligned}$$
(7)

Multi-scale attention embedding propagation Layer

To effectively enhance the modeling capability of complex relationships between users and items in recommendation systems, this paper draws inspiration from advanced feature modeling techniques in the field of computer vision. Specifically, we adapt the multi-scale large kernel attention mechanism from the vision domain into graph neural network-based recommendation models, and propose a novel Multi-Scale Attention Embedding Propagation Layer (MAEP). First, we design the Multi-Scale Large Kernel Attention (MLKA) module, which is inspired by the use of large receptive field convolution kernels to model long-range dependencies. By leveraging a multi-scale mechanism, the module extracts features at different levels of granularity, and uses a gating mechanism to perform weighted fusion of local and global features, thereby effectively alleviating the problem of block effects. We adapt this mechanism to the user-item graph, which enhances the expressive power of the embeddings. Then, we construct the Graph Structure Attention Unit (GSAU), which integrates graph neural networks with a self-attention mechanism to further model the structural relationships between nodes. It employs a recursive message-passing approach to reinforce the multi-level collaborative relations between users and items during the embedding propagation process. The formal definition and proof of MAPE are provided in Appendix A (see supplementary material).

Unlike traditional GNN-based recommendation models that rely on single-scale feature extraction methods, MAPE integrates multi-order neighbor information in a recursive manner through multi-scale attention and graph structure awareness, without the need for explicit partitioning into 1-hop, 2-hop, or 3-hop neighbors. This enables adaptive modeling of neighbors at various distances. MAPE consists of two main components: Multi-Scale Large Kernel Attention (MLKA) and Graph Structure Attention Unit (GSAU). The overall process proceeds through the following steps:

$$\begin{aligned} & N=LN\left( X\right) ,X=X+\lambda _1f_3\left( MLKA\left( f_1\left( N\right) \right) \otimes f_2\left( N\right) \right) \end{aligned}$$
(8)
$$\begin{aligned} & N=LN\left( X\right) ,X=X+\lambda _2f_6\left( GSAU\left( f_4\left( N\right) ,f_5\left( N\right) \right) \right) \end{aligned}$$
(9)

Where, \(LN\begin{pmatrix}\cdot \end{pmatrix}\) denotes Layer Normalization, \(\lambda _{1}\) and \(\lambda _{2}\) are learnable scaling factors, and \(f_i(\cdot )\) represents a pointwise convolution operation to maintain dimensional consistency. The symbol \(\otimes\) denotes element-wise multiplication. Below, we will introduce the two important modules of MLKA and GSAU.

Multi-scale large kernel attention

MLKA is the core component of MAEP. The primary objective of the MLKA module is to capture long-range dependency features through large convolutional kernels, extract hierarchical features via a multi-scale mechanism, and employ a gating mechanism to adaptively aggregate local and global features, ultimately avoiding block artifacts. This module consists of the following three parts:

  1. (1)

    Large Kernel Attention (LKA) module is designed to extract global features of nodes by leveraging large convolutional kernels, particularly to capture long-range dependencies. In our task, the relationships between users and items are often indirect, especially when users’ historical behaviors are sparse or scattered. Capturing long-range dependencies is crucial for understanding these complex interactions. Large convolutional kernels aggregate more contextual information, thereby enhancing the model’s global perception capability. Below is the formula for capturing long-range dependency features using large convolutional kernels:

    $$\begin{aligned} LKA\left( X\right) =\sigma \left( X*W_{l\arg e}+b_{l\arg e}\right) \end{aligned}$$
    (10)

    Where, X is the input feature, \(W_{large}\) is the weight of the large convolutional kernel, \(b_{large}\) is the bias term, * denotes the convolution operation, and \(\mathrm {\sigma }\) is the activation function.

  2. (2)

    Multi-Scale Mechanism (MSM) enhances the model’s perception capability at multiple levels by combining convolutional operations of different scales. Smaller convolutional kernels capture fine-grained local features, while larger convolutional kernels focus on global information. This combination of multi-scale perception enables the model to more comprehensively understand the complex relationships between users and items.

    $$\begin{aligned} MSM\left( X\right) =LKA\left( X\right) +Con\nu _{small}\left( X\right) \end{aligned}$$
    (11)

    Where, \(Con\nu _{small}\begin{pmatrix}X\end{pmatrix}\) is a smaller convolutional operation that captures fine-grained local features. Multi-scale features are fused through addition, ensuring that information from different levels is effectively captured.

  3. (3)

    Gated Aggregation (GA) module adopts a gating mechanism to dynamically fuse local and global features. Specifically, the model learns a trainable gating parameter to adaptively control the fusion ratio between local and global information, thus avoiding excessive dependence on a single source of features and reducing information redundancy. This helps suppress block effects and enhances the model’s representation capacity and convergence stability. In practice, the gating unit is implemented as a lightweight learnable module that efficiently adjusts the output of each layer without introducing significant additional computational overhead.

    $$\begin{aligned} GA\left( X\right) =\beta \cdot LKA\left( X\right) +\left( 1-\beta \right) \cdot Con\nu _{small}\left( X\right) \end{aligned}$$
    (12)

Graph structure attention unit

The GSAU module is another core component of the MAEP that we designed. It mainly captures the relationships between nodes through GNN and self-attention mechanisms, and enhances the embedding representations between nodes through a recursive message passing mechanism. Unlike traditional attention mechanisms that rely on learnable attention parameters updated gradually over training epochs, the attention weights in GSAU are dynamically computed at each layer based on the local graph structure and node features. This mechanism mainly consists of the following three steps:

The first step is node embedding propagation. The representation of each node depends not only on its own features but also on the aggregation of information from its neighboring nodes, enriching its embedding representation. This layer-by-layer propagation mechanism enables nodes to integrate useful signals from their local neighbors, thereby obtaining more expressive representations. In our task, node embeddings are used to represent the state of users or items, while the embeddings of neighboring nodes provide additional contextual information, helping the model to more accurately capture user preferences and item characteristics. The computation of node propagation is as follows:

$$\begin{aligned} e_u^{(t+1)}=\sum _{i\in N_u}\pi _{u,i}\cdot e_i^{(t)} \end{aligned}$$
(13)

Where, \(e_u^{\left( t+1\right) }\) is the embedding of node u at the t+1-th layer, \(e_i^{(t)}\) is the embedding of neighbor node i at the t-th layer, \(N_{u}\) is the set of neighbors of node u, and \(\pi _{u,i}\) is the attention weight between node u and its neighbor node i, representing the influence of node i on node u.The weight is dynamically computed based on the features and graph structure of nodes u and i, and is recalculated at each layer.

The second step is structure-aware weighted propagation based on the adjacency matrix. This process incorporates the graph’s structural information into the attention propagation. The adjacency matrix \(A_{u,i}\) indicates whether there is a connection between node u and node i, and \(d_{i}\) denotes the degree of node i, which is used to normalize the propagation process and maintain model stability. By introducing a structure-aware weighting mechanism, the model relies not only on node features but also leverages the graph’s topology to adjust the propagation weights, thereby enhancing its ability to model structural information. The computation of this process is as follows:

$$\begin{aligned} e_u^{(t+1)}=\sum _{i\in N_u}A_{u,i}\cdot d_i\cdot \pi _{u,i}\cdot e_i^{(t)} \end{aligned}$$
(14)

The third step is information propagation from high-order neighbors. The information is not limited to first-order neighboring nodes but is also integrated from higher-order neighbors through a multi-hop propagation mechanism. In this way, a node’s representation incorporates not only information from its directly connected neighbors but also features from second-order neighbors, enabling the model to capture more complex relationships between nodes. The corresponding formulation is as follows:

$$\begin{aligned} e_u^{(t+1)}=\sum _{i\in N_u}\pi _{u,i}\cdot e_i^{(t)}+\sum _{j\in N_u^{(2)}}\pi _{u,j}\cdot e_j^{(t)} \end{aligned}$$
(15)

where \(N_{u}^{(2)}\) represents the second-order neighbors of node u.

Embedding fusion layer

The purpose of the embedding fusion layer is to perform weighted fusion of embeddings from different levels in the bipartite graph, thereby generating the final user and item embeddings. In Embedding Layer, we define the embeddings of user u as \(z_{u1}\) and \(z_{u1}\) (obtained from the two augmented subgraphs, respectively) and the embedding of item i as \(e_{i}\). After weighted fusion through the multi-scale attention mechanism, the preliminary embeddings \(e_{u1}^{^{\prime }}\), \(e_{u2}^{^{\prime }}\), and \(e_{i}^{^{\prime }}\) are obtained. The specific fusion process can be expressed as:

$$\begin{aligned} & e_u^{\prime }=\sum _{l=0}^L\tau (l)e_u^{(l)} \end{aligned}$$
(16)
$$\begin{aligned} & e_i^{\prime }=\sum _{l=0}^L\tau (l)e_i^{(l)} \end{aligned}$$
(17)

Where, \(e_u^{(l)}\) and \(e_i^{(l)}\) are the embeddings of user and item at the \(l\)-th order, respectively, and \(\tau (l)\) is the weighting coefficient for the embeddings. Inspired by LightGCN, we uniformly set \(\tau (l)\) to \(\frac{1}{L+1}\). After performing \(L\) rounds of propagation on the embeddings using the normalized adjacency matrix \(\varvec{\hat{A}}\) in graph convolution, the final updated embeddings \(e_{u1}^{\prime \prime }\), \(e_{u2}^{\prime \prime }\), and \(e_{i}^{\prime \prime }\) are obtained as follows:

$$\begin{aligned} & e_u^{\prime \prime }=F_u\left( {\hat{{\textbf {A}}}},e_u^{\prime }\right) \end{aligned}$$
(18)
$$\begin{aligned} & e_i^{\prime \prime }=F_i\left( {\hat{{\textbf {A}}}},e_i^{\prime }\right) \end{aligned}$$
(19)

Contrastive learning embedding prediction and training layer

Contrastive learning learns more discriminative embedding representations by reducing the distance between similar samples and increasing the distance between different samples. It uses the self-recognition of nodes as a self-supervised task, providing auxiliary signals for representation learning. In this paper, we combine the multi-scale attention mechanism of GNN and apply an edge drop enhancement strategy. By ignoring the item nodes and enhancing only the user nodes, we generate two different views for each user to construct the contrastive learning task, enabling the model to learn more generalized user representations and improving its ability to model user preferences. In the previous, we have already fused the embeddings to obtain the final user and item embeddings \(e_{u1}^{^{\prime }}\), \(e_{u2}^{^{\prime }}\), and \(e_{i}^{^{\prime }}\). To optimize the embeddings, we employ a contrastive loss to maximize the similarity between positive sample pairs while minimizing the similarity between negative sample pairs. InfoNCE has been widely validated as effective in the field of graph contrastive learning for recommendation, offering good training stability and representation discriminability14,33, while also integrating naturally with our multi-scale embedding propagation structure. Therefore, we adopt InfoNCE as the loss function in this work. The user-side contrastive loss is defined as follows:

$$\begin{aligned} L_{ssl}^{user}=\sum _{u_1,u_2\in U}-\log \frac{\exp \left( s\left( e_{u_1}^{\prime \prime },e_{u_2}^{\prime \prime }\right) /\tau \right) }{\sum _{\nu _2\in U}\exp \left( s\left( e_{u_1}^{\prime \prime },e_{\nu _2}^{\prime \prime }\right) /\tau \right) } \end{aligned}$$
(20)

Where, the similarity between \(s\left( e_{u_1}^{\prime \prime },e_{u_2}^{\prime \prime }\right)\) and \(s\left( e_{u_1}^{\prime \prime },e_{v_2}^{\prime \prime }\right)\) is calculated using cosine similarity:

$$\begin{aligned} & s\left( e_{u_1}^{\prime \prime },e_{u_2}^{\prime \prime }\right) =\frac{e_{u_1}^{\prime \prime }\cdot e_{u_2}^{\prime \prime }}{\left\| e_{u_1}^{\prime \prime }\right\| \left\| e_{u_2}^{\prime \prime }\right\| } \end{aligned}$$
(21)
$$\begin{aligned} & s\left( e_{u_1}^{\prime \prime },e_{v_2}^{\prime \prime }\right) =\frac{e_{u_1}^{\prime \prime }\cdot e_{v_2}^{\prime \prime }}{\left\| e_{u_1}^{\prime \prime }\right\| \left\| e_{v_2}^{\prime \prime }\right\| } \end{aligned}$$
(22)

\(\tau \in \begin{bmatrix}0.1,1\end{bmatrix}\) controls the smoothness of the distribution, and the negative samples \(e_{\nu _{2}}^{\prime \prime }\) are taken from the augmented views of different users.

Based on the final embeddings of users and items, the interaction score is calculated as follows:

$$\begin{aligned} {\tilde{y}}_{ui}=e_u^{\prime \prime }\cdot e_i^{\prime \prime } \end{aligned}$$
(23)

To learn the model parameters, we optimize the Bayesian Personalized Ranking (BPR) loss function27, which is widely adopted in recommendation systems. The BPR loss is defined as follows:

$$\begin{aligned} L_{BPR}=-\sum _{(u,i,j)\in O}\ln \sigma \left( {\tilde{y}}_{ui}-{\tilde{y}}_{uj}\right) +\lambda \left\| \Theta \right\| \end{aligned}$$
(24)

Where, \(O=\left\{ \begin{pmatrix}u,i,j\end{pmatrix}|\begin{pmatrix}u,i\end{pmatrix}\in R^+,\begin{pmatrix}u,j\end{pmatrix}\in R^-\right\}\) represents the pairwise training dataset, \(\sigma (\cdot )\) is the sigmoid function, \({\Theta }\) denotes all learnable parameters, and \(\lambda\) is the L2 regularization coefficient used to prevent model overfitting.

Finally, our objective function is a weighted combination of the BPR loss and the contrastive loss, formulated as follows:

$$\begin{aligned} L=L_{_{BPR}}+\alpha L_{_{ssl}}^{user} \end{aligned}$$
(25)

where \(\alpha\) is a hyperparameter used to balance the weights of the BPR loss and the contrastive loss. In this study, we followed the configuration of the representative contrastive learning-based recommendation model SGL14, and uniformly set \(\alpha\) to 0.1.

During the training process, we have implemented several measures to optimize model performance, including:

  1. (1)

    Early Stopping, to prevent overfitting and improve training efficiency, we employ an early stopping mechanism. If the model fails to significantly improve performance within 50 training epochs, the training process is halted prematurely. This helps save computational resources and avoids overfitting the training data.

  2. (2)

    Optimizer and Learning Rate Scheduling, we use the Adam optimizer to adaptively adjust the learning rate for faster convergence. Additionally, a learning rate scheduling strategy is applied to prevent excessively large learning rates in the later stages of training, ensuring stable optimization.

Experiments

In order to demonstrate the superiority of GR-MC and reveal the reasons for its effectiveness, extensive experiments were conducted and the following research questions were answered:

  • RQ1: How does GR-MC perform compared to other recommendation methods?

  • RQ2: How do the key components of GR-MC impact its performance?

  • RQ3: How do different parameter settings affect the proposed GR-MC?

  • RQ4: How does GR-MC perform under cold-start scenarios?

  • RQ5: How does the time cost of GR-MC compare to other recommendation methods?

Experimental settings

Datasets

This study conducted experiments on five widely used public benchmark datasets: MovieLens-100K, MovieLens-1M, Gowalla, Yelp2018, and Amazon-book. These datasets cover different domains and user scales, with significant differences in the number of users and items as well as interaction density, which can effectively reflect the data sparsity and diversity challenges faced by practical recommendation systems. Detailed statistics of each dataset are shown in Table 1.

Table 1 Statistics of the datasets.
Full size table

MovieLens: This dataset is sourced from the MovieLens website and includes three stable benchmark datasets with different scales: MovieLens-100K, MovieLens-1M, and MovieLens-20M45. Each dataset contains user ratings of movies, movie attributes and tags, as well as demographic features of users. The rating scale ranges from 1 to 5, with a step of 1. In this paper, we select MovieLens-100K and MovieLens-1M for experimentation.

Gowalla: This dataset is sourced from the Gowalla platform’s check-in data, which contains location information shared by users through check-ins46. As a classic dataset in the recommendation domain, in addition to check-in records, this dataset also includes social relationships between users.

Yelp2018: This dataset is an academic benchmark dataset built based on data from the Yelp open platform, containing structured data such as user ratings, review texts, social relationships, and business attributes up to 201828. It is widely used in research on recommendation systems and social network analysis.

Amazon-book: This dataset originates from the Amazon platform, containing user book ratings and review data. It is a widely used public benchmark dataset in recommendation system research. It includes structured data such as user ratings, review texts, and product attributes, making it particularly suitable for studying the performance of recommendation algorithms in sparse data environments47.

To ensure the quality of the dataset, we follow the data processing method used in the NGCF model with a 10-core setting48, meaning that only users and items with at least 10 interactions are retained. For each dataset, 80% of each user’s historical interaction data is randomly selected as the training set, while the remaining 20% is used as the test set. Additionally, 10% of the interaction data from the training set is further randomly sampled to construct the validation set for hyperparameter tuning. For each observed user-item interaction, it is considered a positive sample, and a negative sample is generated by randomly selecting an item that the user has not interacted with using a negative sampling strategy.

Baseline methods

To validate the effectiveness of the proposed GR-MC model, it is compared with seven state-of-the-art baseline models. These baseline models cover different categories of recommendation algorithms, including traditional matrix factorization methods (MF and NeuMF), graph neural network-based recommendation methods with no feature information (NGCF and LightGCN), graph neural network-based recommendation methods with feature information (GC-MC and SGL), as well as self-supervised learning-based SGL and graph attention network-based NGAT4Rec recommendation methods. Specifically, MF and NeuMF are introduced to test the performance of traditional matrix factorization and neural network-based recommendation methods in recommendation tasks, thereby demonstrating the advantages of GNN models in capturing complex relationships between users and items, especially in the absence of explicit feature information. These two baseline models help verify the improvement in recommendation accuracy of GNN over traditional methods. Moreover, NGCF and LightGCN are introduced to compare GNN-based recommendation methods with graph convolution mechanisms and traditional matrix factorization methods, to verify whether GNN models with graph structure information can achieve better performance in capturing complex interactions between users and items. Finally, NGAT4Rec is introduced to evaluate the improvement of the attention mechanism on GNN recommendation methods, and SGL is introduced to verify the role of contrastive learning in enhancing embedding representations and improving model generalization ability. The following outlines these baselines:

  • MF15: It is a widely used baseline method, simple and efficient, commonly applied in various recommendation systems, and can provide good recommendation results even in scenarios with sparse data.

  • NeuMF18: It combines the advantages of traditional matrix factorization and neural network models. Through the multi-layer perceptron (MLP), it can learn more complex nonlinear relationships and enhance the expressive power of the recommendation model, thereby improving the modeling accuracy of user-item interactions.

  • GC-MC49: It combines graph convolution with matrix completion techniques, making full use of graph structural information to enhance the performance of the recommendation system. This method effectively models the implicit relationships between users and items, providing an improvement over traditional matrix factorization.

  • NGCF28: This is a typical graph neural network-based recommendation method that effectively captures higher-order interaction information between users and items through graph convolution networks. The model propagates information within the graph structure, making the embedding representations more precise, and is suitable for handling complex user-item relationships.

  • LightGCN29: As a simplified graph neural network model, it removes complex nonlinear activation functions and multiple message-passing operations, using a simple neighbor aggregation mechanism. This approach can significantly improve computational efficiency while maintaining high recommendation performance, making it particularly suitable for large-scale datasets.

  • GTN50: It automatically generates multi-hop connections (meta-paths) through graph transformation layers, mining potentially useful relationships in heterogeneous graphs without the need for predefined structures, thereby enabling end-to-end node representation learning and enhancing modeling capability in complex graph structures.

  • NGAT4Rec51: This is a recommendation method based on a neighbor-aware graph attention network. By pairwise calculating attention weights between neighbors, it explicitly models implicit correlations and assigns neighbor-aware attention coefficients to enhance the quality of embedding representations. The model combines multiple layers of neighbor-aware graph attention, aggregating multi-hop neighbor signals while simplifying the network architecture.

  • SGL14: It adopts a self-supervised learning strategy, enhancing the generalization ability of the recommendation system through data augmentation on the graph structure. Additionally, contrastive learning effectively improves the discriminative power of the embeddings, thereby enhancing the model’s recommendation performance. SGL introduces three different data augmentation techniques, effectively mitigating the issue of sparse labeled data.

Evaluation metrics

This study uses two commonly used metrics, Recall@K and NDCG@K. Recall@K is used to evaluate the proportion of the K recommended items that match the user’s actual interactions. NDCG@K further incorporates the ranking of the recommended items, giving higher weights to correct recommendations that appear higher in the ranking. The higher the values of these two metrics, the better the quality of the model’s recommendations. In this study, K=20 is selected to analyze the experimental results.

Implementation details

All experiments were conducted in the same experimental environment, with the following specifications: NVIDIA A40 GPU, CUDA 11.7, driver version 515.65.01, Python 3.8.19, and PyTorch 2.0.0.

To ensure fair comparisons, the best hyperparameter settings reported in the original baseline papers are referenced. The Xavier is used for initialization, the Adam optimizer is selected, the batch_size is uniformly set to 1024, regs is set to 1e-5, the initial weight for contrastive learning is set to 0.1, and the learning rate is set to 1e-4. To prevent overfitting, an early stopping strategy is employed to record the best model parameters, which are then used for evaluation on the test dataset.

Comparation experiments (Q1)

In this section, we compare GR-MC with seven baseline models across five datasets. For example, Fig. 2 shows the training loss of GR-MC on the five datasets, while Figs. 3 and 4 present the Recall@20 and NDCG@20 results on MovieLens-100K and Amazon-book, clearly illustrating the training process and advantages of GR-MC. Specifically, the detailed results of GR-MC and the baselines are shown in Table 2, from which it can be observed that our method achieves superior Recall and NDCG on both small-scale datasets (MovieLens-100K and MovieLens-1M) and large-scale sparse datasets (Gowalla, Yelp2018, and Amazon-book).

  • GR-MC demonstrates significantly better overall performance compared to all baseline models. On average, it achieves improvements of 9.98% in Recall@20 and 14.45% in NDCG@20 across the five datasets. Notably, on the MovieLens-1M dataset, NDCG@20 improves substantially by 26.97%, which can be attributed to GR-MC’s enhanced capability to capture user interests, as well as its improved ranking accuracy through dynamic modulation and contrastive signal enhancement. On Amazon-book, a typical long-tail sparse dataset, GR-MC improves Recall@20 and NDCG@20 by 24.69% and 21.90%, respectively, verifying its effectiveness and robustness in complex recommendation scenarios.

  • GNN-based methods show clear advantages in recommendation systems. Unlike MF models, which compute static associations between users and items via inner product, GNNs recursively aggregate information from neighboring nodes, enabling the capture of richer high-order collaborative signals. For example, NGCF introduces a hierarchical neighbor aggregation mechanism that significantly enhances representational capacity, while LightGCN reduces model complexity by removing redundant modules without sacrificing performance, performing particularly well on datasets like Gowalla and Amazon-book. These approaches demonstrate that GNNs can effectively improve node representations, thereby significantly boosting recommendation performance.

  • Compared to the self-supervised baseline SGL, GR-MC further enhances the consistency and discriminability of embedding representations. SGL improves the robustness of user and item embeddings by generating contrastive views of graphs for self-supervised learning. GR-MC, on the other hand, adopts a contrastive learning framework as an auxiliary strategy, integrates user-side enhancement, and designs the MLKA and GSAU modules to further improve the modeling of neighborhood information. Through joint optimization guided by contrastive loss, the model not only achieves global contrastive learning, but also extracts more discriminative local features, ultimately improving recommendation accuracy.

  • From a model design perspective, GR-MC enhances the modeling of crucial neighbor information through the MLKA and GSAU modules while maintaining moderate computational complexity. This targeted enhancement is particularly effective for long-tail sparse datasets such as Amazon-book, where GR-MC demonstrates stronger robustness and accuracy. Overall, these improvements enable GR-MC to maintain excellent performance across various complex recommendation scenarios.

Fig. 2
figure 2

Performance of GR-MC training loss on five datasets.

Full size image
Fig. 3
figure 3

Performance of GR-MC on Movielens-100k Dataset.

Full size image
Fig. 4
figure 4

Performance of GR-MC on Amazon-book Dataset.

Full size image
Table 2 Overall performance comparison, where bold indicates the best performance for each row, underlined indicates the best baseline performance, and %Improv. represents the performance improvement of GR-MC compared to the best baseline.
Full size table

Ablation study (Q2)

In this section, in order to further validate the necessity of the key components in the proposed method, a series of ablation experiments were conducted, as shown in Table 3. These experiments separately evaluate the effects of MLKA and GSAU. Recall@20 and NDCG@20 were used as evaluation metrics for result analysis, leading to the following main conclusions:

  1. (1)

    The advantages of Multi-Scale Large Kernel Attention (MLKA). The ablation experiment was conducted on the MLKA module, and when switched off, the model’s performance declined. The average performance of Recall@20 and NDCG@20 across the five datasets decreased by 6.09%, 8.12%, 4.72%, 12.07%, and 18.44%, respectively. This indicates that MLKA can extract information from multiple scales, enhancing the effectiveness of GNN propagation. Removing this module leads to a reduced ability to extract information, making it difficult for the model to effectively aggregate distant neighbor information, which affects GNN propagation and results in an overall performance drop.

  2. (2)

    The effectiveness of the Graph Structure Attention Unit (GSAU). The ablation experiment was conducted on the GSAU module. After removing GSAU from each dataset, the average performance of the model decreased by 2.92%, 5.61%, 1.41%, 7.98%, and 9.06%, respectively. The drop in experimental results further indicates that while edge dropout, as a data augmentation technique, has significant advantages in improving model robustness, alleviating overfitting, and enhancing long-tail user modeling, it can also lead to a reduction in the neighbors of certain users, affecting the completeness of information propagation. This effect is more pronounced in sparsely-interacted datasets. However, our designed GSAU, through adaptive attention mechanisms and high-order information aggregation strategies, effectively compensates for the information loss caused by edge dropout, allowing the model to still learn crucial interaction information even with reduced neighbors, thus improving recommendation performance.

  3. (3)

    This paper compares three different edge dropout strategies: applying augmentation only to the edges adjacent to user-only, only to the edges adjacent to item-only, and to both user and item nodes simultaneously. Specifically, under the item-only strategy, the average performance on Recall@20 and NDCG@20 across the five datasets drops by 1.43%, 2.05%, 3.04%, 5.41%, and 6.69%, respectively; while under the symmetric strategy, the average drops are 1.14%, 1.06%, 1.65%, 2.68%, and 3.46%. These results indicate that structural perturbation on the user side plays a more critical role in enhancing model generalization and training stability in user-item interaction graphs. This is mainly because user behavior patterns and interest distributions are more diverse, and moderately augmenting their adjacent edges helps improve the robustness of representation learning. In contrast, item nodes are typically denser, and excessive perturbation tends to introduce noise, negatively affecting the accuracy of information propagation. Appendix B (see supplementary material) provides simplified preliminary theoretical analysis of (a) the gradient variance under the edge dropout mechanism and (b) the expected performance gain per training epoch, as an attempt to support these observations.

Table 3 The impact of user-only Edge Dropout, MLKA and GSAU on the performance of the GR-MC model.
Full size table

Model architecture study (Q3)

Effect of layer numbers

The results in Table 4 show that the 3-layer model achieves the highest Recall@20 and NDCG@20, effectively balancing information aggregation and over-smoothing. This indicates that moderately increasing the number of layers can enhance the model’s expressive power. However, performance degrades in the 4- to 6-layer models due to excessive smoothing caused by overly deep networks, which weakens the model’s discriminative ability. Additionally, on sparser datasets such as Amazon-Book and Yelp2018, the 1-layer model performs significantly worse, suggesting that shallow networks struggle to sufficiently capture complex user-item interactions. In contrast, the 3-layer model better leverages neighbor information, resulting in improved recommendation performance. Overall, the 3-layer architecture consistently delivers optimal performance across different datasets; therefore, we adopt a 3-layer propagation depth in this work. At the same time, to further mitigate the overfitting risk potentially caused by deeper networks, we incorporated strategies such as neighbor sampling, user-focused edge dropout, L2 regularization, and early stopping in the model.

Table 4 The impact of the number of embedding propagation Layers (L).
Full size table

Effect of embedding size

Both excessively large and small embedding dimensions can affect the expressive power and computational efficiency of the GR-MC model. Larger embedding dimensions enhance the model’s ability to capture complex user-item relationships, especially improving recommendation accuracy in the multi-scale attention mechanism, but at the cost of increased computational and storage overhead. Conversely, smaller embedding dimensions can improve training efficiency and help prevent overfitting in sparse data scenarios but may be insufficient to represent complex relationships. Therefore, this paper analyzes the impact of different embedding dimensions on the proposed model’s performance by varying the dimension size, e.g., d=32,64,128,256,512, and evaluates performance using Recall@20 and NDCG@20 metrics. Through experiments, a balance between expressive power and computational efficiency is achieved. As shown in Fig. 5, the Recall@20 and NDCG@20 generally improve across five datasets as the embedding dimension increases, but after d=256, further increases yield diminishing performance gains and even marginal declines. Thus, the embedding dimension of 256 is finally adopted, combined with L2 regularization and early stopping mechanisms, to further prevent redundancy and overfitting risks associated with larger embeddings.

Fig. 5
figure 5

The impact of the number of embedding size.

Full size image

Cold start study (Q4)

The cold-start problem is one of the major challenges in recommendation systems, referring to the difficulty of generating personalized recommendations for users with no historical interaction data. To assess the robustness of GR-MC in cold-start scenarios, we conducted user-level cold-start experiments on the Movielens-100K dataset. Specifically, we randomly selected a subset of users and excluded all their interaction data from the training set to simulate a real-world cold-start situation. The model then generated recommendations for these users without relying on any prior behavior data, and we evaluated the results using the Recall@20 metric. As shown in Fig. 6, GR-MC significantly outperforms various baseline methods under the cold-start condition, demonstrating its superior recommendation performance. These results indicate that, through its neighbor-enhanced mechanism and contrastive learning strategy, GR-MC is able to infer user preferences effectively even in the absence of interaction history, achieving robust and accurate recommendations.

Fig. 6
figure 6

Cold start user Recall@20 result.

Full size image

Complexity and time efficiency analysis (Q5)

To comprehensively evaluate the potential computational overhead introduced by incorporating the Multi-Scale Large Kernel Attention (MLKA) and the Graph Structure Attention Unit (GSAU) in GR-MC, this paper records the training time and the total time cost during the testing phase for each model on five datasets, as shown in Table  5, and provides both theoretical and empirical analyses. It should be noted that the testing time includes not only the forward inference on the test data but also the computational cost of calculating evaluation metrics.

In each GNN propagation layer, the core operations of GR-MC are neighbor aggregation and embedding update. Let the total number of user and item nodes be N, the average number of neighbors per node be C, the embedding dimension be d, and the number of attention scales be S. The complexity of each module is as follows:

  • Single GNN layer propagation:

    $$\begin{aligned} {\mathcal {O}}(N \cdot C \cdot d) \end{aligned}$$
    (26)

  • Multi-scale Large Kernel Attention (MLKA):

    $$\begin{aligned} {\mathcal {O}}(S \cdot N \cdot C \cdot d) \end{aligned}$$
    (27)

  • User-focused Edge Dropout for contrastive views:

    $$\begin{aligned} {\mathcal {O}}(2 \cdot S \cdot N \cdot C \cdot d) \end{aligned}$$
    (28)

  • Contrastive loss computation: Let M be the number of nodes sampled for contrastive learning and K the number of negative samples per node.

    $$\begin{aligned} {\mathcal {O}}(M \cdot K \cdot d) \end{aligned}$$
    (29)

Thus, the total time complexity of GR-MC can be approximated as:

$$\begin{aligned} {\mathcal {O}}(2 \cdot S \cdot N \cdot C \cdot d + M \cdot K \cdot d) \end{aligned}$$
(30)

Compared to baseline models, the multi-scale attention strategy in GR-MC introduces additional but controllable overhead, while significantly enhancing the representational capacity of the model. To further demonstrate the above phenomenon, the following section analyzes the time cost of GR-MC from an experimental perspective.

From the experimental results, it can be observed that GR-MC exhibits favorable control over time costs during both training and inference stages. For example, on the MovieLens-1M dataset, the per-epoch training time of GR-MC is 196.3 seconds, which is shorter than that of NGCF. On large-scale sparse graphs such as Amazon-book, GR-MC also outperforms NGCF and NGAT4Rec, validating the practical effectiveness of its structural optimization strategy. In the inference stage, GR-MC maintains high efficiency as well, requiring only 114.7 seconds on the Gowalla dataset, which is about 46% less than NGCF. However, on small-scale datasets like MovieLens-100K, the advantage in inference time is less obvious due to the relatively high proportion of fixed computational overhead, where minimalist models such as LightGCN perform better.

In summary, GR-MC achieves performance improvement while keeping the time cost within an acceptable range, thus meeting the computational efficiency requirements of practical recommendation tasks.

Table 5 The training and testing time (unit: seconds/epoch).
Full size table

Discussion

Our model needs to consider potential social impacts. First, due to the inherent message-passing mechanism in graph neural networks favoring high-degree nodes, the model may unintentionally amplify popularity bias, tending to recommend popular items while neglecting long-tail content. To address this issue, we have incorporated neighbor sampling and regularization strategies in the current design for preliminary mitigation. In the future, we plan to integrate diversity-aware sampling or weighting mechanisms to further balance the popularity distribution in recommendation results. Secondly, modeling user behavior may pose privacy risks, especially when it comes to social relationships or long-term behavioral sequences, where user preference patterns may be indirectly inferred or abused. So in the future, privacy protection technology should be introduced to enhance the usability and security of the model in real recommendation scenarios. In terms of fairness, recommendation models may have performance differences between different user groups, resulting in some groups receiving suboptimal recommendations. To alleviate this issue, this algorithm avoids explicit preference amplification in its design and verifies its stability on multiple datasets at different sparsity levels. In the future, we will introduce explicit fairness constraints or multi-objective optimization strategies to enhance the fairness of recommendations. Although offline experiments have been conducted on five publicly available datasets covering multiple domains and sparsity, simulating diverse real-world scenarios, offline evaluation still cannot completely replace dynamic user feedback in real environments. Therefore, the proposed method will be deployed in the real-time recommendation system for future work.

Conclusion and future work

In this paper, we propose GR-MC to address the challenges of insufficient accuracy and robustness in recommendation tasks under data sparsity and missing neighbor interactions. First, we design a graph structure augmentation operator based on an edge dropout strategy applied solely to user nodes, which helps capture the interaction between users and items more effectively, while also aiding in combating noise and anomalous interactions. Secondly, we design a multi-scale attention embedding propagation mechanism to enhance the model’s ability to capture high-order neighbor information, improving the accuracy of user and item representations. Third, we incorporate contrastive learning as an auxiliary framework into the GNN model, along with a dynamic weighting mechanism, to improve the discriminative power of the learned embeddings. Finally, benefiting from the efficient design of the multi-scale attention mechanism and contrastive learning framework, GR-MC maintains model performance while keeping computational cost within a manageable range, achieving a good balance between effectiveness and resource consumption. Extensive experiments were conducted on five datasets with different sparsity characteristics to further validate the effectiveness and robustness of the proposed algorithm in addressing data sparsity and cold-start problems compared to other baseline methods.

Similar to the effectiveness of machine learning in handling complex nonlinear problems such as unstable motion in frictional processes, user behavior prediction in recommendation systems also faces challenges involving complex relationships and dynamic features. Although this study has achieved promising experimental results, we acknowledge that there is still room for further improvement and extension. First, the current algorithm mainly focuses on modeling multi-scale interactions between users and items within the graph structure, but does not explicitly incorporate temporal or sequential information. This may limit its ability to fully capture the dynamic evolution of user interests over time. In future work, we plan to integrate time-aware modules and sequential modeling methods, combining the multi-scale attention mechanism with temporal information to improve the accuracy and personalization of recommendations. Second, as artificial intelligence continues to advance in the field of recommendation systems, intelligent and dynamic user interest modeling has become an important development trend52. Therefore, the GR-MC framework has great potential to be extended to application scenarios with higher demands for real-time and dynamic recommendations, such as social media and news recommendations. In future research, we will continue to explore the potential of graph neural networks for complex relationship modeling, and integrate multi-dimensional information such as temporal signals to provide more practical ideas and methods for recommendation system research.