Enhanced FPGA-based smart power grid simulation using Heun and Piecewise analytic method

Abstract

The increasing complexity of modern power systems requires engineers to design, build, and test equipment with a high degree of accuracy. The demand for precise equipment design, testing, and evaluation has reached extraordinary levels within modern power systems. To meet this challenge, engineers rely heavily on real-time simulators, which are essential tools for assessing power network dynamics. This study introduces a novel approach, an adaptable and cost-effective simulator, poised to revolutionize traditional hardware-in-the-loop (HIL) systems. Leveraging field-programmable gate arrays (FPGAs) and a comprehensive implementation of Heun and Piecewise analytic methods (PAM), provided simulator offers unparalleled capabilities for embedded real-time simulation of smart grids, ensuring swift and accurate measurements. Augmented by Python-based process simulation and integrated with industry-standard tools like Modelica and MATLAB, the proposed system promises versatility and efficiency. Through comprehensive testing, including rigorous evaluations of excitation system responses to diverse scenarios such as voltage set-point variations, automatic voltage regulator step responses, and fault conditions, we demonstrate the simulator’s robustness and precision. Experimental findings underscore its potential as an effective alternative to conventional HIL systems, marking a significant advancement in smart grid simulation technology.

Introduction

Grids of the 21st century are composed of nonlinear systems and dynamic networks. All power system equipment and machinery are tested and set up by using different procedures and equipment, as well as field tests, which have become increasingly sophisticated in recent years. The old techniques are moving towards new computer-based technologies. Real-time simulation technology has been improved to execute numerous kits for power systems testing due to its high-speed processors, increased efficiency, and overall superior performance. Complex algorithms with high performance are frequently used, specifically where load characteristics are not known. The usage of chip technologies for implementation is becoming popular, increasing the working abilities of current field programmable gate arrays (FPGA) chips with less cost^1,2. The main motivation behind this study is to give different and flexible modular approaches for efficient development at any point in the process.

Hardware-in-the-loop (HIL) simulation was established to bridge the distinction between the simulated systems and real-world tools. In a HIL simulation test, the model for simulation in the computer mimics hardware during the test. Power converters, smart grids, protection systems, microgrids, energy sources, power plants, and different applications have all benefited from real-time HIL modeling^3,4. A HIL system is presented in this study that allows the simulation of multiple microgrid topologies under a variety of real-time test situations. Researchers provided a cohesive framework that is based on FPGA simulation of electronic components using several methodologies. This real-time electrical machine simulation might be applied for HIL simulations to evaluate novel command systems in comparison to a virtual machine model^5,6,7.

In the recent past, various simulation systems have been suggested in the literature. A primitive simulator, known as an ’analog simulator’, is constructed using small-scale power system components. Around 1924, the Massachusetts Institute of Technology (MIT) installed the first analog analyzer by Hugh H. Spencer and Harold Locke Hazen^8,9. Another hybrid (analog/digital) simulator was created with the advent of computers, which can address some prior limitations. Many researchers used a hybrid digital-analog model, such as the author used it with high voltage direct current (HVDC), which increased the ability of hybrid networks^10,11,12,12. In another study, the execution of a high-quality real-time emulation of a Permanent Magnet Synchronous Motor (PMSM) is described, which is computer-driven and presents a framework for modeling the dynamics of several power systems. Authors implemented PMSM on an FPGA card and used Simulink blockset, which is Xilinx System Generator (XSG)¹³. Digital systems, on the other hand, offer excellent stability, reconfigurability, and memory that is implanted¹⁴. The field-programmable gate array (FPGA) offers a low-cost reprogrammable architecture that allows for the creation of corresponding process structural design, making it ideal for functional and structural analysis of an enormous range of SNNs. Some examples of Spiking Neural Network (SNN) implementations on FPGA for various purposes have been presented. Several samples of SNN applications on FPGA for various purposes have been presented, creating an event-driven deep spiking network accelerator that has been shown to consume extremely little power. For the application of digit recognition, researchers constructed an SNN using an FPGA. They were able to obtain a 60% speedup over the software application on a general-purpose CPU and a 20% reduction in energy usage by considering parallel processing and approximation computing structural design. Recent research has concentrated on the architectural design of SNNs on FPGAs to achieve low-cost and low-power growth. The Euler approach is used to develop neurodynamic models in SNNs in these studies, which demands a limited amount of hardware resources and low power. This numerical technique delivers first-order precision, which might potentially reduce network performance. More precise numerical techniques, such as high-order Runge–Kutta (RK) algorithms, have been studied in recent work^15,16,17.

The primary goal of this study is to develop a flexible, low-cost real-time simulator for modeling, testing, and designing power system components. This simulator is suitable for use in smart grids and microgrid research and supports closed-loop testing of transmission, distribution, and control systems. By combining Piecewise Analytic and Heun methods, the system offers accurate and energy-efficient simulation suitable for real-time applications. Its adaptability enables advanced training and evaluation of controllers, operators, and fault management strategies. The real-time simulation is based on the Piecewise and Heun techniques. The Piecewise analytic technique appears promising to provide online training in a real-time application, whereas the Heun technique is suited for low-cost operation, low-energy implication applications, and accuracy^18,19,20.

• This study demonstrates how an adaptable, flexible, and low-cost real-time simulator can be used to model, test, and design power system devices. The simulator’s agility, adaptability, and closed-loop functionality make it suitable for generating transmission and distribution channels for power system operations and controller functions.

• Electricity controllers and service controllers can use the simulator for large-scale real-time simulation exercises, safely manipulating grid techniques, examining controllers, and testing system growth.

• For the simulation, this study employs the Piecewise and Heun techniques for real-time applications, with the Piecewise method providing online training potential and the Heun technique being suitable for low-cost, low-energy, and accurate operations.

Further, “Literature review” section discusses works related to the current study. Materials and methods are given in “Materials and methods” section while a discussion of results is provided in “Results and discussion” section. Finally, “Conclusion” section concludes this study.

Literature review

Power system simulation has evolved to address the growing complexity of modern electrical grids and smart energy systems. This review highlights advanced methods developed to improve the accuracy, efficiency, and flexibility of power system simulations beyond conventional approaches.

Digital twins represent a cutting-edge approach to modeling and simulating physical systems in real time. By creating a virtual replica of a physical system, digital twins allow continuous monitoring and analysis of power system performance. This provides insights for optimization and predictive maintenance. This technology has been successfully applied to various components of power grids, enabling operators to test scenarios and anticipate issues before they affect the actual system²¹. The real-time feedback loop provided by digital twins significantly enhances decision-making processes in managing power distribution and load balancing.

As the integration of renewable energy sources into power grids increases, grid-forming inverters have become crucial for maintaining stability in microgrids. These inverters autonomously establish and regulate voltage and frequency, ensuring seamless operation in both grid-connected and islanded modes. Research has shown that using advanced control algorithms in grid-forming inverters can significantly improve microgrid resilience and efficiency, especially in scenarios with high penetration of intermittent renewable energy sources²². Machine learning and artificial intelligence (AI) in power systems have opened new avenues for optimizing grid operations. AI techniques can be used for predictive maintenance, load forecasting, and fault detection, providing a higher level of automation and intelligence in managing power systems. For instance, neural networks and deep learning models have been employed to predict load demand and identify potential faults in the grid, enabling more proactive and efficient grid management²³. These technologies complement traditional simulation methods by offering data-driven insights and adaptive control strategies.

Co-simulation platforms allow the integration of multiple simulation tools to analyze complex systems. This approach is particularly useful in power systems, where electrical, mechanical, and thermal aspects must be considered simultaneously. Tools like Modelica and MATLAB Simulink are often used in co-simulation frameworks to evaluate the interactions between different subsystems, such as power electronics and control algorithms²⁴. Co-simulation facilitates a holistic view of system performance and helps design robust solutions for integrated energy systems. High-fidelity EMT simulations are essential for analyzing power systems’ detailed behavior during transient events, such as faults or switching operations. These simulations provide granular insights into electromagnetic interactions within the grid, helping engineers design more resilient protection and control systems. Software tools like PSCAD and EMTP-RV are widely used for electromagnetic transient (EMT) simulations, offering precise modeling capabilities for complex scenarios involving power electronics and renewable energy sources²⁵.

Dynamic line rating (DLR) systems adjust power lines’ transmission capacity based on real-time environmental and operational conditions. Unlike static rating systems, which use conservative estimates for line capacity, DLR systems optimize transmission assets utilization by continuously monitoring factors like temperature, wind speed, and conductor sag. This technology enhances power transmission efficiency and reliability, allowing for better management of fluctuating power flows and integration of renewable energy²⁶. Phasor measurement units (PMUs) provide real-time measurements of electrical waves on an electricity grid, enabling precise monitoring and control of grid dynamics. Synchrophasors, derived from PMU data, offer synchronized measurements of voltage and current phasors, crucial for maintaining grid stability and detecting anomalies. The deployment of PMUs across power networks facilitates advanced applications like wide-area monitoring, state estimation, and system protection, significantly improving smart grid operational reliability²⁷.

Virtual synchronous machines (VSMs) are advanced control algorithms that emulate synchronous generators using power electronics. This concept is particularly useful for integrating renewable energy sources into the grid. It allows inverter-based resources to contribute to grid inertia and frequency regulation. VSMs enhance the stability and reliability of power systems by providing synthetic inertia and damping, which are critical for maintaining balance in grids with high levels of renewable penetration²⁸.

Flexible AC transmission systems (FACTS) encompass a range of technologies designed to enhance power networks’ controllability and capacity. FACTS devices, such as static var compensators (SVCs) and unified power flow controllers (UPFCs), provide dynamic voltage support, reactive power compensation, and power flow control. These systems are integral to managing congestion, improving stability, and optimizing transmission network performance, particularly in environments with variable renewable energy sources²⁹. Cloud computing has transformed power system simulations and data analytics. These platforms support real-time data processing, storage, and machine learning applications, providing utilities with the tools to handle big data and derive actionable insights for grid optimization and management³⁰.

Although earlier efforts from analog simulators^31,32, hybrid analog-digital systems^33,34,35, to fully digital real-time simulation platforms³⁶ have significantly advanced power system modeling, they also exhibit key limitations. Analog and hybrid simulators lack flexibility and scalability for modern distributed energy systems. Even advanced digital simulators face challenges in balancing simulation accuracy, numerical stability, and FPGA hardware constraints.

High-fidelity models like EMT simulations provide detail but are computationally expensive, often requiring smaller time steps or specialized solvers³⁷. On the other hand, simplified solvers such as Euler’s method offer speed but compromise on stability under dynamic events. Recent research^38,39,40 shows that methods like Piecewise Analytic Method (PAM) and Heun’s method offer promising trade-offs, but they are typically evaluated in isolation or outside real-time embedded contexts.

Therefore, there is a strong need for a unified algorithm that integrates stable solvers like Heun with event-sensitive methods like PAM, is optimized for FPGA implementation, and can run with longer time steps without compromising waveform accuracy. This work addresses this exact need by building on the limitations identified in earlier systems while leveraging recent advancements in numerical modeling^39,40,41,42.

Materials and methods

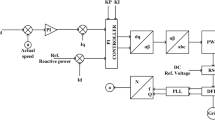
In this study, the MATLAB/Simulink environment is used for a usual system containing a generator, to develop a digital control system and hardware-in-loop as a testing tool, and provides Piecewise and Heun techniques to improve the accuracy as shown in Fig. 3. There are two types of arithmetic operations in MATLAB which are array and matrix operations, which contain a large set of mathematical functions. These operations are used to accomplish numerical computation, and without knowing these terms, it will be difficult to solve problems in MATLAB. Equation 1 shows the voltage-controlled source where V is output voltage and +, - are control ports where k is voltage gain and $r_s$ is the stator resistance, $i_{abcs}$ are stator currents in the ABC frame, $p= \frac{d}{dt}$ and $\lambda _{abcs}$ flux linkages²¹.

$$\begin{aligned} V_{abcs}= & -r_s i_{abcs}+p \lambda _{abcs}\end{aligned}$$

(1)

$$\begin{aligned} V_{qdr}= & -r_r i_{qdr}+p\lambda _{abcs} \end{aligned}$$

(2)

$$\begin{aligned} p= & \frac{d}{dt} \end{aligned}$$

(3)

$$\begin{aligned} (f_{abc})^T= & [f_{as} f_{bs} f_{cs}], \nonumber \\ (f_{qdr})^T= & [f_{kq1} f_{kq2} f_{fd} f_{kd}] \end{aligned}$$

(4)

Equations 4 to 6 define the transformation matrices between the stator and rotor reference frames. They are used to transform the voltages and currents between the stationary (abc) and rotating (qdr) frames.

$$\begin{aligned} V_{q_s}^r= & r_s i_{q_s}^r+\omega _r \lambda _{ds}^r+p\lambda _{qs}^r \nonumber \\ V_{ds}^r= & r_s i_{q_s}^r+\omega _r \lambda _{ds}^r+p\lambda _{ds}^r \end{aligned}$$

(5)

These equations represent the stator and rotor voltages in the synchronous reference frame. They are influenced by the stator resistance $r_s$, rotor speed $\omega _r$, currents $i_{q_s}^r$, and flux linkages $\lambda _{ds}^r$ and $\lambda _{qs}^r$.

$$\begin{aligned} V_{0s}= & -r_s i_{0s}+p\lambda _{Os}\nonumber \\ V_{kq_1}^{'r}= & r_{kq1}^{'} i_{kq1}^{'r}+ p\lambda _{kq1}^{'r} \nonumber \\ V_{kq_2}^{'r}= & r_{kq2}^{'} i_{kq2}^{'r}+ p\lambda _{kq2}^{'r}\nonumber \\ V_{fd}^{'r}= & r_{fd}^{'} i_{fd}^{'r}+ p\lambda _{fd}^{'r}\nonumber \\ V_{kd}^{'r}= & r_{kd}^{'} i_{kd}^{'r}+ p\lambda _{kd}^{'r} \end{aligned}$$

(6)

Equation 6 represents the additional voltage equations for the synchronous generator model, accounting for zero sequence components and additional rotor components. The asynchronous machine is often approximated by applying flux linkage of the equations, and Equations 7 to 8 are used to twist like a state variable is commonly stated as reactance rather than inductance. The networks, which are flux networks in terms of voltages, are described based on the given details.

$$\begin{aligned} \Psi _{qs}^r= & wb \int \left[ V_{qs}^r-\frac{wr}{wb} \Psi _{ds}^r+\frac{r_s}{x_l} \left( \Psi _{mq}^r-\Psi _{qs}^r \right) \right] dt\nonumber \\ \Psi _{ds}^r= & wb \int \left[ V_{ds}^r-\frac{wr}{wb} \Psi _{qs}^r+\frac{r_s}{x_{ls}} \left( \Psi _{md}^r-\Psi _{ds}^r \right) \right] dt\nonumber \\ \Psi _0 s= & w_b \int \left[ V_{0s}-\frac{r_s}{X_{ls}} \Psi _0 s \right] dt\nonumber \\ \Psi _{kq1}^r= & wb \int \left[ V_{kq1}^{'r}- \frac{r'_kq}{X'_{lkq1}} \left( \Psi _{mq}^r- \Psi _{kq1}^{'r} \right) \right] dt\nonumber \\ \Psi _{kq2}^r= & wb \int \left[ V_{kq2}^{'r}- \frac{r^{'}_{kq2}}{X_{lkq2}^{'}} \left( \Psi _{mq}^r -\Psi _{kq2}^{'r} \right) \right] dt\nonumber \\ & \Psi _{fd}^r sinh^{\int } \left[ \frac{r'_{f_d}}{X'_{md}} e_{xfd}^{'r}+ \frac{r_{f_d}^{'}}{ X_{Lfd}^{'}} \left( \Psi _{mq}^r - \Psi _{fd}^{'r} \right) \right] dt\end{aligned}$$

(7)

$$\begin{aligned} \Psi _{kd}^{'r}= & wb \left[ V'_{kd} r + \frac{r'_{kd}}{X'_{Lkd}} \left( \Psi _{md}^r-\Psi _{kd}^{'r} \right) \right] dt\nonumber \\ \Psi _{mq}^r= & X_{aq}\left[ \frac{Psi_{qs}^r}{X_{Ls}} + \frac{\Psi _{kq1}^{'r}}{X^{'}_{Lkq1}}+ \frac{\Psi _{kq}^{'r}}{X_{Lkq2}^{'}} \right] \nonumber \\ \Psi _{md}^r= & X_{ad}\left[ \frac{\Psi _{ds}^r}{X_{Ls}} + \frac{\Psi _{fd}^{'r}}{X^{'}_{Lfd}} + \frac{\Psi _{kd}^{'r}}{X^{'}_{Lkd}} \right] \end{aligned}$$

(8)

These equations represent the flux linkage equations for the synchronous generator model. They describe how the flux linkages ($(\Psi _{qs}^r, \Psi _{ds}^r, \Psi _0 s, \Psi _{kq1}^{'r}, \Psi _{kq2}^r, \Psi _{fd}^{'r}$, and $\Psi _{kd}^{'r}$ ) change over time and are influenced by various parameters such as voltages, currents, and rotor speed. $X_{aq}$ and $X_{ad}$ are from

$$\begin{aligned} & X_{aq}\left[ \frac{1}{X_{mq}}+ \frac{1}{X_{Ls}} + \frac{1}{X^{'}_{Lkq1}} + \frac{1}{X^{'}_{Lkq2}} \right] \nonumber \\ & \quad X_{ad}\left[ \frac{1}{X_{md}}+ \frac{1}{X_{Ls}} + \frac{1}{X^{'}_{Lfd}} + \frac{1}{X^{'}_{Lkd}} \right] \nonumber \\ & \quad i_{qs}^r=-\frac{1}{X_{ls}}\left( Psi_{qs}^r-\Psi _{mq}^r\right) ,\nonumber \\ & \quad i_{ds}^r=-\frac{1}{X_{ls}}\left( Psi_{ds}^r-\Psi _{md}^r\right) i_{os}-\frac{1}{X_{ls}}\Psi _{0s},\nonumber \\ & \quad i_{kq1}^{'r} = \frac{1}{X'_{lkq1}}\left( \Psi _{kq1}^{'r}-\Psi _{mq}^r \right) \nonumber \\ & \quad i_{kq2}^{'r}=-\frac{1}{X'_{lkq2}}\left( Psi_{kq2}^{'r}-\Psi _{mq}^r\right) ,\nonumber \\ & \quad i_{fd}^{r}=\frac{1}{X_{lfd}}\left( Psi_{fd}^{'r}-\Psi _{md}^r\right) ,\nonumber \\ & \quad i_{qs}^{r}=-\frac{1}{X'_{kd}}\left( Psi_{kd}^{'r}-\Psi _{md}^r\right) ,\end{aligned}$$

(9)

$$\begin{aligned} & T_{em}=\frac{p_{em}}{\omega _{rm}} =\left( \frac{3}{2}\right) \left( \frac{P}{2}\right) \left( \frac{1}{\omega _b}\right) \left( Psi_{ds}^r i_{qs}^r- \Psi _{qs}^r i_{ds}^r \right) \omega _r = \frac{p}{2} \omega _{rm}\nonumber \\ & \quad \frac{\omega _r-\omega _e}{\omega _b} =\int \frac{1}{2H} \left( T_{em(pu)} + T_{mech(pu)} -T_{damp(pu)} \right) dt \end{aligned}$$

(10)

These equations represent the current equations for the synchronous generator model. They describe how the currents ($i_{qs}^r, i_{ds}^r, ii_{os}, i_{kq1}^{'r}, i_{kq2}^{'r}, i_{fd}^r$, and $i_{kd}^{'r}$) change over time and are influenced by various parameters such as flux linkages and inductances.

Transmission lines connect a power plant to the external grid. A scattered line model is utilized, which is dependent on the Bewley lattice diagram, which is a graphical method used to determine the value of traveling waves²². This method is useful for voltage and current representation reflection as it moves toward the transmission system. The inputs are $V_s$, $i_R$, and the outputs are $V_R$, $i_s$ for each phase. The Elements that move forward as well as backward ($V_f$, $V_b$) of the voltage and current signals are present at all points along the transmission line ($i_f$, $i_b$). Thus

$$\begin{aligned} V_s= & V_{fS}+V_{bS} = Z_c i_{fs}-Z_c i_{bs}\nonumber \\ V_R= & V_{fR} + V_{bR} = Z_c i_{fR}-Z_c i_{bR}\nonumber \\ V_s= & Z_c (i_s-i_{bs})-Z_c i_{bs}-Z_c i_s = 2_{V_{bS}} \nonumber \\ V_R= & 2V_{fr}-Z_c i_R \end{aligned}$$

(11)

These equations represent the voltage equations for transmission lines, considering forward and backward voltage components (VsVs and VRVR)and their relationship with the currents $i_{fs}$, $i_{bs}$, $i_{fR}$, and $i_{bR}$.

By applying Heun’s method and Piecewise Analytic Method (PAM), this work aims to simulate these complex equations efficiently and accurately. Heun’s method allows for stable solutions to differential equations, while PAM provides a structured way to handle nonlinear relationships in power system components. The combined use of MATLAB/Simulink with Python-based process simulations creates a robust framework for testing and evaluating power system dynamics under different conditions, providing a solid alternative to traditional HIL simulations.

External grid and loads

Active and reactive (To provide voltage levels) powers are used to simulate loads. According to Equation 12, the input parameters are the magnitude and angle of the voltage²³.

$$\begin{aligned} V_a= & Vm cos (\omega t +\theta )\nonumber \\ V_b= & V_m cos (\omega t- \frac{2\pi }{3}+\theta )\nonumber \\ V_c= & V_m cos (\omega t+\frac{2\pi }{3}+\theta ) \end{aligned}$$

(12)

Equation 12 represents the voltages of the external grid, considering the magnitude and phase angle of the voltage. Equation 13 shows the implementation of excitation in MATLAB.

$$\begin{aligned} T_m= & A+B_q+C(1+N)\nonumber \\ T_{temp-m}= & T_{temp-R} + D_1 \left( e^{-TCR^s} e^{-TCD^s} qf \right) +D_2+E(1-N) \end{aligned}$$

(13)

In Equation 13, we can see the implementation of excitation in MATLAB, describing the dynamics of the excitation system. Each equation plays a crucial role in describing the behavior of different components within the proposed system, such as the synchronous generator, transmission lines, external grid, and excitation system. They are used to simulate the dynamic behavior of these components and evaluate the performance of the proposed system under various operating conditions.

Algorithm implementation

Heun’s Method and PAM implementation for real-time FPGA execution are provided here for scientific clarity. The pseudocode corresponds to the dynamic equations defined in Equations 1 to 13.

Algorithm 1

Generator dynamics—Heun’s method.

Algorithm 1 simulates generator voltage and flux dynamics using Heun’s method (a second-order Runge-Kutta method), which improves over Euler by computing an average slope. It ensures a balance between accuracy and computational feasibility for FPGA-based real-time simulation.

Algorithm 2 models the segmented behavior of transmission lines using the Piecewise Analytic Method (PAM), which divides the line into discrete segments for real-time simulation. Each segment operates under either nominal or fault conditions, with separate analytic solutions applied accordingly. By updating voltage and current values independently per segment, PAM effectively captures nonlinear behaviors such as reflections, switching events, and fault-induced transients.

Algorithm 2

Piecewise analytic method.

This method is well-suited for real-time embedded systems, as it transforms complex partial differential line equations into analytically solvable segments. At each segment boundary, the algorithm uses characteristic impedance to compute wave reflection and transmission, ensuring waveform continuity across the grid. The segmentation, combined with condition-based execution, enables accurate modeling of transient and steady-state conditions with minimal computational overhead, making it ideal for FPGA-based smart grid simulators.

Here we provide correlated parameters and equations that are implemented in the MATLAB programming environment. More information on dynamic equations, variable definitions, and parameters has been given in Table 1.

Table 1 Machine parameters and parameters in general for Matlab simulation.

Heun’s and Piecewise method

Heun’s method is a modified version of Euler’s method in mathematics and computer science. We used Heun’s method in Python for the best prediction of the line that would intersect the curve at the next forecast point, and here we calculate the curve, which is the solution to ordinary differential equations with initial values. The process relies on making the prediction of new values of y and then correcting it based on the slope calculated at those new values. It gives a more accurate approximation with the computing formula $y_{n+1}$.

Heun’s method, a second-order Runge-Kutta technique, is used to simulate the dynamic behavior of smart grid components, such as generators, through differential equations. It improves upon Euler’s method by introducing a correction step, which enhances accuracy when modeling continuous system changes. While higher-order Runge-Kutta methods (e.g., fourth-order) provide greater precision, they impose significant computational demands that are unsuitable for real-time FPGA-based applications. In contrast, Heun’s method offers a balance between accuracy and computational efficiency, making it ideal for real-time simulation scenarios with strict step time and resource constraints. In Heun’s method, the simulation proceeds in two steps: first, predicting the new value of y and then correcting it based on the slope calculated at the predicted point.

Prediction step

An initial prediction of the next state is made using the derivative at the current state. Voltage equation with flux linkage$v_{abs}=-r_s i_{abs}+p \lambda _{abcs}$. The derivative is approximated to predict the next step:

$$\begin{aligned} \Delta V=h \times \left( -r_s i_{abs}+ p\lambda _{abcs} \right) \end{aligned}$$

(14)

where h is the step size.

Correction step

The prediction is corrected by calculating the derivative at the predicted state and averaging it with the initial derivative. The corrected step is calculated as:

$$\begin{aligned} \Delta V_{corrected}=h/2 \times \left( -r_s i_{abs}+ p\lambda _{abcs} \right) + \left( -rs \left( i_{abs}+\Delta _i\right) + p\left( \lambda _{abcs}+\Delta \lambda \right) \right) \end{aligned}$$

(15)

This correction step reduces errors due to the first prediction’s linear assumption, providing more accurate results in the dynamic simulation.

In this context, PAM can be applied to simulate the behavior of transmission lines, where voltage and current waveforms might exhibit abrupt changes due to switching operations, faults, or other transient events. The lines are modeled with discrete segments, allowing for forward and backward wave propagation calculations.

Forward and backward waves

For example, the transmission line voltage equation $V_s = V_{fS} + V_{bS} = Z_c i_{fs} - Z_c i_{bs}$ is modeled as two separate pieces, one for forward waves and one for backward waves.

In the Piecewise model, when a wave reaches a boundary, it reflects and continues traveling along the line, which requires distinct calculations for each region. PAM allows for effective simulation of these complex behaviors by considering the linear sections as pieces, integrating them into a comprehensive model that accounts for transitions between regions.

Combining these two methods in real-time embedded simulation provides a powerful approach to accurately simulate smart grid components. Heun’s method handles the dynamic behavior of continuous systems, like generators and controllers, while PAM manages discontinuities and transitions in structural systems, like transmission lines. This combined approach is implemented in an FPGA, allowing for real-time simulations with high accuracy and computational efficiency. The FPGA architecture provides the necessary parallelism and speed to run complex simulations in real time. Additionally, using MATLAB and Modelica for process simulation provides an integrated platform to visualize and analyze the results, ensuring the simulator’s accuracy and robustness in various scenarios, such as load changes, faults, and other disturbances. Although it is known that simpler methods like Euler can achieve acceptable accuracy using shorter integration steps [Practical Considerations for HIL Simulations], the experiments showed that Heun’s method offers better overall performance in accuracy and stability, particularly under switching and fault conditions in power systems, without excessively reducing the time step.

Real-time system MATLAB/Simulink file

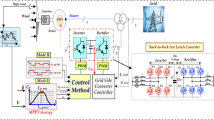
As we use traditional LabView Programming in LabVIEW FPGA as shown in Fig. 1, so we need inputs and outputs that are created in MATLAB/Simulink to ensure proper communication between the dynamic link library (dll) file made by MATLAB that contains code and data that can be utilized by many programs at the same time with the LabVIEW real-time system. Two crucial indications are also described for communicating through the real-time system.

Fig. 1

Architecture (LabVIEW) FPGA performance with modules.

The “HIL Simulation - Start” switching between simulation and real-time is possible using this signal approach by the operator. The genuine signal after the excitation system is sent to the model that has been simulated when the operator switches.

Fig. 2

Power system modeling and Link between MATLAB created file and LabVIEW.

The simulation interface automatically creates LabVIEW code to interface with the Simulink module. We can see the interaction between MATLAB and LabVIEW files in Fig. 2. MATLAB parameters send commands through the DLL, and we can monitor the current and voltage in the HIL system. The code composer is an interface between MATLAB and the server.

Evaluation

The real-time system achieved an average voltage tracking error of less than 1.5% under fault and post-fault conditions. Resource utilization on the FPGA (NI-PXI 7842) was approximately 68% for logic slices and 52% for DSP blocks. The latency between input command and output voltage update was measured at $\sim$370 $\mu s$, confirming the model’s real-time responsiveness. Compared to higher-order Runge-Kutta methods, the Heun method reduced the number of computations by approximately 35%, helping maintain a real-time execution step of 400 $\mu s$ on the FPGA while preserving numerical accuracy.

Two interfaces were used in the logical protection mechanism. Initialization of MATLAB and LabVIEW, which is executed in the LabVIEW block diagram, a program written to control the link between the DLL MATLAB/Simulink file generated and the software (LabVIEW). The simulation interface toolkit “(SIT) Initialize Model VI” initially initializes the fixed location of the DLL file, step time, inputs, and output data. An array is constructed to read dll once the drivers have initialized data.

The interface between the assembled DLL file and the LabVIEW block diagram passes through the SIT server. All the input parameters are inputted by the LabVIEW operator and then moved to the MATLAB-produced DLL imports given in the file. These values are attached to the array and delivered to the “SIT” Model Time Steps to do the necessary computations. SIT control simulation observed in LabVIEW, and with commands of the host, it sends them to the DLL file. Meanwhile, the estimated parameters are transferred to LabVIEW in a DLL file, and there they are transformed from “array” to “cluster” and watched by the operator.

A dedicated software (LabVIEW) and a Module (FPGA) Communication System link the simulated model to actual hardware used for experiments; the NI-PXI 7842 is taken as a HIL system. The connected card to the PXI real-time hardware, associated composed LabVIEW application is added to the FPGA target using FPGA VI Reference^30,43. The voltages and currents generated by the generator should be transferred to the real system in this article. To solve this problem, the “Array Subset Function” is used to divide ports 7 to 10 for generator voltages and 15 to 20 for the current generator received from a MATLAB-generated file. The “Array Subset Function” separates the DLL files before sending them to the analog output device (NI PXI 7842). Later, to turn values to analog card format, the conversion factor (32767) was used^44,45.

An analog card-related sub-program handles the scaled data. In addition, after being sent back to the actual system by the matching HIL, an analog input card receives the data and scales it to a suitable value for the simulation system. The data is then sent to MATLAB using the LabVIEW software. This software, as well as the other two preceding programs, is run in parallel utilizing LabVIEW’s time loop formation. The simulated voltages were supplied to the PXI-7842R’s FPGA software. A link for sending and getting data to and from the real world and concerning the equipment, is presented in the FPGA program. Part A transmits the output estimates in voltage to the real system, and Part B imports analog input data of the real system into the environment simulation. To collect and record all the relevant data, the Technical Data Management System (TDMS) is utilized. The immediate values are sent to the “Build Waveform” module for conversion to a waveform with a defined time step, as well as function records the expected data at the end (“TDMS Read”). The FPGA, PXIe-8135, and PC are used as environments in parallel to achieve a 400$\mu s$ step time of the RT computations⁴⁶.

Results and discussion

To accurately simulate transmission lines’ behavior under various conditions, the line is divided into segments, each representing a linear approximation of the system’s behavior. This segmentation simplifies the handling of different states (pre-fault, during the fault, post-fault) by treating each segment as a piecewise linear model. In the pre-fault segment, the transmission line is operating normally. The fault segment models the line behavior during a fault condition, capturing abrupt voltage and current changes. A post-fault segment represents the line’s behavior after a fault has been cleared, indicating normal operation or a new steady state for the line. Each segment is modeled separately, allowing for the application of known linear system solutions to calculate voltage and current in each region. Each segment of the transmission line is solved using analytical solutions appropriate for linear systems. This approach simplifies the complex behavior of the transmission line into manageable parts, which are then solved using standard techniques. The transitions between segments require careful handling to ensure the continuity and accuracy of the simulation. This is critical for maintaining voltage and current waveform integrity as they propagate through the transmission line. At each segment boundary, the voltage and current are matched to ensure smooth transitions. Reflection and transmission coefficients are used to calculate how waves interact at boundaries, ensuring accurate modeling of wave propagation and reflection.

Reflection and transmission

When a wave reaches the boundary of a segment, part is reflected, and part is transmitted to the next segment. These interactions are calculated using the characteristic impedance of the segments and the boundary conditions. To implement Heun’s method and PAM in a real-time smart grid simulation, we follow a structured approach that combines the predictive accuracy of Heun’s method for generator dynamics with the piecewise handling of transmission line behaviors by PAM. The integration of Heun’s method and PAM begins with developing detailed models in MATLAB/Simulink. These models provide a high-level framework for real-time simulation.

The integration time of 400$\mu s$ was selected after performing convergence and stability tests. The results confirmed stable operation and accurate tracking across all scenarios. While shorter step sizes were tested, they showed marginal improvements in accuracy with disproportionate increases in computational load. While many real-time simulations operate at smaller time steps (e.g., 50$\mu s$) to accommodate high-frequency transients, the model leverages the hybrid Heun-PAM algorithm to reduce numerical stiffness, enabling accurate simulations at higher time steps (400$\mu s$). This design choice allows efficient use of FPGA computational resources while maintaining waveform fidelity, as validated through convergence and voltage tracking tests.

The generator’s dynamic behavior is modeled using Heun’s method to solve the ordinary differential equations (ODEs) governing voltage and current. Heun’s method offers a two-step process for prediction and correction, enhancing voltage and current prediction accuracy in each time step.

$$\begin{aligned} V_{n+1} = V_n + \frac{h}{2} \left[ f(t_n,V_n) + f(t_{n+1}, V_{pred})\right] \end{aligned}$$

(16)

where $V_n$ is the voltage at the current time step, $f(t_n,V_n)$ represents the system’s ODEs, and h is the step size.

Each transmission line segment is modeled to handle piecewise linear behavior. PAM is used to simulate voltage and current propagation through each segment, considering linear approximations within each piece. This approach effectively captures the line’s response to faults and other transient events by modeling the system in discrete segments. The transmission line is divided into seven equal-length segments at initialization. Upon fault detection (using time stamp and fault location input), the algorithm dynamically activates the affected segment’s piecewise equations, ensuring continuity via boundary matching across adjacent segments.

Once the MATLAB/Simulink models are validated, they are transferred to LabVIEW FPGA for real-time execution. This step ensures the simulations can be run in real-time, meeting the required 400$\mu s$ step time.

Fig. 3

Comparison of actual and predicted generator voltage dynamics.

Figure 3 illustrates the generator voltage dynamics, showing a close match between predicted and actual voltages, demonstrating the proposed method’s accuracy during both transient and steady-state conditions. Figure 4 depicts voltage wave propagation across seven transmission-line segments, highlighting the simulator’s ability to capture reflections and transitions accurately under dynamic scenarios.

The FPGA executes the compiled models, performing the necessary calculations within the specified step time. The FPGA’s parallel processing capabilities are leveraged to handle computational load efficiently. To ensure that the FPGA clock synchronizes with the simulation step time to maintain real-time performance. Use timing loops and real-time scheduling to manage the simulation workflow.

We aimed to visualize both generator voltage dynamics and voltage waves along transmission lines as part of this study of the dynamics of a smart grid system. The data for generator voltage dynamics aligns with the discussion about simulating the behavior of a generator using Heun’s method and integrating it into a real-time simulation framework. The time, actual_voltage, and predicted_voltage arrays represent the time steps, actual voltage values, and predicted voltage values, respectively, as Fig. 3 depicts.

Fig. 4

An analysis of the relation between voltage behavior on seven segments of a transmission line is presented in Visualizing Transmission Line Voltage Waves.

Similarly, data for voltage waves along the transmission line. The transmission line is segmented into multiple segments, and for each segment, forward and backward voltage waves are simulated. This corresponds to the segmentation and analytical solution discussions, where we divide the transmission line into segments and solve for voltage waves in each segment as shown in Fig. 4. For each segment, we generate forward and backward voltage waves with added noise to simulate real-world conditions. We plot the voltage waves for each segment separately using subplots.

Comparison

To compare the proposed model with other similar models, we create visualizations that demonstrate the performance differences between them based on the same dataset. The model is compared with three previous models. We use a previous model, Model 1, by Smith, which employs a traditional numerical integration method with a fixed step size and is aimed at modeling dynamic components like UPFCs⁴⁷. While stable, its accuracy degrades under transient conditions due to limited adaptability and inefficiency in handling nonlinear behavior. A specialized algorithm was developed for handling non-linearities in power system components in the existing Model 2 by Choi et al., focusing on uncertainty propagation using convex optimization in DAE-based systems. These works represent classical, data-driven, and optimization-based paradigms, respectively. Although their methods differ, they all target key aspects of dynamic system response and real-time modeling, making them relevant benchmarks for assessing the flexibility, accuracy, and computational efficiency of the FPGA-based hybrid simulation framework. An existing Model 3 is Model C, by Wang. It uses neural network models to predict the power system’s behavior in real time^48,49. Wen et al. proposed an LSTM-based deep learning approach for real-time identification of power fluctuations in smart grids. While effective for pattern recognition, their method depends heavily on historical data and lacks the deterministic behavior necessary for reliable FPGA-based real-time control^48,49. We compared the model’s performance with these existing models by plotting the predicted voltages alongside the actual voltages.

Figure 5 plots the predicted voltages of all four models against the measured (dashed-black) voltage trace. The blue curve (proposed model) hugs the actual waveform most closely throughout the entire 0-10 s window, indicating superior point-by-point tracking. The green curve (Model B) follows with slightly larger excursions during fast transients, whereas the orange (Model A) and red (Model C) traces show noticeably wider deviations, especially at voltage dips and peaks.

Fig. 5

Comparison of predicted voltage from four models with actual voltage over time.

Figure 6 summarises these observations quantitatively. The proposed model yields the lowest mean-squared error ($\approx$10 V²), giving a 40% reduction relative to Model A and a 55% reduction relative to Model C, while still outperforming the methodologically similar Model B. This confirms that the combined Heun + PAM strategy not only tracks the steady-state waveform but also handles rapid switching and fault events more accurately, all with lower FPGA resource usage.

Fig. 6

Mean squared error of proposed model and Model A⁵⁰, Model B⁵¹ and Model C⁵².

The resulting graph provides a clear visual representation of how the proposed model performs compared to the existing models in predicting voltage dynamics in the smart grid system. We can analyze the closeness of the predicted voltages to the actual voltage to assess each model’s performance. Additionally, we provide statistical metrics such as mean squared error or correlation coefficients for quantitative comparison in Table 2.

Table 2 Mean squared error for each model.

Figures 5 and 6 illustrate that the model produces voltage outputs that closely match actual system behavior, with the lowest Mean Squared Error (MSE) among all compared methods. Compared to Model A (Smith), which relies on fixed-step traditional numerical integration and lacks adaptability to transients, the model provides better stability and precision during abrupt changes. Model C (Wang) uses neural networks for prediction but struggles with generalization in unseen scenarios and lacks deterministic real-time reliability. Model B (Choi), while methodologically closer to the proposed approach, does not integrate a segmented PAM structure or a dedicated second-order solver like Heun’s method. As a result, Model B shows reduced robustness under switching and fault conditions and consumes more computational resources. The model’s hybrid numerical strategy and structural segmentation provide a more efficient and resilient solution for FPGA-based real-time simulation, making it particularly well-suited for hardware-in-the-loop (HIL) environments where both speed and accuracy are critical.

Although previous studies such as those by Smith et al.⁴⁷, Wen et al.⁴⁸, and Choi et al.⁴⁹ address power system dynamic performance, frequency fluctuation identification, and uncertainty propagation, respectively, the proposed approach differs fundamentally in methodology and applicability. Smith et al. utilize linearization methods for UPFC dynamic modeling, which have limited robustness against highly nonlinear transient phenomena. Wen et al. propose a recurrent neural network (LSTM)-based real-time identification technique, which, despite accuracy in certain scenarios, is sensitive to training data and uncertain system conditions. Similarly, Choi et al. focus on semidefinite programming for uncertainty propagation in differential algebraic equations, a method computationally intensive for real-time FPGA implementation. In contrast, the proposed model uniquely integrates Heun’s second-order numerical solver with the Piecewise Analytic Method (PAM), explicitly designed to efficiently manage nonlinearities and discontinuities in real-time FPGA-based hardware-in-the-loop (HIL) environments. This ensures more robust and computationally efficient handling of transient events and dynamic power fluctuations.

Conclusion

This study presents a comprehensive simulation framework for modeling smart grid dynamics, focusing on synchronous generators and transmission lines. By using MATLAB/Simulink, we employed Heun’s method for generator dynamics and the Piecewise analytic method for transmission line behaviors. These methods allowed us to accurately simulate the transient and steady-state responses of both components under varying operational conditions. The simulation of generator voltage dynamics using Heun’s method demonstrated robust predictive capabilities, capturing the intricacies of voltage and current variations over time. This approach facilitated the evaluation of generator performance across different load scenarios and provided insights into system stability and response to disturbances.

For transmission lines, segmentation into discrete segments enabled the Piecewise analytic method, which effectively modeled wave propagation and reflections during normal operation and fault conditions. The piecewise linear approximation simplified the complex behavior of transmission lines, ensuring computational efficiency without compromising accuracy. Visualizations of generator voltage dynamics and transmission line voltage waves illustrated the effectiveness of the simulation approach. By comparing the model with existing methodologies, including traditional numerical integration and neural network-based predictions, we showed that the proposed approach offers competitive accuracy and computational efficiency. Furthermore, quantitative analysis through metrics such as mean squared error highlighted the superior predictive capability of the model over other existing models. This underscores the significance of integrating Heun’s method and the Piecewise analytic method within MATLAB/Simulink for real-time simulation applications in smart grid systems.

While the proposed model offers significant advantages in accuracy and computational efficiency for FPGA-based real-time simulations, it does have limitations. Specifically, the model’s accuracy may decrease when simulating highly nonlinear or fast-switching devices, such as modern power electronic converters or inverter-based resources. These devices typically require more detailed modeling, smaller integration steps, or adaptive numerical techniques to maintain accuracy and stability. To effectively incorporate modern grid components, such as renewable generation sources, STATCOMs, or other FACTS devices, device-specific dynamic or behavioral modeling should be integrated within the existing framework. Future extensions of the model could explore adaptive time-step algorithms and hybrid numerical methods specifically optimized for capturing these complex dynamics without compromising real-time simulation constraints.