Introduction

DTH hammer are extensively utilized in mining and tunneling operations for their efficiency in fracturing medium-to-hard rock’s with poor drillability1. Current drilling practices predominantly rely on pneumatic rock drills combined with blasting techniques2, where optimizing energy transfer and rock-breaking efficiency remains a critical challenge. Previous studies have systematically investigated the dynamics of percussive drilling. For instance, Lundberg analyzed energy transfer mechanisms in impact systems, emphasizing the influence of kinetic energy and impact power on drilling efficiency. Wyering et al. developed rock strength estimation methods to enhance drilling speed, correlating mechanical properties with drillability indices3. Yan et al. further explored the coupled effects of thermal, hydraulic, mechanical, and chemical (THMC) fields on rock damage evolution4, while Qu et al. highlighted the significance of bit-rock interfacial mechanics in assessing drillability5. Zhang et al. established a wellbore instability model considering bedding planes and multiple natural fractures, combining the transverse isotropic stress model with the multiple weak surface strength criterion (Jaeger weak surface criterion extension). A weak surface superposition method is proposed to analyze the coupling effect of natural cracks on collapse pressure6. In addition, Zhang et al. established a transverse isotropic wellbore stress model based on the Lekhnitskii-Amadel solution. Researchers compared four intensity criteria: Mohr-Coulomb (MC), Mogi-Coulomb (MGC), modified Lade (ML), and modified Wiebols-Cook (MWC). It was concluded that the collapse pressure is sensitive to the anisotropy of the elastic modulus7,8. Gao et al.9 carried out the research on the fracture characteristics and mine pressure control effect of “surface fracturing-horizontal fracture surface” on high-level thick and hard rock strata (THS) systematically. Whereafter, Gao et al.10 derived the formula of bending strain energy after the equivalent thickness of rock strata decreased, proving that the fracture step distance decreased after fracturing, and the energy release intensity decreased significantly.

Recent advancements in numerical modeling have enabled deeper insights into drill-rock interactions. Wang et al. established a finite element model for pneumatic down-the-hole (DTH) hammers using ABAQUS, evaluating drilling efficiency under varying operational parameters11. However, their model neglected spatial configurations between the drill and rock, limiting its predictive accuracy. Similarly, Bo et al. investigated the mechanical structure of DTH drills but focused narrowly on energy transfer using ANSYS, omitting dynamic fracture mechanics12. Experimental approaches, such as split-Hopkinson pressure bar tests by Xie et al.13, revealed correlations between drilling pressure, rotational speed, and rock fragmentation rates. Meanwhile, Feng et al. and Xu et al. employed customized rotary-cutting devices and cylindrical drill bit models to analyze stress distributions, though their simplified geometries introduced uncertainties in force predictions14,15. Zhang et al. found that the three shape function-corrected MC criteria (MCWW, MCYL, and MCMN) can all predict the true triaxial rock strength with high accuracy (R2 > 0.9), among which the elliptical correction (MCWW) has the best overall performance. The parameter determination method based on conventional triaxial tests is reliable, providing a practical solution for engineering applications16. Notably, Wu et al. addressed limitations of traditional PDC bits in complex strata by developing a dynamic Drucker-Prager (D-P) constitutive model but excluded critical interactions between hybrid bit bodies and rocks, leading to force estimation errors17. Fan et al.18 incorporated the semipermeable characteristics of the wellbore wall and the lateral anisotropy of shale into a unified analytical framework simultaneously. Through the integral transformation-load decomposition method in the Laplace domain, the closed solutions of three load modes were given, and the time-domain responses are obtained by Stehfest inversion, supplemented by COMSOL finite element verification.

Despite these efforts, key gaps persist: (1) Most models oversimplify drill-rock spatial interactions or initial rock surface conditions; (2) The combined effects of structural parameters (e.g., bit geometry, piston dynamics) and operational variables (e.g., impact velocity, rotational speed) remain underexplored; (3) Existing constitutive models often fail to capture high-strain-rate rock behavior under percussive loading. To address these limitations, this study proposes a comprehensive numerical model integrating a bit-piston-rock system with pre-existing boreholes, employing the Holmquist-Johnson-Cook (HJC) constitutive criterion to simulate rock fracture under dynamic loading. Using ANSYS LS-DYNA with APDL scripting, we systematically evaluate impact forces across diverse working conditions, structural configurations, and initial rock geometries. The results provide actionable insights for optimizing drill design and operational parameters, bridging the gap between theoretical simulations and field applications in challenging rock environments.

Rock drilling impact dynamics and rock material constitutive equations

Analysis of the impact dynamics equation for rock drilling

In order to describe the transient dynamic behavior during rock drilling operations using a DTH hammer, a contact dynamic model between the drill bit (tungsten carbide inserts) and the rock surface is developed based on D’Alembert’s principle11,12,19,21 and the finite element method (FEM). This model facilitates the definition of the interaction between the piston of the DTH hammer and the rock target, including appropriate impact boundary conditions.

The general dynamic equilibrium equation governing the drilling system22,23 can be expressed as:

$$M\ddot {U}+C_{1}\dot {U}+KU={F_t}+{f_t}$$
(1)

where: M, C1, and K represent the mass, damping, and stiffness matrices of the system, respectively; U, \(\dot {U}\) and \(\ddot {U}\) denote the displacement, velocity, and acceleration vectors; \({F_t}\) is the contact force vector between the drill bit and the rock; \({f_t}\) denotes the applied drilling load.

This formulation captures the coupled mechanical interaction of the bit-rock interface, accounting for material inertia, damping effects, and elastic-plastic deformation under high-frequency impact loading. By solving this dynamic system, the time-varying stress and displacement distributions at the contact interface can be obtained, which are essential for understanding the rock fragmentation mechanism and optimizing the structural design of the impactor and its operating parameters.

Constitutive model of rock materials

In the context of rock drilling using DTH hammer, accurate modeling of the rock material’s mechanical response under high strain rate and multi-axial stress conditions is critical for predicting drilling performance and bit-rock interaction behavior. Due to the complex, nonlinear, and heterogeneous nature of rock, its deformation and failure characteristics24,25 cannot be adequately described using linear elastic models. Instead, a rate-dependent elasto-plastic constitutive model is adopted to reflect the dynamic response of rock under percussive loading. To accurately simulate the mechanical behavior of rock during the high-frequency impact process induced by a DTH hammer, it is essential to incorporate a suitable constitutive model that captures both the elastic and plastic responses of the rock. In this study, a modified JHC constitutive model is adopted to describe the dynamic behavior of brittle rock under high strain rates, multiple impacts, and complex stress states.

The JHC model integrates the effects of pressure hardening, strain rate sensitivity, and damage evolution, making it suitable for simulating rock fragmentation under dynamic loading. The yield strength of the material is expressed as:

$${\sigma ^*}=\left( {A\left( {1 - D} \right)+B \cdot {P^*}} \right)\left( {1+C\ln {{\dot {\varepsilon }}^*}} \right)$$
(2)

where: \({\sigma ^*}\) is the normalized equivalent stress; A is the normalized cohesive strength; B is the pressure hardening coefficient; \({P^*}\) is the normalized pressure; C is the strain rate coefficient; \({\dot {\varepsilon }^*}\) is the normalized strain rate; D is the damage parameter (ranging from 0 to 1), which evolves as a function of plastic strain and hydrostatic pressure.

The damage evolution in the model accounts for microcrack initiation, growth, and coalescence, which are essential for capturing the rock failure process under impact loading. When the accumulated plastic strain reaches a critical threshold, the damage variable D increases rapidly, leading to a reduction in strength and stiffness, and eventually, rock fragmentation.

In addition, the hydrostatic pressure component is incorporated into the yield surface to reflect the confining pressure effect, which significantly influences the brittle-to-ductile transition in rock behavior. The stress–strain response predicted by the JHC model is validated through numerical simulations and experimental calibration using granite and sandstone specimens, providing a reliable foundation for analyzing rock breakage efficiency in different working conditions. When employing the HJC criterion to model rock material behavior, the dominant failure mode is compressive damage. In the numerical solver, this is implemented by introducing a failure criterion through the keyword *MAT_ADD_EROSION in the material definition of the K file. The material parameters for the rock model are adopted from references26,27,28, as listed in Table 1.

Table 1 Material parameters of rock based on the HJC constitutive model.
Full size table

In rock fracture analysis, a “damage factor” D is typically used to describe the failure and spalling behavior of rock materials29. This factor can be defined based on the variation of the elastic modulus before and after material damage. The stress–strain damage curve of rock material is illustrated in Fig. 1.

Fig. 1
figure 1

Stress–strain damage curve of rock material.

Full size image

The damage factor D is defined as follows:

$$D=1 - \frac{E^\prime}{E}=\left\{ \begin{gathered} 0 \quad (\varepsilon \leqslant \bar {\varepsilon }_{\text{f}}^{\text{p1}}) \hfill \\ 1 - \frac{\sigma }{\bar {\sigma }}\,(\varepsilon>\bar {\varepsilon }_{{\text{f}}}^{{{\text{p1}}}}) \hfill \\ \end{gathered} \right.$$
(3)

where: \(\varepsilon\) and \(\sigma\) denote the strain and stress of the rock, respectively, and \(\bar {\sigma }\)is the stress corresponding to the curve in the figure. E and \(E^{\prime}\)represent the elastic modulus of the rock before and after damage, respectively, and \(\bar {\varepsilon }_{{\text{f}}}^{{{\text{p1}}}}\) denotes the equivalent plastic strain after fracture.

Assuming the equivalent strain before and after rock fracture is used as the fracture criterion, the following relationship can be written:

$${\varepsilon ^{\text{p}}} \leqslant \bar {\varepsilon }_{{\text{f}}}^{{{\text{p1}}}}$$
(4)

where: \({\varepsilon ^{\text{p}}}\) is the equivalent plastic strain before fracture.

In Fig. 3, the segment OA corresponds to the elastic–plastic deformation stage of the rock. When the stress reaches the yield strength limit (point A), the rock begins to undergo damage and yield, and the corresponding stress is \({\sigma _{y0}}\), at which point the damage factor \(D=0\). When the equivalent plastic strain reaches \(\bar {\varepsilon }_{{\text{f}}}^{{{\text{p1}}}}\) after fracture, the total damage factor reaches \(D=1\), indicating complete rock failure. At this point, the corresponding element will be deleted from the computational domain, and the simulation will terminate accordingly.

Numerical modeling and assumptions of the DTH hammer system

Generally, the mechanical structure of a DTH hammer system includes components such as the drill bit, piston, guide sleeve, outer cylinder, air cylinder, valve seat, valve cover, spring, check valve, striking cap, and rear joint, as illustrated in Fig. 2. For the purpose of impact process analysis in rock drilling, the impact system is simplified to consist of the drill bit, piston, and rock. In this study, a three-dimensional (3D) structural model19 of the impact system of the Type 80 DTH hammer was established using Autodesk Inventor. The model was then imported into ANSYS for finite element meshing and preprocessing. Subsequently, LS-DYNA was employed to perform the numerical solution and postprocessing.

Fig. 2
figure 2

Mechanical structure schematic of the impactor–drill bit–rock simulation system. 1-Rock; 2-Drill bit; 3-Piston; 4-Guide Sleeve; 5-Outer Cylinder; 6-Air Cylinder; 7-Valve Seat; 8-Valve Cover;9-Valve Plate; 10-Spring; 11-O-ring; 12-Washer; 13-Check Valve; 14-Striking Cap; 15-Rear Joint.

Full size image

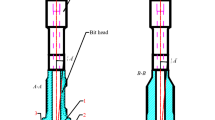
To facilitate numerical simulation, several simplifications and assumptions were made in the finite element modeling process, as referenced in11,17. Due to the significantly higher stiffness of the piston (made of 35CrMoVA29 and carbide buttons compared to the rock, both the piston and the drill bit (including buttons) were treated as continuous, homogeneous, and isotropic elastic materials. Furthermore, button wear was ignored, and the buttons were modeled as rigid bodies. The rock material was assumed to be a continuous, homogeneous, and isotropic elastic–plastic medium, with its mechanical behavior described by the HJC constitutive model. This model accommodates large deformation, high strain rate, and high-pressure conditions. The rock’s failure was defined in LS-DYNA using the keyword *MAT_ADD_EROSION, allowing for automatic deletion of failed elements to simulate the ejection of fragmented rock chips. Other assumptions include the omission of compressed air flow through the passage between the piston and drill bit, and neglecting thermal effects. To ensure continuous contact between the drill bit buttons and the rock surface and to counteract the rebound effect under impact force, an axial thrust force Fr was applied to the drill bit. Based on experimental and theoretical considerations30, this axial impact force was set at 9 kN. Figure 3 illustrate the schematic of the Type 80 DTH hammer system and its corresponding simplified 3D finite element model, the schematic of drill bits and rock (no impact piston), respectively. The element type was defined as Solid164 in ANSYS LS-DYNA using an eight-node hexahedral solid element specifically designed for explicit dynamic analysis (such as impact, explosion, collision, and other high-speed transient events). This type of element can choose two algorithms: the single-point integration algorithm and complete integration algorithm. The single-point integration and complete integration refered to the number of integration points used in Gaussian integration. The single-point integration algorithm was very effective for high strain rate simulation, which can save a lot of calculation time, but it requireed hourglass control. The solution process using the complete integration algorithm was slow and does’t cause the hourglass phenomenon. It is mainly used for materials with a large Poisson’s ratio. To enhance the computational efficiency, this manuscript adopted the single-point integration algorithm to calculate the stress-strain results. The contact surface between the drill bit and the rock was refined to ensure the effectiveness of contact between them. The model boundary was set as follows: fixed displacement constraints and non-reflection boundary condition constraints were applied to the bottom of the rock. The drill bit exerted rotational motion and drilling pressure. The impact piston was applied by an initial velocity along the axis.

Fig. 3
figure 3

Simplified 3D model of the drill bit (buttons)–impact piston–rock (with initial bore)) 1-ANSYS 19.2, available from: https://www.ansys.com/zh-cn/products/fluids/ansys-fluent; 2-AUTODESK INVENTOR 2023, avaliable from: https://www.autodesk.com.cn/products/inventor/overview?term=1-YEAR&tab=subscription. 1-drill bit; 2-column tooth H5(six evenly distibuted, φ14 mm*22 mm); 3-column tooth H1-H4(4-φ13 mm*19 mm); α-drill bit teeth distribution angle; γ-transition angle of rock initial hole modeling; Dhole-initial borehole top diameter (c) the schematic of drill bits and rock (no impact piston).

Full size image

Numerical results analysis of the DTH hammer

Verification and explanation of model accuracy

During the establishment of the analysis model, it was necessary to refine the units of some key contact areas to ensure the stability of the calculation results. The single-factor method was adopted, and the optimization of rock refinement size was selected as an example to prove the accuracy of the model. The initial conditions of the model size remained the same except for the detailed size of the rock. Specifically, the initial working conditions were a numerical model with initial bore hole, an axial impact force \({F_r}\) of 9 kN, a rotational speed \({n_r}\) of 15 rpm, and a piston impact velocity \({v_p}\) of 7.37 m·s−1. The bit configuration was modeled with a column tooth distribution angle α = 0°, transition angle of rock initial hole modeling γ = 21.48°, and an initial bore diameter Dhole=95 mm. By analyzing the above-mentioned different models and the maximum impact force between drill bit and the rock, as well as the number of rock model elements, the size of the rock refinement elements can be determined. The results were listed in Table 2. It can be known that when the refinement size was between 0.925*10−3 m and 1.25*10−3 m, the maximum impact force between drill bit and rock, Ft1max, was between 131.547 kN and 136.510 kN, and the relative change ratio was between 98.19% and 101.90%. Thus, it can be seen that the rock refinement size can be selected within the range of 0.925*10−3 m to 1.25*10−3 m, at which point the accuracy of the model was guaranteed. Taking into account the fine and uniform grid division at the contact points with the drill bit, and also considering the size of the model, the optimized refinement size was selected as 1*10−3 m finally. Thus, the model of drill bits had 213,122 elements and 40,364 nodes, the model of impact piston had 32,960 elements and 38,400 nodes, the model of rock had 451,328 elements and 460,256 nodes. As well as the entire model had 697,410 elements and 539,020 nodes.

Table 2 Model rationality explanation table taking the optimization of rock refinement element size as example with initial bore hole.
Full size table

Analysis of the rock-breaking process by the drill bit

To investigate the dynamic interaction between the drill bit and rock during the percussive drilling process, a numerical model was developed with initial operating conditions set as follows: an axial impact force \({F_r}\) of 9 kN, a rotational speed \({n_r}\) of 15 rpm, and a piston impact velocity \({v_p}\) of 7.37 m·s−1. The bit configuration was modeled with a column tooth distribution angle α = 0°, transition angle of rock initial hole modeling γ = 21.48°, and an initial bore diameter Dhole=95 mm. The stress evolution within the rock at various time points was analyzed to elucidate the rock-breaking mechanism.

Fig. 4
figure 4

Stress contour maps of the rock-bit contact process.

Full size image

As illustrated in Fig. 4, at t = 1.5 ms, the column teeth labeled H1 and H4 initially make contact with the rock surface. At this moment, the maximum von Mises equivalent stress reaches 386.32 MPa (Fig. 4a). Shortly thereafter, at t = 1.63 ms, the peak impact force attains its maximum value of 133.970 kN, indicating the moment of peak resistance during the impact phase. By t = 1.8 ms, all the column teeth are fully engaged with the rock. Localized damage in the rock elements is observed, marking the initiation of material failure as the bit begins to effectively penetrate and crush the rock surface. The maximum von Mises stress increases to 589.77 MPa at this stage (Fig. 4b). As the impact progresses further to t = 2.1 ms and t = 2.4 ms, continued interaction between the bit and rock surface results in an expanding damaged zone (Fig. 4c and d). The cyclic nature of the percussive impact facilitates progressive fragmentation of the rock, demonstrating the repeated failure and detachment of rock particles under sustained dynamic loading. This behavior underpins the efficient material removal mechanism inherent in DTH hammer. It should be particularly pointed out that rock is a typical strain rate-sensitive material. Under the extremely high strain rate of the impact load of the rock drill (much higher than the quasi-static test), the strength of the rock material will be significantly enhanced. Significant stress concentration occurs at impact points, crack tips, material defects or geometric discontinuities. The maximum stress reaching 801.4 Mpa occurs in a certain stress concentration area (such as impact contact points or microcrack initiation points), which is the result of the combined effect of local stress state, strain rate and initial low damage. It reflects the real physical processes under impact loads. The phenomenon observed in Fig. 4 is a typical manifestation of the HJC model accurately simulating the dynamic strength enhancement and progressive damage failure process of rock under impact loads, which is in line with the physical mechanism and model expectations and is not contradictory.

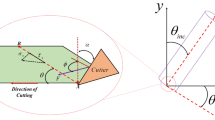
Analysis of maximum impact force under different drill bit teeth distribution angles α

The rock models without initial holes were analyzed under varying distribution angles α of the bit buttons. The maximum forces between the piston and the bit, as well as between the bit and the rock, were extracted for each configuration. The results are illustrated in Fig. 5.

Fig. 5
figure 5

Maximum impact force under different drill bit teeth distribution angles α for models without initial bore holes.

Full size image

When the distribution angle α of the bit buttons ranged from 0° to 177.5°, the maximum impact force Ft1max between the bit and the rock varied between 200.65 kN and 258.97 kN. The ratio of the maximum to the minimum impact force reached 1.291, indicating a significant influence of the button arrangement on drilling performance. A polynomial fitting was performed on the maximum impact force values, yielding a regression with a high correlation coefficient of 98.69% and a relative error range of −9.40% to 8.23%.

$$\begin{gathered} {F_{{\text{t1max}}}}{\text{=217}}.{\text{151+7}}.{\text{5153}}\alpha - 0.{\text{653}}{\alpha ^2}+0.0{\text{245}}{\alpha ^3}{\text{-4}}.{\text{87*1}}{{\text{0}}^{ - 4}}{\alpha ^4}+ \hfill \\ {\text{5}}.{\text{52*1}}{{\text{0}}^{ - 6}}{\alpha ^5} - {\text{3}}.{\text{6}}0{\text{*1}}{{\text{0}}^{ - 8}}{\alpha ^6}+{\text{1}}.{\text{27*1}}{{\text{0}}^{ - 10}}{\alpha ^7} - {\text{1}}.{\text{96*1}}{{\text{0}}^{ - 13}}{\alpha ^8}+{\text{4}}.{\text{1}}0{\text{*1}}{{\text{0}}^{ - 17}}{\alpha ^9} \hfill \\ \end{gathered}$$
(5)

The variation in button distribution angle α reflects the impact of cutting geometry on drilling efficiency. When α is 25°, the impact forces experienced by the bit buttons during the rock-breaking process are minimized, resulting in the most effective rock fragmentation. This configuration is advantageous for reducing the impact stress on both the bit and the buttons, minimizing button wear, and enhancing the overall drilling rate.

Impact force under different piston impact velocities v p

In this analysis, the axial pressure Fr was set to 9 kN, the bit rotational speed nr to 15 rpm, and the button distribution angle α to 0°. The rock was modeled without an initial borehole. For each piston impact velocity vp - which corresponds to a specific impact energy E0 - the maximum impact force between the bit and the rock was extracted, as shown in Fig. 6.

Fig. 6
figure 6

Impact force under different piston impact velocities vp without an initial borehole.

Full size image

The simulation results indicate that when vp ranges from 2.86 m/s to 4.66 m/s, the rock undergoes only elastic deformation without material failure, suggesting insufficient energy transfer for effective rock breakage. As the piston velocity increases beyond this threshold, both rock fracturing and impact force intensify markedly. Notably, a peak in impact force is observed within the range of vp = 5.71 m/s to 8.72 m/s. Within this range, the impact force reaches its maximum values, with three representative velocities − 7.19 m/s, 7.37 m/s, and 7.73 m/s - yielding peak impact forces of approximately 200 kN. These values are relatively stable, indicating an optimal range for energy transfer where rock-breaking efficiency is maximized without significantly increasing mechanical load on the system. The maximum impact force was fitted using a polynomial regression function Ft1max, achieving a high correlation coefficient of 99.87%.

$${F_{{\text{t1max}}}}={\text{1}}0.{\text{371}}+\frac{{{\text{19}}0.{\text{298}}}}{{{\text{1}}+{\text{1}}{0^{{\text{3}}.{\text{584}}}}^*}{{^{{\text{}}}}{{^{(}}^{{\text{4}}.{\text{972}} - }}{{^{{{v_{\text{p}}}}}}^)}}}$$
(6)

The relative error within the range of vp =5.214 m/s to 8.725 m/s was found to be between − 7.46% and 4.34%, demonstrating high predictive accuracy. From a mechanical perspective, considering the force response of both the piston and the drill rod during operation, and in order to reduce the mechanical dimensions of the drill rod and piston assembly, it is recommended that the piston impact velocity be set to one of the following values: 7.19 m/s, 7.37 m/s, or 7.73 m/s. Under these conditions, the corresponding impact energies E0 are 82.65 J, 87.00 J, and 95.70 J, respectively. These settings not only ensure sufficient energy delivery for rock fragmentation but also contribute to prolonging the service life of drilling components by maintaining a balanced dynamic load.

Analysis of impact force under different rotary speeds n r

Rotary speed is a critical parameter in evaluating drilling performance and the efficiency of rock penetration during percussive drilling. In this analysis, the piston impact velocity was set to vp=7.37 m/s, axial thrust to Fr=9 kN, and the bit button arrangement angle to α = 0°. A model without a pre-existing borehole was used to simulate the rock–bit interaction under various rotary speeds. The maximum impact force between the bit and the rock was extracted over time for each condition.

Fig. 7
figure 7

Distribution of maximum impact force under different rotary speeds nr for the model without an initial borehole.

Full size image

As shown in Fig. 7, the maximum impact force ranged from 198.84 kN to 199.59 kN when the rotary speed nr varied between 150 and 250 rpm. Within this range, the fluctuation of impact force was relatively minor, with a peak-to-valley ratio of 1.137. However, as nr continued to increase beyond this range, a noticeable decrease in impact force was observed. In particular, when nr exceeded 1000 rpm, the decline became more significant. This trend is attributed to the enhanced shear and scraping effects exerted by the bit at higher rotary speeds, which facilitates rock fragmentation and thus reduces the peak impact force required per strike. Nonetheless, excessively high rotary speeds may impose structural and dynamic limitations on the drill rod system. Increased rotary motion can result in elevated lateral vibrations and reduce the effective impact energy transferred to the rock, especially if the drill rod lacks sufficient stiffness. Therefore, while higher nr values may enhance rock breakage efficiency through cutting, they should be optimized within mechanical constraints to avoid diminishing returns or structural failures. A polynomial fitting was applied to the maximum impact force data, yielding a regression function with a correlation coefficient of 90.66%.

$${F_{{\text{t1max}}}}={\text{177}}.0{\text{78}}+\frac{{{\text{24}}.{\text{189}}}}{{{\text{1}}+{\text{1}}{0^{ - 0.00{\text{263}}*}}{{^{(}}^{{\text{1176}}.{\text{46}} - }}{{^{n}}^{_{{\text{r}}})}}}}$$
(7)

The relative error for rotary speeds between 0 and 1900 rpm remained within the range of −0.97% to 3.62%, indicating satisfactory model accuracy for predictive analysis.

Maximum impact force under different transition angles γ of the initial borehole

To investigate the influence of the transition angle in the initial borehole on drilling performance, numerical simulations were conducted using a rock model with an initial borehole top diameter Dhole=95 mm. The transition angle γ, defined as the angle between the borehole sidewall and the adjacent rock surface, was varied within the range of 20.9° to 22.1°. The maximum impact force between the piston and the bit, as well as between the bit and the rock, was extracted for analysis, with results illustrated in Fig. 8.

Fig. 8
figure 8

Maximum impact force under the transition angle γ for different rock initial pore modeling.

Full size image

The maximum impact force Ft1max experienced between the bit and the rock varied between 82.608 kN and 133.970 kN, yielding a peak-to-valley ratio of 1.662. A polynomial regression was applied to fit the relationship between the maximum impact force and the transition angle γ, resulting in a high coefficient of determination (R2 = 98.04%).

$${F_{{\text{t1max}}}}= - {\text{27919}}.{\text{359}}+{\text{28}}0{\text{55}}.{\text{2}}0{\text{4}}*\sin \left[ {\frac{{\pi *(\gamma - {\text{1}}00{\text{3}}.{\text{743}})}}{{{\text{33}}.{\text{613}}}}} \right]$$
(8)

The relative error of the fitted curve within the γ range of 20.9° to 22.1° was confined to −2.72% to 1.96%, indicating excellent predictive accuracy. These findings suggest that even slight changes in the borehole transition angle can lead to significant variations in impact force. A more gradual transition (smaller γ) may lead to smoother energy transmission and lower peak loads, while sharper transitions may result in stress concentration zones that increase the drilling resistance. The maximum impact force first increases and then decreases within the given transition angle range. This is mainly because at the initial stage of the increase in the transition angle, stress concentration dominates, causing the maximum impact force to rise. When γ started to increase from 20.9°, the geometric abrupt change at the edge of the borehole intensifies (the angle between the side wall and the rock face becomes steeper). Stress waves were reflected and superimposed at the abrupt interface, forming a local high-stress area, which significantly increased the penetration resistance of the drill bit. When γ increased further, the impact force decreased instead. The main reason was that the impact energy was in a state dominated by dissipation. When γ exceeds the critical value (approximately 21.48°), the overly steep transition zone caused. The contact area between the drill bit and the rock decreased, causing stress waves to scatter at sharp angles rather than be effectively transmitted. At this point, the resistance gain generated by stress concentration was overridden by the force attenuation caused by energy dissipation, and the impact force then decreased. Hence, optimizing the borehole geometry is crucial for enhancing rock fragmentation efficiency and reducing tool wear in percussive drilling operations.

Conclusions

An impact force analysis model for a pneumatic hammer, which includes the piston, drill bit, and rock (considering both cases with and without initial pore modeling), was established using APDL. The model was used to analyze the failure characteristics of rock materials under impact. The distribution of the maximum impact force under various impact motion parameters, different tooth column distribution angles, and transition angles of rock initial pore modeling was examined. The numerical solutions for the maximum impact force were fitted to different curves and equations, followed by a relative error analysis. The influence of different factors on the maximum and minimum values of the impact force was ranked in the following order of significance: transition angle of the rock initial pore modeling, drill bit tooth column distribution angle, and rotational speed. The results indicate that when the initial rock surface is relatively smooth, the maximum impact force reaches a minimum value of 200.65 kN under the conditions where the tooth column distribution angle α0 of the drill bit is 25°, the rotational speed is 15 rpm, and the piston impact velocity is 7.37 m/s (with an impact energy of 87 J). This angle can be considered as the baseline for the structural arrangement of the drill bit tooth column.