Introduction

As shield tunnel engineering progresses toward ultra-large diameters, ultra-shallow burial depths, and ultra-soft soil conditions1,2,3,4, the mechanical performance degradation of segmental linings under complex geological and loading environments has become increasingly pronounced. Investigations have identified the primary causes of segment damage to include ground settlement and segment uplift caused by uneven simultaneous grouting5,6,7, poor assembly quality, material aging, and environmental erosion8,9,10. For example, in the Zhuhai tunnel project, segment uplift in shallow overburden zones reached up to 50 mm, and fluctuations in grouting pressure significantly influenced repair effectiveness. In one metro section, tunnel uplift and segmental ring surface misalignment resulted in a damage rate as high as 30%11,12. Recent studies on segment failure mechanisms13,14,15,16 have led to the adoption of various maintenance strategies, such as grouting reinforcement17,18,19,20, channel steel ring reinforcement21,22,23, and corrugated steel plate reinforcement24,25,26. Existing grouting reinforcement methods mitigate deformation by filling ground voids and enhancing the interaction between surrounding rock and segments27,28,29. These methods are primarily classified as simultaneous30 or secondary grouting31,32,33. Wang and Wang34 addressed issues of water inflow and collapse in tunnels with water-rich, weak surrounding rock, significantly improving soil stability through deep-hole grouting technology. Based on equivalent porosity theory, Ye et al.35 derived formulas for slurry diffusion radius and segmental pressure, demonstrating that grouting effectiveness in the Pearl River area is influenced by multiple parameters. Zhang et al.36 proposed a grouting volume deformation method based on numerical simulation. Practical validation confirmed its feasibility and demonstrated that grouting effectively controls tunnel convergence. Chen et al.37 applied paste grouting to reinforce water-rich gravelly formations. The experimental results confirmed its high adaptability. Building on previous research, Ye et al.38 proposed a unified theoretical model for post-lining grouting slurry diffusion. This model includes multiple stages: filling, permeation, compaction, and fracturing. Tang et al.39 conducted orthogonal experiments on shield tunneling beneath existing masonry structures. He found that deep-hole grouting within the tunnel effectively reinforced the ground while minimizing disturbances to adjacent masonry. Full-face grouting yielded the best results. The radial reinforcement radius should not exceed 5 m, and the reinforcement range before and after structures should be limited to 1.5 times the tunnel diameter.

Existing studies have primarily focused on post-lining grouting techniques and their reinforcement effects behind boreholes in shield tunnels, while largely neglecting grouting reinforcement directly targeting the tunnel segments. This study proposes a structural reinforcement technique using borehole permeation grouting to address damage repair in reinforced concrete segmental linings. Radial grouting channels were drilled through segment cracks, and a modified epoxy resin grout was employed to achieve directional penetration and uniform crack filling. To systematically investigate the mechanical recovery mechanism of damaged segments through grouting reinforcement, a full-scale, two-point symmetrical loading test was conducted in accordance with GB/T 50152-2012 (Standard for Test Methods of Concrete Structures). Two comparative test groups were established: a pre-cracked control group and a grouting-repaired group. Monitoring mid-span displacement–load curves, concrete strain distributions, and crack propagation paths yielded quantitative data for optimizing grouting parameters and evaluating repair performance in shield tunnel segments. The study also addresses a gap in current standards concerning the quantitative evaluation of mechanical properties at the grout–repair interface. The primary objectives of this study are: (1) to validate the effectiveness of fracture-oriented grouting in restoring the mechanical performance of damaged shield tunnel segments; (2) to quantify changes in structural load-bearing capacity before and after repair through full-scale loading tests; and (3) to establish an elastoplastic analytical model for the preliminary prediction of the load-bearing capacity of damaged segments. The central hypothesis posits that, under controlled curing conditions, targeted grouting can substantially improve both the load-bearing capacity and ductility of locally damaged segments, thereby effectively inhibiting crack propagation and extending the service life of tunnel structures.

Design of the test

Metro shield tunnel segment test specimen

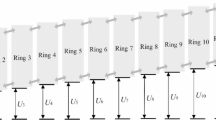
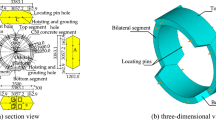
The test specimens were obtained from shield tunnel segments used in a metro project, and were composed of C50 precast concrete. Two standard segments, designated M0 and M1, were selected for bending load tests in this study. Segment M0 was used to determine the ultimate load-bearing capacity through a monotonic loading test. Segment M1 was subjected to a distributed loading test. It was first loaded to a damaged state (80% of its ultimate capacity), then reinforced via grouting, and finally loaded to failure. Figure 1 illustrates the position of the standard segment within the segmental ring. As shown in Fig. 2, the standard segment has an outer diameter of 6200 mm, an inner diameter of 5500 mm, a central angle of 67.5°, a thickness of 350 mm, and a ring width of 1200 mm.

Fig. 1
figure 1

Dimensions of standard block.

Full size image
Fig. 2
figure 2

Standard block diagram of a metro shield tunnel segment.

Full size image

The segments were made of grade C50 concrete with double-layer reinforcement, using 20 mm diameter steel bars. The minimum concrete cover to the outermost reinforcement layer is 35 mm on the outer face and 25 mm on the inner face of the segment. This study evaluates the effectiveness of grouting reinforcement in repairing damaged shield tunnel segments. The interaction between segmental rings was not considered; thus, the loading was applied to a standard segment from a single ring.

Material properties

As shown in Fig. 3, a modified high-fluidity epoxy resin was used as the grouting material, and its properties are listed in Table 1.

Fig. 3
figure 3

Grouting material.

Full size image
Table 1 Material properties of modified epoxy resin.
Full size table

Reinforcement program

Based on the extent and characteristics of damage in the deteriorated segment, pressure grouting was applied to reinforce cracks with widths between 0.1 and 0.2 mm. Along the direction of each of the four cracks, 12 mm diameter and 150 mm deep grouting holes were drilled at 250 mm intervals. Prior to grouting, an air compressor was used to clean dust and debris from the grouting holes and cracks. During grouting, a trial injection was first conducted at a pressure of 0.2–0.3 MPa. Once grout leakage was ruled out, the remaining grouting holes were injected. Grouting was performed continuously until grout overflowed from each hole. For cracks narrower than 0.1 mm, the surface was first polished with sandpaper, then cleaned with an air compressor, and finally wiped with alcohol. Finally, the surface was sealed by brushing on modified epoxy resin. After grouting, the specimens were cured at room temperature for 7 days. Figure 4 shows the inner arc surface after grouting reinforcement, while Fig. 5 presents the segment’s side view.

Fig. 4
figure 4

Inner arc grouting diagram.

Full size image
Fig. 5
figure 5

Lateral grouting diagram.

Full size image

Loading program

The experimental loading system, illustrated in Fig. 6, comprises a fixed-end constraint, a free end, a distribution beam, rigid shims, an electro-hydraulic servo actuator, and a load cell. A simply supported beam configuration was adopted, with the specimen placed horizontally on a dual-support boundary system. The fixed end restrained translational movements along the X, Y, and Z axes and rotational movements about the X- and Y-axes, whereas the free end was restrained only in the Z-direction.

Fig. 6
figure 6

Test loading system.

Full size image

A vertical load F was applied using the electro-hydraulic servo actuator and transferred as a uniformly distributed load through the distribution beam. Due to the cantilever beam effect, a bending neutral axis developed at the fixed end, while the free end exhibited a controllable deflection. The Z-direction displacement constraint effectively suppressed rigid-body motion while allowing translational movement in the X and Y directions. Strain monitoring indicated that the maximum bending strain was concentrated at the upper edge of the cross-section near the fixed end.

A quasi-static, stepwise loading method was employed, in which the load was incrementally increased in 50 kN steps using a servo-controlled system until the specimen reached the target load level. The mechanical response of the specimen during loading is illustrated in Fig. 7. Each load level was maintained for 120 s to ensure structural response stability, during which the timing of crack initiation, crack propagation paths, and the evolution of crack width were recorded.

Fig. 7
figure 7

Schematic of force application on the segment.

Full size image

Test monitoring point layout

A multi-parameter coordinated monitoring system was established for this experiment. A symmetrical sensor layout was adopted, with displacement gauges installed at the segment mid-span, beneath the loading beam, and at the free end to monitor vertical deflection and capture horizontal displacement. Additionally, arrays of circumferential electrical resistance strain gauges were installed on the intrados, extrados, and lateral surfaces to reconstruct the concrete strain field. The specific layout of measurement points on the segment is illustrated in Fig. 8.

Fig. 8
figure 8

Layout of test monitoring points.

Full size image

Analysis of grouting parameters

Key Mechanical Property Indicators

According to the Code for Design of Concrete Structures (GB 50010-2010), the ultimate states of segmental structures are defined as follows: when the maximum crack width on the segment surface reaches 0.2 mm, the structure is considered to have reached the serviceability limit state. If the crack width further increases to a critical value of 2.0 mm, or if concrete crushing occurs, the structure is deemed to have reached the ultimate limit state for load-bearing capacity.

Based on the loading test results presented in Table 2, the cracking and service loads of the two segment specimens prior to reinforcement exhibited similar characteristics, indicating comparable initial damage levels. After reinforcement, specimen M1 demonstrated a significant improvement in load-bearing performance. Specifically, its ultimate load increased from 530 kN before reinforcement to 580 kN after reinforcement, corresponding to a 9.43% increase. The results demonstrate that the adopted reinforcement technique can enhance the segment’s ultimate load capacity by approximately 9.4%, thereby significantly improving its structural performance.

Table 2 Characteristic load values of segments.
Full size table

Analysis of test data

Crack width

The maximum crack width of the reinforced concrete is calculated using the following formula:

$$\begin{array}{c}{\omega }_{max}={\alpha }_{cr}\Psi \frac{{\sigma }_{s}}{{E}_{s}}\left(1.9c+0.08\frac{{d}_{eq}}{{\rho }_{te}}\right)\end{array}$$
(1)

In the equation, \({\alpha }_{cr}\) denotes the structural stress characteristic coefficient, determined according to Reference40; \({E}_{s}\) represents the elastic modulus of the reinforcement; \(\Psi\) is the strain non-uniformity coefficient of the reinforcement, calculated by Eq. (2); \({\sigma }_{s}\) refers to the stress in the reinforcement at the cracked section, obtained from Eq. (3); \({d}_{eq}\) is the equivalent diameter of the longitudinal reinforcement in the tension zone; and \({\rho }_{te}\) is the effective reinforcement ratio, calculated by Eq. (4).

$$\begin{array}{c}\Psi =1.1-\frac{0.65{f}_{tk}}{{\rho }_{te}{\sigma }_{s}}\end{array}$$
(2)
$$\begin{array}{c}{\sigma }_{s}=\frac{M}{0.87{h}_{0}{A}_{s}}\end{array}$$
(3)
$$\begin{array}{c}{\rho }_{te}=\frac{{A}_{s}}{{A}_{te}}\end{array}$$
(4)

When \(\Psi <0.2\), it is taken as 0.2; when \(\Psi >1.0\), it is taken as 1.0. \({f}_{tk}\) denotes the characteristic tensile strength of concrete; \({A}_{s}\) is the cross-sectional area of the longitudinal reinforcement in the tension zone; \({A}_{te}\) represents the cross-sectional area of the member, calculated by Eq. (5), where \(M\) is the mid-span bending moment, determined using Eq. (6).

$$\begin{array}{c}{A}_{te}=0.5bh\end{array}$$
(5)
$$\begin{array}{c}M=\frac{aP}{2}\end{array}$$
(6)

In the equation, \(a=1.225\) m, and \(P\) denotes the load applied by the experimental loading device.

Table 3 compares the theoretical values and experimental measurements of the maximum crack width, demonstrating good agreement between them. Specifically:

Table 3 Comparison of calculated and measured maximum crack width values.
Full size table

For the unreinforced segment M0:

  1. (1)

    When the load increased to 266 kN, the crack width reached the allowable limit of 0.20 mm specified by the code;

  2. (2)

    At a load of 738 kN, the crack width expanded to 0.90 mm, accompanied by localized concrete crushing at the extrados, indicating structural failure.

For the grouted reinforced segment M1:

  1. (1)

    At a load of 625 kN, the crack width developed to 0.70 mm, with accompanying damage to the concrete at the extrados; this load was identified as the failure load.

Comparison of crack propagation between M0 and M1 within the 525–625 kN load range showed that grouting reinforcement reduced the crack width growth rate by 17–23%, confirming its effectiveness in restraining crack development. However, the failure load of the reinforced segment decreased from 738 to 625 kN, a reduction of 15.3%, attributable to the following factors:

  1. (1)

    Drilling-induced damage: Grouting holes (12 mm diameter, 150 mm depth) reduced the effective concrete cross-sectional area, causing stress concentration;

  2. (2)

    Interface failure mechanism: At loads above 580 kN, abnormal fluctuations were observed at strain monitoring points, indicating bond degradation or partial debonding at the interface between the reinforcement layer and concrete.

Segment displacement

Figures 9, 10 and 11 presents the vertical displacements at the segment mid-span and loading points, alongside the horizontal displacement at the free end. As shown in Fig. 9, the failure test involved loading the specimen until failure. In the original (unreinforced) segment, stiffness was highest during the elastic stage, exhibiting a linear load–displacement relationship with minimal displacement. Upon entering the plastic stage, the specimen displayed brittle failure characteristics, rapidly failing after reaching a peak load of 738.7 kN due to the absence of reinforcement.

Fig. 9
figure 9

Vertical displacement at the mid-span of the segment.

Full size image
Fig. 10
figure 10

Horizontal displacement at the free end of the segment.

Full size image
Fig. 11
figure 11

Vertical displacement at the loading points on the segment.

Full size image

In the damage test, the specimen was preloaded to 525 kN to induce initial damage, followed by repair using grouting reinforcement, establishing a reinforcement–failure test. After reinforcement, the specimen’s stiffness partially recovered during the elastic stage, and displacement under identical loads was reduced compared to the damage test. In the plastic stage, reinforcement improved both load-bearing capacity and ductility. Consequently, the peak load increased significantly; the rate of load decrease slowed down, and displacement grew more gradually. The load–displacement curve showed a more gradual decline, indicating that the reinforcement effectively delayed failure.

In the 525–625 kN range, segment displacement growth rate in M1 (repaired) was reduced by approximately 17–23% compared with M0, Indicate an effective increase in strength through grouting, as shown in Fig. 9, Table 3.

Concrete strain

Figures 12, 13 and 14 illustrates the variations in concrete strain on the intrados, extrados, and side surfaces at the mid-span of segments M0 and M1 as the load increases. After preloading to 525 kN, the elastic modulus decreased from 30.2 kN/με (original structure) to 16.8 kN/με, representing a reduction of 44%, while the peak load dropped by 14%. Between 450 and 525 kN, the rate of strain accumulation accelerated during the plastic stage, indicating significant degradation in material stiffness and load-bearing capacity due to pre-damage.

Fig. 12
figure 12

Strain values at the monitoring points on the inner arc of the segment.

Full size image
Fig. 13
figure 13

Strain values at the monitoring points on the outer arc of the segment.

Full size image
Fig. 14
figure 14

Strain values at the lateral monitoring points of the segment.

Full size image

Following reinforcement, the elastic modulus recovered to 19.7 kN/με, approximately 65% of the original value. The peak load increased by 9.4% to 580 kN. At failure, the strain reached − 4200 με, a 68% increase compared to the original specimen (− 2500 με). The load–strain curve displayed a broad plateau, indicating that reinforcement effectively enhanced structural load capacity, ductility, and strain distribution uniformity.

The original specimen exhibited brittle failure, characterized by a sudden 10% load drop post-peak, whereas the reinforced specimen showed ductile failure, with a gradual 13.8% load reduction after the peak. Grouting reinforcement improved the failure mechanism by suppressing crack propagation.

An anomalous strain spike to + 51,210 με at a 530 kN load likely resulted from local debonding of the reinforcement layer or sensor malfunction, suggesting that interface bonding requires optimization for improved long-term stability.

Conclusions

This study proposes a grouting-based repair method for segmental linings in shield tunnels and conducts full-scale flexural testing to evaluate the mechanical performance and failure characteristics of segments before and after repair. The results demonstrate that, under controlled curing conditions, fracture-oriented grouting increases the ultimate load of damaged segments by 9.4%, enhances ductility, and effectively suppresses crack propagation. The proposed elastoplastic calculation matched experimental observations within 10% and can serve as a preliminary reference for structural design. The main conclusions are summarized as follows:

  1. 1.

    Grouting reinforcement increased the ultimate load of the damaged structure by 9.4% and the failure displacement by 68%. The load–displacement curve exhibited a broad plateau, indicating substantial improvements in both load-bearing capacity and ductility. Strain measurements on the intrados revealed a more uniform strain distribution following reinforcement, with peak strain rising from − 1300 to − 4200 με, thereby confirming the effectiveness of the reinforcement material in suppressing crack propagation.

  2. 2.

    The elastic modulus of the reinforced specimen recovered to 65% of the original structure’s value, with interfacial bond performance identified as the primary factor limiting complete stiffness restoration. The failure mode transitioned from brittle to ductile, aligning with the design principle of ‘strong reinforcement, weak base’.

  3. 3.

    Preloading to 525 kN resulted in a 44% decrease in elastic modulus and a 15% reduction in failure load. Although reinforcement partially restored the mechanical properties, abnormal strain responses under high loads suggest potential debonding or interfacial failure within the reinforcement layer, highlighting the necessity to further optimize bonding methods.

  4. 4.

    This study provides empirical data to support the reinforcement design of existing damaged structures and highlights the critical role of interface performance in repair effectiveness. Future research should integrate microscopic analyses (e.g., crack distribution, interfacial bonding conditions) to more effectively elucidate the underlying mechanisms. Moreover, developing novel reinforcement materials and construction techniques is essential for enhancing long-term stability. Although the proposed reinforcement method significantly enhances mechanical performance, its efficacy remains constrained by interfacial bond quality, thereby emphasizing the importance of optimizing both materials and processes in future investigations.

  5. 5.

    This study is based on two full-scale specimens subjected to controlled laboratory loading; therefore, the results primarily reflect short-term mechanical recovery. To facilitate field application, parametric finite element method (FEM) studies across diameters, materials, and strata followed by controlled field trials are recommended.