D2S-DiffGAN: a novel image classification model under limited labeled samples

Abstract

As deep learning technologies gradually penetrate various industries, the issue of data scarcity has become a key factor restricting their widespread application and further development. The existing image classification models typically use the Generative Adversarial Network (GAN) to expand the amount of data. However, the GAN focuses solely on generating spatial domain features, overlooking the complementary role of frequency domain information in image representation. In addition, these models assign the same loss weight to both real and generated samples, failing to effectively reflect the contribution differences of these samples during model training. To address these issues, this paper proposes a fully supervised image classification model (D2S-DiffGAN) under limited labeled samples. First, a dual-domain synchronous GAN (DDSGAN) is constructed that constrains the generator from both the spatial and frequency domains. This ensures that the generated samples satisfy both the visual realism of RGB images and the consistency of frequency domain energy distribution, resulting in more diversity and realism. Second, a multi-branch feature extraction network (MBFE) is designed to capture the local texture features, global semantic features, and cross-channel correlation features of the samples. Meanwhile, an attention module is introduced to dynamically fuse multi-dimensional features, further enhancing the channel feature representation relevant to the task. Finally, a differentiated loss function (DIFF) is proposed, setting different loss weights based on the characteristics of generated samples and real images, thereby more reasonably handling the differences between generated and real samples and optimizing the model training process. Extensive experiments on the SVHN and CIFAR-10 datasets show that the proposed model can still achieve good classification accuracy under limited labeled samples, fully validating its effectiveness.

Introduction

With the rapid development of the Internet and the continuous improvement of computational device performance, deep learning has made significant progress in various fields such as facial recognition¹, speech recognition², and autonomous driving³, marking the entry of human society into the era of artificial intelligence⁴. As a core task of computer vision, image classification has naturally received extensive attention. In recent years, researchers have successively proposed various models ^5,6,7,8,9,10 aimed at achieving autonomous image classification, thereby effectively reducing the labor and additional costs required for image annotation ^11,12,13,14.

Although deep learning-based image classification techniques have achieved remarkable results, their performance is highly dependent on the amount of data used for model training¹⁵. However, in many real-world scenarios, it is challenging to construct large-scale datasets due to issues such as privacy, ethics, and cost¹⁶. For instance, sensitive data in the military domain cannot be publicly disclosed or used freely¹⁷; rare diseases in the medical field involve users’ private information¹⁸, leading to a very limited amount of collected data. Moreover, obtaining images in fields like endangered species conservation is even more different¹⁹. In these cases, traditional fully supervised image classification models tend to overlearn the noise in the training set, making it difficult to extract representative features. This significantly degrades the performance of the model on the test set, resulting in poor practical application results²⁰.

Currently, employing data augmentation techniques to expand the number of samples is a solution when labeled samples are limited. Traditional data augmentation methods primarily include geometric transformations (such as shifting, rotating, scaling, cropping, flipping, etc.) and color transformations (such as erasing, adding noise, blurring, and padding, etc.). Yun et al.²¹ proposed Cutmix that selects a small area from another image to cover the corresponding area of the current image. Wang et al.²² introduced a Random Erasing Network that repeatedly selects specific areas for random erasing. Li et al.²³ proposed a novel Cross-Set Erasing and Inpainting method (CSEI) that uses erasing and inpainting to process images in the support set. Ren et al.²⁴ proposed a Multi-Local Feature Relation Network (MLFRNet), which randomly crops a rectangular area from the original image and then resizes the cropped area to match the original image. However, the images generated by traditional data augmentation methods are highly similar to the original images, which provides very limited information. In addition, classic geometric and color transformations lack the deep understanding of the inherent structure and semantic information of the original images, resulting in generated images that fail to simulate the complex and variable conditions of the real world. Therefore, the performance improvement of small-sample image classification models based on traditional data augmentation is minimal.

To address this issue, the Generative Adversarial Networks (GAN) emerged and have gradually become one of the mainstream data generation models, widely applied to small-sample image classification tasks. Hong et al.²⁵ proposed MatchingGAN, a method that generates new images of the same category by fusing random noise with multiple images of the same category. Li et al.²⁶ proposed an Adversarial Feature Hallucination Network (AFHN) based on Conditional Wasserstein Generative Adversarial Network (cWGAN), which incorporates two new regularizers: a classification regularizer and an anti-collapse regularizer, to enhance the discriminability and diversity of synthetic samples. Pahde et al.²⁷ designed a cross-modal feature generation framework that uses auxiliary modal data to enrich the embedding space in few-shot scenarios. Sharma et al.²⁸ proposed SMOTified-GAN that combines the strengths of SMOTE and GAN to transform the unrealistic or overgeneralized samples generated by SMOTE into data that more closely aligns with the actual distribution. Mi et al.²⁹ proposed a Wasserstein GAN with Confidence Loss (WGAN-CL), which introduces a shortcut stream connection in the GAN structure to expand the model’s solution space and uses confidence loss for model optimization. Hua et al.³⁰ proposed FFGAN, which combines local feature fusion with GAN to improve the quality and diversity of generated images, solving the issue of spatial misalignment in the image generation process. Ding et al.³¹ proposed a GAN model based on Local Outlier Factor (LOF) and information entropy (LEGAN), which uses LOF to detect sparse and dense sample points and performs affine transformations to mitigate mode collapse; while the decentralization constraint based on information entropy is used to enhance the diversity of generated samples. Although GAN-based small-sample image classification models have achieved some success, there are still some shortcomings. On the one hand, the GAN only focuses on the generation of spatial domain features, neglecting the complementary role of frequency domain information in image representation, resulting in generated images with poor diversity and insufficient realism. On the other hand, most GAN-based data augmentation methods treat real and generated samples with equal loss weights, failing to effectively reflect the contribution differences of different samples during model training. This may lead to the generated samples potentially over-influencing the model, thereby reducing its classification performance.

Therefore, this paper proposes a new fully supervised image classification model (D2S-DiffGAN) under limited labeled samples with the following contributions:

• 1. A dual-domain synchronous GAN (DDSGAN) is constructed that constrains the generator from both the spatial and frequency domains. This design ensures that the generated samples satisfy both the visual realism of RGB images and the consistency of frequency domain energy distribution, resulting in more diversity and realism.

• 2. A multi-branch feature extraction network (MBFE) is designed to capture the local texture features, global semantic features, and cross-channel correlation features of samples, and an attention module is introduced to dynamically fuse multi-dimensional features, aiming further to strengthen the channel feature representation relevant to the task.

• 3. A differentiated loss function (DIFF) is proposed, which sets different loss weights for generated and real images based on their distinct characteristics. Through this strategy, the model can more reasonably handle the differences between generated and real samples, thus optimizing the network training process and improving the stability and classification performance of the model.

Basic theory

This section delves into the three core foundational theories that support our paper. Specifically, the Discrete Cosine Transform is an effective method for converting images from the spatial domain to the frequency domain; the Generative Adversarial Network provide theoretical support for the construction of dual-domain synchronous generative adversarial networks; and the Convolutional Block Attention Module enhances feature information relevant to the task, which helps to improve the model’s performance in specific tasks.

Discrete Cosine Transform

Discrete Cosine Transform (DCT) ^32,33,34 can convert images from the spatial domain to the frequency domain, thereby extracting key information and achieving efficient compression. Its specific steps are as follows:

• First, the RGB image is converted to the YCbCr color space to separate the brightness (Y) and chromaticity information (Cb, Cr). The conversion formulas are as follows:

  $$\begin{aligned} & Y = 0.299R + 0.587G + 0.114B \end{aligned}$$

  (1)
  $$\begin{aligned} & Cb = 128 + (-0.168736R - 0.331264G + 0.5B) \end{aligned}$$

  (2)
  $$\begin{aligned} & Cr = 128 + (0.5R - 0.418688G - 0.081312B) \end{aligned}$$

  (3)

• Assuming the input image has a size of ${N} \times {M}$. Second, a two-dimensional DCT is performed on the pixel matrices x(n, p) of the Y, Cb, and Cr channels to obtain the corresponding matrices, respectively. The formula is as follows:

  $$\begin{aligned} X(k,m) = \alpha (k)\alpha (m) \sum _{n=0}^{N-1} \sum _{p=0}^{M-1} x(n,p) \cos \left[ \frac{\pi (2n+1)k}{2N}\right] \cos \left[ \frac{\pi (2p+1)m}{2M}\right] \end{aligned}$$

  (4)

  Where n and p represent the row and column indices of images in the YCbCr color space, respectively, and k and m represent the row and column indices of images in the frequency domain. a(k) and a(m) are the normalization coefficients, which are expressed as follows:

  $$\begin{aligned} \alpha (k) = {\left\{ \begin{array}{ll} \sqrt{\frac{1}{N}}, & k = 0 \\ \sqrt{\frac{2}{N}}, & k \ne 0 \end{array}\right. }, \alpha (m) = {\left\{ \begin{array}{ll} \sqrt{\frac{1}{M}}, & m = 0 \\ \sqrt{\frac{2}{M}}, & m \ne 0 \end{array}\right. } \end{aligned}$$

  (5)

• Finally, the three obtained DCT frequency domain coefficient matrices are combined to form the frequency domain representation of the RGB image.

Generative adversarial network

As shown in Fig 1, the Generative Adversarial Network (GAN)³⁵ is composed of two neural networks: the generator G and the discriminator D. When training reaches an ideal state, G can produce samples that are almost indistinguishable from real data.

Fig. 1

The basic framework of Generative Adversarial Network (GAN).

Specifically, G takes a random noise vector z as input and attempts to map it to a data space that resembles the real data. Its objective function is as follows:

$$\begin{aligned} L_G = \min _{G} \mathbb {E}_{p_z} [\log (1 - D(G(z)))] \end{aligned}$$

(6)

In Eq (6), G(z) represents the generated sample, D(G(z)) represents the probability that D assigns to G(z), and ${p_z}$ represents the prior distribution of z. D takes generated samples and real samples as input and outputs a value $D(\cdot ) \in (0,1)$, which indicates the probability that it believes the input sample is “real.” The loss function of D is as follows:

$$\begin{aligned} L_D = \max _{D} \left[ \mathbb {E}_{p_x} [\log D(x)] + \mathbb {E}_{p_z} [\log (1 - D(G(z)))] \right] \end{aligned}$$

(7)

In Eq (7), x represents the real data, D(x) is the probability that D assigns to x, and ${p_x}$ is the probability distribution of x.

Convolutional block attention module

The attention mechanism allows the model to focus on key information by assigning varying weights to different parts of the input data. As shown in Fig 2, the Convolutional Block Attention Module (CBAM)³⁶ consists of a cascade of a channel attention module and a spatial attention module. First, the channel attention module applies global average pooling and max pooling to extract features from the input feature map $F \in \mathbb {R}^{C \times H \times W}$, which are then processed by a shared MLP (two fully connected layers) to compute channel attention. The channel weights $M_c$ are obtained through the Sigmoid activation function, and the calculation formula is as follows:

Fig. 2

The basic framework of Convolutional Block Attention Module (CBAM).

$$\begin{aligned} M_c = \sigma (W_2(\delta (W_1 F_{\text {avg}})) + W_2(\delta (W_1 F_{\text {max}}))) \end{aligned}$$

(8)

Where $W_1 \in \mathbb {R}^{\frac{C}{r} \times C}$ and $W_2 \in \mathbb {R}^{C \times \frac{C}{r}}$ represent the weights of the two fully connected layers, respectively, and r is the channel reduction rate (with a value of 16). The symbol $\delta (\cdot )$ denotes the ReLU activation function, and $\sigma (\cdot )$ denotes the Sigmoid activation function. The element-wise multiplication of $M_c$ with the input feature map $F \in \mathbb {R}^{C \times H \times W}$ is performed to obtain the channel-refined feature $F'$ with enhanced channels, and the calculation formula is as follows:

$$\begin{aligned} F' = M_c \odot F \end{aligned}$$

(9)

Second, the spatial attention module applies max pooling and average pooling to $F'$ to compress its spatial information, yielding two feature vectors of size $H \times W \times 1$. These vectors are then concatenated along the channel dimension to create a feature map of size $H \times W \times 2$. Following this, a $7 \times 7$ convolutional layer is used to extract spatial relationships. The Sigmoid activation function is utilized to normalize the output, resulting in the spatial weights $M_s$. The formula is as follows:

$$\begin{aligned} M_s = \sigma (f^{7\times 7}(\text {concat}(F_{\text {avg}}^{'}, F_{\text {max}}^{'}))) \end{aligned}$$

(10)

Finally, by performing element-wise multiplication between $M_s$ and $F'$, the final weighted feature map $F''$ is obtained. The formula is as follows:

$$\begin{aligned} F'' = M_s \odot F' \end{aligned}$$

(11)

Our approach

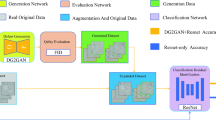
As shown in Fig 3, the proposed image classification model under limited labeled samples consists of four key steps: data preprocessing, data generation, model training, and model evaluation.

Fig. 3

The block diagram of the proposed image classification model under limited labeled samples.

Data preprocessing: First, the limited labeled samples are divided into training and testing sets. Second, the diversity of images in the training set is increased through methods such as rotation, cropping, and flipping, and their pixel values are normalized. Finally, the Discrete Cosine Transform (DCT) is applied to obtain the frequency domain representation of the images in the training set.

Data generation: The images from the training set (RGB spatial domain) and their corresponding frequency domain representations are fed into the DDSGAN to generate high-quality samples (RGB spatial domain).

Model training: Both the images in the training set and the samples generated by DDSGAN are input into the MBFE. This network is responsible for feature extraction and classification tasks, while the DIFF is used to optimize its parameters.

Model evaluation: The test set is used to evaluate the optimized and tuned model, with the aim of verifying its classification performance and generalization ability.

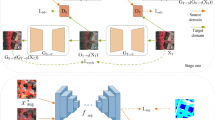
Dual-domain synchronous generative adversarial network (DDSGAN)

Since G in the traditional GAN focuses on learning the underlying distribution patterns of images (RGB spatial domain), the samples generated by it lack controllability in the frequency domain. This limitation can lead to phenomena such as blurring, artifacts (frequency distribution deviations), and unrealistic local texture details in the generated samples. Moreover, it may trigger mode collapse and loss of high-frequency information, thereby resulting in lower-quality generated samples.

To address the above issue, the DDSGAN is proposed, which imposes constraints on G from both the RGB spatial and frequency domains. This design can reduce high-frequency noise artifacts and enhance detailed textures, thereby improving the naturalness and diversity of generated images. As shown in Fig 4, DDSGAN consists of three components: a generator (G), an RGB spatial domain discriminator ($D_S$), and a frequency domain discriminator ($D_F$).

Fig. 4

The architecture of the Dual-Domain Synchronous Generative Adversarial Network (DDSGAN).

Among them, $D_S$ performs traditional adversarial training to accurately distinguish between real images and generated samples in the RGB spatial domain with its loss function defined as:

$$\begin{aligned} L_{D\_S} = \mathbb {E} [\log D_S(x)] + \mathbb {E}[\log (1 - D_S({G(z)}))] \end{aligned}$$

(12)

Where x and G(z) represent the real images and generated samples in the RGB spatial domain, respectively. $D_F$ is responsible for receiving the frequency domain feature representations $x_f$ and $G(z)_f$ corresponding to x and G(z), respectively. Its goal is to accurately identify $x_f$ as “real” and $G(z)_f$ as “fake”. The loss function is expressed as follows:

$$\begin{aligned} L_{D\_F} = \mathbb {E} [\log D_F(x_f)] + \mathbb {E}[\log (1 - D_F({G(z)_f}))] \end{aligned}$$

(13)

In DDSGAN, G not only needs to fool $D_S$ to make the generated images appear realistic in the RGB spatial domain but also needs to deceive $D_F$ so that its spectral distribution aligns with the statistical characteristics of real data. Therefore, G must optimize the adversarial loss in both the spatial and frequency domains simultaneously. Its loss function is as follows:

$$\begin{aligned} L_{G} = \underbrace{\mathbb {E} [\log (1 - D_S(G(z)))]}_{L_{G\_S}} + \underbrace{\mathbb {E} [\log (1 - D_F(G(z)_f))]}_{L_{G\_F}} \end{aligned}$$

(14)

Where $L_{G\_S}$ and $L_{G\_F}$ represent the adversarial losses in the RGB spatial domain and frequency domain, respectively. In summary, the samples generated by DDSGAN not only conform to the characteristics of real images at the pixel level (visual plausibility) but also align with the statistical properties of real images at the frequency level (consistency of energy distribution).

Multi-branch feature extraction network (MBFE)

ResNet-50³⁷ can learn more complex hierarchical features from data, and its residual blocks can effectively alleviate the vanishing-gradient problem, making the training process more stable. However, the shallow structure of ResNet-50 relies solely on a single $7 \times 7$ large convolution kernel for coarse-grained downsampling to extract features from data, which continuously participates in the construction of higher-level semantic features during the hierarchical transmission process. Therefore, when the resolution of the feature map drops sharply, the shallow structure design of ResNet-50 can easily result in the loss of fine-grained local discriminative features.

To address this issue, the MBFE is proposed. In the MBFE, a Local Global Convolutional Attention Block is designed to replace the $7 \times 7$ shallow convolutional structure in ResNet-50 (the rest of which remains consistent with ResNet-50), aiming to extract local details and global information from data more comprehensively. As shown in Fig 5, the specific implementation steps of the Local Global Convolutional Attention Block are as follows:

Fig. 5

The schematic diagram of the Multi-Branch Feature Extraction Network (MBFE) based on ResNet-50.

First, three convolution kernels of different sizes ($3 \times 3$, $5 \times 5$, and $7 \times 7$) are used in parallel to extract feature representations at different scales from the data. Second, the multi-scale information is integrated through feature concatenation to enhance the complementarity of the features. The mathematical expression is as follows:

$$\begin{aligned} F = C_{3 \times 3}^2(X) \oplus C_{5 \times 5}^2(X) \oplus C_{7 \times 7}^2(X) \end{aligned}$$

(15)

Here, $C_{3 \times 3}^2(\cdot )$ represents a $3 \times 3$ convolution that focuses on extracting local texture information; $C_{5 \times 5}^2(\cdot )$ denotes a $5 \times 5$ convolution, used for capturing medium receptive field structures; $C_{7 \times 7}^2(\cdot )$ indicates a $7 \times 7$ convolution, responsible for modeling the global context. X and $\oplus$ represent the input image and the feature concatenation operation, respectively.

Finally, the Convolutional Block Attention Module (CBAM) is introduced to perform adaptive weighting on the concatenated features F, highlighting features relevant to the current task while suppressing redundant information. To more effectively understand the proposed MBFE, Table 1 presents its detailed structure and parameter configuration.

Table 1 The structure and parameter configuration of the Multi-Branch Feature Extraction Network (MBFE).

Differentiated loss function (DIFF)

In image classification tasks, the cross-entropy loss³⁸ assigns the same weight to all samples. This may result in the loss of easily classified samples dominating the overall loss, thereby causing the direction of gradient updates to be biased towards these simple samples. The general form of the cross-entropy loss function is as follows:

$$\begin{aligned} L_{CE} = - \sum _{i} y_i \log (p_i) \end{aligned}$$

(16)

Where $y_i$ represents the true label for the i-th sample, and $p_i$ denotes the probability that the model correctly predicts the i-th sample. Focal Loss³⁹ introduces a regulatory factor to reduce the loss weight of easily classified samples, thereby encouraging the model to pay more attention to hard-to-classify samples, which has achieved significant results in object detection tasks.

Although DDSGAN can generate high-quality samples, there still exists a discrepancy between the generated samples and the real samples. In image classification tasks under limited labeled samples, the number of generated samples is often much greater than that of real samples. To prevent the model parameters from being overly biased toward generated samples and inspired by Focal Loss, the DIFF is proposed. Specifically, the DIFF weights the loss of generated samples and real samples differently, thereby avoiding the dominance of loss of generated samples in the overall loss and preventing the model from overfitting to the generated samples. Its mathematical expression is as follows:

$$\begin{aligned} L_{DIFF} = -w_{\text {real}} \sum _{i \in \text {real}} y_i \log (p_i) - w_{\text {gen}} \sum _{i \in \text {gen}} y_i \log (p_i) \end{aligned}$$

(17)

Here, $w_{\text {real}} = \frac{N_{\text {real}}}{N_{\text {real}} + N_{\text {gen}}}$ and $w_{\text {gen}} = \frac{N_{\text {gen}}}{N_{\text {real}} + N_{\text {gen}}}$ represent the weights assigned to the loss of real samples and the loss of generated samples, respectively. $N_\text {real}$ and $N_\text {gen}$ denote the number of real and generated samples, respectively. By this design, the DIFF effectively balances the impact of generated and real samples on model training.

Experiments and analysis

In this section, we conducted extensive experiments on two public datasets: SVHN and CIFAR-10. To simulate the scenario of limited labeled samples in real-world applications, we randomly sampled different proportions of samples from their training sets for model training. The purpose is to more accurately reflect the performance of the proposed model under limited labeled samples.

Experimental parameter settings and details

All experiments were conducted on a Windows 10 operating system, with a hardware platform equipped with a 13th Generation $\text {Intel}^{\circledR } \text {Core}^{\textrm{TM}}$ i5 processor and an NVIDIA GeForce RTX 3080 graphics card, achieving GPU acceleration through CUDA 11.3. The algorithm implementation is in Python language, based on the PyTorch deep learning framework, and the development environment is PyCharm software. The model training parameters were set as follows: the batch size was uniformly set to 128, the training period consisted of 100 epochs, and an Adam optimizer with a learning rate of 0.0002 and normalization value of 0.5 was used.

To verify the effectiveness of the proposed model under limited labeled samples, it was compared with five existing models: ResNet-50³⁷, Shared DC Discriminator, Shared ResNet Discriminator, EC-GAN⁴⁰ and ICUW-GAN⁴¹. Their specific architectures and parameter counts are as follows:

ResNet-50: It employs ResNet-50 as the backbone for image classification without sample augmentation. The total number of parameters is 25.6 M.

Shared DC discriminator: It uses a GAN for sample augmentation and employs ResNet-50 as the backbone for image classification. The total number of parameters is 31.9 M, with the GAN contributing 6.3 M.

Shared ResNet discriminator: It uses an ACGAN for sample augmentation and employs ResNet-50 as the backbone for image classification. The total number of parameters is 32.4 M, with the ACGAN contributing 6.8 M.

EC-GAN: It proposes a new image generation model based on GAN for sample augmentation and employs ResNet-50 as the backbone for image classification. The total number of parameters is 33 M, with the proposed generation model contributing 7.4 M.

ICUW-GAN: It proposes a new image generation model based on ACGAN for sample augmentation and employs ResNet-50 as the backbone for image classification. The total number of parameters is 33.2 M, with the proposed generation model contributing 7.6 M.

D2S-DiffGAN (Ours): It uses the DDSGAN for sample augmentation and employs the MBFE as the backbone for image classification. The total number of parameters is 35.9 M, with the DDSGAN contributing 8.7 M.

SVHN dataset

The SVHN dataset was constructed by Netzer et al.⁴² as a benchmark dataset for digit recognition. It contains 630,420 color images of house numbers captured from real-world street scenes. All images are 32$\times$32 RGB color images, covering 10 classes representing the Arabic digits 0–9. The dataset consists of 73,257 training images, 26,032 test images, and 531,131 additional images (optional for use), with digit regions precisely annotated using bounding boxes.

First, this paper compares the generative performance of GAN and DDSGAN on the SVHN dataset. As shown in Fig 6, GAN constrains the generator only in the RGB spatial domain, resulting in generated samples with uneven stroke thickness, blurred edges, and high-frequency artifacts. Some images even exhibit missing details or distorted shapes. Additionally, mosaic-like noise blocks appear in the background, and unnatural ring-shaped light spots may emerge. In contrast, DDSGAN generates digit images that better preserve character contours and effectively reduce frequency distribution biases, making the images clearer and more coherent. The local textures appear more realistic, the background retains its granular quality, and the color transitions are smoother.

Fig. 6

Comparative analysis of generative performance between GAN and DDSGAN on the SVHN dataset. (a) GAN; (b) DDSGAN.

Next, to evaluate the performance of the proposed model under limited labeled samples, different proportions of samples were randomly selected from the training set for training each model, and their accuracy on the test set was compared, as shown in Fig 7. It is evident that as the amount of training data increases, the accuracy of all models improves, confirming the fundamental principle that “model performance is positively correlated with data scale.” Moreover, regardless of the sample proportion used for training, D2S-DiffGAN consistently achieves the best performance, demonstrating its effectiveness under limited labeled sample conditions.

Fig. 7

Comparison of the accuracies on the test set when different proportions of samples are randomly selected from the SVHN training set for model training.

Specifically, compared to ResNet-50, D2S-DiffGAN achieves the most significant improvement, indicating its ability to generate high-quality auxiliary samples under limited data conditions. This helps the model learn more diverse features, thereby enhancing classification performance. Both the Shared DC Discriminator and Shared ResNet Discriminator rely on GAN-generated samples, yet their classification accuracy is lower than that of D2S-DiffGAN, suggesting that DDSGAN produces higher-quality samples that effectively improve the model’s generalization ability. Additionally, although EC-GAN and CUW-GAN are more advanced GAN variants, their classification accuracy still falls short of D2S-DiffGAN, further demonstrating the superiority of DDSGAN in this task. Overall, D2S-DiffGAN performs exceptionally well on the SVHN dataset, particularly when labeled samples are extremely limited (5$\%$-15$\%$). This indicates that even in data-scarce environments, D2S-DiffGAN can still generate high-quality auxiliary samples, effectively enhancing the model’s generalization ability and fully validating its effectiveness.

Additionally, the accuracy of each class on the test set was evaluated when only 5$\%$ of the training samples were used to train the proposed model, as shown in Fig 8. The results indicate that the class with the highest accuracy is “1,” likely because it has the fewest strokes and a simple shape, making it easier for the model to recognize correctly. Similarly, the classes “0,” “4,” and “7” also achieve relatively high accuracy, possibly due to their distinct shapes, which make them easier to distinguish from other classes. In contrast, the class with the lowest accuracy is “5,” likely because its shape is easily confused with “3,” “6,” and “8,” leading to a higher classification error rate.

Fig. 8

Comparison of the accuracy of each category on the SVHN test set using only 5$\%$ of the training set samples for the proposed model training.

Finally, a series of ablation experiments were conducted to validate the effectiveness of each module proposed in this paper. Specifically, we designed the following models:

Model 1: Uses a standard ResNet-50 for image classification and updates its parameters with cross-entropy loss.

Model 2: Uses MBFE for image classification and updates its parameters with cross-entropy loss.

Model 3: First employs DDSGAN for data augmentation, then uses a standard ResNet-50 for image classification, updating network parameters with cross-entropy loss.

Model 4: First employs DDSGAN for data augmentation, then uses a standard ResNet-50 for image classification, updating network parameters with DIFF.

Model 5 (D2S-DiffGAN): First employs DDSGAN for data augmentation, then uses MBFE for image classification, updating network parameters with DIFF.

As shown in Table 2, both Model 2 and Model 3 achieve higher classification accuracy than Model 1 across different training set sizes, indicating that both MBFE and DDSGAN effectively enhance classification performance under limited labeled sample conditions. Further observations reveal that as the amount of training data increases, MBFE (Model 2) shows a larger performance improvement, possibly because it can better extract feature information when more data is available. In contrast, the improvement from DDSGAN (Model 3) is relatively smaller, likely due to the diminishing marginal benefits of data augmentation as data volume increases. Additionally, Model 4 achieves higher classification accuracy than Model 3, demonstrating that DIFF contributes to further optimizing model performance. Model 5 achieves the highest accuracy, proving that the combination of DDSGAN, MBFE, and DIFF maximizes model performance improvements.

Table 2 The ablation experiments on the SVHN dataset.

CIFAR-10 dataset

The CIFAR-10 dataset, developed by Krizhevsky et al.⁴³, serves as a benchmark dataset for image classification. It consists of 60,000 color images with a resolution of 32$\times$32 pixels, evenly distributed across 10 classes: airplane, automobile, bird, cat, deer, dog, frog, horse, ship, and truck. Among them, 50,000 images form the training set, while 10,000 images are designated as the test set, ensuring a strict 1:1 ratio of samples for each class.

To further validate the effectiveness of the proposed model, additional comparative experiments were conducted on the CIFAR-10 dataset. First, a visual analysis of the samples generated by GAN and DDSGAN was performed, as shown in Fig 9. It can be observed that the images generated by GAN contain a significant amount of noise, leading to blurred and irregular object edges, which negatively affects perceptual quality. For instance, animal fur appears smudged with blurred textures, object contours become distorted, and in some cases, the generated shapes are incomplete. In contrast, DDSGAN produces smoother images while preserving reasonable structural details, making object shapes more natural and well-defined, with more seamless color transitions.

Fig. 9

Comparative analysis of generative performance between GAN and DDSGAN on the CIFAR-10 dataset. (a) GAN; (b) DDSGAN.

Next, different proportions of samples were randomly selected from the CIFAR-10 training set to train various models, and their accuracy on the test set was compared, as shown in Fig 10. It can be observed that, as the size of the training dataset increases, the test accuracy of all models improves accordingly. Additionally, regardless of the training set size, D2S-DiffGAN consistently achieves the highest accuracy. Notably, in scenarios where only 10$\%$–20$\%$ of the training data is used, D2S-DiffGAN outperforms ResNet-50 by 9$\%$–11$\%$ and surpasses other advanced GAN variants (EC-GAN, ICUW-GAN) by 1.5$\%$–3$\%$. These results indicate that, by leveraging superior sample generation capabilities and the differentiated loss function (DIFF), D2S-DiffGAN can significantly enhance image classification performance under limited labeled data conditions, further validating its effectiveness.

Fig. 10

Comparison of the accuracies on the test set when different proportions of samples are randomly selected from the CIFAR-10 training set for model training.

Furthermore, to further evaluate the performance of the proposed model on the CIFAR-10 dataset in greater detail, we analyzed its per-class accuracy on the test set when trained with only 5$\%$ of the samples, as shown in Fig 11. The results indicate significant differences in classification difficulty across categories. For instance, animal classes (cat, dog, horse) are generally easier to classify, possibly because they exhibit distinct texture and shape features, enabling the model to learn their representations more accurately. In contrast, the classification difficulty varies among transportation-related classes (airplane, automobile, truck), with airplanes being the most challenging to classify. This may be due to variations in viewing angles and complex backgrounds, making it harder for the model to capture consistent class-specific features. Additionally, small animal classes (deer, frog) exhibit lower classification accuracy, likely because their relatively small size and frequent presence in cluttered backgrounds within the CIFAR-10 dataset increase the classification difficulty.

Fig. 11

Comparison of the accuracy of each category on the CIFAR-10 test set using only 5$\%$ of the training set samples for the proposed model training.

Finally, ablation experiments were conducted on the CIFAR-10 dataset to further validate the effectiveness of the proposed modules. The experimental design was consistent with that used for the SVHN dataset, and the results are presented in Table 3. As shown in the results, both Model 2 and Model 3 achieved higher test accuracy than Model 1 across different training set sizes, indicating that MBFE and DDSGAN contribute to improved classification performance, with DDSGAN having a more significant impact. Furthermore, Model 4 outperformed Model 3, demonstrating that DIFF can further optimize classification performance. Model 5 consistently achieved the best performance across all experimental settings, suggesting that MBFE, DDSGAN, and DIFF complement each other, working synergistically to enhance the model’s learning capability from multiple perspectives and improve its generalization ability across different data scales.

Table 3 The ablation experiments on the CIFAR-10 dataset.

Conclusion

Traditional supervised image classification methods typically rely on large-scale labeled datasets to achieve high performance. However, due to privacy protection, ethical constraints, and the high cost of annotation, constructing large labeled datasets is extremely challenging in many application scenarios. To address this issue, this paper proposes a new fully supervised image classification model (D2S-DiffGAN) under limited labeled samples. In D2S-DiffGAN, a Dual-Domain Synchronized Generative Adversarial Network (DDSGAN) is constructed, which imposes constraints on the generator in both the spatial and frequency domains to improve the quality of generated samples. Additionally, a Multi-Branch Feature Extraction network (MBFE) is designed and integrated with an attention mechanism to enhance the extraction of task-relevant channel features. Meanwhile, a Differentiated Loss Function (DIFF) is introduced to adjust the loss weights based on the distinct characteristics of generated and real images, thereby optimizing the network training process.

Experiments on the SVHN and CIFAR-10 datasets demonstrate that: (1) Compared to standard GAN, DDSGAN can generate more realistic samples with clearer edge details and smoother color transitions, highlighting its advantages in data augmentation; (2) When the number of labeled samples is limited, D2S-DiffGAN outperforms existing methods, validating its effectiveness; (3) Ablation studies further analyze the independent contributions of the MBFE, DDSGAN, and DIFF modules, proving that the joint optimization strategy of these three components plays a crucial role in improving model performance.

Although the proposed method achieves significant improvements under limited labeled samples, there are still areas worth further exploration. Future work may investigate the applicability of D2S-DiffGAN to even smaller datasets and integrate more advanced generation and feature extraction techniques to enhance its generalization ability in complex tasks. Additionally, incorporating semi-supervised or self-supervised learning strategies could further reduce dependence on labeled data, expanding the potential applications of this approach.