Introduction

The deterioration of civil structures and infrastructures stems from factors such as excessive loading, environmental conditions, and natural disasters, often resulting in substantial financial losses1,2. Both short- and long-term structural damages contribute to a decrease in structural lifetime, highlighting the monitoring process’s crucial importance3,4. Conventional methods of SHM, which rely on visual inspection, necessitate the services of certified structural inspectors to evaluate buildings and establish maintenance plans; however, these approaches are demanding, subjective, and susceptible to errors5.

Machine Learning (ML) methodologies have significantly advanced, particularly in the areas of system identification, damage detection, and risk assessment6,7. Additionally, Deep Learning (DL) techniques have garnered significant interest, and particularly, their ability for automatic extraction of complex features in high-dimensional data has led to their widespread adoption across various application fields8,9. Zhang et al10. carried out a study proposing an innovative DL technique to model and predict seismic response, which depends on a Long Short-Term Memory (LSTM) recurrent neural network. Qu et al11. presented the rough set theory and an LSTM network to monitor safety in concrete dams. They also developed single-point and multipoint concrete dam deformation prediction algorithms utilizing LSTM. Furthermore, a novel assessment framework was suggested for a predictive model to forecast the deformation of concrete dams. Mao et al12. conducted a study in which a data anomaly detection approach was presented by employing generative adversarial networks and auto-encoders. Pathirage et al13. carried out a study suggesting an approach for damage detection based upon auto-encoders. The results indicated that the method was capable of discerning patterns between the modal information. Bui-Tien et al.14 introduced a novel framework using the Electric Eel Foraging Optimization algorithm to optimize a DL model combining 1DCNN, Gated Recurrent Units, and Residual Networks, enhancing accuracy and efficiency in bridge damage detection.

CNNs, known for their practicality in processing images15,16 and signals17,18,19have been consistently used to examine the behaviors of various structural systems20,21. In this context, CNNs have been frequently used to assess defects in pavement22,23 and structures24,25. Structural cracks are identified as significant parameters that can influence the performance of structures particularly when subjected to repetitive loads26. In a study, Ali et al27. used eight datasets to assess the effectiveness of five DL models, including a suggested CNN model, for crack localization and detection in structures made of concrete. Kim et al28. utilized an architecture based on CNNs for the purpose of identifying cracks on concrete surfaces, verified using 40,000 images. The outcomes have demonstrated a maximum peak accuracy of 99.8%. Yuan et al29. introduced a methodology for measuring the length of fatigue crack, and the effectiveness of the suggested approach was empirically verified using a compact tensile specimen fatigue test. The outcomes substantiated the approach’s ability to accurately and efficiently measure the length of crack. In addition, new CNNs for the classification of pavement cracks utilizing three-dimensional pictures were suggested in a work by Li et al30.. Pavement patches were categorized into five groups using the suggested CNNs, and of the different suggested CNNs, the total accuracies exceeded 94%.

Another application of CNNs observed in articles involved employing this method to analyze time-frequency images31,32. A study by Jamshidi and El-Badry33investigated the use of CNNs in classifying damage severity. The study used time-frequency representations of acceleration data from multiple sensors for CNN damage identifiers. The evaluation of the CNN-based classifier involves employing a dataset containing the response of a concrete beam subjected to impact hammer tests. It was demonstrated that the utilized method could accurately classify damage at different intensities, ranging from slight to severe. Wang et al34. presented a novel approach to structural damage identification in their study, utilizing the IASC-ASCE SHM benchmark. The abilities of deep neural networks and the Hilbert-Huang Transform were combined in the method. The strategy used in the paper showed advantages in accuracy when compared to SVM and ANN.

Typically, predictions in DL are made using a single model. However, by employing ensemble learning, which integrates multiple models, the accuracy of these predictions can be significantly enhanced. The fundamental principle of ensemble learning is to merge several models, resulting in a more resilient and reliable predictive system. Asghari et al35. introduced an innovative deep ensemble learning approach for detecting structural damages. Lie and Zhao36 introduced a technique to enhance the effectiveness of concrete damage detection by utilizing ensemble learning across various semantic segmentation networks. Their approach involved employing five distinct networks to identify coarse concrete cracks and spalling.

While CNN algorithms have shown promising results in damage detection using time-frequency images obtained from wavelet transform of signals, the studies conducted in this area remain insufficient, as numerous CNN algorithms and factors affecting their performance have not been thoroughly investigated in this field; consequently, these studies need to become more comprehensive. Therefore, the objective of this study is to evaluate and compare the efficacy of multiple fine-tuned CNN algorithms in identifying various types of structural damage, aiming to determine which algorithm achieves the highest prediction accuracy. Moreover, this study proposes a novel application of a voting ensemble of CNN models using time-frequency images for structural damage detection. In this study, acceleration data from different case studies, including an actual bridge in Japan, an experimental steel frame, a grandstand simulator, and a benchmark bridge, is utilized. In conclusion, a thorough parametric investigation is carried out regarding factors influencing prediction accuracy. These factors encompass the type of mother wavelet, the number of input images used to train the algorithms, and the duration of records converted to RGB images.

Methodology

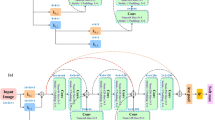
A comprehensive depiction of this research methodology and the algorithms utilized in this investigation is illustrated in Fig. 1. An assortment of CNN-based architectures, including DenseNet 121-based, DenseNet 169-based, DenseNet 201-based, ResNet 50-based, ResNet 101-based, ResNet 152-based, VGG 16-based, and VGG-19-based models, has been employed with the aim of examining the overall capabilities of voting ensemble learning and individual CNNs, as well as contrasting the prediction accuracy of different algorithms for detecting structural damages using time-frequency images derived from wavelet transforms of acceleration response of structures. It should be noted that a dense layer with 1024 neurons was added to well-known CNN architectures before the final output layer. Furthermore, each experiment was repeated Multiple times with different images in training and testing datasets to obviate the necessity for assurance, and the average of them will be presented in the following sections.

Fig. 1
figure 1

An exhaustive overview of the present study.

Full size image

Wavelet transform

Typically, the initial signals are collected in the time domain and sometimes require transformation for subsequent analysis; moreover, the primary objective of employing mathematical transformations is to discern the generative process of the signal by obtaining information within an alternate functional space37. The Wavelet Transform (WT) is a robust technique for investigating the properties of non-stationary signals38. By employing the WT, the signal in the time domain can be transformed into the time-frequency domain, providing further information about both time and frequency characteristics39. The core concept involves employing a mother wavelet \(\:{\varphi\:}\left(\text{t}\right)\).

$$\:{{\varphi\:}}_{{\upalpha\:},{\uptau\:}}=\frac{1}{\sqrt{{\upalpha\:}}}{\varphi\:}\left(\frac{\text{t}-{\uptau\:}}{{\upalpha\:}}\right)$$
(1)

where \(\:{\uptau\:}\) and \(\:{\upalpha\:}\) represent the translation parameter and scale parameter, respectively. Continuous Wavelet Transform (CWT) of a signal \(\:\text{f}\left(\text{t}\right)\) can be given by the following equation40.

$$\:{{\upomega\:}}_{\text{t}}\left({\upalpha\:},{\uptau\:}\right)=\frac{1}{\sqrt{{\upalpha\:}}}{\int\:}_{-{\infty\:}}^{+{\infty\:}}\text{f}\left(\text{t}\right){\varphi\:}(\frac{\text{t}-{\uptau\:}}{{\upalpha\:}})\:\text{d}\text{t}$$
(2)

In this article, CWT is employed to convert the structural response data, obtained from various conditions of the structure, including healthy and various damaged states, into time-frequency images. These images serve as inputs for training the CNN models. By transforming the raw structural response into time-frequency representations, the CWT enables the extraction of detailed features from different states of the structure, facilitating the training process of CNN models to accurately differentiate between different conditions.

Image preprocessing and dataset

Numerous RGB images, each sized 224 × 224 × 3, have meticulously been generated with the utilization of the CWT. These visual representations were derived from the responses extracted from accelerometers positioned within the structures. The quantity of time-frequency images and the specific duration of each record vary and will be elaborated upon extensively in the section dedicated to each considered structure.

Convolutional neural networks

The concept of CNN, a DL method, takes inspiration from the principles of visual neuroscience; furthermore, the CNN architecture typically comprises phases for extracting features and carrying out classification41,42. CNN uses the weight-sharing procedure within its convolutional layers and can lower the quantity of training parameters32. In a convolutional layer, the input layer is convolved with kernels, resulting in the generation of intermediate feature maps through the following process.

$$\:{\text{X}}_{\text{j}}^{\text{L}}=\text{S}(\sum\limits_{\text{i}\in\:{\text{M}}_{\text{j}}}{\text{X}}_{\text{i}}^{\text{L}-1}\text{*}{{\upomega\:}}_{\text{i}\text{j}}^{\text{L}}+{\text{b}}_{\text{j}}^{\text{L}})$$
(3)

where, \(\:{\text{X}}_{\text{i}}^{\text{L}}\) and \(\:{{\upomega\:}}_{\text{i}\text{j}}^{\text{L}}\) indicate the i-th channel of layer L and the i‐th channel of filter j in layer L, respectively. Moreover, S is called the activation function and \(\:{\text{b}}_{\text{j}}^{\text{L}}\) is the bias parameter43. Frequently, a pooling layer is used among a series of consecutive convolutional layers, to mitigate the potential for overlearning44. The size of the input is gradually reduced through pooling layers; furthermore, the pooling layer lowers the quantity of parameters and calculations in the network45. Fully connected layers establish connections connecting each neuron in a particular layer to every individual neuron in a subsequent layer46. Despite the feature extraction role of convolutional and pooling layers in processing input images, it is the fully connected layers taking the responsibility of classifying47,48.

CNNs have evolved with various architectures, each offering unique advantages for image classification. Given the excellent performance of VGG, ResNet, and DenseNet models in image classification, as demonstrated in numerous research papers, these architectures have been chosen for this article. Each of these CNN models has been widely recognized in the field of computer vision. The selection of these architectures in this article is driven by their proven effectiveness across various image classification challenges, aiming to leverage their complementary strengths to achieve state-of-the-art performance.

Fine tuning

Either from scratch or by transfer learning, a CNN model is able to be trained. Transfer learning offers a potent technique to mitigate the reliance of DL approaches on the quantity of available data. Using small-scale datasets or datasets consisting of similar samples, CNNs trained from scratch might experience overfitting, whereas transfer learning is able to mitigate this problem. The utilization of fine-tuning can boost classifier accuracy by transferring knowledge from domains with huge amounts of data49,50. Weights of the model were assigned according to a pre-trained algorithm in the fine-tuning of CNNs, with the exception that a number of the final blocks were left unfrozen to allow for weight adjustments during the training procedure51. In this investigation, all blocks of considered CNNs were frozen except two final blocks.

In the given architecture, the fully connected layer with 1024 neurons is placed before the final classification layer. Additionally, a dropout layer is applied after this dense layer to reduce overfitting by randomly deactivating a subset of neurons during training. After global average pooling compresses the spatial dimensions of the deep features into a vector, this dense layer introduces non-linearity and additional depth, allowing the model to learn more expressive and task-specific feature representations.

Ensemble learning

Ensemble learning refers to a method in ML that various models are combined to create a unified model52. This method boosts the precision and reliability of predictions by integrating multiple models, making it ideal for datasets with small samples and imbalanced distributions53; moreover, it is highly preferred in engineering prediction tasks because of its robustness and superior performance compared to individual models54. Ensemble learning takes advantage of the benefits that different models provide on different data to enhance overall performance53.

A voting classifier functions as a classifier that consolidates the outputs of different ML models, whether they are identical or conceptually diverse, using a majority vote to determine the final prediction55. The voting classifier primarily operates with two techniques, including hard voting and soft voting. In hard voting, the final outcome is determined by counting the class votes from each individual model. The class that garners the majority of votes from the base learners is selected as the final prediction56. Soft voting generates the final prediction by analyzing the probability outputs from each base model. The technique determines the final class by summing the weighted prediction probabilities provided by all classifiers for each possible class. The class with the greatest overall probability is selected as the output label57.

Metrics

The confusion matrix is commonly employed to illustrate how successfully classification algorithms perform. Every component within the matrix denotes the overall number of times the experiments are classified in the related anticipated category. As can be seen, the following equations provide the formula of metrics used to assess the efficacy of different identification models in this paper58.

$$\:\text{R}\text{e}\text{c}\text{a}\text{l}\text{l}=\frac{\text{T}\text{P}}{\text{T}\text{P}+\text{F}\text{N}}$$
(4)
$$\:\text{P}\text{r}\text{e}\text{c}\text{i}\text{s}\text{i}\text{o}\text{n}=\frac{\text{T}\text{P}}{\text{T}\text{P}+\text{F}\text{P}}$$
(5)
$$\:\text{F}1-\text{s}\text{c}\text{o}\text{r}\text{e}=\left(\frac{2\text{*}\text{r}\text{e}\text{c}\text{a}\text{l}\text{l}\text{*}\text{p}\text{r}\text{e}\text{c}\text{i}\text{s}\text{i}\text{o}\text{n}}{\text{r}\text{e}\text{c}\text{a}\text{l}\text{l}+\text{p}\text{r}\text{e}\text{c}\text{i}\text{s}\text{i}\text{o}\text{n}}\right)$$
(6)
$$\:\text{A}\text{c}\text{c}\text{u}\text{r}\text{a}\text{c}\text{y}=\frac{\text{T}\text{P}+\text{T}\text{N}}{\text{T}\text{P}+\text{T}\text{N}+\text{F}\text{P}+\text{F}\text{N}}$$
(7)

where TP, FP, FN, and TN stand for true positive, false positive, false negative, and true negative, respectively.

Sensitivity analyses

In the process of determining the damage type through the approach detailed in this study, it becomes apparent that distinct parameters hold varying degrees of influence on the predictions. This section focuses on investigating the impact of three specific parameters using University of Central Florida (UCF) benchmark structure as a case study. By analyzing these parameters in detail, this article aims to gain an understanding of how they affect the overall predictive performance of the proposed method.

University of central Florida benchmark structure

Numerical simulation makes it possible to calculate the solutions of the models computationally, providing a way to replicate real-world physical behavior59. The bridge model, created at the UCF, was employed in this section to assess the effect of three parameters on the performance of considered individual CNN algorithms60,61. The bridge has been made of two 5.49 m long girders, seven 1.83 m long beams, and six 1.07 m tall columns. The cross sections of all beams and columns correspond to S3 × 5.7 and W12 × 26, respectively. Each structure component was joined by a simple, hinged, fixed, or semi-fixed restraint62. The schematic of the considered structure, is illustrated in Fig. 2.

Fig. 2
figure 2

Schematic of the UCF benchmark model, drawn with the aid of SeismoStruct v202563, website: https://www.seismosoft.com.

Full size image

The structure’s acceleration responses were analyzed in an intact state and five different damaged conditions. These damages involved modifications to the connections between the longitudinal and transverse components, adjustments to the deck’s boundary conditions, and Changes in the stiffness of springs positioned at the supports of the bridge. A force of 10 kN was applied to Node 170 to simulate dynamic excitation, and six accelerometers were utilized to capture the data. The arrangement of sensors, damaged points, and the place of the applied load can be observed in Fig. 3. Furthermore, Table 1 provides comprehensive details on all the states that have been taken into account.

Fig. 3
figure 3

Location of sensors, damages, and the loading.

Full size image
Table 1 Description of the assessed conditions for the UCF benchmark bridge.
Full size table

The networks were trained using time-frequency images generated by CWT with the Bump mother wavelet. The responses were split into 1200 matrices for each condition, with each matrix containing 15 s of acceleration data. An RGB image is generated using one matrix for each condition. Figure 4 provides a representation of the responses of all states, accompanied by their respective time-frequency images.

Fig. 4
figure 4

Samples of the UCF benchmark bridge time-frequency images.

Full size image

Results

In each of the experiments, the algorithms underwent both training and testing with about 80% and 20% of all images, respectively. The average values of accuracy, precision, F1 score, and recall across all experiments conducted for each algorithm have been calculated and are visually represented in Fig. 5.

Fig. 5
figure 5

The outcomes of the various architectures in the UCF benchmark bridge.

Full size image

Figure5 makes it clear that DenseNet201-based algorithm outperformed with the highest accuracy at 99% in predicting the types of damages. Furthermore, the three DenseNet-based methods, boasting an average accuracy of 98.8%, demonstrated superior predictive capabilities for types of damages compared to the others.

Evaluating the influence of number and duration of input acceleration records

The training procedure, computational cost, and accuracy of predictions can be strongly affected by the quantity of input images. A larger dataset can provide richer information, allowing the model to be trained better and make more accurate predictions. However, it is crucial to consider that collecting a huge amount of data entails substantial costs; moreover, it is probable that sufficient data in some structures might not be accessible. Consequently, the network might face difficulties in training correctly with limited image data, impacting its accuracy in recognizing various structural damage types. Furthermore, the duration of records converted to time-frequency images could have an impact on the extent to which the method is capable of accurately anticipating the results. Records with a longer duration may contain more comprehensive information; however, accumulating a significant amount of data still face the same issues previously mentioned. This section concentrates on how variations in record duration and number can affect the algorithms’ outcomes.

In this part, the efficiency of the considered network in forecasting the proper state is evaluated using various Quantities of input images acquired from acceleration responses of the UCF benchmark bridge with different durations. Consequently, the network has been given 100%, 90%, 80%, 70%, 60%, and 50% of the entire dataset, which equals 2400 images in every state, in order to be fine-tuned. It should be noted that each dataset consists of images derived from record with durations of either 6-, 9-, 12-, and 15-second employing Amor mother wavelets. Figure 6 (a) illustrates a three-dimensional representation of the changes in prediction accuracy regarding this matter. Moreover, Fig. 6 (b) shows the radar plot of the prediction accuracy of records with different periods in detecting damage types. Each vertex represents the number of images in each state used in the training and testing process, and each grid indicates the prediction accuracy. It is important to highlight that DenseNet121-based model was utilized in this section, given its proper performance observed in the results and its low number of parameters.

Fig. 6
figure 6

The influence of the number and duration of records on accuracy.

Full size image

Based upon Fig. 6 (a), as the duration of recorded data extends, there is a notable improvement in the accuracy of the results. This trend suggests that longer recording durations provide more comprehensive information, which enhances the performance of the model. Additionally, increasing the number of images used for fine-tuning enhances the precision of the outcomes. With a larger set of images, the model can more effectively identify and learn from patterns and variations, leading to stronger and more precise predictions. However, it is essential to acknowledge the impact of reducing these factors. On average, a shorter duration of records results in an accuracy loss of approximately 4.3%. Similarly, a reduction in the number of input images used for fine-tuning leads to an average accuracy loss of around 2.7%. Figure 6 (b) demonstrates that as the duration of each recording increases, the impact of the number of images on the algorithm’s performance lessens. Specifically, when each recording is 6 s long, increasing the number of images improves performance by 3.6%. However, when the recording length extends to 15 s, this impact drops to 1.7%.

Mother wavelet’s impact on time-frequency images

The deployment of different types of mother wavelet not only leads to changes in the time-frequency images but also might possess an influence on performance of the algorithms. This section examines the effect of changes in mother wavelet types on the outcomes. Accordingly, three different types of commonly used mother wavelet, including Morse, Amor, and Bump, were employed in order to transform the acceleration responses gathered by sensors placed in the UCF benchmark bridge into images. Figure 7 displays the results of this investigation using average prediction accuracy. It is crucial to point out that, based on the superior performance noted in the Sect. “University of central florida benchmark structure”, DenseNet169-based and DenseNet201-based models were selected for use in this section.

Fig. 7
figure 7

The effect of various mother wavelet types on the performance of the considered algorithms.

Full size image

As delineated by the data presented in Fig. 7, the utilization of Bump and Amor mother wavelets yields the highest and lowest values, respectively. Moreover; the Bump mother wavelet appeared to perform slightly better, possibly because of its ability to focus more clearly on relevant frequency bands. Additionally, the results highlight that DenseNet201-based algorithm exhibits less sensitivity to changes in the choice of mother wavelet. Given the beneficial effect of the Bump mother wavelet, this mother wavelet has been used to convert the acceleration responses into time-frequency images in the following case studies.

Case studies

In this part, the potency of the mentioned CNN algorithms, along with the voting ensemble learning method in detecting the damage types has been thoroughly verified through conducting assessments on three different structures, including a steel truss bridge placed in Japan, an experimental five-story steel frame, and Qatar University’s Grandstand Simulator (QUGS). Each structure offers different challenges and conditions, making the assessments comprehensive and reliable in verifying the models’ capabilities.

The old ADA steel truss Bridge

The acceleration responses of the Old ADA bridge in Japan have been utilized in this section in order to verify the efficacy of different algorithms in a real-world bridge64,65. The dimensions of the main span of the bridge, which was erected in 1959 and demolished in 2012, are 59.2 m in length and 3.6 m in width. Prior to the removal of the bridge, different types of damages were artificially simulated, and environmental vibrations were recorded66.

Four various structural health states were taken into account, which are: case I, Intact structure; case A, at the mid-span of the structure, one of the vertical elements was cut to half of its initial section area; case B, the mentioned element was cut entirely; case C, at the 5/8th span, one vertical truss element was wholly cut after reparation of the element mentioned in last cases. In Fig. 8, the damage scenarios are depicted67.

Fig. 8
figure 8

Visualization of damage locations.

Full size image

Responses collected from accelerometers were categorized into four groups, consisting of 672, 456, 584, and 568 five-second segments, respectively, with regard to the availability of data. Figure 9 illustrates examples of the acceleration responses and time-frequency images for the mentioned states.

Fig. 9
figure 9

Samples of the Old ADA bridge time-frequency images.

Full size image

Results

In all of the conducted experiments, the authors utilized 80% of the dataset, which was gathered from all available sensors, for both the training and validation phases. This portion of the data was used to fine-tune the models and ensure they were properly adjusted for optimal performance. The remaining 20% of the dataset was set aside exclusively for testing purposes, allowing for the evaluation of the algorithms’ performance on unseen data. Table 2 provides a clear comparison of the performance of different algorithms in predicting damage types and contains the averages of accuracy, precision, F1_score, and recall of conducted experiments.

Table 2 The outcomes of the various methods in the old ADA bridge.
Full size table

Table 2 distinctly reveals that voting ensemble method, with accuracy rates of 97.5% and 97%, effectively demonstrates its capability in predicting damage types. Additionally, the DenseNet201-based algorithm set itself apart by achieving the highest accuracy of 96.3%, outperforming other CNNs in the case study. Furthermore, Fig. 10 (a) visually presents the confusion matrix from one of the analyses conducted with hard voting ensemble learning, while Fig. 10 (b) displays the ROC curve generated from one of the experiments employing each of the CNN architectures.

In this case study, the recorded training times per epoch showed that DenseNet121-based, DenseNet169-based, and DenseNet201-based models took about 4, 6, and 7 s, respectively. Models based on VGG16 and VGG19 required around 3 and 4 s per epoch, respectively. Similarly, ResNet50-based model completed each epoch in around 3 s, while ResNet101-based and ResNet152-based models required about 6.5 and 9 s, respectively. It is worth noting that these training times were measured during one of the training processes for each model using CNN-based architectures with the Adam optimizer, categorical cross-entropy loss function, and a batch size of 32.

It should be noted that given the differences in the number of images across classes, techniques such as over-sampling, under-sampling, or class weighting were not applied, since classification performance was consistently high and no significant bias toward majority classes was observed.

Fig. 10
figure 10

Results of classifying types of structural damage in the Old ADA bridge: (a) Confusion matrix of test dataset; (b) ROC curve.

Full size image

The experimental five-story steel structure

A detailed laboratory experiment was conducted on a five-story steel frame structure to evaluate its behavior under impact loading conditions. The mentioned study involved capturing various vibration responses, including acceleration, strain, and excitation force, with data being recorded at a sampling rate of 500 Hz for intact state and different damaged scenarios. The structure was built utilizing columns that measure 8 mm by 8 mm and beams that are 6 mm by 6 mm, with twenty of each element included in the design. These elements were assembled into a three-dimensional framework using 40 joints to interconnect them. At the ends of the beams and columns, C-shaped joint mechanisms were used68,69. An image of that experiment is shown in Fig. 11 (a).

Fig. 11
figure 11

(a) The experimental five-story steel structure; (b) Locations and directions of accelerometers and forcing69.

Full size image

To simulate damage, a healthy beam on the third floor of the frame was substituted with a damaged member in each case. Force measurements were obtained using an impact hammer, and acceleration responses of the experimental frame were recorded utilizing 12 accelerometers. Figure 11 (b) illustrates the locations and directions of the accelerometers and that of the applied forces69. The considered beam experienced three different types of structural anomalies:

Case H: The beam’s cross-section was altered to 8 mm by 8 mm.

Case L: The cross-section was further reduced to 4 mm by 4 mm.

Case R: Partial damage was introduced by decreasing the cross-section by 1 mm in both width and depth, in a portion of the beam.

The results from each accelerometer were segmented into 5-second intervals that encompassed the force application period for each case. These segments were then converted into time-frequency images. Figure 12 presents samples of acceleration responses from various states, along with their time-frequency images.

Fig. 12
figure 12

Samples of the experimental Five-Story steel structure time-frequency images.

Full size image

Results

The entire dataset, which included a total of 2200 time-frequency images, was divided into training and testing subsets. Specifically, 80% of the images were used for training purposes, while 20% were set aside for validation and testing. Detailed results from the experiments conducted with each algorithm are outlined in Table 3.

Table 3 The outcomes of the various methods in the experimental 5-story steel frame.
Full size table

Table 3 reveals that the DenseNet121-based algorithm attained the highest accuracy in predicting damage types. Furthermore, the performance of both soft and hard voting ensemble learning methods, which achieved accuracy rates of 98.9% and 98.5% respectively, demonstrates a substantial improvement over the individual algorithms. In this case study, which focuses on various conditions taken place in a beam of the three-dimensional frame, the DenseNet-based models generally demonstrate superior performance compared to the ResNet-based and VGG-based models. In Fig. 13 (a), the confusion matrix is represented, stemming from an analysis that employed hard voting ensemble learning. Meanwhile, Fig. 13 (b) depicts the ROC curve produced from an experiment utilizing each of the considered CNNs.

In one of the training procedures using CNN-based architectures with the Adam optimizer, categorical cross-entropy loss function, and a batch size of 32, the approximate training time per epoch for each CNN architecture was measured independently. DenseNet121-based, DenseNet169-based, and DenseNet201-based models required approximately 5, 7, and 9 s per epoch, respectively. VGG16-based and VGG19-based models completed each epoch in about 4 and 5 s, while ResNet50-based model took 4 s. The deeper ResNet models, namely ResNet101-based and ResNet152-based models, required around 8 and 11.5 s per epoch, respectively.

Fig. 13
figure 13

Results of classifying types of structural damage in the experimental 5-story steel frame: (a) Confusion matrix of test dataset; (b) ROC curve.

Full size image

Qatar university grandstand simulator

It is essential to experimentally test the newly-introduced methods in a controlled laboratory setting before they are applied to real-life structures; QUGS, illustrated in Fig. 14, has been built for this purpose70. This structure, with dimensions of 4.2 m by 4.2 m in plan, was engineered to accommodate 30 spectators. The steel frame is composed of 8 main girders and 25 filler beams, all supported by 4 columns. The 8 girders measure 4.6 m in length, while the 5 filler beams in the lower section are approximately 1 m long. The remaining 20 beams each have a length of 77 cm. The two long columns are about 1.65 m in length71,72,73.

Fig. 14
figure 14

QUGS (Light green represents the girders, whereas the filler beams are depicted in dark green.).

Full size image

In this case study, the structural damage was created by loosening the connection bolts which resulted in a slight change in rotational stiffness at the connections74,75; moreover, different bolts were loosened to create various slight damage cases in the benchmark structure17. It should be noted that a shaker was used to dynamically excite the structure, and an accelerometer placed at each beam-to-girder intersection measured and recorded the vibration response for undamaged and damaged conditions. Six damage conditions, resulting from loosening bolts at one joint of the structure, were randomly selected to evaluate the performance of the considered algorithms. Figure 15 illustrates the locations where these considered damages occurred.

Fig. 15
figure 15

Placement of considered damages in QUGS.

Full size image

The recorded results from each accelerometer were meticulously divided into 25 segments, with each segment consisting of 10-second recordings corresponding to every individual case. To perform the training procedure, these segments were subsequently transformed into time-frequency images by employing the Bump mother wavelet. This transformation was carried out as it leads to the extraction of both time and frequency information. Figure 16 presents samples of the acceleration responses, accompanied by their corresponding time-frequency images.

Fig. 16
figure 16

Samples of the QUGS time-frequency images.

Full size image

Results

It should be borne in mind that the dataset comprised a total of 5,250 images across all cases. Of these, approximately 4,200 images were set aside for training and validation purposes, allowing the models to learn effectively; furthermore, the remaining images were specifically reserved for the testing phase, which facilitates an evaluation of the models’ performance on previously unseen data. Table 4 details the outcomes obtained from all experiments conducted using each algorithm.

Table 4 The outcomes of the various architectures in the QUGS.
Full size table

Table 4 clearly indicates that soft voting ensemble learning achieved an accuracy of 99%, reflecting its highly favorable performance in predicting different damage conditions. Among the individual algorithms assessed, VGG16-based algorithm distinguished itself by achieving the highest accuracy, making it the top performer in this evaluation. In this case study that different damage scenarios featured the same type of damage occurring in various locations within the structure, VGG-based models excelled in accurately identifying different states in comparison to DenseNet-based models and ResNet-based models. In Fig. 17 (a), the confusion matrix is illustrated, derived from an analysis using soft voting ensemble learning, and, Fig. 17 (b) shows the ROC curve obtained from an experiment that evaluated the considered CNNs. In one of the training processes using CNN-based architectures with the Adam optimizer, categorical cross-entropy loss function, and a batch size of 64, the approximate average training time per epoch for each CNN model was recorded to assess computational demand during model fitting. DenseNet121-based and ResNet50-based models each required roughly 6.5 s per epoch. DenseNet169-based and DenseNet201-based models took about 9.5 and 13 s, respectively, reflecting the increased complexity in their deeper architectures. VGG16-based and VGG19-based models required approximately 7 and 9 s, respectively. ResNet101-based and ResNet152-based models, showed around 14 and 20 s per epoch, respectively.

Fig. 17
figure 17

Results of classifying types of structural damage in the QUGS: (a) Confusion matrix of test dataset; (b) ROC curve.

Full size image

Conclusions

The principal goal of the present study is to evaluate the robustness of voting ensemble learning and examine the efficacy of various CNNs utilizing time-frequency images in classifying the health status of structures. To validate the results derived from different algorithms in detecting types of damage, the acceleration responses obtained from three structures were converted into time-frequency images through wavelet transformation. The subsequent step involved training different algorithms using the transformed images. The findings demonstrated that within the considered structures, the utilization of voting ensemble learning, including hard and soft methods, gave rise to average prediction accuracy of 98.2%. Furthermore, in a comparison of various individual CNN architectures, DenseNet201-based algorithm demonstrated the best performance in two case studies, which analyzed different types of damage conditions. Specifically, this algorithm achieved 96.3% and 99% accuracy, respectively, outscoring all other models considered. In the experimental five-story steel structure, which considered damage scenarios within one location, DenseNet121-based algorithm excelled with a 95.4% prediction accuracy, outperforming all other models in this specific structure. The VGG16-based algorithm demonstrated outstanding performance in the last case study, which focused on a single damage type across multiple locations, achieving a 96.2% prediction accuracy and surpassing all other models.

Prior to investigating the mentioned case studies, a comprehensive sensitivity analysis was carried out to assess the parameters that might impact the performance of the algorithms. First, the examination of the final results investigated the utilization of mother wavelets, including Morse, Amor, and Bump. The outcomes showed that the utilization of Bump mother wavelet consistently led to demonstration of the highest accuracy across the considered structure. Additionally, the impact of varying the duration of each record, converted into each RGB image, on prediction accuracy was evaluated, and the investigation revealed that employing records with a duration of 15 s Yielded the highest accuracy compared to durations of 6, 9, and 12 s. Finally, the influence of the quantity of input time-frequency images on accuracy of outcomes was explored, and the findings indicated that a reduction in the number of input data correlated with a decrease in prediction accuracy.