Economic dispatch of multimicrogrid interconnected system based on bilevel robust optimization

Abstract

Driven by the accelerated advancement of microgrid technologies and the surging demand for regional power supply assurance, multi-microgrid (MMG) systems confront significant operational challenges pertaining to economic efficiency and power supply reliability. Based on the assumption that the microgrid adopts the grid-connected mode, this study proposes a bi-level robust optimization framework for interconnected system coordination to address the inherent stochasticity of renewable energy generation in MMG collaborative operations. Primarily, a microgrid-level robust optimization model is formulated to identify adverse boundary conditions through operating cost maximization under internal uncertainty scenarios, thereby yielding a day-ahead scheduling strategy that achieves optimal balance between conservativeness and economic viability. Subsequently, a cooperative optimization paradigm for MMG systems is developed, which enables spatio-temporal optimization of cross-microgrid resource allocation through rigorous analysis of energy exchange constraints and distribution network interconnection dynamics. The solution methodology employs a column-and-constraint generation (C&CG) algorithm integrated with strong duality theory, implementing a master-subproblem alternating iteration mechanism for model decomposition. The simulation results demonstrate that the established multi-microgrid interconnected system can reduce the overall operational cost of the microgrid cluster by up to 28.9%, validating its significant economic and robustness advantages under conditions of electricity price fluctuations.

Introduction

Microgrids, as critical components of modern power systems, integrate distributed renewable energy (DER), energy storage systems (ESS), and flexible loads to establish autonomous “source-grid-load-storage” ecosystems¹. This integration enhances distribution grid resilience and renewable energy accommodation capacity, particularly under high renewable penetration scenarios². The energy transition acceleration has further positioned regional multi-microgrid (MMG) systems as pivotal infrastructure, leveraging their synergistic advantages in energy efficiency optimization, fault isolation, and market participation mechanisms³. Consequently, optimizing MMG operational economy and reliability while addressing renewable generation intermittency constitutes a primary research frontier.

Although increasing the penetration of renewable energy into existing systems offers many benefits, it also introduces stability challenges. The intermittent nature of renewable resources can lead to an imbalance between supply and demand, causing reliability issues, voltage fluctuations, and stability problems in the grid⁴. The existing microgrid scheduling considering uncertainty is mainly realized from the coordinated optimization operation of multiple time scales or the uncertainty optimization methods such as stochastic optimization and robust optimization⁵. Literature⁶ proposes a multi-timescale optimal scheduling method for integrated energy systems based on distributed model predictive control, which considers the complexity of the overall solution of the system with distributed structure, and achieves flexible scheduling of the integrated energy system through the co-ordination of various sub-systems. The paper⁷ combines demand-side management (DSM) and energy management strategies (EMS), and proposes a three-stage stochastic EMS framework to solve the problem of optimal scheduling of grid-connected generating units and minimization of operating costs. In the literature⁸, a two-stage robust optimization framework is constructed for high penetration renewable energy scenarios in Southwest China, and the Benders decomposition algorithm is used to solve the economic optimal solution under extreme weather.

While progress has been made in MMG interconnection scheduling, critical knowledge gaps persist. Literature⁹ proposes a MMG interactive operation strategy based on alternating direction method of multipliers (ADMM) for multi-scenario counties. Literature¹⁰ proposes a distributed regulation model and an upper and lower level interaction and coordination mechanism for multi-park integrated energy systems, and constructs a two-layer optimal dispatch model for multi-park integrated energy systems and distribution grids that considers different interests. In the past two years, the research on multi microgrid has gradually deepened, aiming to improve energy efficiency and reduce costs. Literature¹¹ proposes a techno-economic analysis model for energy storage systems in multi-energy microgrids and employs a decomposition approach to solve the optimization problem while considering investment and maintenance costs of the storage systems. Literature¹² proposes a bi-level noncooperative dispatch strategy that takes into account user satisfaction and willingness to consume renewable energy, aiming to maximize the revenue of microgrid operators and the welfare of users. Literature¹³ investigates stochastic energy management optimization in multi-microgrid systems considering energy efficiency strategies and proposes a two-stage stochastic programming framework integrating independence index and Expected Energy Not Supplied (ENS).

Building upon these foundations, this study develops a bi-level robust optimization model for MMG economic dispatch to optimize the energy management system of microgrids under the worst operating conditions, while taking into account the renewable energy uncertainty and load power fluctuation. The framework introduces microgrid energy interaction and distribution network power mutual aid constraints, considers time-of-day electrovalence and demand response loads, and employs alternating master-subproblem resolution to derive optimal scheduling strategies under worst-case operational scenarios, balancing computational efficiency with solution robustness. The main contributions of this study are manifested in the following aspects:

• 1. To achieve cost-effective and efficient operation under the collaborative operation of heterogeneous microgrids, this paper innovatively constructs a multi-microgrid interconnected system that encompasses microgrid energy interaction and power mutual support. Based on this system, a bi-level robust optimization model is established, which is capable of accurately solving for the globally optimal dispatch scheme under the worst-case scenarios.

• 2. Currently, most existing literature simplifies the model by setting the market electricity price as a fixed value during the optimization process, such as Literature¹⁴. In contrast, this study fully incorporates the time-of-use electricity pricing mechanism into the model construction, making it more in line with the actual power supply conditions of the power system. Meanwhile, by taking full account of the characteristics of demand response loads, it successfully achieves peak shaving and valley filling through scientific and rational dispatch strategies, effectively alleviating the power supply pressure on the grid and enhancing the operational stability and economic efficiency of the power system.

• 3. This study conducts in-depth and detailed discussions and analyses on the impacts of uncertain parameter selection and real-time electricity price fluctuations on the cost of the bi-level robust model, further verifies the robustness of the constructed model when facing complex and variable operating environments, providing a reliable basis for the practical application of the model.

The subsequent content of this paper is organized as follows: Section 2 provides a detailed description of the multi-microgrid interconnected system; Section 3 focuses on elaborating the construction process of the bi-level robust optimization dispatch model; Section 4 introduces the solution methods employed to solve this model; Section 5 conducts deep discussions on the simulation results of the case study; finally, Section 6 summarizes the entire paper and draws conclusions.

Model of MMG interconnected system

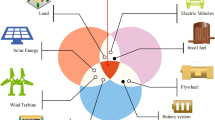
Constructed upon the foundational architecture of single-microgrid systems, the multi-microgrid interconnection system integrates considerations of power equilibrium within individual microgrids alongside inter-microgrid energy interaction. Its operational control framework is structured into two distinct layers: the single-microgrid internal control layer and the multi-microgrid inter-coordination control layer³. The centralized control paradigm employed within the multi-microgrid system is illustrated in Figure 1, wherein each constituent single microgrid incorporates controllable distributed generation units, renewable distributed generation resources, energy storage systems, and load.

Figure 1

Structure of multi-microgrid system.

Controllable distributed generation

Micro gas turbines (MGTs) can be considered as flexible dispatch resources in integrated energy systems due to their flexibility and fast response capability¹⁵. Using micro gas turbines as the controllable distributed generation inside the microgrids, the cost function is expressed by a linear function with the following equation:

$$\begin{aligned} C_{G,t,i}=\begin{bmatrix}a_{i}P_{G,t,i}+b_{i}\end{bmatrix}\Delta t \end{aligned}$$

(1)

Where $C_{G,t,i}$ represents the power generation cost of the i th micro grid MGT in t period; $P_{G,t,i}$ denotes the power generation; $a_{i}$, $b_{i}$ is the cost coefficient; and $\Delta t$ is the scheduling duration, which takes the value of 1h.

The upper and lower output power constraints without considering the climb rate constraint:

$$\begin{aligned} P_{G,i}^{min}\le P_{G,t,i}\le P_{G,i}^{max} \end{aligned}$$

(2)

$P_{G,i}^{max}$ and $P_{G,i}^{min}$ are the upper and lower limits of the MGT output power, respectively.

Energy storage model

In microgrid systems, energy storage can play a role in smoothing fluctuations, shaving peaks and filling valleys, and it is an effective and necessary initiative to deploy energy storage to improve system regulation¹⁶¹⁷. Considering its primary investment cost and operation and maintenance cost, the average charging and discharging cost is expressed as:

$$\begin{aligned} C_{S,t,i}=K_{S,i}[P_{dis,t,i}/\eta _{i}+P_{ch,t,i}\eta _{i}]\Delta t \end{aligned}$$

(3)

Where $C_{S,t,i}$ denotes the charging and discharging cost of the energy storage device within the i th microgrid during t period; $P_{ch,t,i}$ and $P_{dis,t,i}$ are the charging power and discharging power, respectively; $K_{S,i}$ is the charging and discharging cost coefficient; and $\eta _{i}$ denotes the charging and discharging efficiency.

The energy storage constraints mainly consider the energy storage capacity change and charging/discharging power constraints with the following equations:

$$\begin{aligned} & {\left\{ \begin{array}{ll} 0\le P_{dis,t,i}\le U_{S,t,i}P_{S,i}^{max}\\ 0\le P_{ch,t,i}\le [1-U_{S,t,i}]P_{S,i}^{max}& \end{array}\right. } \end{aligned}$$

(4)

$$\begin{aligned} & \eta _i\sum _{t=1}^{N_T}\left[ P_{ch,t,i}\Delta t\right] -\frac{1}{\eta _i}\sum _{t=1}^{N_T}\left[ P_{dis,t,i}\Delta t\right] =0 \end{aligned}$$

(5)

$$\begin{aligned} & E_{S,i}^{min}\le E_{S0,i}+\eta _{i}\sum _{t^{\prime }=1}^{t}\left[ P_{ch,t^{\prime },i}\Delta t\right] -\frac{1}{\eta _{i}}\sum _{t^{\prime }=1}^{t}\left[ P_{dis,t^{\prime },i}\Delta t\right] \le E_{S,i}^{max} \end{aligned}$$

(6)

Equation (4) is the energy storage charging and discharging power constraints, in which $P_{S,i}^{max}$ and $P_{S,i}^{min}$ are the upper and lower limits of charging and discharging power, respectively; $U_{S,t,i}$ denotes the charging and discharging state of the energy storage, which is discharged when taking the value of 1, and recharged when taking the value of 0. Equation (5) shows the capacity constraints at the beginning and end of scheduling, in which $N_T$ is the scheduling period and takes the value of 24h. Equation (6) shows the residual capacity constraints for each time period, in which $E_{S,i}^{max}$ and $E_{S,i}^{min}$ are the upper and lower limits of the energy storage capacity, respectively; and $E_{S0,i}$ is the storage capacity at the initial scheduling moment.

Demand response load

Electricity demand response (DR) mechanisms emphasize bidirectional interactions between the supply-side and demand-side entities within the power grid, wherein the demand-side modulates its load consumption patterns in response to dynamic electricity market pricing signals and grid operational requirements, with the objective of securing compensatory economic incentives¹⁸. The demand response load modulation process must adhere to the following operationally-binding constraints:

$$\begin{aligned} & \sum _{t=1}^{N_{T}}P_{DR,t,i}\Delta t=D_{DR,i} \end{aligned}$$

(7)

$$\begin{aligned} & D_{DR,i}^{min}\le P_{DR,t,i}\Delta t\le D_{DR,i}^{max} \end{aligned}$$

(8)

Where $P_{DR,t,i}$ represents the dispatching power of the i th microgrid in the demand response load in t period; $D_{DR,i}$ is the total electricity demand of the demand response in the dispatch cycle; $D_{DR,i}^{max}$, $D_{DR,i}^{min}$ denotes the upper and lower limits of the electricity demand of the demand response load in time period t. Subject to the constraints being satisfied, the dispatch cost function is expressed as:

$$\begin{aligned} C_{DR,t,i}=K_{DR,i}|P_{DR,t,i}-P_{DR,t,i}^{*}|\Delta t \end{aligned}$$

(9)

Equation (9) expresses the difference between the actual dispatch power of demand response loads and the expected electricity consumption plan in absolute terms. Where $P_{DR,t,i}^{*}$ represents the expected power consumption; $K_{DR,i}$ is the unit dispatch cost of demand response load. Introducing the auxiliary variable $P_{DR1,t,i}$, $P_{DR2,t,i}$ to linearise this equation into Equation (10), $P_{DR1,t,i}$ and $P_{DR2,t,i}$ satisfies the constraints of Equations (11)(12).

$$\begin{aligned} & C_{DR,t,i}=K_{DR,i}\left( P_{DR1,t,i}+P_{DR2,t,i}\right) \Delta t \end{aligned}$$

(10)

$$\begin{aligned} & P_{DR,t,i}-P_{DR,t,i}^*+P_{DR1,t,i}-P_{DR2,t,i}=0 \end{aligned}$$

(11)

$$\begin{aligned} & P_{DR1,t,i}\ge 0,P_{DR2,t,i}\ge 0 \end{aligned}$$

(12)

Power balance model of system

The multi-microgrid interconnection system satisfies load demand through coordinated operation of distributed generation units and inter-microgrid energy exchange mechanisms. When the power output from generation units fails to meet demand, the system initiates inter-microgrid energy transactions and procures supplemental power from the distribution grid. Conversely, when generation capacity exceeds local demand, the system exports surplus power to other microgrids and the distribution grid. This bilateral energy transfer framework, termed “power reciprocity”, effectively reduces overall system-wide generation costs and enhances economic efficiency¹⁹.

The system energy interaction cost and constraints are expressed as:

$$\begin{aligned} & C_{M,t,i}=K_{M,i}\left( P_{buy,t,i}-P_{sell,t,i}\right) \Delta t \end{aligned}$$

(13)

$$\begin{aligned} & {\left\{ \begin{array}{ll} 0\le P_{buy,t,i}\le U_{M,t,i}P_{M,i}^{max}\\ 0\le P_{sell,t,i}\le [1-U_{M,t,i}]P_{M,i}^{max}& \end{array}\right. } \end{aligned}$$

(14)

$$\begin{aligned} & C_{c,t,i}=K_{c,i}(P_{cbuy,t,ij}-P_{csell,t,ji})\Delta t \end{aligned}$$

(15)

$$\begin{aligned} & {\left\{ \begin{array}{ll} 0\le P_{cbuy,t,ij}\le U_{N,t,i}P_{c,i}^{max}\\ 0\le P_{csell,t,ji}\le U_{R,t,i}P_{c,i}^{max}\\ P_{cbuy,t,ij}=P_{csell,t,ji}\\ U_{N,t,i}+U_{R,t,i}\le 1& \end{array}\right. } \end{aligned}$$

(16)

Equation (13) represents the interactive power cost of the distribution grid, $C_{M,t,i}$ represents the power purchase and sale cost of the i th microgrid in t period; $P_{buy,t,i}$ and $P_{sell,t,i}$ are the purchased and sold power, respectively; $K_{M,i}$ represents the day-ahead transaction price of the distribution grid, which adopts the time-sharing tariff policy. Equation (14) is the upper and lower bounds of the interactive power of the distribution network, and $P_{M,i}^{max}$ is the upper limit of the purchased and sold power; $U_{M,t,i}$ indicates the status of electricity purchase and sale within the distribution network, with a value of 1 representing electricity purchase and a value of 0 representing electricity sale. Equation (15) represents the energy interaction cost between microgrids, where $C_{c,t,i}$ represents the interaction cost between the ith microgrid and other microgrids in time period t; $P_{cbuy,t,ij}$, $P_{csell,t,ij}$is the power purchased by microgrid i from j and the power sold by microgrid j to i; and $K_{c,i}$ is the interactive power tariff coefficient. Equation (16) is the interaction power constraint between microgrids, $P_{c,i}^{max}$ is the upper limit of transmission power, $U_{N,t,i}$, $U_{R,t,i}$ indicates the status of electricity purchase and sales on the micro network, and when 0 is taken at the same time, it indicates that there is no power interaction.The interactive power balance constraints are as follows:

$$\begin{aligned} \begin{aligned} P_{G,t,i}+P_{PV,t,i}&+P_{dis,t,i}+P_{buy,t,i}+P_{cbuy,t,ij}\\ &=P_{L,t,i}+P_{ch,t,i}+P_{DR,t,i}+P_{sell,t,i}+P_{csell,t,ji} \end{aligned} \end{aligned}$$

(17)

Model Assumptions

To focus on the core trade-off between economic dispatch and robustness optimization in MMG systems while balancing model tractability and computational efficiency, the following assumptions are made:

• 1. The microgrid operates in grid-connected mode throughout the scheduling horizon, disregarding transient processes during islanding/grid-connected mode transitions.

• 2. Operational cost functions are linearized, neglecting nonlinear dynamics such as microturbine ramp-rate constraints and minimum up/down times.

• 3. The charging/discharging efficiency of the ESS is set as the fixed value 95%, disregarding efficiency degradation caused by temperature fluctuations or equipment aging. Initial state-of-charge (SOC) randomness is not considered.

• 4. The scheduling horizon is defined as 24h with 1h time resolution, disregarding power fluctuations and dynamic adjustments at sub-hourly scales.

Bi-level robust optimization model

A bi-level robust optimization model for energy management of multi-microgrids considering worst-case cost minimization in an ensemble of uncertain load growth rates based on the bilevel structure of multi-microgrid interconnected systems to enhance the robustness of the planning scheme²⁰.

The first model layer is the worst-case scenario optimization layer within a single microgrid. The worst-case scenario optimization model is established for each microgrid, taking into account the volatility of renewable energy output and the range of load changes. The microgrid optimally allocates its own power capacity under the goal of maximizing the microgrid’s own revenue, and at the same time coordinates and optimizes the output of the micro gas turbine and the charging and discharging power of the energy storage, to get the result of the minimum operating cost under the worst-case scenario, which is passed to the upper layer model for scheduling.

The second layer model is the global coordination layer of the multi-microgrid interconnection system. Considering the coupling constraints between the microgrids, it optimizes the power interactions between each microgrid system and the power interactions between the microgrids and the distribution network according to the feedback information from the microgrids in the lower layer, and focuses on solving the problem of economically optimizing the operation of the whole multi-microgrid system in order to achieve the optimal energy management scheme so as to improve the economy and reliability of the system. The optimization objective function of the whole bilevel model is as follows:

$$\begin{aligned} & \min _{\varvec{x}}\{\max _{{\varvec{u}}\in {\varvec{U}}}\min _{{\varvec{y}}\in \Omega (\varvec{x},\varvec{u})}f_{MMG}\} \end{aligned}$$

(18)

$$\begin{aligned} & f_{MMG}=\sum _{i=1}^{m}\sum _{t=1}^{N_{T}}[C_{G,t,i}+C_{S,t,i}+C_{DR,t,i}+C_{M,t,i}+C_{c,t,i}] \end{aligned}$$

(19)

Equations (18)(19) show the bi-level robust optimization model considering renewable energy uncertainty. In the equations, $\varvec{x}$ and $\varvec{y}$ are optimization variables, $\varvec{u}$ represents uncertain variables, $\varvec{U}$ denotes the uncertainty set, and $\Omega$ defines the feasible region for variable $\varvec{y}$, which varies according to different uncertain parameters. The first-level optimization addresses the day-ahead scheduling problem for the multi-microgrid cluster, aiming to determine the optimal scheduling strategy $\varvec{x}$ for the entire system while minimizing the total operational cost. The second-level optimization accounts for uncertainties in renewable energy output and load demand, and derives the minimum operational cost and optimal energy interaction scheme for each generation unit in the worst-case scenario. Specifically in the second-level model, the max problem selects the extreme uncertainty scenarios to capture the most adverse conditions, while the min problem optimizes the operational variables $\varvec{y}$ under given $\varvec{x}$ and $\varvec{u}$ to compute the minimum operational cost $f_{MMG}$ for the MMG system. The detailed expressions for variables $\varvec{x}$, $\varvec{y}$, and $\varvec{u}$ specific to each microgrid are provided in Equations (20)-(21):

$$\begin{aligned} & {\left\{ \begin{array}{ll} \varvec{x}&= \begin{bmatrix} U_{S,t}, U_{M,t}, U_{N,t} \end{bmatrix}^T \\ \varvec{y}& = \begin{bmatrix} P_{G,t}, P_{ch,t}, P_{dis,t}, P_{DR,t}, P_{DR1,t}, P_{DR2,t}, \\ P_{buy,t}, P_{sell,t}, P_{PV,t}, P_{L,t}, P_{cbuy,t}, P_{csell,t} \end{bmatrix}^T \end{array}\right. } \end{aligned}$$

(20)

$$\begin{aligned} & \varvec{U}={\left\{ \begin{array}{ll}\varvec{u}=\left( P_{PV,t},P_{L,t}\right) ^T\\ P_{PV,t}\in \left[ {\hat{P}}_{PV,t}-\Delta P_{PV,t}^{max},{\hat{P}}_{PV,t}+\Delta P_{PV,t}^{max}\right] \\ P_{L,t}\in \left[ {\hat{P}}_{L,t}-\Delta P_{L,t}^{max},{\hat{P}}_{L,t}+\Delta P_{L,t}^{max}\right] & \end{array}\right. } \end{aligned}$$

(21)

Considering that the renewable energy source is photovoltaic (PV) energy, Equation (21) uses a boxed uncertainty set $\varvec{U}$ to represent the power fluctuation range of the system PV output and the actual load. Where $P_{PV,t}$, $P_{L,t}$ is the predicted value of PV and load in time period t; $\Delta P_{PV,t}^{max}$ and $\Delta P_{L,t}^{max}$ are the upper and lower limits of permissible fluctuation deviation corresponding to.

For ease of presentation, based on the above constraints and objective functions, the bi-level robust model of a multi-microgrid system can be expressed in the form of a generic matrix as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \limits _{\varvec{x}}\{\max \limits _{{\varvec{u}}\in {\varvec{U}}}\min \limits _{{\varvec{y}}\in \Omega (\varvec{x},\varvec{u})}\varvec{c}^T\varvec{y}\}\\ s.t.\varvec{D}\varvec{y}\ge \varvec{d}\\ \quad \varvec{K}\varvec{y}=\varvec{g}\\ \quad \varvec{F}\varvec{x}+\varvec{G}\varvec{y}\ge \varvec{h}\\ \quad \varvec{I}\varvec{y}=\varvec{u}& \end{array}\right. } \end{aligned}$$

(22)

Where $\varvec{c}$ is the coefficient matrix corresponding to the objective function; $\varvec{D}$, $\varvec{K}$, $\varvec{F}$, $\varvec{G}$, $\varvec{I}$ are the coefficient matrices of the variables under the corresponding constraints; $\varvec{d}$, $\varvec{g}$, $\varvec{h}$ are the constant column vectors. The first row of constraints corresponds to Equations (2), (6), (8), (12); the second row corresponds to Equations (5), (7), (11), (13); the third row corresponds to Equations (4), (15), (17); and the fourth row corresponds to the values of PV output and load at different times of the day in the prediction scenario.

Solution methodology

For the above multi-microgrid bi-level robust model, the column constraint generation (C&CG) algorithm²¹ is used for solving in this paper. Using this algorithm, the original problem is decomposed into a master problem and a set of sub-problems, and the variables and constraints of the sub-problems are continuously substituted into the master problem in the iterative process for solving alternately, so as to obtain the optimal solution of the original problem, which can obtain a more compact lower bound of the original objective function.

The decomposition master problem is of the form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \limits _{\varvec{x}} \varvec{\alpha } \\ s.t. \varvec{\alpha } \ge \varvec{c}^T \varvec{y}_s \\ \quad \varvec{D}\varvec{y}_s \ge \varvec{d} \rightarrow \varvec{\lambda } \\ \quad \varvec{K}\varvec{y}_s = \varvec{g} \rightarrow \varvec{\gamma } \\ \quad \varvec{F}\varvec{x} + \varvec{G}\varvec{y}_s \ge \varvec{h} \rightarrow \varvec{\nu } \\ \quad \varvec{I}\varvec{y}_s = \varvec{u}_s^* \rightarrow \varvec{\pi } \\ \quad \forall s \le k \end{array}\right. } \end{aligned}$$

(23)

Where k is the current number of iterations; $\varvec{y}_s$ is the solution of the subproblem after the s th iteration; $\varvec{u}_s^*$ is the value of the uncertainty variable $\varvec{u}$ in the worst case scenario obtained after the s th iteration.

The decomposed subproblem takes the form:

$$\begin{aligned} \max _{\varvec{u}\in \varvec{U}}\min _{\varvec{y}\in \Omega (\varvec{x},\varvec{u})}\varvec{c}^T\varvec{y} \end{aligned}$$

(24)

According to the duality theory²², the Lagrange multipliers $\varvec{\lambda }$, $\varvec{\gamma }$, $\varvec{\nu }$, $\varvec{\pi }$ are introduced and the correspondence is shown in Equation (24), the minimization problem in the inner model can be transformed into max form and merged with the outer max problem as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \max \limits _{\varvec{u} \in \varvec{U}, \varvec{\gamma }, \varvec{\lambda }, \varvec{v}, \varvec{\pi }} \varvec{d}^T \varvec{\gamma } + (\varvec{h} - \varvec{F} \varvec{x})^T \varvec{v} + \varvec{u}^T \varvec{\pi } \\ \text {s.t.} \varvec{D}^T \varvec{\gamma } + \varvec{K}^T \varvec{\lambda } + \varvec{G}^T \varvec{v}+\varvec{I}^T \varvec{\pi } \le \varvec{c} \\ \quad \varvec{\gamma } \ge \varvec{0}, \quad \varvec{v} \ge \varvec{0} \end{array}\right. } \end{aligned}$$

(25)

From the pole method, the uncertain variable $\varvec{u}$ is taken to the boundary value of the fluctuation interval when Equation (25) takes its maximum value. In the study of this paper, the worst case scenario can be described as the range of the interval where the PV output is minimum and the load power is maximum, so that the uncertainty set is represented as:

$$\begin{aligned} \varvec{U} = {\left\{ \begin{array}{ll} \varvec{u} = \left( P_{PV,t}, P_{L,t}\right) ^T \\ P_{PV,t} = {\hat{P}}_{PV,t} - Q_{PV,t} \Delta P_{PV,t}^{\max } \\ P_{L,t} = {\hat{P}}_{L,t} + Q_{L,t} \Delta P_{L,t}^{\max } \\ \displaystyle \sum _{t=1}^{N_T} Q_{PV,t} \le \Gamma _{PV} \\ \displaystyle \sum _{t=1}^{N_T} Q_{L,t} \le \Gamma _L \end{array}\right. } \end{aligned}$$

(26)

Where $\varvec{Q}=[Q_{PV,t}, Q_{L,t}]^{T}$ is a binary variable indicating the state of the uncertain variable at time t, and a value of 1 indicates that the boundary value is reached; $\Gamma _{PV}$, $\Gamma _{L}$ are uncertain adjustment parameters, with integer values ranging from 0 to $N_T$. A larger value indicates that the boundary values are reached more frequently, reflecting a more conservative approach. Conversely, a smaller value suggests a riskier scheme. After substituting the expression for the uncertain variable from Equation (26) into Equation (25), a product term involving the binary variable $\varvec{Q}$ and the continuous variable $\varvec{\pi }$ will arise. To linearize this nonlinearity, the Big-M method is applied for simplification. Specifically, auxiliary variable $\varvec{Q^{\prime }}=[Q_{PV,t}^{\prime },Q_{L,t}^{\prime }]^{T}$ and corresponding constraints are introduced, resulting in the following linearized model:

$$\begin{aligned} {\left\{ \begin{array}{ll} \max \limits _{\varvec{u}\in \varvec{U},\varvec{\gamma },\varvec{\lambda },\varvec{v},\varvec{\pi }}\varvec{d}^T\varvec{\gamma }+(\varvec{h}-\varvec{F}\varvec{x})^T\varvec{v}+\hat{\varvec{u}}^T\varvec{\pi }+\varvec{\Delta }\varvec{u}^T\varvec{Q}^{\prime }\\ s.t.\varvec{D}^T\varvec{\gamma }+\varvec{K}^T\varvec{\lambda }+\varvec{G}^T\varvec{\nu }+\varvec{I}^T\varvec{\pi }\le \varvec{c}\\ \quad \varvec{\gamma }\ge \varvec{0},\varvec{\nu }\ge \varvec{0}\\ \quad \varvec{0}\le \varvec{Q}^{\prime }\le \varvec{\overline{\pi }}\varvec{Q}\\ \quad \varvec{\pi }-\varvec{\overline{\pi }}(\varvec{1}-\varvec{Q})\le \varvec{Q}^{\prime }\le \varvec{\pi }& \end{array}\right. } \end{aligned}$$

(27)

Where $\widehat{\varvec{u}}=[{\widehat{P}}_{PV,t},{\widehat{P}}_{L,t}]^{T}$, $\Delta \varvec{u}=[\Delta P_{PV,t}^{max},\Delta P_{L,t}^{max}]^{T}$; $\varvec{\overline{\pi }}$ represents the upper bound of the dual variable $\varvec{\pi }$, the reasonable value of $\varvec{\overline{\pi }}$ is of crucial importance in model construction. An unreasonable value would cause a significant deviation between the results and reality, failing to provide a valid basis for decision-making. Specifically, a too-large $\varvec{\overline{\pi }}$-value weakens the model’s relaxation, increases computational instability, and may lead to larger errors, prolonged solving time, or even non-convergence. Conversely, a too-small $\varvec{\overline{\pi }}$-value may misjudge and interrupt feasible solutions, and affect the model’s ability to solve practical problems. Considering the range of the dual variable $\varvec{\pi }$ and the model’s characteristics, and based on the empirical summarization method combined with case analysis, we determine the value of $\varvec{\overline{\pi }}$ to be 1,000,000, ensuring that the model accurately covers the possible maximum value of $\varvec{\pi }$, improves solving efficiency, and guarantees solving stability and result accuracy.

The C&CG algorithm idea is used to solve the model and the architecture is shown in Algorithm 1.

Algorithm 1

C&CG algorithm architecture.

Case study

The office building type multi-microgrid system provides stable power for user loads, ensures stable load operation, reduces economic losses caused by load shutdowns due to power supply failures, and has positive significance for improving the reliability of power supply and energy consumption management in office buildings²³. Typical daily illumination and load data of two neighboring office and commercial buildings in a certain area are selected to build a bi-level robust optimization model of a multi-microgrid system, and the C&CG algorithm is used to solve the model in combination with MATLAB and CPLEX toolbox to derive a day-ahead scheduling strategy that takes into account the PV output and load uncertainty.

Input data

A multi-microgrid system containing two microgrids is used and the system structure is shown in Figure 1. The dispatch cycle is 1d, and every 1h is a time step. The two microgrids have different renewable energy configuration capacity and load characteristics, the specific configuration parameters are shown in Table 1, the discounted cost unit price of energy storage is $0.38, the cost unit price of microgrid interaction is $0.6, and the market price of purchased and sold electricity is considered in the time-sharing tariff policy, as shown in Figure 2. Considering the PV output and load fluctuation range of 15% and 10%. Set the uncertainty adjustment parameters $\Gamma _{PV}$ and $\Gamma _{L}$ to 6 and 12, respectively, indicating that during the scheduling optimization process, the PV output will attain the minimum value of its predicted interval in 6 specific time periods, while the load power will reach the maximum value of its predicted interval in up to 12 time periods, with both PV output and load power equaling their predicted values during all remaining time intervals. The predicted and actual power of the dual microgrid system are shown in Figure 3.

Table 1 Configuration parameters of the dual microgrid system.

Figure 2

Distribution network purchase and sale electrovalence.

Figure 3

Predicted and actual output of the dual microgrid system.

Results and discussions

Optimization results

Based on the bi-level robust optimization model, the dual microgrid system in the region is simulated. Firstly, the cost and expense when the dual microgrids do not form an interconnected system are analyzed, and it can be obtained that the total operating cost of the dual microgrid system in this case is $12,627, which is higher at this time. The interconnected system composed of two microgrids is simulated, and the optimal scheduling of each microgrid is drawn according to the generation power of each output unit, as shown in Figure 4. The simulation results show that the operating cost of the system is $8978, which is 28.9% lower than the first case. Therefore the multi-microgrid interconnection system can strongly reduce the operating cost of multi-microgrid system with better economy.

Figure 4

Optimal scheduling results of the dual microgrid interconnection system.

As demonstrated in Figure 4, PV generation ceases entirely during the intervals of 1:00–5:00 and 20:00–24:00. During these periods, MG1 primarily fulfills its power demand through coordinated dispatch of micro gas turbines, energy storage systems, and distribution network imports, while exporting surplus energy to MG2 at predefined interaction tariffs. Concurrently, MG2 employs energy storage charging protocols to maintain supply-demand equilibrium.

In contrast, between 6:00 and 19:00, active PV generation enables cost-optimized power management. Given that inter-microgrid exchange tariffs remain below peak electricity pricing thresholds, the system prioritizes internal renewable utilization during supply deficits. Furthermore, surplus photovoltaic energy is exported to the distribution grid at prevailing market rates, achieving dual objectives of enhanced energy utilization efficiency and operational expenditure minimization.

Figure 5 delineates the actual and expected power consumption of the demand response loads in the dual microgrid interconnection system. Combined with the electrovalence shown in Figure 3, analysis reveals that the expected power consumption of the demand response loads is mainly concentrated in the moments when the electrovalence are in the peak hours. Optimal scheduling facilitates load shifting, redistributing consumption to off-peak intervals characterized by valley pricing. This demand-side management strategy yields measurable reductions in energy procurement costs, achieving expenditure savings relative to uncontrolled consumption scenarios.

Figure 5

Demand response load actual and expected power usage.

Optimization model analysis

The selection of uncertain parameters directly affects the conservatism of multi microgrid system optimization scheme, the greater the number of instances when boundary values are reached, the higher the level of conservatism. As illustrated in Figure 3, the PV generation operates for 12h, while the load operates for 24h. Therefore, three sets of uncertainty adjustment parameters are selected as follows: $\Gamma _{PV}=0$, $\Gamma _{L}=0$ indicate that both PV and load power are equal to their predicted values throughout the scheduling optimization process; $\Gamma _{PV}=12$, $\Gamma _{L}=24$ signify that, during all operating periods in the scheduling optimization, PV output consistently takes the minimum value within its predicted interval, while load power consistently takes the maximum value within its predicted interval; $\Gamma _{PV}=6$, $\Gamma _{L}=12$ represent the uncertainty parameter values under a conservative scenario. Simulation comparisons yield the corresponding day-ahead operating costs, as shown in Table 2.

Table 2 Comparison of day ahead scheduling costs under different uncertain parameters.

As evidenced by the comparative data in Table 2, the bilevel robust optimization framework exhibits its minimum operational expenditure when the uncertainty parameter is calibrated to zero, achieving parity with deterministic model costs. A positive correlation is observed between uncertainty parameter escalation and systemic operating cost increments, confirming theoretical consistency under unperturbed conditions. This convergence validates the model’s mathematical rigor in deterministic environments, where its optimal solution aligns precisely with conventional deterministic optimization outcomes. When confronted with external disturbances, the robust model is capable of minimizing real-time scheduling costs and addressing uncertainties by adjusting the level of conservatism in the optimization solution. The higher the degree of uncertainty, the more conservative the resulting solution becomes. Therefore the conservatism of the dual-microgrid interconnection system scheme can be flexibly adjusted by varying the uncertainty parameters of the bi-level robust model.

The results show that the bi-level robust model scheduling cost of the system is higher than the deterministic model. This is due to the fact that the scheduling plan of the robust optimization model mainly takes into account the fluctuation of uncertainties, whereas the deterministic optimization model scheduling plan has certain risks and cannot cope with the complex operation environment during the actual operation. Therefore, when conducting the actual economic analysis, the adjustment cost is introduced to portray the additional payment or reduced revenue of the microgrid due to the deviation of the day-ahead scheduling plan from the actual operating demand.

Table 3 Cost comparison of different optimization models at 1.5/0.7 times of electricity price.

Table 4 Cost comparison of different optimization models at 2/0.5 times of electricity price.

The daily operating cost of a multi-microgrid interconnected system is equal to the sum of the day-ahead dispatch cost and the adjustment cost. Considering the amount of deviation between actual and planned, in real operation, the sale price is lower than the day-ahead price while the purchase price is higher than the day-ahead price. Taking the real-time market electricity purchase and sale prices as 1.5/0.7 times and 2/0.5 times the day-ahead electricity prices, respectively, to simulate real-time price fluctuations. The adjustment costs and daily operating costs of the bi-level robust model and the deterministic model under these corresponding price scenarios are presented in Table 3 and Table 4. Comparative analysis reveals that the bi-level robust model exhibits lower total operating costs, with the proportion of adjustment costs in daily operating costs being lower than that of the deterministic model. Experimental data demonstrate that this conclusion remains valid under scenarios with electricity price fluctuations. Therefore, in practical operations, the bi-level robust model demonstrates superior robustness and economic efficiency.

Conclusions

This study proposes a bi-level robust optimization-based collaborative scheduling framework to address the operational requirements of interconnected multi-microgrid systems, particularly confronting the dual uncertainties of renewable generation intermittency and load demand volatility. The proposed model demonstrates outstanding performance in terms of economic efficiency, providing an effective solution for the development of smart grids and enhancing the stability and reliability of multi-microgrid interconnected systems. The analysis results at this stage indicate that:

• 1. Through establishing an interconnected energy exchange architecture, heterogeneous microgrids can implement synergistic operational mechanisms. This approach leverages differential resource endowments to achieve spatiotemporal load-sharing coordination, effectively reducing peak-hour external grid dependency, while substantially enhancing systemic economic efficiency.

• 2. The developed bilevel robust optimization paradigm employs a box uncertainty set to mathematically characterize fluctuation boundaries of renewable generation and elastic loads. By integrating column-and-constraint generation (C&CG) algorithm with duality theory decomposition, the methodology attains globally optimal scheduling solutions under worst-case scenarios while maintaining computational tractability.

• 3. Parametric sensitivity analysis reveals that uncertainty set configurations critically govern model conservatism. Operational guidelines recommend calibrating uncertainty parameters through historical prediction error distributions or risk-aversion coefficients, thereby mitigating either standby capacity redundancy exceeding 15% or adjustment cost escalation beyond acceptable thresholds.

• 4. Economic viability assessment incorporating real-time adjustment cost metrics demonstrates an inverse correlation between model conservatism level and real-time compensation cost proportion. This empirically validates the framework’s robust optimization efficacy and operational adaptability in volatile environments, providing a methodological foundation for scheduling high-renewable-penetration multi-microgrid system.

However, this study is confined to theoretical models and simulated data. As energy forms in regional multi-microgrid systems become increasingly diversified, transactions between different microgrids may further enhance the operational efficiency of the system. Therefore, in the future, it is necessary to incorporate actual operational data and further consider cooperative game issues among microgrids.