High boost switched capacitor based 13L CG transformerless inverter for cost effective grid integration

Abstract

Transformerless inverter topologies with common ground features in solar photovoltaic and grid-connected systems are increasingly preferred due to their ability to effectively suppress leakage current to approximately zero, eliminate transformer-induced losses, and achieve improved energy conversion efficiency. This article presents a high-boost switched capacitor thirteen-level (13L) common ground transformerless inverter topology (HBSC-13L-CGTLI) with a voltage gain of six and reduced cost. Further, the maximum voltage across the switch is 67% of the output voltage, which reduces the cost of the inverter. The proposed topology does not need any separate circuit for its negative voltage level generation. The proposed topology generates a 13L output voltage at the load terminal using a single DC source, thirteen switches, four switched capacitors and three diodes. A detailed description of operational modes, design of the switched capacitor and filter inductor, and loss analysis of the proposed topology is presented. The performance of the proposed topology is validated through MATLAB/Simulink simulations and experimental results from a 1 kW laboratory prototype under various operating conditions. Finally, a detailed, comprehensive comparison of the different 13L inverter topologies is carried out to demonstrate the superior features of the proposed topology.

Introduction

Multilevel inverters are gaining more attention in both industry and academic fields due to their wide range of medium and high-power applications, such as speed drives, electric vehicles, high voltage power transmission, renewable energy integration, etc. The increasing penetration of renewable energy sources has highlighted the significance of power electronic converters in grid integration systems. These power electronic interfaces, particularly DC-DC and DC-AC converters, are fundamental in achieving efficient and reliable power conversion for clean energy production. Among various advanced converter topologies, multilevel inverters have emerged as a crucial solution for integrating renewable sources with the electrical grid. Due to the limitations of conventional two-level inverters in operating at high frequencies, multilevel inverters have emerged as a viable alternative^1,2. Compared to conventional two-level structures, multilevel inverter configurations offer lower switch voltage ratings, reduced dv/dt stress, higher fundamental component magnitude, improved voltage harmonic profile, minimised electromagnetic interference, and enhanced output power quality. Although multilevel inverters are widely recognised, conventional topologies such as cascaded H-bridge, neutral point clamped (NPC), and flying capacitor (FC) types present several limitations. The key benefit of the series-connected conventional H-bridge configuration is (i) does not need clamping diodes, (ii no series-connected multiple dc-link capacitors, and (iii) absence of flying capacitors. Therefore, the CHB doesn’t need any voltage balancing techniques. However, this topology needs more isolated DC sources to produce higher output voltage levels, while both the NPC structure and the flying capacitor (FC) types suffer from increased component count. Additionally, these structures face challenges with capacitor voltage balancing and sizing issues. Furthermore, these conventional topologies rely heavily on front-end DC-DC circuits to achieve the required grid voltage levels³. To address these limitations, several advanced multilevel transformerless inverter topologies (TLIT) have been reported in the literature, where the integration of switched-capacitor (SC) configurations with a single DC source has emerged as an effective solution for grid-connected solar PV applications. These structures demonstrate enhanced voltage boosting capabilities while maintaining reduced component count, effectively addressing the limitations of conventional multilevel inverters’ topologies^4,5.

In the literature^{6,7,8,9,10,11}, several multilevel transformerless inverter topologies have been proposed using switched-capacitor techniques with a single DC source to achieve voltage boosting capability. The reported topologies in literature^{6,7,8,9,10,11} comprise: a five-level TLIT⁶, a seven-level TLIT with three-fold voltage gain⁷, a nine-level TLIT with double boost capability⁸, an eleven-level hybrid inverter topology for medium voltage applications⁹, a thirteen-level inverter with three-fold voltage boost and reduced component count¹⁰, and a seventeen-level switched-capacitor inverter topology with high voltage gain¹¹. Analysis of these topologies^{6,7,8,9,10,11} shows several limitations. Topology⁶ utilises more switches and H-bridges in its structure, resulting in high voltage stress without boosting capability. While topology⁷ has a lower total standing voltage per unit TSVp.u. voltage, it requires a higher number of switches (12 switches). Topologies^8,9 suffer from high switch count with high voltage rating requirements, with topology⁹ needing additional control circuits for capacitor voltage balancing. Topology¹⁰ shows limitations in ripple current control, while topology¹¹ has increased component count, higher TSV, and high inrush current. Furthermore, these topologies have limited applicability when considering solar PV applications, with none addressing the critical issue of leakage current. As leakage current can cause safety hazards, EMI, and component degradation, its mitigation is essential for compliance with standards like VDE-0126-1-1 through modifications in the structure of the inverter topologies and different pulse width modulation (PWM) techniques.

Through modifications in topology design, one of the prominent methods that emerged is the common-ground type topology^{12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32}, where the grid neutral and PV source negative terminals are connected to a common ground together, resulting in near-zero leakage current. The topologies^{12,13,14,15,16,17,18} generate a five-level output voltage, topologies^{19,20,21,22,23,24,25,26} generate a seven-level output, topologies^{27,28,29,30,31} generate a nine-level output, and topology³² generates a thirteen-level output voltage waveform. All these are common ground topologies designed for solar grid-connected applications, as their common ground structure helps to maximise leakage current suppression. Topology¹² employs six switches but exhibits a significantly high maximum blocking voltage of 1.5 times the input voltage and lacks voltage boosting capability. Topology¹³, while also utilising six switches, maintains a maximum blocking voltage equal to the output voltage but requires additional magnetic components and demonstrates no boosting capability. In¹⁴, a five-level common-ground transformerless inverter is proposed using five switches, a diode, and multiple capacitors, but it uses more capacitors despite generating only five output voltage levels without boosting. The topology in¹⁵ employs one additional switch compared to¹⁴ but requires one capacitor less, with the capacitor voltage stress limited to half of the input voltage. However, it suffers from higher switch voltage stress up to 1.5 times the input voltage and does not offer any voltage boosting capability. The topology in¹⁶ uses the same number of power switches as¹⁵ and the same number of capacitors as¹⁴. It has a maximum switch voltage stress equal to the input voltage and, like^14,15, it does not offer any voltage boosting capability. Topology¹⁷ introduces 5L CG TLIT with boosting capability; however, it is constrained by a high device-to-level ratio (DLR), and its maximum blocking voltage equals the output voltage. Similarly, topology¹⁸, designed as a dual-boost 5L CG TLIT, incorporates six switches but faces limitations with its maximum blocking voltage equalling the output voltage and notably high voltage stress on its components.

Topologies^19,20 represent a seven-level CG TLIT with three-fold boost voltage boosting capabilities. Topology¹⁹ employs nine switches and achieves a voltage boost of three times the input voltage, with its peak inverse voltage across switches maintained at three times the input voltage (equal to the output voltage). Similarly, topology in²⁰ maintains its peak voltage stress within the output voltage range; however, it requires a higher number of power components compared to topology in¹⁹. In²¹, a seven-level common-ground inverter is proposed with triple voltage boosting and inherent capacitor balancing. While it ensures leakage current suppression, it uses more diodes and requires several switches to block voltages up to 3V_dc, increasing overall cost and complexity. Additionally, it suffers from high capacitor charging currents. In²², a seven-level common-ground inverter with dynamic voltage boosting is proposed. Though it enables single-stage boosting, it uses more power components and imposes maximum switch voltage stress of 2V_dc to generate 7L output levels. Despite its advantages of generating a seven-level output voltage with a three-fold voltage gain²³, it suffers from the use of high-rated switches, which leads to a significantly high total standing voltage per unit (TSV_p.u.). This increases the voltage stress on the devices, complicates the selection of components, and can affect overall reliability and cost-effectiveness, especially in higher voltage applications. Similar to²³, the topology in²⁴ requires several high-rated switches, with some rated up to 3V_dc, leading to a high total standing voltage per unit. Additionally, it uses a magnetic component, an inductor for soft charging, which adds to circuit complexity and introduces extra losses. The topology in²⁵ uses 10 switches, one diode, and two switched capacitors. Five of its switches are rated to block 2V_dc, resulting in a high TSV_p.u., which increases voltage stress and impacts cost and reliability. The topology in²⁶ achieves a 7L output with a three-fold voltage boost using a low number of power switches, only six, which significantly reduces switching losses, cost, and control complexity. However, this is achieved at the cost of using more switched capacitors (four in total). In pursuit of higher output voltage levels, topologies^{27,28,29,30,31} implement nine-level inverter structures with a CG connection and a voltage boosting feature. Both the topologies presented in^27,28 are capable of generating nine-level output voltage waveforms; however, their voltage boosting capability is limited to only twice the input voltage, which may restrict their applicability in systems requiring higher step-up gains. Further, the topologies^29,30 can boost the output voltage to four times the input voltage, with topology²⁹ utilising nine switches and topology³⁰ employing ten switches. Though the topology in³¹ offers dynamic voltage boosting, it needs the requirement of magnetic components and a higher number of power switches. Topology³² presents a thirteen-level CG TLIT with a voltage gain limited to three times the input voltage. The aforementioned analysis highlights a critical trade-off in existing topologies: higher switch count yields reduced voltage stress, while fewer components result in increased voltage stress. Addressing this fundamental challenge, this paper presents a thirteen-level inverter topology that optimises both component count and voltage stress, while maintaining enhanced voltage boost capability and leakage current suppression through the CG structure. The key features include,

• 1. It generates a 13 V output with a six-fold voltage boost, i.e., V_o = 6V_dc.

• 2. The MBV_p.u. of each semiconductor device is within the output voltage, i.e., 0.67V_o

• 3. Low TSV_p.u. and maximum conducting devices.

• 4. Least cost of the inverter.

• 5. SC are self-balanced, so no external balancing is needed.

Proposed HBSC-13L-CGTLI topology

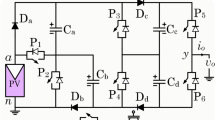
Fig. 1a illustrates the configuration of the proposed HBSC-13L-CGTLI topology. It consists of thirteen switches (S₁–S₁₃), three diodes (D₁–D₃), and four switched capacitors (SCs) (C₁–C₄). The proposed structure can generate a 13L output voltage waveform with a boost factor of 6 using four self-balanced SCs. Among these SCs, C₁ and C₂ are balanced at a voltage equal to the input voltage (V_dc), while C₃ and C₄ are balanced at 2V_dc. Table 1 presents the distinct switching patterns and the status of SCs used to generate the 13L output voltage. The operation of the proposed inverter topology is explained through 13 modes of operation (States 1–13), as depicted in Figs. 1 and 2. State 1 represents zero voltage levels, states 2 to 7 represent positive output levels, and states 8 to 13 represent negative output levels. Additionally, the proposed inverter topology connects the grid’s neutral and the source’s negative terminal to a common ground, thereby effectively suppressing leakage current to nearly zero, making it highly suitable for grid-connected solar PV applications. A detailed explanation of each of the thirteen distinct output voltage levels is provided below.

Fig. 1

(a) Proposed HBSC-13L-CGTLI topology, (b–h) Positive output voltage levels from 0 to + 6V_dc.

Table 1 Switching and capacitor status.

Fig. 2

(a–f) Negative output voltage levels from -V_dc to -6V_dc.

State 1: (zero)

The switches S₅, S₇, and S₁₁ are in a conduction state, and the generated voltage is zero in this state. The switch S₁ is also turned ON, which connects the input voltage source V_dc to SC C₂ in parallel, thereby charging it to V_dc. The corresponding charging path of the SC C₂ is via x-S₁-D₁-n as depicted in Fig. 1b.

State 2: (+ V_dc)

In this state, the switches S₃, S₄, and S₁₁ are switched ON, applying the source voltage across the load terminals to generate a voltage level + V_dc. With switches S₂ and S₃ ON, and S₁ OFF, SC C₁ is charged to V_dc via the path x − S₃ − S₂ − n. Additionally, the SCs C₃ and C₄ are charged to a voltage of + 2V_dc (V_C1 + V_C2), as switches S₅, S_8, and S₁₀ are ON, as shown in Fig. 1c.

State 3: (+ 2V_dc)

To generate the + 2V_dc voltage level, switches S₁, S₄, and S₁₁ are turned ON, and their corresponding load current path is illustrated in Fig. 1d. The input source voltage V_dc and the stored voltage of SC C₁ are added together to supply the load. Simultaneously, as S₁ is ON, SC C₂ charges through the path x − S₁ − D₁ − n. As same as, + V_dc output voltage level, the SCs C3 and C4 are also charged to a voltage of + 2V_dc (V_C1 + V_C2/dc).

State 4: (+ 3V_dc)

To achieve the + 3V_dc output voltage level, the input source V_dc and the voltage across the SC C₃ are summed up, and the respective current flow path is x-S₃-S₄-S₆-S₈-S₁₁-n as depicted in Fig. 1e. Meanwhile, with switches S₂ and S₁₀ turned ON, SCs C₁ and C₄ are charged to a voltage of V_dc and 2V_dc, respectively.

State 5: (+ 4V_dc)

With switches S₁, S₄, S₆, S₈, and S₁₁ switched ON, an output voltage of + 4V_dc output voltage level is achieved. The input source V_dc, along with the voltages of SCs C₁ and C_3, is summed up as illustrated in Fig. 1f. Meanwhile, with switch S₁ turned ON, SC C₂ is charged to V_dc via x-S₁-D₁-n.

State 6: (+ 5V_dc)

The positive terminal of the source and the terminal denoted as ‘y’ are connected to generate a + 5V_dc output voltage level by turning ON the switches S₃, S₄, S₆, S₉ and S₁₁, as depicted in Fig. 1g. This enables the source voltage This enables the source voltage V_dc, to combine with the SC voltages V_C3 and V_C4 to generate an output voltage equal to + 5V_dc. Additionally, with S₂ turned ON, the SC C₁ is charged via the path x − S₂ − S₃ − n.

State 7: (+ 6V_dc)

As far as the last positive level of the proposed inverter is concerned, the switches S₁, S₄, S₆, S₉, and S₁₁ are turned ON, enabling the source voltage V_dc to add up with voltage across capacitors C₁, C₃ and C₄, thereby generating a + 6V_dc output voltage, as illustrated in Fig. 1h. Meanwhile, with switch S₁ turned ON, SC C₂ is charged to V_dc via x-S₁-D₁-n.

State 8: (− V_dc)

During this mode, the voltage across SC C₂ is utilised to generate − V_dc, by turning ON switches S₅ and S₁₂, as depicted in Fig. 2a. Additionally, switch S₃ is also turned ON, which connects the source in parallel with C₁, allowing it to charge to V_dc​. The load current flow path is S₂-S₅-S₇-S₁₀-S₁₂-y-n as depicted in Fig. 2a.

State 9: (− 2V_dc)

To synthesise the − 2V_dc voltage level, the switches S₅, S₇, S₈, and S₁₂are triggered ON, establishing a current path through D-S₅-S₇-S₈-S₁₂-y-n, as illustrated in Fig. 2b. Meanwhile, with switch S₁ turned ON, SC C₂ is charged to V_dc via x-S₁-D₁-n.

State 10: (− 3V_dc)

In this operating state, switches S₅, S₇, S₁₀, and S₁₂ are triggered ON, allowing the voltages of SCs C₂ and C₄ to be utilised to generate − 3V_dc. Similar to State 8, switch S₃ is also turned ON, connecting the source in parallel with C₁ and enabling it to charge to V_dc through x − S₂ − S₃ − n. The load current flow path is S₂-S₅-S₇-S₁₀-S₁₂-y-n, as depicted in Fig. 2c.

State 11: (− 4V_dc)

The stored energy of the SCs C₃ and C₄ is utilised in this state to generate a − 4V_dc output voltage. This can be achieved by turning ON the switches S₅, S₇, S₉, and S₁₂ as shown in Fig. 2d. As same as state 9, SC C₂ is ​charged to V_dc via x-S₁-D₁-n.

State 12: (− 5V_dc)

The second last negative output voltage level, i.e., − 5V_dc, is obtained by utilising the stored energy of SCs C₂, C₃ and C₄, corresponding to V_C2, V_C3, and V_C4, respectively. This is achieved by the on-state switches S₂, S₅, S₇, S₉ and S₁₂ as depicted in Fig. 2e. Here to the SC C₁ is charged to V_dc via x − S₂ − S₃ − n.

State 13: (− 6V_dc)

As far as the last negative level of the proposed HBSC-13L-CGTLI topology is concerned, the switches S₅, S₇, S₉, S₁₂ and S₁₃ are turned ON to add the voltages of all SCs C₁-C₄ as shown in Fig. 2f.

Considering all operational states (1–13) and the respective switching sequences depicted in Figs. 1 and 2, it is observed that the peak inverse voltage (PIV) of each switch remains within the maximum output voltage of 6V_dc, i.e., 0.67V_dc, as listed in Table 2. Considering the PIV of all switches, the quantitative measure of the cumulative voltage stress across all switching devices TSVp.u. of the proposed HBSC-13L-CGTLI topology is computed as,

$$TSV = \sum\limits_{i = 1}^{n} {PIV_{i} } = 33/6 = 5.5$$

(1)

where PIV_i denotes the peak inverse voltage of the i^th switch, and n represents the total number of switches in the circuit.

Table 2 Voltage stresses of switches, diodes and capacitors.

Design of passive components (SCs (C₁-C₄) AND FILTER INDUCTOR (L_f))

Design of SCs (C₁-C₄)

The higher multilevel output voltages have been generated in switched capacitor multilevel inverters based on the charging and discharging of capacitors employed in their circuit structure. So, capacitance selection is an essential parameter in a switched-capacitor multilevel inverter to achieve higher output voltage levels. The capacitances of all four SCs (C₁-C₄) are selected according to their maximum discharging period (MDP). The total stored charge (Q_C) of the SC is expressed as²⁹,

$$Q_{C} = \int\limits_{{t_{{_{1} }} }}^{{t_{{_{2} }} }} {{\text{I}}_{g.pk} \,\,\sin (\omega t)} \,\,dt$$

(2)

where the Q_C represents the total charge stored on the SC, t₁ is the start time of the MDP and t₂ is its end time of the MDP, and I_m is the maximum grid current.

The 13L output voltage waveform of the proposed HBSC-13L-CGTLI topology with its SCs MDP and voltage across SCs (C₁-C₄) are shown in Fig. 3. Fig. 3 shows that the SCs C₁ and C₂ demonstrate MDP of t₅ to (π-t₅) and t₄ to (π-t₄), respectively. Furthermore, SCs C₃ and C₄ operate with symmetrical MDPs of t₂ to (π-t₂), with SC C₃'s MDP occurring in the positive half-cycle and SC C₄ in the negative half-cycle of the output voltage waveform.

Fig. 3

The 13L output voltage waveform along with MDP of SCs C₁-C₄ and voltage across SCs.

The charge of SC C₁ during its MDP, i.e., t₅ to (π-t₅) is written as,

$$Q_{C1} = \int\limits_{{t_{5} }}^{{\pi - t_{5} }} {{\text{I}}_{g.pk} \,\,\sin (\omega t)\,\,dt} = \frac{{{\text{I}}_{g.pk} }}{\omega }\left( {\cos (\omega t_{5} ) - \cos (\omega (\pi - t_{5} )} \right)$$

(3)

The charge of SC C₂ during its MDP, i.e., t₄ to (π-t₄) is written as,

$$Q_{C2} = \int\limits_{{t_{4} }}^{{\pi - t_{4} }} {{\text{I}}_{g.pk} \,\,\sin (\omega t)\,\,dt} = \frac{{{\text{I}}_{g.pk} }}{\omega }\left( {\cos (\omega t_{4} ) - \cos (\omega (\pi - t_{4} )} \right)$$

(4)

Similarly, the charge of SCs C₃ and C₄ during its MDP, i.e., t₂ to (π-t₂) is written as,

$$Q_{C3} = Q_{C4} = \int\limits_{{t_{2} }}^{{\pi - t_{2} }} {{\text{I}}_{g.pk} \,\,\sin (\omega t)\,\,dt} = \frac{{{\text{I}}_{g.pk} }}{\omega }\left( {\cos (\omega t_{2} ) - \cos (\omega (\pi - t_{2} )} \right)$$

(5)

Considering a permissible voltage ripple of 15% and MDP of the SCs, the expression for the capacitor is written as,

$$C = \frac{{Q_{C} }}{{0.15 \times V_{dc} }}$$

(6)

The maximum value of the capacitances of the SCs C₁-C₄ can be expressed as Eqs. (4)-(6):

$$C_{1} = \frac{{{\text{I}}_{g.pk} }}{{0.15V_{dc} \times \omega }}\left( {\cos (\omega t_{5} ) - \cos (\omega (\pi - t_{5} )} \right)$$

(7)

$$C_{2} = \frac{{{\text{I}}_{g.pk} }}{{0.15V_{dc} \times \omega }}\left( {\cos (\omega t_{4} ) - \cos (\omega (\pi - t_{4} )} \right)$$

(8)

$$C_{3} = C_{4} = \frac{{{\text{I}}_{g.pk} }}{{0.15V_{dc} \times \omega }}\left( {\cos (\omega t_{2} ) - \cos (\omega (\pi - t_{2} )} \right)$$

(9)

Design of Filter Inductor L _f

The current through the filter inductor (i_Lf(t)) over one complete cycle, considering the voltage across the inductor V_LF, and the initial inductor current i_Lf (0), is represented as,

$$i_{{L_{f} }} (t) = i_{{L_{f} }} (0) + \frac{1}{{L_{f} }}\int\limits_{0}^{t} {V_{{L_{f} }} \,\,dt}$$

(10)

Considering the maximum output voltage level of the inverter, which corresponds to the zone-f as depicted in Fig. 3, the inductor ripple current is obtained as¹⁸,

$$\Delta i_{{L_{f} }} = \frac{{(5V_{dc} - V_{g} ) \times d_{f} }}{{L_{f} }}$$

(11)

The duty cycle d_f can be obtained by applying the inductor volt-sec balance principle at zone-f, and it is obtained as,

$$\int\limits_{0}^{{d_{f} T_{s} }} {(6V_{dc} - V_{g} )\,\,dt + } \int\limits_{{d_{f} T_{s} }}^{{T_{s} }} {(5V_{dc} - V_{g} )\,\,dt = 0}$$

(12)

$$d_{f} = \frac{{V_{g} }}{{V_{dc} }} - 5$$

(13)

From (10) and (13), the value of the inductor filter (L_f) is calculated as,

$$L_{f} = \frac{1}{{\Delta i_{{L_{f} }} \times f_{sw} }}\left( {11V_{m} - 30V_{dc} - \frac{{V_{m}^{2} }}{{V_{dc} }}} \right)$$

(14)

Loss analysis

In this section, the theoretical total power loss of the proposed HBSC-13L-CGTLI topology is discussed to estimate its efficiency. The efficiency (η) of the proposed HBSC-13L-CGTLI topology, which is a measure of how effectively it converts DC power into AC power while minimising losses, is defined as follows,

$$\% \eta = \frac{{P_{out} }}{{P_{in} }} \times 100 = \frac{{P_{out} }}{{P_{out} + P_{loss} }} \times 100$$

(15)

The total power loss of a multilevel inverter is the sum of conduction and switching losses of switches and diodes, and ripple loss of capacitors.

$$P_{loss} = (P_{con} + P_{sw} )_{(sw/d)} + {\text{P}}_{r}$$

(16)

where P_con and P_sw represent the conduction and switching losses of the switches and diodes, P_r denotes the ripple loss of the capacitor.

Conduction losses

In a multilevel inverter, conduction losses originate from the on-state resistance of semiconductor switches and the equivalent series resistance of capacitors. These losses happen when the switches remain in the on state while conducting current. By applying Kirchhoff’s Voltage Law (KVL) to the equivalent circuits shown in Fig. 4 and considering parasitic elements such as the on-state switch resistance (R_nS), diode resistance (R_nD), capacitor’s internal resistance (R_rC), and the diode’s forward bias voltage drop (V_d), the power loss at different output voltage levels is determined and estimated⁴³ using Eqs. (17)-(31).

Fig. 4

(a) Equivalent circuit of proposed HBSC-13L-CGTLI topology, (b) Equivalent circuit for zero level, (c–h) Equivalent circuit for positive half cycles (+ V_dc to + 6V_dc), (i–n) Equivalent circuit for negative half cycles (-V_dc to -6V_dc).

Considering both switching devices and capacitors, the total conduction loss is mathematically represented as,

$$\begin{gathered} P_{con} = P_{cond,sw} + P_{cond,d} + P_{cond,c} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, = I_{S}^{2} R_{n,S} + I_{D}^{2} R_{n,D} + I_{C}^{2} R_{r,C} \hfill \\ \end{gathered}$$

(17)

where I_S and I_D represent the RMS value of current flowing through the active switching devices and diodes during the conduction period, while I_C denotes the RMS value of current passing through the capacitors. These current components and their respective internal resistances contribute to the overall conduction losses in the proposed topology. Considering the equivalent circuit shown in Fig. 4b for zero-level output voltage generation, four switches, one diode, one DC input source, and a switched capacitor are involved in the conduction path. The corresponding conduction losses can be mathematically expressed as,

$$P_{con,0} = I_{S1}^{2} R_{n,S1} + I_{S5}^{2} R_{n,S5} + I_{S7}^{2} R_{n,S7} + I_{S11}^{2} R_{n,S11} + I_{D1}^{2} R_{n,D1} + I_{C2}^{2} R_{r,C2}$$

(18)

From the equivalent circuit shown in Fig. 4c, the next highest voltage level (+ V_dc) involves six switches, two diodes, and four capacitors in the conduction path. The corresponding conduction losses are given by,

$$\begin{gathered} P_{con + 1} = I_{S2}^{2} R_{n,S2} + I_{S3}^{2} R_{n,S3} + I_{S4}^{2} R_{n,S4} + I_{S5}^{2} R_{n,S5} + I_{S9}^{2} R_{n,S9} + I_{S11}^{2} R_{n,S11} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{D2}^{2} R_{n,D2} + I_{D3}^{2} R_{n,D3} + I_{C1}^{2} R_{r,C1} + I_{C2}^{2} R_{r,C2} + I_{C3}^{2} R_{r,C3} + I_{C4}^{2} R_{r,C4} \hfill \\ \end{gathered}$$

(19)

The conduction loss equations for the remaining positive voltage levels (+ 2V_dc to + 6V_dc) are represented as follows,

$$\begin{gathered} P_{con + 2} = I_{S1}^{2} R_{n,S1} + I_{S4}^{2} R_{n,S4} + I_{S5}^{2} R_{n,S5} + I_{S9}^{2} R_{n,S9} + I_{S11}^{2} R_{n,S11} + I_{D1}^{2} R_{n,D1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{D2}^{2} R_{n,D2} + I_{D3}^{2} R_{n,D3} + I_{C1}^{2} R_{r,C1} + I_{C2}^{2} R_{r,C2} + I_{C3}^{2} R_{r,C3} + I_{C4}^{2} R_{r,C4} \hfill \\ \end{gathered}$$

(20)

$$\begin{gathered} P_{con + 3} = I_{S2}^{2} R_{n,S2} + I_{S3}^{2} R_{n,S3} + I_{S4}^{2} R_{n,S4} + I_{S6}^{2} R_{n,S6} + I_{S8}^{2} R_{n,S8} + I_{S10}^{2} R_{n,S10} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{S11}^{2} R_{n,S11} + I_{C1}^{2} R_{r,C1} + I_{C2}^{2} R_{r,C2} + I_{C3}^{2} R_{r,C3} + I_{C4}^{2} R_{r,C4} \hfill \\ \end{gathered}$$

(21)

$$\begin{gathered} P_{con + 4} = I_{S1}^{2} R_{n,S1} + I_{S4}^{2} R_{n,S4} + I_{S6}^{2} R_{n,S6} + I_{S8}^{2} R_{n,S8} + I_{S10}^{2} R_{n,S10} + I_{S11}^{2} R_{n,S11} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{D1}^{2} R_{n,D1} + I_{C1}^{2} R_{r,C1} + I_{C2}^{2} R_{r,C2} + I_{C3}^{2} R_{r,C3} + I_{C4}^{2} R_{r,C4} \hfill \\ \end{gathered}$$

(22)

$$\begin{gathered} P_{con + 5} = I_{S2}^{2} R_{n,S2} + I_{S3}^{2} R_{n,S3} + I_{S4}^{2} R_{n,S4} + I_{S6}^{2} R_{n,S6} + I_{S9}^{2} R_{n,S9} + I_{S11}^{2} R_{n,S11} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{C1}^{2} R_{r,C1} + I_{C3}^{2} R_{r,C3} + I_{C4}^{2} R_{r,C4} \hfill \\ \end{gathered}$$

(23)

$$\begin{gathered} P_{con + 6} = I_{S1}^{2} R_{n,S1} + I_{S4}^{2} R_{n,S4} + I_{S6}^{2} R_{n,S6} + I_{S9}^{2} R_{n,S9} + I_{S11}^{2} R_{n,S11} + I_{D1}^{2} R_{n,D1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{C1}^{2} R_{r,C1} + I_{C2}^{2} R_{r,C2} + I_{C3}^{2} R_{r,C3} + I_{C4}^{2} R_{r,C4} \hfill \\ \end{gathered}$$

(24)

Following the same approach as positive levels, the conduction losses for all negative voltage levels (-V_dc through -6V_dc) are calculated as follows,

$$\begin{gathered} P_{con - 1} = I_{S2}^{2} R_{n,S2} + I_{S3}^{2} R_{n,S3} + I_{S5}^{2} R_{n,S5} + I_{S12}^{2} R_{n,S12} + I_{D3}^{2} R_{n,D3} + I_{C1}^{2} R_{r,C1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{C2}^{2} R_{r,C2} \hfill \\ \end{gathered}$$

(25)

$$\begin{gathered} P_{con - 2} = I_{S1}^{2} R_{n,S1} + I_{S5}^{2} R_{n,S5} + I_{S7}^{2} R_{n,S7} + I_{S8}^{2} R_{n,S8} + I_{S12}^{2} R_{n,S12} + I_{D}^{2} R_{n,D1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{C2}^{2} R_{r,C2} + I_{C3}^{2} R_{r,C3} \hfill \\ \end{gathered}$$

(26)

$$\begin{gathered} P_{con - 3} = I_{S2}^{2} R_{n,S2} + I_{S3}^{2} R_{n,S3} + I_{S5}^{2} R_{n,S7} + I_{S10}^{2} R_{n,S10} + I_{S12}^{2} R_{n,S12} + I_{S11}^{2} R_{n,S11} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{D1}^{2} R_{n,D1} + I_{C1}^{2} R_{r,C1} + I_{C2}^{2} R_{r,C2} + I_{C4}^{2} R_{r,C4} \hfill \\ \end{gathered}$$

(27)

$$\begin{gathered} P_{con - 4} = I_{S1}^{2} R_{n,S1} + I_{S5}^{2} R_{n,S5} + I_{S7}^{2} R_{n,S7} + I_{S9}^{2} R_{n,S9} + I_{S12}^{2} R_{n,S12} + I_{D1}^{2} R_{n,D1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{C2}^{2} R_{r,C2} + I_{C3}^{2} R_{r,C3} + I_{C4}^{2} R_{r,C4} \hfill \\ \end{gathered}$$

(28)

$$\begin{gathered} P_{con - 5} = I_{S2}^{2} R_{n,S2} + I_{S3}^{2} R_{n,S3} + I_{S5}^{2} R_{n,S5} + I_{S7}^{2} R_{n,S7} + I_{S9}^{2} R_{n,S9} + I_{S12}^{2} R_{n,S12} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{C1}^{2} R_{r,C1} + I_{C2}^{2} R_{r,C2} + I_{C3}^{2} R_{r,C3} + I_{C4}^{2} R_{r,C4} \hfill \\ \end{gathered}$$

(29)

$$\begin{gathered} P_{con - 6} = I_{S5}^{2} R_{n,S5} + I_{S7}^{2} R_{n,S7} + I_{S9}^{2} R_{n,S9} + I_{S12}^{2} R_{n,S12} + I_{S13}^{2} R_{n,S13} + I_{C1}^{2} R_{r,C1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + I_{C2}^{2} R_{r,C2} + I_{C3}^{2} R_{r,C3} + I_{C4}^{2} R_{r,C4} \hfill \\ \end{gathered}$$

(30)

The total conduction losses of the proposed HBSC-13L-CGTLI topology can be calculated by summing up all the individual voltage level losses calculated from Eqns. (18–30) as follows,

$$\begin{gathered} P_{con} = P_{con,0} + P_{con + 1} + P_{con + 2} + P_{con + 3} + P_{con + 4} + P_{con + 5} + P_{con + 6} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + P_{con - 1} + P_{con - 2} + P_{con - 3} + P_{con - 4} + P_{con - 5} + P_{con - 6} \hfill \\ \end{gathered}$$

(31)

Switching losses

Switching losses in semiconductor devices occur due to the finite transition time during turn-on and turn-off processes, where the simultaneous presence of voltage and current leads to power dissipation. These losses are assessed over a fundamental cycle, considering the switching times (t_on and t_off), with turn-off typically contributing more to overall losses. To simplify the analysis, switching losses are often evaluated using a linear approximation of voltage and current variations during the transition periods⁴². Considering energy dissipation during the turn-on and turn-off periods,

$$E_{on,i} = \int\limits_{0}^{{t_{on} }} {v(t)i(t)\,\,dt = } \frac{{V_{s,i} \times I_{on,i} \times t_{on} }}{6}$$

(32)

$$E_{off,i} = \int\limits_{0}^{{t_{off} }} {v(t)i(t)\,\,dt = } \frac{{V_{s,i} \times I_{off,i} \times t_{off} }}{6}$$

(33)

The currents I_on,i and I_off,i represent the current flowing through the ith switch during turn-on and before turn-off, respectively, while V_{s, i} denotes the voltage of the switch in the OFF state.

Considering the number of ON and OFF transitions of the i^th switch over one complete cycle, the switching loss for the i^th switch can be calculated as,

$$\begin{gathered} P_{s,i} = \frac{{\left( {E_{on,i} \times N_{on,i} } \right) \times \left( {E_{off,i} \times N_{off,i} } \right)}}{t} \hfill \\ \,\,\,\,\,\,\,\, = \frac{{V_{s,i} \left[ {\left( {I_{on,i} \times N_{on,i} \times t_{on} } \right) + \left( {I_{off,i} \times N_{off,i} \times t_{off} } \right)} \right]}}{6t} \hfill \\ \end{gathered}$$

(34)

Using (34) and considering the switching frequency f_sw, the overall switching losses of the proposed HBSC-13L-CGTLI topology can be expressed as,

$$P_{s} = f_{sw} \sum\limits_{i = 1}^{13} {\frac{{V_{s,i} \left[ {\left( {I_{on,i} \times N_{on,i} \times t_{on} } \right) + \left( {I_{off,i} \times N_{off,i} \times t_{off} } \right)} \right]}}{6t}}$$

(35)

Capacitor ripple losses

Considering all four SCs, C₁-C₄, the capacitor voltage ripple loss is expressed as⁴³,

$$\begin{gathered} P_{r} = 2 \times f_{o} \left( {\sum\limits_{i = 1}^{n} {C_{i} \times \Delta V_{Ci}^{2} } } \right) \hfill \\ \,\,\,\,\,\, = 2 \times f_{o} \left[ {\left( {C_{1} \times \Delta V_{C1}^{2} } \right) + \left( {C_{2} \times \Delta V_{C2}^{2} } \right) + \left( {C_{3} \times \Delta V_{C3}^{2} } \right) + \left( {C_{4} \times \Delta V_{C4}^{2} } \right)} \right] \hfill \\ \end{gathered}$$

(36)

Comparative assessment

A comprehensive comparative assessment has been performed between the proposed HBSC-13L-CGTLI topology and other 13L inverter output voltage topologies. The topologies are classified into four distinct categories: multi-source 13L inverter topologies^33,34,35, single DC source with three-fold boost topologies^{10,36,37,38,39}, single DC source with six times boost topologies^40,41,42,43, and single DC source with three boost and six boost configurations having common ground features^32,44,45,46 as depicted in Figs. 5, 6, 7 and 8. The comparison encompasses critical parameters including component count (switches (N_sw), drivers (N_dr), diodes (N_d), capacitors (N_c), total component count (T_D)), voltage metrics (TSV_p.u., and MBV_p.u.), ratios (switch-to-level generation (N_sw/N_L), and switch-to-gain number (N_sw/Gain)), capacitor voltage diversity factor (CDF), and number of peak voltage stress switches (PVS). Through this comprehensive comparison study, the advantages and various trade-offs of the proposed topology against existing configurations are thoroughly examined and presented in this section. Comparing various 13L topologies, in the first category, the one proposed in³⁴ uses a minimum of 11 switches, while the remaining two topologies^33,35 use 14 switches. In the second category of three-fold boost 13L inverter topologies,^36,39 generate 13L output using 11 switches, while the topology in³⁷ uses 14 switches. In the third category with six-boost topologies,^32,41 require a minimum of 13 switches, while topology⁴³ uses a maximum of 15 switches to generate a 13L output voltage waveform. In the final category of common ground feature topologies,³² utilises a minimum of 11 switches, followed by the proposed topology, which employs 13 switches to generate a 13L inverter output voltage. The other topologies^44,45,46 in this category use a significantly greater number of switches. Among the common ground featured multilevel inverter topologies in the fourth category, as shown in Fig. 8, when comparing topology³² and the proposed topology with other topologies presented in^33,34,35, these topologies utilise a significantly higher number of power switches to generate a 13L output voltage. Although topology³² employs two switches and one diode fewer than the proposed topology, its voltage boosting capability is only half compared to the proposed topology. Specifically, while the proposed topology achieves six times the input voltage boost, topology³² achieves only three times the input voltage boost.

Fig. 5

A multi-source 13L inverter topology^33,34,35.

Fig. 6

A single DC source with three-fold voltage boost topologies^{10,36,37,38,39}.

Fig. 7

A single DC source with six-fold voltage boost topologies^40,41,42,43.

Fig. 8

A single-source three-fold and six-fold voltage boost CG topologies^32,44,45,46.

Comparing all topologies shown in Figs. 5, 6, 7 and 8, the lowest switch count of 11 is used by topologies proposed in^32,34,36,38, and³⁹. Although these topologies use slightly fewer switches than the proposed topology, their voltage-boosting capability is significantly lower than the proposed topology. Additionally, the topology proposed in³⁴ requires two separate voltage sources to achieve 13L with a boost factor of 2. Furthermore, the proposed topology is extensively compared with existing topologies based on voltage metrics (TSV_p.u. and MBV_p.u.) and performance ratios (switch-to-level generation and switch-to-gain number). While comparing all the topologies with the proposed topology based on voltage metrics, the TSV_p.u. of the proposed topology is 5.5, ranking as the third least, while its MBV_p.u. is 0.67, positioning as the fourth least compared to all other topologies. Although the proposed topology has a TSV_p.u. of 5.5, topologies^36,43, and⁴⁶ demonstrate lower TSV_p.u. value of 5. Though the topology³⁶ has the lowest TSV_p.u. of 5 with an MBVp_.u. of 0.67, its gain is limited to only 3. Similarly, topology⁴³ also achieves a minimum TSV_p.u. of 5; however, it requires 15 power switches in total for its 13L output voltage waveform generation, which is higher than the proposed topology’s requirement of 13 switches. The one in⁴⁶, despite having the least TSV_p.u. of 5, demands approximately 30 power switches, which is significantly higher than the proposed topology. Even with its favourable MBV_p.u. of 0.15, its generalised topology type requires an excessive number of switches. The second-least TSV_p.u. of 5.33 is shared by topologies^10,32, and⁴¹. When comparing topology¹⁰ with the proposed topology, both utilise 13 power switches, but topology 5 achieves only half the voltage gain (3 compared to the proposed topology’s gain of 6), despite having a slightly lower TSV_p.u. Its MBV_p.u. is 0.67, which is comparable to the proposed topology. Similarly, topology⁴¹ also employs 13 switches and demonstrates comparable operational characteristics, though with a slightly lower MBV_p.u. of 0.5 compared to the proposed topology’s 0.67. The topology proposed in³², while maintaining the same switch count of 13, exhibits a TSV_p.u. of 5.3 and a higher MBV_p.u. of 1.0. However, like topology¹⁰, it only achieves a voltage gain of 3, which is half of what the proposed topology delivers (gain of 6). The proposed topology and topology in³⁷ both exhibit a TSV_p.u. of 5.5, which ranks as the third-lowest among all topologies in the comparison. While sharing identical TSV_p.u., topology³⁷ exhibits a higher MBV_p.u. of 1 and requires 14 power switches in contrast to the proposed topology’s 13 switches. Regarding total power device requirements, topology³⁷ utilises 30 devices compared to the proposed topology’s 33.

Significantly, the proposed topology challenges conventional design principles where a higher switch count typically correlates with lower stress levels. Instead, it successfully demonstrates optimal stress management despite utilising a higher component count, representing an innovative approach to topology design. Unlike conventional multilevel inverter designs, where reduced switch count typically leads to increased voltage stress profiles, the proposed topology demonstrates a unique capability to maintain lower voltage stress profiles across switches despite utilising a reduced number of power components, thus challenging the traditional trade-off between component count and voltage stress distribution. When comparing N_sw/N_L, N_sw/Gain across topologies, the proposed topology achieves an N_sw/N_L of 1 and an N_sw/Gain of 2.17, performance levels that are only matched by topologies^41,42 in the existing literature. The proposed topology outperforms most existing configurations with an impressive N_sw/Gain of 2.17, followed closely by topologies^40,43, while all other existing topologies lag significantly behind in this crucial performance metric. The CDF emerges as another crucial comparison metric, owing to its direct impact on inverter cost and size optimisation. This key parameter fundamentally influences the achievement of higher power density at reduced costs. The diversity factor, calculated as the ratio of total capacitor voltages to peak output voltage³², positions the proposed topology at 1, which is in par with the high-boost topologies. The number of peak voltage switches, defined as switches experiencing maximum output voltage, represents another significant evaluation criterion. Analysis shows that the proposed topology, along with topologies^{10,36,40,41,42,43,44}, and⁴⁶, demonstrates superior characteristics as none of their switches require a voltage rating equal to the output voltage.

Notably, in the proposed configuration, the maximum switch voltage stress is limited to 0.67% of the output voltage. Furthermore, a detailed cost function (CF) analysis is conducted using weighted factors under two categories: α = β = 0.5 and α = β = 1.5 and discussed. The CF has been computed³² and expressed as

$$CF = \frac{{(T_{D} + (\alpha * TSVp.u.) + (\beta * CDF) + N_{S} )}}{Gain}$$

(37)

Based on cost function analysis, Eq. 37, topologies^40,41,42,43 and the proposed topology demonstrate optimal cost metrics. Although the proposed topology exhibits marginally higher cost indices compared to topologies^40,41,42,43, it uniquely incorporates common ground characteristics. This facilitates maximum leakage current suppression (~ 0 mA), a critical feature absent in topologies^40,41,42,43, making it particularly advantageous for grid-connected PV applications. The proposed topology demonstrates superior performance compared to existing common-ground configurations^32,44,45,46, with significantly lower cost function values of 6.21 and 7.29 (with weight factors considered). With the considered weight factors α and β, the proposed topology achieves cost function values of 6.21 and 7.29. When compared with other common-ground type topologies^32,44,45,46, the proposed topology demonstrates significantly lower values. This reduction in cost function values indicates the superior performance of the proposed topology over the other CG topologies.

A comprehensive cost comparison analysis was performed for the topologies with a gain of 6^{41,42,43,44,45,46}, with the results documented in Table 3. All topologies were evaluated under identical operating conditions: an input voltage of 60 V, an output voltage of 360 V, and a rated output power of 1 kW. The component selection for each topology was carefully optimised based on these design specifications. The detailed cost analysis, including component-wise breakdown and total system costs, is systematically presented in Table 3 for comparative evaluation. From Table 3, the cost analysis shows that the proposed topology achieves the lowest inverter cost both with and without heatsink considerations. The next lowest cost is observed in topology⁴², followed by topologies^41,43, respectively. Performance evaluation metrics, including Fractional Gain Constant (FGC) and Improved Subtractive Gain Cost (ISGC), were determined⁴⁷ for all topologies under consideration and listed in Table 3. The analysis demonstrates that the proposed topology exhibits superior characteristics with notably higher values of FGC and ISGC parameters. These enhanced metrics conclusively establish the proposed topology’s operational advantages over other configurations.

Table 3 Cost analysis of different high-boost 13L inverter topologies.

Fig. 9 shows the graphical representation that illustrates a comprehensive comparison analysis through a radar chart, evaluating various topologies^{32,41,42,43,44,45,46} and the proposed topology. The comparative analysis encompasses critical parameters, including N_sw, N_sw/N_L, N_sw/Gain, cost of the inverter, and maximum conducting switches (MCS) across all configurations. The comparative analysis through radar chart visualisation demonstrates that the proposed topology exhibits the lowest area coverage compared to other topologies^{32,41,42,43,44,45,46}. This minimal area coverage in the radar chart significantly indicates that the proposed topology emerges as one of the prominent candidates among the different configurations^{32,41,42,43,44,45,46}. The proposed topology demonstrates remarkable characteristics through comprehensive comparative analysis: reduced component count, high voltage boost capability, low CDF, one of the lowest TSV_p.u. and MBV_p.u., and notably the lowest cost inverter among the compared topologies, while achieving the highest FGC and IGSC indices. These distinctive advantages establish it as an optimal candidate for grid-connected solar PV applications.

Fig. 9

Radar chart of comparative analysis of the proposed topology and topologies^{32,41,42,43,44,45,46}.

Results and discussion

The proposed HBSC-13L-CGTLI inverter topology is analysed through simulation using the MATLAB/Simulink platform and experimentally validated using a 1 kW laboratory prototype. The analysis is carried out under steady-state, transient, and grid-connected conditions, and the corresponding results are presented and discussed in this section.

Simulation results

Initially, with an input voltage of 60 V, the proposed inverter topology achieves an output voltage of 360 V with 13 levels as depicted in Fig. 10a. Under present steady-state testing conditions with a resistive load of R = 120 Ω, the corresponding output current reaches a peak value of 3 A with an RMS value of 2.121 A, as illustrated in Fig. 10b. The voltage across the SCs C₁-C₄ is illustrated in Fig. 10c–f, where it can be seen that C₁ and C₂ maintain a balanced voltage at the input voltage level of 60 V, while C₃ and C₄ are balanced at twice the input voltage, specifically at 120 V. The performance of the proposed topology is further evaluated with an RL load Z = 60 + j100 Ω. The results show that the load voltage maintains six-times boost characteristics, achieving 360 V at the output. Under these loading conditions, the load current reaches a peak value of 5.3 A with a corresponding RMS value of 3.76 A, as shown in Fig. 10g,h. Figs. 10 (i–l) depicts that the capacitor voltages C₁ and C₂ are maintained at 60 V, while C₃ and C₄ are maintained at 120 V during RL load operation, with minimal ripple variations as shown in the waveforms.

Fig. 10

Simulation results of (a) Output voltage (v_o) at R = 120 Ω, (b) Load current(i_o) at R = 120 Ω, (c–f) SCs voltage V_C1, V_C2, V_C3, V_C4 at R = 120 Ω, (g) Output voltage (v_o) at Z = 60 + j100 Ω, (h) Load current (i_o) at Z = 60 + j100 Ω, (i–l) SCs voltage V_C1, V_C2, V_C3, V_C4 at Z = 60 + j100 Ω, (m–o) Output voltage (v_o), Load current (i_o) & SCs voltage V_C1, V_C3 at Z = 60 + j100 Ω during step change in input voltage, (p,q) Output voltage (v_o), & Load current (i_o) during change in load from R = 100 Ω to at Z = 60 + j100 Ω, (r,s) Output voltage (v_o), & Load current (i_o) during modulation index change 1.0 to 0.8 at Z = 60 + j100 Ω, (t,u) Output voltage (v_o), & Load current (i_o) during modulation index change 0.8 to 0.5 at Z = 60 + j100 Ω.

To evaluate the dynamic transient operating capability of the proposed topology, different tests are performed, such as varying input voltage conditions, load variations and modulation index (MI) variations. The analysis primarily focused on examining the system’s response to input voltage variations from 54 to 60 V while the load was maintained at Z = 60 + j100 Ω. The resultant waveforms, illustrated in Fig. 10m–o, demonstrate the behaviour during the voltage transition. Fig. 10m demonstrates that when the input voltage is maintained at 54 V, the output voltage stabilises at ~ 325 V, and upon increasing the input to 60 V, the output voltage rises to 360 V. The corresponding current waveforms exhibit peak values of 4.7 A and 5.3 A, respectively, as illustrated in Fig. 10n. Fig. 10(o) presents the capacitor voltage waveforms during the input voltage transition from 54 to 60 V. The results indicate that the capacitor voltages effectively track the changing input voltage while maintaining balanced voltage levels across the operating range. In general, the load conditions are not constant in practical applications. Therefore, the performance of the proposed topology under varying load conditions is tested with two load configurations: a pure resistive load R = 100Ω and an RL load Z = 60 + j100 Ω. The corresponding output voltage and current waveforms are presented in Figs. 10p,q, respectively.

The results demonstrate that the load voltage remains consistently regulated at 360 V throughout the transition, and the current waveform analysis shows that under R load, the current maintains a steady value of 3.6 A. When switched to RL load, the waveform becomes sinusoidal with a peak value of 5.3 A, as depicted in Fig. 10q. The performance of the proposed topology is checked by examining its behaviour across varying modulation indices (MI). The investigation involved systematic transitions of MI from 1 to 0.8, and subsequently from 0.8 to 0.5, while maintaining the RL load of Z = 60 + j100 Ω. The results demonstrated distinct operational characteristics at each modulation index: at MI = 1, the system successfully achieved all 13 levels with corresponding voltage and current values of 360 V and 5.3 A; at MI = 0.8, the level count decreased to 11, yielding voltage and current measurements of 303 V and 4.3 A respectively; and at MI = 0.5, the system operated at 7 levels, producing a voltage output of 185 V with peak current reaching 2.4 A as shown in Figs. 10r–u.

In addition to steady-state and transient response analysis, the grid-connected operation of the proposed topology is evaluated, and the respective results are presented in Figs. 11 and 12, which demonstrate the topology’s performance under various operating conditions. The proposed topology is tested under unity power factor, lagging power factor, and leading power factor conditions, and the corresponding results are depicted in Figs. 11a–c. Furthermore, the topology’s response to reference current variations is examined through step changes from 1.5 A to 5 A, and the results are presented in Fig. 12b. These comprehensive simulation results validate that the proposed topology maintains optimal performance across all operating conditions.

Fig. 11

Simulation results when connected with the grid (a) Output voltage (v_o), grid voltage (v_g), and grid current (i_g) at unity PF, (b) Output voltage (v_o), grid voltage (v_g), and grid current (i_g) at lagging PF, (c) The source current (i_s) while delivering ~ 1 kW real power to the grid.

Fig. 12

Simulation results when connected with the grid (a) Output voltage (v_o), grid voltage (v_g), and grid current (i_g) at leading PF, (b) Output voltage (v_o), grid voltage (v_g), and grid current (i_g) when the reference current is changed from 1.5 A to 5 A.

Power losses occurring in the semiconductor switches and diodes of the proposed 13L inverter were analysed using Piecewise Linear Electrical Circuit Simulation version 4.3.6 (PLEXIM) simulation software⁴⁸ with IKW50N60DTP devices operating at 25 °C at different output power levels. Fig. 13 illustrates the power loss distribution across the semiconductor devices of the proposed 13L inverter topology. The analysis shows that switches S₁-S₅ experience predominant losses due to their position in the capacitor charging path, with diodes D₁-D₃ exhibiting the next significant contribution to power losses. Fig. 14a, b illustrate the power loss analysis of the proposed 13L inverter topology at unity power factor for output powers of 500 W and 1000 W, respectively. The analysis shows total power losses of 14 W at 500 W output and 52 W at 1000 W output. It can be observed from Fig. 14c that the efficiency of the proposed inverter topology decreases as the output power increases, with the highest efficiency achieved at lower power levels.

Fig. 13

Plexim power loss contribution details of switches and diodes of the proposed topology.

Fig. 14

Simulation power loss analysis (a) Power loss distribution at 500 W unity PF, (b) Power loss distribution at 1000 W unity PF, (c) Total power loss and efficiency at 500 W and 1000 W.

Experimental results

The proposed 13L inverter topology was experimentally validated using a laboratory prototype, as shown in Fig. 15. The prototype was designed for a 1 kW output power rating and incorporated SKM75GB063D switching devices, MUR5060 diodes, and HCPL-3120 gate drivers, all interfaced with a Texas Instruments TMS320F28379D digital controller. A soft charging inductor of 33 μH was utilised during the experimental validation to reduce the inrush current. Table 4 lists the specifications of the experimental prototype.

Fig. 15

Experimental prototype of the proposed topology.

Table 4 Specifications of an experimental setup.

The experimental results illustrated in Figs. 16, 17, 18 and 19 demonstrate the performance of the proposed inverter topology. Tests were performed under two loading conditions: a pure resistive load of R = 100 Ω and an inductive load of Z = 60 + j100 Ω at a modulation index (M_a) of 1.0. The experimental measurements at 60 V input demonstrate that the inverter output maintains 360 V while exhibiting peak load currents of 3.6 A and 5.34 A for resistive and inductive loading conditions, respectively. These results, presented in Figs. 16a,b, substantiate the designed voltage gain factor of six in the proposed topology. Further analysis of the voltage and current profiles for the SCs (C₁, C₂, C₃, C₄) is presented in Figs. 16c,d. As shown in Figs. 16c,d, the measured results indicate that capacitors C₁ and C₂ maintain voltage levels at 60 V, while C₃ and C₄ operate at 120 V, with an allowable voltage ripple of 10%, and their charging current profiles remain within the specified limits under inductive loading conditions of Z = 60 + j100 Ω. The dynamic performance of the proposed inverter topology has been analysed under variations in input voltage (from 54 to 60 V), load (from R = 100 Ω to Z = 60 + j100 Ω), and MI variation (from MI = 1 to MI = 0.8), with the corresponding results presented in Figs. 17a–d. While changing the input voltage from 54 to 60 V, initial measurements at 54 V input demonstrated a 13L output voltage waveform with a magnitude of 324 V, corresponding to a peak load current of 4.7 A. Upon increasing the input voltage to 60 V, the system maintained its 13L output configuration while achieving an output voltage of 360 V, with the peak current magnitude escalating to 5.3 A. The experimental results illustrated in Fig. 17b validate that the SC voltages V_C1-V_C4 maintain voltage-balanced operation throughout the input voltage transition period. Next, a load change operation has been performed, transitioning from a pure resistive load of R = 100 Ω to an inductive load of Z = 60 + j100 Ω and the respective waveforms are depicted in Fig. 17c. It can be observed that with a resistive load, the output voltage waveform and output current waveform are in phase, with a current magnitude of 3.6 A. When the load changes to inductive, it follows a sinusoidal pattern, with the peak current value reaching 5.3 A at a power factor of 0.89. Furthermore, the dynamic operating behaviour of the proposed topology was analysed by varying the modulation index (MI) from 1.0 to 0.8 under an inductive load of Z = 60 + j100 Ω, and the corresponding results are presented in Fig. 17d. The analysis shows that when the modulation index is 1.0, the proposed topology fully achieves 13L output voltage levels with a peak voltage of 360 V and a peak load current of 5.3 A. Upon reducing the modulation index from 1.0 to 0.8, the output voltage levels decrease to 11 L, with the output voltage and peak current dropping to 301 V and 4.3 A, respectively. Additionally, the voltages across the switched capacitors C₁ and C₂ during this dynamic operation are illustrated in Fig. 17d.

Fig. 16

Experimental results (a) Output voltage v_o and current i_o and SC voltages V_C2 and V_C3 at load R = 100 Ω, (b) Output voltage v_o and current i_o and SC voltages V_C2 and V_C3 at load Z = 60 + j100 Ω, (c) & (d) voltage and current profile of SCs (C₁-C₄) at load Z = 60 + j100 Ω.

Fig. 17

Experimental results during dynamic operating conditions (a) Output voltage v_o and current i_o and SC voltage V_C1 for a step change in input voltage from 57 to 60 V, (b) Voltage profile of SCs (C₁-C₄) at load Z = 60 + j100 Ω for a step change in input voltage from 57 to 60 V, (c) Output voltage v_o and current i_o for a load change of R = 100 Ω to Z = 60 + j100 Ω, (d) Output voltage v_o and current i_o and SC voltage V_C1 and V_C2 for a change in MI from 1 to 0.8.

Fig. 18

The control scheme for the grid-connected operation of the proposed HBSC-13L-CGTLI.

Fig. 19

Experimental results at grid-connected operation (a) Inverter output voltage v_o, grid voltage and current v_g/i_g at unity PF, (b) Inverter output voltage v_o, grid voltage and current v_g/i_g at leading PF, and (c) Inverter output voltage v_o, grid voltage and current v_g/i_g at lagging PF.

As depicted in the Fig. 18, the control architecture for grid-connected operation is implemented as described in¹⁶. The filtered current i_g is injected into the utility system, where the grid synchronization block manages synchronisation with the utility voltage. This synchronisation enables the transformation block to convert the desired active (P) and reactive (Q) power references into corresponding current components (i_g^ref||) and (i_g^ref⊥), which are then combined to form the total reference grid current (i_g^ref). The actual grid current (i_g)is compared with this reference, and a Proportional-Resonant (PR) controller processes the resulting error to generate the voltage reference V_ref. This reference is used by the PWM block to generate appropriate gate signals, which are fed to the gate driver to control the inverter power switches.

The Proportional–Resonant (PR) controller effectively regulates sinusoidal currents by combining two adjustable parameters: the proportional gain (K_p) and the resonant gain (K_r). It is used as the inner current controller to ensure accurate tracking of the reference current (i_g,ref), typically set for a unity power factor. The PR output feeds into the PWM stage, controlling the inverter’s switching. The PR controllers operate in the stationary reference frame and offer infinite gain at the grid frequency ω_o, eliminating steady-state error.

The standard transfer function is:

$$G_{c} (s) = K_{p} + \frac{{2K_{i} s}}{{s^{2} + \omega_{0}^{2} }}$$

(37)

To ensure digital implementation stability, a damping factor is added:

$$G_{c} (s) = G_{{c_{p} }} (s) + G_{{c_{r} }} (s) = K_{p} + \frac{{2K_{i} \omega_{c} s}}{{s^{2} + 2\omega_{c} s + \omega_{0}^{2} }}$$

(38)

In the proposed HBSC-13L-CGTLI system, the values K_p = 62.83 and K_r = 6283 are chosen via iterative tuning for optimal performance in a 1 kW setup.

The inverter’s output voltage (v_o) waveform, grid voltage (v_g) waveform, and grid current (i_g) waveform under various power factor (PF) conditions such as unity PF, leading PF, and lagging PF conditions of the proposed topology is tested and the respective results are presented in Fig. 19a–c. Fig. 20a–d illustrates the voltage stress profile of the switches (S₁-S₁₃) and diodes (D₁-D₃). These blocking voltage measurements reveal that switches S₁, S₃, S₄, S₅, S₈, S₉, S₁₀, and S₁₃ experience blocking voltage equal to twice the input voltage (2V_dc), switch S₂ blocking voltage equals the input voltage (V_dc), while switches S₆, S₇, S₁₁, and S₁₂, along with diodes D₂ and D₃, maintain a maximum blocking voltage of 67% of the output voltage.

Fig. 20

Experimental results of (a–d) Voltage profile of switches S₁-S₁₃ and diodes D₁-D₃.

Fig. 21a presents the experimental efficiency comparison between the proposed topology and those presented in^41,43. For identical output power conditions, the experimental efficiency of the proposed topology demonstrates superior performance compared to^41,43. Additionally, Fig. 21b illustrates the correlation between simulation and experimental analysis of the proposed topology.

Fig. 21

Efficiency comparison between (a) Proposed topology [P],^41,43, (b) Simulation Vs Experimental.

Conclusion

A single-source, high-boost, switched-capacitor-based 13L CG transformerless inverter topology with a voltage gain of six is proposed. The proposed structure utilises fewer devices compared to other recent topologies with the same output voltage level, achieving sixfold voltage boosting without the use of an H-bridge. The voltage of the switched capacitors is maintained using a series–parallel configuration, thereby validating their self-balancing capability. An important feature of the proposed topology is its use of a reduced number of switches while achieving a high voltage boost. Moreover, the MBV_p.u. of the switches remains within the output voltage, i.e., limited to 67% of the output voltage. A detailed comparison with existing topologies of the same 13L output voltage level shows that the proposed configuration achieves higher voltage gain with reduced power switch count and lower maximum blocking voltage (MBV), resulting in significantly lower overall cost. The experimental prototype of 1 kW was tested across a range of operating conditions, including steady-state, dynamic response, and grid-connected scenarios, demonstrating the effectiveness and practical viability of the proposed topology. The simulation efficiency of the proposed topology is 98.6%, while the measured efficiency is 97.5%, both of which are higher than those of recent topologies at the same output power levels. The proposed topology stands out for its high voltage boost with reduced switches, low MBV_p.u., and cost-efficiency. Combined with the CG feature, it is well-suited for solar PV applications that demand high voltage gain and zero leakage current.