Assessment of Chinese local government disaster resilience based on the D-FAHP method

Abstract

Previous studies on disaster resilience commonly employ the AHP and FAHP methods, but both exhibit limitations when expert evaluation information is incomplete or uncertain. To address this, this study adopts the D-FAHP method to assess the disaster resilience of sub-provincial municipal governments in China. Building on prior research and incorporating critical indicators identified through team fieldwork, we established an evaluation system with 4 criterion layer indicators and 19 scheme layer indicators.The D-FAHP method proves more applicable to complex evaluations under uncertain environments, enhancing the scientific rigor of indicator weight calculation in this study. By integrating indicator weights with expert panel assessments, we conducted a quantitative analysis and evaluation of the disaster resilience of the Qiannan Municipal Government. The comprehensive disaster resilience score reached 87.19, rated as “Good”. Among the four phases, mitigation, preparedness, and recovery demonstrated strong performance, while the response phase requires further improvement. Overall, this study contributes to: (1) Enriching the disaster resilience evaluation indicator system, while empirically validating the critical importance of public disaster prevention education, public disaster response capacity training, crisis management resource reserves, and hazard avoidance-based land use planning; (2) Pioneering the application of the D-FAHP method, an innovative integration scarcely seen in existing disaster resilience assessment research.

Introduction

In 2023, there were a total of 326 major natural disasters worldwide, resulting in 86,473 people died, 93.05 million people were affected, and direct economic losses amounted to US$202.652 billion. Compared with the average of the past 30 years (1993–2022), the frequency of larger natural disasters in 2023 has decreased by 3%, the number of people killed is 73% more, the number of people affected is 53% less, and the direct economic loss is 32% more¹.

This study assesses the capacity of local governments to respond to natural disasters, which include meteorological disasters, geologic disasters, forest fires, and major biological disasters². Governmental emergency response capacity is expressed both in the degree of realization of the emergency management system implemented by the national government and in the ability of the territorial government to cope with specific risks³. From traditional society to modern society and post-modern society, the government function structure from the class rule function gradually to the direction of social management function and social service function center shift phenomenon⁴. The government, as a provider of public services, a formulator of public policy, a manager of public affairs and an exerciser of public power, is in an important special position in crisis management⁵. The Federal Emergency Management Agency has a practice of handling major incidents as locally as possible, that is, local emergency managers are expected to keep the impact of an incident within local boundaries⁶. Because local officials are the first responders to arrive on the scene of an emergency and provide early critical response, local governments have primary functional responsibility in disaster emergency management⁷. To summarize, assessing the disaster resilience of local governments is important to reduce the threat of various disasters to the survival and development of the population.

The four-phase theory of crisis management.The 1978 final report of the National Governors Association (NGA) Emergency Preparedness Program proposed four phases of emergency management: mitigation, preparedness, response, and recovery⁸. Since then, the four-phase theory has become the basic theory of emergency management and has been widely used in emergency management research and practice around the world, although the definitions of the four phases are not exactly the same^5,6,9.

In terms of the construction of the emergency response capacity evaluation index system, the selection and establishment of some index systems are based on the crisis management cycle theory. For example, Deng constructed the framework of urban emergency response capacity evaluation system including 18 classes, 76 attributes and 405 features, and the 18 classes in the evaluation system reflect the idea of crisis management cycle theory¹⁰. Yang established a comprehensive capacity evaluation system for urban disaster emergency management based on process management, which includes three subsystems as well as 12 sub-systems, including pre-disaster early warning capacity evaluation, disaster emergency response capacity evaluation and post-disaster recovery capacity evaluation, and empirically analyzed the emergency response capacity of the governmental departments with a comprehensive evaluation Table¹¹. Henstra constructed an indicator system for evaluating local government emergency management plans, proposing a total of 30 key measurement items from four phases: preparedness, mitigation, response, and recovery¹². Li constructed the evaluation index system of comprehensive emergency response capacity for urban flooding, covering three dimensions of pre-disaster prevention capacity, disaster disposal capacity and post-disaster recovery capacity, with a total of 15 measurement items¹³.

Regarding methodological selection, existing studies have widely employed AHP and FAHP methods. However, these approaches exhibit limitations when expert evaluation information is incomplete or uncertain. D-number theory permits the sum of D-values to be less than 1, with the residual portion accounting for “unknown or unobserved information,” thereby enhancing its capability to handle incomplete data. Hence, this study adopts the D-FAHP method. In the following section, we will introduce the development of D-number theory and the D-FAHP method.

Theoretical foundation

D-S theory

D-S theory is usually referred to as Dempster-Shafer theory, which was jointly developed by Dempster and Shafer.In 1967, Dempster first proposed the framework of upper and lower probability induced by multivalued mapping in his paper, which passes probability measures from the space X to the space S through multivalued mapping, defines the upper probability and the lower probability and introduces the rule of combination of evidence¹⁴. This work provided new tools for dealing with uncertainty and incomplete information, but its mathematical formalization was not yet perfected.In 1976, Shafer further extended Dempster’s ideas in his work, and his core contributions included the discriminative framework, the formal definition of the belief function, and the canonicalization of Dempster’s combinatorial rules, marking the formalization of D-S theory¹⁵. However, the Dempster-Shafer (D-S) theory also exhibits limitations, which motivated the development of D-number theory.

D numbers theory

D Numbers Theory, proposed by Deng in 2012, aims to address the limitations of Dempster-Shafer (D-S) theory in dealing with incomplete information and highly conflicting evidence. The basic probability assignment (m-function) of D-S theory needs to satisfy ∑m(A) = 1, which is not able to deal with the lack of information directly, whereas D Numbers Theory allows the sum of D values to be less than 1, with the remainder representing “unknown or unobserved information”, enhancing the ability to express incomplete information¹⁶.

The definition and properties of D-number are as follows¹⁶:

Definition 1

Let there exist a finite nonempty set Ω with a mapping D:

$$D{\text{ }} \to {\text{ }}\Omega {\text{ }}\left[ {0,1} \right]$$

(1)

Satisfying:

$$\:\sum\:_{B\subseteq\:{\Omega\:}}\text{D}\left(\text{B}\right)\le\:1,\text{D}\left({\uptheta\:}\right)=0$$

(2)

Then the mapping D is called a D-number, where B is a subset of Ω, $\:{\uptheta\:}$ is the empty set. If $\:\sum\:_{B\subseteq\:{\Omega\:}}\text{D}\left(\text{B}\right)=1$, Then it means that the information represented by the number D is complete. If $\:\sum\:_{\text{B}\subseteq\:{\Omega\:}}\text{D}\left(\text{B}\right)<1$, Then it means that the information represented by the D number is incomplete.

Definition 2

Let there exist a D-number D and a nonempty finite set Ω, Then the information completeness Q of D can be quantitatively expressed as:

$$\:\text{Q}=\sum\:_{B\subseteq\:{\Omega\:}}\text{D}\left(\text{B}\right)$$

(3)

Definition 3

Let the discrete set Ω = {b₁, b₂,…, b_i, …, b_n}, Then the special expression for the D-number is:

$$\begin {aligned}{D\left( {\{ {b_1}\} } \right){\text{ }} = {\text{ }}{v_1}} \\ {D\left( {\{ {b_2}\} } \right){\text{ }} = {\text{ }}{v_2}} \\ \ldots \\ {D\left( {\{ {b_i}\} } \right){\text{ }} = {\text{ }}{v_i}} \\ \ldots \\ D\left( {\{ {b_n}\} } \right){\text{ }} = {\text{ }}{v_n}\end {aligned}$$

(4)

It can also be expressed simply as:

$$D{\text{ }} = {\text{ }}\left\{ {\left( {{b_1},{\text{ }}{v_1}} \right),\left( {{b_2},{v_2}} \right),{\text{ }} \ldots ,{\text{ }}\left( {{b_i},{\text{ }}{v_i}} \right),{\text{ }} \ldots ,{\text{ }}\left( {{b_n},{\text{ }}{v_n}} \right)} \right\}$$

(5)

Among these, v_i>0 and $\:\sum\:_{i=1}^{n}{v}_{i}\le\:1$.

The uncertainty problem can be efficiently described by the above expressions for D-numbers.

Definition 4

Let there exist D numbers:

D = {(b₁, v₁₎, (b₂, v₂), …, (b_i,v_i), …,(b_n,v_n)}, Then its integration can be expressed as:

 

$$I(D)=\:{\sum\:}_{i=1}^{n}{b}_{i}{v}_{i}$$

(6)

Prior to presenting the improvements made by D-number theory to fuzzy preference relations, an introduction to fuzzy preference relations is requisite.

Fuzzy preference relation

The fuzzy preference relation is denoted by the symbol “>”, which represents the experts’ preferences for each assessment object by constructing a pairwise comparison matrix.

Let there exist a set of evaluation objects S = {S₁, S₂, …, S_n} with fuzzy preference relations:

$${\mu _R}:{\text{ }}S{\text{ }} \times {\text{ }}S{\text{ }} \to {\text{ }}\left[ {0,{\text{ }}1} \right]$$

(7)

Expressed in matrix form as R = [r_ij]_m×n:

$$\:\text{R}=\left[\begin{array}{cc}\begin{array}{cc}{r}_{11}&\:{r}_{12}\\\:{r}_{21}&\:{r}_{22}\end{array}&\:\begin{array}{cc}\dots\:&\:{r}_{1n}\\\:\dots\:&\:{r}_{2n}\end{array}\\\:\begin{array}{cc}\vdots&\:\vdots\\\:{r}_{n1}&\:{r}_{n2}\end{array}&\:\begin{array}{cc}\vdots&\:\vdots\\\:\dots\:&\:{r}_{nn}\end{array}\end{array}\right]$$

This matrix is satisfying:

(1) r_ij ≥ 0. (2)r_ij + r_ji = 1, ∀ i, j ∈ {1, 2, …, n}. (3)r_ii = 0.5, ∀ ∈ {1, 2, …, n}.

where r_ij denotes the degree of expert’s preference for the importance of S_i with respect to S_j. The assignment of r_ij and its corresponding meaning are as follows:

1) r_ij = 0, S_j is definitely more important than S_i.

2) r_ij ∈ (0, 0.5), S_j is a bit more important than S_i.

3) r_ij = 0.5, S_i and S_j are equally important.

4) r_ij = ∈(0.5,1), S_i is a bit more important than S_j.

5) r_ij = 1, S_i is definitely more important than S_j.

However, the fuzzy preference matrix also has shortcomings, for example, in the case of incomplete or uncertain assessment information of experts, it is impossible to construct a reasonable fuzzy preference matrix, so the application of the fuzzy preference matrix is somewhat limited. Consequently, the fuzzy preference relation enhanced by D-numbers (the D-number preference relation) was put forward.

D-number preference relation

Due to the limitations of fuzzy preference relation in the case of incomplete or uncertain information of expert assessment, DENG proposed a D-number preference relation theory in his research, which extends the fuzzy preference relations with the D-number theory to expand the scope of application of preference relation to the field of uncertain information to cope with the limitations of the fuzzy preference relation, and its corresponding matrix is called the D number preference matrix, or D matrix for short, which is assumed as follows¹⁷.

Let there exist a set of assessment objects S = {S₁, S₂, …, S_n}, Its D-number preference relation can be expressed as follows:

$${R_D}:{\text{ }}S{\text{ }} \times {\text{ }}S{\text{ }} \to {\text{ }}D$$

(8)

Expressed in hexamatrix form as R_D = [D_ij]_m×n:

$$\:{\text{R}}_{\text{D}}=\left[\begin{array}{cc}\begin{array}{cc}{D}_{11}&\:{D}_{12}\\\:{D}_{21}&\:{D}_{22}\end{array}&\:\begin{array}{cc}\dots\:&\:{D}_{1n}\\\:\dots\:&\:{D}_{2n}\end{array}\\\:\begin{array}{cc}\vdots&\:\vdots\\\:{D}_{n1}&\:{D}_{n2}\end{array}&\:\begin{array}{cc}&\:\vdots\\\:\dots\:&\:{D}_{nn}\end{array}\end{array}\right]$$

This matrix is satisfying:

(1) D_ij = {($\:{b}_{1}^{ij}$, $\:{v}_{1}^{ij}$), ($\:{b}_{2}^{ij}$,$\:{v}_{2}^{ij}$), …, ($\:{b}_{m}^{ij},\:{v}_{m}^{ij}$)},D_ji = {($\:1-{b}_{1}^{ij}$, $\:{v}_{1}^{ij}$),(1-$\:{b}_{2}^{ij}$, $\:{v}_{2}^{ij}$), …, ($\:1-{b}_{m}^{ij},\:{v}_{m}^{ij}$)}, ∀ i, j ∈ {1, 2, …, n}.

(2) $\:{b}_{k}^{ij}$ ∈ [0, 1], ∀ k ∈ {1, 2, …, m}.

(3) D_ii = {(0.5, 1.0)}, ∀ i ∈ {1, 2, …, n}.

Where $\:{b}_{k}^{ij}$ denotes the degree of importance of the ith option relative to the jth option as perceived by the Kth expert, and $\:{v}_{k}^{ij}$ denotes the degree of support for that degree of importance by the expert.

Proposed model

D-FAHP method

AHP is a system analysis method combining qualitative analysis and quantitative analysis proposed by A.L.Saaty, an American operations researcher.The key link of AHP is the establishment of judgment matrix, and whether the judgment matrix is scientific and reasonable has a direct impact on the effect of AHP, but there are the following problems: (1) It is difficult to test the consistency of the matrix. (2) When the matrix is not consistent, it is difficult to adjust. (3) The judgment standard of matrix consistency lacks scientific basis. (4) The consistency of matrix is significantly different from the consistency of human thinking¹⁸. In order to solve the above problems, the concept of fuzzy consistency matrix was introduced. The core idea is to use triangular fuzzy numbers to generate judgment matrices, to obtain a more objective fuzzy set consisting of judgment results, and to make the results more consistent with the actual thinking process by comparing the objective analysis process¹⁹. The AHP method that introduces a fuzzy agreement matrix is FAHP, which is a multi-criteria decision-making method that combines fuzzy logic and AHP.

The FAHP method, by introducing fuzzy consistent matrices, makes the results more aligned with the actual human thought process, representing a further development of the AHP. However, the FAHP method cannot handle differentiated opinions within expert groups, such as in the following two scenarios: (1) Eight experts believe that the importance level of S1 compared to S2 is 0.7, while two other experts believe it is 0.6. (2) Eight experts believe that the importance level of S1 compared to S2 is 0.7, while another group of experts considers the evaluation information incomplete or uncertain and does not provide the importance level of S1 compared to S2. In these two cases, the importance level of S1 compared to S2 cannot be represented using ordinary fuzzy preference relations. However, D-FAHP extends fuzzy preference relations using D-number theory, expanding the applicability of preference relations to the domain of uncertain information to address the limitations of fuzzy preference relations, allowing for differentiated opinions within expert groups [24]. D-FAHP can represent the aforementioned two cases as [(0.6, 0.2), (0.7, 0.8)] and (0.7, 0.8), respectively. Thus, this study adopts the D-FAHP method, which can be better applied to complex evaluation and decision-making problems in uncertain environments.

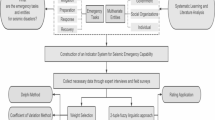
The construction of the evaluation index system

Referring to NGA’s discussion of the four-stage theory of crisis management, this study divides the local government disaster resilience assessment index system into four criterion layers of indicators: mitigation, preparedness, response and recovery⁸. Existing studies have constructed a rich number of emergency response capacity assessment index systems, but some disaster resilience assessment index systems do not include public education on disaster prevention knowledge and disaster response capacity training^13,20,21. Some studies have pointed out that attention should be paid to the cultivation of urban residents’ active participation in disaster reporting in normal times, and that strengthening the disaster prevention and relief ability of urban residents is an effective way to enhance the city’s comprehensive disaster prevention capability, and people’s behavior and response to disasters have become a decisive factor in disaster reduction¹⁰. The public’s behavioral response ability is very important in the whole disaster emergency management system, including the degree of understanding of the disaster, the degree of knowledge of disaster prevention and mitigation, and the ability to save the disaster¹¹.

Some disaster resilience assessment indicator systems do not include resource reserves for crisis management and resource allocation in disaster relief^11,13,22. However, established studies have pointed out that after a disaster, the supply of relief materials is the basic guarantee for rescue and relief, and is a key factor in reducing disaster losses¹⁰. In addition, in the 1997 and 2000 U.S. emergency preparedness assessment of emergency response capabilities, the assessment focused on the 13 management functions of emergency management, including resource management, which shows the importance of resource management in emergency management¹¹.

Some disaster resilience assessment indicator systems do not include hazard avoidance-based land use planning^{11,13,20,23,24}, but some studies have pointed out that the international disaster mitigation strategy has shifted from site-scale engineering “hard” measures to “soft” measures such as regional land use planning restrictions. “Measures”, that is, through the land use planning means to limit the land development behavior, which is the most effective means of preventing geological disasters. Only from the reasonable land use planning to start, limit the land use behavior, assume the responsibility of soil and water conservation, in order to effectively prevent geological disasters or minimize the loss of geological disasters²⁵. Land use planning can prohibit or restrict development in disaster-prone areas, such as flood-prone areas, thereby reducing the risk of people and property being exposed to disasters. In hazardous areas, zoning regulations can prohibit inappropriate development, such as residential construction, and instead designate the land for recreational use. Where development cannot be completely prevented, regulations can limit building density to minimize the number of people and property values at risk²⁶.

Some resilience assessment studies do not include the recovery of governmental functions and service capacities impacted by disaster^{11,13,20,23,24}. However, it has been pointed out that in an emergency situation, most of the studied departments will face office space destruction, manpower shortages due to employee casualties, operational difficulties triggered by the loss of archival equipment, the challenge of extended working hours, and the difficulty of documenting losses and expenditures during the recovery period after a disaster²⁷. And in the aftermath of earthquakes and other disasters, local governments are often swamped with service demands, many of which are related to the immediate impact of the disaster and are handled primarily by fire departments, regular departments, and emergency services. However, a large number of disaster-related needs, as well as regular needs, can also be directed to other functions, which are related to housing, financial support, health services, schooling, and other areas of government responsibility²⁸.

In summary, based on existing studies^{10,11,13,14,20,23,24}, this study added indicators of public education on disaster prevention knowledge and training on disaster response capacity, resource reserves for crisis management, resource allocation in disaster relief, hazard avoidance-based land use planning and the recovery of governmental functions and service capacities impacted by disaster to the indicator system. Four criterion layer indicators, namely mitigation, preparedness, response and recovery, and 19 scheme layer indicators, including public education on disaster prevention, public training on disaster response capacity, disaster monitoring and forecasting, and hazard avoidance-based land use planning, were finally identified. The established evaluation indicator system and its corresponding weight distribution are presented in Table 1.

Table 1 Local government disaster resilience evaluation indicator Weights.

Weighting calculation based on D-FAHP approach

Steps for weight calculation

When using the D-FAHP method, the first step is to solve the indicator weights through the D-number preference relation, and then integrate the indicator weights layer by layer by combining with the FAHP hierarchy structure, and finally obtain the comprehensive weights.

The steps for calculating indicator weights using the D-number preference relation are as follows¹⁷:

Step 1, organize the participating experts to compare the indicators pairwise with reference to the assessment scales in Table 2, and express the importance of the indicators relative to the assessment objectives through the D-number preference relationship, and construct the D-number preference matrix R_D.

Table 2 0.1–0.9 scale method and its meaning.

Step 2, the D-number preference matrix is transformed into a determinant matrix R_C based on the integrated representation of the D-number.

Step 3, constructs a probability matrix R_P based on the determinant matrix R_C, and calculates the preference probabilities between the indicators for pairwise comparisons.

Step 4, the probability matrix R_P is transformed into a triangularized probability matrix $\:{R}_{P}^{T}$ and the indicators are ranked in order of importance.

Step 5, the determinant matrix R_C is represented as a matrix $\:{R}_{C}^{T}$ based on the indicator ranking results.

During the calculation of weights, the inconsistency coefficient I.D. of the D-number preference matrix R_D is calculated using the following equation:

$$\:\text{I}.\text{D}.=\frac{\sum\:_{\text{i}=1,\text{j}<\text{i}}^{\text{n}}{\text{R}}_{\text{P}}^{\text{T}}(\text{i},\text{j})}{\text{n}(\text{n}-1)/2}$$

(9)

where $\:{R}_{P}^{T}(i,j)$ denotes an element in the matrix $\:{R}_{P}^{T}$ and n denotes the number of indicators compared in pairs.

Since there are three levels in the hierarchical structure of the indicator system, namely the target layer, the criterion layer and the scheme layer, when calculating the weights, the weights of the indicators at all levels are integrated layer by layer, and the process is as follows:

(1) Combined with the results of the D-number preference relationship calculation, let the weight vector of the criterion layer indicator U_i relative to the assessment target be A = (a₁, a₂, a₃, a₄), where a_i is the weight of U_i relative to the assessment target, a_i≥0 and $\:\sum\:_{i=1}^{4}{a}_{i}=1$.

(2) Let the weight vector of scheme layer indicator U_ij relative to U_i be B_i = (b_i1,b_i2,…,$\:{b}_{{in}_{i}}$), where b_ij denotes the weight of U_ij relative to U_i, b_ij≥0 and $\:\sum\:_{j=1}^{{n}_{i}}{b}_{ij}=1$, n_i denotes the number of scheme layer indicators U_ij corresponding under the criterion layer indicator U_i.

(3) Let the set of integrated weights of U_ij relative to the assessment objectives, W=(W₁₁,W₁₂,…,W_ij,…,W₄₁,…,$\:{W}_{{4n}_{i}}$), where W_ij=a_ib_ij, which denotes the integrated weights of Uij relative to the assessment objectives, W_ij≥0 and $\:\sum\:_{i=1}^{4}\sum\:_{j=1}^{{n}_{i}}{a}_{i}{b}_{ij}=1$.

Weighting calculations

D-FAHP is a subjective weight assignment method. In this study, the expert panel consists of 10 members, who are the experts participating in the symposium during our team’s investigation at the Emergency Management Bureau of Qiannan. These experts have professional backgrounds in meteorology, geology and other fields, and possess extensive work experience in emergency management.

Firstly, we calculate the weights of the indicators at each criterion level with respect to the target level. In the previous section, we have elaborated in detail the specific steps for calculating the weights using D-FAHP. Therefore, in this section, we will only present the relevant matrices and results:

$$\:{\text{R}}_{\text{D}}=\begin{array}{c}\begin{array}{c}\\\:{\text{B}}_{1}\\\:{\text{B}}_{2}\end{array}\\\:{\text{B}}_{3}\\\:{\text{B}}_{4}\end{array}\left[\begin{array}{cc}\begin{array}{c}{\text{B}}_{1}\\\:\left(\text{0.5,1.0}\right)\\\:\left(\text{0.3,1.0}\right)\end{array}&\:\begin{array}{c}{\text{B}}_{2}\\\:\left(\text{0.7,1.0}\right)\\\:\left(\text{0.5,1.0}\right)\end{array}\\\:\left(\text{0.3,0.8}\right),\left(\text{0.2,0.2}\right)&\:\left(\text{0.4,1.0}\right)\\\:\left(\text{0.2,0.6}\right),\left(\text{0.3,0.4}\right)&\:\left(\text{0.3,0.6}\right),\left(\text{0.2,0.4}\right)\end{array}\begin{array}{cc}{\text{B}}_{3}&\:{\text{B}}_{4}\\\:\left(\text{0.7,0.8}\right),\left(\text{0.8,0.2}\right)&\:\left(\text{0.8,0.6}\right),\left(\text{0.7,0.4}\right)\\\:\begin{array}{c}\left(\text{0.6,1.0}\right)\\\:\left(\text{0.5,1.0}\right)\\\:\left(\text{0.3,1.0}\right)\end{array}&\:\begin{array}{c}\left(\text{0.7,0.6}\right),\left(\text{0.8,0.4}\right)\\\:\left(\text{0.7,1.0}\right)\\\:\left(\text{0.5,1.0}\right)\end{array}\end{array}\right]$$

$$\:{\text{R}}_{\text{C}}=\begin{array}{c}\begin{array}{c}\\\:{\text{B}}_{1}\\\:{\text{B}}_{2}\end{array}\\\:{\text{B}}_{3}\\\:{\text{B}}_{4}\end{array}\left[\begin{array}{cccc}\begin{array}{c}{\text{B}}_{1}\\\:0.5\\\:0.3\end{array}&\:\begin{array}{c}{\text{B}}_{2}\\\:0.7\\\:0.5\end{array}&\:\begin{array}{c}{\text{B}}_{3}\\\:0.72\\\:0.6\end{array}&\:\begin{array}{c}{\text{B}}_{4}\\\:0.76\\\:0.74\end{array}\\\:0.28&\:0.4&\:0.5&\:0.7\\\:0.24&\:0.26&\:0.3&\:0.5\end{array}\right]$$

$$\:{\text{R}}_{\text{P}}=\begin{array}{c}\begin{array}{c}\\\:{\text{B}}_{1}\\\:{\text{B}}_{2}\end{array}\\\:{\text{B}}_{3}\\\:{\text{B}}_{4}\end{array}\left[\begin{array}{cccc}\begin{array}{c}{\text{B}}_{1}\\\:0\\\:0\end{array}&\:\begin{array}{c}{\text{B}}_{2}\\\:1\\\:0\end{array}&\:\begin{array}{c}{\text{B}}_{3}\\\:1\\\:1\end{array}&\:\begin{array}{c}{\text{B}}_{4}\\\:1\\\:1\end{array}\\\:0&\:1&\:0&\:1\\\:0&\:0&\:0&\:0\end{array}\right]$$

Rank the indicators of the criterion layer according to their degree of importance: B1 > B2 > B3 > B4

$$\:{\text{R}}_{\text{P}}^{\text{T}}=\begin{array}{c}\begin{array}{c}\\\:{\text{B}}_{1}\\\:{\text{B}}_{2}\end{array}\\\:{\text{B}}_{3}\\\:{\text{B}}_{4}\end{array}\left[\begin{array}{cccc}\begin{array}{c}{\text{B}}_{1}\\\:0\\\:0\end{array}&\:\begin{array}{c}{\text{B}}_{2}\\\:1\\\:0\end{array}&\:\begin{array}{c}{\text{B}}_{3}\\\:1\\\:1\end{array}&\:\begin{array}{c}{\text{B}}_{4}\\\:1\\\:1\end{array}\\\:0&\:1&\:0&\:1\\\:0&\:0&\:0&\:0\end{array}\right]$$

.

During the weight calculation process, according to Formula (9), the inconsistency coefficient I.D. of the D-number preference matrix R_D is computed as 0.1667 using matrix $\:{R}_{P}^{T}$. Based on existing research, the rationality of the D-matrix is represented by the inconsistency coefficient I.D., and the acceptability of the inconsistency in the decision-making matrix (D-matrix) is determined by the decision-makers, whose subjective requirements define the tolerance level for inconsistency¹⁷. After discussion, the expert group concluded that although the I.D. value is slightly higher than 0.1, upon re-examining the weighting process, it was found that it reflects reasonable and irreconcilable differences in perspectives. These differences stem from the inherent complexity of the decision-making problem, and the current judgments have adequately represented the collective wisdom. Forcing a lower inconsistency might distort the genuine opinions of certain experts.

$$\:{\text{R}}_{\text{C}}^{\text{T}}=\begin{array}{c}\begin{array}{c}\\\:{\text{B}}_{1}\\\:{\text{B}}_{2}\end{array}\\\:{\text{B}}_{3}\\\:{\text{B}}_{4}\end{array}\left[\begin{array}{cccc}\begin{array}{c}{\text{B}}_{1}\\\:0.5\\\:0.3\end{array}&\:\begin{array}{c}{\text{B}}_{2}\\\:0.7\\\:0.5\end{array}&\:\begin{array}{c}{\text{B}}_{3}\\\:0.72\\\:0.6\end{array}&\:\begin{array}{c}{\text{B}}_{4}\\\:0.76\\\:0.74\end{array}\\\:0.28&\:0.4&\:0.5&\:0.7\\\:0.24&\:0.26&\:0.3&\:0.5\end{array}\right]$$

Solve the system of equations from this matrix:

$$\:\left\{\begin{array}{c}\begin{array}{c}\lambda\:({W}_{B1}-{W}_{B2})=0.7-0.5\\\:\lambda\:({W}_{B2}-{W}_{B3})=0.6-0.5\end{array}\\\:\lambda\:({W}_{B3}-{W}_{B4})=0.7-0.5\\\:{W}_{B1}+{W}_{B2}+{W}_{B3}+{W}_{B4}=1\end{array}\right.$$

$\:\lambda\:$>0,$\:{W}_{Bi}\ge\:0$,∀i∈{1,2,3,4}.

Where W_Bi denotes the weight of the ith criterion layer indicator, and $\:\lambda\:$ denotes the credibility of the information, which is related to the cognitive ability of the participating experts about the assessment problem. The assessment expert group in this study consists of emergency management researchers and managers with rich management experience, so $\:\lambda\:$=$\:\lceil\lambda\:\rceil$=2. Therefore, the weight of each criterion layer indicator is obtained as W_B1 = 0.375, W_B2=0.275, W_B3=0.225, W_B4=0.125.In the four indicators of the criterion layer, according to weights in descending order were soothing (B1), preparation (B2), response (B3) and recovery (B4).

Similarly, according to the above steps can be found in each scheme layer indicators for the criterion layer indicators of the weight, as well as relative to the target layer of the integrated weight, the results of the calculation shown in Table 1.

The combined weight vector of indicators for each scheme layer W_C1=(0.077), W_C2=(0.058), W_C3=(0.129), W_C4=(0.111), W_C5=(0.074), W_C6=(0.055), W_C7=(0.035), W_C8=(0.046), W_C9=(0.066), W_C10=(0.075), W_C11=(0.064), W_C12=(0.043), W_C13=(0.012), W_C14=(0.032), W_C15=(0.044), W_C16=(0.031), W_C17=(0.025), W_C18=(0.018), W_C19=(0.008).

Assessment of disaster resilience of Chinese local government

Evaluation process

This study uses the Qiannan municipal government as a case in point. Concerning the rationality of sample size, the majority of existing research on disaster resilience assessment involves only a single sample. Only a very small number of studies are based on multiple samples.However, multi-sample research using D-FAHP demands substantial research resources, as the scoring of each sample must be grounded in the sample’s actual circumstances. Taking this into account, we anticipate expanding the sample size in future research endeavors.Based on the weights of the above scheme layers and with reference to established studies²⁹, the process of assessing the resilience of local governments is as follows:

(1) Establishment of evaluation sets.

Third, the evaluation set V={V₁, V₂, …, V_n} is constructed. According to the characteristics of disaster resilience, this study divides the evaluation set into five levels, V={excellent, good, average, poor, very poor}.

(2) Determination of indicator affiliation.

Indicator affiliation refers to the degree of affiliation of each indicator to the local government resilience evaluation set. This is because not all quantitative evaluations of an indicator by an expert group are consistent. For example, if x experts within the expert group quantitatively evaluate a program indicator, and y experts rate it as excellent, the degree of affiliation of the excellent evaluation is y/x.

(3) Confirmation of fuzzy relationship matrix.

Based on the evaluation results of the experts, the affiliation degree of the five evaluation levels under each scheme layer indicator can be obtained, and the fuzzy relationship matrix of affiliation degree is generated R=(r_ij)_m×n. r_ij denotes the affiliation degree of the ith factor to the jth element.

(4) Calculation of comprehensive evaluation matrix.

In this study, the weighted average fuzzy operator is used in the quantitative calculation of evaluation to calculate the evaluation vector B of the local government’s disaster resilience, and the calculation formula is as follows:

$$B = W\cdot R$$

(10)

(5) Quantitative assessment of local government disaster resilience.

The five evaluations in the evaluation set are replicated to obtain the assignment matrix P, P=(Pi)_5×1. Multiplying the comprehensive evaluation matrix with the assignment matrix yields the quantitative evaluation value of disaster resilience, F³⁰.

$$F=B\cdot P$$

(11)

In order to visualize the results of the evaluations for quantitative analysis, the scores of the five evaluations were graded as shown in Table 3 and P was assigned as P1 = 100, P2 = 90, P3 = 80, P4 = 70, and P5 = 60.

Table 3 Comprehensive evaluation criteria for emergency response capacity.

Case analysis

The expert group’s affiliation scores for local government disaster resilience are shown in Table 4. By multiplying the local weights of the indicators at each scheme layer with the affiliation degree of the corresponding evaluation level and summing them according to the criterion layer of affiliation, the results indicate that: B1=(0.2, 0.438, 0.331, 0.031, 0), B2=(0.234, 0.341, 0.426, 0, 0), B3=(0.144, 0.277, 0.428, 0.151, 0), B4=(0.188, 0.448, 0.352, 0.012,0), The affiliation matrix for scheme layer indicators is:

$$\:\text{R}=\left[\begin{array}{c}\begin{array}{c}{\text{B}}_{1}\\\:{\text{B}}_{2}\end{array}\\\:{\text{B}}_{3}\\\:{\text{B}}_{4}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{cc}0.2&\:0.438\\\:0.234&\:0.341\end{array}&\:\begin{array}{ccc}0.331&\:0.031&\:0\\\:0.426&\:0&\:0\end{array}\\\:\begin{array}{cc}0.144&\:0.277\\\:0.188&\:0.448\end{array}&\:\begin{array}{ccc}0.428&\:0.151&\:0\\\:0.352&\:0.012&\:0\end{array}\end{array}\right]$$

According to Eq. (10), the comprehensive evaluation vector B = W∙R is obtained.

$$\:\text{B}=\left(\text{0.375,0.275,0.225,0.125}\right)\left[\begin{array}{cc}\begin{array}{cc}0.2&\:0.438\\\:0.234&\:0.341\end{array}&\:\begin{array}{ccc}0.331&\:0.031&\:0\\\:0.426&\:0&\:0\end{array}\\\:\begin{array}{cc}0.144&\:0.277\\\:0.188&\:0.448\end{array}&\:\begin{array}{ccc}0.428&\:0.151&\:0\\\:0.352&\:0.012&\:0\end{array}\end{array}\right]$$

B = (0.195,0.376,0.382,0.047,0).

According to Eq. (11), F = B∙P

$$\:\text{F}=\left(\text{0.195,0.376,0.382,0.047,0}\right)\left[\begin{array}{c}\begin{array}{c}100\\\:90\end{array}\\\:80\\\:\begin{array}{c}70\\\:60\end{array}\end{array}\right]=87.19\:\text{c}\text{a}\text{n}\:\text{b}\text{e}\:\text{o}\text{b}\text{t}\text{a}\text{i}\text{n}\text{e}\text{d}.$$

.

Therefore, the disaster resilience of the Qiannan municipal government is good.

Table 4 Membership degree of second-level index,.

Results and discussion

This study employs the D-FAHP method to evaluate the disaster resilience of the Qiannan Municipal Government. The existing disaster resilience assessment indicator system inevitably omits several critical indicators, such as public disaster prevention education and public disaster response capacity training, crisis management resource reserve, disaster relief resource allocation, hazard avoidance-based land use planning, and the Recovery of governmental functions and service capacities impacted by disasters. Based on in-depth field research, we have supplemented these indicators into the local government disaster resilience assessment indicator system. This has resulted in a comprehensive indicator system comprising 4 criterion layers and 19 scheme layers.

After calculating the weights, the indicators at the criterion layer are ranked from highest to lowest weight as follows: Mitigation, Preparedness, Response, and Recovery. This is in line with the basic principle of “prevention first and integration of peacetime and wartime” in emergency management². The calculation results of the weights also confirm the importance of the indicators we added. For example, the comprehensive weight of hazard avoidance-based land use planning is as high as 0.111; the comprehensive weight of public disaster prevention education is 0.077; the comprehensive weight of public disaster response capacity training is 0.058; and the weight of the capacity to rehabilitate government functions and services affected by disasters ranks second among the five indicators in the recovery stage.

Subsequently, a quantitative evaluation was carried out on the disaster resilience of Qiannan Municipal Government. The final evaluation score was 87.19, and the evaluation result was rated as “good”. Specifically, the score in the mitigation stage was 88.07, the score in the preparedness stage was 88.08, the score in the response stage was 84.132, and the score in the recovery stage was 88.12. Currently, the response stage has negatively impacted the final evaluation score. However, to further enhance the disaster resilience of Qiannan Municipal Government, efforts should not only be focused on improving the capabilities in the response stage, but also on optimizing the work in the mitigation and preparedness stages. Notably, it is essential to strengthen the training of the public’s disaster response capabilities and conduct annual reviews of emergency response plans. Moreover, there is a pressing need to further bolster the community-level emergency response forces, which are currently rather weak in Qiannan. In addition, to enhance the efficiency and effectiveness of emergency management, it is necessary to further promote the application of artificial intelligence (AI) and data science in this field³¹. If Qiannan can further enhance its disaster resilience in these aspects, it will offer valuable insights and experiences for the national disaster risk management framework.

In the mitigation stage, disaster monitoring and forecasting received the highest score (90 points) and carried the greatest weight. In modern emergency management, being able to anticipate the approaching of disasters in advance can significantly mitigate disaster losses. Therefore, disaster monitoring and forecasting are of utmost significance. The meteorological department of Qiannan offers a three-tier progressive service framework consisting of “special meteorological information reports → early warning bulletins → short-term and imminent forecasts”. This enables the locking-in of the heavy rainfall trend 48 h in advance. Moreover, Qiannan has allocated responsibilities for 524 mountain flood-prone areas, 310 reservoirs, and 101 ponds based on risk levels, and formulated key flood-prevention layout plans. These measures demonstrated remarkable effectiveness during the heavy rainfall periods of the 2025 flood season. The public disaster response capacity training received the lowest score (84 points). This is because Qiannan has organized numerous disaster response capacity training programs targeting primary and secondary school students, while overlooking the training for grass-roots communities. A study have noted that within 72 h after a disaster, the government should also disseminate self-rescue demonstration videos via social media to enhance the disaster response capabilities of the affected population³². We concur with this perspective. However, we assert that pre-disaster training of disaster response capabilities is even more crucial. Such training should encompass both disaster prevention training and post-disaster adaptability training. Additionally, teachers with specialized training play a pivotal and irreplaceable role in the effective dissemination of disaster education knowledge³³.

In the preparation stage, the comprehensive emergency response plan carried the highest weight and ranked second in terms of scoring (88 points). This is attributable to the fact that the comprehensive emergency response plan serves as a cornerstone for the management of diverse disasters. A well-structured plan framework can offer detailed guidelines for disaster management, thereby enhancing the capacity for disaster resilience.Qiannan has established a “1 + 23” emergency rescue command system, thus formulating a plan system centered around the comprehensive plan and buttressed by specialized plans. Specifically, this encompasses the “General Emergency Response Plan for Emergencies in Qiannan” along with specialized plans such as the “Emergency Response Plan for Communication Assurance in Emergencies in Qiannan” and the “Emergency Response Plan for Sudden Environmental Incidents in Qiannan”. The annual emergency plan review received the lowest score (86 points). This is because the emergency plans in Qiannan have not been subjected to annual reviews; instead, the review cycle typically extends beyond three years.

In the response stage, the coordination capacity in disaster relief operations holds the highest weight; however, it only received a score of 84 points. This is because disaster relief operations are non-linear in nature and necessitate the collaboration of multiple departments and personnel. An orderly execution of disaster relief operations can enhance their efficiency. Nevertheless, when coordinating disaster relief operations, Qiannan did not adhere strictly to the stipulations of the pre-established plan. Instead, the highest-ranking official present at the scene coordinated the work based on personal experience.

Furthermore, during the disaster, the Qiannan Municipal Government did not adequately focus on information from social media. Leveraging social media information can effectively promote cooperation among organizations, volunteers, and the affected population³⁴. The community-level emergency response force rank second in terms of weight, yet they only scored 80 points. This is due to the fact that Qiannan has only one full-time grassroots rescue team. Grassroots disaster relief operations mainly relies on non-full-time personnel, such as government employees and villagers. These two factors are the primary reasons for the relatively low score of 84.1 in the response stage.In the United Kingdom, the Community First Responders (CFR) have made substantial contributions to the rapid emergency response in rural areas through information sharing, technological intervention, and effective communication³⁵. To address the issue of weak grassroots emergency response capabilities, the Qiannan Municipal Government should draw on the advanced experience of the UK and establish semi-professional teams similar to the CFR at the grassroots level.

In the recovery stage, the disaster recovery plan has the highest weight and also attains the highest score (90 points). This is because when post-disaster recovery efforts are grounded in a pre-designed disaster recovery plan, there is no necessity to devise a recovery plan during the actual disaster event. Instead, minor adjustments can be made to the existing recovery plan, thereby enhancing the efficiency of the recovery work. Qiannan leveraging its comprehensive contingency plan framework, has developed detailed plans for the recovery activities related to various disasters. These plans have effectively guided the recovery operations in the aftermath of past disasters. The Recovery of governmental functions and service capacities impacted by disasters ranks second in terms of weight, yet it only scores 86 points. This is because after the government functions and services in Qiannan have been impacted by disasters, no prior arrangements were made regarding office space and working conditions for the restoration activities. As a result, the timeliness of this restoration process cannot be ensured.

Based on the above discussion, the evaluation results ultimately obtained in this study align with the actual disaster response capacity of the Qiannan municipal government, indicating that integrating D-number theory with the FAHP method for assessing local government disaster response capabilities possesses certain feasibility and effectiveness. The integration of this model is relatively uncommon in existing research, representing an innovative attempt to enhance current evaluation methods. Furthermore, the constructed indicator system demonstrates strong timeliness and practical reference value. However, this study has limitations in terms of generalizability, as it only uses Qiannan as a case study, resulting in a single sample source that fails to cover government disaster response practices across diverse geographical, economic, and social contexts. This constrains the extrapolation potential of the conclusions. In subsequent research, expanding the scope of case studies and selecting multiple representative regions for comparative evaluation should be considered to enhance the universality of the model and findings.