A design of multiple color image encryption scheme based on finite algebraic structures

Abstract

This article introduces an innovative method for constructing substitution and permutation boxes and their application in image encryption. In encryption, the essential component that creates confusion is the substitution box(S-box). S-boxes can be constructed using different mathematical structures. An S-box with high nonlinearity enhances confusion in encryption. The nonlinearity of the S-box depends on its mathematical structure; the more nonlinear the structure, the higher the quality of the S-box. Quality can be measured using differential, linear, and statistical attacks. Another main component in image encryption is the permutation box(P-box), which creates confusion by scrambling the image pixels. The proposed scheme is based on the algebraic structure of the Galois field. In this scheme, we utilize the group action over an 8-bit finite field and then apply a bi-linear transformation to construct S-boxes and P-boxes. The proposed encryption scheme satisfies standard cryptographic requirements. Experimental results show that, in comparison with other well-known existing schemes, the method successfully generates many unique, uncorrelated, and secure S-boxes. A security study of the proposed scheme indicates that multiple color-encrypted images can swiftly and effectively mitigate numerous risks, rendering them suitable for real-time applications with stringent security demands.

Introduction

Data transmission serves as the lifeblood of our interconnected world in the modern digital environment. It involves transferring information between devices, systems, and users, facilitating real-time connectivity and access to vast volumes of data. Researchers have become more interested in data privacy over the past 20 years. Cryptography is the tool employed to protect data from unauthorized access. By utilizing cryptography, a secure data transfer system can be established. There are two categories of cryptography for transforming plaintext into cipher text: symmetric cryptography and asymmetric cryptography. In a symmetric cryptosystem, data blocks are transformed into cipher form by using a single key to cipher and decipher the data. Shanon was the first to give the idea of block ciphering in 1949. The Advanced Encryption System (AES) is an example of a block cipher. While doing encryption by using AES, the confusion created by using the permutation box (P-box) and diffusion created by using the substitution box (S-box). The AES S-box is constructed using a finite algebraic structure, an inversion map, and affine transformation¹. In literature, researchers have used various mathematical structures to construct S-boxes. The APA S-box known as Cao and Cui presented affine-power-affine in 2007². While studying the strength of S-boxes, the AES S-box has greater algebraic complexity as compared with the APA S-box. Minh-Triet-Tran and Doan-Khanh Anh-Duc Duong introduced the Gray S-box in 2008³. The Gray S-box and AES S-box have similar cryptographic properties because it is generated by using binary codes derived from the AES S-box. The researcher built it using binary codes derived from the AES S-box. The Gray S-box and AES S-box share similar experimental properties. Still, the Gray S-box demonstrates greater resistance against interpolation and algebraic attacks than the AES S-box. The Fiestel network utilizes the Skipjack S-box⁴, which is based on 32 rounds and was introduced by Phan and Kim in 2009. For the 64-bit block, this type encrypts and decrypts using an 80-bit key. Iqtadar et al. created chaos-based S-boxes⁵. In⁶, a linear fractional transformation is used to make a very nonlinear S-box. In⁷, a novel method for constructing S-boxes over the projective linear group. The proposed method provides a stronger and system-independent cryptographic structure than existing chaos-based S-box designs, as shown in⁸. The authors of⁹ offer a new way to build S-boxes using group actions over finite local rings. They demonstrate that this method is highly effective for cryptography. In¹⁰, an S-box building strategy that utilizes coset diagrams to illustrate how $PSL(2, \mathbb {Z})$ acts on the projective line over $GF(2^9)$ and a structured mapping approach. This gives the S-box strong cryptographic properties. This work builds an S-box utilising tangent delay from elliptic cavity chaotic sequences and a specific symmetric group permutation, as shown in¹². It is tough to break with differential and linear attacks. As mentioned in¹³, this work suggests a complete evaluation criterion to determine how well existing S-boxes function for encrypting images. Using symmetric group permutations on $GF(2^8)$ elements seeded by the Liu J S-box, this study¹⁴ creates 40320 new $8\times 8$ S-boxes that have better nonlinear features for cryptographic use. These S-boxes demonstrate greater resistance against differential attacks but lower resistance against statistical attacks. Iqtadar et al. obtained 40, 320 S-boxes by applying the permutation of $S_{8}$ on the Liu S-box. An S-box is a mapping from $Z^{p}_2$ to $Z^{q}_2$, represented as $\phi : Z^{p}_2\rightarrow Z^{q}_2.$ The p input bits are mapped into the q output bits via this mapping. We denote an S-box as a square or rectangular matrix. An S-box of order $p\times q$presents two possibilities: first, every input value has a unique output; second, multiple inputs may produce the same output. A bijective S-box is onto and one-to-one. In symmetric key cryptosystems, these S-boxes, sometimes known as reversible S-boxes, are very important. In recent years, we have seen an immense volume of data transmitted through digital channels, emphasizing the critical importance of data security. Each day, numerous images containing personal and confidential data are shared. To improve security and efficiency¹⁵, suggested a new chaos-based partial image encryption system that uses an LFT-based S-box and dynamic keys in the LWT domain. A new method for encrypting images was proposed in¹⁶. It utilizes a complete shuffling matrix and combines chaotic systems to achieve robust security and minimal computational complexity. A novel method for encrypting images, utilizing random pixel permutation and 64-bit key sharing to maintain image privacy while ensuring visual quality¹⁷. A quaternion-based PRNG that uses three chaotic systems was proposed in¹⁸ to fix problems with periodicity and make cryptographic security stronger. NIST statistical tests confirmed this. A memory-efficient tri-stage polynomial multiplication accelerator called Meta¹⁹ was proposed to enhance the flexibility and speed of lattice-based cryptography by utilizing fused computing and reconfigurable hardware. A two-factor authentication solution for keyless entry systems was suggested in²⁰. It combines regular credentials with distinctive vibrations caused by a person’s finger, making it harder for hackers to gain access. Colour images often contain sensitive data related to military, medical, and information technology. To safeguard these confidential images, diverse encryption techniques have been developed based on intricate mathematical structures, such as DNA sequences^20,21,22, SCAN-CA²³, and self-adaptive methods. In recent years, we have witnessed advancements and developments in MIE algorithms derived from chaotic systems. Tang et al.²⁴ proposed a method work in which a PNG image might be generated by decomposing numerous grayscale images into bit planes and subsequently encrypting them. In²⁵, Zhang et al. developed an MIE algorithm employing the SIE approach to consolidate all images into one extensive image. Li et al. used compression techniques into an MIE algorithm to enhance encryption efficiency while reducing storage capacity²⁶. Rasul et al. amalgamated all images into a singular, extensive image before structuring them into one-dimensional data for encryption; yet, the experimental data remained inadequate in terms of security²⁷. The methodology employed by Gao et al. utilized optical methods to encrypt multiple images; however, optical encryption is costly and presents specific obstacles and limitations in practical applications²⁸. Sahasrabuddhe encrypted multiple images by partitioning the colour images into smaller segments and arranging them into cubes²⁹. In³⁰, showed a multiple-image encryption technique utilizing 3D Lorenz and 3D Rossler chaotic maps. The method included pixel permutation and bitwise XOR operations utilizing chaotic sequences. Recent works have proposed robust S-box designs using Galois field transformations³¹, and 3D chaotic maps for secure image encryption³². Recent studies proposed strong medical image encryption schemes using mathematically derived S-boxes with fuzzy sets³³ and algebraic group methods³⁴ to enhance security in e-healthcare systems. Recent works have introduced S-boxes using coset graphs and algebraic methods to improve the security of block ciphers and image encryption^35,36. Recent works proposed fast chaos-based image encryption schemes³⁷, revealed and improved weaknesses via chosen-plaintext attacks^38,39, and optimized S-box design for stronger cryptographic security⁴⁰. Recent works have utilized chaotic systems with SHA-512 for image encryption⁴¹ and 4D hyperchaos to design robust cryptographic S-boxes⁴². The coefficients of linear fractional and affine transformations are subject to particular constraints. A recent study proposed a deniable encryption method for DNA storage, utilizing noise channels to conceal true data among fake messages while ensuring secure and accurate decryption in⁴³. In⁴⁴, a novel chaotic map was proposed for generating dynamic S-Boxes with strong cryptographic properties, enhancing resistance against various attacks in data security applications. In⁴⁵, a dynamic S-Box construction utilizing a novel chaotic map and a tweaking approach was proposed, demonstrating strong cryptographic properties and adaptability for real-world data security applications. This study aims to design multiple highly nonlinear S-boxes with diffusion properties, thereby establishing an unrestricted framework. The suggested technique is distinctive as it treats Galois fields (GF) as a group and operates on GF independently. The generation of S-boxes, P-boxes, and a random number key in the proposed scheme solely relies on Galois field structures. Furthermore, the proposed image encryption method includes permutation, substitution, and bitwise XOR of keys in the substituted channels. The numerous existing multiple-image encryption techniques, which solely rely on chaotic structures, encrypt grayscale images. In the proposed scheme, the S-P-boxes are used to encrypt colour images by processing blocks of sizes 4, 9, and 16, as well as an array of single-colour images. In⁴⁶, an image encryption scheme based on non-chain rings and bivariate polynomials is presented to enhance the algebraic complexity of the cryptosystem. In⁴⁷, a novel hybrid approach for color image encryption schemes based on non-chain rings and chaotic structures is discussed. Effective virtual machine migration and user recruiting in cloud and mobile systems are topics covered in recent research^48,49. Additionally, they investigate POS password leaks through Wi-Fi sensing and secure DNA storage through deniable encryption^50,51. In⁵², a multiple image encryption(MIE) scheme based on 2D and 3D representation challenges to guide future research in MIE; also, MIE is a scheme based on S-boxes and DNA sequences discussed in⁵³. The rest of the presented work consists of eight sections. The section 2 provides some basic knowledge related to our suggested scheme. In section 3, we provide extensive detail about the design of the S-boxes discussed, and in section 4, we address the security analysis of the strategies recently suggested. A discussion of the security analysis for the proposed image encryption system is presented in section 6, while section 5 outlines the proposed image encryption scheme. The final section, number 7, provides a comprehensive overview of the recently proposed scheme, along with some previously completed work. Additionally, in section 8, we declare that we do not have any conflicts of interest with other individuals.

Preliminaries

The cryptographic algorithms, mainly based on algebraic structures such as groups, rings, and fields, possess strong cryptographic properties, including invertibility and nonlinearity. If a non-empty set C satisfies the closure, associative, identity, and inverse properties, it is a group in the context of the binary operations addition and multiplication. Furthermore, if a group holds the commutative property, then it is an abelian group under binary operation. A non-empty set is a ring if it is an abelian group under binary operation addition and is a semi-group (closure and associative laws hold). The set real numbers $\mathbb {R}$, set of integers $\mathbb {Z}$, and integral multiple set of integers $n\mathbb {Z}$ are some examples of rings. An abelian group is said to be a field if it holds the left and right distributive laws. The set of rational numbers $\mathbb {Q}$, set of real numbers $\mathbb {R}$, and set of complex numbers $\mathbb {C}$ are the examples of field. Also, $\mathbb {Z}_{p}$ where p is a prime number is a field. An irreducible polynomial is a polynomial that cannot factored into polynomials of smaller degrees over the same field. The degree of the irreducible polynomial is the variable’s highest power. Let $(\mathbb {F},+,.)$ be a field and $g(y)\in \mathbb {F}(y)$ is said to be irreducible polynomial in $\mathbb {F}(y)$, if it can be written as $g(y)=h(y)k(y)$, for $h(y),\quad K(y)\in \mathbb {F}(y)$, both h(y) and k(y) are constant. When applied to the field of real numbers, the polynomial $y2+1$ is irreducible. The Galois field $GF(p^{m})$ is a finite field of order $p^{m}$ by definition, where m is a positive integer and p is a prime number. In addition to being groups, Galois fields are extensions of prime fields. Let us assume that q(y) is a primitive irreducible polynomial of degree m in the prime field $\mathbb {Z}_{p},$ where p is a prime number. The Galois field for the primitive root $\mu$ of polynomial p(y) is defined as follows:

$$\begin{aligned} GF(p^{m}) =\frac{\mathbb {Z}_p[y]}{ \langle q(y) \rangle } =\{b_{0}+b_{1}\mu +b_{2}\mu ^{2}+\cdot \cdot \cdot \cdot \cdot +b_{m-1}\mu ^{m-1}:b_{j} \in \mathbb {Z}_{p}, \forall j= 0,1,2,......,m-1 \} \end{aligned}$$

(2.1)

For $p=2$ and $m=4$, the Galois field is as follows:

$$\begin{aligned} GF(2^{4}) =\frac{\mathbb {Z}_p[y]}{ \langle q(y) \rangle } =\{b_{0}+b_{1}\mu +a_{2}\mu ^{2}+b_{3}\mu ^{3} :b_{i} \in \mathbb {Z}_{2}, \forall \qquad j= 0,1,2,3 \} \end{aligned}$$

(2.2)

Over the finite field $\mathbb {Z}_{2}$, we define a polynomial of degree 4 as $q(y)= b_{4}y^{4}+ b_{3}y^{3}+b_{2}y^{2}+b_{1}y+b_{0}$. Here, $b_{j}\in \mathbb {Z}_{2}$. The primitive irreducible polynomial of degree over the field $\mathbb {Z}_{2}$ can be defined as $q(y)=y^{4}+y+1$. Let $\upmu$ be its primitive root; then we construct Galois field $GF(2^{4})$ have 16 element which are given below:

$$\begin{aligned} q(\mu ) &= \mu ^{4}+\mu +1=0 \\& 0\\& 1\\& \mu \\& \mu ^{2}\\& \mu ^{3}\\& \mu ^{4} = \mu + 1\\& \mu ^{5} = \mu (\mu + 1)= \mu ^{2} + \mu \\& \mu ^{6} = \mu (\mu ^{2} + \mu ) = \mu ^{3} + \mu ^{2}\\& \mu ^{7} = \mu (\mu ^{3} + \mu ^{2}) = \mu ^{4} + \mu ^{3} = \mu ^{3} + \mu + 1\\& \mu ^{8} = \mu (\mu ^{3} + \mu + 1) = \mu ^{4} + \mu ^{2} + \mu = \mu ^{2} + 1\\& \mu ^{9} = \mu (\mu ^{2} + 1) = \mu ^{3} + \mu \\& \mu ^{10} = \mu (\mu ^{3} + \mu ) = \mu ^{4} + \mu ^{2}=\mu ^{2} + \mu + 1\\& \mu ^{11} = \mu (\mu ^{2} + \mu + 1) = \mu ^{3} + \mu ^{2} + \mu \\& \mu ^{12} = \mu (\mu ^{3} + \mu ^{2} + \mu ) = \mu ^{4} + \mu ^{3} + \mu ^{2} = \mu ^{3} + \mu ^{2} + \mu +1\\& \mu ^{13} = \mu (\mu ^{3} + \mu ^{2} + \mu +1)= \mu ^{4} + \mu ^{3} + \mu ^{2} + \mu = \mu ^{3} + \mu ^{2} + 1 \\& \mu ^{14} = \mu (\mu ^{3} + \mu ^{2} + 1) = \mu ^{4} + \mu ^{3} + \mu = \mu ^{3} + 1 \end{aligned}$$

(2.3)

The elements of the $GF(2^{4})$ can also be written as:

$$\begin{aligned} GF(2^{4})=\{0,1,\mu ,\mu ^{2},\mu ^{3},\mu ^{4},\mu ^{5},\mu ^{6},\mu ^{7},\mu ^{8},\mu ^{9},\mu ^{10},\mu ^{11},\mu ^{12},\mu ^{13},\mu ^{14}\} \end{aligned}$$

(2.4)

On the similar pattern we can construct the $GF(2^m)$, where $m={2,3,4,5,6,7,8}$. Similarly $GF(2^{8})$ can be constructed by using the following polynomial:

$$\begin{aligned} GF(2^{8}) =\frac{\mathbb {Z}_2[y]}{ \langle q(y) \rangle } =\{b_{0}+b_{1}y+b_{2}y^{2}+b_{3}y^{3}+b_{4}y^{4}+b_{5}y^{5}+b_{6}y^{6}+b_{7}y^{7}:b_{j} \in \mathbb {Z}_{2}, \forall j= 0,1,2,......,7 \}, \end{aligned}$$

(2.5)

The primitive irreducible polynomial for degree 8 polynomial of $FG(2^{8})$ is $q(y)=y^{8}+y^{4}+y^{3}+y^{2}+1.$ The $GF(2^{8})$ have 256 unique element, each element can be converted to a integer ranges $[0-255],$

$$GF(2^{8})=\{0,1,\mu ,\mu ^{2},\mu ^{3},\mu ^{4},\mu ^{5},\mu ^{6},.........\mu ^{253},\mu ^{254}\}.$$

Suggested technique for designing S-P-boxes

The suggested approach for constructing permutation and substitution boxes depends on linear fractional transformations, group actions, the Galois field $GF(2^{8})$, and inversion maps. The action of a group G on a set X is as follows:

$$\phi :G\times X \longrightarrow X$$

$$(1)\quad\quad\phi (\sigma _{e},d(z))=(d(z))^{\sigma _{e}} =d(z):where \sigma _{e} \in G, d(z) \in X$$

$$(2)\quad\quad\phi (\sigma , \sigma (\rho ,d(z)))=\phi (\sigma o\rho ,d(z))=(d(z))^{\sigma o \rho }$$

The proposed approach includes the following steps as a whole:

• (1) Construct the Galois field $GF(2^{8}).$

• (2) Taking the action of group G on the set X, here we take $G=GF(2^{8})$ and $X=GF(2^{8})$, then the action of G on X under addition is given below:

  $$\phi :G\times X \longrightarrow X$$

  defined as:

  $$\phi (a,x)=(a+x),$$

  where $a\in G$ and $x\in X.$

• (3) Taking the action of G on X under multiplication is given below:

  $$\phi :G\times X \longrightarrow X$$

  defined as:

  $$\phi (a,x)=(a.x)=d(z),$$

  where $a\in G$ and $x\in X.$

• (4) Defines the inversion map is below:

  $$\phi : GF(2^{8})\longrightarrow GF(2^{8}),$$
  $$\phi (d(z))=(d(z))^{-1}=y, \quad where \, d(z)\in GF(2^{8}).$$

• (5) Use the linear fractional transformation to the elements of the inversion map:

  $$\varPhi : GF(2^{8})\longrightarrow GF(2^{8}),$$

  defined by:

  $$\varPhi (y)=\dfrac{a.y+b}{c.y+d}=z,$$

  where $a,b,c,d \& z\in GF(2^{8}).$

The inversion map and linear fractional transformation create randomness in the elements of GF due to their non-linear behavior. The desired S-boxes are from step 5, which exhibits high nonlinearity. After constructing $GF(2^{8})$ in step 1, we utilize the action of $GF(2^{8})$ on itself through addition. The output of step 2 is again a GF. In step 3, we apply the action of $GF(2^{8})$ on itself through multiplication, resulting in another GF output in Step 3. The group action of $GF(2^{8})$ on itself through addition and multiplication represents a linear transformation. To introduce a non-linear component in our proposed scheme, we map each element of $GF(2^{8})$ to its inverse. For constructing S-boxes with robust cryptographic properties, including ideal nonlinearity and resistance against differential and linear attacks, we apply a linear fractional transformation to the inverse elements of $GF(2^{8}).$ Finally, we generate numerous S-boxes for each value of a, b, c, and d, exhibiting high nonlinearity. Table 1 shows the newly constructed S-box. The flowchart illustrating the newly proposed S-box scheme is in Fig. 1.

Algorithm 1

Pesudocode of the Proposed S-box Scheme

Table 1 The Proposed S-box structure.

Fig. 1

Flowchart of the Proposed S-P-box Generation Scheme.

S-box security analysis

The security evaluation of S-boxes, essential components of symmetric key cryptography systems, involves multiple assessments to ensure resistance against various types of attacks. Strong nonlinearity plays a crucial role in preventing linear cryptanalysis; thus, thoroughly investigating characteristics such as non-linearity and assessing an S-box’s deviation from a linear function is essential. In contrast to differential cryptanalysis, differential analysis measures the likelihood that different input differences will result in specific output differences, calculated through the differential approximation probability (DAP). The linear approximation probability (LAP) measures the strength of the S-box against the linear attacks, which calculates the probability of linear approximations between input and output differences. The proposed S-boxes also undergo Strict Avalanche Criteria (SAC) to ensure the slight change in the input bit results in a bigger change in the output. The bit independence criteria (BIC) increases resistance to numerous cryptographic attacks by establishing minimal correlations between input and output bits. To ensure the resistance and cryptographic strength of the proposed S-boxes, S-boxes undergo numerous cryptographic analyses that are explained in detail in the following sections (Table 2).

Table 2 Comparison of the Proposed S-box with Several well-known Existing Methods.

Nonlinearity(NL)

The nonlinearity of an S-box, or substitution-box, in cryptography is an essential property for measuring the strength of an S-box. It means that changes in the input bits to the S-box do not result in predictable or proportional changes in the output bits. This lack of a simple linear relationship makes it significantly more difficult for attackers to analyze and exploit patterns in the encryption process. When creating safe block ciphers, nonlinear S-boxes are essential because they strengthen the encryption scheme’s defenses against cryptographic attacks, such as differential and linear cryptanalysis.

$$S : GF(2^{8})\longrightarrow GF(2^{8})$$

The nonlinearity(NL) of the S-box can be found over the Galois field $GF(2^{8})$ by the using the following relation:

$$\begin{aligned} NL(S)=min(\sigma ,\mu ,\xi ){\beta \in GF(2^{n})\arrowvert \sigma .S(\beta )\ne \mu .\beta \otimes \xi }, \end{aligned}$$

(4.1)

where $\sigma \in GF(2^{n}),$ $\mu \in GF(2),$ $\xi \in GF(2^{n})\backslash {0}$ and ‘.’ denote dot product over GF(2).

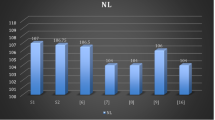
For an S-box, the optimal nonlinearity value is 120 over GF$(2^{8}).$ A S-box with high NL can generate better confusion in the data. An S-box can pass other cryptographic tests without perfect NL. A perfect NL S-box may not fulfill the criteria for other cryptographic attacks. The NL of S-box $S_{1}$ produced using the recommended method was measured in this case. The S-box $S_{1}$ has an average NL value of 112. Table 3 provides the NL of the recently proposed scheme along with a comparison with other published studies.

Table 3 Nonlinearity Analysis of the Proposed S-box and Comparison with Existing Schemes.

Linear Approximation Probability (LAP)

In the field of cryptographic analysis, a crucial metric that examines the quality of the S-box is linear approximation probability. The assessment evaluates the probability of a linear relationship existing between input and output bits within an S-box. The mathematical representation of LAP is below:

$$\begin{aligned} LP(S)=\dfrac{1}{2^{n}}\{max_{\alpha ,\beta }[M(\alpha ,\beta )]\} \end{aligned}$$

(4.2)

where

$$\begin{aligned} M(\alpha ,\beta )=[\#\{\mu \in GF(2)^{8}|\alpha .\mu =\beta *\cdot S(\mu )\}-2^{n-1}] \end{aligned}$$

(4.3)

where $\alpha \in GF(2)^{8},$ $\beta \in GF(2)^{8}\backslash {0}$ and $``\cdot ''$ represents the dot product over GF(2).

The cryptographically strong S-box has a low LAP value. Table 2 provides the LAP value of the suggested scheme along with a comparison to other published studies, demonstrating the proposed S-box’s resistance to linear attacks.

Differential Approximation Probability (DAP)

The differential attack is an effective cryptanalysis technique by analyzing the connections between the cipher image with the corresponding plain image. The S-box, an important nonlinear component of image encryption, should be resistant to attacks. The differential approximation probability (DAP) assesses an S-box’s capacity to resist differential attacks. The DAP of the substitution box is calculated by using the following mathematical formula:

$$\begin{aligned} DAP(\delta \alpha \longrightarrow \delta \beta ) = \frac{\alpha \in X | S(\alpha ) \otimes S(\alpha \times \delta \alpha ) = \delta \beta }{2^{m}} \end{aligned}$$

(4.4)

For every input differential $(\delta \alpha _i)$, this suggests a unique output differential $(\delta \beta _i)$ ensuring a uniform mapping probability for every i. A lower DAP value of an S-box indicates good resistance against differential attacks. The DAP values of the proposed S-boxes are provided in Table 4, showing values closer to the ideal range. Additionally, Table 2 compares S-boxes from the proposed scheme with those from published work, demonstrating that the suggested S-boxes have lower DAP values. Hence, we can conclude that the proposed S-boxes are resistant to differential attacks.

Table 4 Differential Approximation Probability (DAP) of the Proposed S-box.

Strict Avalanche Criterion(SAC)

SAC measures the impact of a slight change in the input of a cryptographic function, typically an S-box, on the output. According to the strict avalanche criterion, a function’s output bits should change with a 50% probability for each change in the input bit. An encryption technique can be readily broken by constructing a relationship between the inputs and outputs if there is no strict avalanche effect. If a cryptographic function demonstrates a high diffusion level, it fulfills the SAC criterion. This criterion ensures that even little modifications to the input result in significant and unexpected changes to the output. The SAC of an S-box for an $8\times 8$ dependent matrix is determined through the following equations:

$$\begin{aligned} M = [m(i,j)]_{i=1,j=1}^{8,8} \end{aligned}$$

(4.5)

where

$$\begin{aligned} m(i,j)=\{\dfrac{1}{2^{n}}[\alpha (S_{i}(s+h_{j})+S_{i}(s))]|h_{i}\in GF(2)^{8}\cdot \alpha (h_{j})=1\quad and\quad 1\leqslant i, j\leqslant 8\} \end{aligned}$$

(4.6)

where $\alpha (h_{j})$ is the number of non-zero bits in $h_{j}.$ A cryptographic function that meets the SAC is anticipated to have a high degree of diffusion, ensuring that even minor changes in the input cause significant and unpredictable changes in the output. If all the entries of the $8\times 8$ SAC matrix are close to 0.5, then the SAC test is fulfilled. The SAC values of the proposed S-boxes are shown in Table 5. The maximum and minimum values of the suggested S-box are 0.545 and 0.43, respectively. The numerical values indicate that S-boxes satisfy the SAC test. Furthermore, the SAC values of the newly constructed S-boxes are equal to those of other well-known existing S-boxes listed in comparison Table 2.

Table 5 Strict Avalanche Criterion (SAC) Analysis of the Proposed Scheme.

Bit Independence Criterion(BIC)

An S-box is said to satisfy BIC if the output bits of the S-box are statistically independent of any subset of its input bits. In other words, BIC ensures that no linear or algebraic relationship exists between the input and output bits, making it resistant to crypt-analysis techniques based on linear and algebraic equations. S-boxes that meet the bit independence criterion contribute to the robustness and security of cryptographic systems by thwarting attempts to exploit linear dependencies, thereby enhancing their resistance to attacks. The BIC test is said to be fulfilled for the suggested scheme if the BIC value of the S-box is close to 0.5. Table 6 shows the maximum and minimum values of the BIC for the proposed and other well-known S-boxes. Table 2 shows that the BIC values of the newly suggested S-boxes are 0.5000034, 0.49998, and 0.50456, which is very close to an optimal value. The numerical values of BIC ensure that the suggested S-boxes can resist common attacks.

Table 6 Bit Independence Criterion (BIC) Analysis of the Proposed Scheme.

Proposed image encryption scheme

Color image encryption secures digital images with multiple color channels, such as RGB or CMYK, to protect their confidentiality during transmission or storage. Image encryption involves applying encryption algorithms that extend traditional grayscale encryption methods to maintain the integrity and privacy of each color component. Effective color image encryption techniques should ensure that the encrypted image maintains its visual appearance while concealing the original content through robust encryption mechanisms, thus preventing unauthorized access and ensuring the privacy of sensitive color image data.

• (1) Take an RGB image of size $M\times N\times 3$ consisting of red (R), blue (B), and green (G) channels. Each plain image channel is considered a gray image of order $M\times N.$ In the first step, divide the RGB image into three primary channels; each channel can be encrypted in its own right. The entries of each channel are the pixel values of the image.

• (2) To scramble the pixels of the plain image, we use permutation on the primary image or shuffle the pixel values. We use the algebraic structure to produce a series of pseudo-random numbers. The $GF(2^{8})$ have 256 distinct elements in ascending order. To create diffusion in the image encryption, a sequence of random numbers using P-boxes is constructed over the Galois field(GF) of 256 elements, as discussed in the S-P-boxes scheme. After applying the permutation on red (R), blue (R), and green (G) channels, we obtained the permuted red $(P_R)$, permuted $(P_B)$, and permuted green $(P_G)$ channels. Combining the three permuted channels, we get the permuted image denoted by $P_I$, as shown in Fig. 3.

• (3) The substitution plays a vital role in encryption. It occurs through the replacement of image entries from a lookup table. In our proposed scheme, S-boxes are used for substitution. In encryption, substitution creates confusion in the scheme. In our proposed scheme, we use three separate S-boxes for substitution on each permuted channel. After substitution, we obtained substituted red channel $S_R,$ blue channel $S_B$, and green channel $S_G$. Figure 3 shows the resulting images after combining the substituted red, blue, and green channels.

• (4) Random numbers play a fundamental role in various science, technology, and mathematics fields. These numbers are unpredictable and lack any discernible pattern, making them crucial in statistical analysis, simulations, and cryptography applications. In computer programming, random numbers introduce an element of chance, creating dynamic, non-deterministic behavior in games, simulations, and algorithms. True randomness, often generated through physical processes like radioactive decay or atmospheric noise, is challenging, so pseudo-random number generators are commonly used in computer systems. These generators produce sequences that appear random, providing a practical way to introduce unpredictability into software applications. Random numbers are essential for technical purposes and have a role in decision-making, such as random survey sampling or drawing lots to make impartial choices. Overall, random numbers are a vital tool for solving a wide range of problems and adding a touch of uncertainty to our digital world. Regarding image encryption, various types of random numbers are employed in cryptography to enhance the security of the encryption process. True random and pseudo-random numbers are the two main types of random numbers. Pseudo-random numbers are generated based on algorithms and a starting sample value. Although they appear random, pseudo-random numbers are deterministic; thus, if the starting point is known, they are unable to attack. True random numbers, on the other hand, come from unpredictable physical processes like radioactive decay or electrical noise. True random numbers are safer for cryptographic applications since they show no noticeable pattern and are less vulnerable to prediction attacks.

• (5) We generate the random numbers from the proposed scheme over the Galois field. These random numbers are considered a key, or a bit, with the substituted channels of an RGB plain image. The generated random numbers, ranging from $[0-255]$ and appearing in a random sequence, are applied to each substituted channel. After the bit xor operation, we use the Matlab command to concatenate the three encrypted channels of the color image; then, we obtain an encrypted image. Figure 3 shows the plan, permuted, substituted, and ciphered images of butterfly, baboon, and peppers. The entire innovative technique of image encryption is based on S-Boxes generated through the action of groups on the Galois field GF(256). A flowchart depicting the entire procedure is presented in Fig. 2.

• (6) Numerous image encryption techniques encrypt only one image. In a practical sense, a series of images should be encrypted. Simple strategies for generating a series of random numbers, scrambling the image pixels, and bitwise XOR operations are used to encrypt multiple images. The drawback of these methods is that, instead of providing a mathematically exact recovery, the reconstruction approach theoretically approximates the original image, resulting in poor image quality. Specifically, the random iterative method necessitates a high number of projections, which increases the imaging time. Additionally, the approaches frequently used for gathering image data and encrypting it using an algorithm imply that the person encrypting the images must be aware of the correct key. This increases the risk of keys leaking. To overcome this issue, we proposed a technique based on finite algebraic structures. The scheme first takes the input of multiple color images in the form of one or combined images as a block of $2^{n}, 3^{n},...$, where n is a positive integer. These images are divided into three color channels: red, green, and blue. These color channels of each image undergo permutation and substitution steps utilizing the S-P-boxes constructed by the proposed scheme mentioned in Section 3. Each color layer of multiple images is bit-wise xor with one of the S-boxes, whose elements are highly random in order. Make a string of 256 elements, with one of the S-boxes excepting the S-boxes used for substitution. Finally, combine the encrypting layers of each image, and we obtain the ciphered multiple images. The confusion component of the scheme enhanced the security of the multiple images. The plain, permuted, substituted, and ciphered blocks of images of order $2\times 2$, $3\times 3$, and $4\times 4$ are shown in Fig. 4. Moreover, multiple plain and encrypted images are shown in Fig. 5. The source of the images used in the proposed scheme is available in the references^{66,67,68,69,70,71,72,73}, all blocks of images are resized by using the Matlab code.

Fig. 2

Flowchart of the Proposed image encryption scheme.

Fig. 3

(a) Original (plain) images of Butterfly⁶⁸, Baboon⁷¹, and Peppers⁷²; (b) Permuted versions of the images; (c) Substituted images after the confusion stage; (d) Final ciphered images after applying the complete encryption scheme.

Fig. 4

(a) Original image blocks of sizes $2^2$, $3^2$ and $4^2$; (b) Permuted blocks; (c) Substituted blocks after the confusion step; (d) Final ciphered images after the complete encryption process.

Algorithm 2

Pseudocode for the Proposed Multiple Image Encryption Scheme

Security analysis of ciphered images

The security analysis of a ciphered image involves the evaluation of its resistance to various cryptographic attacks. Calculated images should exhibit strong diffusion, confusion, and resistance to statistical analysis to ensure the confidentiality and integrity of the underlying content. Assessing the security of a ciphered image involves scrutinizing properties such as entropy, correlation, and sensitivity to alterations. An effective encryption scheme should produce random images and display no discernible patterns, making them robust against known and chosen plaintext attacks. To guarantee that the ciphered image is resistant to both unauthorized access and cryptographic attacks, a comprehensive security analysis helps determine the robustness and dependability of the encryption process.

Fig. 5

Original and Corresponding Encrypted Images^68,69,70,73.

Key space analysis

Keyspace analysis in image encryption is a vital component in evaluating the security of image encryption methods. The keyspace includes all possible keys used to encrypt and decrypt the image. A larger key space implies greater security, as it renders brute-force attacks computationally impractical. Only those with the correct decryption key can restore the original image, thanks to image encryption techniques that utilize a robust key space to safeguard the content from unauthorized access. The researcher must asses the keyspace’s size and unpredictability to determine how vulnerable the algorithm is to various types of attacks. A well-designed image encryption system requires a key space that is sufficiently large and well-distributed to resist attacks and maintain the confidentiality and integrity of the ciphered images. In our proposed scheme, we use three keys for encrypting a plain image. We use the S-P boxes to encrypt the plain image. We generate each S-P box by using the parameters (a, b, c, d, m, n), each of which consists of 8 bits, i.e., $(a,b,c,d,m,n)\in (GF(2^8))^6$ and have $2^{48}$ possible configuration for a single S-box or P-box. In the proposed scheme, we use one P-box for permutation, three different S-boxes for substitution, and one P-box for bitwise XOR operation with the substituted RGB channels. We used two P-boxes and three S-boxes in the entire proposed scheme, so the total keyspace is $(2^{45})^5=2^{240}$. In other words, we have enough key space to protect confidential data from adversaries.

Entropy analysis

A practical method for evaluating the security and unpredictability of encrypted images is entropy analysis. Entropy is a statistical measure of the amount of disorder or randomness in data. An encrypted image with a high entropy value is more resistant to statistical attacks because it has a more complicated and unpredictable distribution of pixel values. Cryptographers aim to maximize the entropy of encrypted images, ensuring that they appear random and lack patterns that attackers could exploit. High entropy in encrypted images also signifies strong diffusion and confusion properties, essential for preserving the confidentiality of the original content. Therefore, entropy analysis is a crucial step in evaluating the quality and security of image encryption algorithms, helping to ensure that they are robust against various cryptanalysis techniques and can maintain data integrity and confidentiality. Mathematically, calculate the entropy of a ciphered image by using the following formula:

$$\begin{aligned} E(I)=-{\sum }^{q-1}_{\imath =0}{\sum }^{q-1}_{\jmath =0}p(\imath ,\jmath )log_{a}p(\imath ,\jmath ). \end{aligned}$$

(6.1)

The above equation can be used to determine the entropy E(I), where “a” denotes the base of the logarithm and $p(\imath ,\jmath )$ denotes the probability of a pixel in a color image. The entropy of the ciphered images is presented in Table 7, which also includes a comparison with published work earlier. The optimal value of entropy is 8. The ciphered images in our recently proposed method have an entropy of approximately 8, which suggests that they are resilient to statistical attacks.

Table 7 Comparative Entropy Analysis (in pixels) of the Proposed Scheme and Existing Methods.

Histogram analysis

Histogram analysis is employed to examine the distribution of pixel intensities in an encrypted image. It offers information about the statistical properties, which helps evaluate the encryption scheme’s security and unpredictability. We examine the histograms of ciphered images to assess the resistance of the suggested encryption method to statistical attacks. Figure 6 presents a histogram analysis comparing the unencrypted images of butterfly, Baboon, and Pepper with their encrypted counterparts. The histograms of the ciphered images are substantially different from those of the matching original images, with an essentially uniform distribution. As a result, it becomes clear that the suggested method is quite resistant to statistical attacks.

Fig. 6

RGB histogram comparison between original and ciphered Images: (a) Original color images of Butterfly⁶⁸, Baboon⁷¹ and Peppers⁷²; (b) RGB histogram of the original images; (c) Encrypted images; (d) RGB histogram of encrypted images.

Correlation analysis

To assess the security and efficacy of encryption methods used on images, correlation analysis is essential in the field of image encryption. It evaluates the degree to which the pixel values of the encrypted and original images are correlated. A robust encryption scheme should minimize discernible patterns or correlations between corresponding pixel positions in the two images. High correlations indicate vulnerabilities and potentially reveal information about the original image. Successful image encryption algorithms strive to break such correlations, rendering statistical analysis and attacks more challenging. By quantifying these correlations, researchers and cryptographers can assess the strength of an encryption algorithm and determine whether it can withstand various crypt-analytic techniques. Thus, correlation analysis is vital for ensuring the robustness of image encryption methods and maintaining the confidentiality and security of the encrypted content. The correlation analysis of red, green, and blue channels of plain image Lena and its ciphered channels are shown in Figs. 7 and 8. The numerical values of the correlation analysis for test images butterfly, baboon, and pepper, as well as their block images and ciphered images, are given in Table 8. We also provide a comparison of the designed technique with other published work.

Fig. 7

Correlation plots of adjacent pixels in the Red (R), Green (G), and Blue (B) channels of the original RGB image of Baboon. The first, second and third rows represents the correlations between vertically, horizontally, and diagonally adjacent pixels, respectively.

Fig. 8

Correlation plots for neighboring pixels in the Red (R), Green (G), and Blue (B) channels of the original RGB image of Baboon⁷¹. The first, second and third rows illustrate the correlations among vertically, horizontally, and diagonally adjacent pixels, respectively.

Table 8 Comparative Correlation Analysis of RGB Channels for the Proposed and Existing Techniques.

NPCR and UACI

The NPCR (Normalized Pixel Change Rate) and UACI (Unified Average Changing Intensity) are important metrics for evaluating image encryption techniques. These metrics assess the sensitivity and randomness of pixel changes in the encrypted image when a single bit in the plaintext image is altered. A higher NPCR value implies that the encryption algorithm causes more pixel changes, making it more resistant to tampering and cryptanalysis. On the other hand, a higher UACI value signifies a greater dispersal of pixel value differences, indicating more robust diffusion properties in the encryption process. Together, NPCR and UACI provide a quantitative means of measuring the quality and security of image encryption algorithms. Effective encryption methods should exhibit high NPCR and UACI values, indicating robustness against alterations and high diffusion. This ensures that even small changes in the plain text result in significant modifications in the cipher text while maintaining a uniform distribution of pixel value differences. The following mathematical formula can calculate the NPCR and UACI of the newly suggested scheme:

$$\begin{aligned} NPCR=\frac{1}{M\times N}\left[ \sum _{m,n}E(m,n)\right] \times 100\% \end{aligned}$$

(6.2)

where E(l, m, n) is of size $M\times N\times 3$ defined by, and $I_1$ and $I_2$ are the ciphered images corresponding to one byte deviating from the original plain images.

$$\begin{aligned} UACI=\frac{1}{M\times N}\left[ \sum _{m,n}\frac{I_{1}(m,n)-I_{2}(m,n)}{255}\right] \times 100\% \end{aligned}$$

(6.3)

Table 9 presents the NPCR and UACI values pixels wise of the newly suggested method, demonstrating robust resistance to differential attacks.

Table 9 Comparison of NPCR and UACI Metrics Between the Proposed Scheme and Existing Methods.

Peak to Noise Attacks(PSNR)

Peak Signal-to-Noise Ratio (PSNR) is a commonly used metric in data compression and transmission to assess the quality of encrypted or reconstructed images. A quantitative evaluation of image fidelity is provided by PSNR, which calculates the ratio of a signal’s peak strength to noise intensity. In image encryption, PSNR can assess how well an encryption algorithm preserves image quality despite introducing cryptographic noise or distortions during the encryption process. A higher PSNR value indicates reduced distortion and improved image quality. However, due to the similarity between the original and encrypted images, achieving a high PSNR can occasionally compromise security. This is because it may indicate a weaker encryption technique. Striking a balance between security and image quality is essential when considering PSNR in image encryption, as exceptionally high PSNR values may inadvertently expose vulnerabilities in the encryption process. The PSNR values of the proposed method can be assessed using the subsequent mathematical formula:

$$\begin{aligned} PSNR\doteq 10.\log _{10}(\frac{(Max\quad pixel\quad value)^{2}}{\sqrt{MSE}}). \end{aligned}$$

(6.4)

The Mean Square Error (MSE) is defined as follows:

$$\begin{aligned} MSE\doteq \frac{1}{M \times N}\sum _{i=1}^M \sum _{i=1}^M[I(i,j)-I'(i,j)], \end{aligned}$$

(6.5)

.

The PSNR values are presented in Table 10, where I(i, j) and $I'(i,j)$ denote the pixel values of the encrypted and unencrypted images, respectively. This suggests that the proposed encryption system can transmit images with enhanced security.

Table 10 PSNR Comparison between the Proposed Scheme’s Original (O), Decrypted (D), and Ciphered (C) Images.

Occluded attacks

Occluded attacks in image encryption involve deliberately exploiting hidden or partially obscured regions within an encrypted image. These attacks target situations where the encryption process might not have fully concealed certain areas of the image, potentially revealing sensitive information. Occluded attacks are particularly challenging to defend against because they exploit weaknesses in the encryption algorithm’s ability to conceal content effectively. Effective image encryption schemes must ensure that all areas of the encrypted image are equally resistant to cryptanalysis. Occluded attacks emphasize the importance of robust encryption techniques that maintain security even in the presence of hidden or partially concealed data. Researchers and cryptographers strive to develop encryption methods that can withstand occluded attacks, thereby bolstering the security of sensitive image data. Figure 9 shows the decryption of the ciphered images, and if the unauthorized person changes the data, the receiver can understand the original message. Table 11 shows the PSNR values of the test image of Baboon for different levels of cropping. When we cropped data from various parts of the images on decryption, the results demonstrated that the proposed scheme could recover the original data. We can conclude that the proposed work is resilient to a cropping attack.

Fig. 9

Resistance to occlusion attack: (a–h) Occluded encrypted images; (i–p) Corresponding decrypted images.

Table 11 PSNR Values of Decrypted Images under Different Levels of Cropping.

Computation analysis

The efficiency of an algorithm is measured by its computational complexity, which examines how much time and space it requires, proportional to the size of the input, to find the best possible solutions. It serves as a benchmark for comparing algorithms, enabling the determination of which strategy is most effective for a specific set of computational tasks. The time-based complexity of this method is determined by the size of the input image, denoted by (M), as well as the number of intermediate data structures that are produced as a result of bit-wise operations, replacements, and permutations. Given that ‘m’ represents the size of the random number or permutation data, ‘n’ represents the size of S-boxes, ‘l’ represents the size of the data from substitutions, ‘r’ represents the size of the ‘key’, and ‘s’ represents the total number of elements in bit-wise XOR and concatenation, the overall time complexity of the operations is $O(M + 3m + 3n + 3l + r + 3s)$. Furthermore, the memory that is required to hold the input image and its channels, in addition to the numerous intermediate matrices that are formed during S-box operations, replacements, and permutations, has a substantial impact on the space complexity of the technique. About $O(M + 5m + n + 2l + r + 2s)$ is the space complexity, where M is the picture size and ‘m’, ‘n’, ‘l’, ‘r’, and ‘s’ are the sizes of intermediate data structures that are created at various points during the process. Moreover, the suggested scheme takes 8 seconds to encrypt the image on a standard PC; it should take less time on more advanced systems.

Randomness test for cipher

Cryptosystem security assessments rely on features such as extended duration, high complexity, uniform distribution, and productivity. For digital image randomness testing, NIST SP $800-22$ is utilized on a block of $4\times 4$ images with the specific aim of fulfilling these requirements. Many subcategories are included in a portion of these tests. Many initial keys are utilized for the figure randomness check. While conducting all of the NIST tests, we used the ciphered Baboon 24-bit digital image. The encrypted data is a color image of the block, which is $4\times 4$ units in size and $256\times 256\times 3$ units in size. Table 12 displays the results of the tests. Considering these findings, it can be concluded that our proposed approach for digital image encryption successfully passes the NIST tests. We can determine that our predicted digital image encryption tool’s efficiency passes the NIST test by analyzing these results.

Table 12 Cryptographic Randomness Test of the Encrypted Image of Block of 4 × 4.

Conclusion

We introduced a simple and innovative scheme for constructing substitution and permutation boxes. These S-P-boxes have confusion and diffusion properties. The newly built S-boxes have good resistance against well-known attacks. The nonlinearity of the proposed s-box is 112, which is the minimum. Following our proposed scheme, we obtain hundreds of S-boxes of nonlinearity 112. The non-linearity of the newly generated S-boxes is the same as that of well-known S-boxes like AES and gray. A comparison of non-linearity, LAP, DAP, BIC, and DAP values of the newly generated S-box with some published work related to S-boxes. The comparison Tables 2, 3, 4, 5, and 6 show that the recently suggested scheme can generate hundreds of S-boxes and have greater security against linear, differential, and statistical attacks. The numerical values of the linear, differential, and statistical analysis are very close to optimal values. Therefore, we can utilize the newly suggested S-boxes for encryption purposes, enhancing confusion during the substitution process. Further, the proposed scheme for S-P-boxes can generate several highly secure S-boxes. These S-P-boxes create confusion and diffusion in data encryption. The recommended image encryption technique ensures the secure transfer of digital images. The primary foundation of the suggested approach is Galois fields and their actions on Galois fields. Three channels are identified in the color image: red (R), green (G), and blue (B). The distinct substitution of the three suggested S-boxes in each channel complicates the encryption procedure. In the first step, P-boxes are used for permuting the pixels of each channel. P-boxes produce diffusion within the encryption process. To generate confusion, it is possible to utilize the recently proposed S-boxes for each channel. Three S-boxes are applied to each of the permuted channels. In the last step, one P-box is bitwise xor with the substituted channels. After performing all the above steps and concatenating the three encrypted channels, we get the ciphered image of the plain image. The suggested method can encrypt images containing any type of digital data. Several well-known experimental tests are applied to the proposed scheme. The proposed scheme withstands various attacks, including key space analysis, differential attacks, linear attacks, and statistical attacks. The experimental values of the proposed scheme and their comparison with some of the well-known published works are shown in Section 6. According to Section 6, the proposed scheme is secure, fast, and suitable for real-time applications. Visual content in videos is constantly changing. Future developments of the suggested method may find use in audio and video encryption. Furthermore, the proposed method’s hardware implementation offers an intriguing direction for further study. Moreover, collaborating with other groups in the Galois field can be an exciting endeavor.