Examination of hydrological variations and their effect on water shortage trends and water-energy production using convolutional neural network and ISSA

Abstract

This research has explored the impacts of insufficient water that is attributed to climate change, as well as industrial growth in power generation. This makes use of Global Circulation Models (GCMs) to project future climate changes and employs the Standardized Precipitation Index (SPI) to determine drought severity. ISSA and CNN work together with him to model and predict changes in reservoir capacity over time. Thus, sustainable hydropower planning in a changing climate shall be achieved. It predicts that from 2025 to 2035, hydrological variability will surely increase since droughts will increase in occurrence and severity compared to the baseline period of 2003 to 2023. It is also expected that SPI values will reach <-1.5, which would indicate the emergence of reduced precipitation volumes of up to 40% below that of the baseline level, as a definitive trend towards drought in the near- to mid-term drought projections (2025–2035). More SPI values above + 1.0, which correlate with precipitation anomalies over 20% above the baseline average, indicate early near-term (2024–2026) and mid-term (2034–2036) wetter conditions. The SSP5 future scenario indicates a relatively drier future, with less water precipitation, higher evaporation rates, and elongated periods of lower reservoir depths. This optimized CNN model provides an accurate, reliable reservoir dynamics simulation (R2 = 0.89, NSE = 0.80) that is essential for a precise hydropower forecasting. Hydropower generation peaks around 2026 under SSP1, declining by about 0.7 billion kWh by 2030 and slightly stabilizing above that level by 2040. Such results indicate how pertinent it is for adaptive water-energy management, bearing in mind the increasing hydrological variability induced by climate change.

Introduction

The global issue of water scarcity is threatening the sustainability of water resources and socioeconomic development driven by climate change and increasing human pressures¹. Climate change alters important hydrological patterns like precipitation, evaporation, and evapotranspiration rate, as well as the availability of water². This level of change has an unequal impact on sectors of agriculture, industry, and domestic supply, particularly in arid and semi-arid zones where limited water resources already exist. Properly managing the situation is going to require a very high level of understanding about the complex relationship between climate change and water scarcity for the future proactive and sustainable management of such strategies³.

Human activities make water shortages much worse, in addition to changes in the weather. Population growth, urbanization, and agricultural practices are all things that make individuals require additional water. Thus, water resources can become overused and poorly distributed. This imbalance makes it very hard for sustainable development to occur, especially in places where water is already hard to get. These human-made stresses, together with the effects of climate change, put higher demands on water systems. This makes it clear that it’s necessary to take action now to make sure that water is safe for both current and future generations⁴.

Large-scale infrastructure, particularly dam construction, is complicated further by these global and regional pressures, as it entails fundamentally changing natural hydrological systems; these alterations from dams, which are lifeblood projects used for hydropower generation, water supply, flood control, and navigation, profoundly modify natural river flows⁵. Dams change the way rivers flow, move sediment, and interact with the environment, which changes the physical, chemical, and biological properties of river systems over time. For example, major rivers in East, Southeast, and Southern Asia already experience significant decreases in sediment transport annually as a result of damming, causing wide river fragmentation and environmental degradation. Critically, the combined impact of these infrastructural changes and climate variability, as altered streamflow and sediment yield demands, requires integrated studies to understand their cumulative effect on water supply security⁶.

The change in natural river flow caused by dams can significantly impact regional water patterns. It often increases water scarcity by altering how water is distributed and its quality. Therefore, it is essential to look at water availability trends before and after building dams. This helps us understand the long-term effects on water security. These studies can give valuable insights into how infrastructure projects change local water conditions and affect ecosystems downstream⁷.

Understanding these global drivers of climate change, informed by human activities and structures, is essential in the development of appropriate mitigation and adaptive management strategies for the local hydrology. Mitigation can be implemented through water conservation, alternative water source exploration, or new water management strategies. The approach to sustainable water management must recognize whether the environmental sacrifice and the outweighed benefit of larger-scale implications and major infrastructure are worth it. When informed of the water shift pace, we can assess the biophysical consequences of required ecological impact assessments and cost-based assessments with low-cost practices. This may lessen the impact of water source degradation and the consequences of scarcity⁸. Yet, the complexity and inherent non-linearity of these interacting systems make it an uphill task for a common modeling approach.

Most recently, artificial intelligence, in particular, brain networks, has come to give us new tools that are highly powerful for application in hydrological modeling.

They can learn excellently and detect complex patterns. Applications have included streamflow simulation⁹. , water quality prediction¹⁰, and water quality prediction¹⁰, among other uses of these models in hydrology. These systems excel at synthesizing large volumes of multivariate data, including hydrological parameters, environmental conditions, and records of construction activities, to identify complex, non-linear patterns that govern river flow and surface water levels. By learning from historical data, neural networks can not only analyze pre- and post-dam construction impacts but also project future streamflow and reservoir levels. This predictive capability is instrumental for proactive, adaptive water management¹¹.

Furthermore, neural networks can be incorporated into real-time monitoring systems that detect inconsistencies and changes in hydrological measures, acting to notify early warning and timely remediation actions. These models can also assist risk assessments for dam construction while allowing decisions based on understanding future adverse impacts to streamflow and water levels when dams are erected. Overall, neural networks are an effective mechanism to better understand the complex relationships between land and infrastructure, and the hydrology in these systems, for better decision-making to support sustainable water resource management¹².

Recent studies have focused increasingly on disentangling the interplay among water scarcity, dam infrastructure, climate change, and hydrological systems, a nexus that is directly relevant to the problems addressed in this study. Collectively, these studies demonstrate that dams are critical for water and energy security; however, they simultaneously disrupt riverine ecosystems, ultimately creating more water stress under the effects of climate change.

For instance, in a study by Singh et al.¹³The Bisalpur Dam was shown to have significantly reduced the peak discharge and average river water levels of the Banas River, based on statistical trend analysis. They maintained that major water infrastructure projects should be subject to rigorous environmental impact assessments, as their work further corroborates many others that have demonstrated interrupting flow regimes downstream, causing immediate impacts on water availability, and consequent severe ecological degradation.

Similarly, Oliveira et al.¹⁴ found that in the Maranhão watershed of Portugal, a 1D-CNN machine-learning model could forecast daily inflows and peak flows. In contrast, the physics-based MOHID-Land model outperformed during dry periods, as well as on monthly averages. The study advocates a hybrid modelling approach that combines data-driven and process-based models to exploit their respective strengths. This is becoming an essential trend for improving accuracy across different hydrological conditions. According to Veldkamp et al.¹⁵, hydro-climatic variability was responsible for at least 79% of annual variability in global water scarcity, especially at regional and global levels, between 1960 and 2000. The influence of human (anthropogenic) factors on water scarcity, water demand, and population growth has increased with time. The study highlights the dynamic interactions between past natural climate processes and changing societal adaptations, thereby reinforcing the need for an integrated assessment framework that considers climatic uncertainty and evolving human pressures on water resources.

Deng and Zhao¹⁶ investigated the Heihe River Basin in China and found significant challenges, including supply-demand imbalances, inefficient water use, and weak institutional frameworks. Standard solutions include scientific, policy, and management approaches. Their findings emphasize that water scarcity must be confronted using technology as well as reforms in governance, allocation methods, and stakeholder participation, especially in transboundary basins, where competition over these resources tends to run high.

Wang et al.¹⁷ found human activities to influence 52.35% of the annual streamflow fluctuations in the Han River Basin, while climate dominates during seasons, hence emphasizing the need for adaptive management. Based on insights like these, this study develops a unique CNN-ISSA machine learning model that simulates the capacity of a reservoir under diverse climate scenarios. This hybrid tool brings actionable, real-time forecasting to strengthen the resilience of water-energy systems against increasing drought and hydrological variability.

This foundation enchants the study as it directly addresses the growing global challenge of water scarcity with its resultant destabilization to hydropower production, which has become one of the pillars of renewable energy systems that are now increasingly threatened by climate variability. Water scarcity, dam infrastructure, and climate change have already been well established in research concerning their critical linkages^{11,12,13,14,15}; however, there is still a significant gap in developing localized, high-accuracy predictive tools capable of informing adaptive water-energy management under future climate uncertainty.

This is the rationale driving the introduction of an innovative hybrid modeling framework, which combines a Convolutional Neural Network (CNN) synergistically with the Improved Spring Search Algorithm (ISSA) to simulate and forecast reservoir capacity dynamics under different forecasted climate scenarios (SSP1 and SSP5) to convert global-scale climate risks into actionable, site-specific insights. Meanwhile, ISSA optimizes hyperparameters for the model and improves population-based search efficiency, ensuring substantial performance even in complex hydrological systems with rich historical data.

Virtual modeling is done by combining CMIP6 climate projections with SPI data from the Standardized Precipitation Index for drought assessment and further validating results using the HEC-ResSim model for reservoir inflow. The multi-scale synthesis realized by this methodology provides a holistic, evolving view of the water-energy nexus, as it not only quantifies reduced potential in hydropower generation because of hydrological variability and intensified droughts but also provides a decision-support system to optimize reservoir operation and planning of energy portfolios and designing climate-resilient infrastructure.

Ultimately, this research contributes a scalable, data-driven strategy to mitigate the adverse effects of global warming on hydropower reliability, enabling more sustainable and adaptive management of water and energy sources in an increasingly erratic climate.

Materials and methods

Region study and data description

All the historical meteorological and hydrological data used for training and validating the CNN-ISSA model comprise a period of twenty-one years stretching from 2003 to 2023. The dataset incorporates daily and monthly records of variable quantities such as precipitation, reservoir inflow (runoff), evaporation rates, and storage capacity of the Xinfengjiang Reservoir. This period was chosen to ensure calibration of the model on the most recent and highest-quality observational data. Such data reveal hydrological variability in the present-day and thus provide a strong basis for the future projections of the SSP1 and SSP5 climate scenarios. This period from 2003 to 2023 has been consistently referred to throughout the paper as the “baseline period” against which future projections (2024–2040) are measured for various metrics such as SPI, WSI, reservoir capacity, and hydropower generation.

The observed meteorological and hydrological data used in this study, including daily and monthly records of precipitation, reservoir inflow (runoff), evaporation rates, and reservoir storage capacity for the period 2003–2023, were obtained from the CMA (China Meteorological Administration). Future climate projections under the SSP1 and SSP5 scenarios are derived in an ensemble of four CMIP6 Global Climate Models (ACCESS-CM2, CESM2, MIROC6, UKESM1-0-LL) downloaded from the Earth System Grid Federation (ESGF) portal. The Guangdong Provincial Water Resource Department provided the hydropower generation data and reservoir operational parameters. This ensures robustness and traceability of our modeling framework through multi-source data integration.

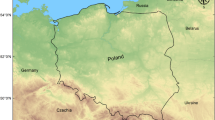
Water management is crucial for socio-economic development, especially in areas experiencing water scarcity. The implementation of innovative strategies for reservoir procedures is essential to solving water scarcity challenges. The Xinfengjiang Reservoir plays a significant role in addressing water scarcity challenges in the area. Although the reservoir has been created to aid in water supply and control of floods, it has caused some environmental and geological problems. The Xinfengjiang Reservoir, also famous for Wanlü Lake, is an artificial lake situated in Heyuan, Guangdong, China. It has been designed by damming the Xinfeng River, which is a tributary of the Dong River. Figure 1 depicts the geographical position.

Fig. 1

The Xinfengjiang Dam position (Image © 2025 Google Earth).

China’s dedication to sustainable electricity generation is highlighted by its advanced hydropower infrastructure, which can produce about 0.99 billion kWh of hydropower each year. Moreover, it features an average streamflow of approximately 195.7 m³/s each year. The Xinfengjiang Reservoir (Wanlü Lake) receives 1,927 mm of rainfall each year, and a noteworthy portion of it occurs from April to June. The average temperature in a year is about 21.83 °C, with monthly 24-hour averages varying from 13.1 °C in January to 28.5 °C in July. The reservoir’s entire capacity of storage is 13.89 billion m³, and its efficient capacity of storage is 6.49 billion m³. The estimated average rate of evaporation between 2003 and 2023 is 67 mm. In July 2014, the highest monthly rate of evaporation was observed at 157.3 mm, whereas in December 2018, the lowest monthly rate of evaporation was recorded at 6.4 mm.

Assessment of global warming on climate variables

The CMIP6 (the Coupled Model Intercomparison Project Phase 6) is a framework that enables the simulation and comprehension of past, present, and future climate changes. The CMIP6 utilizes a group of climate models that make predictions based on different Shared Socioeconomic Pathways (SSPs)¹⁸. These pathways take into account other potential future progress in demographics, technology, economics, and environmental policies¹⁹. The models available in CMIP6 simulate a broad range of climate parameters, including air temperature, wind speed, humidity, rates of evaporation, and soil moisture. It is essential to consider certain variables to accurately predict drought situations and water availability for hydropower production in the future²⁰. The study utilizes some of the CMIP6 models for simulating climate variables as listed in Table 1.

Table 1 The CMIP6 model employed in this investigation.

SSPs scenarios have represented various pathways of greenhouse gas emissions and future societal progress. The features of the SSPs scenarios have been illustrated in Fig. 2.

Fig. 2

The feature of the SSPs scenarios.

The flowchart of climate variable prediction is demonstrated in Fig. 3.

Fig. 3

The flowchart of climate variable prediction.

We are aware that GCMs are typically coarse-scale models, which can limit their direct application in local-scale hydrological impact assessments. However, in this study, we used four CMIP6 GCMs (ACCESS-CM2, CESM2, MIROC6, UKESM1-0-LL) that were representative of regional climate and appropriately expressed large-scale climate variability that affected the hydrology of the Xinfengjiang Reservoir basin region. While downscaling techniques (e.g., bias correction and statistical or dynamical downscaling) can refine climate information, the main aim of this study was to evaluate long-term trends and relative change in the basin under SSP1 and SSP5 scenarios and not high-resolution spatial modelling. We also used the ensemble mean from multiple GCMs to avoid biases from individual models and produce more robust predictions about future drought and reservoir dynamics.

Before being integrated into the CNN-ISSA modeling framework, the raw outputs of the four selected CMIP6 General Circulation Models (GCMs) (namely, ACCESS-CM2, CESM2, MIROC6, UKESM1-0-LL) underwent statistical bias correction for local-scale reliability in climate projections. Given that despite their global merit, GCMs operate at coarse spatial resolution (~ 100–200 km) and express considerable bias compared to the local station data in mean, variance, and extremes, QM was used to adjust systematic biases in GCM-simulated distributions of precipitation, temperature, and evaporation so that their cumulative distribution functions (CDFs) are the same as those derived from the observed historical data (2003–2023) for the Xinfengjiang basin. Selection of these four GCMs was not arbitrary; preliminary evaluations of their hindcast performance (1980–2014) in reproducing the seasonal cycle, interannual variability, and spatial patterns of precipitation and temperature over South China were the basis for this criterion. Models with the highest skill scores (that is, lower RMSE, higher correlation) for the region of interest were favored to ensure that the ensemble represents local climate dynamics with some credibility. While dynamical downscaling provides greater spatial resolution, the computational expense makes it unfeasible for multi-model, multi-scenario ensemble studies. Therefore, QM-based statistical downscaling was adopted as a feasible and computationally less costly method that is also widely validated to downscale the GCM projections for the purpose of analyzing our reservoir-scale hydrological simulations.

Meteorological, agricultural, and hydrological drought evaluation

Meteorological drought is described by a lack of dryness and precipitation, which is often the initial indication of a drought. Epochs of considerably below-normal precipitation are typically the first sign of a drought. Agricultural drought connects meteorological drought to its agricultural effects by concentrating on rainfall scarcities and soil water shortages²¹. Hydrological drought is linked to rainfall scarcities that affect water resources and reservoirs. Figure 4 illustrates the trend of drought.

Fig. 4

The trend of drought.

The measurement of rainfall over different time intervals is done using the SPI, which is used as a tool to examine and control conditions of drought. Meteorological drought’s main sign is the rainfall shortage for any location, which the SPI is designed to quantify. This index compares total observed rainfall through a particular epoch (monthly, annual, seasonal) with long-term records of rainfall for that epoch.

SPI values are presented as standard deviations from the average, with negative values demonstrating lower than average rainfall and positive values demonstrating higher than average precipitation. Depending on the SPI, it can reveal either hydrological drought or conditions of agricultural drought. Shorter periods (1–3 months) represent soil moisture (conditions of agricultural drought), while more extended periods (12 months or more) represent effects on the availability of water (hydrological drought). The SPI reveals hydrological situations, including levels of groundwater and storage of reservoirs, more accurately with longer accumulation epochs. This is because it is not just the immediate conditions of soil moisture that are revealed in the SPI. The ranges of SPI values and their related categories of drought are illustrated in Table 2.

Table 2 The range of SPI values.

Water scarcity assessment

In this study, the Water Scarcity Index (WSI) has been defined in terms of total annual water withdrawal (including municipal, agricultural, and industrial demands) in relation to total annual renewable freshwaters for the Xinfengjiang basin. The index, being dimensionless, states the extent to which human water consumption affects the natural water supply system in percentage²². Since higher WSI values indicate greater amounts of available water consumed, there is increased competition and scarcity²³. For example, a WSI of 40% denotes annual withdrawal from the basin of 40% of the renewable water, while 60% remains for environmental flows and system resilience. This standardized definition of which physical elements correspond to the Falkenmark Indicator is better for a more robust and internationally comparable metric than precipitation anomalies alone. The severity categories presented in Table 3 (i.e., Low, Moderate, High Scarcity) will be applied to this calculated WSI to classify levels of water stress under the current and future states of climate change, providing clear thresholds for water managers and policymakers to trigger adaptive changes in their behavior.

Table 3 Organization of drought conditions based on the WSI.

The Water Scarcity Index (WSI) is assessed using the standardized Falkenmark Indicator. In mathematical terms, the WSI is the percentage of total annual water withdrawal (WW) to total renewable yearly freshwater resources (RWR); thus:

$$\:WSI\:\left(\%\right)=\frac{WW}{RWR}\times\:100$$

where: $\:WW$ is the total volume of freshwater withdrawn annually for municipal, agricultural, and industrial use within the Xinfengjiang basin (in billion m³/year). $\:RWR$ Is the total volume of renewable freshwater resources available annually in the basin, primarily derived from surface runoff and reservoir inflow (in billion m³/year).

The metric, based on human activity, states how much of the available water resources are consumed. The higher the percentage, the more scarcity and competition for water resources. The classification thresholds, such as Low, Moderate, or High Scarcity from Table 3, will consequently be applied to the computed WSI in order to classify the communities in terms of their water stress. This is a standard method applied in global water resource assessments regarding the implications of the conditions and is consistent with that used by Veldkamp et al.¹⁵ in their work on international water scarcity events under changing socioeconomic and hydro-climatic conditions.

Evaluation of the impact of drought severity and water scarcity trends on reservoir capacity

Neural network models have substantial utility in predicting reservoir capacity because they can effectively identify complex relationships and patterns contained in the data. They are naturally adept at identifying classes of patterns and detecting nonlinear relationships and dependencies that may not be found using other approaches. By utilizing historical data, neural network models can make more accurate estimates of reservoir capacity, information that can be invaluable in preparing for flood and drought scenarios. Because of their ability to adapt to changing conditions and an ongoing stream of new data, neural network models make sense for applications in dynamic and temporal systems such as hydrology. Neural networks can “mine” all relevant input features automatically from the data; therefore, manual engineering is not a requirement, and essential signals concerning reservoir capacity are more likely to be captured. Also, neural networks can catch nonlinear relationships in hydrological systems, and because of this, they are able to create better, richer predictions than simple linear models can. Finally, neural networks fit nicely in applications involving time series forecasting, which makes them a good fit for predicting future flow rates and water levels based upon past or historic values The simulation of the parameters governing the capacity of water reservoirs is an essential exercise for professionals to determine the best way to manage water behind dams and accurately estimate the power production capacity of hydropower facilities. The increasing demand for water and the variability in water consumption necessitate the use of reservoir simulation parameters in the investigation of water resources. These models are based on the relationships within aquatic systems, hydroelectric power, and basin hydrology.

In this research, a well-optimized CNN model has been employed to simulate reservoir capacity. It takes into account the correlations and patterns between precipitation and water scarcity. The resulting output is straightforward and easily understandable. It enables the analysis of drought severity and trends in water scarcity concerning reservoir capacity. The proposed method is forecasted in the subsequent sections. The model requires historical data such as rainfall, runoff, and evaporation, along with other hydrological data, to predict the capacity of the reservoir under various scenarios.

Convolutional neural network

The one-dimensional convolution neural network (1D-CNN) model employed in this study is designed solely for modeling future time-series predictions of hydrological variables and is distinctively different from the well-used 2D-CNN approach for image recognition. Where the 2D convolutions scan through spatial grids (e.g., pixels in an image), the 1D-CNN processes the time-series inputs by means of convolutional filters applied along the temporal axis of features such as daily precipitation, evaporation, historical reservoir inflow, and the like. This architecture has been found to be effective in capturing local temporal patterns and dependencies in hydrological sequences, as recently confirmed in studies such as Oliveira et al.²⁴, which successfully applied a 1D-CNN for daily streamflow forecasting. Hence, the “local connectivity” and hierarchical feature learning of the CNN, as referred to in the original text, are used to automatically extract relevant temporal features from the multivariate time series so that the model can learn complex, non-linear relationships governing the behavior of reservoirs without requiring manual feature engineering. Indeed, this offers an answer for a data-driven model dealing with sequential and autocorrelated environmental variables such as hydrological data.

Convolutional layer

Convolutional layers for learning temporal features by convolving a set of learnable filters over the input time series data are the basic building blocks of any 1D-CNN architecture. Each such filter moves along the temporal dimension (which is defined as the timeline of time steps) of the input, performing a discrete convolution operation to obtain a one-dimensional feature map. Of utmost importance, the weights and biases of each filter are stretched across all the time steps in the sequence so that, regardless of the filter’s position, the same temporal pattern will be recognized. Such parameter sharing drastically minimizes the number of trainable parameters in comparison to a fully connected network. For a particular convolutional layer, the output feature map obtained via filter m at time step t is computed as follows:

$$\:{y}_{t,m}=f\left({b}_{m}+{\sum\:}_{k=1}^{K}{\sum\:}_{i=1}^{\left(f-1\right)}{W}_{k,m,i\:.}{x}_{t-i,k}\right)$$

(1)

where, $\:\varvec{x}\in\:\:{\text{R}}^{{T}_{in\:\times\:k}}\:$defines the input sequence of length $\:{T}_{in}$ in which K denotes the dimension of features (e.g., precipitation, evaporation), $\:f$ indicates the filter size (temporal receptive field), $\:{W}_{k,m,i\:.}$ Represents a weight which connects feature k with temporal offset i to filter m, $\:{b}_{m}$ is the scalar bias for filter m, and $\:f(\cdot\:)$ Illustrates a non-linear activation function (e.g., ReLU).

The length of the output feature map $\:{T}_{out}$ is determined by the input length $\:{T}_{in}$, filter size F, stride S, and padding P:

$$\:two{W}_{out}=\frac{{T}_{in}-F+2P}{S}+1$$

(2)

For every one of the M filters, the layer learns F × K weights and one bias, which gives a total of $\:F\times\:K\:$weights and one bias, resulting in $\:(F\times\:K+1)\times\:M$ total trainable parameters. This design allows the automatic extraction of hierarchical temporal features from multivariate hydrological data.

After the convolutional layer, a pooling layer (max-pooling, in this case) follows in order to reduce the temporal dimensionality of the feature maps, thus reducing the computational burden and overfitting effect. Max pooling operates by sliding a window of size. $\:{F}_{P}$ over each 1D feature map and selecting the maximum value within that window. The output length $\:{T}_{Pool}$ after pooling is given by:

$$\:{T}_{Pool}=\left[\frac{{T}_{out}-{F}_{P}}{{S}_{P}}\right]+1$$

(3)

where $\:{S}_{P}\:$is the pooling stride. The depth (number of feature maps, $\:M$ ) remains unchanged.

FC layer

In the context of the 1D-CNN architecture we use to forecast reservoir capacities, the final regression layer that performs fully-connected (FC) operations integrates the high-level temporal features extracted by the preceding set of convolutional and pooling operations into a single scalar output- the amount of predicted reservoir storage volume (in billion m³). Different from those tasks, such as image classification, the FC layer will not output values as probabilities against categories; it instead performs a weighted summation of all flattened features from the previous layer in generating a continuous number prediction. A regression loss function, for instance, mean squared error, is used to optimize model parameters through training by determining the difference between the predicted reservoir capacity and the observed capacity. FC layers are recognized for their significant number of trainable parameters, an inherent problem that may make this model prone to overfitting since it memorizes training data patterns but has minimal generalization to unseen data. To remedy this predicament, dropout regularization is employed in every iteration of training; this involves the temporary deactivation of a portion of the neurons in this layer. As a result, the network distributes learning across multiple redundant pathways, which strengthens networks during generalization, being crucial for later performance on out-of-sample climate data.

Performance index

The process of optimizing a CNN consists of identifying the optimum values for the hyperparameters so that the difference between the desired output and actual output is minimized. This involves using a performance index that measures whether a model has made a correct prediction. Once this is established, an optimization technique is applied to improve accuracy, with the primary aim being to minimize prediction errors.

$$\:Max\underset{\overrightarrow{{H}_{p}}\in\:{R}^{i}}{\text{max}}CNN\left(\overrightarrow{{H}_{p}},\overrightarrow{W},T{d}_{i}\right)$$

(4)

here, the hyperparameter vector of the $\:{i}^{th}$ dimension is indicated by $\:{H}_{p}$. The trained data is represented by $\:T{d}_{i}$, $\:i<{i}^{max}$. The weight vector is illustrated by $\:CNN$. The $\:{i}^{max}$ has specified the variable explained by the user in such a way that it balances complication and correctness, which results in equilibrium.

A higher value reflects greater model complexity, while a lower value suggests reduced accuracy, making the selection of an appropriate CNN structure dependent on carefully choosing the maximum iteration parameter $\:{i}^{max}$A progressive approach using a CNN tailored for assessing drought severity on water scarcity trends has been recommended as the most effective method.

Improved spring search algorithm

The research involves coordinating an artificial system using the Spring Search Algorithm (SSA) over time intervals, defining the problem space clearly, and applying spring force laws to represent data transmission. The optimization technique developed has the capacity to solve a variety of optimization problems with solution locations in the search space. The resulting solutions can be compared based on their spring stiffness, which represents our cost function. The SSA algorithm can be implemented in two universal stages: first, constructing a time-dependent artificial model by choosing the relevant variables and governing laws, and then executing the algorithm until the final stopping condition is reached. This methodical approach to exploring a problem space in an optimization context allows for systematic space exploration and optimization, which is desirable in complex optimization problems.

Ordering variables, specifying laws, and setting the system

The system’s space uses a multi-dimensional coordinate system to model the optimization problem in which potential solutions can occupy any point. The search is modeled as a system of objects connected by springs where each object has a location as well as a stiffness coefficient. As it is hard to determine the actual location of the objects, we simply found the stiffness between the connected objects and inferred spring values based on them, which served to keep us on track during the search for an optimal solution.

The system function operates under physical parameters comparable to those found in nature. For example, Hooke’s law states that deformation is proportional to the force applied as long as the elastic limit of the material is not exceeded. While we might experience variations beyond the elastic limit, Hooke’s law was applicable in all possible variations for this study. The methodology of determining an object’s position at any moment in time is to sum all the previous displacements along with the coefficients based on the principles of force and motion. This method reduces some complex optimization scenarios into a dynamic model based on physics that basically replicates and visualizes movement through the solution space and illustrates how users can track movement.

$$\:{Z}_{j}=({z}_{j}^{1},\:.\:.\:.\:,\:{z}_{j}^{d},\:.\:.\:.\:,\:{z}_{j}^{n})$$

(5)

Here, the variable $\:{z}_{j}^{d}$ indicates the $\:{j}^{th}$ object’s location in the $\:{d}^{th}$ dimension. The solution space has explained the primary location of every object randomly. The current objects aim to return to a stable location through the force of the spring.

The following equation has been utilized for computing the spring’s stiffness coefficient:

$$\:{G}_{j,i}={G}_{max}\times\:\left|{V}_{n}^{j}-{V}_{n}^{i}\right|\times\:\text{m}\text{a}\text{x}({V}_{n}^{j},{V}_{n}^{i})$$

(6)

here, the spring’s stiffness coefficient between $\:i$ and $\:j$ objects have been demonstrated by $\:{G}_{j,i}$. The maximum value of the spring’s stiffness coefficient has been illustrated by $\:{G}_{max}$. The $\:i$ and $\:j$ cost functions have been represented by $\:{V}_{n}^{j}$ and $\:{V}_{n}^{i}$, respectively. The equations below have been employed to normalize the cost function.

$$\:{V}_{n}^{{\prime\:}j}=\frac{{v}_{cos}^{j}\:}{\text{m}\text{i}\text{n}\left({v}_{cos}\right)}$$

(7)

$$\:{V}_{n}^{j}=\text{min}\left({V}_{n}^{{\prime\:}j}\right)\times\:\frac{1}{{V}_{n}^{{\prime\:}j}}$$

(8)

Here, the performance index is illustrated by $\:{V}_{cos}$, and the performance index of $\:{j}^{th}$ Object is represented by $\:{v}_{cos}^{j}$.

It is possible to model the issue in an m-dimensional space, where each parameter has specific coordinates. By comparing performance indexes, it is determined which points are more robust on either side of an object. More robust points indicate better positions, leading to two general forces acting on each coordinate left and right calculated using Eq. (8) and Eq. (7), respectively. They have been utilized in the $\:{j}^{th}$ object.

$$\:{{V}_{total}^{i,d}}_{R}=\sum\:_{j=1}^{{n}_{R}^{d}}{G}_{j,i}{z}_{j,i}^{d}$$

(9)

$$\:{{V}_{total}^{i,d}}_{L}=\sum\:_{l=1}^{{n}_{L}^{d}}{G}_{l,i}{z}_{l,i}^{d}$$

(10)

here, the total quantity of the right forces is indicated by $\:{{V}_{total}^{i,d}}_{R}$. The variable $\:{{V}_{total}^{i,d}}_{L}$ illustrates the total quantity of left forces applied to the $\:{i}^{th}$ object in $\:{d}^{th}$ dimension. The variables $\:{n}_{L}^{d}$ and $\:{n}_{R}^{d}$ indicate the $\:d$ dimension of the left and right robust points, respectively. The variables $\:{z}_{l,i}^{d}$ and $\:{z}_{j,i}^{d}$ illustrate the distance of $\:{i}^{th}$ object from left and right robust points. The variables $\:{G}_{l,i}$ and $\:{G}_{j,i}$ illustrate the spring’s stiffness coefficient that are related to the $\:{i}^{th}$ object. The Hooke law in the $\:{d}^{th}$ dimension is computed as follows:

$$\:d{Z}_{R}^{i,d}=\frac{{{V}_{total}^{i,d}}_{R}}{{{G}_{equal}^{i}}_{R}}$$

(11)

$$\:d{Z}_{L}^{i,d}=\frac{{{V}_{total}^{i,d}}_{L}}{{{G}_{equal}^{i}}_{L}}$$

(12)

Here, the variables $\:d{Z}_{L}^{i,d}$ and $\:d{Z}_{R}^{i,d}$ represent the displacement of the $\:{i}^{th}$object to the left and right side of the d^th dimension, respectively. The total displacement would be computed showed in the equation below:

$$\:d{Z}^{i,d}=d{Z}_{L}^{i,d}+d{Z}_{R}^{i,d}$$

(13)

here, the variable $\:d{Z}^{i,d}$ demonstrates the $\:{i}^{th}$ object’s final displacement in the $\:{d}^{th}$ dimension. The $\:z$ direction can be negative or positive:

$$\:{Z}_{new}^{i,d}={Z}_{0}^{i,d}+{r}_{1}\times\:d{Z}^{i,d}$$

(14)

Here, the variable $\:{Z}_{new}^{i,d}$ illustrates the system point’s new location with $\:{i}^{th}$ object and $\:{d}^{th}$ dimension. Moreover, the variable $\:{Z}_{0}^{i,d}$ illustrates the $\:{i}^{th}$ object’s main equilibrium point with $\:d$ dimension. The variable $\:{r}_{1}$ illustrates a random amount that ranges from 0 to 1, and it is employed to avoid random mode.

The formula below demonstrates that when reaching equilibrium, objects and springs experience a small displacement due to slipping. The displacement is minimal at the final stage:

$$\:{Z}^{i,d}={Z}_{new}^{i,d}+\frac{2\times\:\left(T-t\right)}{T}\times\:\left(-0.2+{r}_{2}\times\:0.4\right)\times\:{Z}_{new}^{i,d}$$

(15)

here, the updated location of the $\:{i}^{th}$ objects within dimension $\:d$ is illustrated by $\:{Z}^{i,d}$. The variable $\:T$ illustrates the maximum number of iterations. The current number of iterations is illustrated by $\:t$. The variable $\:{r}_{2}$ illustrates a random amount that ranges from 0 to 1, and it is employed to avoid random mode.

Variables upgrade and time passing

All objects are initially placed randomly within a defined search space. Each object’s displacement is calculated using specific equations (Eqs. 2–6), and it is then moved to its new position. The spring stiffness between objects is updated at each step based on Eq. (2). The algorithm starts by initializing the system and a population of candidate solutions. Each candidate’s performance is evaluated and normalized. Movement laws and spring forces are updated for each candidate, and displacements are calculated to update their positions. This process repeats until the stopping criterion is met, at which point the best solution is returned, and the algorithm ends.

Improved spring search algorithm

A new approach called the Improved Spring Search (ISSA) algorithm has been introduced in this investigation, which aims to address the original SSA’s limitations and increase its efficacy. One significant improvement is the addition of a nonlinear adaptive weight factor that adjusts the search space based on each solution’s fitness. This adjustment helps avoid premature convergence and increase population diversity, which ultimately means better performance. The improved formula can yield positive or negative value for $\:z$:

$$\:{Z}_{new}^{i,d}={Z}_{0}^{i,d}+{w}_{i}\times\:{r}_{1}\times\:d{Z}^{i,d}$$

(16)

here, the $\:{i}^{th}$ The weight factor is illustrated by $\:{w}_{i}$ and it is attained by the formula below:

$$\:{w}_{i}=\frac{\overline{\text{F}}-{\text{F}}_{\text{i}}}{\overline{\text{F}}-\underset{\_}{\text{F}}},i=\text{1,2},\dots\:,{N}_{P},\:$$

(17)

here, the maximum fitness value is illustrated by $\:\overline{\text{F}}$ and the minimum fitness value is demonstrated by $\:\underset{\_}{\text{F}}$. The $\:{i}^{th}$ Candidate’s fitness value is represented by $\:{\text{F}}_{\text{i}}$.

The algorithm dynamically adjusts search spaces using a weighting factor allocating wider ranges to weaker candidates and narrower ones to stronger candidates to optimally balance exploration and exploitation. The second enhancement includes the use of chaotic map, including $\:\beta\:$ instead of $\:{r}_{2}$ using the formula below:

$$\:{Z}^{i,d}={Z}_{new}^{i,d}+\frac{2\times\:\left(T-t\right)}{T}\times\:\left(-0.2+\beta\:\times\:0.4\right)\times\:{Z}_{new}^{i,d}$$

(18)

here, singer chaotic map has been employed as follows:

$$\:\beta\:=\gamma\:\left(7.86{p}_{k}-23.31{{p}_{k}}^{2}+28.75{{p}_{k}}^{3}-13.30{{p}_{k}}^{4}\right),{p}_{0}\in\:\left[0,\:1\right],\:\gamma\:=1.07$$

(19)

here, the iteration amount is illustrated by $\:k$.

The utilization of this mechanism results in an improved speed of convergence for location updates.

Algorithm validation

A methodological validation stage was developed to quantitatively measure the performance of the ISS algorithm. The assessment was performed using the MATLAB R2017b 64-bit version application on a computer system consisting of an Intel Core i7 CPU at 2.6 GHz, 16GB RAM, and 64-bit operating system. The primary purpose of this phase of development is to assess the efficiency and robustness of the algorithm on a variety of optimization tasks of various attributes and complexities. In order to assess the performance of the ISS, twelve benchmark functions from the “CEC-BC-2017 test suite” were utilized. The benchmark functions allowed comparisons of performance to be made, the benchmark functions included unimodal, multimodal, rotated, shifted, hybrid problems of various dimensions and optima. The algorithm’s performance was compared with five state-of-the-art metaheuristic algorithms, each inspired by natural behaviors, including War Strategy Optimization (WSO)²⁵, Supply-Demand-Based Optimization (SDO)²⁶, Growth Optimizer (GO)²⁷, Butterfly Optimization Algorithm (BOA)²⁸.

Model input structure and data preprocessing

The CNN-ISSA model is trained and tested with historical daily time-series weather data from 2003 to 2023. The input features comprise four hydro-meteorological parameters of significance: (1) daily precipitation (mm); (2) daily reservoir inflow (m³/s); (3) daily evaporation (mm); and (4) previous day reservoir storage (billion m³). These parameters were specifically chosen for their physical relevance to reservoir operation and hydropower potential. This scaling was done using Min-Max normalization to equalize the magnitude across the variables and facilitate faster convergence of the models. The authors state that the case was framed as a supervised time-series forecasting problem using a sliding window approach: For each prediction, the model takes in a sequence of the last 30 consecutive days of multivariate input data (that is, a 30 × 4 matrix) to predict the reservoir storage capacity on day 31. This led to an input tensor for the 1D-CNN with dimensions (batch size, 30, 4), where 30 is the length of the temporal sequence and 4 is the number of input features. The output target is one scalar predicting reservoir capacity in units of billion m³ for the next day. The entire dataset was split chronologically into training (2004–2018, ~ 70%), validation (2019–2020, ~ 10%), and test (2021–2023, ~ 20%) sets to keep time dependencies intact and evaluate the model’s ability to generalize for unseen future conditions. This well-thought-out structure allows the 1D-CNN to learn complex temporal patterns and interdependencies on multiple hydrological variables and thus lay a solid foundation for simulating reservoir behavior in the face of climate change scenarios.

Hydropower production

Hydropower generation is the process of transforming the kinetic and potential energy of water into electrical energy through the use of turbines and generators. Hydropower generation is a function of flow rate and water head and the turbine and generator’s efficiency. The hydropower generation equation is defined mathematically as:

$$\:P=\eta\:\rho\:QgH$$

(20)

Here, power output is illustrated by $\:P$ (W). The variable $\:\eta\:$ demonstrates the turbine and generator’s effectiveness, which is equal to 0.8. The water density is indicated by $\:\rho\:$ (kg/m3). The rate of water flow is illustrated by $\:Q$ (kg/m³). The water head is illustrated by $\:H$ (m). The acceleration is demonstrated by $\:g$ that is caused by gravity (m/s²).

Results

Assessing the impact of global warming on climate variables

Figure 5 presents the annual climate variations in various future periods, taking into account the base period of 2003–2023. The findings presented give clear insight into expected annual climate anomalies for different future periods calculated from an ensemble of four CMIP6 models (ACCESS-CM2, CESM2, MIROC6, UKESM1-0-LL). To avoid giving seemingly precise estimates for single values, each metric is shown to the ensemble means, with the ranges among models signifying uncertainty in projections. Under the SSP1 scenario, the ensemble mean annual precipitation is projected to slightly drop to about 1923 mm (range: 1916–1930 mm) from a baseline mean of 1930.5 mm (range: 1921–1938 mm). Under SSP5, the reduction in precipitation is larger, with an ensemble mean of about 1915 mm (range: 1900–1925 mm), which very clearly points to, and is statistically more robust in implying, a drying trend. The ensemble mean of temperature for the baseline is 22.06 °C (range: 21.85–22.29 °C), rising under SSP1 to 22.18 °C (range: 22.00–22.38 °C) and further to 22.39 °C (range: 22.15–22.58 °C) under SSP5. Similarly, evaporation increases from baseline mean 6.83 mm (range: 6.50–7.09 mm) to 6.91 mm (range: 6.59–7.15 mm) under SSP1, and to 7.09 mm (range: 6.78–7.29 mm) under SSP5. Although modest shifts in ensemble means occur under SSP1, the SSP5 climate projections indicate a conditionally drier and warmer future associated with enhanced shifts in the central tendency, alongside coherent narrowing or shifting of the entire inter-model distribution toward higher temperature, evaporation, and lower precipitation. This indicates that SSP5 represents a more severe and certain trajectory of hydroclimatic stress than SSP1.

Fig. 5

The annual climate variables change under different SSPs.

Also, Fig. 6 shows the error bars clearly show the spread of values from the four individual GCMs, highlighting the uncertainty in the projections and preventing the misinterpretation of the ensemble mean as a single, deterministic forecast.

Fig. 6

Annual Climate Variables Change Under Different SSPs (Ensemble Mean ± Inter-Model Range).

Assessing drought severity

This research will focus on communicating drought severity in order to ascertain how droughts might impact future water scarcity trends. The research will provide an in-depth contribution to drought analysis, which is essential for creating a strong water conservation plan and sustainable management of water resources to deal with a possible drought. The study uses the SPI to quantify drought severity, which measures precipitation deficit for different time scales. The findings are presented in Fig. 7 providing a comprehensive view of projected drought conditions in 3 periods.

In SSP-suitable months within the short term (Months), SPI values indicate moderately dry conditions with values as low as -1.5 (December days), by ~-30% from the Near Normal boundary, up to moderately wet (+ 1.5 in July) or ~ + 30% from the Near Normal boundary conditions in regard to the baseline. On the other hand, SSP5 would indicate a slight trend towards increasingly extreme drying conditions, e.g., -2.0 (Jan/Nov/Dec), where >-40% or lower from Near Normal boundary falls within the possible ‘’Severity’’ or ‘’Extreme severity’’ drying categories, possibly having less marked wet periods (e.g., + 0.2, ~+5% from average).

The SSP1 projections indicate that severe hydrological droughts will occur in the near to mid-term (2025–2035) with SPI values dropping as low as -1.5 to -2.0, indicating precipitation deficits of around 30–40% from baseline average realizations in 2003–2023. In contrast, conditions would be moderately wet early in the near term (about 2024–2026) and mid-term (2034–2036), with an SPI exceeding + 1.0. Projected over these periods, precipitation is going to exceed baseline levels by more than 20%. Under SSP5, a trend toward dryness is continued over the course, with an SPI often reaching − 2.0 or lower at mid- to late-term (2030–2040), indicating a greater frequency and severity of hydrological droughts with rainfalls falling below the baseline by more than 40%. Only mild wet periods are found, with maximum SPI values attaining + 0.8 ( ~ + 15% above baseline), mainly during mid-term (2034–2036).

On average, compared to baseline (2003–2023), increasing drought severity is projected across the board, with SSP5 more so than SSP1. Moderate deviations should still be expected by SSP1, which even indicates specific dry years (-30% to -40%), as well as some wet ones (+ 20% or higher). SSP5 primarily shows a tendency toward extensive negative deviations and relatively minor positive deviations, which suggests a drier future to the baseline conditions with even more intense and frequent droughts.

Fig. 7

Projected Drought Conditions (SPI) for Short, Mid, and Long-term Periods under SSP1 and SSP5 Scenarios.

Assessing water scarcity

The WSI is a crucial tool for assessing water shortage in a region. It takes into account various factors, including the availability of water resources and the demand for water in the context of socioeconomic conditions. The SSPs are scenarios that project different futures based on varying levels of socioeconomic challenges for mitigation and adaptation to climate change. The study uses the WSI index to quantify water scarcity, which is presented in Fig. 8 provides a comprehensive analysis of projected drought conditions in 3 periods.

Water Scarcity Index (WSI) results obtained illustrate a trend of increasing water scarcity through the short, mid, and long terms as obtained under SSP1 and SSP5 scenarios from the 2003 to 2023 baseline. Due to these growing trends, the most severe conditions exist under SSP5. In the short-term of both scenarios, seasonal variability is displayed; however, in SSP5, the WSI values remain higher throughout the entire assessment, where January and December exhibit the highest levels of scarcity (approximately 40–50% WSI, representing a 100%+ increase from the baseline’s normal < 20% range for these months) compared to SSP1 (approximately 30–40% WSI, about 50–100% higher than baseline values). For mid-term conditions, both scenarios project an increasing trend of water scarcity above baseline conditions, with a more pronounced increment of 9.4% in winter scarcity for the SSP5 scenario than the 4.8% increase projected under SSP1, indicating water stress levels possibly 50–100% higher than the baseline mean.

In the long-term (2030–2040), WSI values are expected to vary between 20% and over 80%, representing a huge rise when compared to the baseline values in the period from 2003 to 2023, during which WSI averaged between 0% and 40%. Therefore, across both scenarios, water scarcity ramps up with time, with the SSP5 scenario consistently predicting WSI values higher than SSP1 by 10–15% points. From the late 2030s to early 2040s, WSI values under SSP5 witnessed an exceeding of the 80% mark, indicating a shift from high water scarcity conditions to extreme water scarcity conditions when compared to the baseline values. This represents an increase of over 100% compared to the baseline WSI average of around 20–30%, with the value in SSP5 remaining consistently 10–15% higher than in SSP1, thus illustrating how a high-emission pathway can push water scarcity to levels of severity twice or even greater than those experienced in the baseline period.

Fig. 8

Projected Water Scarcity Conditions (WSI) for Short, Mid, and Long-term Periods under SSP1 and SSP5 Scenarios.

Assessing drought severity on water scarcity trends

Suggested optimization model validation

We run every test function through a number of iterations on every algorithm to ensure that consistent and reliable results are obtained. It is common practice in the metaheuristic optimization field to set the number of runs to 25. The quality and robustness of the solutions found are indicated by the Mean, Best, and standard deviation (StD) of the objective function value output from each algorithm. We are primarily interested in the metrics (Mean, Best, and StD). We provide a detailed analysis of the results that our proposed ISS method produced in Table 4, as opposed to other leading methods that we examined. This table identified the Mean, Best, and StD values for each algorithm across a range of functions and ranked each algorithm based on its Mean ranks. In addition, the table highlighted the overall best-performing results for each function in bold font. Table 4 ultimately provided the comparison of the results output by the ISS algorithm with all other algorithms considered in this study.

Table 4 Comparison of the outcomes of the ISS algorithm and the other algorithms.

The ISS algorithm, which has been widely adopted in metaheuristic optimization approaches, consistently exhibits high performance on a large number of test problems. It often finds the minimal Mean and Best values, demonstrating a remarkable ability to locate optimal solutions. For the F1 problem, the ISS method has the lowest best value (0.72) and a competitive mean value (7.24) when compared to the other methods, e.g., WSO, SDO, GO, and BOA algorithms. The performance metrics suggest that the ISS algorithm not only found the optimal solution, but also provided a generally strong performance across the other nine iterations of detail-based problems. The standard deviation of the International Space Station (ISS) on the F1 mission was lower than that of the Solar Dynamics Observatory (SDO) and Big Observation of Apes (BOA), which would indicate that the information obtained by the ISS and F1 was much more consistent. The ISS method shows its stability and reliability by producing the ideal best value of 0.00 on functions like F5, F6, and F12, always retaining this value and maintaining this level of confidence with a Mean of 0.01 or less and a standard deviation of 0.00. However, there are some situations when other algorithms beat others. For example, BOA was the only algorithm to have the greatest value (24.41) on function F8, but it was also the only algorithm with the highest mean value, suggesting less consistency. The performance of the ISS algorithm is impressive, especially when we consider the high-ranking positions. Considering these findings in the context of particular optimization problems could provide a better perspective on the practical applicability and effectiveness of the ISS method in comparison to alternatives.

Simulation of water scarcity trends by the optimal model

Close agreement in Fig. 9 holds for simulated (CNN-ISSA) and observed reservoir capacity from 2007 to 2023, capturing major peaks and troughs like the extreme drought in 2011 when observed storage went below 2.5 billion m³ and the high-capacity state around 2018 when adequate reservoir levels surpassed 5.0 billion m³. This close visual and statistical agreement was validated under assessed training data (2004–2018) and testing data (2019–2023) and showed that the model was capable of not only retrieving general seasonal trends, but also accurately resolving extreme hydrological events that are highly significant for operational planning regarding water and power. The model’s ability to reproduce those historical stress points gives reason to believe that it would be reasonably reliable for forecasting future reservoir behavior under climate variability, justifying the use of such modeling for adaptive management and drought mitigation preparedness.

Fig. 9

The reservoir capacity simulation from 2007 to 2023.

As a result, this model is promising to predict efficient reservoir capacities from 2024 to 2040. The accuracies of the model simulations, along with the associated errors, are detailed in Table 5.

Table 5 The correctness of the hydrological model’s effectiveness.

The optimized CNN model has shown strong performance in simulating reservoir capacities. This is evident from the minimal error and good fit values during training and testing. The model’s effectiveness is indicated by an RMSE of 0.59, an R2 of 0.90, and a Nash-Sutcliffe Efficiency of 0.85 in the training phase. Additionally, the model’s ability to predict future data is confirmed with an R2 value of 0.89 during testing. An NSE of 0.80 further demonstrates the model’s capability to simulate observed runoff data. In summary, the optimized CNN model is very effective at predicting runoff with high accuracy, as shown by its performance metrics.

Forecasting water reservoir capacity

In Fig. 10, we have illustrated the prediction of reservoir capacity for the period, 2024–2040, with two scenarios, SSP1 and SSP5. The SSP1 Scenario is relatively stable, with lower fluctuations in reservoir capacity. The minimum capacity is experienced around 2033, when reservoir capacity appears to fall just below about 3 billion m³. The maximum capacity seemed to happen around 2036, when reservoir capacity peaked, just above 4.5 billion m³. In contrast, the SSP5 Scenario demonstrates greater fluctuations around higher reservoir capacities than the SSP1 Scenario. The minimum capacity is also seen around 2033, but at a slightly higher value compared with the SSP1 Scenario. However, when you look at maximum capacity in the SSP5 Scenario, it is considerably higher than the maximum that is seen under the SSP1 Scenario, with a maximum between approximately 5.5 billion m³ and 2036. As shown by the SSP1 and SSP5 projections, we expect to see variable reservoir capacities. Those trends are significant because they directly affect the reliability of hydropower generation. When the reservoir is low, there may not be enough water for the available hydropower to meet energy demand. However, high reservoir levels have the potential to allow an increase in hydropower generation capacity.

Fig. 10

Forecasting reservoir capacity from 2024 to 2040 under two scenarios.

Future hydropower generation

The hydropower potential has been influenced by various climate scenarios as presented in Fig. 11.

According to SSP1, hydropower generation is estimated to reach a near-term peak, just below 0.9 billion kWh, in the early period (2024–2027) before a drop in the mid-term (2028–2032) to around 0.7 billion kWh, about 22% lower than the peak. In the late mid-term (2033–2037), generation will partially recover before more subsequent peaks fall below the first maximum. The end of the projection period (2038–2040) will witness generation stabilizing at slightly above 0.7 billion kWh, an approximate 20% long-term decline compared to the early near-term peak.

For the SSP2 scenario, hydropower follows a similar trend, with a peak also around 2026 but at a lower value than the SSP1 peak. The decline into the year 2030 is also noted, as is the trough, which is identical to the trough of the SSP1. As pointed out in the first scenario, an increase in hydropower towards 2035 has been witnessed. By 2040, hydropower generation will refer to the hydropower generation from the SSP1 scenario. The information contained in this document helps to develop and assess possible trends in hydropower production and also assists in key energy planning and policy development. The variability in generation also speaks to the need for flexible energy systems. It has broader implications regarding complementary renewable energy systems as a means to provide a stable energy supply.

Fig. 11

The hydropower potential forecasting by different climate scenarios.

Practical implementation and policy implications

Due to extreme precipitation and water shortages anticipated in the future, especially under the SSP5 scenario, proactive and integrated actions and policies are urgently required on the ground. Adaptive management of the water-energy nexus should provide emphasis on flexible reservoir operation, striking a balance between hydropower generation and ecological flows and municipal/agricultural supply. However, investments in climate-resilient infrastructure, including wastewater reuse, desalination, and managed aquifer recharge, are critical for drought supply shock buffering. In addition, diversifying the energy mix with complementary renewables (e.g., solar and wind) can help tackle the grid instability caused under periods of low hydropower generation. Furthermore, effective management of transboundary basins such as the Dong River requires enhanced cooperation towards regional data-sharing, coordinated operation, and equitably established water allocation frameworks. These integrated strategies represent a functional policy pathway for enhancing systemic resilience, and their repeat mentions in the Discussion section may now become an unnecessary distraction, allowing Sect. 5 to solely focus on a synthesis of scientific findings, model performances, and research limitations.

The study also identifies some inherent limitations that must be considered when implementing the process in practice. The CNN model relies heavily on historical hydrological data of good quality, which will create uncertainties in areas where such data are scarce. The time-consuming nature of the ISSA algorithm could limit its use for real-time applications where high-performing computing resources are not available. Strong performances were achieved in the Xinfengjiang Reservoir study; however, to apply the model to other basins, it must be recalibrated for local differences in climate, topography, and operations. Therefore, contextual adaptation and capacity-building are vital for scaling up this tool in new regions.

Discussion

In the face of climate changes corresponding to SSP1 and SSP5, a novel hybrid modeling framework, CNN-ISSA, has been developed to simulate reservoir capacity and forecast hydropower generation, in order to provide vital information for the Xinfengjiang Reservoir. Results forecast a progressive increase in hydrologic variability from 2025 to 2035, with SPI projected to fall in the range of − 1.5 to − 2.0 (indicating 30–40% precipitation deficits), particularly under SSP5. The SSP5 scenario will also push WSI values above 80% by the late 2030s, indicating a change to extreme water scarcity. Although some moderate wet periods (SPI > + 1.0) are predicted around 2024–2026 and 2034–2036, their intensity and duration are further reduced under SSP5 in a clear trend towards persistent aridification.

CNN-ISSA showed good prediction capabilities (R² = 0.89–0.90, NSE = 0.80–0.85) in reconstructing past reservoir dynamics and projecting future trends. Under SSP1, the reservoir capacity shows less variability, with a peak near 4.5 billion m³ in 2036; under SSP5, however, larger fluctuations in higher capacity (~ 5.5 billion m³) and more irregular low-storage interfacing periods were recorded. Hydropower generation is projected to peak around 2026, under both scenarios (~ 0.9 billion kWh under SSP1), and to drop by ~ 22% by 2030 before partially rebounding. By 2040, hydropower generation is projected to stabilize at slightly above 0.7 billion kWh, indicating a more fundamental reduction in reliability under the amassed effects of climate stress.

These results emphasize the model’s potential for being utilized in decision support toward operational planning and risk assessment. Convergence speed and solution accuracy favored ISSA over other metaheuristics, while CNNs modeled the nonlinear responses of hydrology. However, the model’s performance depends on data quality and availability of computational resources and its generalizability requires calibration for the specific basin. This is a strong emphasis on a careful context-based implementation as opposed to the standard one-size-fits-all deployment.

In conclusion, this study builds a bridge between global climate evolution scenarios and reservoirs in integrated forecasting, thereby promoting localized adaptation to climate change. Furthermore, it quantifies how those processes are increasing the risks of climate change and water scarcity for energy security, thereby supporting the technical foundation for the integrated adaptive policies proposed in Sect. 4. Future efforts should, therefore, incorporate high-resolution downscaling and investigate transfer learning for enhanced model reliability in poorly informative and topographically intricate areas.

Conclusion

This study delves into how global warming affects local water systems, especially when it comes to making water and energy. The study examines hydrological drought over three, six, and twelve months using GCMs and the SPI. A hybrid modeling approach that combines the Enhanced ISSA with a CNN is used to model and predict how reservoir capacity will change as the climate changes. This makes it possible to look closely at how a lack of water affects the production of hydropower. The research anticipates a trend toward increased hydrological variability, including periods of intense drought (SPI <- 1.5) that may occur in the near and mid-term (2025–2035). This is especially true under SSP5, where in several instances, SPI is anticipated to dip below − 2.0. Moderate wet conditions (SPI > + 1.0) are projected to occur in the early near-term (2024–2026) and in the mid-term (2034–2036), although such conditions would be less accentuated under SSP5. As a whole, the region is progressively transitioning toward droughts and water scarcity (WSI > 80%), with a higher probability during the 2030s under high-emission scenarios. The WSI also raises increasing concerns about water availability because the WSI under the SSP5 scenario was always higher than the WSI under the SSP1 scenario. The ISSA optimization algorithm performed well, as it had the lowest Mean and Best values for objective functions for the algorithms tested. Furthermore, the optimized CNN model performed very well with respect to its accuracy in simulating reservoir capacities. This is crucial to hydropower generation forecasting related to trends, energy planning, and policy making.

The hybrid CNN–ISSA model has limitations as it requires a high quality of historical data availability. If a region has low data availability, then performance might be reduced. Additionally, the computational complexity of the ISSA algorithm might be prohibitive for real-time applications without available computational resources. The model may be applied in new regions; however, calibrating the model in a new area may be necessary due to climate, topography, and dam operational differences. Ultimately, though, the model will provide helpful support to adaptive water and energy management. It will help optimize reservoir operations, develop early warning drought systems, assist hydropower planning, and help with climate-resilient infrastructure. It also plays a supportive role in transboundary water cooperation and integrated policy development, which is relevant in tackling the global water-energy nexus under increasing climate uncertainty. The critical thing to note is that there are limitations to the use of raw outputs from GCMs since they are not downscaled to reflect hydrological response in space or time. Such an approach can indicate broad-scale climate trends. Still, we recommend high-resolution downscaling for future local hydrological processes and the accuracy of the predictions of variability and changes in reservoir inflows or drought severity caused by climate change in areas with complex geomorphology and localized climatic variation.