Reconfigurable intelligent surface-assisted N-ary Alamouti

Abstract

Reconfigurable intelligent surface (RIS)-assisted transmission has become a novel concept for future wireless communications. The multiple-input multiple-output (MIMO)-based RIS-assisted Alamouti (RIS-Alamouti) scheme has been recently proposed in the literature. The RIS-Alamouti scheme models the conventional Alamouti scheme with two transmit antennas and $N_r$ receive antennas. In this paper, we propose a novel MIMO-based scheme, hereinafter referred to as the N-ary RIS-assisted Alamouti (N-RIS-Alamouti) scheme. In the proposed N-RIS-Alamouti scheme, $\log _2N$ additional information bits can be conveyed by transmitting a pair of N-ary phase shift keying (NPSK) symbols in one of two transmit antennas over four time slots. The pair of NPSK symbols can be regarded as one channel’s additional phase component over four time slots. The proposed N-RIS-Alamouti scheme not only preserves the error performance of the RIS-Alamouti scheme but also enhances its spectral efficiency; hence, it allows the transmission of a larger number of bits per channel use without trading off on reliability. The achievable order N of the N-RIS-Alamouti scheme increases as the number of receive antennas increase meaning that a larger spectral efficiency is achievable for a larger number of receive antennas. Simulation results show that at a bit error rate (BER) of $2\times {10^{-5}}$, the proposed 128-RIS-Alamouti and 256-RIS-Alamouti with 64-ary phase shift keying and 64 reflector elements achieve the BER performance of the RIS-Alamouti for two and three receive antennas, respectively. Equivalently, an additional 7 bits and 8 bits are transmitted in four time slots, respectively.

Introduction

Reconfigurable intelligent surfaces (RISs) have evolved as a promising technology in wireless communications¹. Several classes of RISs exist. The class of phase-adjustable RISs can be thought of as a planar surface composed of several passive elements. Each element represents a reconfigurable scatterer that is able to modify the impinging signal with an adjustable phase shift. Each element can be programmed and controlled by using external stimuli. Consequently, several phase-adjustable RIS-based or RIS-assisted wireless communication systems have been proposed^2,3. The access-point (AP)-based RIS-assisted single-input multiple-output (SIMO)² or multiple-input multiple-output (MIMO) systems are significantly different from the existing conventional SIMO or MIMO systems. The AP-based RIS-assisted SIMO or MIMO systems do not require a dedicated source for radio frequency (RF). In the remainder of the paper, our focus will be on phase-adjustable AP-based RISs.

There are numerous RIS-assisted SIMO or MIMO systems that have been proposed in the literature. These systems are, for example, the RIS-assisted Alamouti scheme^3,4, the RIS-assisted and index modulation-based VBLAST system³, three RIS-assisted index modulation (RIS-IM) schemes: an RIS-assisted space shift keying scheme, RIS-assisted spatial modulation², RIS-based quadrature reflection modulation⁵, RIS-assisted space-time block coding (STBC) and differential space-time block coding (DSTBC)⁶ and space-time block coded RIS-based received spatial modulation (SM)⁷. Similar to the conventional Alamouti scheme, the RIS-assisted Alamouti scheme with ${N_r}$ receive antennas employs a linear maximum-likelihood (ML) detector and achieves a diversity order of $2N_r$. The RIS-assisted IM scheme was implemented by use of the conventional IM principle for selecting the indices of multiple receive antennas to improve the spectral efficiency. The RIS-assisted STBC and DSTBC have been proposed to enhance error performance in⁶. Finally, the space-time block coded RIS-based received SM has been proposed to enhance data transmission compared to the traditional RIS-assisted SM. In this paper, we primarily focus on improving the spectral efficiency of the RIS-Alamouti scheme.

Very recently, an enhanced spectral efficiency scheme, N-ary Alamouti space-time block coding (N-STBC), was proposed⁸. The proposed N-STBC scheme requires four time slot transmissions or two consecutive Alamouti block transmissions. In the N-STBC scheme, there exists $\log _2{N}$ additional information bits which are mapped into one pair of N-ary phase shift keying (NPSK) space-time labelling diversity (STLD) signals which was proposed in⁹. The pair of NPSK STLD signals are transmitted via one of the two transmit antennas during two consecutive block transmissions. To further improve the error performance of the N-STBC scheme, in⁵, golden codewords are applied to transmissions. Motivated by the spectral efficiency advantage of the N-STBC scheme, in this paper, we propose a novel transmission scheme, referred to as the N-ary RIS-assisted Alamouti (N-RIS-Alamouti) scheme. Compared to the RIS-Alamouti scheme, the proposed N-RIS-Alamouti scheme further enhances the spectral efficiency, while the proposed N-RIS-Alamouti still maintains the same error performance of the RIS-Alamouti at high signal-to-noise ratios (SNRs). Again, the proposed N-RIS-Alamouti scheme preserves the linear ML detection.

The novelty of the proposed N-RIS-Alamouti scheme is that $\log _2N$ additional information bits can be conveyed by transmitting a pair of NPSK symbols in one of two transmit antennas over four time slots. In practical application of the proposed N-RIS-Alamouti scheme, the pair of NPSK symbols can be regarded as extra channel phases. Note that, introducing the extra channel phases will not increase implementation complexity at the transmitter, while improving spectral efficiency.

The remainder of the paper is organized as follows: In Section System model, we present system models, which include STLD and the proposed N-RIS-Alamouti scheme. In Section Signal detection, we discuss signal detection with perfect channel state information (CSI) and imperfect CSI. In Section Error Performance Analysis of the RIS-Alamoutiand N-RIS-Alamouti Schemes, we present the formulation of the closed-form average bit error probability (ABEP) of the RIS-Alamouti and derive the error performance bound of the proposed N-RIS-Alamouti schemes. Simulation and theoretical ABEP are demonstrated in Section Numerical results and conclusions are finally drawn in Section Conclusion.

Notation: $[\cdot ]^T$, $(\cdot )^H$, $|\cdot |$ and $\Vert \cdot \Vert _F$ represent the transpose, Hermitian, Euclidean and Frobenius norm operations, respectively. $(\cdot )^*$ represents the complex conjugate. $E\{\cdot \}$ is the expectation operation. $\Re \{\cdot \}$ is the real part of a complex argument and $j=\sqrt{-1}$. $Q(\cdot )$ represents the Gaussian Q-function. $\min _{a}(\cdot )$ evaluates the minimum of the argument with respect to a.

System model

STLD is a key component in the proposed N-RIS-Alamouti scheme. As preliminaries, in this section, we briefly present the design of the pair of STLD symbols, and then describe in detail the proposed N-RIS-Alamouti scheme.

Design of the pair of STLD symbols

STLD is an STBC with two transmit antennas. In the conventional STLD system, there are two pairs of STLD symbols. These STLD symbols are either M-ary quadrature amplitude modulation (MQAM) or M-ary phase shift keying (MPSK). However, in this paper, only MPSK is applied in the passive RIS-assisted transmission schemes.

Let the input information bit stream be $\varvec{b}=[\begin{matrix}b_{1}&\cdots&b_{{r}} \end{matrix}]$, $r=\log _2{M}$, where M is the order of MPSK. Let $\varvec{\bar{\chi }}_M$ be the signal set of the MPSK. Then bit stream $\varvec{b}$ is fed into two bit-to-symbol mappers, $\Omega _M^k, k\in [1:2]$, which maps the r input information bits onto constellation points from $\varvec{{\bar{\chi }}}_M$, and yields a pair of STLD symbols, $(x_{\varvec{b}}^1, x_{\varvec{b}}^2)$, where $x_{\varvec{b}}^k=\Omega _M^{k}(\varvec{b})$ and $E\{|x_{\varvec{b}}^k|^2\}=1, k\in [1:2]$.

Since $x_{\varvec{b}}^k$ are MPSK symbols, we may also express the symbol as $x_{\varvec{b}}^k=e^{j\theta ^k}$. Then the pair of the STLD symbols is written as $(e^{j\theta ^1}, e^{j\theta ^2})$.

Normally, the first mapper $\Omega _M^1$ is the Gray coded mapper, while the second mapper $\Omega _M^2$ is designed for a specific modulation scheme⁶. The design of the second mapper $\Omega _M^2$ has been discussed in the literature. As an example, the two mappers for one pair of 16PSK STLD (cf. Fig. 1 in⁶) is shown in Fig. 1.

In Fig. 1, there are 16 legends $q_x, q\in [0:15], x\in [0:15]$. q in $q_x$ stands for the corresponding decimal index of the input information bits and x is denoted in $e^{j\frac{2\pi }{16}\times {x}}$. There are two types of symbol pairs in Fig. 1.

Type I: $\Omega _M^{1}(\varvec{b})=\Omega _M^{2}(\varvec{b})$.

Suppose that the input information bits are 0011 which is equivalent to $q=3$. The subscript of $q=3$ is $x=2$. So we have $\Omega _M^{1}({0011})=\Omega _M^{2}({0011})= e^{j\frac{2\pi }{16}\times {2}}$. Then the pair of 16PSK STLD symbols is $(e^{j\frac{2\pi }{16}\times {2}}, e^{j\frac{2\pi }{16}\times {2}})$.

Type II: $\Omega _M^{1}(\varvec{b})\ne {\Omega _M^{2}(\varvec{b})}$.

Suppose that the input information bits are 0010 which is equivalent to $q=2$. From Fig. 1, we have $\Omega _M^{1}({0010})=e^{j\frac{2\pi }{16}\times {3}}$ and $\Omega _M^{2}({0010})= e^{j\frac{2\pi }{16}\times {11}}$. Then the pair of 16PSK STLD symbols is $(e^{j\frac{2\pi }{16}\times {3}}, e^{j\frac{2\pi }{16}\times {11}})$.

Fig. 1

Two bit-to-symbol mappers of 16PSK.

N-ary RIS-assisted Alamouti system

In this subsection, we present the proposed N-RIS-Alamouti scheme. Similar to the N-ary Alamouti STBC scheme discussed in⁵, we introduce a dimension (a pair of coupled phase offsets) of order N into one of two transmit antennas per four time-slots, which in this paper, is referred to as N-RIS-Alamouti.

Fig. 2

System model of the N-ary RIS-assisted Alamouti scheme.

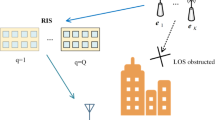
The proposed N-RIS-Alamouti scheme models a $2\times {N_r}$ MIMO system, where $N_r$ is the number of antennas at the receiver, $N_r\ge {2}$. In the proposed N-RIS-Alamouti scheme, an unmodulated carrier signal is transmitted from a low-cost RF signal generator located close to the source (S) unit. Figure 2 shows the block diagram of the proposed N-RIS-Alamouti scheme which is the same as the RIS-Alamouti system as discussed in³. However, the N-RIS-Alamouti scheme employs four time slots for transmission. In Fig. 2, $r_s$ and $r_d$ denote the distance between S and the passive RIS and the distance between the RIS and the destination (D), respectively. The distance $r_s$ is chosen close to the passive RIS which makes the channel between the source and the RIS to be line-of-sight (LOS).

In the proposed N-RIS-Alamouti scheme, there are five input information bit streams, $\varvec{b}_i,i\in [1:5]$. Four of the bit streams, $\varvec{b}_i,i\in [1:4]$, will be sent to one Gray coded bit-to-symbol mapper, $\Omega _M$, which maps $\log _2M$ bits of each of these bit streams to MPSK symbols, $e^{j\theta _i}=\Omega _M(\varvec{b}_i), i\in [1:4]$. Bit stream $\varvec{b}_5$ will be sent to either a bit-to-symbol mapper, $\Omega _N$ if $N=4$ or two bit-to-symbol mappers, $\Omega _N^l, l\in [1:2]$ if $N\ge {8}$. For $N=4$, the bit-to-symbol mapper $\Omega _N$ maps $\log _2N$ bits of bit stream $\varvec{b}_5$ into a 4PSK symbol, $e^{j\theta _5(p)}=\Omega _N(\varvec{b}_5)$ and $p\in [1:N]$ which denotes the index of the bit stream $\varvec{b}_5$. For $N\ge {8}$, the two bit-to-symbol mappers, $\Omega _N^l, l\in [1:2]$ map $\log _2N$ bits of bit stream $\varvec{b}_5$ into a pair of NPSK symbols, $(e^{j\theta _5^1(p)},e^{j\theta _5^2(p)})$, where $e^{j\theta _5^l(p)}=\Omega _N^l(\varvec{b}_5)$. There are two codeword matrices in the proposed N-RIS-Alamouti scheme. The $l^{th}$ codeword matrix of the proposed N-RIS-Alamouti scheme is given by:

$$\begin{aligned} \varvec{X}_l=\left[ \begin{matrix}e^{j\theta _{2l-1}} & e^{j\theta _5^l(p)} \times {e^{j\theta _{2l}}}\\ -e^{-j\theta _{2l}} & e^{j\theta _5^l(p)} \times {e^{-j\theta _{2l-1}}}\end{matrix}\right] , l\in [1:2]. \end{aligned}$$

(1)

Note that in (1), for $N=4$, $e^{j\theta _5^1(p)}=e^{j\theta _5^2(p)}=e^{j\theta _5(p)}$. In (1), a pair of NPSK symbols, $(e^{j\theta _5^1(p)},e^{j\theta _5^2(p)})$, is transmitted through the second transmit antenna over two block time slots (four time slots). The pair of NPSK symbols conveys $\log _2N$ additional information bits to the receiver.

In (1), let $e^{-j\tilde{\theta }_{2l-1}}=e^{j\theta _5^l(p)} \times {e^{-j\theta _{2l-1}}}$ and $e^{j {\tilde{\theta }_{2l}}}=e^{j\theta _5^l(p)} \times {e^{j\theta _{2l}}}$, where $\tilde{\theta }_{2l-1}=\theta _{2l-1}-\theta _5^l(p)$. The $l^{th}$ and ${\tilde{\theta }_{2l}}=\theta _5^l(p)+{\theta _{2l}}$ codeword matrix given in (1), is further written as:

$$\begin{aligned} \varvec{X}_l=\left[ \begin{matrix}e^{j\theta _{2l-1}} & {e^{j\tilde{\theta }_{2l}}}\\ e^{-j(\theta _{2l}+\pi )} & {e^{-j\tilde{\theta }_{2l-1}}}\end{matrix}\right] , l\in [1:2], \end{aligned}$$

(2)

In Fig. 2, the passive RIS has L elements which are partitioned into two parts. Each part has L/2 elements. Based on the N-RIS-Alamouti encoding, in each time slot, each part is adjusted to a common reflection phase value. The transmission is over four time slots. As an example, the first and the second RIS parts are adjusted to a common reflector phase $\theta _1$ and ${\tilde{\theta }_{2}}$ and $-(\theta _2+\pi )$ and ${\tilde{\theta }_{1}}$ in the first two time slots and phase $\theta _3$ and ${\tilde{\theta }_{4}}$ and $-(\theta _4+\pi )$ and ${\tilde{\theta }_{3}}$ in the second two time slots, respectively. The proposed N-RIS-Alamouti models the Alamouti with MPSK by adjusting the phases of the RIS elements to modify the phases of the RF carrier signal. Through adjusting the phases of each RIS part, the Alamouti scheme can be implemented by use of a single RF signal generator instead of two full RF chains at the transmitter. It is assumed that the RIS is blind with respect to the channel state information (CSI).

The signal transmission of the N-RIS-Alamouti takes two block transmissions (four time slots). In Fig. 2, $h_{i,k}^l, k\in [1:N_r], l\in [1:2]$ is the channel coefficient between the $i^{th}$ element of the RIS and the $k^{th}$ receive antenna at D during the $l^{th}$ block transmission. All $h_{i,k}^l$ are statistically independent of each other. It is assumed that $h_{i,k}^l$ is the small-scale fading coefficient which is modelled as complex Gaussian random variables (RVs) distributed as $CN (0,1)$. It is further assumed that the channel coefficient remains constant over two time slots, and takes on an independent value in another two time slots. Based on the $l^{th}$ codeword matrix given in (2), the received signal at the $k^{th}$ receive antenna in the $l^{th}$ block transmission can be written as:

$$\begin{aligned} r_{1,k}^l&=\sqrt{P_t}\left[ e^{j\theta _{2l-1}}A_{1,k}^{l}+{e^{j\tilde{\theta }_{2l}}A_{2,k}^{l}}\right] +n_{1,k}^l, \end{aligned}$$

(3.1)

$$\begin{aligned} r_{2,k}^l&=\sqrt{P_t}\left[ e^{-j(\theta _{2l}+\pi )} A_{1,k}^{l}+{e^{-j\tilde{\theta }_{2l-1}}A_{2,k}^{l}}\right] +n_{2,k}^l. \end{aligned}$$

(3.2)

In (3.1) and (3.2), $A_{1,k}^{l}=\sum _{i=1}^{L/2}{h_{i,k}^l}$ and $A_{2,k}^{l}=\sum _{i=1+L/2}^{L}{h_{i,k}^l}$. Since $h_{i,k}^l$ is modelled as a complex Gaussian RV distributed as $CN (0,1)$ and all $h_{i,k}^l$ are statistically independent of each other, then $A_{i,k}^l$ is also modelled as a complex Gaussian RV distributed as $CN (0,\frac{L}{2})$. $n_{t,k}^l$ is the complex additive white Gaussian noise (AWGN) RV distributed with $CN (0,N_0)$, where $N_0$ is the single-sided noise power spectral density. $P_t=P_L{E_s}$, where $E_s$ is the average transmitted RF signal energy. $P_L$ is the total path gain from S to the RIS and further to D which is given by³:

$$\begin{aligned} P_L=\frac{\lambda ^4}{256\pi ^2r_s^2r_d^2}, \end{aligned}$$

(4)

where $\lambda$ is the wavelength of the operating frequency $f_c$. We then have $\lambda =\frac{v_c}{f_c}$, with $v_c$ the light transmission speed.

Signal detection

In this section, we maily focus on signal dection with perfect CSI and imperfect CSI for the proposed N-RIS-Alamouti scheme.

Signal detection with perfect CSI

In this subsection, we assume that the CSI is perfectly estimated at the receiver. Both sides of (3.1) and (3.2) are divided by $\sqrt{P_t}$, then (3.1) and (3.2) are rewritten as:

$$\begin{aligned} \tilde{r}_{1,k}^l&=e^{j\theta _{2l-1}}A_{1,k}^l+e^{j\tilde{\theta }_{2l}}A_{2,k}^l+\tilde{n}_{1,k}^l, \end{aligned}$$

(5.1)

$$\begin{aligned} \tilde{r}_{2,k}^l&=e^{-j(\theta _{2l}+\pi )}A_{1,k}^l+e^{-j\tilde{\theta }_{2l-1}}A_{2,k}^l+\tilde{n}_{2,k}^l, \end{aligned}$$

(5.2)

where $\tilde{r}_{t,k}^l=\frac{r_{t,k}^l}{\sqrt{P_L{E_s}}}$ and $\tilde{n}_{t,k}^l=\frac{n_{t,k}^l}{\sqrt{P_L{E_s}}}$. $\tilde{n}_{t,k}^l$ is a complex Gaussian RV distributed as $CN (0,\frac{N_0}{{P_L}{E_s}})$.

In the following discussion, we focus mainly on the detection of the N-RIS-Alamouti scheme. It is assumed that the CSI is known at the receiver. The ML detection is a joint detection of the phase offsets $e^{j\theta _5^l(p)}$ and the transmitted four symbols $e^{j\theta _m}, m\in [1:4]$. Consequently, the joint detection includes two steps:

Step 1: Given a pair of phase components $(e^{j\theta _5^1(p)},e^{j\theta _5^2(p)})$ detecting the transmitted four symbols $e^{j\theta _m}$.

Given the CSI and $e^{j\theta _5^l(p)}$, (5.1) and (5.2) are rewritten as:

$$\begin{aligned} \tilde{r}_{1,k}^l&=e^{j\theta _{2l-1}}A_{1,k}^l+e^{{j\theta }_{2l}}\tilde{A}_{2,k}^l+\tilde{n}_{1,k}^l, \end{aligned}$$

(6.1)

$$\begin{aligned} \tilde{r}_{2,k}^l&=-(e^{j\theta _{2l}})^*A_{1,k}^l+(e^{{j\theta }_{2l-1}})^*\tilde{A}_{2,k}^l+\tilde{n}_{2,k}^l, \end{aligned}$$

(6.2)

where $\tilde{A}_{2,k}^l=e^{j\theta _5^l(p)}\times {{A}_{2,k}^l}$.

Obviously, (6.1) and (6.2) are the received signals for the conventional Alamouti scheme with MPSK transmission.

Let $\tilde{\varvec{r}}_{i}^l=[\tilde{r}_{i,1}^l \cdots \tilde{r}_{i,N_r}^l]^T$, $\varvec{A}_{1}^l=[A_{1,1}^l \cdots A_{1,N_r}^l]^T$, $\tilde{\varvec{A}}_{2}^l=e^{j\theta _5^l(p)}\times {\varvec{A}_{2}^l}=[\tilde{A}_{2,1}^l \cdots \tilde{A}_{2,N_r}^l]^T$ and $\tilde{\varvec{n}}_{i}^l=[\tilde{n}_{i,1}^l \cdots \tilde{n}_{i,N_r}^l]^T$. Then the combined signals are given by:

$$\begin{aligned} z^{2l-1}&=[(\varvec{A}_1^{l})^H{\tilde{\varvec{r}}_1^{l}}+(\tilde{\varvec{r}}_2^{l})^H\tilde{\varvec{A}}_2^{l}], \end{aligned}$$

(7.1)

$$\begin{aligned} z^{2l}&=[(\tilde{\varvec{A}}_2^{l})^H{\tilde{\varvec{r}}_1^{l}}-(\tilde{\varvec{r}}_2^{l})^H\varvec{A}_1^{l}]. \end{aligned}$$

(7.2)

Finally, the estimated symbol is given by:

$$\begin{aligned} \hat{x}_l^{p}=\mathcal {D}_{PSK}\left( z^l\right) , \end{aligned}$$

(8)

where $\mathcal {D}_{PSK}\left( \cdot \right)$ is the MPSK demodulator function. $l\in [1:4]$. $\hat{x}_l^{p}$ stands for the estimated symbols given the pair of phase components $(e^{j\theta _5^1(p)},e^{j\theta _5^2(p)})$.

Step 2: Jointly detecting the transmitted four symbols $e^{j\theta _m}$ and the pair of the phase components $e^{j\theta _5^l(p)}$.

To facilitate the discussion, we define the detected symbol vector as $\hat{\varvec{x}}^p=(\hat{x}_1^{p}, \hat{x}_2^{p}, \hat{x}_3^{p}, \hat{x}_4^{p})$ for a given pair of the phase components $(e^{j\theta _5^1(p)}, e^{j\theta _5^l(p)})$. Considering MPSK, we further have $\hat{x}_l^{p}=e^{j\theta _l^p}$.

Let $\hat{\varvec{x}}=(\hat{x}_1, \hat{x}_2, \hat{x}_3, \hat{x}_4)$ and $\hat{\varvec{s}}=(e^{j\theta _5^1(p)}, e^{j\theta _5^2(p)})$ be the finally estimated symbol vectors. Finally, the estimation of the transmitted signals $e^{j\theta _m}$ and $(e^{j\theta _5^1(p)},e^{j\theta _5^2(p)})$ is given by:

$$\begin{aligned} {[}\hat{\varvec{x}},\hat{\varvec{s}}]=\min _{e^{j\theta _5^1(p)},e^{j\theta _5^2(p)}\in {\varvec{\chi }}_N}{\sum _{l=1}^{2}}{(ED_{2l-1}+ED_{2l})}, \end{aligned}$$

(9)

where:

$ED_{2l-1}={\Vert \tilde{\varvec{r}}_{1}^l-(e^{j\theta _{2l-1}^{p}}\varvec{A}_{1}^l+e^{j\theta _5^l(p)}\times {e^{j\theta _{2l}^{p}}\varvec{A}_{2}^l)}\Vert _F^2}$,

$ED_{2l}={\Vert \tilde{\varvec{r}}_{2}^l-(-e^{-j\theta _{2l}^p}\varvec{A}_{1}^l+e^{j\theta _5^l(p)}\times {e^{-j\theta _{2l-1}^{p}}\varvec{A}_{2}^l)}\Vert _F^2}$ and $\varvec{\chi }_N$ is the signal set of the pair of $(e^{j\theta _5^1(p)},e^{j\theta _5^2(p)})$.

Signal detection with imperfect CSI

In this subsection, we assume that the CSI is not perfectly estimated at the receiver. The imperfect CSI in Alamouti based wireless cooperation networks has been discussed in¹⁰. The channel estimation model in¹⁰ will be applied in this paper.

Let $\hat{\varvec{A}}_{k}^l$ be the estimation of ${\varvec{A}}_{k}^l$ at the receiver, $k\in [1:2]$. It is assumed that the entries of $\hat{\varvec{A}}_{k}^l$ are also complex Gaussian RVs. Similar to¹⁰, the channel estimation model is given by

$$\begin{aligned} \hat{\varvec{A}}_{k}^l={\varvec{A}}_{k}^l+\varvec{e}_{k}^l \end{aligned}$$

(10)

where $\varvec{e}_{k}^l$ is the channel estimation error vector, where $\varvec{e}_{k}^l=[e_{k,1}^l \cdots e_{k,N_r}^l]^T$. Each entry $e_{k,m}^l, m\in [1:N_r]$ of $\varvec{e}_{k}^l$ also is a complex Gaussian RV distributed as $CN(0,\sigma _{e}^2)$.

From (10), it is seen that $e_{k,m}^l$ in the channel estimation model is a parameter to measure the quality of the channel estimation. The smaller the value of $e_{k,m}^l$, the more accurate the channel estimation.

The signal detection algorithm with imperfect CSI estimation is the same as the one with perfect CSI in previous subsection except for replacing $\hat{\varvec{A}}_{1}^l$ with ${\varvec{A}}_{1}^l$ and $\hat{\tilde{{\varvec{A}}}}_{2}^l$ with $\tilde{\varvec{A}}_{2}^l$, where $\hat{\tilde{{\varvec{A}}}}_{2}^l=e^{j\theta _5^l(p)}\times {\hat{\varvec{A}}_{2}^l}$

Error performance analysis of the RIS-Alamouti and N-RIS-Alamouti schemes

Error performance of the RIS-Alamouti scheme

The error performance of the RIS-Alamouti has been analyzed in³. The average symbol error probability (ASEP) $P_e^s$ of MPSK for the RIS-Alamouti with one receive antenna is given in (9) of³. For the RIS-Alamouti scheme with $N_r$ independent receive antennas, (9) of the ASEP in³ is easily modified as:

$$\begin{aligned} P_e^s=\frac{1}{\pi }{\int _0^{(M-1)\pi /M}{\left( \frac{1}{1+\left( \frac{\sin (\pi /M)^2}{\sin (\eta )^2}\frac{P_L LE_s}{2N_0}\right) }\right) ^{2N_r}}}d\eta . \end{aligned}$$

(11)

However, (11) is not a closed-form expression. In the following discussion, we apply the trapezoidal rule to (11) to yield a closed-form expression for the ASEP. Applying the trapezoidal rule into (11), we have:

$$\begin{aligned} P_e^s=\frac{b}{n\pi }\left[ \frac{f\left( b\right) }{2}+\sum _{k=1}^{n-1}{f\left( \frac{b}{n}k\right) }\right] , \end{aligned}$$

(12)

where $f(x)={\left( {1+\left( \frac{\sin (\pi /M)^2}{\sin (\eta )^2}\frac{P_L LE_s}{2N_0}\right) }\right) ^{-2N_r}}$ and $b=\frac{(M-1)\pi }{M}$.

Finally, the ABEP $P_e^b$ is approximately given as:

$$\begin{aligned} P_e^b\approx \frac{P_e^s}{\log _2M}. \end{aligned}$$

(13)

Lower error probability Bound of the N-RIS-Alamouti scheme

The lower error probability bound of the N-STBC Alamouti without the Golden codeword has been discussed in⁵. In⁵, the phase component $e^{j\theta _5^l(p)}$ of the fading channel is treated as an interference. Following the same approach, $e^{j\tilde{\theta }_{2l}}=e^{j\theta _5^l(p)}\times {e^{j\theta _{2l}}}$ and $e^{j\tilde{\theta }_{2l-1}}=e^{j\theta _5^l(p)}\times {e^{j\theta _{2l-1}}}$ in (5.1) and (5.2) can be written as $e^{j\theta _{2l}}+\epsilon _1$ and $e^{j\theta _{2l-1}}+\epsilon _2$, respectively. Then (5.1) and (5.2) are rewritten as:

$$\begin{aligned} \tilde{r}_{1,k}^l&=e^{j\theta _{2l-1}}A_{1,k}^{l}+{e^{j\theta _{2l}}A_{2,k}^{l}}+\hat{n}_{1,k}^l, \end{aligned}$$

(14.1)

$$\begin{aligned} \tilde{r}_{2,k}^l&=-e^{-j\theta _{2l}}A_{1,k}^{l}+{e^{-j\theta _{2l-1}}A_{2,k}^{l}}+\hat{n}_{2,k}^l, \end{aligned}$$

(14.2)

where $\hat{n}_{1,k}^l=\tilde{n}_{1,k}^l+{\epsilon _1}\times {A_{2,k}^{l}}$ and $\hat{n}_{2,k}^l=\tilde{n}_{2,k}^l+{\epsilon _2}\times {A_{2,k}^{l}}$.

(14.1) and (14.2) are equivalent to the conventional Alamouti transmission. In (14.1) and (14.2), both $\epsilon _1$ and $\epsilon _2$ are RVs. If the CSI is known at the receiver, both ${\epsilon _1}\times {A_{2,k}^{l}}$ and ${\epsilon _2}\times {A_{2,k}^{l}}$ are also RVs, which may be regarded as additional noise components. Compared to the conventional Alamouti transmission, (14.1) and (14.2) have additional noise components which are caused by the pair of STLD NPSK symbols. So the error probability of the RIS-Alamouti scheme is the lower error probability bound of the N-RIS-Alamouti scheme.

Numerical results

In this section, we present the simulated bit error rate (BER) vs. SNR results for the proposed N-RIS-Alamouti scheme in the quasi-static Rayleigh fading channel with AWGN as described in Section System model. The ABEP is calculated based on (13). The setups and the pathloss models in the N-RIS-Alamouti scheme, are the same as the ones in³. We set $r_s=1$ m and $r_d=9$ m. The pathloss gain is calculated based on (4). It is also assumed that the CSI is fully known at the receiver. The legend, (MPSK, L, $N_r$) N-RIS-Alamouti, in all figures of this section denotes the N-RIS-Alamouti with MPSK, L reflector elements and the number of receive antennas $N_r$ at the destination. (MPSK, L, $N_r$) 1-RIS-Alamouti stands for the RIS-Alamouti proposed in³. The legend BER denotes the simulated BER. The legend $\beta$ denotes the spectral efficiency which is defined as the number of bits transmitted per antenna per transmission time slot. Finally, the legend “w/o L” stands for N-RIS-Alamouti scheme without STLD NPSK symbols, $e^{j\theta _5^1(p)}=e^{j\theta _5^2(p)}$.

In all simulations, the constellation mappers for 16PSK is shown in Fig. 1 of Section System model. The constellation mappers for 32PSK and 64PSK are shown in Figs. A1 and A2, respectively, in the Appendix. Actually, the second constellation mapper of 64PSK is easily derived from Fig. A2. Let the second mapper of 64PSK be $\Phi _{64}$ and the second mapper of 128PSK be $\Phi _{128}$. In this paper, the second constellation mapper of 128PSK $\Phi _{128}$ is derived from the second constellation mapper $\Phi _{64}$ of 64PSK, which is given by:

$$\begin{aligned} \Phi _{128}(1:64)&=\Phi _{64}, \end{aligned}$$

(15.1)

$$\begin{aligned} \Phi _{128}(65:128)&=64+\Phi _{64}. \end{aligned}$$

(15.2)

Similarly, the second constellation mapper $\Phi _{256}$ of 256PSK is easily derived from $\Phi _{128}$.

Error performance of the RIS-Alamouti

In this subsection, we present the error performance of the RIS-Alamouti schemes with $N_r$ receive antennas. The simulation results and theoretical ABEP given by (13) are shown in Fig. 3 for 16PSK and 64PSK with $N_r=2$, respectively.

Fig. 3

Validation of the BER vs. SNR for the RIS-Alamouti scheme.

From Fig. 3, as expected it is seen that the theoretical ABEP given by (13) matches the simulated BER very well below the BER of $10^{-2}$ .

RIS-Alamouti vs N-RIS-Alamouti

In this subsection, we compare the N-RIS-Alamouti scheme with the RIS-Alamouti scheme in terms of the bit error performance and spectral efficiency. The simulation results are shown in Figs. 4 and 5 for 16PSK and 64PSK, respectively. In this subsection, we set $N_r=2$. From Fig. 4, it is observed that the 32-RIS-Alamouti scheme with 16PSK achieves the error performance of the 1-RIS-Alamouti scheme for two different surface sizes, $L=64$ and $L=256$. However, the spectral efficiency of the 32-RIS-Alamouti scheme with 16PSK is 2.625, while the spectral efficiency of 1-RIS-Alamouti scheme with 16PSK is 2.

Based on (3.1) and (3.2), the ratio of the equivalent channel variance between (16PSK,256,2) N-RIS-Alamouti and (16PSK,64,2) N-RIS-Alamouti is 4, which makes the (16PSK,256,2) N-RIS-Alamouti with 16PSK achieve an SNR gain of 6 dB compared to (16PSK,64,2) N-RIS-Alamouti. This is validated in Fig. 4. Similar results are observed from Fig. 5 for the N-RIS-Alamouti scheme with 64PSK.

In this subsection, we further demonstrate the N-RIS-Alamouti schemes without STLD NPSK symbols, $e^{j\theta _5^1(p)}=e^{j\theta _5^2(p)}$. From Figs. 4 and 5, it is seen that the error performance of the N-RIS-Alamouti schemes with STLD NPSK symbols $(e^{j\theta _5^1(p)}, {e^{j\theta _5^2(p)}})$ achieves an SNR gain of 2 dB compared to the N-RIS-Alamouti schemes without STLD NPSK symbols. So the N-RIS-Alamouti with STLD NPSK symbols also achieves labelling diversity.

Fig. 4

BER vs. SNR of the N-RIS-Alamouti with $N_r$ and 16PSK.

Fig. 5

BER vs. SNR of the N-RIS-STLD with $N_r$ and 64PSK.

N-RIS-Alamouti order N vs. the number of receive antennas

In this subsection, we investigate how the number of receive antennas affects the order N of the N-RIS-Alamouti scheme. In all simulations, we set $L=64$. The simulated BERs of the N-RIS-Alamouti schemes with 16PSK and 64PSK for different $N_r$ are shown in Fig. 6 and 7, respectively. From Fig. 6, it is seen that the 32-RIS-Alamouti scheme, not the 64-RIS-Alamouti, with 16PSK matched the error performance of 1-RIS-Alamouti for $N_r=2$ at high SNRs. However, 64-RIS-Alamouti with 16PSK also achieves the error performance when the number of receive antennas is increased to $N_r=3$ for the 1-RIS-Alamouti. Similarly, it is observed from Fig. 7 that the 128-RIS-Alamouti and 256-RIS-Alamouti with 64PSK match the error performance of the 1-RIS-Alamouti at high SNRs for $N_r=2$ and $N_r=3$, respectively. So the achievable order N of the N-RIS-Alamouti scheme increases as the number of receive antennas increases.

Fig. 6

BER vs. SNR of the N-RIS-Alamouti with $N_r$ and 16PSK.

Fig. 7

BER vs. SNR of the N-RIS-STLD with $N_r$ and 64PSK.

Hence, larger orders, i.e. spectral efficiencies, can be achieved as $N_r$ increases.

N-RIS-Alamouti with perfect CSI vs. N-RIS-Alamouti with imperfect CSI

In this subsection we take N-RIS-Alamouti scheme with $N=1$ and $N=32$ for 16PSK and $N_r=2$ as examples to investigate how the imperfect CSI affects the error performance of the N-RIS-Alamouti scheme. In our simulations we set $L=256$. The simulated BERs of the N-RIS-Alamouti schemes with 16PSK and $N_r=2$ for different estimated $\sigma _e^2$ are shown in Fig. 8.

Fig. 8

BER of the N-RIS-STLD with $N_r=2$ and 16PSK vs $\sigma _e^2$

From Fig. 8 it is seen that:

• In the systems, N-ary RIS-Alamouti scheme imperfect CSI estimation results error floor at high SNRs;

• The smaller the variance of the channel information estimation error the lower the error floor.

• The error performance will not show error floor for perfect channel estimation.

Conclusion

In this paper, the N-ary RIS-Alamouti scheme was proposed. In the proposed N-RIS-Alamouti scheme, the additional information bits were conveyed by a pair of STLD NPSK symbols. The pair of STLD NPSK symbols was further merged into one channel’s phase component. Compared to the RIS-Alamouti scheme, the proposed N-RIS-Alamouti scheme not only preserves the error performance of the RIS-Alamouti scheme but also enhances its spectral efficiency. Simulation results showed that the achievable order N of the N-RIS-Alamouti scheme increases as the number of receive antennas increases allowing significantly large spectral efficiencies to be achieved. For example, at a BER of $2\times {10^{-5}}$, the proposed 256-RIS-Alamouti with 64PSK and 64 reflector elements achieve the error performance of the RIS-Alamouti for three receive antennas. Equivalently, an additional 8 bits are transmitted in four time slots.