Introduction

Everyday life involves numerous decision-making scenarios, particularly when selecting the optimal policy from various evaluation criteria1,2,3,4. This process often requires analyzing which criteria are most critical and then employing the AHP5,6 a fundamental MCDM technique, to determine the best approach for criteria analysis7,8,9,10. The AHP is a widely used technique that helps DM evaluate options based on multiple factors11,12,13,14,15. Developed in the 1970s, AHP has gained widespread adoption due to its comprehensive and logical approach. The AHP framework involves the following steps:

  • Hierarchical Problem Organization: The DM must structure the problem hierarchically, breaking it into goals, criteria, and alternatives.

  • Pairwise Comparisons: Pairwise comparisons between criteria and alternatives are conducted to create a judgment matrix.

  • Consistency Testing: It is necessary to evaluate and modify the judgement matrix’s consistency until satisfactory

  • Synthesis of Comparisons: The process synthesizes comparisons across layers to obtain the final weights of the alternatives.

An AHP user employs pairwise comparisons using the discrete 9-value scale method developed by Saaty16, resulting in a recognized Pairwise Weighting Matrix (PWM). This systematic approach ensures a rational and structured decision-making process.

Despite its widespread use, AHP has faced criticism because DMs often struggle to produce rigorously consistent comparisons17. This issue becomes particularly challenging when dealing with multiple criteria and alternatives. To address the problem, Saaty18 introduced the Consistency Ratio (CR), which indicates the likelihood that the matrix ratings result from random chance.

Saaty set the threshold of the Consistency Ratio (CR) at 0.1, and19 discusses the rationale for deeming this threshold satisfactory. Consequently, changing an inconsistent comparison matrix becomes an essential and intriguing process. To convert inconsistent comparison matrices into consistent ones, there are two standard methods:

  1. (1)

    Re-evaluation of the Comparison Matrix: In this method, the decision-makers (DMs) adjust the values of the comparison matrix during re-evaluation. The process requires them to reassess and provide new judgments to establish updated matrix values. However, this method does not guarantee consistency and often requires iterative adjustments until uniformity is achieved.

  2. (2)

    Modification of the Original Matrix: This approach involves systematically modifying the original Matrix using specific techniques to satisfy the consistency criteria. Researchers have proposed various methods for adjusting inconsistent matrices, including strategies for resolving multiplicative preference inconsistencies11,20,21,22,23,24,25.

These approaches aim to improve consistency and enhance the credibility of the PCM in decision-making processes.

This article introduced a novel distance formula based on the Cosine Distance metric. This effort drew inspiration from the effectiveness of cosine similarity matching in speaker authentication26,27,28,29. Notably, the authors30 demonstrated that in GMM-supervector space, cosine distances are more accurate than Euclidean distances. Additionally, researchers have successfully evaluated the effectiveness of cosine distance for speaker diarization using the CallHome telephone corpus31,32.

Building on this foundation, we propose a cosine distance formula combined with the Grey Wolf Optimization Algorithm to address and repair inconsistencies in the PCM.

We propose the GWO algorithm33,34,35 to find a replacement matrix that satisfies the consistency test while remaining as close as possible to the basic Pairwise Comparison Matrix (PWM). Researchers have effectively modified this algorithm to tackle non-differentiable optimization issues, where the search space is continuous and lacks gradient information. We refer to this process as GWO-AHP.

GWO is one of the latest SI-based algorithms, proposed by Mirjalili36 in 2014. The GWO algorithm models the behaviour of grey wolves in nature to find the optimal path for hunting prey. It employs a natural technique that organizes a pack of wolves into different roles according to their hierarchical structure37. The roles of the wolves, which guide the hunting process, define the GWO pack’s four groups: Alpha, Beta, Delta, and Omega, with Alpha being the best hunting option available.

In the initial GWO study, the population was divided into four groups to replicate the natural leadership structure of grey wolves. Extensive testing by the algorithm’s designers revealed that incorporating four groups yielded the best average performance on benchmark problems and on a set of low-dimensional real-world case studies.

The GWO search technique, similar to previous SI-based algorithms, begins by generating an arbitrary group of grey wolves. The four wolf groupings are then identified based on their positions and distances from the desired prey. Each wolf, updated during the search process, represents a potential solution. Furthermore, GWO employs critical operations governed by two factors to balance exploration and exploitation while avoiding stagnation in local optima.

GWO has a distinct mathematical foundation, although it shares similarities with other population-based techniques for finding the global optimum. It mimics the movement of solutions around one another in an n-dimensional search space, analogous to how grey wolves naturally pursue and encircle their prey. Unlike PSO, which uses both position and velocity vectors, GWO requires only one position vector, reducing memory requirements. Additionally, while PSO tracks the best solution for each particle and the overall best solution, GWO retains only the top three solutions.

This article is organized as follows: The next section presents the inconsistency of the PCM. Section 2.1 defines the objective of reducing PCM inconsistency, followed by Sect. 2.2, which introduces the inconsistency correction of PCM using cosine distance. Section “Objective to reduce the inconsistency of PCM” details the PCM inconsistency repair using the GWO algorithm, with Section “Inconsistency correction of PCM by cosine distance” defining the Grey Wolf Optimization algorithm. Section “Main results and analysis” discusses the results, including examples in Section “Special case: PCM of order 6 with”. The performance analysis of GWO examines the PCM of order 6 for the special case matrix. Finally, the study uses graphs and tables to compare GWO with PSO and ANTAHP.

Inconsistency of the pairwise comparison matrix

One of the most essential aspects individuals face is making sensible decisions, as these decisions impact not only their own future but also the futures of others. Researchers have proposed several decision-making strategies that aim to replicate similar processes to assist people in making informed choices. Thomas Saaty developed the AHP, a MCDM approach that has been extensively studied and applied across various industries38. In addition to aiding decision modelling, this method includes a consistency ratio (CR), which serves as a critical acceptance-rejection criterion for the PCM. DMs use it to determine whether to accept or reject judgments.

A mathematical framework that combines pairwise comparisons is called a PCM. Formally, a PCM is a positive reciprocal matrix \(A= {\left({a}_{ij}\right)}_{n\times n}\), here \({a}_{ij }>0\) represents the unbiased evaluation of the ratio of \({w}_{i}\) to \({w}_{j}\). Keep in mind that \({a}_{ii}=1 \forall i\) and \(a_{ij} = 1/a_{ji} \forall i,j\) are assumed to be true. Thus, the construction of a PCM is as follows:

$$A = \left\{ {\begin{array}{*{20}l} {a_{11} } \hfill & {a_{12} } \hfill & {..} \hfill & {..} \hfill & {..} \hfill & {a_{1n} } \hfill \\ {a_{21} } \hfill & {a_{22} } \hfill & {..} \hfill & {..} \hfill & {..} \hfill & {a_{2n} } \hfill \\ . \hfill & . \hfill & . \hfill & {} \hfill & {} \hfill & . \hfill \\ . \hfill & . \hfill & {} \hfill & . \hfill & {} \hfill & . \hfill \\ . \hfill & . \hfill & {} \hfill & {} \hfill & . \hfill & . \hfill \\ {a_{n1} } \hfill & {a_{n2} } \hfill & {..} \hfill & {..} \hfill & {..} \hfill & {a_{nn} } \hfill \\ \end{array} } \right\}$$
(2.1)

Since \({\lambda }_{max}\) is the principal eigenvalue of the reciprocal PCM of \(n\times n\), the consistency index can be computed in the following manner:

$$CI= \frac{{\lambda }_{\text{max}}-n}{n-1}$$
(2.2)

Saaty showed that a DM is completely consistent if

$${a}_{ij}.{a}_{jk}={a}_{ik} \forall i,j,k=1, 2, 3, \dots \dots n, {\lambda }_{\text{max}}=n$$
(2.3)

Additionally, if the person making the decisions is not perfectly consistent, then

$${\lambda }_{\text{max}}>n.$$
(2.4)

According to Saaty, the consistency ratio is

$$CR=\frac{CI}{RI}$$
(2.5)

The average value of \(CI\) derived by positive reciprocal PCM is denoted by \(RI\), which represents random processes generated using a scale of 1 to 9. Table 1 displays the average RI for different values of n39.

Table 1 The Random index by saaty.
Full size table

According to Saaty, a DM shows sufficient consistency if their CR value is less than 0.10. We do this to guarantee that perturbations cover only one order of magnitude. Experts also recognize that organizations cannot achieve novel ideas if the CR threshold is too low18.

Objective to reduce the inconsistency of PCM

The objective function for creating the modified PWM from the original depends on two crucial factors. The consistency ratio rate comes first. One attains perfect consistency when the maximum eigenvalue equals the number of criteria/size of matrices \(\left({\lambda }_{max}=n\right)\), occurs when \(CR=0\).1, the initial goal is to minimize CR. However, we only pursue CR at a rate of less than 0.1. The second is to reduce the difference between the modified and original Matrix. Maintaining the original judgment requires keeping modified matrices close to their original matrices. There are several other ways to calculate the distance between two matrices, including the square distance, the root mean square error, and the Hamming distance between two genotypes. The distance between two matrices is measured in this study using the Cosine Distance (\({d}_{cosine}).\) The reason \({d}_{cosine}\) is preferred in this study is because, as40,41 mentioned, when classifying data with comparable features, the term “similarity” refers to the actual similarities and is frequently employed. Utilizing similarity measures can help increase the accuracy of information retrieval by determining how similar two objects are. If two matrices are the same, \({d}_{cosine}\) will be zero; if \({d}_{cosine}\) is smaller, it means that the two matrices are more similar.

Inconsistency correction of PCM by cosine distance

When using AHP to establish criterion weights, it is necessary to address inconsistencies. Experts often recommend three corrective measures to reduce inconsistency: First, identify the judgment that exhibits the highest inconsistency. Second, specify the parameters needed to amend the decision. Third, request committee members to revise their evaluations. You might need to repeat these steps multiple times to achieve satisfactory results.

The objective is to create a modified matrix that meets the consistency criteria while preserving the experts’ original judgments. Since the PCM is reciprocal, the decision variables in the optimization model are the elements of the Matrix’s lower triangle, which range from 1/9 to 9.

There are numerous techniques to quantify the distance between the substitute matrix and the original Matrix; this article employs the following cosine distance metric:

Cosine Distance = 1 − Cosine Similarity.

To calculate the cosine similarity, divide the vectors’ dot product by their magnitudes’ product:

$$\text{Cosine} \text{Similarity}= \frac{\sum_{i,j=1}^{n}\left({a}_{ij}.{b}_{ij}\right)}{\sqrt{\sum_{i,j=1}^{n}{({a}_{ij})}^{2}}\sqrt{\sum_{i,j=1}^{n}{({b}_{ij})}^{2}}}$$

where \({a}_{ij}\) are the elements of the original matrix A, \({b}_{ij}\) are the elements of the modified matrix B.

The result of the cosine similarity ranges between.

  • The vectors are directed in the same direction when the value is 1.

  • The vectors are orthogonal if the value is 0.

  • The vectors are pointing in opposing directions when the value is -1.

Cosine similarity derives from cosine distance. The cosine distance is defined as

$${d}_{\text{cosine}}({a}_{ij},{b}_{ij})= 1-\frac{\sum_{i,j=1}^{n}\left({a}_{ij}.{b}_{ij}\right)}{\sqrt{\sum_{i,j=1}^{n}{({a}_{ij})}^{2}}\sqrt{\sum_{i,j=1}^{n}{({b}_{ij})}^{2}}}$$
  1. 1.

    The cosine distance is zero when the vectors are equal, or the cosine similarity is one.

  2. 2.

    The cosine distance is one when the cosine similarity is zero (the vectors are orthogonal).

  3. 3.

    The cosine distance is two when the cosine similarity is -1, meaning that the vectors point in opposing directions.

The objective function aims to minimize the distance between the modified matrix B and the original Matrix A while improving consistency by bringing the principal eigenvalue closer to the number of comparison elements. The objective function value (OFV) incorporates these two elements in the following form:

$$OFV={d}_{\text{cosine}}({a}_{ij},{b}_{ij})+ {\lambda }_{\text{max}}-n$$
(2.6)

s.t

$$\frac{1}{9} \le {a}_{ij }\le 9$$
(2.7)
$${a}_{ij}= \frac{1}{{a}_{ji}}$$
(2.8)
$${a}_{ii}=1$$
(2.9)
$$\left|{a}_{ij}-{b}_{ij}\right|\le \epsilon$$
(2.10)

where \({a}_{ij}\) are the elements of the original matrix A, \({b}_{ij}\) are the elements of the modified matrix B, and \(n\) is the order of the Matrix.

The maximum difference range for the 1–9 scale is set at \(\epsilon =\) 2.0. This parameter controls the range of possible differences for each PCM judgement. To boost the chance of a successful correction, we can adjust the value of \(\epsilon\) based on the DM’s preference level. In certain exceptional cases, where the CR value is significantly higher, we cannot correct the CR to be less than 0.1 for a bit of \(\epsilon\).

PCM inconsistency repairing by the GWO algorithm

The repair procedure utilizes the cosine distance formula and the GWO algorithm to address the inconsistent PCM. Since cosine distance focuses on vector direction rather than magnitude, it is a highly effective distance metric for high-dimensional or sparse datasets. The GWO method, a swarm intelligence (SI) technique, begins the optimization process with arbitrary solutions. Each solution includes a vector that keeps the problem’s parameter values constant. Every iteration starts by calculating the objective value for each solution. As a result, the desired value is stored in a single variable linked to each solution.

In 2014, Mirjalili36 presented the GWO algorithm. It adheres to the grey wolf (Canis lupus) pursuit strategy and leadership hierarchy. Being gregarious, grey wolves once lived in packs of five to twelve. Alpha (α), beta (β), delta (δ), and Omega (ω) are the four varieties of grey wolves into which the entire group can divide. In the pack’s social hierarchy, Alpha is the most significant rank, and Omega is the next lowest level. Alpha is the term for the male or female leader of a pack of grey wolves42. The leader wolf chooses hunting, sleeping locations, and other matters, and the pack must abide by them. Both male and female Betas are subordinate wolves to the Alpha, and they are most likely the best choice to take the place of an alpha in the event of an alpha wolf’s ageing or death. Betas are in charge of upholding discipline in the prey and reiterating the Alpha’s orders.

Additionally, they provide the Alpha with feedback. The grey wolf rating places Omega at the bottom. The final wolves permitted to consume are these. A wolf who is neither an \(\alpha\), \(\beta\), nor \(\omega\) is called a delta (\(\delta\)) (or subordinate) wolf. Although inferior to \(\alpha\) and \(\beta\), \(\delta\) wolves rule \(\omega\).

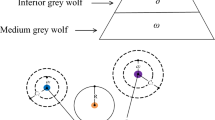
Group hunting is another fascinating social trait of grey wolves, in addition to their social structure. Figure 1 illustrates the primary stages of hunting by grey wolves37:

Fig. 1
figure 1

Grey wolf hunting mechanism.

Full size image

Chasing and surrounding is the initial stage of hunting. GWO uses two points in an n-dimensional space to express this mathematically. It adjusts one point’s location dependent on another. To replicate this, the equation below is suggested:

$$X\left(t+1\right)=X\left(t\right)-A\cdot D$$
(3.1)

In this equation, \(X\left(t+1\right)\) represents the wolf’s next location, \(X\left(t\right)\) Represents its present position, \(A\) is a coefficient matrix, and \(D\) is a vector based on the prey’s position. \(\left({X}_{p}\right)\), determined as follows:

$$D=\left|C\cdot {X}_{p}\left(t\right)-X\left(t\right)\right|$$
(3.2)

where

$$C=2 \cdot {r}_{2}$$
(3.3)

It is essential to notice that the vector \({r}_{2}\) is generated randomly from the interval [0,1]. These two formulas allow one solution to go around another. Because the equations use vectors, we can apply them to any dimension. Figure 2 illustrates a possible grey wolf location for a prey item.

Fig. 2
figure 2

Encircling mechanism of grey wolves.

Full size image

The above equations’ random elements replicate the various step sizes and wolf movements. Equations defining their values are as follows:

$$A=2a \cdot {r}_{1}-\text{a}$$
(3.4)

a is a vector whose value drops directly from 2 to 0 throughout the run. The vector \({r}_{1}\) It generates at random from the interval [0,1].

In GWO, the three best solutions in the population \(\alpha\), \(\beta\), and \(\delta\) —are assumed to have a reasonable estimate of the location of the global optimum for optimization problems, even though the exact location is unknown. Keeping this in mind, the other wolves must adjust their positions as described below:

$$X\left(t+1\right)=\frac{\left({X}_{1}+{X}_{2}+{X}_{3}\right)}{3}$$
(3.5)

where \({X}_{1},\) \({X}_{2}\) and \({X}_{3}\) are calculated with the help of the following Eq. (3.6).

$$\begin{gathered} X_{1} = X_{\alpha } \left( t \right) - A_{1} .D_{\alpha } \hfill \\ X_{2} = X_{\beta } \left( t \right) - A_{2} .D_{\beta } \hfill \\ X_{3} = X_{\delta } \left( t \right) - A_{3} .D_{\delta } \hfill \\ \end{gathered}$$
(3.6)

where \({D}_{\alpha }\), \({D}_{\beta }\) and \({D}_{\delta }\) are calculated with the help of the following Eq. (3.7).

$$\begin{gathered} D_{\alpha } = \left| {C_{1} .X_{\alpha } - X} \right| \hfill \\ D_{\beta } = \left| {C_{2} .X_{\beta } - X} \right| \hfill \\ D_{\delta } = \left| {C_{1} .X_{\delta } - X} \right| \hfill \\ \end{gathered}$$
(3.7)

In a two-dimensional search space, Fig. 3 illustrates how a search agent modifies its position based on \(\alpha\), \(\beta\) and \(\delta\). As shown, the final position would be randomly located within a circle defined by the \(\alpha\), \(\beta\) and \(\delta\) positions in the search space. In other words, the \(\alpha\), \(\beta\) and \(\delta\) wolves determine the prey’s location, while the other wolves adjust their positions sporadically relative to the prey.

Fig. 3
figure 3

Position updating in Grey Wolf Optimization.

Full size image

The GWO algorithm regularly updates the results using Eqs. (3.5–3.7). Before computing \(\alpha , \beta\) and \(\delta\), you should determine the difference between the current solution and these values using Eq. (3.6). Next, confirm the contributions of \(\alpha\), \(\beta\) and \(\delta\) to the solution’s location update using Eq. (3.7). Regardless of the outcomes’ objective value or locations, GWO’s key governing variables (A, C, and a) are updated prior to the location updates.

The primary objective of exploitation is to refine the potential solutions found during the exploration stage by evaluating the neighbourhood of each solution. For the solutions to converge toward the global optimum, GWO must make minor adjustments. The main challenge in this context is the balance between exploration and exploitation. Therefore, to accurately estimate the global optimum of a particular problem during optimization, an algorithm must be capable of managing and reconciling these competing properties. Exploration primarily relies on the GWO regulating parameter, variable \(C\). This parameter always yields a value between 0 and 2, influencing the prey’s contribution to determining its following location. The influence becomes larger when \(C<1\), causing the solution to move closer to the prey. Since this option produces random values independent of the number of iterations, exploration takes precedence over exploitation if local optima become stagnant.\(a\) is an additional regulating parameter that encourages research, which decreases linearly from 2 to 0. The range of variable \(A\) swings between the range of \(\left[-2, 2\right]\) because of its arbitrary components. Prioritizing exploitation occurs when \(1<A<1\), whereas encouraging exploration occurs when \(A>1\) or \(A<1\), as shown in Fig. 4. Figure 5 shows the pseudo code for the GWO algorithm.

Fig. 4
figure 4

Attacking prey versus searching for prey.

Full size image
Fig. 5
figure 5

Gray Wolf Optimization Algorithm’s Pseudo code.

Full size image

Main results and analysis

The proposed Cosine Distance Formula and GWO algorithm can be applied to real-world applications to address the inconsistency of the PCM. In Section “Illustrative examples”, this proposed solution uses various matrices to correct the PCM’s inconsistency. We also apply the proposed method in Section “Special case: PCM of order 6 with” to a highly inconsistent specific matrix, briefly discussing its convergence history with figures and tables to illustrate the significance of the convergence level of the suggested method. Additionally, we compare the proposed methodology with well-known algorithms, such as PSO and Ant Colony Optimization (ACO).

Illustrative examples

In this section, we use examples from widely published relevant articles to illustrate the implementation of the proposed framework and compare the results.

Example 1

PCM of order 4 with \(\epsilon =2\)

The first PCM from43 represents the Matrix of pairwise preference ratios for four criteria considered essential for constructing the National Laboratory Animal Centre. The criteria are: Price (C1), Organization (C2), Technical Score (C3), and Question and Answer (Q&A) (C4). The original PCM is illustrated below in Table 2. The original PCM (Table 2) has \(CR=0.14\) and \({\lambda }_{\text{max}}=4.38\).

Table 2 The original Matrix of order 4.
Full size table

We apply the proposed GWO algorithm using the selected control parameter set for 300 iterations. The GWO procedure runs ten consecutive times to execute the repair shown in Table 2. We then select the run that provides the best value for optimizing the objective function. We set the swarm size to 30.

Analyses the substitute matrix with the original Matrix, the original PWM has \({\lambda }_{max}=4.38\) and \(CR=0.14\). In contrast to the Table. 3, the substitute PWM resulted in \({\lambda }_{max}=4.027912 CR= 0.010338\), and the Optimization Best Fitness value = 0.066072. Comparing the original and substitute matrices, the difference between the original and substitute matrices is 0.038160. using the GWO algorithm with \(\epsilon =2\), the mean and S.D. of the corrected terms are 0.71 and 0.93, respectively.

Table 3 Substitute the Matrix of order 4.
Full size table

Table 4 shows the results of running this algorithm ten times for the initial matrix A. The standard deviation (S.D.) and mean of the correction elements, CR, and OFV are minimal, and Table 4 shows that all ten runs were successful. Figure 6 shows the optimized best value for the minimum CR and the difference between the original and substituted Matrix.

Table 4 Results of ten algorithm runs on the initial matrix A (Order 4), showing minimal standard deviation and mean values for the corrected elements, Consistency Ratio (CR), and Objective Function Value (OFV).
Full size table
Fig. 6
figure 6

3D plot of the Difference term, CR and OFV for the Substitute Matrix of order 4.

Full size image

Example 2

PCM of order 5 with \(\epsilon =2\)

The second PCM from43 represents the Matrix of pairwise preference ratios for five criteria. The Original PCM is illustrated below in Table 5. The original PCM (Table 5) has \(CR=0.330499\) and \({\lambda }_{\text{max}}=6.480636\).

Table 5 Original Matrix of order 5.
Full size table

We use the chosen control parameters to apply the GWO algorithm for 300 iterations. We run the GWO procedure consecutively ten times to perform the repair shown in Table 5. We then select the run that provides the best value for optimizing the objective function. We set the swarm size to 30.

On analyzing the original and substitute matrices, the original PWM has \({\lambda }_{max}=6.480636\) and \(CR=0.330499\). In contrast to the Table 6, the substitute PWM resulted in \({\lambda }_{max}= 5.242061\) and \(CR=0.054032\), and the Optimization Best Fitness value = 0.285249. Comparing the original and substitute matrices, the difference between the original and substitute matrices is 0.043188. using the GWO algorithm with \(\epsilon =2\), the mean and S.D. of the corrected terms are 1.30 and 0.87, respectively.

Table 6 Substitute the Matrix of order 5.
Full size table

“Supplementary Table S1” shows the results of running this algorithm ten times on the initial matrix A. The S.D. and mean of the correction elements, CR, and OFV are minimal, and “Supplementary Table S1” indicates that all ten runs were successful. Figure 7 displays the optimized best value for the minimum CR and the difference between the original and substituted Matrix.

Fig. 7
figure 7

3D plot of the Difference term, CR and OFV for the Substitute Matrix of order 5.

Full size image

Example 3

PCM of order 8 with ε = 2.

The Third PCM from43 represents the pairwise preference ratio matrix for five criteria. The Original PCM is illustrated below in Table 7. The original PCM (Table 7) has \(CR=0.169213\) and \({\lambda }_{\text{max}}=9.670136\).

Table 7 Original Matrix of order 8.
Full size table

We apply the GWO algorithm using the selected control parameters for 300 iterations. The GWO algorithm runs ten consecutive times to perform the repair shown in Table 7. We then select the run that provides the best value for optimizing the objective function. We set the swarm size to 30.

On analyzing the original and substitute matrices, the original PWM has \({\lambda }_{\text{max}}=9.670136\) and \(CR=0.169213\). In contrast to Table 8, the substitute PWM results in \({\lambda }_{\text{max}}=8.223738\) and \(CR=0.022668\), and the Optimization Best Fitness value = 0.274920. Comparing the original and substitute matrices, the difference between the original and substitute matrices is 0.252252. using the GWO algorithm with \(\epsilon =2\), the mean and S.D of the corrected terms are 0.93 and 0.78, respectively.

Table 8 Substitute the Matrix of order 8.
Full size table

“Supplementary Table S2” shows the results of running this algorithm ten times on the initial matrix A. The standard deviation and mean of the correction elements, CR, and OFV are minimal, and “Supplementary Table S2” indicates that all ten runs were successful. Figure 8 displays the optimized best value for the minimum CR and the difference between the original and substituted Matrix.

Fig. 8
figure 8

3D plot of the Difference term, CR and OFV for the Substitute Matrix of order 8.

Full size image

Special case: PCM of order 6 with \({\varvec{\epsilon}}=3.0.\)

At the same time, there are some highly inconsistent matrices, like the Matrix \(A\) used in43 with \(CR= 0.546487\). We cannot find a satisfactory solution using this GWO to correct with \(\upepsilon =2.0\). So, we take \(\upepsilon =3.0\) to perform the GWO algorithm on Matrix \(A\). The Original PCM is illustrated below in Table 9. The original PCM (Table 9) has \(CR=0.546487\) and \({\lambda }_{\text{max}}=9.388221\).

Table 9 Original Matrix of order 6.
Full size table

We apply the GWO algorithm using the selected control parameters for 300 iterations. The GWO algorithm runs ten consecutive times to perform the repair shown in Table 9. We then select the run that provides the best value for optimizing the objective function. We set the swarm size to 30.

Analyzing the original and substitute matrices, the original PWM has \({\lambda }_{max}=9.388221\), and \(CR=0.546487\). In contrast to Table 10, the substitute PWM resulting in \({\lambda }_{max}=6.455061\) and \(CR=0.073397\), and the Optimization Best Fitness value = 0.581101. Comparing the original and substitute matrices, the difference between the original and substitute matrices is 0.126040. using the GWO algorithm with \(\epsilon =3\), the mean and S.D of the corrected terms are 1.4844 and 1.2125, respectively.

Table 10 Substitute the Matrix of order 6.
Full size table

“Supplementary Table S3” shows the results of running this algorithm ten times on the initial matrix A. The standard deviation and mean of the correction elements, CR, and OFV are minimal, and “Supplementary Table S3” indicates that all ten runs were successful. Figure 9 displays the optimized best value for the minimum CR and the difference between the original and substituted Matrix.

Fig. 9
figure 9

3D plot of the Difference term, CR and OFV for the Substitute Matrix of order 6.

Full size image

Performance analysis of GWO for the special case matrix

The GWO algorithm properly balances exploration and exploitation by employing the variable, ensuring its convergence. Furthermore, the three best solutions consistently guide other solutions toward the most promising areas of the search space. As a result, there is a significant likelihood that the population’s objective value will improve throughout optimization. For optimization challenges, GWO calculates the global optimum. Figures 10 and 11 show the convergence of the grey wolves to obtain the best optimized objective function value (OFV) and the best CR value, respectively, in just 94 iterations.

Fig. 10
figure 10

The convergence history of objective function value (OFV).

Full size image
Fig. 11
figure 11

The convergence history of the consistency ratio.

Full size image

These figures show that the convergence of responses displays a fascinating phenomenon due to the adaptation process of the primary regulating parameter \((A)\). By analyzing Figs. 10 and 11, We may observe that the number of iterations gradually alters solutions. This demonstrates how GWO appropriately maintains a balance between exploration and exploitation. Finally, because the GWO obtained the best OFV and CR at the 94th iteration, Fig. 12 only shows iterations 1–94. After this, the GWO achieves the best CR value.

Fig. 12
figure 12

The convergence history of the consistency ratio up to 94 iterations.

Full size image

Comparison with PSO and ANTAHP

We also compare our findings with those of alternative approaches. Girsang et al.43 present the results of PSO with the Taguchi method and ANTAHP using an example of an inconsistent PWM, as narrated in Table 9 with CR = 0.546487. Tables 11 and 12 illustrate the comparison between the PSO + Taguchi method and ANTAHP, as suggested by Yang et al. and Girsang et al., respectively. Yang et al.44 repaired the PWM such that its CR = 0.019 and Di = 0.3577, while Girsang et al.43 repaired the PWM to have CR = 0.094 and Di = 0.1720. The GWO also performs a repair, yielding CR = 0.069825 and Di = 0.134232. The team sets the swarm size to 30. The findings indicate that GWO prioritizes performance to obtain a matrix that is closer to the original than those proposed by Yang et al. and Girsang et al.43. The Di of GWO is more petite than those of Yang et al.44 and Girsang et al.43. However, in striving to get closer to the original Matrix, the consistency ratio of GWO is higher than that of PSO and the Taguchi method but smaller than ANTAHP.

Table 11 Comparison of GWO CR with PSO + Taguchi method and ANTAHP.
Full size table
Table 12 Comparison of GWO Di with PSO + Taguchi method and ANTAHP.
Full size table

Nevertheless, it remains a consistent matrix. The results’ standard deviation (SD) is minimal compared to the mean (less than 5%), indicating that all data points are very close to the expected value. Tables 11 and 12 compare GWO’s CR and Di (Difference between the original and substituted Matrix) with ANTAHP and PSO + Taguchi.

Conclusion and future scope

This work proposes a novel framework based on a swarm intelligence (SI) optimization algorithm, GWO, inspired by the behaviour of grey wolves, along with a new distance formula utilizing the Cosine Distance metric. This framework aims to propose a comprehensive repair procedure that makes an inconsistent PCM consistent while minimizing the differences between the original and substitute matrices.

The framework we propose offers the following advantages over previous work on inconsistency repair:

  • In this study, we use the cosine distance formula because utilizing similarity measures can help increase the accuracy of information retrieval by determining how similar two objects are.

  • With the parameter \(\epsilon\) introduced in this article, DMs can achieve consistency by adjusting it to suit their preferences. This allows them to control the difference between the elements of the original Matrix and the substitute matrix according to their specific requirements.

According to the experimental data, we get better outcomes for the Matrix with a CR of 0.546487; the GWO does a repair, which results in CR = 0.069825 and Di = 0.134232. While ANTAHP fixed the PWM to have CR = 0.094 and Di = 0.1720, PSO fixed the PWM so that its CR = 0.019 and Di = 0.3577. The team carried out this procedure thirty times. Results demonstrate that GWO’s performance is given precedence over those suggested by PSO and ANTAHP to produce a matrix that is more similar to the original.

We evaluate our approach using multiple experimental data points and compare it with data from related research for validation. The results demonstrate that this approach outperforms previously used methods based on ANTAHP and PSO.

Furthermore, applying this novel framework to PCM of varying orders yields superior results. The accompanying figures and tables illustrate an excellent convergence rate, further validating the framework’s effectiveness. These findings also show that the proposed method aligns more with the original matrices than existing methods.

While researchers have extensively studied consistency in PCM, there remains scope for improving the existing consistency ratio (CR). Future work could explore using the K-Nearest Neighbours (KNN) algorithm to identify the underlying causes of inconsistency in pairwise comparisons. After placing the sources of inconsistency, you can apply other algorithms to enhance the consistency ratio (CR) effectively. Specifically, the current model requires parameter \(\epsilon\) (maximum correction range) to ensure that the difference between the original and modified PCM elements remains minimal. Without applying \(\epsilon\), the modified Matrix may deviate significantly from the decision maker’s original judgments. This limitation indicates that the model, in its current form, cannot guarantee optimal proximity to the expert’s intent unless \(\epsilon\) is defined correctly. Future work will explore adaptive or dynamic correction mechanisms to address this issue more flexibly.