Introduction

Evaluation of rupture risk for cerebral aneurysms is crucial for ensuring suitable clinical outcomes1. Morphological parameters are currently used to evaluate the rupture risk of cerebral aneurysms because of their simple calculation process2,3,4. In particular, aspect ratio and size ratio of aneurysms are two crucial morphological parameters correlated with rupture risk5,6,7,8.

Although morphological parameters have been widely used to predict the rupture risk of cerebral aneurysms, these parameters exhibit certain limitations in evaluating aneurysm irregularities because of their simple calculation process9. Morphologies of cerebral aneurysms vary individually and tend to be irregular in shape. Multiple studies have shown that morphological irregularities in cerebral aneurysms—such as blebs, daughter sacs, marked lobulation, and non-axisymmetric shapes—are strongly associated with rupture risk10,11,12. Huang et al. conducted a systematic review and meta-analysis of intracranial aneurysms and demonstrated that irregular aneurysm morphology is significantly more common in ruptured than in unruptured aneurysms, confirming irregularity as a robust morphological marker of rupture risk13. However, conventional morphological parameters, such as the aspect ratio and size ratio cannot fully represent aneurysm irregularities. Although studies have been conducted to develop morphological parameters that can evaluate aneurysm irregularities,14,15 these parameters are not sufficient for evaluating aneurysm irregularity.

In a previous study, a new morphological parameter—the mass moment of inertia—was introduced to effectively evaluate aneurysm irregularity9. The results of that study revealed that the mass moment of inertia can quantitatively describe the size, daughter sac, and irregularity of a complex-shaped aneurysm by considering the characteristics of the three-dimensional (3D) aneurysm shape. However, artificial neural networks (ANNs) trained with the mass moment of inertia could not achieve comparable performance in rupture risk evaluation unless hemodynamic parameters were used to train the ANN model.

The goal of this study is to develop new morphological parameters that quantitatively assess the degree of aneurysm irregularity. To achieve this, we developed novel morphological indexes (NMIs) by modifying the mass moment of inertia to more effectively characterize aneurysm irregularity, thereby eliminating the need for complex hemodynamic analyses. We then evaluated the ability of these NMIs to capture morphological irregularity through rupture risk prediction and compared their predictive performance with that of conventional morphological parameters, including aspect ratio, bottleneck ratio, volume-to-ostium ratio, and size ratio, using ANN.

Methods

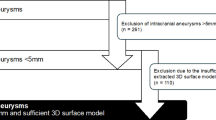
The study protocol was approved by our institutional review board of Yongin Severance Hospital, (No. 9-2024-0008). The requirement for written informed consent from the included patients was waived. In addition, all methods were performed in accordance with the relevant guidelines and regulations (STROBE). Between March 2020 and July 2023, 456 cerebral aneurysms were registered. All data were prospectively recorded in databases and reviewed retrospectively. The following criteria were considered for inclusion of cases in the study: (1) age > 18 years, (2) saccular aneurysm located in the anterior circulation, and (3) availability of digital subtraction angiography (DSA) source data of patients for computer-aided design program. The criteria for exclusion were as follows: (1) non-saccular aneurysm, (2) aneurysm in the posterior circulation, and (3) previous history of surgical clipping or coil embolization.

Novel morphological indexes for evaluating aneurysm morphology

Three NMIs—ANI, aneurysm-to-neck index; AVI, aneurysm-to-vessel index; AII, aneurysm irregularity index—were devised by modifying the mass moment of inertia and product of inertia to effectively evaluate aneurysm morphologies, such as aneurysm size and irregularity because the mass moment of inertia and the product of inertia can describe the aneurysm morphology by evaluating the distance of a mass from the rotating axis and the symmetry of the shape with respect to a specific plane.

The mass moment of inertia and product of inertia was first calculated according to the calculation process presented in a previous study for calculating the NMIs9. Detailed explanations of the mass moment of inertia and product of inertia and the calculation process of both equivalent mass moment of inertia and NMIs are provided in Supplementary Materials. The manipulation process of the 3D aneurysm model for calculating the mass moment of inertia is depicted in Supplementary Figure S4. First, DSA was performed for the 3D reconstruction of an aneurysm. A digital imaging and communications in medicine (DICOM) date of a cerebral aneurysm obtained from DSA was automatically converted to stereolithography (STL) data using 3D Slicer after applying an appropriate signal intensity threshold. The aneurysm was then manually isolated from the parent artery using a CAD software by an experienced clinician. Second, the interior of each aneurysm was removed to generate a thin-walled model. The inertia matrix, comprising both the mass moment of inertia and the product of inertia, was then automatically calculated using the CAD software. To provide a more comprehensive representation of aneurysm morphology, the equivalent mass moment of inertia was finally computed.

The equivalent mass moment of inertia was normalized using the diameters of the aneurysm neck and parent vessel, as the relative size differences between these structures significantly influence rupture risk. Based on this normalization, two indexes were defined: the Aneurysm-Neck Index (ANI) and the Aneurysm-Vessel Index (AVI). ANI represents the ratio of the equivalent mass moment of inertia to the mass moment of inertia of aneurysm neck diameter, and its value increase as the neck diameter decreases (Fig. 1A). AVI is defined as the ratio of the equivalent mass moment of inertia to the mass moment of inertia of parent vessel diameter, reflecting how large the aneurysm is relative to the vessel size (Fig. 1B).

Fig. 1
figure 1

Physical meanings of novel morphological indexes: (A) \(\:ANI\), (B) \(\:AVI\), and (C) \(\:AII\).

Full size image

A third index, the Aneurysm Irregularity Index (AII), was introduced to quantify morphological irregularity. AII is calculated by normalizing the equivalent mass moment of inertia with the standard deviation of the mass moments of inertia along the x, y, and z axes. Aneurysms with high irregularity exhibit greater variability across these axes, resulting in a higher standard deviation and, consequently, a larger AII value (Fig. 1C). The definitions and physical interpretations of these morphological parameters are summarized in Supplementary Table S1.

Commercial computer-aided design program CATIA (V5-6R2021; Dassault Systems, Paris, France) was used to automatically calculate the mass moment of inertia and product of inertia. Meshmixer (version 11.0.544; Autodesk, San Rafael, CA, USA) was used to manipulate the 3D aneurysm model16. Furthermore, conventional morphological parameters, such as aspect ratio, size ratio, bottleneck ratio, and volume-to-ostium ratio, were calculated to compare the rupture risk prediction performances of conventional and moment-based morphological parameters.

Rupture risk prediction model using artificial neural network (ANN)

ANNs have been widely used in developing various prediction models on clinical applications because it can evaluate a complex influence of various parameters17. For this reason, ANNs has been used to develop a rupture risk prediction model for cerebral aneurysms. The rupture risk prediction model developed in this study consisted of five layers containing input and hidden layers with a rectified linear unit activation function and one output layer with a sigmoid function for binary classification. A total of 456 cerebral aneurysms were randomly divided into 319 training (257 unruptured and 62 ruptured aneurysms) and 137 test (110 unruptured and 27 ruptured aneurysms) datasets. Three ANN models were constructed to compare the rupture risk prediction performances of various morphological parameters. The three models included an ANN model trained with the NMIs (NMI model, 3 predictors), an ANN model trained with the conventional morphological parameters (MORPH model, 4 predictors), and an ANN model trained with both NMIs and conventional morphological parameters (NMI + MORPH model, 7 predictors).

Statistical analysis

The rupture risk prediction performance of the ANN models was evaluated by calculating the receiver operating characteristic (ROC) curve and its area under the receiver operating characteristic (AUROC)18. Furthermore, the Youden’s index was used to determine the cut-off value of the rupture criterion19. IBM SPSS Statistics was used to perform statistical analyses (version 24.0; IBM Corp., Armonk, NY, USA).

Results

The training dataset comprised 319 aneurysms (mean maximum diameter: 5.22\(\:\pm\:\)2.11 mm) from 297 patients (218 women and 79 men); their mean age was 61.7 years (range: 26–91 years). The test dataset had 137 aneurysms from 135 patients (99 women and 36 men, mean maximum diameter: 5.57\(\:\pm\:\)2.33 mm); their mean age was 59.4 years (range: 27–85 years).

Table 1 presents the means and standard deviations of each morphological parameter. The box-and-whisker and dot plots for conventional morphological parameters and NMIs were also shown in Supplementary Figure S5 and S6. The values of all the parameters for ruptured aneurysms were higher than those for unruptured aneurysms. Furthermore, the differences in conventional morphological parameters and NMIs between unruptured and ruptured aneurysms were statistically significant.

Table 1 Mean and standard deviation of the morphological parameters of unruptured and ruptured aneurysms.
Full size table

Figure 2 displays the ROC curves for all ANN models. The AUROC of MORPH model was 0.850 (95% CI, 0.812–0.888), and the highest AUROC was obtained for NMI model (AUROC: 0.951; 95% CI, 0.930–0.973). However, in case of NMI + MORPH model, the AUROC decreased compared with that of NMI model (AUROC: 0.888; 95% CI, 0.86–0.916). Based on the cut-off value, the sensitivity and specificity of each ANN model were 92.9% and 92.0% for NMI model, 72.3% and 87.9% for MORPH model, and 85.7% and 88.0% for NMI + MORPH model.

Fig. 2
figure 2

Receiver operating characteristic (ROC) curves and their area under the receiver operating characteristic (AUROC) values of ANN models. NMI model was trained with ANI, AVI and AII. In addition, MORPH model was trained with AR, BR, VOR, and SR. The NMI + MORPH model was trained with both novel morphological indexes and conventional morphological parameters. The NMI model showed the best performance in predicting the risk of rupture. However, even though both novel morphological parameters and conventional morphological parameters were used to train the model, its performance decreased significantly.

Full size image

Furthermore, the cross-validation analysis was conducted to access the generalization performance by splitting the data into three folds. Supplementary Table S2 shows the sensitivity and specificity of each ANN models trained with each fold and their ROC values. The results demonstrate that our ANN model is robust within the current dataset.

Discussion

Various morphological parameters have been used to determine aneurysm rupture risk by evaluating geometric features. Dhar et al. and Zheng et al.3,15 performed rupture risk prediction from the aspect ratio of aneurysm using ROC curves and achieved good prediction performance (AUROC of Zheng et al.: 0.683, AUROC of Dhar et al.: 0.703). Ashkezari et al.20 developed machine learning models to evaluate the performance of major parameters of aneurysm rupture. To train their rupture risk prediction model, they used various parameters, such as aspect and size ratios, as well as hemodynamic parameters. Consequently, they achieved an increase in the AUROC of the rupture risk prediction model up to 0.84. However, although many parameters were used to develop the rupture risk prediction model, the performance on rupture risk prediction of the model was insufficient.

These conventional morphological parameters cannot effectively evaluate the irregularity of cerebral aneurysms. Rupture risk evaluation of the ruptured and unruptured groups used in this study proved this limitation. Although the MORPH model exhibited decent rupture risk prediction performance, its performance did not reach that of the NMI model. Furthermore, although additional morphological parameters were employed in training the NMI + MORPH model, its performance deteriorated in comparison with that of the NMI model. This phenomenon might be due to the fact that conventional morphological parameters are insufficient to assess the irregularities of cerebral aneurysms.

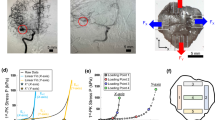
Figure 3 depicts examples of ruptured aneurysms with irregular shapes and rupture risk values evaluated using the ANN models. When the rupture risks of the ruptured aneurysms were evaluated using the MORPH model, a low rupture risk was observed even though the aneurysms ruptured. However, when the NMI model was used to evaluate the rupture risk, it accurately predicted ruptured aneurysms. These results indicate that the NMIs could effectively evaluate aneurysm irregularities that cannot be described using conventional morphological parameters. This phenomenon could be attributed to the NMIs being developed based on the mass moment of inertia because the previous study had confirmed that the mass moment of inertia could quantitatively describe aneurysm irregularity9.

Fig. 3
figure 3

Examples of ruptured aneurysms having irregular shapes, and their rupture risk values evaluated using ANN models. The numbers below the aneurysms represent a probability of rupture predicted by each ANN model. The higher the value, the higher the probability of rupture. Although these are ruptured aneurysms, they were predicted as unruptured aneurysms when the MORPH model was used. On the other hand, they were successfully predicted when the NMI model was used.

Full size image

While the mass moment of inertia is the most powerful morphological parameter for the evaluation of aneurysm irregularity, hemodynamic parameters may also help improve performance of rupture risk evaluation9. However, hemodynamic parameters such as wall shear stress are required to perform computational analyses, such as computational fluid dynamics and fluid-structure interaction;21 for this reason, their application in the clinical field is limited owing to the complex processes. Therefore, NMIs were newly devised based on the mass moment of inertia to improve rupture risk prediction performance and clinical practicality.

We complemented additional parameters, such as the diameters of the aneurysm neck and parent vessel, to allow relative evaluation of aneurysm morphology. Supplementary Figure S7 displays two ROC curves of the rupture risk prediction models trained with the NMIs and mass moments of inertia (\(\:{I}_{xx},\:{I}_{yy},\:\)and \(\:{I}_{zz}\)). The AUROC of the rupture risk prediction model trained for the mass moment of inertia was 0.789. However, when the NMIs were used to train the rupture risk prediction model, the rupture risk prediction performance significantly increased.

Furthermore, \(\:AII\) was developed to effectively evaluate aneurysm irregularities using the standard deviation of the mass moments of inertia in x, y, and z axes. Supplementary Figure S8 displays a comparison of the aspect ratio and \(\:AII\) for representative ruptured and unruptured aneurysms of similar size. Although the irregularity of the ruptured aneurysm was greater than that of the unruptured aneurysm, similar aspect ratios were obtained. Nevertheless, the \(\:AII\) of the ruptured aneurysm was greater than that of the unruptured aneurysm. This comparison confirmed that \(\:AII\) can quantitatively represent the degree of aneurysm irregularity.

Limitations

The aneurysm-segmentation workflow was not fully automated. Although mass moment of inertia and product of inertia can be calculated automatically in commercial CAD software, isolating the aneurysm from the parent artery was performed manually by experienced clinicians, introducing potential operator-dependent variability. Currently, several studies have been conducted to develop an artificial intelligence-based segmentation, which offer promising solutions to reduce such variability.

An age-old limitation in rupture risk studies is the inability to determine the exact morphology of aneurysms immediately prior to rupture. While it would be more meaningful to include aneurysms in the cohort of rupture as ‘ruptured cases’, there is currently no reliable method to predict imminent rupture. Ethical constraints also prevent delaying treatment purely for observational purposes, making it difficult to collect sufficient longitudinal data. As a result, all ruptured aneurysms, including those used in this study, were obtained post-rupture, which may compromise the accuracy of aneurysm morphology.

To minimize discrepancies between pre- and post-rupture shapes, ruptured aneurysms were carefully selected by experienced clinicians. Furthermore, in 8 out of 83 ruptured cases, pseudo-sacs, representing blood leakage post-rupture, were removed to restore an approximation of the original aneurysm shape (Supplementary Figure S9). While an angiographic study has reported that aneurysm morphology remains largely unchanged after rupture,22 its limited sample size hinders the generalizability of this finding. Therefore, it is possible that the geometries used in this study may not fully represent the true pre-rupture state. Given these limitations, future prospective studies, ideally involving multi-institutional collaboration, are essential to capture pre- to post-rupture morphological changes and to improve the accuracy of rupture risk prediction models.

Conclusion

We newly introduced the NMIs based on the normalised mass moment of inertia to evaluate aneurysm morphologies such as the aneurysm size and irregularity. The NMIs effectively described aneurysm irregularities that could not be evaluated using conventional morphological parameters. When the rupture risk prediction performance of the NMIs was examined using ANN models, it showed considerable performance improvement. Consequently, the NMIs can quantitatively evaluate aneurysm irregularities.