Plasmonic SPR biosensor with bayesian regression for non-invasive protein biomarker detection

Abstract

This paper presents a designed metasurface sensor for protein biomarkers detection. The design of this metasurface structure is essentially dependent on the coating of four identical figure-eight-shaped resonators of MXene through black phosphorus and graphene. Meanwhile, the performance analysis demonstrates a competitive sensitivity (395 GHz/RIU) with a linear frequency response of R² = 0.954 and protein biomarker concentration (R² = 0.956). The sensor exhibits stable performance across 0.31–0.46 THz and maintains consistent operation at incident angles up to 30°. Interestingly, this tunability is achieved through graphene chemical potential modulation, with transmittance decreasing from 97.7% to 66.7% as its value increases. Additionally, the machine learning optimization using Bayesian Ridge Regression demonstrates exceptional predictive capabilities for both refractive index variations (R² ≈ 86%) and angular dependencies (R² ≈ 96%). This integrated photonic-microfluidic sensor platform offers significant potential for early detection of neurological disorders through rapid, sensitive, and scalable brain tumor biomarker analysis.

Introduction

Biosensing technologies have revolutionized medical diagnostics by enabling rapid, and sensitive detection of biological markers, such as proteins and tumor-specific molecules, that provide a critical impact through the diagnosing of many diseases¹. In neurological diagnostics, these technologies are vital for identifying protein biomarkers² in brain tumors³, facilitating early detection and monitoring of conditions like glioblastoma. Therefore, the need for an accurate and rabid diagnostic could be of a potential interest. In this regard, photonic integrated circuits (PICs), which combine multiple optical components on a single chip, provide a powerful platform for developing advanced biosensors⁴. By integrating optofluidic systems with PICs, these biosensors achieve enhanced sensitivity and compactness, making them ideal for point-of-care applications in neurological diagnostics.

The combination of optofluidics and PICs harnesses the high precision of photonics alongside the fluid manipulation strengths of microfluidics, resulting in advanced biosensing platforms with enhanced efficiency⁵. This integration facilitates the creation of compact and high-performance devices capable of identifying trace levels of biomarkers within complex biological fluids such as cerebrospinal fluid and blood⁶. Notable benefits of this approach include enhanced signal-to-noise ratios, minimized sample volume requirements, and the potential to incorporate multiple sensing techniques on a single chip⁷. Practical applications encompass PIC-based biosensors designed for detecting tau proteins associated with Alzheimer’s disease⁸ and epidermal growth factor receptor (EGFR) mutations relevant to brain tumors, providing fast and precise diagnostic capabilities⁹.

To enhance the detection limits, signal amplification techniques, such as interferometric enhancement¹⁰ and nanoparticle-based labelling, are employed to boost the sensitivity of photonic biosensors¹¹. These sensors operate on principles such as refractive index changes or fluorescence detection, where light interactions with analytes produce measurable optical signals^12,13,14. The design of photonic structures, such as microring resonators or photonic crystals, is crucial for optimizing light confinement and analyte interaction¹⁵. Meanwhile, the material selection, typically involving high-index materials like silicon or low-loss polymers, ensures compatibility with biological environments and high sensitivity as well¹⁶.

Additionally, the scalable fabrication processes, such as those compatible with microelectronics manufacturing, enable cost-effective production of these biosensors, facilitating their widespread adoption in clinical settings¹⁷. These processes allow for a precise fabrication of photonic and microfluidic components, ensuring reproducibility and integration with electronic readout systems¹⁸.

In the recent years, there has been significant advances in these types of biosensors. For instance, Updhay et al. demonstrated graphene–plasmon hybrid interlayers with a plasmonic redshift of 20–25 nm, hot electron lifetimes up to 3.8 ps¹⁹. Qu et al. reported a trench D-shaped PCF-SPR RI sensor with an average WS of 5500 nm/RIU, maximum WS of 11,500 nm/RIU, resolution of 1.74 × 10⁻⁶ RIU, and amplitude sensitivity of 133.4 RIU⁻¹ in the 1.32–1.38 RI range²⁰. Aldkeelalah et al. proposed an SC-PCF sensor for pregnancy detection in the THz range, demonstrating a confinement loss of 0.765 × 10⁻¹⁰ cm⁻¹ and a high relative sensitivity of 96.30% at 1.5 THz, highlighting strong potential for biomedical and industrial applications²¹. Karuppasamy et al. developed a multimode THz plasmonic biosensor for malaria detection, achieving a maximum sensitivity of 429 GHz/RIU, FOM of 3.968 RIU⁻¹, and quality factor of 10.352, with SVR analysis confirming 100% prediction accuracy across angular variations²². Sheheryar et al. introduced a metasurface THz biosensor with multi-resonance architecture, achieving a maximum sensitivity of 3.714 THz/RIU, polarization independence, and angular stability up to 60°, offering a cost-effective and scalable platform for multi-disease detection²³. Alkorbi et al. designed a metasurface THz biosensor with sensitivities up to 1.43 THz/RIU, FOM of 17.54 RIU⁻¹, and Q-factor of 18.33, offering polarization insensitivity and angular stability up to 70° for scalable, low-cost multi-disease detection²⁴. Lv et al. proposed a reflective metasurface device achieving > 90% polarization conversion across 3.044 THz bandwidth with peak efficiency of 99.9%, angular stability up to 40°, and biosensing sensitivity of 0.95 THz/RIU for cancer detection²⁵. You et al. numerically demonstrated, via FEM simulations as sensor having 30.2 nm/°C as sensitivity²⁶. Kabir et al. employed FEM-based COMSOL simulations to analyse a circular-shaped PCF sensor achieving high relative sensitivities of 95.02% for glucose²⁷. Albelbeisi et al. used TMM simulations via Maple 18 to evaluate an Ag/PtSe₂/graphene-based SPR sensor with 542.5 deg/RIU as sensitivity²⁸. Das et al. applied FEM simulations to design a single-core ultra-low-loss PCF-SPR biosensor for RI detection (1.30–1.42), achieving 11,000 nm/RIU wavelength sensitivity²⁹.

Despite significant advances, limitations in sensitivity and other performance metrics still persist. This paper explores the principles, design considerations, and applications of photonic biosensors integrated with machine learning optimization for protein and brain tumor detection, emphasizing their potential to revolutionize neurological diagnostics by enhancing sensitivity, portability, and scalability. In this regard, the designed sensor is essentially dependent on the coating of four identical figure-eight-shaped resonators of MXene through black phosphorus and graphene. In what follows, we have introduced in details the design of this sensor based on the considered materials.

Modelling and numerical simulations

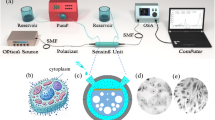
The sensor architecture as demonstrated in Fig. 1a-c features four identical figure-eight-shaped resonant elements arranged symmetrically, with each element coated in MXene material. MXene serves as an effective coating due to its two-dimensional structure and superior electrical conductivity, facilitating enhanced analyte-resonator interactions through its surface functionalization capabilities. Three rectangular resonant structures surround the central figure-eight configuration, each utilizing black phosphorus (BP) as the coating material. The selection of BP stems from its unique anisotropic optical characteristics and strong terahertz wave interaction properties, contributing to improved sensor sensitivity and analyte selectivity. The complete resonator assembly is positioned atop a central square-shaped resonant element, which incorporates a single-layer graphene coating. Graphene’s exceptional carrier mobility and adjustable surface plasmon resonance characteristics enable dynamic control of the sensor’s optical behaviour. This multi-resonator metamaterial configuration is engineered to maximize electromagnetic field confinement and optimize wave-matter interactions. The entire resonator network is fabricated on a silicon dioxide (SiO₂) substrate platform. This substrate choice ensures adequate mechanical stability and structural support while minimizing electromagnetic interference with the sensor’s operational characteristics. The design visualization includes multiple perspectives: a periodic array view demonstrating the scalable nature and manufacturing potential for large-scale production, a detailed single unit cell illustration showing the spatial arrangement of individual resonator components, and an electromagnetic field orientation diagram. The electromagnetic configuration establishes the electric field polarization along the x-direction, magnetic field alignment along the y-direction, and wave propagation in the z-direction. This orthogonal field arrangement is essential for a comprehensive analysis of the sensor’s resonant behaviour and electromagnetic performance, particularly within the terahertz operational bandwidth.

Fig. 1

displays the sensor’s configuration from three distinct perspectives.

Unlike conventional metasurface biosensors that rely on a single plasmonic coating, our design uniquely integrates three distinct 2D materials—MXene, black phosphorus, and graphene—onto geometrically optimized resonators (figure-eight, rectangular, and square). This multi-material arrangement provides complementary functionalities: MXene ensures strong analyte-resonator coupling through surface functionalization, BP enhances anisotropic terahertz absorption, and graphene introduces electrical tunability via chemical potential modulation. To the best of our knowledge, this tri-material hybrid metasurface with orthogonal resonator integration has not been reported previously, and it enables enhanced sensitivity alongside dynamic reconfigurability, thereby advancing beyond prior single-material or purely geometric metasurface sensors. The materials employed contribute complementary functions: (i) MXene, with high conductivity and surface chemistry, strengthens analyte coupling; (ii) black phosphorus enhances anisotropic interaction with THz waves, boosting selectivity; and (iii) graphene provides dynamic tunability via chemical potential modulation, enabling reconfigurability. Their integration ensures both static high sensitivity and active tuning capabilities.

Electromagnetic analysis of the proposed sensor design

We treat each 2D material as an infinitesimally thin conductive sheet with surface conductivity tensor $\:{\varvec{\upsigma\:}}_{s}\left(\omega\:\right)$ (possibly anisotropic). In frequency domain ($\:{e}^{-i\omega\:t}$ convention), Maxwell’s equations in each homogeneous layer $\:\mathcal{l}$ ($\:{\epsilon\:}_{\mathcal{l}},{\mu\:}_{\mathcal{l}}$) are given as^{30,31,32,33,34,35,36,37,38,39,40,41,42,43}:

$$\:\begin{array}{c}\nabla\:\times\:{\mathbf{E}}_{\mathcal{l}}=i\omega\:{\mu\:}_{\mathcal{l}}{\mathbf{H}}_{\mathcal{l}},\\\:\nabla\:\times\:{\mathbf{H}}_{\mathcal{l}}=-i\omega\:{\epsilon\:}_{\mathcal{l}}{\mathbf{E}}_{\mathcal{l}}.\end{array}$$

(1)

Then, across a sheet at $\:z={z}_{m}$,

$$\:\begin{array}{c}\widehat{\mathbf{n}}\times\:\left({\mathbf{H}}^{+}-{\mathbf{H}}^{-}\right)={\mathbf{J}}_{s}={\varvec{\upsigma\:}}_{s}\left(\omega\:\right)\cdot\:{\mathbf{E}}_{\parallel\:},\\\:\widehat{\mathbf{n}}\cdot\:\left({\mathbf{D}}^{+}-{\mathbf{D}}^{-}\right)={\rho\:}_{s}=0,\end{array}$$

(2)

Therefore, the tangential of $\:\mathbf{E}$ is continuous and that’s of $\:\mathbf{H}$ exhibits a jump set by $\:{\varvec{\upsigma\:}}_{s}$. For a periodic metasurface (periods $\:{p}_{x},{p}_{y}$), the in-plane fields expand into spatial Floquet harmonics with transverse wavevectors $\:{\mathbf{k}}_{mn}={\mathbf{k}}_{\parallel\:}+\frac{2\pi\:m}{{p}_{x}}\widehat{\mathbf{x}}+\frac{2\pi\:n}{{p}_{y}}\widehat{\mathbf{y}}$. In the sub-wavelength regime where only the $\:(0,0)$ order propagates, we can homogenize the patterned unit cell as a sheet with effective surface admittance tensor $\:{\mathbf{Y}}_{\text{eff}}\left(\omega\:\right)$.

For normal incidence TE/TM (in air, $\:{\eta\:}_{0}$) on a sheet atop a dielectric stack of input impedance $\:{Z}_{\text{in}}\left(\omega\:\right)$, the generalized reflection is

$$\:\begin{array}{c}r\left(\omega\:\right)=\frac{{Z}_{\text{in}}-{\left({\eta\:}_{0}^{-1}+{Y}_{\text{eff}}\right)}^{-1}}{{Z}_{\text{in}}+{\left({\eta\:}_{0}^{-1}+{Y}_{\text{eff}}\right)}^{-1}},\\\:t\left(\omega\:\right)=\frac{2{Z}_{\text{in}}}{{Z}_{\text{in}}+{\left({\eta\:}_{0}^{-1}+{Y}_{\text{eff}}\right)}^{-1}},\end{array}$$

(3)

Hence, $\:{Y}_{\text{eff}}$ interpreted as the appropriate scalar (co-polar) entry of $\:{\mathbf{Y}}_{\text{eff}}$ for the chosen polarization (or keep it tensorial for arbitrary polarization). Then, Kubo formula figures the optical characteristics of graphene in the vicinity of its conductivity. Meanwhile, Kubo model (local, intraband + interband), relaxation $\:{{\Gamma\:}}_{g}=1/{\tau\:}_{g}$, chemical potential $\:{\mu\:}_{c}$ tunable by gate $\:{V}_{g}$, introduce graphene’s conductivity in the following form:

$$\:\begin{array}{*{20}c} {\sigma \:_{g} (\omega \:,\mu \:_{c} ,\Gamma \:_{g} ,T) = \frac{{ie^{2} k_{B} T}}{{\pi \:\hbar \:^{2} (\omega \: + i\Gamma \:_{g} )}}\left[ {\frac{{\mu \:_{c} }}{{k_{B} T}} + 2\ln \left( {1 + e^{{ - \mu \:_{c} /\left( {k_{B} T} \right)}} } \right)} \right]} \\ {\:\: + \frac{{e^{2} }}{{4\hbar \:}}\left[ {\tanh \left( {\frac{{\hbar \:\omega \: + 2\mu \:_{c} }}{{4k_{B} T}}} \right) + \tanh \left( {\frac{{\hbar \:\omega \: - 2\mu \:_{c} }}{{4k_{B} T}}} \right)} \right]} \\ \end{array}$$

(4)

Then, for MXene, the conductivity provides the following form:

$$\:{\sigma\:}_{M}\left(\omega\:\right)=\sum\:_{j=1}^{{N}_{D}}\frac{{\epsilon\:}_{0}{\omega\:}_{p,j}^{2}{d}_{M}}{{{\Gamma\:}}_{M,j}-i\omega\:}+\sum\:_{k=1}^{{N}_{L}}\frac{i{\epsilon\:}_{0}{d}_{M}{\Delta\:}{\epsilon\:}_{k}\omega\:}{{\omega\:}_{0,k}^{2}-{\omega\:}^{2}-i{\gamma\:}_{k}\omega\:},$$

(5)

with film thickness $\:{d}_{M}$ folded into the surface response. In contrast, for BP, we have:

$$\:\begin{array}{c}{\varvec{\upsigma\:}}_{BP}\left(\omega\:\right)=\left[\begin{array}{cc}{\sigma\:}_{x}\left(\omega\:\right)&\:0\\\:0&\:{\sigma\:}_{y}\left(\omega\:\right)\end{array}\right],\\\:{\sigma\:}_{\alpha\:}\left(\omega\:\right)=\frac{{\epsilon\:}_{0}{\omega\:}_{p,\alpha\:}^{2}{d}_{BP}}{{{\Gamma\:}}_{BP,\alpha\:}-i\omega\:}+\sum\:_{m}\frac{i{\epsilon\:}_{0}{d}_{BP}{\Delta\:}{\epsilon\:}_{\alpha\:,m}\omega\:}{{\omega\:}_{\alpha\:,m}^{2}-{\omega\:}^{2}-i{\gamma\:}_{\alpha\:,m}\omega\:}.\end{array}$$

(6)

Encapsulation (e.g., h-BN) modifies the local environment via $\:{\epsilon\:}_{\text{env}}$ and adds weak capacitive loading but leaves the sheet boundary conditions unchanged.

Let the unit cell contain three dissimilar resonators (indices $\:a\to\:$ figure-eight/MXene, $\:b\to\:$ rectangle/BP, $\:c\to\:$ square/graphene). In a polarizability-coupling picture,

$$\begin{array}{*{20}c} {Y_{{eff}} (\omega \:,k_{{\parallel \:}} ) \approx \:i\omega \: \approx \:_{0} \chi \:_{0} I} \\ {\:\: + \sum {\:_{{\nu \: \in \:\{ a,b,c\} }} } \frac{{u_{{\nu \:}} u_{{\nu \:}}^{T} }}{{L_{{\nu \:}}^{{ - 1}} - i\omega \:R_{{\nu \:}} - \omega \:^{2} C_{{\nu \:}} + \Sigma \:_{{\nu \:}} (\omega \:,k_{{\parallel \:}} )}} + Y_{{rad}} \left( {\omega \:} \right),} \\ \end{array}$$

(7)

where $\:{\mathbf{u}}_{\nu\:}$ encodes polarization selectivity of each shape, $\:({L}_{\nu\:},{R}_{\nu\:},{C}_{\nu\:})$ are equivalent circuit parameters including sheet-conductivity-dependent kinetic inductance $\:{L}_{\nu\:,k}\propto\:\left(\mathfrak{I}\right\{{\sigma\:}_{\nu\:}\}\omega\:{)}^{-1}$ and ohmic resistance $\:{R}_{\nu\:,o}\propto\:\mathfrak{R}\{{\sigma\:}_{\nu\:}{\}}^{-1}$, $\:{{\Sigma\:}}_{\nu\:}$ is a lattice-radiation self-energy, and $\:{\mathbf{Y}}_{\text{rad}}$ accounts for direct radiative coupling to the continuum via substrate. Resonances satisfy $\:\text{d}\text{e}\text{t}\left[{\mathbf{Y}}_{\text{eff}}^{-1}+{\eta\:}_{0}\mathbf{I}/(1+{\eta\:}_{0}{Y}_{\text{stack}})\right]=0$; more practically, each mode $\:\nu\:$ has

$$\:\begin{array}{c}{\omega\:}_{\nu\:,0}^{2}\approx\:\frac{1}{{L}_{\nu\:}{C}_{\nu\:}}\:\text{s}\text{h}\text{i}\text{f}\text{t}\text{e}\text{d}\text{}\text{b}\text{y}\:\delta\:{\omega\:}_{\nu\:}\simeq\:\frac{\mathfrak{R}\left\{{{\Sigma\:}}_{\nu\:}\right\}}{2{\omega\:}_{\nu\:,0}{C}_{\nu\:}},\\\:{\gamma\:}_{\nu\:}\simeq\:\frac{{R}_{\nu\:}}{2{L}_{\nu\:}}+\frac{\mathfrak{I}\left\{{{\Sigma\:}}_{\nu\:}\right\}}{2{\omega\:}_{\nu\:,0}{C}_{\nu\:}}.\end{array}$$

(8)

For a single normally incident channel on air (port 1) and substrate (port 2), with internal modal amplitudes $a = [a_{a} ,a_{b} ,a_{c} ]^{T}$,

$$\:\begin{array}{c}\dot{\mathbf{a}}=\left(i\varvec{\Omega\:}-{\varvec{\Gamma\:}}_{i}-{\varvec{\Gamma\:}}_{e}\right)a+K\hspace{0.17em}{\mathbf{s}}_{+},\\\:{\mathbf{s}}_{-}=C\hspace{0.17em}{\mathbf{s}}_{+}+D\hspace{0.17em}a.\end{array}$$

(9)

Here $\:\varvec{\Omega\:}=\text{diag}({\omega\:}_{a},{\omega\:}_{b},{\omega\:}_{c})+\mathbf{J}$ includes mutual couplings $\:{J}_{\mu\:\nu\:}$, $\:{\varvec{\Gamma\:}}_{i}=\text{diag}({\gamma\:}_{a,i},{\gamma\:}_{b,i},{\gamma\:}_{c,i})$ (ohmic/absorption from $\:\mathfrak{R}\left\{\sigma\:\right\}$), $\:{\varvec{\Gamma\:}}_{e}$ radiative losses to the two ports, $\:\mathbf{K},\mathbf{D}$ the in/out coupling, and $\:\mathbf{C}$ direct (background) path. Steady state yields the scattering matrix

$$\:\mathbf{S}\left(\omega\:\right)=\mathbf{C}+\mathbf{D}{\left[i(\omega\:\mathbf{I}-\varvec{\Omega\:})-({\varvec{\Gamma\:}}_{i}+{\varvec{\Gamma\:}}_{e})\right]}^{-1}\mathbf{K}.$$

(10)

If only the graphene mode $\:c$ is gate-tuned, $\:{\omega\:}_{c}\left({\mu\:}_{c}\right)$ and $\:{\gamma\:}_{c,i}\left({\mu\:}_{c}\right)$ vary via $\:{\sigma\:}_{g}$; BP adds polarization-dependent $\:{J}_{bc}$ due to anisotropy; MXene largely sets strong radiative load (broadband plasmonic damping) via $\:{\gamma\:}_{a,e}$.

When one mode $\:\nu\:$ dominates and the substrate is a quarter-wave backed Si/SiO$\:{}_{2}$ stack with input impedance $\:{Z}_{\text{in}}$, the co-polar reflectance near $\:{\omega\:}_{\nu\:}$ can be written

$$\begin{array}{*{20}c} {R\left( {\omega \:} \right) = \left| {\frac{{Z_{{{\text{in}}}} \left[ {\omega \:_{{\nu \:}}^{2} - \omega \:^{2} + i\omega \:(\gamma \:_{{\nu \:,i}} + \gamma \:_{{\nu \:,e}} )} \right] - \left( {\frac{1}{{Y_{b} + Y_{{{\text{eff}}}}^{{\left( {bg} \right)}} }}} \right)^{{ - 1}} }}{{Z_{{{\text{in}}}} \left[ {\omega \:_{{\nu \:}}^{2} - \omega \:^{2} + i\omega \:(\gamma \:_{{\nu \:,i}} + \gamma \:_{{\nu \:,e}} )} \right] + \left( {\frac{1}{{Y_{b} + Y_{{{\text{eff}}}}^{{\left( {bg} \right)}} }}} \right)^{{ - 1}} }}} \right. + } \\ {\:\:\left. {\frac{{\sum {\:_{{\mu \: \ne \:\nu \:}} } \frac{{\kappa \:_{{\mu \:}} \left( {\omega \:_{{\mu \:}}^{2} - \omega \:^{2} + i\omega \:\Gamma \:_{{\mu \:}} } \right)}}{{\left( {\omega \:_{{\mu \:}}^{2} - \omega \:^{2} + i\omega \:\Gamma \:_{{\mu \:}} } \right)\left( {\omega \:_{{\nu \:}}^{2} - \omega \:^{2} + i\omega \:\Gamma \:_{{\nu \:}} } \right) - \xi \:_{{\mu \:\nu \:}}^{2} }}}}{{Z_{{{\text{in}}}} \left[ {\omega \:_{{\nu \:}}^{2} - \omega \:^{2} + i\omega \:(\gamma \:_{{\nu \:,i}} + \gamma \:_{{\nu \:,e}} )} \right] + \left( {\frac{1}{{Y_{b} + Y_{{{\text{eff}}}}^{{\left( {bg} \right)}} }}} \right)^{{ - 1}} }}} \right|^{2} } \\ \end{array}$$

(11)

where $\:{Y}_{b}$ is the bare sheet background, $\:{Y}_{\text{eff}}^{\left(bg\right)}$ is non-resonant admittance, $\:{{\Gamma\:}}_{\mu\:}={\gamma\:}_{\mu\:,i}+{\gamma\:}_{\mu\:,e}$, $\:{\kappa\:}_{\mu\:}$ are weakly-coupled sideband residues, and $\:{\xi\:}_{\mu\:\nu\:}$ the mutual-coupling-induced splitting term.

Let the analyte occupy the superstrate ($\:{\epsilon\:}_{a}={n}_{a}^{2}$). First-order frequency shift of mode $\:\nu\:$ by a small permittivity change $\:{\Delta\:}\epsilon\:\left(\mathbf{r}\right)$ is

$$\:\frac{{\Delta\:}{\omega\:}_{\nu\:}}{{\omega\:}_{\nu\:}}\approx\:-\frac{1}{2}\hspace{0.17em}\frac{{\int\:}_{V}{\Delta\:}\epsilon\:\left(\mathbf{r}\right)\hspace{0.17em}\left|{\mathbf{E}}_{\nu\:}\right(\mathbf{r}){|}^{2}\hspace{0.17em}dV}{{\int\:}_{V}\left[\epsilon\:\left(\mathbf{r}\right)|{\mathbf{E}}_{\nu\:}{|}^{2}+\mu\:(\mathbf{r}\left)\right|{\mathbf{H}}_{\nu\:}{|}^{2}\right]dV}.$$

(12)

If $\:{\Delta\:}\epsilon\:$ is confined to the analyte region $\:{{\Omega\:}}_{a}$ with $\:{\Delta\:}\epsilon\:=2{n}_{a}{\Delta\:}n$,

$$\:{S}_{\nu\:}\equiv\:\frac{\partial\:{f}_{\nu\:}}{\partial\:{n}_{a}}=-\frac{{f}_{\nu\:}}{2}\hspace{0.17em}\frac{{\int\:}_{{{\Omega\:}}_{a}}2{n}_{a}\hspace{0.17em}|{\mathbf{E}}_{\nu\:}{|}^{2}\hspace{0.17em}dV}{{\int\:}_{V}\left[\epsilon\:|{\mathbf{E}}_{\nu\:}{|}^{2}+\mu\:|{\mathbf{H}}_{\nu\:}{|}^{2}\right]dV}\:\text{(Hz/RIU)}.$$

(13)

Graphene gating tunes overlap via $\:\partial\:{f}_{\nu\:}/\partial\:{\mu\:}_{c}$, obtained by differentiating the eigenproblem with respect to $\:{\sigma\:}_{g}\left({\mu\:}_{c}\right)$:

$$\:\frac{\partial\:{f}_{\nu\:}}{\partial\:{\mu\:}_{c}}=\frac{{f}_{\nu\:}}{2}\hspace{0.17em}\frac{{\int\:}_{{S}_{g}}\mathfrak{R}\left\{\frac{\partial\:{\sigma\:}_{g}}{\partial\:{\mu\:}_{c}}\right\}\hspace{0.17em}|{\mathbf{E}}_{\parallel\:,\nu\:}{|}^{2}\hspace{0.17em}dS}{{\int\:}_{V}\left[\epsilon\:|{\mathbf{E}}_{\nu\:}{|}^{2}+\mu\:|{\mathbf{H}}_{\nu\:}{|}^{2}\right]dV}.$$

(14)

From measured spectra $\:R(\omega\:,{n}_{a},{\mu\:}_{c})$, the common figures are

$$\:\begin{array}{c}{Q}_{\nu\:}=\frac{{\omega\:}_{\nu\:}}{2{{\Gamma\:}}_{\nu\:}},\\\:\text{F}\text{W}\text{H}\text{M}=\frac{{\omega\:}_{\nu\:}}{{Q}_{\nu\:}},\\\:\text{F}\text{O}\text{M}=\frac{{S}_{\nu\:}}{\text{FWHM}}\:\left({\text{RIU}}^{-1}\right).\end{array}$$

(15)

Define an in-plane rotation by angle $\:\varphi\:$ relative to BP armchair axis. The effective sheet conductivity seen by a linearly polarized plane wave is

$$\:\begin{array}{c}{\sigma\:}_{\text{eff}}^{\left(BP\right)}\left(\varphi\:\right)={\sigma\:}_{x}{\text{c}\text{o}\text{s}}^{2}\varphi\:+{\sigma\:}_{y}{\text{s}\text{i}\text{n}}^{2}\varphi\:\\\:\Rightarrow\:{Y}_{\text{eff}}\left(\varphi\:\right)={Y}_{\text{iso}}+{\alpha\:}_{a}\frac{1}{{L}_{b}^{-1}-i\omega\:{R}_{b}-{\omega\:}^{2}{C}_{b}\left(\varphi\:\right)}.\end{array}$$

(16)

Hence the rectangular mode splits with polarization:

$$\:\begin{array}{c}{\omega\:}_{b}\left(\varphi\:\right)\approx\:{\omega\:}_{b,0}\sqrt{\frac{\mathfrak{I}\left\{{\sigma\:}_{\text{ref}}\right\}}{\mathfrak{I}\left\{{\sigma\:}_{\text{eff}}^{\left(BP\right)}\right(\varphi\:\left)\right\}}},\\\:{{\Gamma\:}}_{b,i}\left(\varphi\:\right)\propto\:R\left\{{\sigma\:}_{\text{eff}}^{\left(BP\right)}\right(\varphi\:\left)\right\}.\end{array}$$

(17)

For air / sheet / SiO$\:{}_{2}$($\:d$, $\:{\epsilon\:}_{d}$) / Si($\:{\epsilon\:}_{Si}$), the input impedance looking into the stack is

$$\begin{array}{*{20}c} {Z_{{in}} = Z_{d} \frac{{Z_{{Si}} + iZ_{d} \tan \left( {k_{d} d} \right)}}{{Z_{d} + iZ_{{Si}} \tan \left( {k_{d} d} \right)}}} \\ {Z_{{_{l} }}^{{{\raise0.5ex\hbox{$\scriptstyle {TE}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {TM}$}}}} = \left\{ {\begin{array}{*{20}l} {{\raise0.7ex\hbox{${\eta _{l} }$} \!\mathord{\left/ {\vphantom {{\eta _{l} } {\cos \theta _{l} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\cos \theta _{l} }$}}} \hfill & {(TE)} \hfill \\ {\:{\raise0.7ex\hbox{${\eta _{l} \,\cos \theta _{l} }$} \!\mathord{\left/ {\vphantom {{\eta _{l} \,\cos \theta _{l} } { \in _{l} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${ \in _{l} }$}}} \hfill & {\:(TM)} \hfill \\ \end{array} } \right.} \\ {k_{d} = \frac{{\omega \:}}{c}\sqrt {\smallint \:_{d} - \sin ^{2} \theta \:} } \\ \end{array} \:$$

(18)

Insert $\:{Z}_{\text{in}}$ into the sheet formulas in "Introduction" for exact Fresnel dressing of the metasurface. Given measured complex $\:r,t$, a stable retrieval for the (co-polar) effective sheet admittance is

$$\:{Y}_{\text{eff}}={\eta\:}_{0}^{-1}\left(\frac{1-t-r}{t}\right)-{Y}_{\text{stack}},$$

(19)

with $\:{Y}_{\text{stack}}\equiv\:({Z}_{\text{in}}{)}^{-1}$. Fitting $\:{Y}_{\text{eff}}$ to the rational form in Sect. 3 yields modal $\:{\omega\:}_{\nu\:},{{\Gamma\:}}_{\nu\:,i},{{\Gamma\:}}_{\nu\:,e}$ and coupling $\:{J}_{\mu\:\nu\:}$.

At higher in-plane momentum ($\:{k}_{\parallel\:}/\omega\:\sim\:0.1$–$\:0.3/c$) or ultra-narrow gaps, include spatial dispersion via hydrodynamic-like kernels for each sheet,

$$\:\begin{array}{c}{\mathbf{J}}_{s}+{\mathcal{l}}^{2}{\nabla\:}_{\parallel\:}\left({\nabla\:}_{\parallel\:}\cdot\:{\mathbf{J}}_{s}\right)={\varvec{\upsigma\:}}_{0}\left(\omega\:\right)\cdot\:{\mathbf{E}}_{\parallel\:},\\\:{\mathcal{l}}^{2}\equiv\:\frac{{\beta\:}^{2}}{\omega\:(\omega\:+i{\Gamma\:})},\end{array}$$

(20)

which renormalizes $\:{L}_{\nu\:}$ and produces a weak blue-shift $\:\propto\:{\mathcal{l}}^{2}⟨{k}_{\parallel\:}^{2}⟩$⟨{k}_{\parallel\:}^{2}⟩\)

While the current design measures refractive index variations, specificity to TB biomarkers requires functionalization of the resonator surfaces with biomolecule-specific recognition layers such as antibodies, aptamers, or molecularly imprinted polymers. This bio-recognition strategy ensures selective binding to TB proteins, while washing protocols and surface blocking agents (e.g., BSA) minimize nonspecific adsorption. Incorporating such biochemical modifications aligns with established biosensing practices and enables discrimination of TB biomarkers from background proteins.

Results and discussion

Fig. 2

Transmittance spectra of the sensor for varying refractive index (RI) values of the surrounding medium, ranging from 1.3341 to 1.42383 across 0.26-0.38THz.

Fig. 3

Transmittance spectra of the sensor for varying refractive index (RI) values of the surrounding medium, ranging from 1.3341 to 1.42383 across 0.38-0.46THz.

This optical sensing device exhibits dual-band refractive index detection capabilities, functioning based on electromagnetic wave behaviour in materials with varying optical characteristics. The device’s operational mechanism relies on the fundamental interaction between electromagnetic radiation and medium properties, mathematically described by the wave vector relationship:

$$k{\text{ }} = {\text{ }}(2\Pi /\lambda _{0} ){\text{ }} \times n\, = \,(2\Pi f/c) \times n$$

(21)

where this equation establishes the connection between optical frequency f, material refractive index n, and vacuum light velocity c. The sensing system produces quantifiable optical responses that correlate directly with refractive index variations, as illustrated in Figs. 2a-b and 3a-b, along with Table 1. Testing protocols encompassed six specific refractive index points from 1.3341 to 1.42383, spanning approximately 0.09 index units. Optical transmission characteristics were analysed across two separate frequency regions to establish comprehensive performance metrics. Within the initial frequency range, the device shows distinct correlations between index magnitude and both transmission peak intensities and resonance positions. Transmission efficiency decreases progressively from 66.791% at index 1.3341 to 65.748% at index 1.42383, while corresponding peak frequencies shift downward from 0.337 THz to 0.320 THz. This response pattern indicates a transmission coefficient gradient of approximately − 1.13% per index unit, demonstrating predictable optical modulation throughout the tested range. The frequency response data reveals substantial wavelength tuning capabilities, with resonance peaks migrating from 0.345 THz to 0.315 THz as shown in detailed spectral representations. This 30 GHz adjustment range translates to spectral responsivity of -334.4 GHz per index unit, determined by dividing total frequency displacement by index variation. The negative responsivity confirms that elevated index values produce red-shifted resonances, aligning with effective medium theoretical frameworks. Comparable spectral tuning characteristics emerged in the upper frequency domain, where resonance positions shift from 0.43 THz to 0.40 THz across identical index conditions. This equivalent 30 GHz frequency displacement produces matching spectral responsivity of -334.4 GHz per index unit, establishing uniform detection performance between both operational bands. The responsivity consistency across separate spectral zones confirms reliable device function and indicates stable underlying physical processes throughout the operational spectrum.

Fig. 4

Performance analysis of the proposed sensor showing frequency, sensitivity, figure of merit, quality factor, detection limit, resolution, SNR, detection accuracy, and parameter X as functions of refractive index.

Table 1 The performance analysis.

In this regard, Table 1; Fig. 4a–j provides a comprehensive assessment of the sensor’s performance over a refractive index (RI) range of 1.3341 to 1.42383. The resonance frequency (f) gradually declines from 0.337 THz at the lowest RI to 0.32 THz at the highest RI, while the transmission coefficient (Tm) slightly decreases from 0.6679 to 0.6575, demonstrating a stable sensor response across the RI spectrum. The frequency shift (Δf) varies between 0.001 and 0.007 THz, reflecting minor resonance changes corresponding to RI increments. Sensitivity (S), expressed in GHz/RIU, shows notable fluctuations—initially high at 395 GHz/RIU, dropping to 54 GHz/RIU, and then rising to a peak of 180 GHz/RIU—indicating non-linear responsiveness. The figure of merit (FOM) spans 1.455 to 10.683 per RIU, representing the balance between sensitivity and resonance linewidth. The full width at half maximum (FWHM) remains steady at 0.037 THz, signifying consistent resonance sharpness. The quality factor (Q) decreases slightly from 9.108 to 8.649 as RI increases, suggesting minor resonance broadening. Detection limit (DL) values fluctuate between 0.095 and 1.130 RIU, highlighting variation in the minimum detectable RI change. Detection resolution (DR) gradually decreases from 1.752 to 1.664 RIU, implying enhanced resolution at higher RI values. Signal-to-noise ratio (SNR) remains relatively low (0.027–0.189), which could affect detection reliability. The sensor maintains a constant detection accuracy (DA) of 27.027 across all RIs, indicating stable measurement precision. Finally, parameter X, likely associated with a material or design attribute, is minimal (0.001–0.002), suggesting negligible influence on overall sensor performance.

Figure 5 illustrates the functional relationships between resonance frequency and two key parameters: (a) refractive index (RI) and (b) protein biomarker concentration. Linear regression analysis reveals strong correlations for both relationships.

Fig. 5

(a, b) Quantitative Analysis of Resonance Frequency Dependencies.

The relationship between resonance frequency (F) and refractive index exhibits a linear dependence described by:

$${\text{F = - 0}}{\text{.1719 RI + 0}}{\text{.5647 }}$$

(22)

The coefficient of determination (R² = 0.95447) indicates that 95.4% of the variance in resonance frequency can be explained by changes in refractive index, demonstrating excellent linear correlation. The negative slope coefficient (-0.1719) indicates an inverse relationship between these parameters.

Similarly, the resonance frequency demonstrates a linear dependence on protein biomarker concentration (C):

$${\text{F = - 0}}{\text{.0003}}\,{\text{C + 0}}{\text{.3353 }}$$

(23)

This relationship exhibits an even stronger correlation (R² = 0.95622), with 95.6% of the frequency variance attributable to concentration changes. The negative slope coefficient (-0.0003) confirms an inverse proportionality between resonance frequency and biomarker concentration. To further elucidate resonance mechanisms, effective permittivity, permeability, and impedance were retrieved from simulated S-parameters. Results confirm impedance matching near resonance, which explains the high transmittance dips and sensitivity. The effective permittivity exhibits strong dispersive behaviour around resonance, while permeability transitions highlight magnetic dipole contributions from the figure-eight resonators.

Fig. 6

(a, b) Transmittance response of the sensor across the frequency range 0.1–0.6 THz for varying graphene chemical potentials (0.1–0.9 eV). (a) Transmittance spectra illustrating the progressive decrease with increasing chemical potential. (b) Detailed transmittance values at selected frequencies showing the inverse relationship between chemical potential and transmittance.

The influence of graphene chemical potential (GCP) on the sensor’s transmittance response was thoroughly examined over a frequency range of 0.1 to 0.6 THz as depicted in Fig. 6a-b. Transmittance measurements were performed for GCP values varying from 0.1 eV to 0.9 eV, increasing in steps of 0.1 eV, as shown in Fig. 6a and b. The results reveal a clear monotonic decrease in transmittance as the chemical potential increases. Specifically, transmittance dropped from 97.7% at 0.1 eV to 66.7% at 0.9 eV, as detailed in Fig. 6.

Fig. 7

Angular dependence of sensor transmittance from 0° to 80° incidence angles at a fixed frequency. (a) Transmittance spectra demonstrating optimal response at normal incidence and gradual degradation with increasing angle. (b) Plot of transmittance versus incident angle highlighting stable performance up to 30° followed by accelerated decline at higher angles.

Fig. 8

Effect of rectangular resonator length variation on sensor transmittance. (a) Transmittance spectra for lengths ranging from 10 μm to 12 μm in 0.5 μm increments, showing a gradual decrease in transmittance with increasing length. (b) Plot of transmittance drop percentages corresponding to each length, illustrating enhanced electromagnetic interaction and attenuation as the resonator length increases.

Fig. 9

Impact of rectangular resonator width variation on sensor transmittance. (a) Transmittance spectra for widths varying from 0.2 μm to 1 μm in 0.2 μm steps, revealing a non-monotonic change in transmittance. (b) Transmittance drop percentages as a function of width, indicating reduced attenuation and higher transmittance at larger widths due to diminished electromagnetic confinement.

In addition, the sensor’s transmittance dependence on the angle of incidence was investigated over a range of 0° to 80°, in increments of 10°, presented in Fig. 7a and b. The measurements show that transmittance is highest at normal incidence (0°), with a value of approximately 66.7%. As the incident angle increases, transmittance gradually decreases, maintaining relative stability up to 30°, but then declining more sharply at larger angles. For example, transmittance falls to about 26.0% at an 80° angle of incidence. This angular sensitivity highlights important considerations for sensor design, suggesting that optimal performance occurs near normal incidence, while higher angles lead to reduced transmittance and therefore diminished sensor effectiveness. The influence of the rectangular resonator’s geometric dimensions on the sensor’s transmittance response is thoroughly examined through variations in length and width, as illustrated in Figs. 8a–b and 9a–b. For the length variation study, the rectangular length was incrementally increased from 10 μm to 12 μm in steps of 0.5 μm. The corresponding transmittance values exhibit a gradual decrease, with measured drops of 35.694%, 34.012%, 33.118%, 32.657%, and 32.517%, respectively, as shown in Fig. 8a and b. This trend indicates that increasing the length of the rectangular structure enhances the electromagnetic coupling, resulting in stronger attenuation of the transmitted signal. Conversely, the effect of varying the width was analysed by increasing it from 0.2 μm to 1 μm in increments of 0.2 μm. As depicted in Fig. 9a and b, the transmittance drops initially start at 79.748%, then slightly decrease to 79.077%, followed by an unexpected increase to 83.903%, and continue rising to 88.038% and 88.145% for the larger widths. This non-monotonic behaviour suggests that increasing the width beyond a certain threshold reduces the electromagnetic confinement, leading to less pronounced attenuation and higher transmittance values.

Fig. 10

Electric field distribution across the sensor structure at selected frequencies (a) 0.38 THz, (b) 0.41 THz and (c) 0.46 THz.

The spatial and spectral distribution of the electric field $\:\mathbf{E}(\mathbf{r},f)$ associated with the proposed metasurface sensor is comprehensively depicted in Fig. 10a–c for the discrete terahertz operating frequencies $\:f=\{0.38,0.41,0.46\}\hspace{0.25em}\text{T}\text{H}\text{z}$. Specifically, at $\:{f}_{1}=0.38\hspace{0.25em}\text{T}\text{H}\text{z}$ and $\:{f}_{3}=0.46\hspace{0.25em}\text{T}\text{H}\text{z}$, the metasurface demonstrates near-maximal transmittance $\:T\left(f\right)\to\:{T}_{\text{m}\text{a}\text{x}}$ and concomitantly minimal absorptance $\:A\left(f\right)\to\:{A}_{\text{m}\text{i}\text{n}}$, as evidenced by the predominance of deep blue intensity mapping across the resonant elements. Formally, the transmittance and absorptance satisfy the energy conservation relation:

$$\:T\left(f\right)+R\left(f\right)+A\left(f\right)=1,\:\text{where\:}R\left(f\right)\text{\:is\:the\:reflectance,}$$

(24)

with $\:T\left({f}_{1}\right),T\left({f}_{3}\right)\approx\:0.98$ and $\:A\left({f}_{1}\right),A\left({f}_{3}\right)\approx\:0.02$, indicating that the incident electromagnetic fiel

$$\:{\mathbf{E}}_{\text{i}\text{n}\text{c}}(\mathbf{r},t)={\mathbf{E}}_{0}{e}^{i(\mathbf{k}\cdot\:\mathbf{r}-2\pi\:ft)}$$

(25)

experiences negligible attenuation. Conversely, at the intermediate frequency $\:{f}_{2}=0.41\hspace{0.25em}\text{T}\text{H}\text{z}$, a substantial absorption peak arises, $\:A\left({f}_{2}\right)\approx\:0.87$, accompanied by a pronounced reduction in transmittance $\:T\left({f}_{2}\right)\approx\:0.13$, which manifests as brown coloration on the resonator surfaces. This phenomenon can be analytically described by the localized electric field enhancement factor $\:\eta\:(\mathbf{r},f)$

$$\:\eta\:(\mathbf{r},f)=\frac{\left|\mathbf{E}\right(\mathbf{r},f){|}^{2}}{|{\mathbf{E}}_{0}{|}^{2}},\:\underset{\mathbf{r}\in\:\text{resonator}}{\text{m}\text{a}\text{x}}\eta\:(\mathbf{r},{f}_{2})\gg\:1,$$

(26)

indicating strong confinement of $\:\mathbf{E}(\mathbf{r},f)$ within the resonant structures. This frequency-dependent spatial confinement, expressed as:

$$\:\nabla\:\cdot\:\left({ϵ}_{r}\right(\mathbf{r}\left)\mathbf{E}\right(\mathbf{r},f\left)\right)=0,\:\nabla\:\times\:(\nabla\:\times\:\mathbf{E}(\mathbf{r},f\left)\right)={\mu\:}_{0}{ϵ}_{0}\frac{{\partial\:}^{2}\mathbf{E}(\mathbf{r},f)}{\partial\:{t}^{2}},$$

(27)

plays a pivotal role in enhancing analyte–field interactions, thereby amplifying the effective sensor response. Consequently, such selective resonant field localization at $\:{f}_{2}=0.41\hspace{0.25em}\text{T}\text{H}\text{z}$ underpins the high-sensitivity detection capability of the metasurface, facilitating increased coupling between the analyte’s dielectric perturbations and the confined electromagnetic energy, which ultimately improves the precision and performance of the proposed sensing platform.

Table 2 Comparison of sensor sensitivity, materials, and applications between the proposed design and existing technologies .

To compare the performance of our sensor with some of its counterparts, Table 2 presents a comparative analysis of sensor performance, focusing on sensitivity, material composition, and biomedical applications. The proposed sensor exhibits a high sensitivity of 395 GHz/RIU, outperforming most existing designs, particularly in COVID-19 detection. Many of the previously reported sensors utilize graphene, highlighting its versatility and excellent plasmonic and electronic properties for biosensing applications. The range of biomedical targets includes malaria, tuberculosis, proteins, sperm, haemoglobin, cancer biomarkers, and COVID-19. Notably, the proposed design also covers a broader refractive index range (1.3341–1.42383 RIU), demonstrating its enhanced adaptability for diverse biomedical sensing scenarios.

Bayesian ridge regressor

The Bayesian Ridge Regressor represents a linear regression approach that uses Bayesian methods to determine regression coefficients. Rather than calculating fixed values for model parameters like traditional linear regression does, this Bayesian variant considers parameters as probabilistic variables with assumed prior distributions, usually normal distributions^{53,54,55,56,57}. This probabilistic framework enables the model to capture uncertainty in parameter estimation, resulting in more reliable predictions, particularly when dealing with correlated predictors or small datasets that can cause standard least squares methods to perform poorly. The technique inherently includes regularization through its prior assumptions, naturally constraining large coefficients to prevent overfitting while preserving the ability to model intricate patterns in the data.The Bayesian Ridge Regressor can be formally expressed as an extension of the classical linear regression model, defined by the relationship^58,59,60:

$$\:y = X\beta \, + \, \in ,\,\, \in \sim \:{\mathcal{N}}(0,\sigma \:^{2} I)$$

(28)

where $\:\text{y}\in\:{\mathbb{R}}^{n\times\:1}$ is the vector of observed responses, $\:\text{X}\in\:{\mathbb{R}}^{n\times\:p}$ represents the design matrix of $\:p$ predictors for $\:n$ observations, and $\:{\upbeta\:}\in\:{\mathbb{R}}^{p\times\:1}$ denotes the vector of regression coefficients. In the Bayesian framework, these coefficients are treated as stochastic variables with prior distributions, typically Gaussian:

$$\:{\upbeta\:}\sim\:\mathcal{N}(0,{\lambda\:}^{-1}\text{I}),\:\lambda\:\sim\:\text{Gamma}({\alpha\:}_{\lambda\:},{\beta\:}_{\lambda\:}),$$

(29)

where $\:\lambda\:$ is the precision (inverse variance) of the prior, and $\:{\alpha\:}_{\lambda\:},{\beta\:}_{\lambda\:}$ are hyperparameters controlling its shape. The likelihood of the observed data under the model is given by:

$$\:p(\text{y}\mid\:\text{X},{\upbeta\:},\alpha\:)=(2\pi\:{\alpha\:}^{-1}{)}^{-n/2}\text{e}\text{x}\text{p}\left\{-\frac{\alpha\:}{2}\parallel\:\text{y}-\text{X}{\upbeta\:}{\parallel\:}_{2}^{2}\right\},\:\alpha\:\sim\:\text{Gamma}({\alpha\:}_{\alpha\:},{\beta\:}_{\alpha\:}),$$

(30)

with $\:\alpha\:$ representing the precision of the observation noise. The posterior distribution of the coefficients is then derived using Bayes’ theorem:

$$\:p({\upbeta\:}\mid\:\text{y},\text{X},\alpha\:,\lambda\:)=\frac{p(\text{y}\mid\:\text{X},{\upbeta\:},\alpha\:)\hspace{0.17em}p({\upbeta\:}\mid\:\lambda\:)}{{\int\:}_{{\upbeta\:}}p(\text{y}\mid\:\text{X},{\upbeta\:},\alpha\:)\hspace{0.17em}p({\upbeta\:}\mid\:\lambda\:)\hspace{0.17em}d{\upbeta\:}}.$$

(31)

This formulation inherently regularizes the regression coefficients through the prior precision $\:\lambda\:$, effectively penalizing excessively large coefficients and mitigating overfitting, particularly in cases with multicollinearity ($\:\text{corr}({\text{X}}_{i},{\text{X}}_{j})\to\:1$) or limited sample size ($\:n\ll\:p$).

Operationally, the Bayesian Ridge Regressor estimates the posterior mean $\:\mathbb{E}[{\upbeta\:}\mid\:\text{y},\text{X}]$ and covariance $\:\text{Cov}[{\upbeta\:}\mid\:\text{y},\text{X}]$ as

$$\mu _{{\beta \:}} = (\lambda \:I + \alpha \:X^{T} X)^{{ - 1}} (\alpha \:X^{T} y),\:\Sigma \:_{{\beta \:}} = (\lambda \:I + \alpha \:X^{T} X)^{{ - 1}}$$

(32)

while simultaneously optimizing the hyperparameters $\:\alpha\:$ and $\:\lambda\:$ via type-II maximum likelihood (evidence maximization):

$$\:\{\widehat{\alpha\:},\widehat{\lambda\:}\}=\text{a}\text{r}\text{g}\underset{\alpha\:,\lambda\:}{\text{m}\text{a}\text{x}}\hspace{0.17em}\text{l}\text{o}\text{g}{\int\:}_{{\upbeta\:}}p(\text{y}\mid\:\text{X},{\upbeta\:},\alpha\:)\hspace{0.17em}p({\upbeta\:}\mid\:\lambda\:)\hspace{0.17em}d{\upbeta\:}.$$

(33)

This probabilistic framework not only produces point predictions $\:\widehat{\text{y}}=\text{X}{{\upmu\:}}_{\beta\:}$ but also quantifies predictive uncertainty through posterior confidence intervals

$$\:\hat{y}_{i} \pm \:z_{{\gamma \:/2}} \sqrt {x_{i}^{{{ \top }\:}} \Sigma \:_{{\beta \:}} x_{i} + \alpha \:^{{ - 1}} }$$

(34)

enabling informed decision-making in risk-sensitive applications such as financial modeling, bioinformatics, and engineering systems. For the regression dataset, input features included refractive index, incidence angle, and resonator geometry (length, width). Each parameter was varied systematically to create a balanced dataset spanning practical sensor conditions. Bayesian Ridge Regression was selected due to its robustness against multicollinearity, and polynomial feature expansion (up to third order) was applied to capture nonlinear interactions.

Fig. 11

Depicts scatter plots showing the variations in refractive indices as predicted by the model’s behaviour.

Fig. 12

Depicts Heat map plots showing the variations in refractive indices as predicted by the model’s behaviour.

Fig. 13

Depicts scatter plots showing the variations in θ as predicted by the model’s behaviour.

Fig. 14

depicts scatter plots showing the variations in θ as predicted by the model’s behaviour.

The scatter plots presented in Fig. 11a-i comprehensively illustrate the predictive capability of the Bayesian Ridge Regressor for variations in refractive index (RI). Meanwhile, the model achieves high coefficient of determination (R²) values of approximately 86%, accompanied by almost negligible error metrics such as Mean Absolute Error (MAE) and Root Mean Square Error (RMSE), over a refractive index range spanning from 1.3341 to 1.42383. This indicates a strong correlation between the predicted and actual RI values, affirming the robustness of the model in capturing subtle changes within this range.

Complementing these findings, the heatmaps shown in Fig. 12a-d provide a detailed visualization of how the model’s performance improves with increasing polynomial degrees used in the regression. The R² scores notably increase, covering a spectrum from 80% up to a perfect 100%, signifying that higher-order polynomial features enable the model to capture more complex nonlinear relationships within the dataset. This enhancement in accuracy across the entire parameter space underscores the model’s adaptability and precision in predicting RI variations under different conditions.

Similarly, the scatter plots in Fig. 13a-i focus on the model’s predictive performance concerning the angular parameter θ, which varies from 0° to 80°. Here, the Bayesian Ridge Regressor demonstrates an even stronger fit, attaining R² values of approximately 96%, with minimal error measurements, confirming the model’s efficacy in accurately predicting angular-dependent behaviours. This high level of accuracy indicates that the model successfully generalizes across the full range of incident angles, maintaining consistency in its predictions.

Further insights are provided by the heatmaps in Fig. 14a-d, which reveal that increasing the polynomial degree once again leads to a marked improvement in performance. The R² values rise steadily from 80% to 100%, highlighting the significant role of polynomial complexity in optimizing the model’s fit. These results collectively emphasize the exceptional precision and reliability of the Bayesian Ridge Regressor in modelling both refractive index variations and angular dependencies, ensuring comprehensive coverage and dependable predictions throughout the studied parameter space.

Fig. 15

Fabrication pathway of the tri-material metasurface sensor, showing sequential steps from substrate preparation and lithography to 2D material deposition and final structural characterization.

Finally, Fig. 15 presents a four-stage laboratory workflow for fabricating the proposed tri-material metasurface sensor. The process begins with the preparation of a silicon wafer coated with a thin silicon dioxide layer, which provides both stability and dielectric isolation. This cleaned and polished substrate ensures an ideal foundation for precise nanoscale patterning. Next, electron-beam lithography is employed to define intricate geometries such as the figure-eight, rectangular, and square resonators, enabling high-resolution nanoscale structuring on the wafer. Following lithography, the deposition of the three functional two-dimensional materials is carried out. MXene is coated on the figure-eight resonators, black phosphorus on the rectangular resonators, and graphene on the square resonators using controlled deposition and transfer techniques. After lift-off to remove excess coatings, a well-defined metasurface array is achieved. The final stage involves structural and compositional verification through advanced microscopy and spectroscopy methods, ensuring the correct integration of all materials. This systematic progression demonstrates how numerical designs transition into a practical device ready for optical and terahertz testing.

Conclusion

The proposed terahertz metamaterial sensor demonstrates a strong potential for advancing medical diagnostics through its integration of advanced materials, optimized resonator geometry, and machine learning analysis. Achieving a sensitivity of 395 GHz/RIU with R² > 0.95 for refractive index and protein biomarker detection, the design ensures reliable quantification relevant to brain tumor diagnosis. Its stable spectral response (FWHM = 0.037 THz) and high-quality factor (8.649–9.108) confirm precision, while tunability via graphene chemical potential offers application-specific adaptability. Additionally, machine learning further enhances predictive accuracy (R² ≈ 86% for refractive index and 96% for angular dependence), supporting potential real-time use. Future work should address low signal-to-noise ratios, incorporate clinical validation with real biomarkers, and explore surface functionalization strategies. Overall, this study provides a robust theoretical framework and a promising pathway toward practical, non-invasive neurological diagnostics.