Investigation on dynamical perspective of soliton solutions to the nonlinear integrable Akbota equation through a generalized analytical technique

Abstract

In this study, we investigate the nonlinear integrable Akbota equation (NLIAE), which is an important equation due to its energy-based nature and applications across various fields of science and engineering. Novel soliton solutions are investigated using the auxiliary equation method (AEM) applied to the NLIAE. The obtained soliton solutions exhibit unique, interesting, and diverse physical structures in the context of solitons, solitary, and traveling waves. To understand the physical implications of the derived solutions, a detailed computational analysis is performed, and several solutions are graphically represented in three formats contour, two–dimensional, and three–dimensional using numerical simulations with the aid of Mathematica. The graphical analysis reveals that the derived solutions possess novel physical structures of solitary waves and solitons, including periodic waves, kink waves, peakon bright and dark waves, singular bright and dark solitons, anti–kink waves, mixed kink–bright waves, and mixed anti–kink bright waves. The obtained results are expected to have potential applications in various domains of physical science and engineering, such as optics, ocean engineering, fluid mechanics, nonlinear dynamics, soliton and fractal theory, and other areas of nonlinear science. The findings demonstrate that the AEM is not only effective and straightforward but also an efficient tool for obtaining soliton solutions of various integrable equations, outperforming several existing methods. Moreover, this research presents novel solutions that reveal physical behaviors not previously reported in the literature.

Introduction

The study of soliton solutions of nonlinear evolution equations continues to attract researchers, fostering deeper understanding of nonlinear systems and inspiring innovations across various scientific domains. The theories of solitons and fractal waves, which arise from the investigation of nonlinear partial differential equations (NLPDEs), reveal remarkable physical phenomena^1,2,3,4. Solitary waves maintain their shape and velocity during propagation. In the 19th century, Scott Russell and later Norman Zabusky introduced the concept of solitary waves for the first time. A solitary wave is a self-reinforcing wave that appears in diverse fields such as optics, particle physics, nonlinear dynamics, plasma physics, and fluid dynamics^5,6,7,8,9. A soliton is a special type of solitary wave characterized by exceptional strength and stability, offering promising applications in quantum computing, optical systems, and communication technologies. The accurate understanding and physical interpretation of many natural and engineering phenomena strongly depend on the systematic investigation of NLPDEs^{10,11,12,13,14}. The fundamental processes of nonlinear phenomena, such as energy transfer, temporal localization, the presence of topological regimes, and steady-state deviations can be described through explicit and analytical formulations of NLPDEs. The main concept of concentration models, followed by their extended versions often referred to as dispersive interaction models, was developed several decades ago. In recent years, the role of nonlinear evolution equations (NLEEs) in scientific research has become increasingly significant. They have found wide-ranging applications in mathematical physics, mathematical biology, optical fiber systems, mechanics, hydrodynamics, and chemical physics, providing a powerful framework to explain complex behaviors in these fields^{15,16,17,18,19}.

Researchers have discovered that nonlinear partial differential equations (NLPDEs) can be effectively used to characterize various nonlinear physical phenomena. NLPDEs serve as essential tools for investigating nonlinear behaviors across diverse scientific fields. Disciplines such as fluid mechanics, meteorology, chemistry, biological sciences, engineering, plasma physics, optics, and the aerospace industry employ NLPDEs to model and describe complex physical processes^{20,21,22,23,24}. Several well-known NLPDEs have been developed to represent different dynamic processes and nonlinear activities, including the Chen–Lee–Liu equation²⁵, the three–dimensional mKdV–ZK model²⁶, the damped Korteweg–de Vries equation²⁷, the Kudryashov–Sinelshchikov equation²⁸, the Schrödinger equation²⁹, and the Jaulent–Miodek hierarchy equation³⁰. These equations are widely applied to simulate a broad range of physical events and dynamical systems exhibiting nonlinear characteristics. Analysts and researchers continue to explore intermediate approaches that attract significant attention due to their extensive applications across multiple disciplines of modern science and engineering.

The study of NLPDEs is particularly interesting because no single efficient method can be universally applied to all such equations; therefore, each equation often needs to be investigated individually. Generally, three main approaches are used to analyze NLPDEs: numerical, qualitative, and analytical methods. In recent years, significant progress has been made in developing various efficient and powerful analytical techniques to obtain exact and approximate solutions of NLPDEs. Some of the well-known methods include the $(\varphi ^{'}/\varphi , 1/\varphi )-$expansion method³¹, the extended modified auxiliary equation mapping method³², the improved $F-$expansion method^33,34,35, the extended simple equation technique^36,37, the Sardar sub-equation approach³⁸, the extended direct algebraic mapping method^39,40,41, the $(G'/G)$-expansion approach⁴², the Kudryashov auxiliary equation method⁴³, the extended modified rational expansion method⁴⁴, the tanh–coth approach⁴⁵, the $(-\Phi (\eta ))$-function technique⁴⁶, the Riccati–Bernoulli sub-optimal differential equation method⁴⁷, the Jacobi elliptic function expansion technique⁴⁸, and the modified auxiliary equation method⁴⁹. In addition to these, several other analytical and semi-analytical techniques have also been employed to study and analyze nonlinear models^50,51,52.

Among these methods, the auxiliary equation method (AEM) has emerged as one of the most effective and versatile analytical tools for obtaining exact solutions of NLPDEs. The AEM is highly regarded for its simplicity, flexibility, and ability to generate a wide range of soliton, periodic, and other nonlinear wave solutions. Unlike many traditional approaches, the AEM does not require complex transformations or restrictive assumptions, making it suitable for a broad class of nonlinear models. Moreover, the method can be easily extended or modified to produce novel types of exact solutions, which reveal important physical characteristics of nonlinear systems. Therefore, in this study, we apply the AEM to explore novel soliton solutions of the nonlinear integrable Akbota equation (NLIAE) and to analyze their diverse physical structures and behaviors.

Moreover, in recent years, mathematicians and researchers have carried out extensive studies on nonlinear partial differential equations (NLPDEs). In particular, many experts have focused on investigating chaotic behavior, optical soliton solutions, and solitary wave solutions of NLPDEs, leading to several significant findings. However, research on the chaotic dynamics, optical solitons, and solitary wave structures of more complex NLPDEs is still in its early developmental stage. Motivated by these ongoing studies, the present work investigates the optical soliton theory and solitary wave solutions of the complex nonlinear Akbota equation. This research is built upon the theoretical foundation established by earlier studies on optical soliton theory. The nonlinear Akbota equation^{53,54,55,56,57,58,59,60} is expressed as follows:

$$\begin{aligned}&\alpha q_{\text {xx}}+\beta q_{\text {xt}}+\text {iq}_t+\gamma q v=0,\nonumber \\&v_x-2\epsilon \left( \alpha \left| q|^2{}_x+\beta \right| q|^2{}_t\right) =0. \end{aligned}$$

(1)

Here $\alpha ,~\beta , \gamma$ are constants and $\varepsilon =\pm 1.$ The v(x, t),  q(x, t) represent the real and complex unknown functions, respectively. The nonlinear Akbota equation can be transformed into other well-known nonlinear equations under specific conditions. For instance, when $\alpha =0,$ then Eq. (1), change into nonlinear Kuralay equation and when $\beta =0,$ Eq. (1) change into nonlinear Schrödinger equation.

The nonlinear Akbota equation, which is a well-known Heisenberg ferromagnet type equation, is particularly useful for studying the geometry of curves and surfaces, as well as nonlinear phenomena in magnetic systems. Several researchers have conducted extensive investigations and reported a variety of solutions to the integrable Akbota equation in previous studies. Such as, Kong and Guo obtained analytical wave solutions, including semi-rational, rogue, and breather wave solutions, to the integrable Akbota equation using the Darboux transformation approach⁵³. Mathanaranjan et al. constructed conservation laws, optical soliton solutions, and stability results for the nonlinear Akbota equation using an extended auxiliary equation approach⁵⁴. Faridi et al. presented solitonic wave profiles by employing an improved Sardar sub-equation scheme⁵⁵. Tariq et al. determined exact solutions of the nonlinear integrable Akbota equation using two distinct methods: the Sardar sub-equation and the modified Khater techniques⁵⁶. Li and Zhao investigated bifurcation structures, chaotic behavior, and solitary wave solutions for the Akbota equation using analytical methods⁵⁷. Faridi et al. further explored solitonic and solitary wave solutions over a wide range of cases using the $\phi ^{6}$ method⁵⁸. Another study reported soliton solutions of the nonlinear Akbota equation through three different techniques namely, the general projective Riccati method, the Sardar sub-equation approach, and the $(\frac{G^{'}}{G^{2}})-$expansion methods⁵⁹. More recently, Iqbal et al. investigated optical soliton solutions of the nonlinear Akbota equation using the improved F–expansion method⁶⁰.

In the present work, we investigate novel optical soliton solutions of the nonlinear Akbota equation using a new auxiliary equation technique. The proposed method proves to be highly efficient, comprehensive, and capable of producing a wider range of exact solutions compared to existing approaches. The obtained soliton solutions exhibit diverse physical structures, including periodic waves, kink and anti–kink waves, peakon bright and dark solitons, singular bright and dark solitons, as well as mixed kink–bright and mixed anti–kink bright solitons. These results not only reveal rich and complex nonlinear dynamics but also highlight the versatility of the proposed approach in capturing various physical configurations. Moreover, the solutions derived in this study are novel, accurate, and physically meaningful, offering valuable insights into complex real-world nonlinear phenomena described by nonlinear mathematical models.

The remaining part of this paper organized as follows. The auxiliary equation approach is explain in section 2. While Section 3 presents the formulation of the governing equation. In Section 4, we explore the soliton solutions obtained through the AEM. Section 5 provides the numerical simulations of the derived solutions, and Section 6 compares the constructed results with those obtained using other existing methods. Finally, Section 7 concludes the paper with some remarks and future perspectives.

Brief summery of enhanced approach

The nonlinear equation with partial derivative of space and time consider as

$$\begin{aligned} R(q, q_{t}, q_{x}, q_{tt}, q_{xx},...)=0. \end{aligned}$$

(2)

While R called function of polynomial to the $q_{t}, q_{x}.$ To get the nonlinear ordinary differential equation (NLODE), then apply the transform of wave as

$$\begin{aligned} q(x,t)=\hbar \left( \zeta \right) e^{i \varTheta },~~~ \varTheta = -\kappa x +\Lambda t, \quad \quad \zeta = x-\wp t. \end{aligned}$$

(3)

Where $\kappa , \Lambda ,\Xi ,$ and $\wp$ are parameters. Substituting Eq. (3) in Eq. (2), then obtain nonlinear ordinary differential equation (NLODE) as

$$\begin{aligned} S\left( \hbar , \hbar _{ \zeta }, \hbar _{ \zeta \zeta }, \hbar _{ \zeta \zeta \zeta }, ...\right) =0. \end{aligned}$$

(4)

Let us the solution in generalized form of Eq. (4) given as

$$\begin{aligned} \hbar ( \zeta )=\sum _{i=0}^n b_i \varphi ^i\left( \zeta \right) . \end{aligned}$$

(5)

The function $\varphi (\zeta )$ satisfying the given equation.

$$\begin{aligned} \left( \varphi ^{'}(\zeta )\right) ^2=\nabla _1 \varphi ^{2} ( \zeta )+\nabla _2 \varphi ^{3} (\zeta )+\nabla _3 \varphi ^{4} ( \zeta ). \end{aligned}$$

(6)

While $\nabla _1,~\nabla _2,~\nabla _3,$ are parameters. The Eq. (6) having these exact solutions as

Case–I

$$\begin{aligned} \varphi (x)=-\frac{\nabla _1 \nabla _2 \text {sech}^2\left( \frac{\sqrt{\nabla _1} \zeta }{2}\right) }{\nabla _2^2-\nabla _1 \nabla _3 \left( 1-\tanh \left( \frac{\sqrt{\nabla _1} \zeta }{2}\right) \right) {}^2},~~\text {when}~~\nabla _1>0. \end{aligned}$$

Case–II

$$\begin{aligned} \varphi (x)=\frac{2 \nabla _1 \text {sech}\left( \sqrt{\nabla _1} \zeta \right) }{\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}-\text {sech}\left( \sqrt{\nabla _1} \zeta \right) -\nabla _2},~~\text {when}~~\nabla _2^2-4 \nabla _1 \nabla _3>0. \end{aligned}$$

To calculate the value of integer n then apply the homogeneous balance rule on Eq. (4). Substitute the Eq. (5) in Eq. (4) and collect each cofactors of $\varphi ^{i}(\zeta ),$ then to secure the algebraic equations then make each cofactors equal to zero. To calculate the unknown values to solve the algebraic equations through any computation tool. Inserting the calculated values in Eq. (5) and examined the exact solutions of Eq. (2).

The formulation of governing model

Wave transform for the Eq. (1), taken as

$$\begin{aligned}&q ( x,t )= \Phi ( \zeta ) e^{i \vartheta (x, t)}, \quad \quad v( x,t )= \varphi (\zeta ),\nonumber \\&\vartheta = -\kappa x+ \omega t, \quad \quad \zeta =x-\nu t. \end{aligned}$$

(7)

While $\omega , \kappa ,$ and $\nu$ are parameters. Applying Eq. (7) on Eq. (1) then separate the real and imaginary part of obtaining ordinary differential equation as

$$\begin{aligned} & \left( -\kappa ^{2} \alpha -\omega +\kappa \beta \omega + \gamma \varphi \right) \Phi +\left( \alpha -\beta \nu \right) \Phi ^{''} =0, \end{aligned}$$

(8)

$$\begin{aligned} & \left( -2 \kappa \alpha - \nu +\kappa \beta \nu + \beta \omega \right) \Phi ^{'}=0, \end{aligned}$$

(9)

$$\begin{aligned} & -4 \varepsilon \left( \alpha -\beta \nu \right) \Phi \Phi ^{'}+\varphi ^{'} =0. \end{aligned}$$

(10)

From Eq. (9), we obtained as

$$\begin{aligned} \omega =\frac{ 2 \kappa \alpha + \nu -\kappa \beta \nu }{\beta }. \end{aligned}$$

(11)

Integrate Eq. (10) under $\varsigma ,$ and consider integration constant is zero, secured as

$$\begin{aligned} \varphi =2 \varepsilon (\alpha -\beta \nu )\Phi ^{2}. \end{aligned}$$

(12)

Insert Eq. (12) and Eq. (11) in Eq. (10), we obtained as

$$\begin{aligned} \left( - \nu +\kappa (-2+\kappa \beta ) (\alpha -\beta \nu ) \right) \Phi +2 \beta \gamma \varepsilon (\alpha -\beta \nu )\Phi ^{3}+\beta (\alpha -\beta \nu )\Phi ^{''} =0. \end{aligned}$$

(13)

Where $(\alpha -\beta \nu )\ne 0.$ Now our main purpose to extract the soliton solutions of IAE with proposed approach.

Construction of soliton solutions of governing equation

Applied homogeneous balance rule on Eq. (13), examined $n=1.$ The generalized solutions given as

$$\begin{aligned} \Phi ( \zeta )=b_0+b_1 \varphi (\zeta ). \end{aligned}$$

(14)

Substitute the Eq. (14) in Eq. (13) and collect each cofactors of $\varphi ^{i}(\zeta ),$ then secured the algebraic equations by making each cofactors equal to zero. Solved these equations through Mathematica tool and calculated the unknown values as

Class–I

$$\begin{aligned} b_0= -\frac{\nabla _2}{4 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }},~~b_1= -\frac{\sqrt{\nabla _3}}{\sqrt{\gamma } \sqrt{\epsilon }},~~\nu = \frac{\alpha \left( \beta \nabla _2^2-8 \nabla _3 \kappa (\beta \kappa -2)\right) }{\beta ^2 \nabla _2^2-8 \nabla _3 (\beta \kappa -1)^2},~~\nabla _1= \frac{\nabla _2^2}{4 \nabla _3}. \end{aligned}$$

(15)

Where $\gamma <0.$ The optical soliton solutions are examined in complex functions form of Eq. (1) through inserting the Eq. (15) into Eq. (14).

$$\begin{aligned} q_{1}(x,t)&=\left( \frac{\nabla _2 \left( \frac{4 \nabla _1 \nabla _3 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2}-1\right) }{4 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }} \right) e^{i (t \omega -\kappa x)}, \end{aligned}$$

(16)

$$\begin{aligned} v_{1}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\nabla _2 \left( \frac{4 \nabla _1 \nabla _3 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2}-1\right) }{4 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }} \right) ^{2} , \end{aligned}$$

(17)

$$\begin{aligned} q_{2}(x,t)&=\left( \frac{\frac{8 \nabla _1 \nabla _3 \text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2-\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}+\text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }-\nabla _2}{4 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }} \right) e^{i (t \omega -\kappa x)}, \end{aligned}$$

(18)

$$\begin{aligned} v_{2}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\frac{8 \nabla _1 \nabla _3 \text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2-\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}+\text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }-\nabla _2}{4 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }} \right) ^{2}. \end{aligned}$$

(19)

Fig. 1

Graphical representation of $q_{1}(x,t)$ in peakon dark and periodic wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=2, \nabla _{2}=4, \nabla _{3}=2, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1$.

Fig. 2

Graphical representation of $v_{1}(x,t)$ in peakon bright soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=2, \nabla _{2}=4, \nabla _{3}=2, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1, \alpha =1, \beta =1$.

Class–II

$$\begin{aligned} b_0= \frac{\nabla _2}{4 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }},~~b_1= \frac{\sqrt{\nabla _3}}{\sqrt{\gamma } \sqrt{\epsilon }},~~\nu = \frac{\alpha \left( \beta \nabla _2^2-8 \nabla _3 \kappa (\beta \kappa -2)\right) }{\beta ^2 \nabla _2^2-8 \nabla _3 (\beta \kappa -1)^2},~~\nabla _1= \frac{\nabla _2^2}{4 \nabla _3}. \end{aligned}$$

(20)

Where $\gamma <0.$ The optical soliton solutions are examined in complex functions form of Eq. (1) through inserting the Eq. (20) into Eq. (14).

$$\begin{aligned} q_{3}(x,t)&=\left( \frac{\nabla _2 \left( \frac{4 \nabla _1 \nabla _3 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) {}^2-\nabla _2^2}+1\right) }{4 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }}\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(21)

$$\begin{aligned} v_{3}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\nabla _2 \left( \frac{4 \nabla _1 \nabla _3 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) {}^2-\nabla _2^2}+1\right) }{4 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }} \right) ^{2}, \end{aligned}$$

(22)

$$\begin{aligned} q_{4}(x,t)&=\left( \frac{\nabla _2-\frac{8 \nabla _1 \nabla _3 \text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2-\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}+\text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }}{4 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }}\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(23)

$$\begin{aligned} v_{4}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\nabla _2-\frac{8 \nabla _1 \nabla _3 \text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2-\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}+\text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }}{4 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }} \right) ^{2}. \end{aligned}$$

(24)

Fig. 3

Graphical representation of $q_{2}(x,t)$ in three different periodic wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=-2, \nabla _{2}=5, \nabla _{3}=1, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1$.

Fig. 4

Graphical representation of $v_{2}(x,t)$ in periodic wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=-2, \nabla _{2}=5, \nabla _{3}=1, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1, \alpha =1, \beta =1$.

Class–III

$$\begin{aligned} b_0=&b_0,~~b_1= -\frac{\sqrt{2} \sqrt{\beta } b_0 \sqrt{\nabla _3} \sqrt{\alpha -\beta \nu }}{\sqrt{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu }},~~\gamma = \frac{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu }{2 \beta b_0^2 \epsilon (\beta \nu -\alpha )},\nonumber \\&\nabla _1= \frac{2 \left( \frac{\alpha }{\beta \nu -\alpha }+(\beta \kappa -1)^2\right) }{\beta ^2},~~\nabla _2= -\frac{2 \sqrt{\nabla _3} \sqrt{2 \kappa (\beta \kappa -2) (\alpha -\beta \nu )-2 \nu }}{\sqrt{\beta } \sqrt{\alpha -\beta \nu }}. \end{aligned}$$

(25)

The optical soliton solutions are examined in complex functions form of Eq. (1) through inserting the Eq. (25) into Eq. (14).

$$\begin{aligned} q_{5}(x,t)&=b_0 \left( \frac{\sqrt{2} \sqrt{\beta } \nabla _1 \nabla _2 \sqrt{\nabla _3} \sqrt{\alpha -\beta \nu } \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\sqrt{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu } \left( \nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2\right) }+1\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(26)

$$\begin{aligned} v_{5}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( b_0 \left( \frac{\sqrt{2} \sqrt{\beta } \nabla _1 \nabla _2 \sqrt{\nabla _3} \sqrt{\alpha -\beta \nu } \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\sqrt{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu } \left( \nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2\right) }+1\right) \right) ^{2} , \end{aligned}$$

(27)

$$\begin{aligned} q_{6}(x,t)&= b_0 \left( 1-\frac{\sqrt{\alpha -\beta \nu }}{\left( -\nabla _2 \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) +\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3} \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) -1\right) }\right. \nonumber \\&\left. \frac{2 \sqrt{2} \sqrt{\beta } \nabla _1 \sqrt{\nabla _3} }{\sqrt{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu } } \right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(28)

$$\begin{aligned} v_{6}(x,t)&= 2 \varepsilon (\alpha -\beta \nu ) \left( b_0 \left( 1-\frac{\sqrt{\alpha -\beta \nu }}{\left( -\nabla _2 \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) +\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3} \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) -1\right) }\right. \right. \nonumber \\&\left. \left. \frac{2 \sqrt{2} \sqrt{\beta } \nabla _1 \sqrt{\nabla _3} }{\sqrt{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu } } \right) \right) ^{2}. \end{aligned}$$

(29)

Fig. 5

Graphical representation of $q_{4}(x,t)$ in three different periodic wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=-2, \nabla _{2}=3, \nabla _{3}=1, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1$.

Fig. 6

Graphical representation of $v_{4}(x,t)$ in periodic wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=-2, \nabla _{2}=-5, \nabla _{3}=2, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1, \alpha =1, \beta =1$.

Class–IV

$$\begin{aligned} b_0=&b_0,~~b_1= \frac{\sqrt{2} \sqrt{\beta } b_0 \sqrt{\nabla _3} \sqrt{\alpha -\beta \nu }}{\sqrt{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu }},~~\gamma = \frac{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu }{2 \beta b_0^2 \epsilon (\beta \nu -\alpha )},\nonumber \\&\nabla _1= \frac{2 \left( \frac{\alpha }{\beta \nu -\alpha }+(\beta \kappa -1)^2\right) }{\beta ^2},~~\nabla _2= \frac{2 \sqrt{\nabla _3} \sqrt{2 \kappa (\beta \kappa -2) (\alpha -\beta \nu )-2 \nu }}{\sqrt{\beta } \sqrt{\alpha -\beta \nu }}. \end{aligned}$$

(30)

The optical soliton solutions are examined in complex functions form of Eq. (1) through inserting the Eq. (30) into Eq. (14).

$$\begin{aligned} q_{7}(x,t)&=b_0\left( 1-\frac{\sqrt{2} \sqrt{\beta } \nabla _1 \nabla _2 \sqrt{\nabla _3} \sqrt{\alpha -\beta \nu } \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\sqrt{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu } \left( \nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2\right) }\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(31)

$$\begin{aligned} v_{7}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( b_0\left( 1-\frac{\sqrt{2} \sqrt{\beta } \nabla _1 \nabla _2 \sqrt{\nabla _3} \sqrt{\alpha -\beta \nu } \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\sqrt{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu } \left( \nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2\right) }\right) \right) ^{2} , \end{aligned}$$

(32)

$$\begin{aligned} q_{8}(x,t)&= \left( b_0 \left( \frac{\nabla _1 \sqrt{\alpha -\beta \nu }}{ \left( -\nabla _2 \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) +\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3} \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) -1\right) }\right. \right. \nonumber \\&\left. \left. \frac{2 \sqrt{2} \sqrt{\beta } \sqrt{\nabla _3} }{\sqrt{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu }}+1\right) \right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(33)

$$\begin{aligned} v_{8}(x,t)&= 2 \varepsilon (\alpha -\beta \nu ) \left( b_0 \left( \frac{\nabla _1 \sqrt{\alpha -\beta \nu }}{ \left( -\nabla _2 \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) +\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3} \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) -1\right) }\right. \right. \nonumber \\&\left. \left. \frac{2 \sqrt{2} \sqrt{\beta } \sqrt{\nabla _3} }{\sqrt{\kappa (\beta \kappa -2) (\alpha -\beta \nu )-\nu }}+1\right) \right) ^{2}. \end{aligned}$$

(34)

Fig. 7

Graphical representation of $q_{5}(x,t)$ in kink and periodic wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=2, \nabla _{2}=4, \nabla _{3}=2, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1, b_{0}=1$.

Fig. 8

Graphical representation of $v_{5}(x,t)$ in anti–kink wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=2, \nabla _{2}=4, \nabla _{3}=2, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1, \alpha =1, \beta =1, b_{0}=1$.

Class–V

$$\begin{aligned} b_0= 0,~~b_1= -\frac{\sqrt{\nabla _3}}{\sqrt{\gamma } \sqrt{\epsilon }},~~\nabla _1= \frac{\frac{\alpha }{\alpha -\beta \nu }-(\beta \kappa -1)^2}{\beta ^2}. \end{aligned}$$

(35)

Where $\gamma <0.$ The optical soliton solutions are examined in complex functions form of Eq. (1) through inserting the Eq. (35) into Eq. (14).

$$\begin{aligned} q_{9}(x,t)&=\left( \frac{\nabla _1 \nabla _2 \sqrt{\nabla _3} \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\sqrt{\gamma } \sqrt{\epsilon } \left( \nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2\right) }\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(36)

$$\begin{aligned} v_{9}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\nabla _1 \nabla _2 \sqrt{\nabla _3} \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\sqrt{\gamma } \sqrt{\epsilon } \left( \nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) {}^2\right) } \right) ^{2}, \end{aligned}$$

(37)

$$\begin{aligned} q_{10}(x,t)&=\left( \frac{2 \nabla _1 \sqrt{\nabla _3}}{\sqrt{\gamma } \sqrt{\epsilon } \left( \nabla _2 \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) -\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3} \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) +1\right) }\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(38)

$$\begin{aligned} v_{10}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{2 \nabla _1 \sqrt{\nabla _3}}{\sqrt{\gamma } \sqrt{\epsilon } \left( \nabla _2 \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) -\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3} \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) +1\right) } \right) ^{2}. \end{aligned}$$

(39)

Fig. 9

Graphical representation of $q_{6}(x,t)$ in three different periodic wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=-2, \nabla _{2}=-3, \nabla _{3}=1, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1, b_{0}=1$.

Fig. 10

Graphical representation of $v_{6}(x,t)$ in periodic wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=-2, \nabla _{2}=5, \nabla _{3}=1, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1, \alpha =1, \beta =1, b_{0}=1$.

Class–VI

$$\begin{aligned} b_0=b_0,~~b_1= -\frac{\sqrt{\nabla _3}}{\sqrt{\gamma } \sqrt{\epsilon }},~~\nu = \frac{\alpha \left( 1-\frac{1}{2 \beta ^2 b_0^2 \gamma \epsilon +(\beta \kappa -1)^2}\right) }{\beta },~~\nabla _1= -4 b_0^2 \gamma \epsilon ,~~\nabla _2= 4 b_0 \sqrt{\gamma } \sqrt{\nabla _3} \sqrt{\epsilon }. \end{aligned}$$

(40)

Where $\gamma <0.$ The optical soliton solutions are examined in complex functions form of Eq. (1) through inserting the Eq. (40) into Eq. (14).

$$\begin{aligned} q_{11}(x,t)&=\left( b_0+\frac{\nabla _1 \nabla _2 \sqrt{\nabla _3} \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\sqrt{\gamma } \sqrt{\epsilon } \left( \nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2\right) }\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(41)

$$\begin{aligned} v_{11}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( b_0+\frac{\nabla _1 \nabla _2 \sqrt{\nabla _3} \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\sqrt{\gamma } \sqrt{\epsilon } \left( \nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2\right) } \right) ^{2}, \end{aligned}$$

(42)

$$\begin{aligned} q_{12}(x,t)&=\left( b_0+\frac{2 \nabla _1 \sqrt{\nabla _3}}{\sqrt{\gamma } \sqrt{\epsilon } \left( \nabla _2 \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) -\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3} \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) +1\right) }\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(43)

$$\begin{aligned} v_{12}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( b_0+\frac{2 \nabla _1 \sqrt{\nabla _3}}{\sqrt{\gamma } \sqrt{\epsilon } \left( \nabla _2 \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) -\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3} \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) +1\right) } \right) ^{2}. \end{aligned}$$

(44)

Fig. 11

Graphical representation of $q_{7}(x,t)$ in anti–kink dark and periodic wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=2, \nabla _{2}=4, \nabla _{3}=2, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1, b_{0}=1$.

Class–VII

$$\begin{aligned} b_0= b_0,~~b_1= -\frac{\nabla _2}{4 b_0 \gamma \epsilon },~~\nu = \frac{\alpha \left( 2 \beta b_0^2 \gamma \epsilon +\beta \kappa ^2-2 \kappa \right) }{\beta ^2 \kappa ^2+2 \beta ^2 b_0^2 \gamma \epsilon -2 \beta \kappa +1},~~\nabla _1= -4 b_0^2 \gamma \epsilon ,~~\nabla _3= -\frac{\nabla _2^2}{16 b_0^2 \gamma \epsilon }. \end{aligned}$$

(45)

The optical soliton solutions are examined in complex functions form of Eq. (1) through inserting the Eq. (45) into Eq. (14).

$$\begin{aligned} q_{13}(x,t)&=\left( \frac{\nabla _1 \nabla _2^2 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{4 b_0 \gamma \epsilon \left( \nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) {}^2\right) }+b_0\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(46)

$$\begin{aligned} v_{13}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\nabla _1 \nabla _2^2 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{4 b_0 \gamma \epsilon \left( \nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2\right) }+b_0\right) ^{2}, \end{aligned}$$

(47)

$$\begin{aligned} q_{14}(x,t)&=\left( \frac{\nabla _1 \nabla _2}{2 b_0 \gamma \epsilon \left( \nabla _2 \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) -\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3} \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) +1\right) }+b_0\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(48)

$$\begin{aligned} v_{14}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\nabla _1 \nabla _2}{2 b_0 \gamma \epsilon \left( \nabla _2 \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) -\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3} \cosh \left( \sqrt{\nabla _1} (x-\nu t)\right) +1\right) }+b_0 \right) ^{2}. \end{aligned}$$

(49)

Class–VIII

$$\begin{aligned} b_0=-\frac{\sqrt{\nabla _1}}{2 \sqrt{\gamma } \sqrt{\epsilon }},~~b_1= -\frac{\nabla _2}{2 \sqrt{\gamma } \sqrt{\nabla _1} \sqrt{\epsilon }},~~\nu = \frac{\alpha \left( \beta \nabla _1-2 \beta \kappa ^2+4 \kappa \right) }{\beta ^2 \nabla _1-2 \beta ^2 \kappa ^2+4 \beta \kappa -2},~~\nabla _3= \frac{\nabla _2^2}{4 \nabla _1}. \end{aligned}$$

(50)

Where $\gamma <0.$ The optical soliton solutions are examined in complex functions form of Eq. (1) through inserting the Eq. (50) into Eq. (14).

$$\begin{aligned} q_{15}(x,t)&=\left( \frac{\sqrt{\nabla _1} \left( \frac{\nabla _2^2 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2}-1\right) }{2 \sqrt{\gamma } \sqrt{\epsilon }}\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(51)

$$\begin{aligned} v_{15}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\sqrt{\nabla _1} \left( \frac{\nabla _2^2 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) {}^2}-1\right) }{2 \sqrt{\gamma } \sqrt{\epsilon }}\right) ^{2}, \end{aligned}$$

(52)

$$\begin{aligned} q_{16}(x,t)&=\left( \frac{\sqrt{\nabla _1} \left( \frac{2 \nabla _2 \text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2-\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}+\text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }-1\right) }{2 \sqrt{\gamma } \sqrt{\epsilon }}\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(53)

$$\begin{aligned} v_{16}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\sqrt{\nabla _1} \left( \frac{2 \nabla _2 \text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2-\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}+\text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }-1\right) }{2 \sqrt{\gamma } \sqrt{\epsilon }}\right) ^{2}. \end{aligned}$$

(54)

Fig. 12

Graphical representation of $q_{8}(x,t)$ in three different periodic wave soliton structure visualized in contour, two and three dimensional plotting with $\nabla _{1}=-3, \nabla _{2}=3, \nabla _{3}=1, \kappa =2, \nu =1.5, \epsilon =1.5, \omega =1, \gamma =1, b_{0}=1$.

Class–IX

$$\begin{aligned} b_0= \frac{\sqrt{\nabla _1}}{2 \sqrt{\gamma } \sqrt{\epsilon }},~~b_1= \frac{\nabla _2}{2 \sqrt{\gamma } \sqrt{\nabla _1} \sqrt{\epsilon }},~~\nu = \frac{\alpha \left( \beta \nabla _1-2 \beta \kappa ^2+4 \kappa \right) }{\beta ^2 \nabla _1-2 \beta ^2 \kappa ^2+4 \beta \kappa -2},~~\nabla _3= \frac{\nabla _2^2}{4 \nabla _1}. \end{aligned}$$

(55)

Where $\gamma <0.$ The optical soliton solutions are examined in complex functions form of Eq. (1) through inserting the Eq. (55) into Eq. (14).

$$\begin{aligned} q_{17}(x,y)&=\left( \frac{\sqrt{\nabla _1} \left( 1-\frac{\nabla _2^2 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2}\right) }{2 \sqrt{\gamma } \sqrt{\epsilon }}\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(56)

$$\begin{aligned} v_{17}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\sqrt{\nabla _1} \left( 1-\frac{\nabla _2^2 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2^2-\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) ^2}\right) }{2 \sqrt{\gamma } \sqrt{\epsilon }}\right) ^{2}, \end{aligned}$$

(57)

$$\begin{aligned} q_{18}(x,t)&=\left( \frac{\sqrt{\nabla _1} \left( 1-\frac{2 \nabla _2 \text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2-\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}+\text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }\right) }{2 \sqrt{\gamma } \sqrt{\epsilon }}\right) e^{i(t \omega -\kappa x)}. \end{aligned}$$

(58)

$$\begin{aligned} v_{18}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{\sqrt{\nabla _1} \left( 1-\frac{2 \nabla _2 \text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2-\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}+\text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }\right) }{2 \sqrt{\gamma } \sqrt{\epsilon }} \right) ^{2}. \end{aligned}$$

(59)

Class–X

$$\begin{aligned}&b_0= -\frac{\sqrt{\nabla _1}}{2 \sqrt{\gamma } \sqrt{\epsilon }},~~b_1=b_1,~~\nu = \frac{\alpha \left( \beta \nabla _1-2 \beta \kappa ^2+4 \kappa \right) }{\beta ^2 \nabla _1-2 \beta ^2 \kappa ^2+4 \beta \kappa -2},\nonumber \\&\nabla _2=2 b_1 \sqrt{\gamma } \sqrt{\nabla _1} \sqrt{\epsilon },~~\nabla _3= b_1^2 (-\gamma ) \epsilon . \end{aligned}$$

(60)

Where $\gamma <0.$ The optical soliton solutions are examined in complex functions form of Eq. (1) through inserting the Eq. (60) into Eq. (14).

$$\begin{aligned} q_{19}(x,t)&=\left. \left( \frac{b_1 \nabla _1 \nabla _2 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) {}^2-\nabla _2^2}-\frac{\sqrt{\nabla _1}}{2 \sqrt{\gamma } \sqrt{\epsilon }}\right) \right. e^{i(t \omega -\kappa x)}, \end{aligned}$$

(61)

$$\begin{aligned} v_{19}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( \frac{b_1 \nabla _1 \nabla _2 \text {sech}^2\left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _1 \nabla _3 \left( \tanh \left( \frac{1}{2} \sqrt{\nabla _1} (x-\nu t)\right) -1\right) {}^2-\nabla _2^2}-\frac{\sqrt{\nabla _1}}{2 \sqrt{\gamma } \sqrt{\epsilon }} \right) ^{2}, \end{aligned}$$

(62)

$$\begin{aligned} q_{20}(x,t)&=\left( -\frac{2 b_1 \nabla _1 \text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2-\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}+\text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }-\frac{\sqrt{\nabla _1}}{2 \sqrt{\gamma } \sqrt{\epsilon }}\right) e^{i(t \omega -\kappa x)}, \end{aligned}$$

(63)

$$\begin{aligned} v_{20}(x,t)&= 2 \varepsilon (\alpha -\beta \nu )\left( -\frac{2 b_1 \nabla _1 \text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }{\nabla _2-\sqrt{\nabla _2^2-4 \nabla _1 \nabla _3}+\text {sech}\left( \sqrt{\nabla _1} (x-\nu t)\right) }-\frac{\sqrt{\nabla _1}}{2 \sqrt{\gamma } \sqrt{\epsilon }} \right) ^{2}. \end{aligned}$$

(64)

Graphical illustration of the obtained solutions

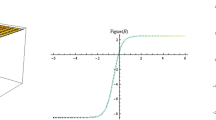
In this section, we present a graphical analysis of the obtained solutions, with particular focus on examining the effects of the governing model’s physical parameters on the explored solutions. An important aspect of this study is that the figures serve to demonstrate the physical structure and formation of the nonlinear model rather than to ensure precise accuracy for a specific real-world or experimental scenario. The main goal is to represent the dynamic and geometric structures of the proposed model. Graphical representations play a central role in understanding the physical behavior of the examined solutions. We illustrate the structures of selected solutions for the complex function q(x, t) and real function v(x, t),  using three types of plots: contour, two-dimensional, and three-dimensional visualizations. The parameter values used in the functions were implemented via Mathematica. As shown in Figs. 1–12, the solutions exhibit diverse and novel physical structures, including periodic waves, kink waves, peakon bright and dark solitons, singular bright and dark solitons, anti–kink waves, mixed kink bright waves, mixed anti–kink bright waves, and mixed anti–kink dark waves. The remaining solutions represent a variety of other nonlinear wave phenomena, including different types of solitons and solitary waves. The graphical illustrations confirm the effectiveness and versatility of the proposed methodology. The approach demonstrates the capability to analyze complex nonlinear problems efficiently with the aid of advanced symbolic computation tools.

Results and discussion

In the past studies some of research has been done and researchers secured different kinds of results for the nonlinear Akbota equation, including trigonometric, elliptic, rational, and hyperbolic functions in the form of traveling waves, kink and anti–kink waves, dark and bright soliton solutions. Such as, using the Darbox equation method, Kong and Guo got the analytical wave solutions for the Akbota equation and these solutions included semi–rational and rogue breather wave solutions⁵³. Mathanaranjan et al. constructed the conversion law, optical soliton solutions, and stability solutions to the nonlinear Akbota equation through an extension of auxiliary equation scheme⁵⁴. Faridi et al. represented the solitonic wave profile through improved Sardar sub equation scheme⁵⁵. Tariq et al. to determine the exact solutions of the nonlinear integrable Akbota equation by using two different techniques, the Sardar sub equation and modified Khatar methods⁵⁶. Li and Zhao found the bifurcation, chaotic behavior, and solitary wave solutions for the Akbota equation using the analysis method⁵⁷. Faridi et al. secured the solitonic wave and spanned a diverse range of solitary solutions by utilizing $\phi ^{6}$ method⁵⁸ and another study determined soliton solutions of nonlinear Akbota equation by applying three different techniques, namely, general projective Riccati, Sardar sub equation and $(\frac{G^{'}}{G^{2}})-$expansion methods⁵⁹. Recently, Iqbal et al. explored the optical soliton solutions of nonlinear Akbota equation by applying the improved F–expansion method⁶⁰. But our demonstrated solutions to the nonlinear integrable Akbota equation have distinct arrangements in the shape of periodic waves, kink waves, peakon bright, peakon dark, singular bright and dark, anti–kink waves, mixed kink bright waves, and mixed anti–kink bright waves, mixed anti–kink bright waves, and mixed anti–kink dark waves, and in different structure of periodic solitons.

Our proposed method is more powerful, simple, straightforward, effective, and easy to determine the solutions for nonlinear evolution equation. Based on the above discussion and relationship that the examined solutions are novel, more generalized and did not examined in the past studies through other approaches.

Conclusion

In this study, the soliton behavior of the newly integrable Akbota equation (IAE) has been theoretically investigated. The obtained solutions are expressed in terms of hyperbolic functions and represent a variety of nonlinear wave structures, including periodic waves, kink waves, peakon bright and dark solitons, singular bright and dark solitons, anti–kink waves, mixed kink bright waves, mixed anti–kink bright waves, and mixed anti–kink dark waves, as well as different structures of periodic solitons. The physical structures of selected solutions have been visualized using three types of plots: two–dimensional, three–dimensional, and contour representations. The constructed solutions have potential applications across multiple fields, including engineering, physical sciences, quantum physics, solid-state physics, plasma physics, optical systems, communication systems, ocean engineering, and the modeling of various phenomena in mathematical physics. The computations and analyses confirm that the proposed technique is effective, powerful, straightforward, and versatile for obtaining solutions of various nonlinear partial differential equations arising in diverse areas of physical and nonlinear sciences.