Introduction

Soil erosion is a major environmental concern that threatens ecosystems, reduces agricultural productivity, and degrades water quality in river systems1,2. Globally, an estimated 2.8 metric tons of soil are lost per hectare each year due to erosional processes3. Countries with tropical rainforest climates, such as Malaysia, are particularly susceptible to erosion because of consistently hot and humid conditions. Intense and frequent rainfall in such regions enhances the capacity of raindrops to detach and transport soil particles4. Besides rainfall as an external erosive force, cohesive forces and antecedent soil moisture also influence erosion resistance, as soils with higher cohesion and moisture content tend to be less susceptible to slaking. Therefore, the estimation of soil erosion is crucial for effective land management and conservation planning.

Various models have been developed to quantify soil erosion under different environmental and land-use conditions. A key parameter in erosion estimation models such as Revised Universal Soil Loss Equation (RUSLE) is the soil erodibility factor, commonly known as the K factor, which quantifies the susceptibility of soil particles to detach and transport by the erosive agents5. The K factor represents the influence of the intrinsic soil properties, both physical and chemical, on soil erosion. While direct measurement of the K factor using a standardized plot provides accurate results, it is often impractical due to time and cost constraints6. To address these limitations, various studies have explored alternative methods to estimate soil erodibility7. Among these, a commonly adopted method is the Wischmeier equation and nomograph, which estimates the K factor based on four key soil characteristics, including particle size distribution, structural, organic matter content, and permeability8. A modification to the Wischmeier equation is the Tew equation9, developed for Malaysian soil series, and is recommended by the Department of Irrigation and Drainage, Malaysia, to estimate the soil erodibility factor in the region10. However, these empirical methods still require soil sampling and subsequent laboratory analysis, which is laborious, time-consuming, and costly. As a result, there has been increasing interest in developing predictive relationships between the K factor and easily measurable soil properties.

One such property is the soil plasticity, indicated by the plasticity index (PI), which reflects the cohesiveness and water retention behavior of the soil. These characteristics are closely associated with the erosion resistance of soil, yet the relationship of plasticity of soil to its erodibility is understudied in both tropical and subtropical environments. The plasticity index serves as a vital parameter in the classification and characterization of the soils, offering useful information about their engineering behavior11. Beyond its conventional use in soil classification, the Atterberg Limits (liquid limit, plastic limit, and plasticity index) are widely recognized for their role in evaluating key geotechnical properties such as shear strength, bearing capacity, compressibility, and susceptibility to volume changes due to shrinkage and swelling12.

In recent years, the Atterberg Limits have gained attention as potential indicators of soil vulnerability to degradation processes driven by both natural environmental conditions and human activities13. Studies involving common soil types have highlighted that the liquid and plastic limits can be effectively used to assess the aggregate vulnerability of the soil to erosional processes14,15. Studies conducted using the Erosion Function Apparatus (EFA) demonstrated that the rate of erosion is influenced by several physical properties, including the plasticity index, degree of compaction, and level of saturation16,17,18. Among these, the plasticity index and the associated soil cohesiveness play a pivotal role in determining the resistance of soil to erosive forces. Adhikari & Osouli19 found that the erosion rate decreased when the plasticity index increased. Curtaz et al.15 suggested that the soils with low cohesion, when exposed to saturation, tend to become more prone to degradation processes such as erosion and strength loss, particularly under intense rainfall.

Manyiwa and Dikinya20 quantified K factor and basic soil properties for six eroded and non-eroded sites to assess erosion in tropical soils in semi-arid conditions. It was observed that the eroded soils had a higher plasticity index compared to the non-eroded soils. Similarly, the sites with low plastic limit were less erodible, probably due to flat surfaces with vegetation cover. Khoirullah et al.21 suggested a negative correlation (R2 = 0.4988) between the empirically measured K factor and the plasticity index of soil. Their correlation was based on the 14 samples of distinct soil types, demonstrating that a high erodibility value was associated with a low value of plasticity index. In their study to associate undrained shear strength with the erodibility of slopes, Couto et al.22 explored the correlations of physical and chemical properties of soil with the empirically measured K factor. The study demonstrated a low significant negative correlation between plasticity index and the K factor (R2 = 0.2627 for erodible, R2 = 0.3371 for non-erodible), suggesting that the high plasticity soils were less erodible due to enhanced aggregate stability. Rosli and Ibrahim23 studied the correlation of physical parameters of soil to its erosion across the riverbanks utilizing the erosion pin technique. The study was based on the erosion rate from the ten sites across the riverbank of Sungai Pusu, Malaysia. No correlation (R2 = 0.027) was found between PI and erosion rate, and it was suggested that PI is not a potential indicator of erosion rate for the study area. Baudson et al.24 analyzed the geotechnical properties of the tailings in relation to surface erosion. It was found that high erodibility was associated with high amounts of silt and fine sand in addition to low plasticity. A similar observation was made by Thounaojam and Ibotombi25 in their study on the influence of clay on K factor, suggesting that an increase in clay content, typically associated with higher plasticity index and organic matter content, corresponds to a decrease in erodibility.

Studies have shown that Atterberg limits are generally influenced by various soil properties, with clay content and organic matter being among the most significant factors13,26. Clay soils typically exhibit a tendency to flocculate, promoting aggregation and thereby reducing their susceptibility to erosion. However, in the case of dispersive clays, the opposite behavior is observed as they are highly prone to erosion27,28. These clays tend to deflocculate upon contact with water, causing the breakdown of inter-particle attractions. As a result, individual clay particles become suspended and are easily transported by flowing water, leading to significant soil loss. The degree of dispersion in such soils has been observed to increase with higher Atterberg Limits, particularly the plasticity index29. A direct relationship between the dispersion ratio and plasticity index suggests that dispersive soils may exhibit high plasticity values while still being highly erodible. In this context, the present study aims to evaluate the correlation between the PI and the K factor based on soil samples collected from different locations in Melaka and Selangor, Malaysia.

Methodology

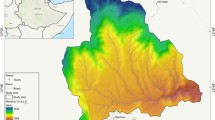
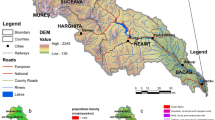
Soil samples were collected from different locations across Melaka Tengah (Melaka) and Sugai Langat Basin (Selangor), to encompass a wide range of soil types and environmental conditions, thereby enhancing the generalizability of the findings and the robustness of the developed correlation. The sampling locations were selected randomly within the targeted regions to maximize soil variability and include as many soil series as possible. The sampling locations are shown in Fig. 1. The samples were taken with the help of a hand auger to a depth of 100 cm. The samples were extracted and immediately sealed in plastic bags to preserve their in situ moisture content.

Fig. 1
figure 1

Study Area: Sampling Stations (a) Selangor, (b) Melaka Tengah. (Map generated using QGIS Desktop version 3.34).

Full size image

All collected samples were air-dried and pulverized to pass through a 2 mm sieve before laboratory testing. The particle size distribution was determined following ASTM standards. Coarse fractions (greater than 75 μm) were analyzed using dry and wet sieve analysis. Wash sieving was conducted following ASTM D1140-17 to quantify the portion finer than 75 μm. For finer fractions (less than 75 μm), hydrometer analysis was carried out according to ASTM D422-63 to determine the distribution of silt and clay particles. Organic matter content was determined using the oxidation method, in which soil samples were treated with a 30% hydrogen peroxide (H2O2) solution. The Atterberg Limits, including Liquid Limit (LL), Plastic Limit (PL), and Plasticity Index (PI), were determined using ASTM D4318-17.

The soil erodibility factor (K) was calculated using the Tew equation, a regionally adapted empirical formula recommended by the Department of Irrigation and Drainage (DID), Malaysia. This equation is tailored for Malaysian soil conditions and integrates key soil properties such as particle size distribution, structure, permeability, and organic matter content. The Tew equation for soil erodibility is expressed as:

$$\:K=\left[1.0\times\:{10}^{-4}\left(12-OM\right){M}^{1.14}+4.5\left(s-3\right)+8\left(p-2\right)\right]/100$$

where “K” represents soil erodibility in [(ton/ac.) (100 ft.ton.in/ac.hr)], “OM” represents soil organic matter content, and “M” in the equation can be described as a particle size parameter which can be determined as [(% silt + % very fine sand) (100 - % clay)], “s” represents the soil structure code, and “p” represents the soil permeability code. The K factor can be multiplied by a conversion factor of 1/7.59 to convert into SI units of [(ton/ha) (ha.hr/MJ.mm)].

Statistical analysis was performed using IBM SPSS Statistics v27. A regression analysis was conducted to examine the relationship between the PI and the K factor. The predictive performance of the developed regression model was assessed using several statistical indices, including the coefficient of correlation (r), coefficient of determination (R2), adjusted R2, Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Square Error (RMSE). These metrics were computed to evaluate the model’s accuracy, goodness-of-fit, and error distribution.

Results and discussion

Distribution of soil properties

The descriptive statistics of the collected soil samples are presented in Table 1, providing an initial understanding of the variability within the soil samples. The results indicate considerable variability across the measured soil properties. Sand content ranged from 9.74% to 69.42% with a mean of 41.25%, suggesting a wide range of textural variation from fine to coarse. Silt and clay contents also exhibited notable variation, ranging from 6.36 to 84.31% and 0.73–53.43%, respectively. The standard deviations of 17.58% and 13.49% of silt and clay, respectively, further reinforce the heterogeneity of soil types in the study area. The soil organic matter content (SOM) had a relatively low mean value of 1.65%, with a positively skewed distribution, indicating that most samples contained low SOM, but a few had distinctly higher concentrations. This is confirmed by the high kurtosis value of 12.48, suggesting a leptokurtic distribution with frequent values clustered near the mean and heavy tails.

Regarding Atterberg limits, the mean LL and PL were 45.27% and 26.76%, respectively, while the PI averaged 18.74%, with values ranging from 6.17% to 35.00%. These PI values imply that the soils largely fall into the intermediate to high plasticity categories, which can significantly influence their erosion susceptibility. The K factor ranged from 0.01 to 0.06 (ton/ha)(ha.hr/MJ.mm), with a mean value of 0.0307. The near-zero skewness and kurtosis indicate a nearly normal distribution for K, which suggests a relatively even spread of erodibility values among the samples.

Table 1 Summary of descriptive statistics.
Full size table
Fig. 2
figure 2

Box normal plot for PI and K factor.

Full size image

Figure 2 presents the box plots and normal distribution curves for PI and K factor, providing a visual and statistical overview of the data distribution, central tendency, and spread. The box plot for PI shows a median around 18%, with the interquartile range extending from approximately 13% to 24%. The median PI value suggests that the central tendency of PI in the studied samples falls within a range typically associated with soils of medium to high plasticity. The PI distribution shows a positively skewed pattern, evidenced both by the right-leaning tail of the density curve and the skewness from Table 2. The box plot reveals a longer upper whisker, suggesting the presence of higher outliers or extreme values above the third quartile. This skewness implies that a considerable portion of the soil samples has lower plasticity, while fewer samples exhibit exceptionally high plasticity. Given that higher PI values generally correlate with increased clay content, these outliers may represent clay-rich soils of expansive nature possessing greater shrink-swell potential and lower permeability, which, despite high plasticity, could still be prone to erosion.

In contrast, the normal distribution curve of the K factor displays a nearly symmetrical and mesokurtic distribution, somewhat skewed to the right, with a slightly flatter peak than a normal distribution, supported by the near-zero skewness and kurtosis values in Table 2. The density plot in Fig. 1 confirms this near-normal distribution, with the data centred closely around the mean and showing a relatively even spread on both sides. The Whiskers indicating a high degree of relative dispersion and suggesting the presence of extreme values at both ends. Despite the long whiskers, the inter quartile range (IQR) which lies approximately between 0.02 and 0.04 is relatively narrow, implying that the middle 50% of the K values are tightly clustered. The median close to 0.03 line lies near the centre of the box, further confirming the balanced spread of K values around the mean.

Correlation analysis

The Pearson correlation analysis, presented in Fig. 3, reveals statistical relationships among soil texture parameters, Atterberg limits, and erodibility factor. The K factor demonstrates a strong positive correlation with PI (r = 0.790 at p < 0.01), suggesting that PI is a reliable predictor of soil erodibility. Although, contrary to the available literature on PI-K correlation21,22,25, this is consistent with theoretical aspect, as highly plastic soils, particularly those rich in clay content tend to exhibit greater swelling potential and expansiveness, that makes the soil prone to erosional processes30,31. The strong linear association implies that as plasticity increases, so does the susceptibility of soil to erosion.

The K factor demonstrates a significantly negative correlation with sand content, suggesting that the coarse textured soils are less erodible, likely due to improved infiltration and the heavy size of the individual sand particles, which are difficult to detach and transport32. Conversely, the strong positive correlation between clay content and K indicates that soils with higher clay content are more erodible. This might be due to the susceptibility of some clay minerals to swelling and dispersion, leading to surface sealing and increased runoff, ultimately enhancing erosion. The non-significant correlation between silt and K suggests that silt content alone may not be a strong predictor of soil erodibility in this study area, possibly due to its interaction with other soil properties. The correlation analysis of soil texture parameters and soil erodibility indicate that the relationship strengthens when these parameters are assessed collectively rather than individually. This suggests the presence of synergistic effect among soil properties33. The interdependence arises because an increase in one particle size fraction inherently reduces the proportion of other fractions.

The significant positive correlations of liquid limit and plastic limit with K further support the influence of soil consistency on erodibility. Higher liquid and plastic limits, indicative of a greater proportion of fine particles and higher plasticity, are associated with increased erodibility.

Fig. 3
figure 3

Pearson correlation matrix.

Full size image

Regression analysis

Table 2 summarizes the regression model where the PI is used to predict the K. In the regression analysis, the plasticity index (PI) was transformed using the natural logarithmic function, i.e., \(\:\text{l}\text{n}\left(PI\right)\). During data processing, it was observed that the logarithmic transformation better captured the variance in the K factor. To maintain linearity and simplify the regression model, the transformed variable \(\:\text{l}\text{n}\left(PI\right)\) was used as the independent variable in place of the original PI. The model shows a strong positive correlation between PI and K, with an r value of 0.821 and R2 of 0.673, indicating that 67.3% of the variance in the K factor can be explained by the PI. The adjusted R2 of 0.664 accounts for the degrees of freedom and suggests a good fit of the model to the data. The standard error of the estimate is 0.00711, which is relatively low, suggesting a good predictive accuracy. The F-change value is 72.128 with p < 0.001, indicating that the model is statistically significant, meaning that PI provides substantial explanatory power for the variation in K.

The ANOVA test results from Table 3 further confirm the model’s significance, showing that the regression model accounts for a significantly larger portion of the variance than the residual error. The coefficients table provides an understanding of the relationship’s direction and strength. The positive regression coefficient for PI quantitatively shows that as soil plasticity increases, so does the predicted soil erodibility. This could be linked to the increased susceptibility of higher plasticity soils to dispersion and detachment, as discussed earlier. The t-statistic for PI is large and statistically significant (p < 0.001), confirming that PI is a strong individual predictor of K. The standardized beta coefficient of 0.821 further emphasizes the dominance of PI in predicting soil erodibility.

Table 2 Summary of regression model.
Full size table
Table 3 Summary of ANOVA and coefficients of regression model.
Full size table
Fig. 4
figure 4

Correlation between plasticity index and erodibility factor.

Full size image

Figure 4 presents the scatter plot illustrating the relationship between PI and the K factor. The plot confirms the positive linear trend, suggesting that soils with higher plasticity values tend to exhibit greater susceptibility to erosion. This visual representation reinforces the statistical findings from the regression analysis. However, the scatter of the data points around the trendline highlights the complexity of soil erodibility. While plasticity is a significant predictor, the unexplained variance suggests the involvement of other potential soil properties and environmental factors. These could include the specific mineralogy of the clay fraction, the soil structure, the presence and type of organic matter, and the influence of climate and topography at the sampling locations.

Table 4 presents key performance metrics used to evaluate the accuracy and explanatory power of the regression model. The r and R2 values of 0.821 and 0.673, respectively, indicate a strong positive relationship between the ln-transformed PI and the K factor. The adjusted R2 of 0.664 suggests that approximately 66.4% of the variability in K is explained by PI alone, after accounting for the degrees of freedom.

The error metrics support the model’s reliability, with an MAE of 0.00587 and an RMSE of 0.00691, reflecting low average prediction error. The MSE, at 0.0000477, also confirms the model’s good fit. These values demonstrate the model’s adequacy for estimating soil erodibility using plasticity index and provide a solid basis for its application in erosion prediction studies.

Table 4 Summary of performance metrics.
Full size table
Fig. 5
figure 5

Scatter plot for unstandardized residuals versus predicted K values.

Full size image
Fig. 6
figure 6

Normal P-P plot of standardized residuals.

Full size image

To evaluate the statistical validity of the regression model beyond performance metrics, diagnostic checks were conducted to assess whether the assumptions of linearity, homoscedasticity, and normality of residuals were satisfied. Figure 5 presents the scatter plot of unstandardized residuals against the predicted K values. The residuals appear randomly dispersed around the horizontal axis with no discernible pattern, curvature, or funnelling effect. This supports both the linearity of the relationship between PI and K and the homoscedasticity (constant variance) assumption of the model.

The Normal P–P plot, as illustrated in Fig. 6, compares the observed cumulative probabilities of the standardized residuals with those expected from a normal distribution. The data points closely follow the 45º reference line, indicating that the residuals are approximately normally distributed. This confirms the normality assumption, which underpins the reliability of coefficient estimates and significance tests. Together, these diagnostic plots reinforce the statistical soundness of the linear regression model used in this study, supporting the interpretation and generalizability of the derived relationship between plasticity index and soil erodibility factor.

Conclusion

This study investigated the relationship between plasticity of soil with its erodibility in the tropical soils of Central Malaysia, aiming to establish a simple predictive model for erosion susceptibility. The correlation analysis revealed a significant positive correlation between PI and K, with the regression model explaining 67.3% variance in the erodibility. The observed relationship suggests that highly plastic soils in the study area may exhibit increased susceptibility to erosion due to factors such as dispersive clay mineralogy or swelling-induced surface sealing. These mechanisms enhance runoff and particle detachment despite the inherent cohesiveness associated with plasticity. The strong linkage between PI and K highlights the dual role of clay content, while it can promote aggregate stability, certain clay threshold under tropical conditions may exacerbate erosion through physicochemical interactions. Despite providing a statistically significant predictive model, approximately 33% unexplained variance indicates the contributions from unmeasured variables such as clay mineralogy, soil structure, and microtopography.

Notably, the study identified regional specificity as a critical factor. The use of the Tew equation, calibrated for Malaysian soils, and the unique climatic and mineralogical conditions of the sampling sites likely influenced the divergence from global trends. This reinforces the necessity of region-specific erosion models that account for local soil characteristics and environmental dynamics. However, this research supports the use of Atterberg limits, particularly PI, as a cost-effective proxy for estimating soil erodibility in tropical regions. Such an approach can streamline erosion risk assessments, aiding land managers and policymakers in prioritizing conservation efforts. Future studies should integrate mineralogical analyses, field-based erosion measurements, and multi-variable modelling to refine predictive accuracy and address the interplay between plasticity, dispersion, and environmental drivers.