Introduction

The advancement of digital technology has led to the widespread adoption of colour laser printers in commercial, governmental, and everyday office settings. Notably, although colour laser printers have substantially improved printing precision and colour fidelity, they have also contributed to technological sophistication in document forgery. For example, they have been illicitly used to produce counterfeit currency, propaganda materials, contracts, and paper documents. The development of techniques to visualise, decode, and forensically examine the counterfeit protection system (CPS) on colour-laser-printed documents provides a novel approach for document authentication. These techniques are anticipated to play an increasingly vital role in criminal investigations and legal proceedings. CPS patterns on printed documents distinctly vary across different brands of colour laser printers in terms of dot matrix morphology, contour patterns, and spatial arrangements. In forensic practice, the evidential examination framework for CPS identification remains predominantly reliant on morphological analysis paradigms. This approach heavily depends on the manual identification of morphological features within the basic dot matrix unit (BDMU). During examination, examiners are required to manually annotate the geometric contours of the BDMU and subsequently compare characteristics such as outline shape, arrangement, and size to trace the brand of the printing device, It typically requires approximately 1 to 3 min for relatively proficient questioned document identification personnel to identify and differentiate a colour laser-printed document, as illustrated in Fig. 11. However, this process faces critical limitations. Annotated contour features often considerably vary between different examiners owing to subjective cognitive differences. Additionally, examiners must determine the orientation between the CPS image and the paper feed direction of the printer to enhance identification accuracy. However, accurately assessing the paper-feed orientation is challenging and compromises operational efficiency.

Fig. 1
figure 1

CPS Measurement method (a) Xerox (b) Hp (c) Epson.

Full size image

Recently, intelligent evidence comparison methods based on information technology have emerged as a prominent research focus in forensic science2. Current research on CPS differentiation or classification for colour-laser-printed documents remains predominantly centred on morphological-feature-based examination. However, the integration of information technology has progressively steered CPS analysis toward automation and digitisation. Researchers have established database-driven computer-aided identification systems capable of automatic CPS decoding and retrieval for comparative analysis3. Initially, CPS examination used to heavily rely on microscopes or video spectral comparators to observe yellow dot patterns. In a previous study, researchers employed the vertical pattern separation (VPS) method to classify CPS from seven colour-laser-printer brands by measuring the distance between repeating units4. Beusekom et al. advanced this approach using horizontal pattern separation and VPS to construct an automated CPS classification database. However, its coverage was limited to only three brands: Xerox, Dell, and Epson5. Li et al. greatly extended this methodology by introducing coordinate axis positioning and boundary region distance measurements. They defined four classification features (orientation, shape, arrangement, and distance), leading to the proposal of the "CPS contour location measurement method"6,7. This method determines the morphology of the BDMU by locating the CPS matrix on printed documents and subsequently identifying features such as BDMU contour shape and typographical arrangement. Despite resolving the challenge of differentiating colour-laser-printer brands using CPS, this approach exhibits substantial limitations owing to its manual operational paradigm. When handling large volumes of evidence, examiners must manually calibrate the coordinate system and measure grid spacing for each frame, necessitating intensive manual intervention and prohibitive time consumption. Within the context of judicial authentication, the operational inefficiencies of existing models represent a critical shortfall, ultimately hampering the widespread application and sustainable development of this technology.

The rapid advancement of artificial intelligence (AI) is shifting document examination toward greater automation and precision. In domains such as handwritten content recognition8, handwriting analysis9, the integration of AI not only enhances automation but also noticeably enhances examination accuracy and efficiency. Therefore, AI systems provide more reliable technical support for forensic authentication and evidentiary analysis. A subsequent study enhanced the accuracy of the model to 88.7% by incorporating Wiener filtering for noise reduction and four-directional GLCM feature extraction10. Ferreira et al. proposed a heterogeneous feature fusion framework, deploying multiple simple convolutional neural network (CNN) architectures in parallel to process sample images enhanced through frequency-domain augmentation, morphological reconstruction, and GLCM transformation. This approach achieved high precision in detecting characters "a" and "e" and demonstrated robust performance against noisy data11.Ferreira et al. proposed three techniques: multidirectional/multiscale gray-level co-occurrence matrices (GLCM_MD/MDMS), convolution texture gradient filter (CTGF), and “frame” region analysis, without the need for high-resolution scanning. Validated on a dataset of 1184 TIFF images printed by 10 printers, the fusion of CTGF and GLCM_MDMS achieved an accuracy of 98.47% when applied to frames12.Building on this method, Joshi et al. replaced traditional scanners with smartphone cameras for document acquisition. Further, they trained a deep CNN model using dual-channel inputs combining raw letter images and their noise residual images to enhance the feature learning capability of the model13.Abady et al. proposed a text-independent Source Printer Identification (SPI) algorithm based on ensemble learning for document forgery detection. It extracts features using Histogram of Oriented Gradient (HOG, global) and Local Binary Pattern (LBP, local), and adopts classifiers such as DT, SVM, and AdaBoost. The algorithm is validated on a dataset of 1200 documents printed by 20 printers14.Abady et al. proposed three CNN-based techniques by identifying the inherent physical features of printers, which were tested using three datasets containing 10 to 30 types of printers. This work has realized the identification of source printers without character segmentation and with adaptation to small datasets15.Li et al. used ImageXpert to measure 33 metrics of laser-printed characters, applying random forest and scatter plots to distinguish printer sources, aiding forensic document analysis16.

In contrast to the aforementioned studies, this study leveraged CNNs to identify the morphological arrangement features of CPS dot matrices in colour-laser-printed documents for differentiating printer brands. An improved ShuffleNet V2 model was used to extract and learn complex CPS features without manual feature engineering, thereby considerably enhancing recognition efficiency while maintaining high accuracy. This method is adaptable to diverse CPS encoding patterns across mainstream printer brands, ensuring broad applicability. The transparency and reliability of the model was validated via interpretability analysis. This approach effectively mitigates human cognitive bias and increases examination accuracy and efficiency. Additionally, it provides more precise and stable technical support for CPS identification in colour- laser-printed documents, promoting the digitalisation and intelligence-driven development of physical evidence examination.

Experimental data

Dataset acquisition

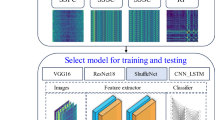
Printing samples were produced using colour laser printers manufactured by eight brands that represented over 95% of the market share: Canon, Dell, Epson, HP, Ikon, Konica, Ricoh, and Xerox. Specifically, the samples included: 56 print files from 12 Canon printer models; 42 print files from 7 Dell printer models; 50 print files from 9 Epson printer models; 60 print files from 20 HP printer models; 53 print files from 11 Ikon printer models; 53 print files from 13 Konica printer models; 50 print files from 7 Ricoh printer models; and 61 print files from 22 Xerox printer models.The samples were scanned using an Epson C65 scanner at a resolution of 600 dpi and saved in JPG format. The scanned files were opened in Photoshop software. To isolate the yellow and black components, the cyan and magenta values were adjusted to − 100, while the yellow and black values were set to + 100. Optimal visualisation was achieved by adjusting the RGB and blue curves within the colour curves panel and maximising the brightness and contrast. The input images were compressed to 224 × 224 pixels prior to model training or validation. As experimental results indicated that using the original full-size images yielded suboptimal performance, a portion of each image was cropped to serve as the sample.From each printed document, one to three 800 × 800 pixel images with different backgrounds were cropped as samples.

Data augmentation

Given the relatively limited number of original samples for each brand of colour-laser-printed documents, directly training the model with the raw dataset may yield suboptimal results. this paper employed data augmentation techniques after creating the samples to balance the dataset distribution,Data augmentation techniques were employed to mitigate the risk of overfitting and to address potential class imbalance that could lead the model to be unduly influenced by specific data types. These techniques served to balance the dataset distribution and increase the overall sample size, thereby enhancing the generalisation capabilities of the model. The dataset was augmented using various methods, including flipping, rotation, translation, blurring, brightness and contrast level adjustment, and the addition of Gaussian and salt-and-pepper noises. This process resulted in a final augmented dataset comprising 4,444 images. Subsequently, the augmented dataset was divided into training and testing sets using an 8:2 split ratio. Table 1 lists the number of samples in the training and testing sets for each brand.

Table 1 Dataset distribution.
Full size table

Network architecture design and improvements

ShuffleNet V2 network architecture

ShuffleNet V217 retains the operations employed in ShuffleNet V1, such as depthwise separable convolution, channel shuffling, and grouped convolution18, while refining the fundamental residual block structure to reduce computational complexity and enhance model accuracy. As a representative lightweight CNN architecture, its core innovation lies in constructing a modular structure that synergistically optimises feature reuse and channel interaction. As illustrated in Fig. 2, the network achieves efficient computation in feature space through two structural units: the standard and downsampling units. Each unit adopts a three-stage processing paradigm: feature splitting, branch processing, and information fusion. First, the standard unit equally partitions the input feature map along the channel dimension into two sub-feature streams. The main processing branch follows the computational logic of "feature compression → spatial feature extraction → feature expansion". Channel dimensionality reduction is performed via 1 × 1 pointwise convolution. Lightweight spatial feature modelling is achieved using 3× 3 depthwise separable convolution with a stride of 1. Channel dimensionality expansion is completed through 1 × 1 pointwise convolution. The parallel bypass branch maintains a direct feature pathway, preserving the integrity of shallow features through identity mapping. During the feature fusion stage, outputs from both branches are integrated via channel concatenation. A channel shuffle mechanism is introduced to break inter-group information barriers, facilitating effective cross-channel feature interaction. To address spatial-resolution reduction requirements, the downsampling unit adapts the design principles of the standard unit. The main branch reduces feature map dimensions by setting the stride for the depthwise separable convolution to 2. The bypass branch innovatively integrates a cascade structure comprising a depthwise separable convolution (stride 2) and 1 × 1 pointwise convolution. This design ensures downsampling functionality while maintaining channel-dimensionality compatibility. Critically, concatenated outputs from both branches undergo channel shuffling, preserving original spatial topology while enabling effective cross-resolution feature fusion. This dual-path collaborative mechanism reduces computational complexity while mitigating information loss inherent in traditional downsampling operations. The ShuffleNet V2 architecture comprises Conv1, MaxPool, Stage 2, Stage 3, Stage 4, Conv5, and FC layers. Stages 2–4 are constructed by stacking the standard and downsampling blocks: Stage 2 and Stage 4 each contain four blocks, while Stage 3 contains eight blocks. In the ShuffleNet V2 1 × configuration, the output channel dimensions for the Conv1, MaxPool, Stage 2, Stage 3, Stage 4, Conv5, and FC layers are 24, 24, 116, 232, 464, 1024, and 1000, respectively. Building upon this foundation, we designed a CPS recognition model for colour-laser-printed documents.

Fig. 2
figure 2

Basic Residual Units of Shufflenet V2 (a) Standard unit (b) Downsampling unit.

Full size image

Model improvements

The as-constructed colour-laser-printed document (CPS) dataset presents several challenges, including complex image backgrounds and a high degree of visual similarity among CPS patterns across certain brands. These factors drastically hinder recognition, preventing existing models from achieving optimal identification performance. We modified the ShuffleNet V2 architecture to simultaneously enhance recognition accuracy and maintain training efficiency. The improved model, termed ShuffleNet_OD_CA, incorporates targeted structural enhancements, as illustrated in Fig. 3.

Fig. 3
figure 3

Shufflenet V2 Schematic diagram of the structure.

Full size image

Note: Stage 2, Stage 3, and Stage 4 are all composed of a downsampling unit, a base unit, and a CoordAttention.

The foundational improvement involves replacing the depthwise separable convolution in the main branch of the core building block of ShuffleNet V2 with omni-dimensional dynamic convolution (ODConv)19. Concurrently, as all convolution operations within the main branch maintained consistent input and output channel dimensions, the initial and terminal 1 × 1 pointwise convolutions were utilised for channel adjustment but solely used for information fusion. Consequently, retaining the terminal pointwise convolution structure following the convolution replacement becomes redundant, as illustrated in Fig. 4. Therefore, the pointwise convolution operation performed at the end of the main branch was removed. Subsequently, a coordinate attention (CoordAttention) mechanism20 was integrated at the terminal position of each stage in the network. Using these enhancement strategies, the accuracy of the network model was improved while maintaining training efficiency. The following sections elucidate the modifications applied to the ShuffleNet V2 architecture by detailing both the CoordAttention mechanism and the ODConv operation.

Fig. 4
figure 4

ODConv structure.

Full size image

Conventional convolution employs a fixed number of kernels, limiting its adaptability to the spatial structure of input data. To address this bottleneck, dynamic convolution mechanisms21 achieve parameter dynamism through an attention-driven kernel fusion strategy. This approach enhances computational accuracy without increasing computational overhead, enabling lightweight CNNs to perform efficiently. ODConv extends this concept by introducing dynamic adjustments not only in the number of convolution kernels but also across spatial dimensions, input channels, and output channels. It can be conceptualised as a parallel multi-head attention mechanism operating simultaneously across all four dimensions of the kernel space. Research demonstrates that the attentional weights learned by ODConv across these four dimensions are mutually complementary, thereby appreciably improving the feature extraction capability of the network.

ODConv comprehensively enhances feature-extraction capabilities by dynamically and synergistically optimising the four dimensions of convolutional kernels—spatial position, input channel, output channel, and kernel quantity—through a multidimensional attention mechanism and parallel processing strategy. Its workflow can be summarised as follows: after extracting basic spatial information via standard convolution, global average pooling (GAP) is applied to the input features to generate a compressed global representation vector. Subsequently, the dimensionality of this vector is reduced, and the vector is activated using a fully connected layer. Four parallel branches then separately compute attention weights for the four dimensions of the kernel. Each branch contributes distinctively. Spatial weights amplify local detail perception, input channel weights filter critical feature sources, output channel weights modulate filter importance, and kernel quantity weights assess multi-kernel collaborative contributions. This forms a complementary four-dimensional dynamic modulation mechanism. All attention weights are applied to the original kernels via element-wise multiplication, achieving adaptive multi-dimensional parameter adjustment. The modulated kernel outputs undergo weighted fusion and layer normalisation, ultimately generating an efficiently fused feature map that simultaneously preserves spatial details, channel interdependencies, and multi-kernel collaborative characteristics. This mechanism dynamically calibrates kernel parameters through multidimensional attention, effectively enhancing the flexibility and robustness of feature representation. The attention mechanisms across different kernel dimensions are visualised in Fig. 5 and formally defined in Eq. (1).

$$y = (\sum\nolimits_{i = 1}^{n} {\alpha_{si} \odot \alpha_{ci} \odot \alpha_{si} \odot \alpha_{wi} } ) * X$$
(1)
Fig. 5
figure 5

Diagrams Illustrating Four Types of Attention Scalar Actions.

Full size image

In Eq. (1), \(\text{R}\) represents the kernel-wise attention scalar, while \(\alpha_{{s_{i} }} \in R^{k \times k} ,\alpha_{{c_{i} }} \in R^{{c_{{i_{n} }} }} ,and\alpha_{{f_{i} }} \in R^{{c_{{o_{ut} }} }}\) denote the attention weights applied to the spatial dimensions, input channels, and output channels of the convolution kernels, respectively. The multiplicative operation \(\odot\) signifies element-wise multiplication across the dimensions within the kernel space.

Previous channel attention mechanisms, such as squeeze-and-excitation22 and convolutional block attention module23, primarily model inter-channel dependencies by emphasising important feature channels while suppressing redundant features. By contrast, CoordAttention preserves the positional information of critical channel features while enriching global spatial layout awareness. As depicted in Fig. 6, this module operates through a dual-branch attention mechanism: one branch captures cross-channel relationships with spatial location embeddings, while the other generates position-sensitive attention maps for spatial coordinate modelling. This design allows CoordAttention to effectively incorporate coordinate information into channel attention. This results in a position-sensitive channel weighting paradigm with enhanced discriminative feature localisation within complex backgrounds—which is crucial for CPS recognition tasks under intricate printing patterns.

Fig. 6
figure 6

CoordAtention Module.

Full size image

CoordAttention performs global pooling on the input feature map separately along the horizontal and vertical directions using two pooling kernels of sizes (H,1) and (1, W), respectively. Consequently, feature maps are obtained in both directions, enabling the compression of global information features for positional information encoding. This step generates two feature vectors: \(z^{h} \in R^{C \times H \times 1} and{\kern 1pt} z^{w} \in R^{C \times 1 \times W}\).

$${\text{z}}_{\text{c}}^{\text{h}}=\frac{\sum_{0\le \text{i}\le \text{W}}{\text{x}}_{\text{c}}(\text{h},\text{i})}{\text{W}}$$
(2)
$${\text{z}}_{\text{c}}^{\text{w}}=\frac{\sum_{0\le \text{j}\le \text{H}}{\text{x}}_{\text{c}}(\text{j},\text{w})}{\text{H}}$$
(3)

The two obtained feature maps are concatenated, and a 1 × 1 convolution followed by non-linear activation is applied to the merged feature layer to generate the intermediate feature map f.

$$f = \delta \, (Conv(Concat(z^{h} ,z^{w} ))) \in R^{{\frac{C}{r} \times (H \times W)}} ,$$
(4)

where r denotes the channel reduction ratio and \(\updelta\) represents the activation function. The feature map f is decomposed into its horizontal component \({\text{f}}^{\text{h}}\in {\text{R}}^{\text{C}/\text{r}\times \text{H}}\) and vertical component \({\text{f}}^{\text{w}}\in {\text{R}}^{\text{C}/\text{r}\times \text{W}}\). These components are then processed using 1 × 1 convolution followed by a Sigmoid function to generate the attention weights.

$${\text{g}}^{\text{h}}=\upsigma (\text{Conv}({\text{f}}^{\text{h}}))\in {\text{R}}^{\text{C}\times \text{H}\times 1}$$
(5)
$${\text{g}}^{\text{w}}=\upsigma (\text{Conv}({\text{f}}^{\text{w}}))\in {\text{R}}^{\text{C}\times 1\times \text{W}}$$
(6)

The horizontal and vertical attention weights are broadcast to the original spatial dimensions and undergo element-wise multiplication with the input feature map. Therefore, the final output y enhances feature responses at important positions.

$${\text{y}}_{\text{c}}(\text{i},\text{j})={\text{x}}_{\text{c}}(\text{i},\text{j})\times {\text{g}}_{\text{c}}^{\text{h}}(\text{i})\times {\text{g}}_{\text{c}}^{\text{w}}(\text{j})$$
(7)

Experimental models and evaluation metrics

We used the Windows 10 operating system with 16 GB RAM, an Intel(R) Core(TM) i5-10300H CPU @ 2.50 GHz, and an NVIDIA GeForce RTX 2060 GPU (6 GB VRAM). Python was used as the programming language, with PyTorch version 1.7.1 and CUDA version 11.0.

The Adam optimiser was employed the initial learning rate (lr) was set to 0.001, with weight decay configured as 5 × 10⁻5, which integrates advantages from both Momentum and RMSProp optimisers. By computing the first-moment estimates (mean) and second-moment estimates (uncentered variance) of gradients, Adam adaptively assigns parameter-specific learning rates, ensuring computational efficiency24. The Cross entropy loss function was introduced to refine the model, as it directly quantifies the disparity between model predictions and ground-truth labels while effectively mitigating vanishing gradient issues—a characteristic that renders it widely applicable in multi-class classification tasks25. The batch size was set to 16, considering model training speed, stability, generalisation capability, and GPU VRAM constraints. Based on preliminary experiments, the number of epochs was fixed at 50 to optimise training time and prevent overfitting. The StepLR learning rate scheduler was selected to adjust the learning rate at equal intervals and was configured with step_size = 7 and gamma = 0.1.Given that this task differs considerably from the task based on the ImageNet dataset, transfer learning was not applied in model training.

Accuracy, precision, recall, and the F1 score were selected to evaluate the performance of the colour-laser-printer classification model. Additionally, model parameters and floating point operations (FLOPs) and Inference time for a single picture were used to measure model complexity.

Results analysis

Ablation study

An ablation study was conducted to investigate the impact of integrating ODConv and CoordAttention on the performance of the ShuffleNet V2 model. Using ShuffleNet V2 as the baseline model, ODConv and CoordAttention were sequentially incorporated to validate the contribution of each module to model performance. The results are presented in Table 2. As shown in Table 2, replacing the depthwise separable convolution operation in the basic module of ShuffleNet V2 with ODConv increased model accuracy by 6%, precision by 5.73%, recall by 7.31%, and F1-score by 6.13%. Additionally, it reduced both the number of parameters and FLOPs. Adding the CoordAttention mechanism to ShuffleNet V2 increased model accuracy by 2.83%, precision by 2.94%, recall by 4.09%, and F1-score by 3.12%, with a slight increase in the number of parameters and FLOPs. Compared to the baseline model, the improved model—ShuffleNet_OD_CA—which replaces the depthwise separable convolution operation with ODConv and incorporates the CoordAttention mechanism, exhibited a 7.36%, 7%, 8.74%, and 7.69% increase in accuracy, precision, recall, and F1-score, respectively. The new model also reduced both the number of parameters and FLOPs.

Table 2 ShuffleNet_OD_CA model ablation experiments.
Full size table

Performance comparison of different models

To further validate the recognition effectiveness of the improved model for the CPS in colour- laser-printed documents, the performance of the model was compared to that of other models, including DenseNet12126, EfficientNet_b027, Inception_v328, MobileNet_V29, ResNext50_32 × 4d30, ResNet5031, Xception32, and MobileNetV3_small_10033, under identical experimental conditions.To make more full use of the limited dataset, reduce the bias introduced by fixed dataset partitioning, and verify the generalization ability of the model, 5 different random numbers were used to partition the training set and test set for training and testing the model. The random number seeds are 123,43,100,256,450. The results are presented in Table 3. Among the lightweight network models, the ShuffleNet_OD_CA model constructed in this study outperformed the other models. The numbers of FLOPs and parameters and inference time were slightly higher for the ShuffleNet_OD_CA than for MobileNetV3_small_100. By contrast, the latter markedly differed from ShuffleNet_OD_CA in terms of accuracy, precision, recall, and F1-score. Compared to traditional CNNs, ShuffleNet_OD_CA exhibited an accuracy comparable to that of Xception, which was higher than those of other models. Furthermore, the precision, recall, and F1-score of ShuffleNet_OD_CA were 0.17%, 0.14%, and 0.16% higher than those of Xception, respectively, representing the highest performance among all models. Hence, the model proposed in this study demonstrated superior performance in recognising CPS in colour-laser-printed documents.

Table 3 Comparison of the performance of different models.
Full size table

CPS recognition model performance and inter-class misclassification analysis

To further analyse the recognition performance of the model on CPS patterns from different brands, the model was used to classify the 884 images in the test set. The results are presented in Table 4. Concurrently, to analyse the issue of misclassification between categories, a confusion matrix was employed to visualise the degree of confusion between different classes, as shown in Fig. 7.There are 6 recognition errors for Dell and Epson. The reason may be that when the samples are rotated by 180 degrees, their key recognition dot matrix patterns may be consistent in composition with other small dots, thus resulting in errors in machine recognition.For the recognition errors between Dell, Epson and HP, the reason may be that the basic unit of the tracking hidden code dot matrix of HP is a combined dot matrix, composed of 2 15 × 8 dot matrices and 1 W-shaped dot matrix. Since the dot matrix display is not clear, the machine only recognizes the 15 × 8 dot matrices and fails to recognize the W-shaped dot matrix, leading to misrecognition.

Table 4 Experimental results of the model on the test set.
Full size table
Fig. 7
figure 7

Confusion matrix.

Full size image

As observed in Table 4, the recognition accuracy of the model for CPS in colour laser-printed documents across all eight brands exceeds 85.05%, with recall rates surpassing 85.04%, precision rates above 84.26%, and F1-scores higher than 87.92%. The model achieves notably higher recognition accuracy for Canon and Konica brands, reaching 94.39% and 94.07%, respectively. The accuracies observed for Epson and Dell brands are lower than those achieved for others. Overall, the model demonstrates satisfactory performance in recognising CPS patterns in colour- laser-printed documents.Confusion matrix as shown in Fig. 7

Application testing of the CPS recognition model

To further verify the usability of the model in this study, the trained ShuffleNet_OD_CA model was loaded for recognition, and tested using samples that have not been used in either the training set or the test set. Due to the high difficulty in obtaining tracking hidden code samples, the number of test samples for each brand is inconsistent. A total of 92 test images were used, including 10 for Canon, 11 for Dell, 11 for Epson, 12 for HP, 11 for Ikon, 12 for Konica, 12 for Ricoh, and 13 for Xerox. The recognition accuracy and average inference time were statistically analyzed, with the results shown in Table 5.

Table 5 Test Results.
Full size table

As can be seen from the table, the model exhibits good overall performance: it can accurately recognize all images of Dell and Epson, while its recognition accuracy for HP and Ricoh is relatively lower, both at 83.33%. Overall, the average recognition accuracy across the 8 categories is 91.44%, and the average inference time is 36.56 ms.

Conclusion

Compared with previous studies, which mostly used image grayscale values and the inherent physical characteristics of printers to identify color laser printers and adopted a small sample size, this study emploied a deep learning model to identify the tracking hidden codes of color laser printers from different brands. A dataset of CPS patterns in documents printed by eight color laser printers of different brands with the highest market share was constructed. An improved network based on the ShuffleNet V2 model architecture was proposed. ODConv was used to replace depthwise separable convolution in basic modules and CoordAttention mechanism was introduced at the end of each stage. Ablation experimental results showed that replacing ODConv and adding CoordAttention mechanism improved the accuracy, precision, recall, and F1-score of the model. The improved model ShuffleNet_OD_CA maintained the high accuracy of the base model, while achieving a more lightweight network structure. The enhanced model exhibited an accuracy, precision, recall, and F1-score of 91.18%, 91.49%, 91.04% and 91.14%, respectively, on the test set, with 8.03 × 10⁷ FLOPs and 1.82 × 10⁶ parameters. The accuracy of the model far exceeded that of the other lightweight models, with fewer parameters than those required for traditional CNN models. Future research will further expand the number of samples and use printed documents from more brands and models of color laser printers to train and test the model, thereby providing support for case investigation.