A cooperative ECC-based authentication protocol for VANETs

Abstract

Vehicular Ad Hoc Networks (VANETs) play a critical role in Intelligent Transportation Systems (ITSs), enabling secure communication between vehicles and roadside infrastructure. However, in dense traffic environments, conventional centralized Vehicle-to-Infrastructure (V2I) authentication schemes impose a significant computational burden on Roadside Units (RSUs), leading to authentication delays and degraded service quality. To address this challenge, we propose a cooperative V2I authentication protocol that delegates part of the computational workload to nearby trusted vehicles. A novel dual-verification mechanism, based on asymmetric delegation and a concealed perturbation point, ensures correctness even in the presence of misbehaving or colluding helpers. This structure differs from previous cooperative authentication models by introducing redundancy and verifiability into offloaded computations. In contrast to prior RSU-centric or fog-layer solutions, our protocol distributes workload without compromising security guarantees. The proposed scheme supports batch authentication and group session key establishment, enabling efficient and scalable secure communication for both V2I and V2V scenarios. Moreover, it incorporates dynamic pseudonym updates and flexible certificate revocation, achieving strong privacy protection with conditional traceability. Formal security analysis under the Real-Or-Random (ROR) model demonstrates robustness against impersonation, replay, and tampering attacks. Simulation results confirm that our protocol reduces RSU-side computation overhead by over 20% under comparable conditions, offering a lightweight and practical solution for real-time authentication in dynamic vehicular networks.

Introduction

Vehicular Ad Hoc Networks (VANETs) are integral to the advancement of Intelligent Transportation Systems (ITSs), enabling secure Vehicle-to-Infrastructure (V2I) communications for safety-critical tasks such as collision avoidance and traffic optimization^1,2. However, in dense urban environments, real-time V2I authentication remains a significant bottleneck due to the limited scalability of centralized designs.

Traditional V2I schemes rely entirely on Roadside Units (RSUs) to perform cryptographic computations for each authentication request. Under heavy traffic, this centralized burden leads to RSU overload, causing delays that compromise real-time responsiveness³ and expose the system to denial-of-service (DoS) attacks⁴. While recent efforts have introduced lightweight cryptographic primitives and batch verification to mitigate these issues, most approaches still center computation at the RSU, offering limited adaptability in highly dynamic or large-scale deployments.

Furthermore, as the number of vehicles increases, the linear growth in RSU workload severely limits scalability. Although pseudonym-based techniques are widely employed to protect vehicle privacy, many existing schemes lack strong unlinkability, rendering them vulnerable to long-term tracking and correlation attacks. Thus, robust authentication protocols must support efficient pseudonym updates and scalable credential management.

We observe that previously authenticated vehicles within RSU range are often underutilized, despite possessing idle computational resources. Motivated by this, we propose a cooperative V2I authentication framework in which RSUs offload part of the authentication task to nearby trusted vehicles. To safeguard against potential forgery by malicious helpers, we introduce a dual-verification mechanism based on asymmetric delegation and a concealed random perturbation point. To the best of our knowledge, this is the first cooperative V2I protocol that combines perturbation-based asymmetric computation with cross-verification to detect helper-side forgery even when helpers are not fully trustworthy.

The proposed scheme further integrates batch authentication, group session key establishment, dynamic pseudonym updates, and certificate revocation, enhancing authentication efficiency, resistance to tracking, privacy protection, and system manageability in real-world VANET deployments.

The main contributions of this work are summarized as follows:

• We propose a cooperative V2I authentication framework in which RSUs delegate partial computations to nearby vehicles. To ensure correctness and detect forgery even when helpers are not fully trustworthy, we introduce a dual-verification mechanism that combines a concealed perturbation point with asymmetric delegation to two independent helpers, one executing the full computation and the other a partial check. Compared to existing protocols, this design enhances accountability and robustness under cooperative settings.

• The protocol supports essential features such as batch authentication, group session key establishment, dynamic pseudonym updates, and certificate revocation, all integrated into a cooperative framework optimized for high-density vehicular environments. These capabilities enhance scalability, privacy, and manageability in real-time deployments.

• We provide a formal security analysis under the Real-Or-Random (ROR) model and conduct extensive simulation experiments. Results show that our scheme reduces RSU-side computational overhead and authentication latency by more than 20%, while maintaining low delay and packet loss, demonstrating its lightweight design and practical viability.

Related work

In recent years, the design of secure and scalable authentication frameworks for VANETs has received increasing attention, driven by the growing demands of dynamic, high-density scenarios^5,6,7,8. Traditional V2I authentication schemes typically centralize all cryptographic operations at RSUs, which causes computational bottlenecks and degraded responsiveness under traffic congestion^2,9,10. Although some schemes mitigate these limitations by adopting lightweight cryptographic primitives or leveraging fog/edge computing^3,5,10,11,12, the authentication logic still remains largely RSU-centric. To further improve efficiency, batch verification techniques, especially those based on certificateless and blockchain models, have been introduced^13,14,15. However, most of these models treat vehicles as passive participants and do not support active, verifiable delegation of authentication tasks. In parallel, privacy-preserving methods such as pseudonym updates^16,17, anonymous key exchange^18,19, and certificate revocation^20,21 have been widely adopted to enhance unlinkability and traceability. Multi-factor and group-based cryptographic mechanisms have also been explored²², including the lattice-based multi-signature scheme²³, which offers post-quantum security and strong anonymity, and the certificateless group signature scheme²⁴, which reduces communication and storage overhead. In vehicular cloud environments, efficient anonymous announcement protocols have been developed to balance privacy and performance²⁵. Despite these advances, most studies explore vehicles largely as passive participants and do not support active, verifiable delegation of authentication tasks. Recent V2X works with RSU-assisted handling²⁶ likewise remain RSU-centric and do not adopt helper-based offloading for V2I authentication. Suo et al.² and Yan et al.¹⁰ proposed partial offloading or trust-path validation, but the core authentication logic still remains at the RSU. Explicitly leveraging nearby trusted vehicles to compute critical operations while preserving verifiability and forgery resistance is less commonly addressed. Moreover, mechanisms for verifying helper-side correctness, especially under non-fully-trusted assumptions, are rarely specified.

To address these gaps, our work proposes the first cooperative V2I authentication protocol that integrates perturbation-based asymmetric delegation with dual verification. The design enables two independent helpers, one executing the full delegated task and another performing partial validation, to collaboratively complete authentication while allowing RSUs to cross-verify results using a concealed perturbation point. This structure ensures correctness and forgery resistance without assuming full trust in helpers. As shown in Table 1, our proposed protocol is the only scheme that simultaneously supports cooperative vehicle-side computation, batch authentication, dynamic pseudonym update, and a dual-verification structure. This design reduces RSU-side workload, maintains secure authentication under helper uncertainty, and improves scalability. Simulation results further validate our design: RSU computation and delay are reduced by over 20% compared to the baseline RSU-only model, while maintaining low packet loss and stable latency across varying traffic densities.

Table 1 Comparison of Representative VANET Authentication Schemes.

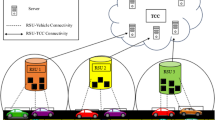
System model

System framework

The system architecture of the proposed authentication protocol for VANETs is illustrated in Fig. 1, which involves the following entities:

• Trusted Authority (TA): A fully trusted entity responsible for system initialization, key generation, vehicle registration, and revocation management. TA issues cryptographic credentials to vehicles and maintains a revocation list to trace or remove misbehaving entities.

• RSU: A semi-trusted infrastructure node deployed along roadways, responsible for communicating with vehicles. Each RSU is equipped with a tamper-proof device (TPD) to protect its own cryptographic material. During authentication, the RSU verifies the trust credential provided by the vehicle, performs mutual identity authentication, and establishes a secure session key with the vehicle. To reduce its computational burden, the RSU may delegate certain lightweight operations to nearby trusted vehicles.

• Vehicle: Each vehicle is equipped with an on-board unit (OBU) that supports sufficient computing and storage capabilities. The OBU includes a TPD for securely storing private keys and sensitive information. Vehicles can initiate mutual authentication with RSUs, present trust credentials for verification, and establish session keys. Additionally, previously authenticated vehicles may be selected by RSUs to assist in partial computations.

Fig. 1

System Framework of the protocol.

Threat model

We consider Dolev-Yao (DY) adversary model²⁷, where the adversary A has full control over the communication channel. The threats are modeled as follows:

Adversary A can eavesdrop, intercept, and block any message transmitted over the channel between vehicles and RSUs.

Adversary A can replay previously captured messages or inject forged messages in an attempt to impersonate legitimate entities or disturb the authentication process.

Adversary A may attempt to impersonate a legitimate vehicle or RSU by crafting protocol-compliant messages.

Adversary A may compromise a vehicle or RSU to extract private keys or credentials.

Adversary A may attempt to compromise one helper vehicles to forge partial authentication results.

Proposed protocol

In this section, we present a cooperative ECC-based authentication protocol for VANETs. The protocol comprises five main phases: Initialization and RSU Registration, Vehicle Registration, Mutual Authentication and Key Agreement, Batch Verification and V2V Group Key, and Pseudonym Renewal and Malicious Vehicle Tracing. The notations used throughout the protocol are summarized in Table 2. To provide an overview of the message exchanges among the participating entities (i.e., TA, vehicles, and RSUs), the complete message flow of the protocol is illustrated in Fig. 2. To prevent forgery even if a helper vehicle misbehaves or colludes, we introduce a dual-channel structure in which the RSU independently assigns a perturbation point R, splitting the delegated tasks such that no helper can reconstruct the complete response. This contrasts with prior works that assume full trust in at least one helper or lack forgery detection.

Table 2 Notation Table.

Fig. 2

Protocol flow in the proposed scheme.

Initialization and RSU registration

TA first selects an elliptic curve E, defined over a finite field ${\mathbb {F}}_p$ where p is a large prime number. The curve E is specified as: $E: y^2 = x^3 + ax + b \mod p, \quad a,b \in {\mathbb {F}}_p$ Let G denote an additive cyclic group of order q on E, and select a generator $P \in G$. TA randomly chooses an administrator private key $x_t \in {\mathbb {Z}}_q$ and computes the corresponding administrator public key as $P_{pub} = x_t \cdot P$. Next, TA selects secure hash functions $h(\cdot )$ and symmetric encryption and decryption algorithms $Enc(\cdot )$, $Dec(\cdot )$ (e.g., AES). For each RSU, TA randomly selects a private key $x_R \in {\mathbb {Z}}_q$ and computes the corresponding public key $R_{pub} = x_R \cdot P$. Then TA publishes the system parameters:$\textrm{Params} = \{ P_{pub}, Rlist_{pub}, G, P, p, q, h(\cdot ), Enc(\cdot ), Dec(\cdot ) \}$ and securely distributes each RSU’s private key $x_R$ to its corresponding RSU via secure channel. RSUs store private key in TPD. $Rlist_{pub}$ is updated accordingly with the update of the RSU’s public key.

Vehicle registration

In the vehicle registration phase, the process begins with $V_i$ securely transmitting its real identity $RID_{V_i}$ to the Trusted Authority (TA) over secure channel, as illustrated in Fig. 3.

Fig. 3

Vehicle Registration.

After receiving the real identity $RID_{V_i}$, TA randomly selects $k \in {\mathbb {Z}}_q$ and computes $C_{V_i} = k \cdot P$. It then calculates a verification component as $D_{V_i} = \bigl (x_t \cdot h(RID_{V_i} \Vert C_{V_i} \Vert P_{pub}) + k \bigr ) \bmod q$, the addition here is arithmetic addition. TA stores $\{RID_{V_i}, C_{V_i}\}$ into the revocation list RvkList for future reference and sends the message $M_1\{D_{V_i}, C_{V_i}\}$ back to $V_i$ over a secure channel.

After receives $D_{V_i}$ and $C_{V_i}$ from TA, $V_i$ first verifies their correctness by checking the equality $D_{V_i} \cdot P = h(RID_{V_i} \Vert C_{V_i} \Vert P_{pub}) \cdot P_{pub} + C_{V_i}$, ensuring the integrity of the information received from TA. Subsequently, $V_i$ randomly selects a pseudonym identity $PID_{V_i}$. It computes the authentication parameters including $S = h(PID_{V_i} \Vert C_{V_i})$, $F_{V_i} = S \cdot C_{V_i}$. $E_{V_i} = S D_{V_i} \bmod q$ and $Z_{V_i} = S h(RID_{V_i} \Vert C_{V_i} \Vert P_{pub}) \bmod q$ computed using mathematical multiplication. These parameters serve as the basis for subsequent authentication. $RID_{V_i}$, $D_{V_i}$ and $C_{V_i}$ are stored in TPD.

Mutual authentication and key agreement

The Part 1 of mutual authentication and key agreement phase is illustrated in Fig. 4. In this phase,$V_i$ first queries the public key list $Rlist_{pub}$ to verify the legitimacy of the RSU’s public key $R_{pub}$, and then initiates the authentication process. $V_i$ randomly selecting $a_v \in {\mathbb {Z}}_q$ and computing $A = a_v \cdot P$. It then computes $B = h(a_v \cdot R_{j_{pub}} \Vert PID_{V_i})$, and calculates $C = E_{V_i} + a_v$, the addition here is arithmetic addition. To ensure freshness and prevent replay attacks, $V_i$ generates a timestamp $T_1$. Subsequently, it computes $D = B \oplus C$, $E = Z_{V_i} \oplus h(B \Vert T_1)$, and $F = h(A \Vert T_1 \Vert C \Vert E)$. These values form the message $M_2\{A,D,E,F,F_{V_i},T_1\}$, which $V_i$ sends to $\text {RSU}_j$.

Fig. 4

Authentication and Key Agreement - Part 1.

Upon receiving the message, $\text {RSU}_j$ first checks the validity of the timestamp $T_1$ to ensure message freshness. It then computes $B' = h(A \cdot x_{R_j} \Vert PID_{V_i})$ and $C' = D \oplus B'$, followed by recovering $Z_{V_i} = E \oplus h(B' \Vert T_1)$. Finally, $\text {RSU}_j$ verifies the correctness of the received values by checking the equality $F {\mathop {=}\limits ^{?}} h(A \Vert T_1 \Vert C' \Vert E)$. This verification ensures that the message originated from $V_i$ and that its contents have not been tampered with during transmission. Then RSU randomly selects $r \in {\mathbb {Z}}_q$, computes $R = r \cdot P$.

The second part of the mutual authentication process, which involves multi-vehicle cooperation, is illustrated in Fig. 5. In this phase, $\text {RSU}_j$ generates a timestamp $T_2$. It computes $G_1 = h(Z_{V_i} \Vert SK_{V_1} \Vert T_2)$ and $H_1 = {Enc}_{SK_{V_1}}(T_2\Vert Z_{V_i}\Vert A\Vert F_{V_i})$, where $SK_{V_1}$ is the session key for vehicle $V_1$. Similarly, $\text {RSU}_j$ computes $G_2 = h(Z_{V_i} \Vert SK_{V_2} \Vert T_2)$ and $H_2 = \textrm{Enc}_{SK_{V_2}}(T_2\Vert Z_{V_i}\Vert R)$ for vehicle $V_2$. The messages $M_3$ and $M_4$ are transmitted to $V_1$ and $V_2$, $V_1$ and $V_2$ are randomly selected trusted vehicles. Upon receiving these messages, $V_1$ and $V_2$ decrypt them to obtain $(T_2 \Vert Z_{V_i}\Vert A\Vert F_{V_i}) = \textrm{Dec}_{SK_{V_1}}(H_1)$ and $(T_2 \Vert Z_{V_i}\Vert R) = \textrm{Dec}_{SK_{V_2}}(H_2)$. Both vehicles verify the timestamp $T_2$ to confirm message freshness and integrity. They then validate $G_1 {\mathop {=}\limits ^{?}} h(Z_{V_i} \Vert SK_{V_1} \Vert T_2)$ and $G_2 {\mathop {=}\limits ^{?}} h(Z_{V_i} \Vert SK_{V_2} \Vert T_2)$. Subsequently, $V_1$ computes $L_1 = Z_{V_i} \cdot P_{pub} + A + F_{V_i}$, and $V_2$ computes $L_2 = Z_{V_i} \cdot P_{pub}+R$. Each vehicle generates a new timestamp ($T_3$ and $T_4$) and computes $N_1 = h(L_1 \Vert SK_{V_1} \Vert T_3)$ and $N_2 = h(L_2 \Vert SK_{V_2} \Vert T_4)$.

The response messages $M_5\{L_1, N_1, T_3\}$ and $M_6\{L_2, N_2, T_4\}$ are transmitted back to $\text {RSU}_j$. Finally, $\text {RSU}_j$ verifies these responses by checking the validity of the timestamps $T_3$ and $T_4$, and validating $N_1 {\mathop {=}\limits ^{?}} h(L_1 \Vert SK_{V_1} \Vert T_3)$, $N_2 {\mathop {=}\limits ^{?}} h(L_2 \Vert SK_{V_2} \Vert T_4)$. and The verification of $L_1 {\mathop {=}\limits ^{?}} L_2 -R + A + F_{V_i}$ checks the correctness of $V_1$ and $V_2$ results to prevent single-point dishonesty.

The final part of the mutual authentication process, as shown in Fig. 6. In this phase, $\text {RSU}_j$ verify the vehicle by checking whether $C'\cdot P {\mathop {=}\limits ^{?}} L_1$ holds. The correctness is ensured by the following equation:

$$\begin{aligned} \begin{aligned} C' \cdot P&= (E_{V_i} + a_v) \cdot P \\&= E_{V_i} \cdot P + a_v \cdot P \\&= S (x_t h(RID_{V_i}\Vert C_{V_i}\Vert P_{pub})+ k) \cdot P + A\\&= S h(RID_{V_i}\Vert C_{V_i}\Vert P_{pub})x_t \cdot P + S\cdot C_{V_i}+ A\\&= Z_{V_i} \cdot P_{pub} + F_{V_i} + A\\&= L_1. \end{aligned} \end{aligned}$$

Then RSU derives the session key as $SK_{V_i} = h(B'\Vert r \cdot A\Vert PID_{V_i}\Vert ID_{R_j})$. $\text {RSU}_j$ then generates a timestamp $T_5$ to protect against replay attacks and computes a verification hash $U = h(SK_{V_i}\Vert B'\Vert T_5)$.

Fig. 5

Authentication and Key Agreement - Part 2.

Fig. 6

Authentication and Key Agreement - Part 3.

The message $M_7\{T_5, R, U\}$ are sent back to $V_i$ over a public channel. Upon receiving them, $V_i$ first verifies the validity of the timestamp $T_5$. It then computes $SK_{V_i} = h(B\Vert a_v \cdot R\Vert PID_{V_i}\Vert ID_{R_j})$, and verifies the correctness of the received verification hash by checking $U {\mathop {=}\limits ^{?}} h(SK_{V_i}\Vert B\Vert T_5)$. Vehicle i and $\text {RSU}_j$ complete their mutual authentication.

Batch verification and V2V group key

In the mutual authentication process between RSU and vehicles, RSU can perform batch authentication of multiple vehicles simultaneously. When RSU authenticates n vehicles at the same time, it sends encrypted messages to trusted vehicles. Upon decryption, each trusted vehicle obtains each vehicle’s $Z_{V_i}$. Using these values, Trusted vehicle $V_1$ aggregates the computations by calculating $L_1$ collectively via batch computation, represented as $\sum _{i=1}^{n} L_1 = \sum _{i=1}^{n} \bigl (Z_{V_i} \cdot P_{pub} + A + F_{V_i}\bigr )= \sum _{i=1}^{n} Z_{V_i} \cdot P_{pub} + \sum _{i=1}^{n}A + \sum _{i=1}^{n}F_{V_i}$. Trusted vehicle $V_2$ aggregates the computations$\sum _{i=1}^{n} L_2 = \sum _{i=1}^{n} Z_{V_i} \cdot P_{pub}$. The aggregation of authentication requires each of $V_1$ and $V_2$ to perform one point multiplication, which is nearly equivalent to the computational cost of a single authentication. Later, RSU performs batch verification of the vehicles by checking the aggregated equation $\left( \sum _{i=1}^{n} C'_{i}\right) \cdot P {\mathop {=}\limits ^{?}} \sum _{i=1}^{n}L_1$, the RSU completes the authentication of n vehicles in batch. For vehicles involved in batch authentication, RSU not only generates session keys for each individual vehicle, but also establishes a V2V Group Key $GK= h(\sum _{i=1}^{n} C'_{i})$ for the entire batch group. This enables fast and secure vehicle-to-vehicle communication within the group. RSU distributes the V2V Group Key by encrypting it with the each vehicle’s session key.

Pseudonym renewal and malicious vehicle tracing

After a period of time or the vehicle enters the new RSU’s area, it updates its pseudonym identity to enhance privacy and security. The vehicle randomly selects a new pseudonym $PID_{V_i}^{\text {new}}$ to distinguish it from the previous identity. Based on this new pseudonym, the vehicle recalculates $S^{\text {new}} = h(PID_{V_i}^{\text {new}} \Vert C_{V_i})$. Subsequently, the vehicle computes the updated authentication parameters, including $F_{V_i}^{\text {new}} = S^{\text {new}} \cdot C_{V_i}$, $E_{V_i}^{\text {new}} = S^{\text {new}} D_{V_i} \bmod q$, and $Z_{V_i}^{\text {new}} = S^{\text {new}} h(RID_{V_i} \Vert C_{V_i} \Vert P_{pub}) \bmod q$. These updated parameters replace the previous parameters and are used for vehicle-to-RSU authentication.

When a vehicle is identified as malicious, the RSU initiates the revocation process by transmitting the vehicle’s $F_{V_i}$ to the Trusted Authority (TA). Upon receiving this value, the TA accesses the revocation list RvkList, which contains records of $\{RID_{V_i}, C_{V_i}\}$ tuples for all registered vehicles. The TA systematically iterates through each stored $C_{V_i}$, computing $F_{V_i}^* = h(PID_{V_i} \Vert C_{V_i}) \times C_{V_i}$. If a computed $F_{V_i}^*$ matches the reported $F_{V_i}$ from the RSU, the TA successfully correlates the malicious vehicle’s pseudonym with its real identity $RID_{V_i}$. Consequently, the TA updates the revocation list to prevent future authentication attempts by the malicious vehicle. This process ensures secure and reliable vehicle identity management, while safeguarding the integrity of the vehicular network.

Security analysis

Informal security proof

Mutual Authentication: During RSU’s verification of the vehicle’s identity, it first computes $B' = h(A \cdot x_{R_j} \Vert PID_{V_i})$ using its private key $x_{R_j}$, extracts $Z_{V_i}$ and C, and with the assistance of trusted vehicles, verifies the equality $C' \cdot P = Z_{V_i} \cdot P_{pub} + F_{V_i} + A$ using the TA’s public key $P_{pub}$. The vehicle computes the session key $SK_{V_i}=h(B\Vert a_v \cdot R\Vert PID_{V_i}\Vert ID_{R_j})$ and verifies $U=h(SK_{V_i}\Vert B\Vert T_5)$ to confirm the correctness of the session key. Since $B = h(A \cdot x_{R_j} \Vert PID_{V_i})$, the vehicle confirms that RSU possesses the private key $x_{R_j}$ paired with the recorded public key $R_{j_{pub}}$, thereby achieving mutual authentication and sharing the session key.

Anonymity: The pseudonym $PID_{V_i}$ is randomly selected and periodically updated. The values $Z_{V_i}$ and $F_{V_i}$ used in authentication also change with the pseudonym, where $S = h(PID_{V_i} \Vert C_{V_i})$, $F_{V_i}^{\text {new}}=S^{\text {new}}\cdot C_{V_i}$ and $Z_{V_i}^{\text {new}}=S^{\text {new}}\cdot h(RID_{V_i}\Vert C_{V_i}\Vert P_{pub})\bmod q$, ensuring vehicle anonymity.

Unlinkability: Each time, the vehicle transmits values A, D, E, F computed using randomly chosen $a_v$, which prevents linkage to previous data. The authentication certificate $C=E_{V_i}+a_v$ also resists tracking of the vehicle identity. $F_{V_i}$ varies with each pseudonym update, making it untraceable.

Identity Traceability Prevention: Without TA involvement, an attacker cannot deduce the vehicle’s real identity from the pseudonym $PID_{V_i}$ and authentication data $A,D,E,F,F_{V_i}$; only the TA, with knowledge of the master key, can reveal the vehicle identity.

Forward Security: The session key $SK_{V_i}$ is derived via the Diffie-Hellman protocol using the vehicle’s temporary private key and the RSU’s public key, and is never transmitted over public channels. The inclusion of RSU’s private key signature and regular updates of the vehicle’s pseudonym and private key further ensure long-term security.

Resistance to Vehicle Impersonation: The vehicle’s authentication certificate C is computed using random values, pseudonym, and the original certificate $D_{V_i}$ issued by the TA, where $E_{V_i}=S\cdot D_{V_i}\bmod q$. This certificate can be verified using the TA’s public key, making impersonation infeasible.

Resistance to RSU Impersonation: RSU must use its private key $x_{R_j}$ to compute $B'$ and derive the session key $SK_{V_i}$, which cannot be forged by an attacker, thus preventing RSU impersonation.

Replay Attack Resistance: All authentication messages include timestamps, and recipients verify the freshness of the timestamps to prevent replay attacks.

Resistance to DoS Attacks: Trusted vehicles assist in the RSU’s authentication computation, mitigating denial-of-service attacks caused by mass authentication requests.

Resistance to Sybil Attacks: The scheme defends against Sybil attacks by assigning each vehicle a unique session key $SK_{V_i}=h(B|a_v \cdot R|PID_{V_i}|ID_{R_j})$, generated through a Diffie-Hellman exchange between the RSU and the vehicle. This key is bound to the current pseudonym and updated with each pseudonym change. As the key cannot be forged without private values, even with past keys or messages, an attacker cannot impersonate other vehicles or create multiple fake identities, thus preventing Sybil attacks.

TPD Assumption and Tolerance: The proposed protocol assumes that both RSU and vehicles are equipped with tamper-proof devices (TPDs) to securely store long-term secrets. While TPDs are widely adopted and considered resilient to physical attacks, we recognize that practical deployments may face partial compromise risks. To mitigate such threats, our protocol employs ephemeral ECC keys and session-specific hashes to ensure forward secrecy. Moreover, the dual-verification design, using a concealed perturbation point and split delegation, offers robustness even when one helper becomes compromised, preventing forgery through isolated key leakage.

Defense Against Single-Point Dishonesty. To prevent a single trusted vehicle from manipulating the cooperative authentication result, two independent vehicles compute distinct values $L_1$ and $L_2$. A random perturbation point $R$, generated by the RSU and disclosed only to one vehicle, is embedded into $L_2$ such that the RSU verifies the correctness by checking whether $L_1 = L_2 + A + F_{V_i} - R$. Specifically, the perturbation point $R$ is constructed by selecting a random scalar $r \in {\mathbb {Z}}_q$ and computing $R = r \cdot P$, where $P$ is the generator of the elliptic curve group $G$. This guarantees that $R$ is uniformly distributed and cryptographically secure. The vehicle computing $L_1$ knows $A + F_{V_i}$ but has no access to $R$, while the vehicle computing $L_2$ knows $R$ but does not know $A + F_{V_i}$. As a result, neither vehicle can forge the other’s output. This mutual blindness prevents a single dishonest vehicle from generating both $L_1$ and $L_2$ that satisfy the verification equation, thereby achieving robustness against single-point forgery and enhancing both integrity and privacy of the cooperative authentication process.

Formal security proof

We provide a formal security analysis of the proposed cooperative authentication protocol under the Real-Or-Random (ROR) model²⁸. To instantiate our protocol in practice, we adopt widely accepted cryptographic parameters. Elliptic curve operations are executed over the secp256r1 curve, which provides a 256-bit key length and 128-bit security strength against the Elliptic Curve Discrete Logarithm Problem (ECDLP). For symmetric encryption and message authentication, we use AES with a 128-bit key (AES-128) and HMAC-SHA-256, respectively. All hash computations are performed using SHA-256, which generates 256-bit outputs. In our protocol, the AES-128 session key is derived by taking the first 128 bits of a SHA-256 hash output.

Let A be a probabilistic polynomial-time (PPT) adversary that aims to compromise the semantic security of the session key established among a vehicle $V_i$, a roadside unit $RSU_j$, and cooperative vehicle $V_1$, $V_2$. The protocol employs ephemeral ECC-based key generation, a collision-resistant hash function modeled as a random oracle, and assumes that both vehicles and RSUs are equipped with TPDs that securely store secret value and remain resistant to physical attacks.

Adversary Capabilities: The adversary A is allowed to issue the following queries:

• Execute($V_i$, $RSU_j$, $V_1$, $V_2$): Simulates passive eavesdropping by returning all exchanged messages.

• Send(($V_i$, $RSU_j$, m): Sends a forged message m to entity $V_i$, $RSU_j$; if valid, returns the protocol response.

• Hash(M): Models the hash function as a random oracle.

• Corrupt($V_i$)/Corrupt($RSU_j$): Attempts to extract secret information, which is protected by TPD; only brute-force guessing is feasible.

• Test($V_i$, $RSU_j$): Returns either the real session key or a random value based on a hidden bit b.

Theorem 1

The advantage of any PPT adversary A in breaking the semantic security of the proposed protocol under the ROR model is bounded by: $Adv_A^{\text {ROR}} \le \frac{q_h^2}{2^{l_h}} + \frac{(q_s + q_e)^2}{n} + \frac{q_s}{2^{2l_{sk}-1}}. + \frac{q_s}{2^{l_k-1}} + 2 \cdot Adv_A^{\text {ECDLP}} + \frac{2}{q}$

Let $q_h$, $q_s$, $q_e$, and $q_c$ denote the number of queries made to the Hash, Send, Execute, and Corrupt oracles. We define a sequence of games $Game_0$ to $Game_5$ to bound the adversary’s success probability:

$Game_0$ describes the real execution of the protocol. The adversary’s advantage is defined as

$$\begin{aligned} Adv_A^{\text {ROR}} = \left| 2 \cdot \Pr [\text {Win}_0] - 1 \right| . \end{aligned}$$

(1)

$Game_1$ simulates a passive eavesdropping attack. Since the session keys are derived from ephemeral ECC secrets which are not transmitted over public channels, the adversary cannot derive the session key. Therefore,

$$\begin{aligned} \Pr [\text {Win}_0] = \Pr [\text {Win}_1]. \end{aligned}$$

(2)

$Game_2$ models the adversary’s attempt to forge valid protocol messages by using the Hash and Send queries. According to the birthday bound, $l_h$ is the output length of the hash function, we obtain

$$\begin{aligned} \left| \Pr [\text {Win}_2] - \Pr [\text {Win}_1] \right| \le \frac{q_h^2}{2^{l_h + 1}} + \frac{(q_s + q_e)^2}{2n}. \end{aligned}$$

(3)

$Game_3$ considers forgery attacks on the cooperative authentication result. Since each helper vehicle uses an independent session key and the protocol can defense against single-point dishonesty, an adversary must correctly guess both session keys to forge a valid result. Given the randomness of key selection, $L_{sk}$ is the bit length of the session key, the advantage is bounded by:

$$\begin{aligned} \left| \Pr [\text {Win}_3] - \Pr [\text {Win}_2] \right| \le \frac{1}{2^{2l_{sk}}}. \end{aligned}$$

(4)

$Game_4$ handles the adversary’s Corrupt queries against $V_i$ or $RSU_j$. As private credentials are protected by TPDs,$l_k$ is the length of the secret value stored in the vehicle, the success probability is bounded by

$$\begin{aligned} \left| \Pr [\text {Win}_4] - \Pr [\text {Win}_3] \right| \le \frac{q_s}{2^{l_k}}. \end{aligned}$$

(5)

$Game_5$ models the adversary’s effort to solve the ECDLP, yielding

$$\begin{aligned} \left| \Pr [\text {Win}_5] - \Pr [\text {Win}_4] \right| \le Adv_A^{\text {ECDLP}}. \end{aligned}$$

(6)

$Game_6$ models a forgery attempt where the adversary controls one of the cooperative helper vehicles and attempts to forge a valid cooperative authentication result by constructing a pair $(L_1, L_2)$ that satisfies the RSU’s verification check. In order to do so, the adversary must ensure that the forged values fulfill the hidden relation determined by the random perturbation point R, which is generated by the RSU and revealed only to one legitimate helper vehicle. Because R is a uniformly random elliptic curve point of q bits, and is unknown to the adversary, any successful forgery of $(L_1, L_2)$ that passes verification requires correctly guessing the value of R. Thus, the adversary’s advantage in this game is bounded by:

$$\begin{aligned} \left| \Pr [\text {Win}_6] - \Pr [\text {Win}_5] \right| \le \frac{1}{q}. \end{aligned}$$

(7)

At the end, the session key can only be obtained by guessing:

$$\begin{aligned} \Pr [Win_6] = \frac{1}{2}. \end{aligned}$$

(8)

We derive the total advantage:

$$\begin{aligned} Adv_A^{\text {ROR}}&= \left| 2 \cdot \Pr [\text {Win}_0] - 1 \right| \nonumber \\&= 2 \cdot \left| \Pr [\text {Win}_1] - \Pr [\text {Win}_6] \right| \nonumber \\&\le 2 \cdot \big ( \left| \Pr [\text {Win}_2] - \Pr [\text {Win}_1] \right| + \left| \Pr [\text {Win}_3] - \Pr [\text {Win}_2] \right| \nonumber \\&\quad \quad \ + \left| \Pr [\text {Win}_4] - \Pr [\text {Win}_3] \right| + \left| \Pr [\text {Win}_5] - \Pr [\text {Win}_4] \right| + \left| \Pr [\text {Win}_6] - \Pr [\text {Win}_5] \right| \big ) \end{aligned}$$

(9)

Substituting inequalities (3)-(8), we obtain:

$$\begin{aligned} Adv_A^{\text {ROR}} \le \frac{q_h^2}{2^{l_h}} + \frac{(q_s + q_e)^2}{n} + \frac{q_s}{2^{2l_{sk}-1}}. + \frac{q_s}{2^{l_k-1}} + 2 \cdot Adv_A^{\text {ECDLP}} + \frac{2}{q} \end{aligned}$$

(10)

Under the results, the proposed protocol is secure against both passive and active adversaries in the ROR model.

Robustness under practical limitations

To ensure the robustness of the proposed delegation mechanism in practical VANET deployments, we further analyze its core assumptions and handling strategies. If an initially selected helper vehicle returns an incorrect or unverifiable result, the RSU will promptly discard it and reselect another available vehicle for assistance. The protocol assumes that at least one of the two selected helper vehicles is honest. In realistic urban traffic conditions, the number of vehicles within the RSU’s communication range can be approximated by a Poisson distribution. Suppose k vehicles are available at a given time, and each independently has a probability $p_h$ of being honest and capable (i.e., equipped with valid credentials and a tamper-proof device). The probability that at least one of the two selected helpers is honest is $1 - (1 - p_h)^2$. Under a conservative estimate with $p_h = 0.7$, this probability reaches 91%. In practice, RSUs can prioritize recently authenticated or higher-reputation vehicles as preferred helpers to further increase the likelihood of honest participation.

In rare situations where no eligible helper is available, such as during low vehicle density or poor connectivity, the RSU falls back to standalone mode, performing the full authentication computation itself. In this case, the RSU directly verifies the legitimacy of the vehicle by checking the encrypted credential through the equation $C' \cdot P = Z_{V_i} \cdot P_{pub} + A + F_{V_i}$. Although this increases its computational load, the correctness and security of the protocol are preserved, and such a fallback is already supported by the system design. Moreover, if a helper vehicle disconnects or fails to respond during the authentication process, the RSU will discard the partial result and revert to full local computation. Adaptive timeout thresholds based on vehicle mobility and local density can be employed to improve reliability. To complement the above design-level resilience mechanisms, we conduct simulations in later sections to empirically evaluate the performance impact of our cooperative mechanism under various helper densities and dynamic vehicular topologies. The results confirm that the protocol maintains low latency and overhead, even in high-mobility conditions. These evaluations further support the practical deployability of the scheme in real-world VANET environments.

Our protocol assumes that both RSU and vehicles are equipped with TPDs, which securely stores cryptographic keys and performs essential operations. While TPDs are widely adopted in real-world vehicular networks and provide strong hardware-level protection, it is crucial to acknowledge potential threats such as physical compromise or side-channel attacks. To mitigate such risks, we design our protocol so that even if the TPD of a single vehicle is compromised, the attacker cannot impersonate other vehicles or forge valid session keys without also breaking the helper vehicle computations or the RSU’s dual verification process. Moreover, the TPD does not store long-term session data or secret material that could affect other vehicles’ security if leaked. This containment ensures that a compromised TPD only endangers its own session security, without breaking system-wide trust. In future deployments, the use of emerging technologies such as physically unclonable functions (PUFs) or remote attestation may further strengthen the resilience of TPDs against hardware-level attacks.

Performance analysis

This section presents a comprehensive performance evaluation of the proposed authentication protocol in terms of computational cost, communication overhead, and network behavior under dynamic vehicular conditions. Comparisons are made against four representative schemes^{3,20,29,30,31,32}.

Security features

Table 3 compares the security properties of our proposed scheme against four existing protocols. Our scheme achieves comprehensive protection across ten critical security aspects. It ensures mutual authentication by verifying that the RSU possesses its private key during session key derivation. It provides strong anonymity and unlinkability through frequent pseudonym updates and embedding randomized ephemeral values in each session. The use of ephemeral keys and fresh randomness in session key generation offers robust forward security, preventing compromise of past sessions even if long-term keys are leaked. We also design a novel defense against single-point dishonesty in cooperative authentication by engaging two helper vehicles and introducing a hidden perturbation point, allowing the RSU to verify consistency and thwart forgery attempts by a single dishonest participant. Valid authentication certificates can only be generated by vehicles possessing credentials issued by the TA, ensuring strong resistance to impersonation attacks. RSUs must also demonstrate possession of their private keys, protecting against RSU impersonation. Freshness checks based on timestamps ensure replay attack resistance, and offloading partial authentication computation to cooperative vehicles enhances DoS attack resilience. Overall, our scheme outperforms the compared protocols in terms of completeness and practicality under dynamic vehicular network conditions.

Table 3 Security Feature Comparison.

Computational cost analysis

To ensure fairness in evaluation, the operation times for all schemes are based on the settings adopted by Miao et al.³³ and Wang et al. (2025)³². We use the following notations to represent the computation time of cryptographic operations: $T_H$ for SHA-256 hash operations, $T_{EM}$ for ECC-based scalar multiplication, $T_{AES}$ for AES-128 encryption/decryption, $T_{BP}$ for bilinear pairing, $T_{EX}$ for exponentiation in group ${\mathbb {G}}_T$, $T_{SM}$ and $T_{PA}$ for scalar multiplication and point addition in group ${\mathbb {G}}_1$, respectively, and $T_{e1}$, $T_{e2}$, and $T_{et}$ for exponentiation in ${\mathbb {G}}_1$, exponentiation in ${\mathbb {G}}_2$, and modular exponentiation in ${\mathbb {G}}_T$. The typical execution times are: $T_H \approx 0.001$ ms, $T_{EM} \approx 0.141$ ms, $T_{AES} \approx 0.013$ ms, $T_{BP} \approx 3.111$ ms, $T_{EX} \approx 0.138$ ms, $T_{SM} \approx 0.141$ ms, $T_{PA} \approx 0.00072$ ms, $T_{e1} \approx 0.566$ ms, $T_{e2} \approx 3.855$ ms, and $T_{et} \approx 0.867$ ms. These values are obtained under experimental settings using optimized cryptographic libraries and reflect average execution efficiency. All compared schemes are evaluated under the same cost model to ensure fairness and consistency in computational analysis. As summarized in Table 4, the evaluation considers the vehicle-side, RSU-side, and cooperative vehicle-side computational load. The comparison results show that our proposed scheme achieves the lowest total computational cost among all evaluated protocols. This is primarily attributed to the introduction of trusted cooperative vehicles, which assist in part of the authentication computation, thereby significantly reducing the computational burden on the RSU. The cooperative vehicle performs partial computation and returns the result, which is then verified and aggregated by the RSU to generate the final authentication response, ensuring both efficiency and security. As a result, the total cost of our scheme is only 1.025 ms, outperforming all other schemes. Figure 7 illustrates the RSU-side computational cost comparison. Although Wang (2022) et al.’s scheme reports a slightly lower RSU cost (0.426 ms vs. 0.598 ms in ours), its vehicle-side cost is significantly higher (0.709 ms), resulting in an unbalanced workload distribution. In contrast, our scheme achieves a better balance between the RSU and the vehicle, supports dynamic revocation, and maintains strong performance in dense vehicular environments. To better capture RSU-side computation under different conditions, we define two modes: independent mode and cooperative mode. In the independent mode, the RSU performs all authentication tasks itself, including signature verification and session key derivation, resulting in a total cost of $6T_{EM} + 3T_H \approx 0.831$ ms. In the cooperative mode, some computation is offloaded to helper vehicles, and the RSU-side cost is reduced to $4T_{EM} + 2T_{AES} + 8T_H \approx 0.598$ ms, which is already listed in Table 4. These two values are used in our simulations to model the RSU’s average computational load under varying helper densities, providing a realistic and flexible evaluation. Unless otherwise stated, the subsequent simulations reported in Packet Loss Rate and End-to-End Delay use a common timing basis: per-role constants for the vehicle, helper, and RSU (cooperative) are taken verbatim from Table 4, whereas the RSU (independent) timing derived from the operation-cost breakdown at the end of this subsection. End-to-end delay is computed as the application-layer round-trip time with the corresponding cryptographic times subtracted under the same basis.

Table 4 Computation Cost Comparison.

Fig. 7

RSU-side computational cost comparison among schemes.

Communication cost analysis

To comprehensively evaluate the communication performance, we compare representative schemes in terms of communication overhead at the vehicle, RSU, and cooperative vehicle sides. The communication element sizes are standardized based on^3,32: a hash output is 32 bytes, an AES ciphertext is 16 bytes, a non-pairing ECC point is 20 bytes, and both timestamp and identity are 4 bytes; elements in the pairing groups ${\mathbb {G}}_1$, ${\mathbb {G}}_2$, and ${\mathbb {G}}_T$ occupy 32, 64, and 64 bytes, respectively, and values in ${\mathbb {Z}}_q^*$ are 32 bytes. In our scheme, the vehicle transmits three hash values, one ECC point, and one timestamp to the RSU, i.e., $3|hash|+|G|+|T|=120$ bytes, and the RSU replies with one timestamp, one ECC point, and one hash value, i.e., $|T|+|G|+|hash|=56$ bytes; in addition, the RSU sends two hash values and two AES ciphertexts to cooperative vehicles, i.e., $2|hash|+2|AES|=96$ bytes, and receives two timestamps, two hash values, and two ECC points in return, i.e., $2|T|+2|hash|+2|G|=112$ bytes. For comparison under the same unitization, Xie (2023)³ uses $4|G|+|hash|+|AES|+|T|=132$ bytes on the vehicle to RSU and $3|G|+3|hash|+|AES|+|ID|+|T|=180$ bytes on the RSU to vehicle path; Wang (2022) uses $3|G|+3|hash|+|T|=160$ bytes uplink and $2|G|+|hash|+|ID|+|T|=80$ bytes downlink; Feng (2024) is bidirectional and symmetric with $3|{\mathbb {G}}_1|+|{\mathbb {G}}_T|+2|{\mathbb {Z}}_q^*|+|T|+|hash|=260$ bytes per direction; Bao (2024) transmits $2|{\mathbb {G}}_1|+9|{\mathbb {Z}}_q^*|+|T|+|\texttt {msg}|+|\texttt{scp}|=389$ bytes from the vehicle to the RSU without a verification reply; Liang (2024) reports $2|{\mathbb {G}}_2|+|mod|+|T|+|hash|=228$ bytes on the vehicle side for the authentication step; Rani and Tripathi (2024)³¹ under our sizes count the vehicle request as $2|{\mathbb {G}}_1|+|T|+|ID|=72$ bytes and the RSU-side traffic across the phase as 1792 bits $=224$ bytes; Wang (2025) uses $2|ID|+4|{\mathbb {G}}_1|+2|T|=144$ bytes per direction on the vehicle to RSU.In contrast, the other schemes do not involve cooperative authentication. As shown in Fig. 8, on the V2I path our per-side communication is small by design: the vehicle sends 120 bytes and the RSU returns 56 bytes, which are lower than those of other schemes under the same unitization. When the helper exchange is also counted, the RSU sends 96 bytes to helpers and receives 112 bytes in return, and the system-level total becomes 384 bytes. This increase stems from the cooperative exchange yet remains moderate and acceptable, because part of the traffic is shifted to cooperative vehicles, which alleviates the RSU burden, avoids hotspots, and improves stability in dense, dynamic deployments.

Fig. 8

Comparison of communication overhead.

Storage overhead analysis

To assess the storage efficiency of our protocol, we analyze the temporary storage overhead incurred during each authentication session. In our scheme, the vehicle needs to store a pseudonym, an encrypted certificate, a temporary private key, and a session key. Since the temporary private key is discarded after authentication, the effective per-session storage overhead on the vehicle side is limited to the pseudonym, certificate, and session key, totaling 96 bytes. On the RSU side, the storage includes the pseudonym and the corresponding session key, which must be maintained until expiration or renewal thresholds are reached. The cooperative vehicles do not store any authentication-related data, further reducing system-wide memory consumption.

For comparison, we evaluate the temporary storage requirements of several representative schemes. As shown in Table 5, Wang (2025) and Wang (2022) require vehicles and RSUs to store certificates, pseudonyms, and session keys, totaling 96–128 bytes per session. Feng (2024) employ zero-knowledge proof components and ciphertexts, leading to 64–96 bytes of storage per side. Although Xie (2023) achieves low vehicle-side storage (32 bytes), its reliance on blockchain recording yields the highest RSU-side footprint (192 bytes per session). In addition, Bao (2024) require the RSU to buffer the verification tuple during checking, which is about 354 bytes per session on the RSU side, while the vehicle maintains a minimal sender footprint of about 64 bytes. Liang (2024) use pairing-group elements at verification; under the same accounting this corresponds to about 96 bytes on the vehicle and about 160 bytes on the RSU per session. Rani (2024) report per-session temporary storage of about 96 bytes on the vehicle and about 64 bytes on the RSU. As summarized in Table 5, our protocol maintains a small and well-balanced per-session footprint.

Table 5 Storage Overhead Comparison Among Protocols.

Table 6 Energy Consumption Comparison Among Protocols.

Energy consumption analysis

This section evaluates the energy consumption of the proposed scheme and compares it with representative baseline protocols. Following the methodology adopted by Miao et al.³³, the total energy overhead $E_{\text {total}}$ is calculated as the sum of computational and communication energy, $E_{\text {total}} = E_{\text {comp}} + E_{\text {comm}}$. Computational energy is derived from the number of cryptographic operations executed by the vehicle, RSU, while communication energy is estimated from the number of transmitted and received bytes using empirical per-byte costs of 5.9 $\mu$J for transmission and 4.7 $\mu$J for reception. Based on these profiles, Table 6 reports the total energy across the compared protocols. Our scheme attains a total energy of $5.49\,\text {mJ}$, substantially lower than Wang (2025) at $18.67\,\text {mJ}$ and Feng (2024) at $13.82\,\text {mJ}$, and close to lightweight designs such as Wang (2022) at $3.91\,\text {mJ}$ and Xie (2023)³ at $5.20\,\text {mJ}$. For completeness, Bao (2024) and Liang (2024) yield $28.89\,\text {mJ}$ and $25.12\,\text {mJ}$, respectively, while Rani (2024) yields $4.68\,\text {mJ}$.

We also quantify the burden on cooperative vehicles in our scheme. The helper’s computation energy is approximately $0.187\,\text {mJ}$. For communication, the helper transmits 112 bytes and receives 96 bytes, giving $E_{\text {comm}}^{\text {helper}} \approx 112\times 5.9~\mu \text {J} + 96\times 4.7~\mu \text {J} \approx 1.112\,\text {mJ}$. Hence the helper totals about $1.299\,\text {mJ}$, roughly $24\%$ of the overall $5.49\,\text {mJ}$. This level is acceptable and imposes a minimal burden on helper nodes. By offloading intensive computations from RSUs, the cooperative mechanism not only improves scalability but also yields system-level energy savings, supporting the practicality of the design in resource-constrained vehicular settings.

Packet loss rate and end-to-end delay

To evaluate the performance of the proposed authentication protocol in a realistic urban vehicular environment, we conducted simulations using OMNeT++ 5.6.2, SUMO 1.8.0, and Veins 5.2 on a workstation equipped with an Intel i7-12700F CPU, 32 GB RAM, and Windows 10. This SUMO/OMNeT++/Veins toolchain follows common practice.The road topology was generated in SUMO based on the real-world map surrounding Dalian University of Technology and imported into Veins, as illustrated in Figs. 9 and 10. The communication overheads calculated in the Communication Cost Analysis section and shown in Fig. 8 were directly used to configure the packet sizes of transmissions between vehicles, RSUs, and helper nodes, ensuring that communication cost was faithfully represented in the Veins simulations. Two RSUs were deployed at fixed positions and configured via the omnetpp.ini file to enable V2I interaction. IEEE 802.11p was adopted as the wireless communication protocol, and the total simulation duration was set to 1800 seconds. To simulate dynamic vehicle mobility, we generated three sets of vehicles each using SUMO’s randomTrips.py script, covering consecutive 600 s intervals. To approximate cryptographic processing delay, we employed a delay-based model using precomputed costs from Table 4, assigning latency values to vehicles, RSUs, and helper vehicles, respectively. These delays were embedded into OMNeT++ message handlers to emulate authentication latency. In each authentication round, every helper vehicle was allowed to assist with at most four sessions to simulate a practical delegation threshold. Additionally, pseudonym refresh was simulated by introducing a new set of the same number of vehicles every 600 seconds. This effectively emulates periodic pseudonym updates while preserving unlinkability and simplifying the simulation. Representative code snippets from the application layer implementations of RSUs, main vehicles, and helper vehicles are shown in Fig. 11, and the overall simulation configuration is summarized in Table 7.

Fig. 9

SUMO-based road network.

Fig. 10

Veins simulation scenario.

Fig. 11

Representative application-layer code snippets for the RSU, main vehicle, and helper vehicle in OMNeT++.

Table 7 Simulation Parameters Setting.

Figures 12 and 13 report performance under traffic densities from 20 to 100 vehicles. Results are averaged over two RSUs. We compare the proposed scheme with three representative non-cooperative protocols from the literature, namely Feng 2024²⁹, Wang 2022²⁰, and Rani 2024³¹. Across all densities, the proposed scheme achieves the lowest packet-loss rate, Wang follows, Rani is higher, and Feng is the highest. The gap grows at high load because every curve rises more steeply from 80 to 100 vehicles, yet our scheme remains clearly below the baselines. The end-to-end delay in Fig. 13 is computed from the application-layer round-trip time after subtracting the cryptographic computation times at the vehicle, the RSU, and the helper. These processing times are taken from Table 4 and are incorporated as event-level delays in the model. Helper coordination adds a modest latency compared with non-cooperative designs, but the increase stays within a real-time budget for V2I and evolves smoothly with load. Notably, our curve shows only a slight bend around 80 vehicles, reflecting improved channel access from coordination before increasing toward 100 vehicles; the baselines exhibit a steadier rise. As traffic density increases from light to heavy, all protocols exhibit a smooth upward trend in both packet loss and end-to-end delay; compared with the other protocols, our scheme maintains a milder growth rate and smaller fluctuations, indicating that the coordination overhead does not amplify with load and that no congestion-induced instability is observed. Overall, the comparative results that the proposed protocol can sustainably maintain a low packet-loss rate and an acceptable end-to-end latency in practical vehicular networks.

Fig. 12

Packet loss rate in protocols.

Fig. 13

End-to-end delay in protocols.

To further investigate the performance trade-offs of the proposed protocol in practical deployments, we conduct a set of simulations by varying the density of helper vehicles. A total of 100 vehicle nodes are deployed in the simulation scenario, categorized into two types: those authenticating directly with the RSU, and those utilizing nearby trusted vehicles for delegated authentication. We adjust the helper density from 0% to 100% and examine its impact on RSU-side computation time and end-to-end delay.

The end-to-end delay is measured directly through the OMNeT++/Veins simulation platform, while the RSU’s computational load is estimated using a weighted linear model based on helper density. Under the hybrid assignment, the end-to-end delay as a function of helper density can be approximated by a convex combination:

$$\begin{aligned} {\overline{T}}_{\text {end-to-end}}(\rho )\;\approx \;(1-\rho )\,{\overline{T}}_{\text {end-to-end}}^{\text {indep}} \;+\;\rho \,{\overline{T}}_{\text {end-to-end}}^{\text {coop}}, \end{aligned}$$

where ${\overline{T}}_{\text {end-to-end}}^{\text {indep}}$ and ${\overline{T}}_{\text {end-to-end}}^{\text {coop}}$ denote the mode-specific baseline end-to-end delays under the same network setting. Specifically, the average RSU computation time $T_{\text {RSU}}$ is calculated as:

$$\begin{aligned} T_{\text {RSU}} = (1 - \rho ) \cdot T_{\text {indep}} + \rho \cdot T_{\text {coop}}, \end{aligned}$$

where $\rho$ denotes the proportion of vehicles using cooperative authentication. The values of $T_{\text {indep}} = 0.831$ ms and $T_{\text {coop}} = 0.598$ ms are defined in Section “Computational Cost Analysis”, corresponding to the RSU computation time in independent and cooperative modes, respectively.

Fig. 14 shows that increasing the helper-vehicle density monotonically reduces the RSU-side computation time through offloading, following an linear trend from the no-helper case to full participation. The end-to-end delay increases as the number of cooperative authentications grows, reflecting the additional relay, short buffering, and channel contention introduced by coordination. It rises the most during the initial move from no helpers to a low helper density, then the curve flattens and the growth becomes sublinear through the medium-to-high range. This shape identifies a favorable benefit-cost region at medium to high densities, where each additional helper continues to provide comparable RSU relief while inducing progressively smaller increments in end-to-end delay. In practice, operating in that region markedly relieves the RSU while keeping the growth of end-to-end latency within an acceptable real-time envelope.

Fig. 14

Impact of helper vehicle density on RSU-side computation time and end-to-end communication delay.

Conclusion

This paper presents a lightweight, privacy-preserving V2I authentication scheme using elliptic curve cryptography (ECC), optimized for dynamic and dense VANET environments. By securely delegating part of the authentication workload to cooperative vehicles, the protocol significantly alleviates RSU-side computation without sacrificing security, leveraging a dual-verification model to detect partial misbehavior.

The scheme supports batch authentication, group key establishment, dynamic pseudonym updates, and malicious vehicle exclusion, offering both scalability and privacy protection. Formal security analysis under the Real-Or-Random (ROR) model confirms resistance to impersonation, replay, and single-point dishonesty. Our simulation results show over 20% reduction in RSU-side computation overhead compared to baseline protocols, while maintaining low packet loss and stable end-to-end delay under varying traffic and cooperation conditions. These results validate the protocol’s practicality and deployability in real-world, dynamic vehicular environments.