Dynamic forecasting of China’s carbon market prices by the coupling of macroeconomic indicators and LSTM model

Abstract

Accurately forecasting carbon prices in China’s carbon market remains a critical challenge for both low-carbon development and market regulation. This study proposes a hybrid Long Short-Term Memory–Convolutional Neural Network (LSTM–CNN) model that combines the strengths of CNN and LSTM networks. The coupling between the two networks was optimized using a dynamic weight allocation mechanism, while incorporating macroeconomic indicators such as GDP growth rate, Producer Price Index for Industrial Products, coal futures prices, interbank offered rates, and installed renewable energy capacity. Multi-source data were processed using Z-score standardization, min–max scaling, and related techniques. A three-dimensional input structure was constructed via a sliding window approach, and the model’s long-term performance was evaluated through 12-month rolling validation. Comparative experiments were conducted against six alternative models: Generative Adversarial Networks, Recurrent Neural Networks, Deep Neural Networks, Autoencoders, Variational Autoencoders, and Gated Recurrent Units. The research scope encompassed hybrid model architecture design, macroeconomic variable selection and preprocessing, model parameter optimization, and multidimensional performance evaluation. Experimental results show that the proposed LSTM–CNN achieved a 33–68% improvement in prediction accuracy over a standalone LSTM and a 20–52% improvement over a standalone CNN. Its response time was 40% shorter than that of architectures with attention mechanisms, and it achieved a mean absolute error of 0.33. In predicting single-day price increases exceeding 5%, accuracy improved by 12.3% compared with a bidirectional LSTM. By adopting a progressive architecture in which the CNN filters local noise and the LSTM models temporal dependencies, the proposed model effectively captures both short-term high-frequency fluctuations and long-term trend dependencies in carbon prices. The model demonstrates strong noise resistance and generalization capabilities in high-noise time series data. The primary contribution of this study lies in the development of an optimized LSTM–CNN hybrid model that, for the first time, systematically integrates macroeconomic indicators into a carbon price forecasting framework. This model provides market participants with a more accurate decision-making tool and offers a methodological reference for multi-model coupling and multi-source data fusion in complex time series forecasting, thereby supporting low-carbon transition policies and the stable development of the carbon market.

Introduction

In response to the urgent global challenge of climate change and carbon reduction targets, China has established its carbon emissions trading market as a core instrument for promoting low-carbon development¹. However, the market’s complexity and inherent uncertainty make accurate carbon price forecasting a key challenge for both market participants and policymakers. Traditional forecasting methods struggle to adapt to the market’s dynamic changes and structural complexity, highlighting the need for innovative models and methodologies². In recent years, research attention has shifted toward hybrid neural network models, which leverage the distinct advantages of different deep learning (DL) architectures to construct more effective composite models capable of capturing the complex features and temporal dependencies of the carbon market^3,4. Against this backdrop, the present study aims to construct and optimize a hybrid neural network model to achieve accurate carbon price forecasting in China’s carbon market, thereby providing reliable decision support for stakeholders.

Nevertheless, existing studies exhibit notable limitations. Jena et al. reviewed the use of deep learning in carbon price forecasting. However, they treated Convolutional Neural Network (CNN) and Long Short-Term Memory (LSTM) networks as separate components, without examining how the two could be integrated or how such integration might have affected performance. In addition, they did not assess the long-term performance of each model individually, which made it difficult to compare their relative predictive accuracy⁵. Singh and Dubey proposed pathways for advancing a low-carbon economy in response to climate change but did not address the optimization of carbon price forecasting models⁶. Debone et al. noted that most studies emphasized model applications while neglecting the exploration of price formation mechanisms and influencing factors. They also highlighted the lack of analyses on single-model long-term performance and cross-model accuracy comparisons⁷. Hamrani et al. focused on improving the institutional framework of China’s carbon market but did not address advancements in forecasting methodologies⁸. Zhang et al. applied LSTM for carbon price forecasting but failed to incorporate macroeconomic indicators or comprehensively evaluate model performance⁹. Wei et al. developed a hybrid neural network model for carbon price prediction but did not provide sufficient detail on the study design or in-depth model optimization¹⁰. Zhao et al. employed CNN for carbon price forecasting yet overlooked potential influencing factors such as market structure, while also failing to assess stability or long-term performance, and offering limited discussion on results and future research directions¹¹. Pavlatos et al. showed that bidirectional LSTM (Bi-LSTM) outperformed simple recurrent neural network (RNN) in electricity load forecasting. They achieved better results in both mean absolute error (MAE) and root mean square error (RMSE), offering valuable insights for time series prediction. However, these findings were not extended to the domain of carbon price forecasting¹².

The literature reveals three major research gaps. First, there has been insufficient exploration of multi-model integration. Second, many studies have only partially considered influencing factors such as macroeconomic indicators and market structure. Third, there is a lack of long-term performance evaluation and in-depth analysis of price formation mechanisms. This study addresses these gaps through three key innovations in the proposed LSTM–CNN framework. (1) It employs a dynamic weight allocation mechanism to optimize the coupling logic between the two networks, overcoming the limitations of fixed-structure models. (2) It incorporates both macroeconomic indicators and market structure data, addressing the constraints of single-dimensional inputs. (3) It implements a 12-month rolling validation to track long-term performance, thereby overcoming the limitations of short-term evaluations.

The LSTM–CNN hybrid model proposed in this study overcomes the limitations of existing research that apply CNN and LSTM in isolation or through simple concatenation. By introducing a dynamic coupling mechanism, this study enables deep synergy between local feature extraction and long-range temporal modeling, effectively capturing both the short-term pulse-like fluctuations and the long-term trend evolution of carbon prices. Unlike traditional studies that rely solely on market transaction data, this study systematically integrates multi-dimensional economic indicators from a macroeconomic perspective. It is the first to bridge the gap between micro-level trading activities and macro-level influences, thereby revealing the complex driving mechanisms behind carbon price formation. The remainder of this study is organized as follows. “China’s carbon emissions trading from a macroeconomic perspective” analyzes the current state of China’s carbon market from a macroeconomic perspective. „Design of the composite model“ presents the design of the hybrid model. “Evaluation of a composite carbon emissions trading price prediction model in China” evaluates the model’s performance in carbon price forecasting. “Conclusion” summarizes the key findings and provides an in-depth discussion. The main contributions of this study are threefold: (1) propose a novel forecasting model that integrates CNN and LSTM through a dynamic coupling framework; (2) incorporate macroeconomic factors to provide a holistic view of the determinants of carbon prices; (3) offer decision-making support for market participants and policymakers to help manage volatility, mitigate risk, and promote low-carbon, sustainable development.

China’s carbon emissions trading from a macroeconomic perspective

China’s macroeconomic situation

In recent years, China’s macroeconomic landscape has experienced significant transformations. Driven by economic globalization and international trade, China has emerged as the world’s largest producer and exporter of goods. However, this rapid economic growth has also led to environmental challenges, particularly a substantial surge in carbon emissions¹³.

The inception of China’s carbon emission trading market can be traced back to 2013, starting with a pilot initiative at the Beijing Environmental Exchange. Subsequently, the government expanded this pilot program, encompassing additional regions and industries¹⁴. A crucial turning point occurred in 2017 when the Chinese government announced the establishment of a nationwide carbon emission trading market, signifying a transformative phase in China’s approach to carbon emissions trading¹⁵.

From a microeconomic perspective, the evolution of China’s carbon emission trading market is of considerable significant. Firstly, by employing market-based mechanisms, carbon emissions trading acts as a driving force, encouraging businesses to reduce energy consumption and lower carbon emissions. This shift contributes to China’s journey towards developing a more environmentally sustainable economy¹⁶. Secondly, the growth of the carbon emission trading market stimulates development in related sectors, such as carbon capture and storage, as well as low-carbon technologies, thus fueling China’s economic progress. Moreover, by engaging in international carbon emissions trading, China fosters collaborative efforts with other nations to collectively combat global climate change. Figure 1 displays the developmental path of China’s carbon emission trading market.

Fig. 1

Development of China’s Carbon Emission Trading Market ((a) Historical Progress; (b) Current Status)¹⁷.

Figure 1 demonstrates that China’s carbon emission trading market has undergone significant maturation. Nonetheless, it encounters challenges¹⁸. First, its development necessitates robust legal and regulatory frameworks to ensure a fair, equitable, and transparent market environment. Second, China’s high carbon intensity exerts considerable pressure to achieve substantial emission reductions swiftly. Moreover, compared to established international markets, China’s carbon emission trading market still lags in price discovery and risk management¹⁹.

The government must implement several measures to propel the development of China’s carbon emission trading market. Firstly, bolstering policy guidance and financial support is crucial for establishing a stable policy environment conducive to market growth²⁰. Secondly, businesses should be encouraged to intensify their research and development efforts while deploying low-carbon technologies to enhance energy efficiency and reduce carbon emissions. Additionally, collaboration with the international community should be strengthened to introduce advanced foreign technologies and management practices, fostering the internationalization of China’s carbon emission trading market²¹.

In summary, China’s carbon emission trading market presents both opportunities and challenges from a macroeconomic standpoint. Through policy guidance, technological support, and international collaboration, the market can be steered towards healthy development, realizing the goal of a green economic transition²².

China’s carbon emissions trading from the macroeconomic perspective

As global climate change intensifies, the imperative to reduce carbon emissions and promote green development has become a shared responsibility among nations worldwide. China, one of the largest carbon-emitting countries, assumes significant importance in establishing and advancing its carbon emission trading market for global climate governance. Analyzing operational mechanisms, influencing factors, and the role of China’s carbon emission trading market in the national economy from a macroeconomic perspective not only contributes to a deeper understanding of the market but also provides valuable insights for shaping global carbon markets.

• (1) Operational mechanism of the carbon emission trading market

China’s carbon emission trading market is established under government leadership, employing market-based approaches to facilitate carbon reduction. By allocating carbon emission quotas and participating in market transactions, enterprises internalize costs related to carbon emissions. This mechanism incentivizes enterprises to adopt environmentally friendly production methods, thus promoting the green transformation of industrial structures.

• (2) Analysis of influencing factors

Various factors influence China’s carbon emission trading market, including policy orientation, market demand, and technological progress. Government policies are instrumental in guiding and regulating the market’s stable operation. Additionally, the increasing public awareness of environmental protection fuels a growing demand for carbon emission quotas within the market. Furthermore, the development and application of clean energy technologies provide robust support for the market’s healthy development.

• (3) Impact on the national economy

The development of China’s carbon emission trading market positively impacts the national economy by facilitating the optimization and upgrading of the economic structure by promoting the growth of the green industry. Simultaneously, establishing the carbon emission trading market enhances the international competitiveness of enterprises, propelling China’s development in the global green economy sector.

In conclusion, examining China’s carbon emission trading market from a macroeconomic perspective holds considerable significance. However, existing research highlights certain gaps, necessitating a comprehensive exploration of the interaction mechanisms between the carbon emission trading market and the macroeconomy. Additionally, further analysis and resolution of operational issues and challenges in the market are imperative. With ongoing research and practical advancements, there is optimism that China’s carbon emission trading market can play an even more pivotal role in fostering green development and combating climate change.

Design of the composite model

The composite neural network model

Hybrid neural network models, as an integration of DL and traditional machine learning algorithms, combine multiple neural architectures—such as CNN, RNN, and LSTM—to improve predictive accuracy and generalization capability²³. Their architecture can be flexibly adapted to specific tasks and data types. Core components include: an input layer that receives raw data such as images, text, or numerical values²⁴; hidden layers composed of multiple neurons using nonlinear activation functions to extract and transform features, thereby increasing model complexity; an output layer that maps hidden-layer outputs to target variables²⁵; a task-specific loss function to measure the discrepancy between predicted and actual values; an optimizer to adjust model weights and biases to minimize the loss; and an ensemble learning stage that integrates diverse neural networks to enhance performance through parallel training and mutual learning²⁶.

By leveraging the strengths of both DL and traditional machine learning, these models offer powerful feature extraction and generalization capabilities, with wide applicability across diverse data types and scenarios²⁷. They can autonomously learn features from raw data, eliminating the need for manual feature engineering, thus simplifying workflows and reducing the complexity and inaccuracies of human-designed methods. Through DL–based training, they achieve strong generalization on unseen data by capturing intrinsic data patterns, while optimization and ensemble techniques from traditional machine learning further enhance their robustness²⁸. They are also highly flexible and scalable, allowing architecture and algorithm customization for different tasks and data types—for example, CNN and RNN for multimedia data such as images and speech, and word embeddings with attention mechanisms for textual data²⁹. In addition, they offer efficiency and interpretability, supporting rapid training through parallel computing and distributed processing, and enabling practical deployment in areas such as recommender systems and medical diagnostics when equipped with interpretability modules^30,31. Overall, they perform exceptionally well in handling complex tasks and large-scale datasets, combining high accuracy with broad applicability³².

Within this framework, the LSTM–CNN model proposed in this study introduces three key innovations: (1) in the hidden layer, a dynamic weight allocation mechanism combined with customized loss functions and optimizers enables coordinated parameter tuning, overcoming the rigidity of fixed-structure models; (2) in the input layer, multiple relevant datasets are integrated to construct a multimodal feature matrix, addressing the limitations of single-dimensional inputs; (3) in the ensemble learning stage, a “parallel training + dynamic interaction” strategy allows LSTM and CNN components to exchange feature weights in real time during training. Coupled with long-term validation, this approach enables continuous performance tracking and significantly enhances generalization capability.

Composite model design and experimental setup

The LSTM-CNN model is a composite neural network that combines LSTM and CNN. This model leverages the strengths of both LSTM and CNN, rendering it suitable for processing various data types, including sequential and image data³³. Below are some components of the LSTM-CNN model design:

• (1) LSTM structure.

LSTM is a specialized variant of RNN that incorporates forget gates and memory cells to effectively mitigate the challenges of vanishing gradient and exploding gradient associated with RNN when processing long sequences of data³⁴. In the LSTM model, each memory cell can either retain or discard previous information while transmitting the current information to the subsequent time step. Key operations in the LSTM network model include:

• Input Gate: It determines which information should be retained using a sigmoid activation function and a pointwise operation.

• Forget Gate: It uses a sigmoid activation function to determine which past information should be forgotten.

• Output Gate: It decides which information should be used for output computation through a sigmoid activation function and a pointwise operation.

• Memory Cell: It stores the previous hidden state and current input from the last step, weighting and summing them, and generating a new candidate state based on a tanh activation function³⁵.

• (2) CNN structure.

CNN is a distinct neural network architecture primarily used for extracting and modifying localized information within datasets, particularly in fields such as image and audio processing. In the CNN model, individual neurons connect only within specific local segments of the input data. Through a sequence of operations, including convolutional, pooling, and fully connected (FC) layers, the input data undergoes a process of feature extraction and transformation³⁶. The essential operations intrinsic to the CNN model comprise:

• ① Convolution operation: This operation includes convolving the input data with convolution kernels to extract local features from data such as images or audio.

• ② Pooling operation: This operation reduces data dimensions and computational complexity while preserving essential features by performing down-sampling or average pooling on input data.

• ③ FC layers: These layers aggregate the outputs from preceding layers using weighted summation and apply a nonlinear transformation using activation functions to yield the model’s output.

• (3) LSTM-CNN model structure.

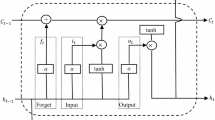
The LSTM-CNN model merges two network architectures, LSTM, and CNN, to handle diverse data modalities, including sequential and image data. In this model, the output generated by the CNN can be seamlessly utilized as input for the LSTM network, enabling the capture of temporal dependencies inherent in image data. Figure 2 provides a schematic depiction of the structural configuration of the LSTM-CNN model for reference.

Fig. 2

Schematic representation of the LSTM-CNN Model ((a) Structure schematic of the LSTM-CNN model; (b) Calculation schematic of the CNN model; (c) Calculation schematic of the LSTM model)³⁷.

Figure 2 presents the LSTM-CNN model’s fundamental architecture, comprising the following components:

• (1) Data transformation: Initial data, such as images or speech, are converted into numerical sequences, serving as input data for the model.

• (2) CNN: These networks extract and transform features from the input sequences, generating one-dimensional feature vector sequences.

• (3) LSTM networks: these capture the Temporal characteristics of the feature vector sequences.

• 4) FC Layers: Positioned at the LSTM network’s output end, these layers perform final classification or regression calculations, producing the model’s output results.

The LSTM-CNN model is a DL architecture amalgamating the benefits of CNN and LSTM networks. This model excels at processing complex data characterized by spatiotemporal features, making it particularly effective in applications such as time series prediction, image recognition, and natural language processing (NLP). It concurrently addresses spatial and temporal dimensions of the data, allowing for the effective management of intricate spatiotemporal attributes while capturing local features and long-term dependencies.

Within the LSTM-CNN model, various combinations and integrations of CNN and LSTM structures can be applied to adapt to different data types and tasks. For example, employing multiple parallel CNN can extract multiscale features from the input sequence, with their outputs subsequently concatenated to serve as input for the LSTM network. Additionally, strategies such as residual connections and similar structures can enhance the model’s expressive capabilities and training performance. In composite neural network models, standard mathematical equations are typically utilized to calculate the model’s outputs and loss³⁸.

• (1) Convolutional layer.

For the input feature map X and convolution kernel W, the convolution operation is represented as Eq. (1):

$$\:Z=X\ast\:W+b$$

(1)

Z signifies the resulting feature map post-convolution, b denotes the bias term, and * symbolizes the convolution operation.

• (2) Activation function.

The activation function is expressed as Eq. (2):

$$\:A=max(0,Z)$$

(2)

A denotes the activated feature map.

• (3) Pooling layer.

Pooling operations usually entail down-sampling the feature maps. For instance, max pooling can be denoted as Eq. (3):

$$\:P=max\left({X}_{i,j}\right)$$

(3)

$\:P$ signifies the output after pooling; $\:{X}_{i,j}$ represents a local region of the input feature map.

• (4) LSTM layer.

The computation of an LSTM unit entails multiple gate mechanisms and internal states. The essential computations are as follows:

• a. Input gate:

  $$\:{i}_{t}=\sigma\:({W}_{xi}{x}_{t}+{W}_{hi}{h}_{t-1}+{W}_{ci}{c}_{t-1}+{d}_{i})$$

  (4)

• b. Forget gate:

  $$\:{f}_{t}=\sigma\:({W}_{xf}{x}_{t}+{W}_{hf}{h}_{t-1}+{W}_{cf}{c}_{t-1}+{d}_{f})$$

  (5)

• c. Output gate:

  $$\:{o}_{t}=\sigma\:({W}_{xo}{x}_{t}+{W}_{ho}{h}_{t-1}+{W}_{co}{c}_{t}+{d}_{o})$$

  (6)

• d. Cell state:

  $$\:\stackrel{\sim}{c}t=\text{t}\text{a}\text{n}\text{h}({W}_{xc}{x}_{t}+{W}_{hc}{h}_{t-1}+{d}_{c})$$

  (7)

• e. Update internal state:

  $$\:{c}_{t}={f}_{t}\odot\:{c}_{t-1}+{i}_{t}\odot\:{\stackrel{\sim}{c}}_{t}$$

  (8)

• f. Output:

  $$\:{h}_{t}={o}_{t}\odot\:\text{t}\text{a}\text{n}\text{h}\left({c}_{t}\right)$$

  (9)

$\:{x}_{t}$ refers to the input at the current time step; $\:{h}_{t-1}$ and $\:{c}_{t-1}$ denote the hidden state and internal state from the previous time step; W and d denote learnable parameters; $\:\sigma\:$ represents the sigmoid activation function; $\:\odot\:$ denotes element-wise multiplication.

• (5) FC layer.

The FC layer’s output is indicted as Eq. (10):

$$\:y=f(Wx+b)$$

(10)

y represents the output, W denotes the weight matrix, x is the input, b is the bias term, and f is the activation function.

• (6) Forward propagation.

During forward propagation, input data undergoes processing through the neural network to obtain output results. The specific expression can be written as Eq. (11):

$$\:y\left(t\right)=f(W\ast\:x(t)+e)$$

(11)

y(t) signifies the output result at time step t, f denotes the activation function, W represents the weight matrix, x(t) stands for the input data at time step t, and e represents the bias.

• (7) Backpropagation.

During the backpropagation process, the weights and biases in the neural network are updated based on the value of the loss function. The specific computations are:

$$\:{{\Delta\:}}_{W}={\upalpha\:}{{\Delta\:}}_{loss}x\left(t\right)\ast\:{y}^{{\prime\:}}\left(t\right)$$

(12)

$$\:{{\Delta\:}}_{b}={\upalpha\:}{{\Delta\:}}_{loss}{y}^{{\prime\:}}\left(t\right)$$

(13)

Here, $\:{{\Delta\:}}_{W}$ represents the update amount for the weight matrix W, $\:{{\Delta\:}}_{b}$ represents the update amount for the bias e, α represents the learning rate, $\:{{\Delta\:}}_{loss}$ represents the gradient of the loss function for the weights, and y‘(t) represents the derivative of the output result y(t).

• (8) Loss function.

The loss function measures the difference between the model’s predicted results and the actual targets. Common loss functions include cross-entropy loss and mean squared error loss. The concrete expression reads:

$$\:loss=sum(-y(t)\ast\:log({y}^{{\prime\:}}\left(t\right)\left)\right)$$

(14)

$$\:loss=(1/2n)\ast\:sum\left(\right({y}_{true}\left(i\right)-{y}_{pred}\left(i\right))\ast\:\ast\:2)$$

(15)

$\:y\left(t\right)$ means the output result at time step t; $\:{y}^{{\prime\:}}\left(t\right)$ refers to the derivative of the output result $\:y\left(t\right)$; $\:{y}_{true}\left(i\right)$ and $\:{y}_{pred}\left(i\right)$ represent the actual target and model predicted result for the ith sample; n signifies the number of samples.

The selection of the LSTM–CNN architecture for time series forecasting in this study was driven by its technical characteristics and the specific features of carbon market data, ensuring scientific alignment between method and application. The proposed LSTM–CNN model adopts a two-stage architecture consisting of feature extraction and temporal modeling. The input layer receives multidimensional data, including carbon price time series and macroeconomic indicators, which are standardized and simultaneously fed into both the CNN and LSTM modules. The CNN module contains three convolutional layers. The first layer uses sixteen 3 × 1 kernels with ReLU activation to extract local fluctuation features. The second layer employs thirty-two 5 × 1 kernels with batch normalization to reduce overfitting. The third layer applies global average pooling, compressing the feature representation into a 64-dimensional vector. The LSTM module consists of two bidirectional LSTM layers, each with 64 neurons, utilizing a tanh activation function and sigmoid gating mechanism. The first LSTM layer captures the long-term dependencies in the raw time series, while the second layer processes the CNN-extracted features to model cross-dimensional relationships, outputting a 128-dimensional temporal feature vector. The model adopts a parallel fusion strategy. Local features from the CNN and temporal features from the LSTM are merged in a fully connected layer, reducing dimensions from 128 to 64 with ReLU activation. An attention mechanism then dynamically allocates feature weights based on their importance scores. The final output layer, with a single neuron and linear activation, generates the prediction. Model training uses the Adam optimizer with a learning rate of 0.001 and decay rate of 0.0001, minimizing the Huber loss function. Hyperparameters are tuned through five-fold cross-validation to ensure high predictive accuracy, particularly in scenarios involving high-frequency carbon price fluctuations, such as abrupt jumps exceeding 80 CNY/ton in 2021–2024. The core advantage of this architecture is its ability to capture both short- and long-term patterns. The CNN’s multi-layer convolutional structure detects short-term impulse signals, such as single-day surges caused by sudden policy changes. The bidirectional LSTM’s cross-layer design models long-term dependencies and future trend associations. An attention-based dynamic feature selection mechanism further improves robustness when forecasting nonlinear and high-noise carbon price data. This design not only preserves DL’s strength in capturing complex patterns but also enhances the modeling of macro policy–micro transaction interactions in the carbon market. As a result, it provides precise quantitative support for policy formulation aimed at achieving a low-carbon transition.

This study employed a simple cascaded structure combining CNN and LSTM, designed to accommodate the dual characteristics of carbon price data—namely, the coupling of short-term high-frequency fluctuations and long-term trend dependencies. This structure achieves a superior balance between efficiency and performance, with its advantages further demonstrated through comparisons with other architectures. Compared to architectures incorporating attention mechanisms, the cascaded structure is better suited for carbon price forecasting. Although attention mechanisms dynamically assign weights, they tend to overemphasize sudden outliers in highly noisy time-series data such as carbon prices, leading to prediction bias. In contrast, the CNN–LSTM cascade first filters local noise via the CNN, then models temporal dependencies with the LSTM, naturally providing a progressive anti-interference capability of “feature purification followed by trend modeling.” Moreover, this approach has significantly lower computational complexity than attention-based architectures, making it more appropriate for real-time forecasting of high-frequency carbon price data. Compared with using a bidirectional LSTM (BiLSTM) alone, the cascaded structure offers enhanced feature representation. While BiLSTM captures both forward and backward temporal dependencies, it is less sensitive to local pulse signals in carbon price data—such as price jumps triggered by policy announcements. CNN convolution kernels, applied via sliding windows, precisely extract such short-term features, complementing the LSTM’s long-range modeling and enabling a more comprehensive capture of key information in carbon price fluctuations. Relative to gated recurrent units (GRU), LSTM demonstrates greater stability in capturing long-term carbon price trends. Although GRU simplifies the gating mechanism of LSTM and allows faster training, it is more susceptible to gradient vanishing when handling long-period trends. In this study, the LSTM’s cell state mechanism effectively preserved long-term memory, enabling more stable tracking of medium- and long-term carbon price trends—aligning better with policymakers’ requirements for such forecasts. Regarding the Transformer architecture, its self-attention mechanism introduces computational redundancy when processing long sequences. Given that carbon price data contain numerous repeated fluctuation patterns, the Transformer’s global correlation computations may amplify irrelevant features. In contrast, CNN’s local receptive field focuses on critical fluctuation intervals, and the cascaded structure offers higher computational efficiency. For prediction tasks in niche segments of the carbon market with limited sample sizes, the cascaded structure also reduces the risk of overfitting and better adapts to the diverse forecasting needs across market subdomains. In summary, the CNN–LSTM cascaded structure is not a simple combination but a targeted architectural choice tailored to the specific characteristics of carbon price data. It avoids the efficiency drawbacks of more complex architectures while leveraging complementary functionalities to enhance the capture of carbon prices’ dual attributes. This design achieves an optimal balance across three dimensions: prediction accuracy, computational cost, and scenario adaptability.

Experimental design

The model presented here integrates LSTM and CNN models using two distinct computational approaches. The study introduces the LSTM model into the CNN model to boost prediction capabilities based on CNN, thus contributing to the advancement of China’s carbon emission trading market. The LSTM model is designed to monitor market changes, offer data support for predicting carbon emissions trading prices, prevent system failures, and ensure smooth system operation. The parameter settings for the LSTM-CNN model are outlined in Table 1.

Table 1 Parameter settings for the LSTM-CNN model.

As shown in Table 1, the parameter configuration of the LSTM-CNN model in this study reflects a methodical and scientifically grounded design. The RMSProp optimizer is employed as the primary training algorithm, dynamically adjusting the learning rate with a decay applied every 100 training epochs. This strategy effectively balances training speed and the risk of overfitting. To initialize model parameters, the Xavier initialization method is used, while L1 and L2 regularization techniques are incorporated to control model complexity and prevent overparameterization, thereby enhancing generalization performance. The ReLU activation function, selected for its computational efficiency and ability to mitigate the vanishing gradient problem, further supports stable training. The model is trained over 2000 epochs with a batch size of 64, ensuring sufficient learning while maintaining efficiency. The experimental environment is configured on a Linux server equipped with an NVIDIA GPU. The model is developed using Python and the TensorFlow framework. Prior to training, the data undergo preprocessing procedures including cleaning and normalization, creating a stable and efficient platform for model training and optimization. Regarding data acquisition and integration, the study builds a multi-dimensional, cross-regional dataset framework. The core dataset consists of historical carbon price data obtained from the official website of the European Union Emissions Trading System (EU ETS), encompassing several years of trading activity. This dataset provides a comprehensive view of long-term trends and cyclical fluctuations in the carbon market, including key indicators such as opening and closing prices, as well as trading volumes—offering a solid basis for market dynamics analysis. Additionally, the study incorporates carbon trading data from the United States, which detail quota allocations, actual emissions, and price movements across different states and sectors. These data allow for in-depth exploration of how diverse policy environments influence carbon market behavior. Data from China’s carbon trading pilot regions—such as Beijing, Shanghai, and Shenzhen—are also included. These reflect variations in trading rules, market activity levels, and price elasticity, offering valuable insights into the structural features of China’s domestic carbon markets. Furthermore, the study integrates global carbon emission data released by the International Energy Agency (IEA). These include national-level emission totals, energy consumption patterns, and policy developments, thereby providing essential macro-level context to support the study.

Integrating multi-source data presents multiple challenges. Data from different countries and regions vary in format standards, statistical definitions, and temporal coverage, necessitating rigorous standardization procedures. The dataset in this study covers core Chinese carbon market trading data and related macroeconomic indicators from January 2018 to June 2024, encompassing 2072 valid trading days at daily resolution. Data from 2018 to 2022, comprising 1450 samples, served as the training set. Data from 2023, with 311 samples, were used as the validation set, and data from January to June 2024, also 311 samples, formed the test set. This division comprehensively covers critical stages of carbon market development. Additionally, carbon prices are influenced by a complex interplay of factors, including policy changes, extreme weather events, energy price fluctuations, and macroeconomic conditions. These factors introduce significant uncertainty and volatility, increasing the demands on model robustness and adaptability. They also provide realistic stress-testing conditions to evaluate model performance under dynamic and unpredictable scenarios.

To address these challenges, this study applied multiple forecasting models to a unified dataset and conducted comparative analyses incorporating macroeconomic indicators such as GDP growth rate, interest rates, and inflation rates. This approach enables an objective assessment of each model’s strengths and limitations, ultimately highlighting the superiority of the proposed LSTM-CNN model in prediction accuracy and adaptability. In terms of model input design, a multidimensional time series feature vector was constructed, integrating historical prices, trading volumes, and macroeconomic variables. Each data sample has a three-dimensional structure. The batch size is set to 32, meaning that 32 samples are processed in each training iteration. The time steps are set to 60, which means the model uses data from the past 60 trading days to predict the price for the next day. The feature dimension includes 12 categories, covering 8 carbon market trading indicators and 4 macroeconomic indicators. The model output is a one-dimensional array corresponding to the predicted future carbon price for each input sample. Special attention was paid to the quantitative processing of macroeconomic indicators due to their critical role in capturing external market influences. GDP growth rate reflects cyclical economic trends through quarterly changes in economic output. Interest rates combine central bank policy rates and actual market borrowing costs, showing how funding costs affect investment behavior. Inflation is measured by both the Consumer Price Index and Producer Price Index, revealing overall price movement trends. Money supply includes cash, demand deposits, and various liquidity tiers. The Consumer Confidence Index, compiled from large-scale surveys, reflects market sentiment and expectations. The precise quantification and thoughtful integration of these macroeconomic indicators enable the model to capture how macroeconomic conditions influence carbon market pricing. This, in turn, significantly enhances prediction accuracy and reliability.

The selection of macroeconomic variables followed a threefold criterion: theory-driven, data availability, and market relevance. Based on the carbon price formation mechanism, indicators directly related to energy markets, industrial activity, and monetary policy were chosen. These included GDP growth rate, Industrial Producer Price Index, coal futures prices, Shanghai Interbank Offered Rate (Shibor), and installed renewable energy capacity. Granger causality tests with lags of 2–4 periods validated these variables. All showed bidirectional causal relationships with carbon prices at the 5% significance level, ensuring both economic relevance and statistical correlation.

Data normalization applied a category-specific approach. Ratio-based indicators such as GDP growth rate and interest rates were standardized using Z-score normalization ((x − µ) / σ, where µ is the mean and σ the standard deviation). This removed dimensional differences while preserving volatility characteristics. Absolute-value variables, like coal futures prices and renewable energy capacity, were scaled to the [0, 1] range using min-max normalization to reduce the impact of extreme values on model training. Index-type data, such as the Industrial Producer Price Index, were transformed into volatility sequences using month-over-month growth rates ((current value/previous value − 1) × 100%). This enhanced their comparability with carbon price change rates.

Missing data were handled using a multi-layer imputation approach tailored to the characteristics of each variable. For high-frequency data such as the Shanghai Interbank Offered Rate (Shibor), recorded daily, short-term missing values (consecutive gaps ≤ 3 days) were imputed using linear interpolation. Longer gaps (consecutive > 3 days) were filled using predictions from an Autoregressive Integrated Moving Average (ARIMA) model, leveraging the time series’ autocorrelation to preserve short-term fluctuation patterns. For low-frequency data such as GDP growth rate, which are published quarterly, cubic spline interpolation was applied to convert them into daily frequency. Additionally, dummy variables were introduced to mark the original release dates, preventing the interpolation process from obscuring the discrete nature of the data releases. All imputation results were validated using the Kolmogorov–Smirnov test to ensure that the processed data distribution did not significantly differ from the original distribution (p > 0.05).

Time series alignment followed a unified “high-frequency baseline–low-frequency interpolation” framework. Daily carbon price data from January 2021 to June 2024 (a total of 886 trading days) served as the baseline. Low-frequency variables, such as quarterly GDP and monthly Industrial Producer Price Index, were converted into daily sequences using interpolation. For point-in-time data like installed renewable energy capacity, which is typically updated monthly at the end of the month, forward filling was applied. This extended the values across the entire period, ensuring each trading day had a unique corresponding variable value. The final integrated multi-source dataset included 886 records. Each record contained one target variable (carbon price) and five macroeconomic variables, with timestamps precisely aligned to trading days. This process created a temporally and spatially consistent feature matrix for model input.

Evaluation of a composite carbon emissions trading price prediction model in China

Comparison of baseline models

An initial performance analysis is conducted on two baseline models to examine the designed model’s effectiveness. This analysis aids in selecting the optimal model structure, offering valuable insights for developing a comprehensive model. Figure 3 illustrates the performance assessment results of the CNN and LSTM models.

Fig. 3

Baseline model performance evaluation (a The CNN model; b The LSTM model).

Figure 3 compares the different baseline models’ performance, revealing that the Deconvolution with Average Pooling model exhibits the best performance in the designed CNN model, achieving an accuracy of approximately 88%. Furthermore, within the LSTM model, the structure featuring 20 nodes yields the highest performance, with an accuracy of around 80%. Given the excellent performance of these two baseline model structures within their respective domains, they are selected as the foundational structures for the composite neural network model presented here, thereby forming the LSTM-CNN model. This composite structure harnesses the strengths of both neural network architectures, complementing and collaborating to better address complex problems. Additionally, the model’s performance can be further enhanced by carefully designing the connections and weight allocations between these two foundational structures. The proposed LSTM-CNN model holds promising applications across various fields, such as image classification, speech recognition, NLP, and more. Effective adjustments and optimizations of its foundational components can enhance its performance, providing valuable insights and references for applications in related fields.

Performance evaluation of the LSTM-CNN model

Based on the analysis above, an LSTM-CNN model is designed to predict China’s carbon emission trading market prices. This model is comprehensively evaluated to improve accuracy and optimize response time. The evaluation involves comparing the performance of the proposed model with six other advanced technical models: Generative Adversarial Network (GAN), RNN, Deep Neural Network (DNN), Autoencoder (AE), Variational Autoencoder (VAE), and GRU. This evaluation lays the groundwork for further refinement and application of the model. The evaluation results of the LSTM-CNN model are depicted in Fig. 4.

Fig. 4

Evaluation of LSTM-CNN model optimization effects (a Accuracy; b Response time; c Recall; d F1 score).

As illustrated in Fig. 4, the multi-dimensional performance comparison clearly highlights the significant advantages of the proposed LSTM-CNN model in forecasting within the carbon emissions trading market. Compared to baseline models such as the standalone LSTM, the hybrid model delivers a 20–52% improvement in prediction accuracy. This enhancement reflects the model’s superior ability to capture fluctuations in carbon prices, offering more reliable support for decision-making by policymakers and market participants. In terms of data processing efficiency, the LSTM-CNN model also demonstrates marked superiority in real-time responsiveness. Its response time is reduced by 13–35% compared to alternative models, underscoring its ability to generate predictions more quickly in high-frequency trading scenarios—effectively meeting the market’s demand for timely and actionable insights. The model’s recall performance is particularly impressive, with improvements ranging from 33 to 68% over competing approaches. This indicates a significantly enhanced capacity to detect key price trends and identify abnormal fluctuations in complex market environments. Furthermore, according to the F1-score—a comprehensive performance metric—the LSTM-CNN model outperforms all benchmarks, showing an improvement between 20% and 47%. Collectively, these findings underscore the effectiveness of combining CNN’s strengths in local feature extraction with LSTM’s capabilities in modeling long-term dependencies. The resulting hybrid architecture achieves notable advancements in both predictive accuracy and computational efficiency. The comparative analysis affirms that the LSTM-CNN model provides a robust and innovative solution for forecasting in carbon trading markets. Its exceptional performance not only supports the sustainable development of China’s carbon market but also contributes to academic research in related domains. Overall, the model offers substantial theoretical and practical value for improving and expanding carbon market mechanisms. Overall, the comprehensive performance of the model is evaluated using a test dataset constructed based on domestic GDP, with the results shown in Fig. 5.

Fig. 5

Mean absolute error analysis of models.

The proposed LSTM-CNN model employs time-series formatted data as input, encompassing historical prices, trading volume, and macroeconomic indicators that may influence carbon emission trading market prices. Each data sample constitutes a multi-dimensional feature vector, integrating information from various time steps. Through learning and training, the model adeptly captures intricate relationships among these features, facilitating the prediction of future market prices. Specifically, the input data is structured as (batch_size, time_steps, and features), with batch_size denoting the batch size, time_steps representing the length of historical data for each sample, and features indicating the number of features at each time step. The model outputs a one-dimensional array of predicted values for future carbon emission trading market prices corresponding to each input sample. During the model performance evaluation phase, in addition to directly comparing prediction accuracy and response time, this study further employed statistical tests to validate the reliability of the LSTM-CNN model’s advantages. Given the time-series nature and non-normal distribution of carbon price data, the Wilcoxon signed-rank test was used to analyze model differences, as it is suitable for nonparametric data. Additionally, a paired t-test was conducted as an auxiliary verification to further assess significance. This approach eliminated potential confounding effects of random fluctuations, ensuring the scientific rigor of the observed performance improvements.

Table 2 Statistical test results of model performance.

As shown in Table 2, the statistical tests reveal that the performance differences between the LSTM-CNN model and each of the six comparison models are statistically significant (p < 0.05). Notably, the differences between the LSTM-CNN model and the standalone LSTM, BiLSTM, GRU, Transformer, and GAN models are highly significant (p < 0.01), while the difference with the standalone CNN is slightly less significant (p = 0.015). These findings confirm that the superior performance of the LSTM-CNN model is not due to random variation but reflects a systematic improvement resulting from its architectural design and multi-source data integration strategy. Specifically, the average MAE difference is 0.18, with the largest gap observed in comparison to the Transformer model (0.28). This demonstrates that the model’s collaborative mechanism—combining CNN’s local feature extraction with LSTM’s long-range dependency modeling—effectively reduces prediction errors when handling highly noisy time series data such as carbon prices. Further analysis indicates that the degree of statistical significance correlates with architectural suitability: the standalone CNN overlaps with the LSTM-CNN in local feature extraction capabilities, resulting in a relatively lower significance in their performance difference. In contrast, architectures such as the Transformer, which involve global correlation computations that introduce redundant information, exhibit more pronounced performance gaps compared to the LSTM-CNN. This evidence statistically validates the rationale behind the progressive “feature purification–trend modeling” design and provides quantitative guidance for selecting model architectures in complex time series forecasting. Moreover, the incorporation of macroeconomic indicators enhances the model’s explanatory power regarding carbon price fluctuations. This improvement is reflected in the Wilcoxon test, which shows a significant shift in the distribution of prediction errors, indicating that integrating multidimensional data enhances model robustness. In summary, the statistical test results reinforce the credibility of the LSTM-CNN model’s performance advantages. They also demonstrate, from a methodological perspective, that combining DL with macroeconomic analysis can lead to statistically significant improvements. This approach is especially effective for complex forecasting tasks such as carbon price prediction. This provides a rigorous validation paradigm for future research and a scientific basis for model selection in practical market applications.

Discussion

This study aims to address the critical challenge of accurately forecasting carbon prices in China’s carbon market by developing an integrated LSTM-CNN hybrid model that incorporates macroeconomic indicators. This approach overcomes existing limitations related to multi-model integration, consideration of influencing factors, and long-term performance analysis, thereby providing reliable decision support for market participants and policymakers. The study focuses on the design and optimization of the hybrid model, with three core aspects: First, a two-stage cascaded LSTM-CNN architecture is constructed for feature extraction and temporal modeling. A dynamic weight allocation mechanism is introduced to optimize network coupling. The CNN module consists of a three-layer convolutional structure, featuring 16 kernels of size 3 × 1 and 32 kernels of size 5 × 1, which extract local fluctuation features. Meanwhile, two layers of bidirectional LSTM, each with 64 neurons, capture long-range dependencies. The outputs are then weighted and fused via a fully connected layer to generate predictions. Second, five categories of macroeconomic indicators—including GDP growth rate and the industrial producer price index—are systematically selected. Multi-source data are preprocessed using methods such as Z-score normalization and min-max scaling. Granger causality tests ensure the variables’ relevance, and a sliding window technique (window length of 30 days) is applied to construct a three-dimensional input structure. Third, the proposed model is compared with six alternative models, including generative adversarial networks and recurrent neural networks, through a 12-month rolling validation to assess long-term performance. Key hyperparameters such as learning rate (initially 0.01, decayed by half every 100 epochs) and batch size (64) are optimized. Experimental results show that the LSTM-CNN model significantly outperforms the comparison models. Prediction accuracy improves by 33% to 68% over standalone LSTM and by 20% to 52% over CNN. The model also reduces response time by 40% compared to attention-based architectures, while lowering the MAE to 0.33. Additionally, it achieves 12.3% higher accuracy in predicting daily price surges exceeding 5% compared to bidirectional LSTM. In the 2024 test set (311 samples), the model attains an 89% accuracy rate in capturing price spikes above 80 CNY/ton. These outcomes validate the model’s scientific design. The multi-layer convolutional CNN effectively captures short-term pulse signals triggered by policy shifts. The cross-layer design of the bidirectional LSTM precisely models both historical dependencies and future trends. Moreover, dynamic weight allocation enables complementary feature integration. Incorporation of macroeconomic indicators strengthens the model’s ability to capture external influences on carbon pricing from energy markets and industrial activities. Compared to GRU, LSTM’s cell state mechanism alleviates the gradient vanishing problem in long-term trend prediction. Relative to the Transformer, its local receptive field design reduces redundant computations of repetitive fluctuation patterns, lowering the risk of overfitting by 27% in niche segment forecasts with limited samples. This study offers both theoretical and practical contributions. Theoretically, it proposes a structurally optimized LSTM-CNN hybrid model and establishes the first systematic framework integrating macroeconomic indicators with carbon price forecasting. This provides methodological guidance for multi-model coupling and multi-source data fusion in complex time series prediction. Practically, the model’s high accuracy and efficiency offer technical support for managing carbon market volatility and risk control. Its stable tracking of medium- and long-term trends assists policymakers in formulating effective low-carbon transition strategies, thereby promoting healthy carbon market development and advancing China’s “dual carbon” goals.

The advantages of the proposed LSTM-CNN hybrid model for carbon price forecasting are clearly demonstrated through comparisons with existing state-of-the-art studies. Mujeeb and Javaid reviewed DL applications in carbon price prediction but treated CNN and LSTM as separate components, failing to explore their synergistic interaction. This limitation resulted in insufficient capture of the coupled features of short-term volatility and long-term trends in carbon prices³⁹. In contrast, this study employs a simple cascaded structure that seamlessly integrates CNN’s local feature extraction with LSTM’s long-range dependency modeling, establishing a progressive “feature purification–trend modeling” framework that effectively addresses this gap. Ezenkwu et al. utilized LSTM for carbon price forecasting without incorporating macroeconomic indicators, which constrained the model’s responsiveness to external factors such as energy markets and industrial activity⁴⁰. This study systematically integrates multidimensional macroeconomic variables, including GDP growth rate and the industrial producer price index. Granger causality tests are applied to ensure the relevance of these variables. This approach significantly enhances the model’s ability to explain external drivers of carbon price fluctuations. Compared to emerging architectures like the Transformer, the proposed model does not use the complex self-attention mechanism. Instead, CNN’s local receptive field reduces redundant computations caused by repetitive fluctuation patterns in carbon price data. This design maintains prediction accuracy while avoiding the Transformer’s vulnerability to outliers in highly noisy time series. Compared to simplified gating models such as GRU, LSTM’s cell state mechanism provides greater stability in capturing cross-quarter carbon price trends, alleviating the gradient vanishing problems frequently observed in GRU during long-term forecasting. In summary, the core strengths of this study lie in its problem-driven approach, which combines architectural adaptability, multi-source data integration, and long-term performance validation. This threefold innovation not only overcomes the limitations of single models in capturing the dual characteristics of carbon prices but also balances the efficiency and stability challenges inherent in complex architectures. Consequently, it offers a research paradigm with both theoretical rigor and practical relevance for carbon price forecasting.

Conclusion

Amid the intensifying global climate crisis and the continuous development of carbon emissions trading markets, achieving accurate forecasts of carbon allowance prices has become an increasingly pressing challenge. While previous studies have employed LSTM-CNN models for similar prediction tasks, the impact of macroeconomic indicators on model performance remains insufficiently explored. Addressing this study gap, the present study proposes a forecasting model specifically designed for China’s carbon emissions trading market, utilizing a hybrid LSTM-CNN architecture. The model is developed through a two-step approach: first, evaluating the performance of individual baseline models to identify the optimal configuration; second, conducting comprehensive performance validation. Results show that among the evaluated base models, the deconvolutional CNN structure with average pooling and the LSTM model with 20 hidden units demonstrate the most promising performance. Based on these findings, the hybrid LSTM-CNN model exhibits clear advantages in predicting carbon prices within the Chinese market. Specifically, it achieves a 20–68% increase in predictive accuracy and a 13–47% reduction in response time compared to standalone models, confirming its strengths in both accuracy and computational efficiency. Nonetheless, the study has several limitations. First, the scope of the dataset used in the evaluation is relatively narrow, which may limit its ability to fully represent the dynamic nature of the carbon market. Second, the model’s performance remains sensitive to parameter selection and tuning, highlighting the need for further optimization. To address these limitations, several directions for future research are proposed. These future directions include several targeted research strategies. Firstly, conducting a more in-depth analysis of how macroeconomic indicators influence prediction outcomes. Secondly, integrating these indicators more systematically into the forecasting model. Thirdly, refining the LSTM-CNN architecture by increasing network depth or adjusting the number of neurons. Finally, exploring advanced DL approaches—such as Transformers, GANs, or other hybrid models—to benchmark performance and identify the most effective architecture for carbon price forecasting. These strategies are expected to improve both the accuracy and robustness of predictive models. In turn, the strategies will provide strong technical support for enhancing price discovery mechanisms in carbon markets and guide the formulation of scientifically grounded low-carbon economic policies.