Introduction

Opencast coal mining accounts for 93% of coal production in India, leading to an increase in waste dump formations and associated stability issues. CIL has removed over 1148 million cubic meters of overburden in recent years, increasing the risk of dump instability1. Maintaining a stable overburden dump (OB) is critical in mining regions, and effective dump management is required to prevent slope failure and associated hazards2. The dump becomes steeper, and the slope becomes more dangerous due to an increase in the stripping ratio and limitations on available land. There have been multiple reports of catastrophic human and property losses due to dump failure. It has an impact on the surrounding environment and impedes the continuing mining operations, which leads to decreased productivity and higher expenses associated with rehandling waste, large dump trucks, and excavators3.

In 2016, a catastrophic dump failure in Rajmahal coalfield resulted in 23 fatalities1. Similarly, Jayant opencast mine experienced a severe dump failure in December 2008, burying five mine workers4. Slope and dump failures have recently begun to exhibit an increasing tendency, according to a review of accidents in opencast mines (DGMS 2020) Accordingly, comprehensive evaluation of dump stability is currently receiving global attentions5,6,7.

Adding benches to the dump, rather in forming a single heap, is the standard technique for waste dump stabilisation in mining locations. This increases the dump’s FOS. Cohesion and friction angle, two strength controlling characteristics, are frequently thought of as crucial governing factors in dump stability2,8. To generalize and evaluate the slope’s overall strength and weakness, many slope stability studies used the FOS9,10,11. Slope stability evaluations are notoriously difficult and time-consuming due to the complexity of the calculations involved. Finding the FOS of a given slope requires a combination of analytical and numerical techniques12,13. Failures are often triggered by excessive load, hydrostatic pressure, poor dump configuration, and lack of space for proper disposal1. Consequently, a viable alternative to limit equilibrium or numerical methods that provide fast and reliable findings is urgently required5.

Machine learning, a subfield of AI, provides a different way to approach slope stability analysis by learning from data and making predictions without the need for explicit rules or equations. The majority of slope stability analyses used the data-driven technique14. The classification predictive models were used by most researchers for slope stability analysis whereas few studies were available on safety factor prediction15,16. The effectiveness of different machine learning models in predicting the safety factor was also determined to be higher for the artificial dump slope compared to the residual soil slope that occurs naturally17.While ML models offer significant advantages in slope stability analysis, they are not without limitations. The accuracy of these models heavily depends on the quality and quantity of the input data, and their performance can vary with different soil conditions and slope characteristics. Additionally, traditional methods like numerical simulations and expert-based models still play a crucial role in validating and complementing ML predictions, ensuring a comprehensive approach to slope stability assessment18.Combining machine learning algorithms with more traditional approaches like finite element methods or limit equilibrium methods (LEM) allow more precise and efficient analysis using hybrid methods14,19. Hybrid models were adopted by various researchers, and it showed that the machine learning models were performed well by the datasets generated from limit equilibrium analysis and finite element analysis17,19,20,21,22,23,24,25,26,27,28.

However, there are always going to be constraints when employing machine learning techniques. While models based on machine learning have seen extensive application, certain studies have relied on a limited sample size as given in Table 1, potentially impacting the ML model’s ability to generalize29. The database is the most critical constraint for machine learning algorithms. The learning rate is enhanced with a larger database. Due to the wide range of possible values for the input parameters used in geotechnical engineering, it is essential that the database used to build highly accurate models have ample coverage in both the training and testing sets30. Furthermore, the majority of machine learning models have been crafted through the expertise of individuals with specialized knowledge, employing a method of experimentation and refinement. Indeed, comprehensive procedures, such as data pre-processing18, feature engineering31, ML algorithm selection32 and hyperparameter tuning, are integral to the practical implementation of ML. Model selection and hyperparameter tuning continue to pose challenges for achieving success in ML-based modelling33. According to the no-free-lunch theorem34, no algorithm can be superior to all others across every problem.

Table 1 Different slope stability analysis using ML approaches.
Full size table

The latest advancements in AI for evaluating slope stability should make use of hybrid intelligence or other AI methods with appropriate performance, minimal governing factors, and easy operation15. One major advantage is that they can effectively manage big and diverse datasets, combine a plethora of influencing factors, and capture intricate data connections18,31,32. Demir and Sahin34 found that data increases model performance, with random forest (RF) performing best out of five machine learning methods for predicting slope stability. In their investigation of machine learning methods for slope stability analysis, Kurnaz et al.42 discovered that the Auto Gluon package’s weighted ensemble learning approach produced the most precise outcomes33. Ma et al.40, found that AutoML (H2O-AutoML) offers a robust automated approach for the development of machine learning (ML) models and the analysis of slope stability concerning circular mode failure. The performance of tree-based ensemble models demonstrated greater accuracy in predictions compared to traditional machine learning methods17,25,26,29,30,43,44. Gao and Ge suggested that the use of novel hybrid ensemble methods would be a better option to assess the stability of complex rock slopes15.

This paper’s significant contribution is emphasized as follows:

A comprehensive database comprising 2250 datasets has been developed through parametric studies aimed at predicting dump slope stability. An AutoML approach has been proposed for model selection in predicting dump slope stability, utilizing the updated dataset. The six top-performing models were optimized using Bayesian optimization with a Gaussian process to identify the best version of each individual model and these optimized models were employed for the stacking ensemble learning model. A different AutoML method was introduced for stability prediction, eliminating the necessity for manual trial and error. It was noted that this AutoML approach surpassed both the stacked random forest metamodel and the individual base models in performance.

This paper is structured as follows (Fig. 1): Sects. “Database preparation” and “Exploratory data analysis” provide an overview of the updated database and the exploratory data analysis. Sects. “Methodology” and “Model interpretation” provide methodology and model interpretation. Sect. “Results and discussions” provide the results and discussions. In Sect. “Conclusions”, the conclusions of the study are presented and outlined potential avenues for further work.

Fig. 1
figure 1

Structure of the paper.

Full size image

Database preparation

It is well-known that limiting equilibrium methods can be used numerically to estimate the stability of both natural and artificial slopes. The shear strength along a sliding surface is computed using the Mohr–Coulomb strength formula. The shear stress upon failure is the material’s shear strength. To achieve a condition of limit equilibrium, the mobilized shear stress must be less than or equal to the shear strength45. In LEM, FOS is calculated as given formula in Eq. (1),

$${\text{FOS}} = \frac{{\tau_{f} }}{\tau } = \left( {c^{\prime} + \sigma^{\prime}tan\phi^{\prime}} \right)/\tau$$
(1)

where, the mobilized shear stress, shear strength, cohesion, normal stress, and friction angle produced at the sliding surface are represented by τf, τ, c’, σ’ and ϕ’, respectively.

With the advent of the conventional technique in 1936, numerous LEMs were created for the purpose of analyzing slope stability. Among these advancements include the Generalized LE (GLE) approach created by Chugh46, as well as Bishops, Janbu, Morgenstern-Price, and Spencer. Though all LEMs rely on assumptions about the interslice normal and shear forces, the main distinction among them is in how these forces are computed. The FOS is found via horizontal force equilibrium, and Janbu’s simplified technique is commonly used for both circular and non-circular failure surfaces47.

However, probabilistic analysis provides a good understanding of the overburden material properties, which are very varied. The FOS of soil/rockfill embankments, such as ore stockpiles and waste rock dumps, can be calculated using limit equilibrium (LE) analysis48,49. Mine tailing dumps at Enyigba, Southeastern Nigeria, were the subject of a limit equilibrium (LE) slope stability analysis conducted by Igwe and Chukwu50. At various points along the dump’s slope, which ranged from 30° to 60°, a constant shear strength parameter was measured. When it was dry, FOS was 1.27–1.33; when it was rainy, it dropped to 1.10–1.29. It is possible that the sample disruption led to inaccurate laboratory determinations of cohesion and friction angle values in this investigation. Therefore, taking the probabilistic analysis into consideration could have explained the attributes’ associated fluctuation. Probabilistic analysis can manage the uncertainties in important factors like shear strength (cohesion, c, in kPa), friction angle (ϕ, in degrees), unit weight (γ, in kN/m3), and hydraulic properties51.

Based on limit equilibrium, the five factors that were used to determine the FOS of the slope were as follows: overall slope angle (β), overall bench height (H), cohesion (c), angle of internal friction (ϕ) and unit weight of soil material (γ). The evaluation was conducted using Slide software. For parametric study Janbu’s simplified method with 50 number of slices was adopted in SLIDE software. According to Table 2, a grand total of 2250 parametric scenarios covering a variety of slope parameter ranges were used to construct the datasets. In order to get the complete database ready for additional investigation utilizing ML algorithms, the FOS that was obtained for several parametric features was utilized. Table 2 also provides a statistical summary of all input and outcome factors that were used in this investigation. The dump slope stability prediction model’s parameter ranges (see Table 3)were established after thorough literature research which were based on real case studies on dump slopes in different Indian coal mines3,5,47,49,51,52.

Table 2 Statistics of dataset.
Full size table
Table 3 Dataset selection considering actual slope failure case studies.
Full size table

Table 1 indicates different factors like overall slope angle, overall bench height, angle of internal friction, unit weight and cohesion are important for slope stability. The inherent moisture content of coal mine dump material which is the natural water content influenced the shear strength values and dump slope stability52. Hence in this study all machine learning models took moisture content as an input parameter, along with five parameters.

Exploratory data analysis

One way to see the probability density of continuous variables in detail is with a Kernel Density Estimate (KDE) graphic. The article’s data visualization is based on the dump dataset using KDE Plot. The probability density of a continuous variable was demonstrated using the KDE Plot, which is sometimes called the Kernel Density Estimate. For a continuous variable, it displays the probability density at different levels. It takes a dataset’s underlying distribution and smooths it out. Figure 2 shows a KDE plot, which is a visual representation of data distribution that sheds light on its shape, central tendency, and dispersion. The plots indicate peaks and distribution ranges that aid in identifying underlying patterns and trends in the dataset, offering a smooth and thorough picture. This is achieved by applying kernel density estimations.

Fig. 2
figure 2

Data structure.

Full size image

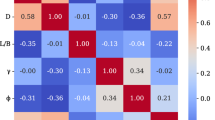
Data distributions for independent and dependent variables are shown using density curves in a violin plot, as seen in Fig. 3. Each curve’s width represents the relative frequency of data points in that area. More data points are suggested by a greater breadth, which suggests higher density. In a violin plot, the median line is the line that runs through the centre. It is useful for figuring out general trends. As illustrated in Fig. 4. a correlation matrix analyses and interprets interactions between variables in a dataset all at once.

Fig. 3
figure 3

Data set distributions.

Full size image
Fig. 4
figure 4

Feature correlations.

Full size image

Methodology

Lazy predict for model selection

One popular Python package, Lazy Predict, provides 42 ML models and automates ML. Because of the size of this dataset, the authors were able to do extensive testing to determine which forecasting models collaborate best with it53. There isn’t a “one size fits all” model because data variability impacts the models’ applicability. It can be challenging to choose the finest ML model from the many that are available. This self-sufficient ML method speeds up the process of finding solutions.

This AutoML model made use of both the training set, which comprised 80% of the dataset, and the testing set, which comprised 20% of the dataset. The R2 scores and runtimes of the models are evaluated by the lazy prediction mechanism after they get these datasets. One can find the top models in Table 4. The dataset takes six inputs and utilizes FOS as an output. The R2 value was used to choose the best six models. Automatic hyperparameter calibration model suggestions are provided by this algorithm. Afterwards, ML models were hyperparameter tweaked based on this algorithm’s recommendations. The authors were able to create reliable ML models for the research by following this procedure. The stability of dump slopes based on prediction of FOS was the primary goal of optimizing these ML models. (See Fig. 5).

Table 4 ML models performance using Lazy predict.
Full size table
Fig. 5
figure 5

Model selection using Lazy predict.

Full size image

Hyperparameter tuning for model optimisation

A machine learning algorithm usually turns a problem into an optimization problem and uses optimization techniques to solve it. The optimization function defines numerous hyperparameters before learning that affect how the machine learning algorithm aligns the model with the data. Hyperparameters are different from internal model parameters like neural network weights, which are learned from data during model training. Before training, the goal was to find hyperparameter settings that optimize data performance in a realistic timeframe. Hyperparameter optimization or tuning is this process. This greatly affects ML algorithm prediction accuracy54.

Complex hyperparameter tuning is an optimization problem with an unknown or black-box objective function. Traditional optimization methods like Newton or gradient descent are inapplicable. Bayesian optimization is an efficient algorithm for this type of optimization55. By combining prior information about the unknown function with data from samples, this method applies Bayesian principles to obtain posterior information on the distribution of the function. Subsequently, utilizing this posterior information, we can infer the points at which the function achieves its optimal value. The findings indicate that the Bayesian optimization algorithm surpasses other global optimization algorithms56. Consequently, the authors utilized Bayesian optimization grounded in Gaussian processes to adjust the hyperparameters of machine learning models.

Table 4 lists six base ML models which hyperparameters are optimised by Bayesian search—Gaussian process with fivefold cross-validation. Resampling through cross-validation is used for model evaluation and hyperparameter selection. According to fivefold cross-validation, the dataset is divided into five equal-sized folds. All aspects of the training and evaluation procedure are double-checked five times. A more comprehensive evaluation of the model’s performance is within reach. Model performance and hyperparameter tuning efficiency estimation are both enhanced by averaging the coefficient of determination and mean square error (MSE) across five iterations with five folds.

Model performance

This study considers model evaluators such as R2, MSE, RMSE, MAE, and MAPE to determine the prediction of FOS of dump slope. In Eqs. (2–6), one can see the formulae that were used to evaluate these performance measures.

$$R^{2} = 1 - \frac{SSR}{{SST}}$$
(2)
$$MSE = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {x_{i} - y_{i} } \right)^{2} }$$
(3)
$$RMSE = \sqrt{\frac{1}{n}} \sum\nolimits_{i = 1}^{n} {\left( {x_{i} - y_{i} } \right)^{2} }$$
(4)
$$MAPE = \frac{100}{n}\sum\nolimits_{i = 1}^{n} {\left| {\frac{{x_{i} - y_{i} }}{{x_{i} }}} \right|}$$
(5)
$$MAE = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left| {x_{i} - y_{i} } \right|}$$
(6)

where,

SSR = sum of squared residuals.

SST = total sum of squares

$$x_{i} = actual value for ith data$$
$$y_{i} = predicted value for ith data$$

Machine learning models

The four primary steps for implementing the suggested six base machine models are as given Fig. 6 and stacked random forest ensemble model for FOS prediction have been highlighted. Partitioning the database into training (80%) and test sets (20%) was the initial step. Second, Bayesian optimisation-Gaussian process was used to determine the best model hyperparameters when training. Additionally, five-fold cross-validation (CV) was used to reduce the possibility of discrepancy that may occur from randomly picking the dataset. Thirdly, five widely-used performance metrics—R2, MAE, MSE, MAPE, and RMSE—were used to assess the trained model’s efficacy. The model prediction outcomes were subsequently explained using SHAP.

Fig. 6
figure 6

Predictive machine learning models.

Full size image

Base ML models

Nusupport vector regressor (NuSVR)

NuSupport Vector Regression is a regression-focused SVM. It extends Support Vector Regression (SVR). NuSVR manages the model complexity-prediction accuracy trade-off differently than normal SVR. The “nu” parameter in NuSVR lets users set the number of support vectors and error tolerance for training57. The statistical learning theory-based SVM reduces structured risk, experience risk, and confidence range. This improves the learning machine’s generalization and model accuracy with less samples58.

Here, the authors go over how to build a dump slope stability model in Python using the NuSVR methodology. The authors used Bayesian Optimization and fivefold cross-validation to find the best hyperparameters. The optimal values of the Nu-SVR-BO model’s hyperparameters are shown in Table 5.

Table 5 Optimal values for hyperparameters of NuSVR model.
Full size table

Light GBM (LGBM)

Another method developed by Microsoft Research Asia59 that made use of the gradient boosting decision trees (GBDT) framework was LGBM. The purpose of this endeavour is to improve the efficiency of computations, which will ultimately result in improved solutions for prediction problems that include vast amounts of data. By employing a pre-sorting technique, the GBDT algorithm selects and partitions indicators. This method can exactly determine the separation point, but it requires more time and memory. LGBM saves memory and speeds up training with a histogram-based technique and a tree leaf-wise growth approach with a maximum depth constraint. LGBM consistently outperforms traditional methods and even some other machine learning models. LGBM is known for its speed and efficiency, making it a strong choice for large datasets60.

Here the authors detail the steps used to create a Python-based dump slope stability model with the LGBM methodology. With the help of Bayesian Optimization and fivefold cross-validation, the hyperparameters were found. Table 6 displays the hyperparameter values that work best for the LGBM -BO model.

Table 6 Optimal values for hyperparameters of Light GBM model.
Full size table

Gradient boosting (GBM)

A popular integrated learning technique, the GBM model builds many trees with different attributes to help with decision-making. To minimize loss, each tree considers the most current residuals and the conclusions of all trees that came before it before learning on its own. In both regression and classification settings, gradient tree boosting is useful since it is a generalization of the lifting approach that works with any differentiable loss function. It seems that the GBM model’s slope stability predictions have produced promising results38,61.

GBM uses numerical optimization to find a loss-function-minimizing prediction model. To minimize the loss function, the GBM rule iteratively adds a “weak learner,” or tree, at each level. After creating the model with an initial estimate, regression minimizes loss function with a decision tree. Each stage refines residuals from the previous model with a new decision tree. Exploiting a buyer, the person repeats rules until they reach the highest level. Each phase cannot amend the selection criteria specified in earlier phases since the procedures are final. GBM works best when a shrinkage parameter, or learning rate, minimizes choice tree size at each iteration cycle. Shrink operation in the GBM reveals that smaller stages are more accurate. Lower distances may improve model accuracy. Arguments return zero to one. The value is inversely proportional to iteration variability; thus, a smaller shrink requires more iterations to converge. Feature organization caused the GBM rule’s recent prophetic increase62. A carefully selected subsample informs the selection tree each iteration instead of the entire educational dataset. When there were enough observations, each generation consumed 50% of the dataset through knowledge evasion on average. A sub-sample fraction’s diverse values must be investigated to discover how lowering statistical parameters affects model quality. The sub-sampling strategy increases GBM model performance and reduces algorithm compute cost by a similar ratio63.

Using Bayesian Optimization and fivefold cross-validation methods, this section describes how the GBM approach is applied in a Python environment to build a dump slope stability model. The goal is to discover the ideal hyperparameters. The optimal settings of the GBM -BO model’s hyperparameters are shown in Table 7.

Table 7 Optimal values for hyperparameters of GBM model.
Full size table

Extreme gradient boosting (XGB)

Chen and Guestrin’s64 XGB ruleset offer a novel approach to implementing the Gradient Boosting technique, specifically K Regression and classification trees. A “sturdy” learner can be produced through additive education methods by combining all of the predictions of a group of “vulnerable” starters, according to the set of rules. To start with, XGB optimizes the processing resources while attempting to prevent overfitting. This is frequently accomplished by reducing the complexity of the target capabilities in order to combine predictive and regularization phrases while maintaining the highest possible processing rate. All the way through education level, XGB functions often undergo parallel calculations63.

In order to create a dump slope stability model, this section describes how the XGB approach was applied in a Python environment. The hyperparameters were determined using Bayesian Optimization and fivefold cross-validation procedures. Table 8 shows the optimal settings of the XGB -BO model’s hyperparameters.

Table 8 Optimal values for hyperparameters of XGB model.
Full size table

Histogram gradient boosting (HGB)

The proposed method leverages histogram-based techniques to optimize gradient boosting ensembles, reducing computational complexity. Instead of processing individual data points, histogram-based methods group continuous features into discrete bins. This significantly reduces the number of calculations required for each iteration. By discretizing features into histograms, the algorithm lowers memory usage, making it feasible to train models on large datasets without excessive resource consumption. Since fewer computations are needed per iteration, HGB trains faster while maintaining high predictive accuracy. HGB scales well with high-dimensional data, making it suitable for complex machine learning tasks65.

Here the authors show how to build a dump slope stability model in Python using the HGB technique, finding the best hyperparameters with Bayesian Optimization and fivefold cross-validation. The optimal settings of the HGB-BO model’s hyperparameters are displayed in Table 9.

Table 9 Optimal values for hyperparameters of HGB model.
Full size table

Extra tree regressor (ETR)

To increase prediction accuracy and decrease the likelihood of overfitting, ETR makes use of a cluster of random decision trees that have been fitted to different parts of the dataset. By combining the results of each tree, this clever method creates a final model that is more powerful than the sum of its parts66,67. This method is an example of a learning algorithm, and it has proven repeatedly that even a basic algorithm may provide good results. This finding, meanwhile, is very dependent on the details of the data that were provided67,68.

In order to create a dump slope stability model, this section describes how the ETR methodology was applied in a Python environment. The hyperparameters were determined using Bayesian Optimization and fivefold cross-validation procedures. Table 10 shows the optimal settings of the ETR -BO model’s hyperparameters.

Table 10 Optimal values for hyperparameters of ETR model.
Full size table

Convergence plot

A convergence plot is a graphical representation of the evolution of a time step or error estimate in machine learning. This tool allows for the visualization of algorithm performance, helping to assess whether the results are stabilizing at constant values. Figure 7a–f shows how the error minimized with increasing the iterations in optimisation algorithm for different machine learning models.

Fig. 7
figure 7figure 7

(a) NuSVR convergence plot. (b) Light GBM convergence plot. (c) GBM convergence plot. (d) XGB convergence plot. (e) HGB convergence plot. (f) ETR convergence plot.

Full size image

Dependence plot

Figure 8a, b show the evolution of the model’s hyperparameter variables and their optimal values with red star in a dependency plot.

Fig. 8
figure 8

(a) Dependence plot for Light GBM model. (b) Dependence plot for ETR model.

Full size image

Learning curve

A machine learning model’s learning curve illustrates how the model’s prediction error evolves with changes to the size of the training set. It is evident from the learning curves for different ML models(as shown in Fig. 9a–f that the training score curve and the validation score curve converge as the size of the training set increases. This is something that can be seen clearly. Adding more training data improves the validation score.

Fig. 9
figure 9figure 9

(a) Learning curve for NuSVR model. (b) Learning curve for Light GBM model. (c) Learning curve for GBM model. (d) Learning curve for XGB model. (e) Learning curve for HGB model. (f) Learning curve for ETR model.

Full size image

Stacking ensemble

By utilizing a meta-learner, a stacking ensemble integrates the forecasts of several base learners69. Training numerous base learners is the first step, and training a meta-learner to optimally aggregate their outputs is the second70. The first step is to gather the predictions made by the base learners after they have trained independently on the same dataset using various techniques or hyperparameter setups. Training a meta-learner with the basis learners’ predictions as features is the second stage. In order to arrive at final predictions, this meta-model (Random Forest) figures out how to integrate or weight the results of the foundation models. Improving prediction accuracy by merging heterogeneous base learners through a meta-learner and so minimizing generalization mistakes is the underlying premise of stacking ensemble71 (Fig. 10). By combining the best features of several base models and reducing the impact of their flaws, stacking EL (as shown in Fig. 10) can achieve better results than any one model in the ensemble72.

Fig. 10
figure 10

Stacked random forest ensemble model.

Full size image

Figure 11 learning curve makes it very evident that, as the size of the training set increases, both the training score curve and the validation score curve converge. Adding more training data improves the validation score. Figure 11 shows that with a cross-validation score of 0.9989, the R2 value converged.

Fig. 11
figure 11

Learning curve for stacking regressor model.

Full size image

H20 AutoML

In order to make AutoML more accessible, several open-source systems have been created, including Auto-Keras, Auto-PyTorch, Auto-Sklearn, Auto-Gluon, and H2O AutoML73. H2O AutoML’s strength in processing big and complex datasets has been highlighted in previous research40,74,75 through its ability to swiftly search for the ideal model without relying on manual trial and error. In addition, H2O AutoML includes a user interface that even those without technical knowledge can use to automatically train and fine-tune models, as well as import and split datasets, find the answer column, and more. Therefore, the current study employed H2O AutoML to analyze the stability of dump slopes.

To build ML models for dump slope stability regression, this work used the H2O AutoML method. The first step was to randomly split the database into half, with 80% going into training and 20% into testing. A variety of ML models were created and programmed, including GLM, DRF, XGB, Deep Learning, and GBM. The authors used the standard fivefold CV to boost performance and dependability and built stacked ensembles using the top-performing models and every tuned model. Mode performance accuracy could be leader boarded. The leader models were tested on the testing dataset after storage. The best model was gradient boosting regressor.

Model interpretation

Sensitivity analysis

For a 120 m overall bench height and 35° overall slope angle, Fig. 12 shows how the FOS is affected by slope parameters. A material attribute’s normalized fluctuation from its minimum to maximum value, spanning from 0 to 100%, is represented by the percentage of range (%) on the x-axis and the factor of safety (FOS) on the y-axis. The influence of input factors on slope stability can be better understood through sensitivity analysis. The combination of slope inclination and height was the subject of a sensitivity study, as shown in Table 11. This study’s dataset was developed using the sensitivity analysis results, which were based on the provided overall slope angle (β) and overall bench height (H).

Fig. 12
figure 12

Sensitivity plot.

Full size image
Table 11 Overall bench height and slope angle for parametric study.
Full size table

For a 120 m overall bench height and 35° overall slope angle, Monte Carlo simulation was used to spread the uncertainties in the input across the dump slope stability model. Dump material properties were represented as random variables characterized by designated probability distributions, as seen in Table 12.

Table 12 Material properties distribution.
Full size table

The mean of the resulting distribution of FOS was 0.914, and the standard deviation was 0.22, as seen in Fig. 13. The authors figured out that the probability of failure (PoF), which is the percentage of realizations with FoS < 1.0, was 63.33%.

Fig. 13
figure 13

FOS distribution plot.

Full size image

Model interpretation using SHAP

This study used the Shapley additive explanations (SHAP) approach to assess the impact of features on machine learning model prediction due to its rapid implementation for tree-based models. In coalitional game theory, Shapley values determined how much each attribute contributed to the prediction76,77. Qualities with higher positive SHAP ratings usually affect the forecast more. Figure 14 shows SHAP values for six input features. Each scattering point on the diagram represents a sample, and the red dots indicate elevated relevant characteristic values. However, blue represents low feature values. Red sample points near positive SHAP values show that the angle of internal friction (ϕ) significantly affects the dump slope’s factor of safety (FOS). Higher friction angle increases dump slope stability. However, several red-marked sample locations are in the area with negative SHAP values for the overall slope angle. All evidence indicated the dump slope’s stability is threatened by the slope angle.

Fig. 14
figure 14

Impact of input features on output.

Full size image

The friction angle ϕ is the primary factor in predicting the factor of Safety (FOS), followed by overall slope angle, cohesion, and overall bench height. Higher bench geometry can affect dump slope stability; however, the shear strength parameters (ϕ and c) have a positive impact among the six features. Figure 14 also states the six features’ relevance. The order of these six features reveals that each is valuable in its own way. To anticipate FOS, the friction angle ϕ is the most important element, followed by slope angle, cohesion, and bench height.

Figure 15 confirms that bench geometry(overall bench height and overall slope angle) and shear strength parameters (ϕ and c) are crucial for assessing dump slope stability.

Fig. 15
figure 15

Relative importance of input features.

Full size image

One helpful visual for comprehending the impact of a specific characteristic on the model’s predictions is the dependence plot, as seen in Fig. 16 of SHAP. The correlation between the value (x-axis) and Shap value (y-axis) of a feature, which represents the feature’s influence on the prediction, is shown in a SHAP dependence plot. Alterations to that feature’s impact on model predictions are illustrated by each point, which stands in for a row in the dataset. The non-linear interactions between features and predictions can be better detected with its help. It colours the dots depending on another characteristic to highlight how features interact with one other. It reveals which characteristic values aid in prediction and which ones hinder it. In Fig. 16a, f once can see that SHAP values grow in relation to feature values, which implies that larger feature values lead to the value of output to be more, and in Fig. 16c, d it can be seen that SHAP values fall in relation to feature values, which means that larger feature values lead to the value of output to be declined. Complex, non-linear interactions are indicated by a curved or scattered relationship (see Fig. 16b, e).

Fig. 16
figure 16figure 16

(a–f) Dependence plot (SHAP).

Full size image

Results and discussions

Comparative study between individual ensemble, stacking ensemble and H2O AutoML

Table 13 provides a summary of the eight models’ prediction performance. For predicting dump slope stability, the H2O AutoML and stacking ensemble usually outperforms standalone ensemble models. Enhancing prediction accuracy by merging varied base learners through a meta-learner and so limiting generalization mistakes is the main advantage of stacking ensemble models over other ensemble models. In addition, H2O AutoML’s user interface enables non-technical users to accomplish tasks such as importing and splitting datasets, finding the answer column, and automatically training and fine-tuning models. An issue that arises often during model training is overfitting, which weakens the models’ ability to generalize as the training data has significantly greater predictive performance than the testing data78. If the prediction accuracies of the training and testing data are significantly different, overfitting may happen. Table 13, fourth column, shows that for all eight models, there are less than 0.1 absolute differences between training and testing R squared prediction accuracies. Despite the lack of a universally accepted definition of overfitting in engineering practice79, this study found that the eight models had relatively small differences (less than 0.1) in their forecast accuracies80.

Table 13 R2 metric of all models.
Full size table

Now that each ML model has been fine-tuned on the training datasets, one can evaluate its effectiveness. It is possible to compare the performance of several ML models using these quantitative parameters(see Table 14). To evaluate the performance of ML models, number of additional statistical metrics, like MSE, MAPE, RMSE, and MAE were used. Table 14 displays the statistical metrics for all of the models. To measure how well the models work, many different statistical measures are employed. Compared to other ensemble models, these results point to H2O AutoML as the most accurate.

Table 14 Statistical metrics of all models.
Full size table

In Fig. 17a–h the x axis represents the real values of 50 observations, and the y axis represent the predicted values of FOS. Figure 17a–h compares the predicted and actual outcomes produced by each of the ML models. It is clear that all the models have produced quite accurate FOS estimates. Consequently, the XGB model achieved the worst accuracy (R2 = 0.7453). Additionally, with an R2 value of 0.998937, the H2O AutoML model delivered the best accuracy. Accuracy between these two models has been provided by other models.

Fig. 17
figure 17figure 17figure 17figure 17

(a–h) Original value vs. Predicted values.

Full size image

To determine if a regression model is suitable, regression analysts employ residual plots, which are graphical tools. They are useful for seeing the differences between the expected and actual values (the residuals) and for finding issues with the model. Whether the model’s assumptions are satisfied and the model fits the data well can be ascertained by analysing the distribution and patterns of residuals. The gradient boosting model was more suitable regression model than XGB model for this study as shown Fig. 18a, b. The error in prediction was less in case GBM model.

Fig. 18
figure 18

(a, b) Residual plots.

Full size image

Conclusions

First of all, the authors conducted the data preprocessing of 2250 raw data to transform into a clean, structured and usable format in exploratory data analysis for further processing. In order to predict the FOS of dump slopes in opencast coal mines, this study examined the use of advanced ML models such as GBM, LGBM, XGB, HGB, NuSVR, ETR, with stacked random forest meta model, and H2O AutoML. In order to build the stacking ensemble model, the authors first employed Bayesian optimization—a Gaussian process-to fine-tune the hyperparameters of six foundational machine learning models. The fivefold CV method enhanced the generalizability of the regression models and six potentially significant indicators like cohesion (c), internal friction angle (ϕ), unit weight (γ), overall bench height (H), natural moisture content (m), and overall slope angle (β) were chosen. One last step was to use the SHAP method to do the sensitivity analysis. The main conclusions are as follows:

  • It was suggested that an AutoML method for building ML models and selecting the optimal model for each dataset. With AutoML, one need not worry about establishing a pipeline by hand for ML algorithm selection and hyperparameter tweaking; the system can handle model development and pipeline searches with ease. Traditional models that were manually tweaked and models that were optimized using metaheuristics were beaten by the trained H2O AutoML model. Automated ML model building, model selection and dump slope stability tests were all successfully accomplished with using AutoML.

  • Lazy predict Auto-ML’s predictions are comparable to those of standalone ML models, with the exception of XGB regressor and NuSVR, where they diverge.

  • Compared to other base learners, the stacking ensemble model has a high accuracy value. This study demonstrated the importance of ensemble ML approaches for evaluating and predicting complex dump slope stability. In order to improve computational efficiency, it is required to integrate the super learner function in practical applications due to the huge number of computations and long training period of the stacking model.

  • SHAP study found that factors such cohesiveness (c), unit weight (γ), total bench height (H), and natural moisture content (m) were important in determining dump slope stability, whereas the internal friction angle (ϕ) and overall slope angle (β) were crucial. The stability of the dump slope is more affected by the prediction variables, such as internal friction angle (ϕ), overall slope angle (β), cohesion (c), and overall bench height (H), which are geotechnical material variables and slope geometry, with relevance scores of 0.2, 0.15, 0.06, and 0.03 respectively.

  • The non-linear interactions between input features and predictions can be better detected with the help of SHAP analysis. It colours the dots depending on another characteristic to highlight how features interact with one other. It reveals which characteristic values aid in prediction and which ones hinder it.

  • The standard modelling approaches have a hard time dealing with the complicated, nonlinear, high-dimensional relationship between slope stability and influencing factors. Because of its adept handling of this relationship and its capacity to generate reliable prediction outcomes, the ensemble learning method is a good fit for assessing dump slope stability.

To build an AutoML approach and enhance its generalizability and dependability, future research should incorporate samples and parameters that are crucial, such as the distribution of grain size, rainfall and other external or trigger factors.