Introduction

Road safety continues to be a global public health concern, with nearly 1.19 million fatalities recorded worldwide in 2021, of which 66% were among individuals aged 18–59 years1. Analysis of contributory factors indicates that driver-related errors dominate, with over-speeding and drunken driving alone responsible for more than 75% of fatalities. Broadly, road crash causation can be categorized into four domains: driver, vehicle, roadway and traffic conditions, and environment. Among these, driver behavior is the most critical factor2, particularly in the form of aggressive and risk-taking maneuvers such as speeding, tailgating, abrupt lane changes, and red-light violations3. These behaviors, often driven by frustration, anger, or the desire to save time, substantially increase the likelihood and severity of crashes4.

Over the years, researchers have conducted various studies and suggested that driving behavior could be classified into three broad styles: aggressive, defensive, and moderate5,6,7. Aggressive driving is associated with risky maneuvers and high crash potential; defensive driving emphasizes vigilance, compliance with rules, and safety margins, while moderate driving represents a balance of the two8. Aggressive driving is closely linked to psychological factors, which makes its identification and quantification inherently complex. Traditionally, two primary approaches have been adopted to assess aggressive or risky driving tendencies: (i) self-reported measures such as the Driving Behavior Questionnaire (DBQ) and Driving Style Inventory (DSI), and (ii) analysis of driver kinematic data. The questionnaire-based methods aim to capture a driver’s traits, attitudes, and mental state while driving.9 developed the Dula Dangerous Driving Index (DDDI) to identify aggressive drivers, concluding that individuals with higher levels of anger and aggression are more likely to engage in risky maneuvers. Similarly,10 introduced the Multidimensional Driving Style Inventory (MDSI), which classifies drivers into eight styles, including risky, patient, and speedy.11 proposed the Prosocial and Aggressive Driving Inventory (PADI) to measure prosocial and aggressive tendencies among undergraduate students. Despite their widespread use, the validity and reliability of these self-reported approaches have been questioned by several researchers12,13,14, primarily due to response bias and the tendency of participants to provide socially desirable answers. Although simple to administer, questionnaire-based investigations remain prone to subjectivity, reducing their robustness. More importantly, these methods are unsuitable for real-time detection and mitigation of aggressive driving, thereby limiting their practical utility in preventing crashes under dynamic traffic conditions.

With advancements in sensing and data-logging technologies, attention shifted to vehicle kinematics, including speed, acceleration, jerk, and lane-changing patterns, collected under controlled (simulator) and naturalistic driving (NDS) conditions. NDS is particularly valuable for capturing real-world behavior without experimental bias15,16. Using such data, several studies distinguished aggressive from normal drivers via thresholds on speed, acceleration, and jerk17,18,19. More recently, machine learning models such as econometric models, fuzzy logic, SVM, ANN, RF, k-NN, and clustering20,21,22,23,24, have been widely applied for classification, anomaly detection, and segmentation. For example,21 improved accuracy with semi-supervised SVM;22 found SVM outperforming k-NN, fuzzy, RF, and ANN;23 identified behavioral risk predictors from crash/near-crash events; and25 showed strong performance from SVM, DT, and RF using velocity and acceleration inputs. Clustering approaches include k-means26, graph-based auto-encoder27, kernel fuzzy c-means28, and RF-based clustering29. Extending beyond purely kinematic clustering,30 incorporated demographic and personality factors and, using negative binomial regression with k-means, grouped drivers into three risk categories. Likewise,31 used vehicle kinematics (speed, brake pedal, acceleration, steering angle) with hierarchical clustering and a quasi-Poisson regression model to stratify drivers into behavioral groups. Trajectory-based studies further extend these approaches.32 used GPS data to detect anomalous trajectories,33 employed vision-based data and clustering to classify stopping behaviors,34 proposed an unsupervised Deep Embedded Trajectory Clustering network (DETECT), and35 applied dynamic clustering to NGSIM data to capture behavioral shifts under varying conditions.36 combined clustering with risk evaluation metrics (stability, car-following, and lane-changing risk) to develop driver risk profiles. Under Indian conditions, few researchers37,38 have used vehicular trajectory data to investigate micro-level behaviors, highlighting the profound effects of traffic heterogeneity.

From the above literature, it is evident that (i) NDS and trajectory-based approaches offer reliable and real-time insights into driving behavior, and (ii) clustering and machine learning methods are effective for behavioral classification. However, it is also observed that most studies on driving behavior remain driver-centric, classifying individuals as aggressive, cautious, or safe without accounting for how their behavior varies at specific roadway locations. Such an approach overlooks the fact that road traffic crashes are often concentrated at black spots, where driving behavior and roadway conditions interact in complex ways. Traditional hotspot-based crash prediction models primarily rely on historical crash records to identify high-risk locations, often constrained by underrated nature of crash records, which can limit their effectiveness for proactive safety management39,40. Similarly, surrogate safety studies focus on observable conflict indicators (e.g., time-to-collision, post-encroachment time) but may not capture latent behavioral patterns across different vehicle types41,42. To overcome these limitations, the present study developed a location-based behavioral clustering framework, leveraging trajectory-derived kinematic features to uncover underlying driving styles at specific roadway segments. This approach not only complements existing hotspot identification methods by adding behavioral depth but also enables proactive safety profiling even in areas with limited crash history. By shifting the focus from crash outcomes to behavioral precursors, our model offers a novel lens for understanding and mitigating roadway risk. When used together, crash prediction models and surrogate safety measures can pinpoint where and when potential risks arise, while behavioral clustering explains which road users are more likely to contribute to those risks and the nature of their driving behaviours, thus supporting both proactive safety diagnosis and crash hotspot identification. Another limitation in existing research is the vehicle-specific nature of most models. Studies usually focus on a single class of vehicles, making it difficult to capture the dynamics of heterogeneous traffic streams that dominate Indian roads. This restricts the scalability of such approaches for real-world deployment.

Therefore, the present study seeks to address these gaps by developing a unified machine learning model, which is defined as a single ML model capable of analyzing and classifying driving behaviors across multiple vehicle classes simultaneously. The objectives of this paper are two-fold: (i) to design a robust model that analyzes and classifies driving profiles at specific roadway locations based on their risk levels, and (ii) to establish a unified framework that eliminates the need for separate models for each vehicle class. Principal Component Analysis (PCA) is applied for dimensionality reduction, and four clustering techniques: K-Means, Density-Based Spatial Clustering of Applications with Noise (DBSCAN), Mean Shift, and Deep Embedded Clustering (DEC) are employed to classify location-specific behaviors into ‘Aggressive,’ ‘Cautious,’ and ‘Safe.’ By shifting the focus from driver-centric to location-centric behavioral analysis, this study offers valuable insights into risky behaviors at high-crash locations, thereby supporting proactive interventions for crash hotspot treatment and improving overall road safety.

The remainder of this paper is organized as follows: Section Data collection and preprocessing presents the location and process of data collection, its preprocessing, assessment of vehicle composition, and application of oversampling to address class imbalance. Section Methodology details the methodology including feature engineering, data normalization, the implementation of Principal Component Analysis (PCA), and provides a brief outline of the clustering techniques employed in this study. Section Results and discussion reports the experimental results, including comparative analyses of individual vehicle classes using both the original and oversampled datasets to identify the two best-performing methods, which are then further evaluated on the combined dataset. Finally, Section Summary and conclusions concludes the paper with a summary of key findings, limitations, and directions for future research.

Data collection and preprocessing

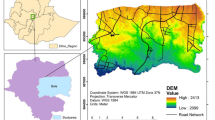
The data for the proposed study were collected from an urban six-lane divided arterial road (Maraimalai Adigalar Bridge) located in Saidapet, the southern part of the city Chennai, India. A 250 m long and 12 m wide road segment was chosen as there were no nearby intersections, bus stops, parked vehicles, or other side elements that could alter drivers’ conduct or the driver’s behavior. Additionally, a separate pedestrian walkway was available to restrict vehicle-pedestrian interaction. The traffic video was recorded between 10:00 am and 3:30 pm, but a 30-minute segment of the video (from 2:45 pm to 3:15 pm) was processed to extract vehicular trajectories and was utilized in this study. This time window of 30 minutes captured a representative mix of driving behaviors—such as vehicle following, lane changes and lateral shift behaviors—under medium traffic conditions. This provided a limited yet diverse dataset, which was utilized for initial model development in this study. To extract the trajectory data from the video, a semi-automated tool named Trajectory Extractor43 was used, which captures vehicle coordinates, dimensions, and vehicle class at an interval of 0.5 seconds. Key steps involved in the Trajectory Extractor44 are as follows:

  • Identify vehicle boundaries manually using a Windows-based graphical interface,

  • Select image points along each vehicle’s edge using a mouse,

  • Calibrate spatial mapping using four reference points with known real-world coordinates,

  • Transform selected image points into real-world coordinates via coordinate transformation,

  • Compute vehicle location, dimensions, and classification across frames,

  • Derive kinematic parameters (speed and acceleration) at 0.5-second intervals,

  • Visualize the process using the Trajectory Extractor interface (see Fig. 1).

Fig. 1
figure 1

Study location (Maraimalai Adigalar Bridge) along with the user interface of Trajectory Extractor43.

Full size image

Once vehicle position data are extracted, a smoothing procedure was applied to handle missing observations caused by occlusions, reduce the influence of measurement errors, and enable accurate computation of derived variables such as speed and acceleration. The Locally Weighted Regression (LWR) method was utilized for trajectory smoothing45. LWR applies a polynomial regression model to a window of \(N\) observations before and after the measurement point of interest, \(t_0\). The trajectory function in the neighbourhood of this point is given by:

$$\begin{aligned} x(t) = f_{t_0}(t,\beta _{t_0}) + \epsilon _{t_0,t}, \end{aligned}$$
(1)

where \(f_{t_0}(t,\beta _{t_0})\) = fitted position at time \(t\) estimated by the local regression function centered at time \(t_0\), \(\beta _{t_0}\) = vector of parameters of the fitted curve to be estimated, and \(\epsilon _{t_0,t}\) = normally distributed error term. The parameters \(\beta _{t_0}\) are estimated using a weighted least squares estimator with \(N\) observations around \(t_0\):

$$\begin{aligned} \beta _{t_0} = \arg \min _{\beta } \left[ X_{t_0} - f_{t_0}(t, \beta ) \right] ' W_{t_0} \left[ X_{t_0} - f_{t_0}(t, \beta ) \right] , \end{aligned}$$
(2)

where \(X_{t_0}\) = column vector of \(N\) position observations used to estimate the trajectory function centered at \(t_0\), \(f_{t_0}(t, \beta )\) = corresponding vector of fitted values, \(W_{t_0}\) = diagonal matrix with elements corresponding to weights assigned to each observation. The observation weights are determined by a tricube function based on the distance from the point of interest \(t_0\):

$$\begin{aligned} w(t_0, t) = 1 - \left( \frac{|t - t_0|}{d} \right) ^3, \end{aligned}$$
(1)

where \(w(t_0, t)\) is the weight assigned to the observation at time \(t\), and \(d\) is the distance to the nearest point outside the window of points considered for fitting the curve.

Finally, the processed data includes 16512 distinct vehicle trajectories extracted at a time resolution of 0.5 s. The trajectories data provide vehicle’s spatial position, speed, and acceleration/deceleration values in both the longitudinal and lateral directions. From Fig. 2, showing the vehicle compositions within the dataset, it can be observed that 50.6% are motorcycles, 29.1% are cars, 14.5% are auto-rickshaws, 3.9% are buses, and 2% are combined LCVs and trucks. Since the composition of buses, LCVs, and trucks is minimal, these classes of vehicles are excluded from further analysis in this present study.

Fig. 2
figure 2

Vehicle composition at the selected study location.

Full size image

Among the selected three vehicle classes, the percentage share of cars and auto-rickshaws is less than that of motorcycles. Addressing this class imbalance and for fair comparison between the vehicle classes and models, an oversampling technique, the Synthetic Minority Over-Sampling Technique (SMOTE), was applied at the aggregate (vehicle-level) feature space, rather than on the raw trajectory data. This is mainly because applying SMOTE at the raw trajectory level would not effectively address class imbalance, as it would preserve the same number of vehicles per class. Oversampling was not applied to the motorcycle class, as it already had the highest samples. Instead, it was applied only to the underrepresented classes—cars and auto-rickshaws. After oversampling, the final sample distribution consisted of 41.8% motorcycles, 34.2% cars, and 24% auto-rickshaws. Table 1 shows the descriptive statistics of the longitudinal speed and acceleration and Fig. 3 shows the speed profile of the selected vehicle class to be used in the analysis. From Table 1, it can be observed that the average speed of vehicles is about 5.88 m/s and the maximum speed is about 15.22 m/s. Also, it is noteworthy that different vehicle types exhibit varying average speeds. Specifically, cars demonstrate the highest mean speed at 6.13 m/s, followed by motorcycles at 6.0 m/s. On the other hand, auto-rickshaws maintain the slowest speed of 5.06 m/s.

Table 1 Descriptive Statistics of the Collected Data43.
Full size table
Fig. 3
figure 3

Speed vs. time profile for different classes of vehicles.

Full size image

Methodology

This study employs a multi-stage clustering framework to identify latent patterns in the dataset. Dimensionality reduction is first performed using Principal Component Analysis (PCA), after which clustering is conducted with four complementary methods: K-means, DBSCAN, Mean Shift, and Deep Embedded Clustering (DEC). The combination of these approaches ensures robustness by capturing centroid-based, density-based, adaptive, and representation-driven structures within the data. The overall procedure is summarized in Algorithm 1, which outlines the sequential steps from dimensionality reduction to clustering and evaluation.

Algorithm 1
figure a

Framework for Driver Behavior Clustering and Classification.

Full size image

Feature Importance

In this study, we concentrated on four parameters: speed and acceleration, in both lateral and longitudinal directions, while employing clustering algorithms. To construct the input feature set, 16 variables were generated by combining four kinematic parameters—longitudinal speed, lateral speed, longitudinal acceleration, and lateral acceleration—with four statistical descriptors: minimum, maximum, mean, and standard deviation. These features were selected based on their relevance to risk-related driving behaviors, such as speeding, abrupt lane changes, and sudden acceleration or deceleration, which are commonly associated with aggressive or unsafe driving. Since these features had varying units and scales (e.g., speed in m/s and acceleration in m/s2), they were normalized, ensuring equal contribution of each feature to the PCA, preventing features with larger magnitudes from excessively influencing the resulting principal components. The normalization was performed using the Standard Scaler transformation, defined as:

$$\begin{aligned} x'_{j} = \dfrac{x_j - \mu _j}{\sigma _j}, \end{aligned}$$
(2)

where \(x'_{j}\) is the normalized value, \(x_j\) is the original feature value, \(\mu _j\) is the mean of the feature (across all samples), and \(\sigma _j\) is the standard deviation of the feature.

In order to reduce dimensionality and retain the most informative variables, Principal Component Analysis (PCA) was applied to the derived 16 standardized features, resulting in 16 Principal Components (PCs), labeled PC1 to PC16. Each PC is a linear combination of the original features, with PC1 capturing the maximum variance and PC16 the least. Preliminary inspection of component loadings identified 9 influential features, which were retained for further analysis. PCA was reapplied on this reduced feature set to examine loading strength, and a cumulative explained variance plot (Fig. 4a) was generated to determine the optimal number of principal components (PCs). The results indicate that the first five PCs explain more than 90% of the total variance, with the corresponding feature loadings presented in Table 2.

Figure 4 shows the results obtained from PCA: the number of important PCs and the correlation circle, illustrating the loading of the features in the first two components (PC1 and PC2). The length of each feature line/arrow denotes the magnitude/strength, while the direction of the feature lines represents the sign of the correlation (positive or negative). From Fig. 4b, it can be observed that PC1 (X-axis) is dominated by speed-related features, and PC2 is influenced by longitudinal acceleration-related features. Thus, we can conclude that PC1 is speed-dominating, while PC2 is longitudinal acceleration-dominating. Thus, these new axes, represented by PC1 on the X-axis and PC2 on the Y-axis, are subsequently used for cluster visualization.

Fig. 4
figure 4

Principal Component Analysis results.

Full size image
Table 2 Feature loading rate on the selected PCs.
Full size table

K-Means clustering

Due to its simplicity, ease of implementation, and high interpretability, the k-means clustering approach is one of the most widely used techniques to solve clustering-related problems46. It is an iterative algorithm that divides the un-labelled datasets into k distinct non-overlapping subgroups (clusters) so that points with similar properties belong to only one group. The algorithm assigns a data point to a cluster such that the sum of the square distance (Euclidean distance) between the data point and the cluster centroid is minimal. The algorithm operates as follows:

  • Initiation Step: Select k different points randomly from a given data set and treat them as initial centroids of the clusters.

  • Expectation Step (E-Step): Calculate the Euclidean distance of each data point from the K cluster centroids. Assign each data point to a cluster whose distance is minimum.

  • Maximization Step (M-Step): Calculate the mean and variance of each cluster and then update it with the centroid of that cluster. This means reassigning each data point to the newest closest centroid of each cluster.

  • Repeat steps 2 and 3 till there is no change in centroids or till the algorithm reaches the maximum number of iterations.

To determine the optimal number of clusters, the Elbow Method was applied using the Within-Cluster Sum of Squares (WCSS), which quantifies the sum of squared distances between each point and its cluster centroid, thereby reflecting intra-cluster dispersion. The aim is to select the number of clusters that minimizes WCSS, with the distortion score used as the evaluation metric. Although widely adopted, k-means struggles with non-linear patterns, depends heavily on initial centroids, and performs poorly in high-dimensional spaces where Euclidean distance becomes less discriminative. As dimensionality increases, data sparsity and distance variation reduce cluster compactness while computational complexity grows47.

Density-based spatial clustering of applications with noise (DBSCAN)

DBSCAN is a density-based clustering algorithm that groups points by density and spatial proximity, capable of detecting clusters of arbitrary shapes and handling noise without requiring the number of clusters in advance48. The various steps involved in the algorithm are as follows:

  • Parameter selection: The key parameters are \(\epsilon\) (distance threshold) and MinPts (minimum number of points to form a dense region).

    • \(\epsilon\): Maximum distance to consider two points as neighbors. Often determined using a k-distance plot, where a sharp increase suggests the optimal \(\epsilon\).

    • MinPts: Minimum number of points for a core region. A rule of thumb is MinPts \(\ge D+1\), with higher values (e.g., 2D) for noisy or high-dimensional data.

  • Core point identification: A point with at least MinPts neighbors within \(\epsilon\) is marked as a core point.

  • Density-connected components: Clusters are formed by expanding from core points to include all density-reachable points.

  • Border and noise points: Points within \(\epsilon\) of a cluster but not meeting MinPts are border points; others are labeled noise.

  • Complexity: With efficient data structures (e.g., kd-tree), the average complexity is \(O(n \log n)\), while the worst case is \(O(n^2)\)49.

Mean shift clustering

Mean-shift clustering is one of the powerful unsupervised learning techniques for data clustering and density estimation50. The steps involved in the algorithm can be described as follows:

  • Initialization: Each data point is assigned a kernel, typically a Gaussian function, with a specified bandwidth parameter. The bandwidth determines the kernel’s size and influences the resulting clusters’ shape and granularity. The bandwidth parameter is normally chosen or optimized through techniques such as cross-validation, where different bandwidth values are tried, and the one that maximizes a clustering criterion such as Silhouette score or minimizing a cost function like the DBI is selected. Alternatively, techniques like the Silverman’s rule of thumb or grid search can be employed to find an optimal bandwidth51,52

  • Shifting: The mean shift vector is calculated for each data point by computing the weighted average of the data points within the kernel’s range. The kernel function and the distances between the data points determine the weights. The mean shift vector represents the direction toward the higher-density region i.e. vector pointing towards the centroid of the density.

  • Updating: The current data point is shifted toward the direction of the mean shift vector. The kernel function and the distances between the data points determine the magnitude of the shift. This process is iteratively applied to all data points until convergence is reached.

  • Convergence: The shifting process continues until the data points no longer move significantly or a predetermined number of iterations is reached. Convergence implies that the data points have settled into the modes of the density. estimate.

Unlike k-means clustering, this algorithm does not require prior knowledge of the number of clusters. Instead of assigning data points to fixed cluster centers, mean-shift identifies clusters based on density estimation, iteratively shifting points towards higher-density regions until convergence is reached.

Deep embedded clustering (DEC)

Deep embedded clustering is a powerful technique that combines deep learning and clustering to achieve end-to-end unsupervised learning53. The algorithm has two main components: the deep embedding component and the clustering component. The former aims to learn a compressed input data representation, which captures complex non-linear relationships and informative features. While the latter component essentially is a standard clustering algorithm that operates on the embedded data to group similar data points into clusters. A simple implication of the model architecture can be seen in Fig. 5.

Fig. 5
figure 5

Architectural Diagram showing the working of Deep Embedded Clustering (DEC).

Full size image

The deep learning part comprises of an auto-encoder which is a neural network architecture used for dimensionality reduction and feature learning. It is trained layer by layer in an unsupervised manner where each layer is trained by reconstructing the input from the previous layer’s representation. This layer-wise pre-training helps in learning hierarchical representations of the data. In DEC, an auto-encoder is first pre-trained on the dataset to make it learn an initial set of learned representations. Similarly, the clustering component of the algorithm is trained on the dataset to obtain an initial set of cluster centroids. The cluster centroids and learned auto-encoder representations would be used to obtain the probability distribution of each data point belonging to a cluster which is then ultimately used for training. The procedure involved is described below:

  • Embedding Calculation: The learned auto-encoder obtains the embedding or latent representation of the input data. Let’s denote the embedding of the data points as \(z_i\), where i represents the index of the data point.

  • Cluster Centroids: The cluster centroids, denoted as \(\mu _j\), are initialized or updated during optimization and obtained using the k-means algorithm. These centroids represent the centers of the clusters in the embedding space.

  • Pairwise Distances: The pairwise distances between each data point’s embedding (\(z_i\)) and the cluster centroids (\(\mu _j\)) are calculated using the Euclidean distance.

  • Similarity Calculation: A similarity between each data point and each cluster centroid is calculated based on the pairwise distances calculated in the previous step. One commonly used similarity measure is the Gaussian kernel function:

    $$\begin{aligned} S_{ij}=\exp {\frac{-||z_i-\mu _j||^2}{2\sigma ^2}}, \end{aligned}$$
    (3)

    where \(S_{ij}\) represents the similarity between data point i and cluster centroid j, ?.? denotes the Euclidean distance, and \(\sigma\) is the bandwidth parameter that controls the width of the Gaussian kernel.

  • Soft Assignment Probabilities: The similarity scores obtained above are normalized to obtain soft assignment probabilities for each data point to each cluster. The probabilities are calculated using the softmax function:

    $$\begin{aligned} p_{ij}=\left( \frac{s_{ij}^2}{\Sigma _{j=1}^Ks_{ij}^2} \right) , \end{aligned}$$
    (4)

    where \(p_{ij}\) represents the soft assignment probability of data point i to cluster j, K is the total number of clusters, and \(\Sigma s_{ij}^2\) denotes the sum of squared similarities for data point I over all clusters.

  • Probability Distribution: The probability distribution, denoted as \(q_{ij}\), is obtained by applying a Student’s t-distribution to the pairwise similarities of the embedded points:

    $$\begin{aligned} q_{ij}=\frac{\left( 1+||z_i-z_j||^2\right) ^{-\alpha }}{\Sigma _{k=1}^N\left( 1+||z_i-z_k||^2 \right) ^{-\alpha }}, \end{aligned}$$
    (5)

    where \(\alpha\) is a parameter that controls the tail heaviness of the distribution, N is the total number of data points.

  • Loss Function: The objective function of DEC combines the data reconstruction loss (measures the dissimilarity between the input data and its reconstruction by the decoder network) and the Kullback-Leibler (KL) divergence54 as the clustering loss (measures the dissimilarity between the target distribution and the distribution of cluster assignments.

    $$\begin{aligned} J_{cluster}=\Sigma _{i=1}^K \Sigma _{j=1}^K p_{ij}\log \left( \frac{p_{ij}}{q_{ij}}\right) , \end{aligned}$$
    (6)
    $$\begin{aligned} J_{recon}=-\Sigma _{i=1}^Nx_i \log (\hat{x}_i) + (1-x_i) \log (1-\hat{x}_i) \end{aligned}$$
    (7)

    where \(p_{ij}\) represents the soft assignment probability of data point i to cluster j, and \(q_{ij}\) denotes the target probability distribution obtained by applying a Student’s t-distribution to the pairwise similarities of the embedded points, \(x_i\) represents the input data, \(\hat{x}_i\) is the reconstructed output, and N is the number of data points. The objective of DEC is to optimize the clustering and embedding processes jointly. The final loss function is as follows:

    $$\begin{aligned} J=J_{recon}+\lambda J_{cluster}, \end{aligned}$$
    (8)

    where \(J_{recon}\) represents the data reconstruction loss of the auto-encoder, \(J_{cluster}\) denotes the clustering loss, and \(\lambda\) is a trade-off parameter that balances the two components. Table 3 shows the list of parameters used in the DEC architecture. Algorithm 2 outlines the complete process involved in the DEC model implementation.

Algorithm 2
figure b

DEC-based method for Driver Behaviour Classification.

Full size image
Table 3 Parameters of DEC architecture used.
Full size table

Results and discussion

Upon implementing the above-mentioned clustering algorithms, the obtained results are organized to provide a systematic evaluation of the clustering methods across vehicle classes. To start with, the performance of all four clustering approaches is presented for individual vehicle datasets under both original and oversampled conditions, enabling a comparative assessment of their effectiveness. In the next level, the best identified clustering methods were subsequently applied to the unified dataset, thereby facilitating an evaluation of their ability to capture location-specific driving safety profiles across multiple vehicle classes.

Individual

K-Means algorithm

For the individual vehicle classes, the K-Means algorithm was first applied as detailed in Algorithm ?? to assess location-specific driver behavior patterns. Figure 6 shows the elbow plot, indicating the selection of three clusters as the optimal number of clusters. Figure 7 presents the clustering results on the first two principal components (PC1 and PC2) derived from trajectory data. Each dot in the plots (Fig. 7) represents an individual driving instance, projected into the reduced feature space. From Figures, it can be observed that the three color-coded clusters represent distinct categories of driving behavior. The safe driving behavior is represented by green, cautious behavior by blue and the aggressive behavior with the red. The behavioral labels “Aggressive,” “Cautious,” and “Safe” were assigned based on the distribution of principal component scores derived from normalized kinematic features. Specifically, PC1 captured speed-related variables, while PC2 reflected acceleration characteristics. Clusters with high PC1 and PC2 values were labeled “Aggressive,” indicating moderate to high speeds combined with rapid acceleration or deceleration, traits commonly associated with risky driving. Clusters with low PC1 and PC2 scores were labeled “Safe,” representing consistent, low-speed driving with minimal acceleration fluctuations. The “Cautious” category was characterized by relatively higher speeds (PC1) but lower acceleration (PC2), suggesting deliberate driving with minimal abrupt maneuvers.

Fig. 6
figure 6

Elbow plot.

Full size image
Fig. 7
figure 7

K-Means Clustering Results.

Full size image

To check the validity of the cluster plots and to evaluate the internal cohesion and separation between the clusters, the Silhouette Score, DBI, CHI were computed. The Silhouette value ranges between –1 and +1, where values greater than 0.50 indicate good clustering, while values between 0.25 and 0.50 represent fair or moderate clustering. For DBI, values less than 1 are considered very good, whereas values between 1 and 2 denote moderate clustering quality, and higher CHI values indicate more compact and well-separated clusters. For the original dataset, motorcycles achieved a Silhouette score of 0.192 with a DBI of 1.658 and CHI of 258, suggesting weaker clustering quality. Cars showed slightly better results with a Silhouette of 0.254, DBI of 1.295, and CHI of 272, while auto-rickshaws exhibited the highest clustering quality among the original data classes, with a Silhouette of 0.396, DBI of 1.185, and CHI of 127. After applying oversampling to balance the class distribution, the clustering performance improved noticeably. Motorcycles recorded a Silhouette of 0.298, DBI of 1.152, and CHI of 463, while cars showed further improvement with a Silhouette of 0.316, DBI of 1.024, and CHI of 517. Overall, the evaluation indices across all classes fall within acceptable ranges, confirming that the clusters are well-formed and reliable, with oversampling significantly enhancing the cohesion and separation of underrepresented vehicle classes such as motorcycles.

DBSCAN

This section presents the clustering results obtained using the DBSCAN algorithm for the three vehicle classes. Figure 8 shows the k-distance plot that is used to select the optimal hyperparameter, epsilon value. Figure 9 show the clustering outcomes on the original and oversampled datasets obtained from DBSCAN.

Fig. 8
figure 8

K-Distance plot for optimal value of epsilon.

Full size image

From Fig. 9, it can be observed that, even at the optimal epsilon, DBSCAN is unable to form multiple distinguishable clusters. Instead, it formed a single dominant cluster (red dots) with the remaining points classified as noise (black dots). This limitation highlights DBSCAN’s sensitivity to data density and its inadequacy in handling datasets with uneven distribution or overlapping clusters. Consequently, the evaluation indices provide limited interpretability: the Silhouette score ( 0.40) and DBI (<1) nominally indicate moderate cohesion and separation, but these metrics are rendered largely meaningless in the context of a single cluster. Similarly, the CHI value, below 30, reflects the absence of between-cluster dispersion. Overall, DBSCAN fails to capture the inherent heterogeneity of the vehicle trajectories, whereas K-Means demonstrates more effective partitioning in such scenarios.

Fig. 9
figure 9

DBSCAN Clustering Results.

Full size image

Mean shift algorithm

This section presents the clustering results obtained using the Mean-Shift algorithm for the three vehicle classes. Figure 10 show the clustering outcomes on the original and oversampled datasets obtained from Mean Shift algorithm. From Fig. 10, it can be observed that both the original and oversampled datasets yield results similar to those obtained with DBSCAN. Specifically, Mean-Shift forms a single dominant cluster (red dots), with only a few scattered points lying outside this cluster. In contrast to K-Means, which requires the number of clusters to be predefined, Mean-Shift and DBSCAN automatically estimate the number of clusters based on the local density of data points. This density-dependent behavior likely explains their inability to partition the data into multiple distinct clusters. With only one cluster formed, the cluster group does not provide meaningful information regarding driver categorization; for instance, the red cluster cannot be interpreted as representing aggressive drivers. The limited performance of Mean-Shift is further corroborated by the evaluation metrics, which lose significance in this context due to the absence of multiple clusters and, consequently, no basis for assessing inter-cluster separation.

Fig. 10
figure 10

Mean Shift Clustering Results.

Full size image

DEC

This section presents the clustering results obtained using the DEC algorithm for all three vehicle classes. Figure 11adepicts the cluster plot for the original dataset, while Fig. 11bshows the results for the oversampled dataset. Compared to DBSCAN and Mean-Shift, DEC demonstrates superior clustering performance. As indicated in Figure 4, speed-related features have positive loadings on the first principal component (PC1), so higher PC1 values correspond to increased vehicle speeds. Similarly, acceleration-related features align with the second principal component (PC2). In the original dataset (Fig. 11a), DEC forms three distinguishable clusters with minimal overlap: red dots represent aggressive drivers, blue dots moderate drivers, and green dots safe drivers. Aggressive drivers tend to cluster at moderate PC1 and higher PC2 values, reflecting medium speeds coupled with rapid acceleration, whereas safe drivers cluster at lower speeds with medium acceleration. In the oversampled dataset, the decision boundaries are largely influenced by PC1, suggesting that speed plays a dominant role in distinguishing aggressive, cautious, and safe driving categories. The evaluation metrics further confirm the superior performance of DEC in both datasets, with Silhouette scores ranging from 0.25 to 0.5, DBI between 1 and 2, and CHI exceeding 300, indicating well-formed and meaningful clusters.

Fig. 11
figure 11

DEC Clustering Results.

Full size image
Table 4 Evaluation metrics for individual vehicle classes across clustering models.
Full size table

Table 4 summarizes the clustering evaluation metrics for individual vehicle classes across the four algorithms: K-Means, DBSCAN, Mean-Shift, and DEC. From Table 4, it can be observed that K-Means and DEC provide the most reliable clustering for individual vehicle classes, with improved performance after oversampling. Silhouette scores, DBI, and CHI indicate that these algorithms form compact and well-separated clusters, particularly for motorcycles and cars. In contrast, DBSCAN and Mean-Shift generally produce a single dominant cluster with scattered points, resulting in poor inter-cluster separation and limited interpretability. Overall, DEC demonstrates the best balance of cohesion and separation, highlighting its effectiveness in categorizing heterogeneous driving behaviors.

Combined data

As observed from the analysis of individual datasets, K-Means and DEC emerged as the most effective models. Consequently, these two clustering approaches were applied to the combined dataset, created by merging data from individual vehicle classes and adding a one-hot encoded feature, ‘vehicle type,’ to differentiate between the various vehicle categories. The obtained results are presented in this section.

K-means

The results of the K-means algorithm applied to the combined dataset are shown in Fig. 12 for the original and oversampled cases. From Fig. 12a, it can be observed that for motorcycles, the aggressive and safe categories are relatively well-separated, with some overlap between them. However, the cautious category completely overlaps with the other two categories, making it less distinguishable. Aggressive vehicles tend towards moderate speed and higher acceleration, whereas safe vehicles tend towards lower speed and lower acceleration values. A similar trend is observed for the other two vehicle classes as well. From Fig. 12b, it can be observed that the decision boundary of the clusters for all vehicle classes is separated, with aggressive drivers occupying the upper portion, while safe drivers occupy the lower portion of the PC2 axis, representing acceleration. The cautious driving category is very low in number and is mainly scattered among the safe and aggressive categories. The corresponding Silhouette score is 0.229 for the original dataset and 0.22 for the oversampled dataset. The DBI improves from 1.50 to 1.37, while the CHI increases markedly from 532 to 850, indicating improved cluster stability, stronger within-cluster cohesion, and greater inter-cluster separation after oversampling.

Fig. 12
figure 12

K-Means Clustering (Combined Dataset) Results.

Full size image

DEC

The results of the DEC algorithm applied to the combined dataset are shown in Fig. 13 for the original and oversampled cases. These figures indicate that for motorcycles and cars, DEC effectively forms three distinct clusters, classifying drivers as aggressive, cautious, and safe. In contrast, for autorickshaws, the model mainly forms two clusters (safe and aggressive) with a very few data points falling in the cautious category. Consistent with the earlier K-Means and DEC results (presented for individual data), aggressive drivers are generally associated with moderate speed (PC1) and higher acceleration (PC2), safe drivers exhibit lower speed and acceleration, while the cautious category tends toward higher speed with lower acceleration. Also, evaluation metrics proved the superiority of this model, achieving a highest CHI of 880 for the oversampled case, with Silhouette score and DBI under acceptable limits. The evaluation metrics further confirm the superiority of DEC over K-Means. THE DEC achieves a Silhouette score of 0.34 for the original dataset and 0.30 for the oversampled dataset. The DBI improves from 1.65 to 1.20, while the Calinski–Harabasz Index (CHI) reaches 880 in the oversampled case, the highest among all models, demonstrating enhanced cluster stability, cohesion, and separation. Aligned with the previous k-means and DEC clustering results, aggressive drivers/vehicles are associated with moderate speed (PC1) and higher acceleration (PC2), safe drivers/vehicles exhibit lower speed and acceleration, while the cautious driving category tends towards higher speed with lower acceleration values. The evaluation metrics proved the superiority of this model, achieving a highest CHI of 880 for the oversampled case, with Silhouette score and DBI under acceptable limits. Table 5 shows the summary of evaluation metrics obtained for all the models for the combined dataset.

Fig. 13
figure 13

DEC Clustering (Combined Dataset) Results.

Full size image
Table 5 Evaluation metrics for combined class clustering.
Full size table

Overall, from Table 5, it can be observed that, both K-Means and DEC provide meaningful clustering of driver behaviors in the combined dataset. K-Means separates aggressive and safe drivers reasonably well, but the cautious category remains indistinct, with oversampling only moderately improving cohesion (CHI rising from 532 to 850, DBI dropping from 1.50 to 1.37). On the other hand, DEC delivers clearer and more consistent clusters, effectively identifying all three categories for motorcycles and cars, while autorickshaws show two dominant clusters. Its performance metrics confirm superiority: a higher Silhouette score (0.34 on the original dataset), improved DBI (1.20 after oversampling), and the highest CHI of 880. In summary, while both models perform satisfactorily, DEC proves more robust and effective, making it the preferred clustering approach.

Table 6 presents the percentage distribution of behavioral categories: Safe, Cautious, and Aggressive, across three vehicle types (Motorcycles, Cars, and Auto-Rickshaws) at the same roadway segment. From Table 6, it can be observed that:

Table 6 Behavioural Characteristics of DEC clustering (Combined Data) results.
Full size table

  • Motorcycles exhibit a higher proportion of Cautious behavior (51.02%) and a moderate share of Aggressive behavior (10.16%), likely due to their maneuverability and frequent speed adjustments.

  • Cars are more evenly distributed, with 42.31% classified as Safe, 45.73% as Cautious, and 11.97% as Aggressive, reflecting a balanced driving style.

  • Auto-Rickshaws show a dominant Safe behavior (80.57%) and minimal Cautious behavior (6.57%), possibly due to their lower speed and operational constraints.

Summary and conclusions

This study developed and evaluated an unsupervised learning framework to classify location-specific driving behaviors across multiple vehicle classes. Trajectory data collected in Chennai, India, over a 30-minute period formed the basis of the analysis. Four kinematic parameters: speed, longitudinal acceleration, and lateral acceleration were extracted for16,512 vehicles spanning six classes. To ensure sufficient representation, only motorcycles, cars, and autorickshaws were retained, while buses, trucks, and light commercial vehicles were excluded due to their low sample sizes. For the three selected vehicle classes, 16 kinematic features were derived for each driver using four statistical descriptors (minimum, maximum, mean, and standard deviation). Standard scaling and Principal Component Analysis (PCA) were applied to reduce dimensionality, with the first five principal components accounting for over 90% of the variance. PC1 primarily captured speed-related features, while PC2 reflected acceleration-related features, enabling visualization of the clustering outcomes. Four datasets: three vehicle-specific and one combined dataset were prepared and analyzed using four clustering algorithms: K-Means, DBSCAN, Mean Shift, and DEC. The evaluation of clustering performance through Silhouette Score, DBI, and CHI revealed that DBSCAN and Mean Shift consistently failed to form meaningful clusters, instead collapsing the data into a single group. In contrast, K-Means and DEC effectively classified drivers into ‘Aggressive,’ ‘Cautious,’ and ‘Safe’ categories across both individual and combined datasets. Aggressive driving behaviors were characterized by moderate speeds and higher acceleration, safe behaviors by lower speeds and lower accelerations, while cautious behaviors typically showed higher speeds coupled with lower acceleration.

The best results were achieved on the combined oversampled dataset, where K-Means and DEC delivered strong performance with CHI values of 850 and 880, respectively. DEC demonstrated the highest overall effectiveness, forming clearer clusters and achieving superior evaluation metrics. Importantly, the unified DEC model was able to classify behaviors across multiple vehicle classes simultaneously, removing the need for separate models and offering a simplified yet accurate framework for location-based driver behavior analysis. In conclusion, the findings highlight the potential of DEC as a robust tool for identifying risky driving behaviors at specific roadway segments. By linking behavioral patterns to locations, the proposed framework supports the detection of driving hotspots where aggressive or unsafe practices are concentrated, thereby providing actionable insights for proactive safety interventions. In heterogeneous traffic conditions, analyzing the vehicle class-wise distribution of safe, cautious, and aggressive drivers helps pinpoint which vehicle types pose higher risks. This allows for targeted measures—such as focused driver training, stricter enforcement, awareness campaigns, and insurance—based incentives or penalties-rather than relying on generalized approaches.

Although the findings are promising, several directions remain for future research. Expanding the dataset to cover longer durations, varied roadway conditions, and diverse geographic regions, particularly within the Indian context would strengthen the model’s robustness. Rather than relying solely on video-based trajectory data for speed and acceleration, an Intelligent Transportation System (ITS) can be integrated to enable advanced data collection using Global Positioning System (GPS), Inertial Measurement Unit (IMU), and other state-of-the-art sensors for capturing detailed kinematic information. Incorporating contextual factors such as roadway geometry, weather, traffic conditions and driver demographics could yield a more nuanced understanding of behavior and ensure its applicability in large-scale, real-world deployments. Ultimately, such a unified location-based modeling approach can directly support black spot identification and corridor-level safety management, enabling more targeted and effective road safety strategies.