Introduction

GNSS radar is a new type of environmental object detection tool that uses GNSS signals as the transmitting source and radar mode as the signal processing method to perform object detection. Specifically, GNSS radar can complete all-weather, full-coverage object detection monitoring tasks and has low equipment cost and human resource, which received extensive attention1. However, the initial design of the GNSS signal is not for radar or for environmental object detection, so its shortcomings are obvious compared to general radar signals, including narrow bandwidth (leading to low resolution), low SNR, etc. Focusing on these characteristics, the current research on static imaging of GNSS radar mainly focuses on increasing the resolution and improving the SNR. Under this background, the research of GNSS radar mainly includes GNSS-R (GNSS reflectometry), GNSS- SAR (GNSS synthetic aperture radar) imaging and RDM for moving targets. The receiver can be placed on the ground, in the air or on the satellite2.

At present, research on air moving target detection is mainly based on ground-based active detection radar3. However, the use of space-based systems for moving target detection has the characteristics of wide area, high efficiency, and all-day detection. Many scientists have studied the GNSS-R method on dynamic target state analysis. Since the theory of GNSS radar was proposed, researchers have used air balloons as a moving platform to collect GNSS signals for imaging experiments. Reference4 studied the influence of signal scattering mode and antenna polarization on target detection in GNSS-R. In 2018, the University of Birmingham in the United Kingdom proposed a theoretical framework for moving target positioning based on bistatic distance measurement, which gave prediction accuracy. Positioning is achieved through multidelay technology and has been verified by experiments5. Reference6,7,8proposed a novel joint detection and localization method for maritime moving ships. Liu F K et al. using multiple satellites to establish a coordinate system and employing a space-time mixed integration method, the effective echo integration of multiple bases is achieved, which increases the tracking accuracy of moving targets9. Reference10,11realizes the geometric model of GNSS passive radar deformation monitoring and optimizes the carrier phase parameters.

The core method of GNSS bistatic radar for moving target detection is to use the RDM generated by the reflected signal of the geostationary satellite12. Therefore, research on improving the detection accuracy of moving targets mainly focuses on the noising decrease method of RDM. Lu X proposed an efficient scheme to remove impulse noise pixels in range doppler images, which provide higher SNR and robustness in range doppler images13. Reference14proposed a machine learning based tracking filter performance improvement method in RDM images. Reference15Propose a repair method for RDM graph when clock is asynchronous. LEE K M introduced an a signal processing method for the reconstruction of the corrupted R-D map owing to the FMCW radar’s asynchronization15. Reference16 investigated the impact of multiple parameters on the delay waveform of the DDM (delay–Doppler map) in GNSS-R of sea waves. Liu C L applied the RDM of the spaceborne GNSS-R to realize the object detection of the target position on the sea surface. For detection, according to the generation principle of spaceborne DDM, research has realized its inverse process, that is, reconstructing the image of the scattering area from the DDM to achieve the purpose of detecting sea surface targets17. These methods optimize and reconstruct the characteristics of the RDM to solve problems, but these studies all focus on the direct signal which does not support for imaging, and the accuracy of the same satellite signal is limited and does not consider receiving multiple signals at the same time. Meanwhile, the characteristics of the RDM imaging are generally adopted in the commonly RDM improve algorithm, and the image processing method is employed to enhance the signal strength. In the literature18,19, a longer observation interval is used in exchange for a smaller scanning bandwidth in SAR radar imaging, which gains a higher range resolution. Reference20 proposes an upgraded theory and implementation method for fixed point attention technology for detecting small mobile drones by improving the R-D diagram. Compared with the general closed-loop overflow cancellation method, this method improves the SNR by 16.7dB. However, due to the fact that GNSS signals are continuous wave signals with very weak signal strength, the above method is only applicable to pulse wave signals or strong signal RDM enhancement methods in specific scenarios, and is not suitable for improving the SNR of GNSS reflection signal RDM spectra.Reference12 proposed a method to improve the SNR of RDM through image fusion and transfer. Firstly, in the distance compression process, the distance is divided into multiple small segments based on the time trajectory for compression. Then, each segment is imaged separately, and distance compensation and Doppler compensation are performed separately after imaging. The SNR of the image is improved by 4.3dB. However, the above method compensates at the later stage of image processing and does not take into account the RDM noise caused by the cross-correlation of GNSS signals, nor does it utilize the unique advantages of GNSS signals and dual base acquisition models.

In this paper, GNSS reflected signal model is proposed, which adopted mixed satellite signals. In addition, RDM spectral noise reduction is realized by successively deducting correlated noise level.

In this paper, the GNSS radar bistatic model is used for object detection detection of moving targets in the air. The main innovations are as follows:

  1. (1)

    Improvement of the SNR of the moving target RDM so that the improvement of the detection accuracy, the noise power of the GNSS RDM is reduced, and the detectability of the moving target is improved.

  2. (2)

    Different from the improved signal source in radar moving targets or the RDM noising decrease algorithm, which based on prior background noise, the proposed algorithm successively deducts correlated noise level after performing range compressions, which is suitable for radars with multiple transmitters.

GNSS passive radar dynamic target object detection method

GNSS radar object detection model

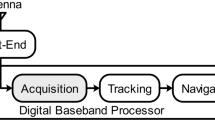
The GNSS radar object detection model is shown in Fig. 1. This model adopts the bistatic radar signal receiver. The signal transmitting source is the GNSS satellite, and the object detection target is the air target, such as an aircraft or drone group. The receiving rack is located on the ground, and it is divided into two channels -direct and reflected channels, which collect signals at the same time. The direct signal is received by a right-handed circularly polarized (RHCP) antenna, and the reflected signal is received by a left-handed circularly polarized (RHCP) antenna.

Fig. 1
figure 1

GNSS radar object detection model.

Full size image

GNSS radar moving target RDM imaging principle

Suppose the GNSS signal representation is shown in Eq. (1), where A represents the signal amplitude, i represents the satellite number, C represents the pseudo random noise code, D represents the navigation bit, f represents the doppler frequency, P represents the carrier phase, and n represents the background noise.

$$\:{\text{S}}^{\text{i}}(\text{t},{\upmu\:})=\text{A}{\text{C}}^{\text{i}}(\text{t},{\upmu\:}){\text{D}}^{\text{i}}\left(\text{t}\right)\cdot\:\text{exp}(\text{j}\left(2{\uppi\:}\text{f}\text{t}\right)+\text{P}\left({\upmu\:}\right))+\text{n}(\text{t},{\upmu\:})$$
(1)

Then, the representative formulas of the GNSS direct signal and reflected signal are (2) and (3), respectively:

$$\:{\text{S}}_{\text{D}}^{\text{i}}(\text{t},{\upmu\:})={\text{A}}_{\text{D}}{\text{C}}^{\text{i}}(\text{t},{\upmu\:}){\text{D}}^{\text{i}}\left(\text{t}\right)\cdot\:\text{exp}(\text{j}\left(2{\uppi\:}{\text{f}}_{\text{D}}\text{t}\right)+{\text{P}}_{\text{D}}\left({\upmu\:}\right))+{\text{n}}_{\text{D}}(\text{t},{\upmu\:})$$
(2)
$$\:{\text{S}}_{\text{F}}^{\text{i}}(\text{t},{\upmu\:})={\text{A}}_{\text{F}}{\text{C}}^{\text{i}}(\text{t},{\upmu\:}){\text{D}}^{\text{i}}\left(\text{t}\right)\cdot\:\text{exp}(\text{j}\left(2{\uppi\:}{\text{f}}_{\text{F}}\text{t}\right)+{\text{P}}_{\text{F}}\left({\upmu\:}\right))+{\text{n}}_{\text{F}}(\text{t},{\upmu\:})$$
(3)

The RDM consists of the distance domain of the abscissa and the doppler domain of the ordinate, and the distance domain is obtained by matched filtering, which is the echo signal is subjected to the Fourier transform operation, then operate autocorrelation with the Fourier transform of the local signal that is generated with the receiver. After that, doppler domain is the Fourier result of the distance domain in the azimuth direction.

From this, the expressions of the distance dimension and doppler dimension are shown in Eq. (4) and Eq. (5) respectively. Where\(\:{\text{S}}_{\text{r}}^{\text{i}}\) represents the reflected signal,\(\:{\text{S}}_{\text{r}\text{e}\text{f}}\) indicates the synchronized local signal,\(\:\text{C}{\text{F}}_{\text{R}}\) represents the distance compression pulse,\(\:{\text{D}}_{\text{R}}\) represents navigation data,\(\:{{\upomega\:}}_{\text{e}}\) represents the doppler frequency of each range domain,\(\:{\Phi\:}\) represents the carrier phase, and T is the observation time of the moving target.

$$\:{\text{S}}_{\text{R}}^{\text{i}}\left(\text{t},{\upmu\:}\right)={\text{S}}_{\text{F}}^{\text{i}}\left(\text{t},{\upmu\:}\right){\text{S}}_{\text{r}\text{e}\text{f}}^{\text{i}}\left(\text{t},{\upmu\:}\right)=\text{C}{\text{F}}_{\text{R}}\left[{\text{t}}_{\text{i}}-{\uptau\:}\left({\upmu\:}\right)\right]{\text{D}}_{\text{R}}\left[{\text{t}}_{\text{i}}-{\uptau\:}\left({\upmu\:}\right)\right]\text{e}\text{x}\text{p}\left(\text{j}\left({{\upomega\:}}_{\text{e}}\left({\upmu\:}\right){\text{t}}_{\text{i}}+{\Phi\:}\left({\upmu\:}\right)\right)\right)$$
(4)
$$\begin{aligned} \:{\text{S}}_{{{\text{doppler}}}} & = \int\limits_{{ - {\text{T}}/2}}^{{{\text{T}}/2}} {{\text{CF}}_{{\text{P}}} \left( {{\text{t}}_{{\text{i}}} - \tau \left( \mu \right)} \right){\text{D}}_{{\text{P}}} \left( {{\text{t}}_{{\text{i}}} } \right) \cdot {\text{exp}}\left( {{\text{j}}\left( {\omega _{{\text{e}}} \left( \mu \right){\text{t}}_{{\text{i}}} + \Phi \left( \mu \right)} \right)} \right) \cdot {\text{exp}}\left( { - {\text{j}}\omega \mu } \right){\text{d}}\mu } \\ & = \int\limits_{{ - {\text{T}}/2}}^{{{\text{T}}/2}} {{\text{CF}}_{{\text{P}}} \left( {{\text{t}}_{{\text{i}}} - \tau \left( \mu \right)} \right){\text{D}}_{{\text{P}}} \left( {{\text{t}}_{{\text{i}}} } \right) \cdot {\text{exp}}\left( {{\text{j}}\left( {\omega _{{\text{e}}} \left( \mu \right){\text{t}}_{{\text{i}}} - \omega \mu + \Phi \left( \mu \right)} \right)} \right){\text{d}}\mu } \\ \end{aligned}$$
(5)

In the azimuth compression process of generating RDM spectra, Fourier transform is required to transform the signal into the frequency domain. However, the Doppler frequencies of stationary and moving objects are different, so there is a clear distinction between the RDM spectra of stationary and moving objects.

RDM noise reduction algorithm

In the algorithm, it is necessary to simultaneously receive signals from several satellites. Due to different satellite orbit heights and attitudes and the space interference encountered by signals to the ground, the strength of the received navigation reflection signals also varies greatly. In this paper, through select weak signals and strong signals to purify the noise based on the autocorrelation characteristics of the GNSS codes of the signals should be feasible. Then the noise of strong signals can be cancelled by purified noise. The flowchart of the algorithm idea is shown in Fig. 2. First, the received satellite signal is been capturing and tracking, then the high-frequency carrier component generated by the strong signal demodulation and the pseudorandom code correlation operation component information of the two satellites are obtained. In the third step, the signal is been noise reduced operated by autocorrelation characteristics of GNSS code. The signal is then circled by recaptured, tracked, and noise-reduced again. The signal noise is significantly reduced after two to three cycles commonly. The number of cycles is set according to the performance and efficiency of processing equipment.

Fig. 2
figure 2

Flow chart of the RDM noise reduction algorithm.

Full size image

The specific steps of the algorithm are as follows:

  1. (1)

    Assume that the weak signal is received by the No. 1 satellite, and the strong signal that needs to cancel the noise is received by the No. 2 satellite. The signal Equation are expressed as (6) and (7), where the amplitude and code phase of the No. 1 and No. 2 satellites are\(\:{\text{A}}_{1},{\text{A}}_{2}\) and \({\text{PN}}_{1} ({\text{t}}),{\text{PN}}_{2} ({\text{t}})\) respectively, the doppler frequency are \(\cos \;\upomega _{1} {\text{t,}}\cos \;\upomega _{2} {\text{t}}\), i represents the satellite number of any other satellite, r(t) represents the received signal, PN(t) represents the pseudo random code, n(t) represents the simulated signal noise, and t is the acquisition time.

    $$\:\text{r}\left(\text{t}\right)\text{P}{\text{N}}_{1}\left(\text{t}\right)={\text{A}}_{1}\text{cos}{{\upomega\:}}_{1}\text{t}+{\sum\:}_{\text{i}=2}^{\text{N}}{\text{A}}_{\text{i}}\text{P}{\text{N}}_{\text{i}}\left(\text{t}\right)\cdot\:\text{cos}{{\upomega\:}}_{1}\text{t}\cdot\:\text{P}{\text{N}}_{1}\left(\text{t}\right)+\text{n}\left(\text{t}\right)\text{P}{\text{N}}_{1}\left(\text{t}\right)$$
    (6)
    $$\begin{gathered} \:{\text{r}}\left( {\text{t}} \right){\text{PN}}_{2} \left( {\text{t}} \right) = {\text{A}}_{2} {\text{cos}}\omega _{2} {\text{t}} \hfill \\ + \sum\limits_{{{\text{i}} = 3}}^{{\text{N}}} {{\text{A}}_{{\text{i}}} {\text{PN}}_{{\text{i}}} \left( {\text{t}} \right) \cdot {\text{cos}}\omega _{1} {\text{t}} \cdot {\text{PN}}_{2} \left( {\text{t}} \right) + {\text{A}}_{1} {\text{cos}}\omega _{1} {\text{t}} \cdot {\text{PN}}_{1} \left( {\text{t}} \right){\text{PN}}_{2} \left( {\text{t}} \right) + {\text{n}}\left( {\text{t}} \right){\text{PN}}_{2} \left( {\text{t}} \right)} \hfill \\ \end{gathered}$$
    (7)
  2. (2)

    Equation (8) can be obtained by deforming Eq. (7), after the GNSS signal is captured and tracked, “\({\text{A}}_{2} \cos \;\upomega _{2} {\text{t}}\)”, “\({\text{A}}_{1} \cos \;\upomega _{1} {\text{t}} \cdot {\text{PN}}_{{\text{2}}} {\text{(t)}} \cdot {\text{PN}}_{{\text{2}}} {\text{(t)}}\)” can be obtained in Eq. (9).

    $$\begin{gathered} \:{\text{r}}\left( {\text{t}} \right){\text{PN}}_{2} \left( {\text{t}} \right) - {\text{A}}_{2} {\text{cos}}\omega _{2} {\text{t}} - {\text{A}}_{1} {\text{cos}}\omega _{1} {\text{t}} \cdot {\text{PN}}_{1} \left( {\text{t}} \right){\text{PN}}_{2} \left( {\text{t}} \right) \hfill \\ = \sum\limits_{{{\text{i}} = 3}}^{{\text{N}}} {{\text{A}}_{{\text{i}}} {\text{PN}}_{{\text{i}}} \left( {\text{t}} \right) \cdot {\text{cos}}\omega _{{\text{i}}} {\text{t}} \cdot {\text{PN}}_{2} \left( {\text{t}} \right) + {\text{n}}\left( {\text{t}} \right){\text{PN}}_{2} \left( {\text{t}} \right)} \hfill \\ \end{gathered}$$
    (8)
  3. (3)

    Assume that there is no cross-correlation relationship between No. 3-N satellites, that is, \(\sum\nolimits_{{{\text{i}} = 3}}^{{\text{N}}} {{\text{A}}_{{\text{i}}} {\text{PN}}_{{\text{i}}} ({\text{t}}) \cdot \cos \;\upomega _{{\text{i}}} {\text{t}} \cdot {\text{PN}}_{2} ({\text{t}}) = 0.}\) According to the generation rule of the autocorrelation characteristic in GNSS code, it can be obtained that \({\text{n}}({\text{t}}) \cdot {\text{PN}}_{2} ({\text{t}}) \cdot {\text{PN}}_{2} ({\text{t}}) = {\text{n}}({\text{t}})\) which is the pure noise signal of the No. 1 satellite. On this basis, this feature is used to cancel the noise of the No. 2 satellite signal.

  4. (4)

    Through tracking \({\text{r}}({\text{t}}) - {\text{n}}({\text{t}})\) again and estimating the carrier phase, the carrier phase with higher accuracy is obtained to generate the RDM.

  5. (5)

    Cycle steps (1)-(4)again, after 2–3 cycles, the cross-correlation parameters of the No. 3-N satellites are further canceled, and the SNR of RDM generated by No. 2 satellite increases significantly.

The method in the previous section takes advantage of the autocorrelation properties of GNSS codes and the forward scatter signal that is discarded in general is been exploited. The main purified noise is the cross-correlation interference noise of the GNSS signal. The SINR(Signal to Interference plus Noise Ratio) before and after noise reduction are derived as follows.

From Eq. (6), the SINR of satellite No. 1 before the noise reduction algorithm can be expressed as Eq. (9).

$$\:\text{S}\text{I}\text{N}{\text{R}}_{\text{s}\text{i}\text{g}\text{n}\text{a}\text{l}\_\text{b}\text{e}\text{f}\text{o}\text{r}\text{e}}=\frac{{\text{A}}_{1}\text{cos}{{\upomega\:}}_{1}\text{t}}{{\sum\:}_{\text{i}=2}^{\text{N}}{\text{A}}_{\text{i}}\text{P}{\text{N}}_{\text{i}}\left(\text{t}\right)\cdot\:\text{cos}{{\upomega\:}}_{\text{i}}\text{t}\cdot\:\text{P}{\text{N}}_{1}\left(\text{t}\right)+\text{n}\left(\text{t}\right)\text{P}{\text{N}}_{1}\left(\text{t}\right)}$$
(9)

In this noise reduction algorithm, it is assumed that the noise interference is divided into two parts: one is the interference caused by other satellites, and the other is Gaussian white noise. The core of this algorithm is to reduce or eliminate the interference caused by other satellites through the autocorrelation of the signal, and white noise still exists in the system. Therefore, the signal SINR after noise reduction can be expressed as Eq. (10).

$$\:\text{S}\text{I}\text{N}{\text{R}}_{\text{s}\text{i}\text{g}\text{n}\text{a}\text{l}\_\text{a}\text{f}\text{t}\text{e}\text{r}}=\frac{{\text{A}}_{1}\text{cos}{{\upomega\:}}_{1}\text{t}}{\text{n}\left(\text{t}\right)\text{P}{\text{N}}_{1}\left(\text{t}\right)}$$
(10)

Comparing Eq. (9) and Eq. (10), the interference noise of other satellites in the denominator basically disappears, and the SINR is obviously enhanced after the noise reduction algorithm adopted.

After RD imaging, the SINR of RDM before and after noising decreased can be expressed as Eqs. (11) and (12) respectively. Therefore, it can be concluded that the SINR of RDM spectrum before and after noise reduction is consistent with the SINR of the GNSS signal.

$$\:\text{S}\text{I}\text{N}{\text{R}}_{\text{R}\text{D}{\text{M}}_{\text{b}\text{e}\text{f}\text{o}\text{r}\text{e}}}={\int\:}_{-\text{T}}^{\text{T}}\frac{{\text{A}}_{1}\text{cos}{{\upomega\:}}_{1}\text{t}}{{\sum\:}_{\text{i}=2}^{\text{N}}{\text{A}}_{\text{i}}\text{P}{\text{N}}_{\text{i}}\left(\text{t}\right)\cdot\:\text{cos}{{\upomega\:}}_{\text{i}}\text{t}\cdot\:\text{P}{\text{N}}_{1}\left(\text{t}\right)+\text{n}\left(\text{t}\right)\text{P}{\text{N}}_{1}\left(\text{t}\right)}\text{d}\text{t}$$
(11)
$$\:\text{S}\text{I}\text{N}{\text{R}}_{\text{R}\text{D}{\text{M}}_{\text{a}\text{f}\text{t}\text{e}\text{r}}}={\int\:}_{-\text{T}}^{\text{T}}\frac{{\text{A}}_{1}\text{cos}{{\upomega\:}}_{1}\text{t}}{\text{n}\left(\text{t}\right)\text{P}{\text{N}}_{1}\left(\text{t}\right)}\text{d}\text{t}$$
(12)

Based on the derivation of SINR above, the probability of the detected object being identified in the RDM spectrum can be further derived. Assuming that the probability of no detecting the imaging GNSS signal is \(\:{\text{H}}_{0}\), then the expression before noise reduction is \(\:{\text{H}}_{0}\)shown in Eq. (13). If the power of intersymbol interference is \(\:{{\upsigma\:}}_{\text{i}}^{2}\), and the power of white noise is \(\:{{\upsigma\:}}_{1}^{2}\), then the mean value is 0, and the variance is \(\:\text{v}\text{a}\text{r}=\sum\:_{\text{i}=2}^{\text{N}}{{\upsigma\:}}_{\text{i}}^{2}+{{\upsigma\:}}_{1}^{2}\), then the false alarm probability threshold \(\:{\text{P}}_{\text{f}}\) is Eq. (14); The probability of detecting the imaging GNSS signal is \(\:{\text{H}}_{1}\), and the expression before noising reduction \(\:{\text{H}}_{1}\) is shown in Eq. (15), then the \(\:\text{m}\text{e}\text{a}\text{n}={{\upmu\:}}_{1}\), variance \(\:\text{v}\text{a}\text{r}=\sum\:_{\text{i}=2}^{\text{N}}{{\upsigma\:}}_{\text{i}}^{2}+{{\upsigma\:}}_{1}^{2}\), and false alarm probability threshold \(\:{\text{P}}_{\text{f}}\) is given in Eq. (16). Where \(\:\text{Q}\left({\cdot\:}\right)\) is the joint probability density function and \(\:{\upepsilon\:}\) is the signal detection threshold.

$$\:{\text{H}}_{{0}_{\text{b}\text{e}\text{f}\text{o}\text{r}\text{e}}}={\sum\:}_{\text{i}=2}^{\text{N}}{\text{A}}_{\text{i}}\text{P}{\text{N}}_{\text{i}}\left(\text{t}\right)\text{cos}{{\upomega\:}}_{\text{i}}\text{t}\cdot\:\text{P}{\text{N}}_{1}\left(\text{t}\right)+\text{n}\left(\text{t}\right)\text{P}{\text{N}}_{1}\left(\text{t}\right)$$
(13)
$$\:{\text{P}}_{{{\text{f}}_{0}}_{\text{b}\text{e}\text{f}\text{o}\text{r}\text{e}}}=\text{Q}\left(\frac{{\upepsilon\:}}{\sqrt{{\sum\:}_{\text{i}=2}^{\text{N}}{{\upsigma\:}}_{\text{i}}^{2}+{{\upsigma\:}}_{1}^{2}}}\right)$$
(14)
$$\:{\text{H}}_{{1}_{\text{b}\text{e}\text{f}\text{o}\text{r}\text{e}}}={\text{A}}_{1}\text{cos}{{\upomega\:}}_{1}\text{t}+{\sum\:}_{\text{i}=2}^{\text{N}}{\text{A}}_{\text{i}}\text{P}{\text{N}}_{\text{i}}\left(\text{t}\right)\text{cos}{{\upomega\:}}_{\text{i}}\text{t}\cdot\:\text{P}{\text{N}}_{1}\left(\text{t}\right)+\text{n}\left(\text{t}\right)\text{P}{\text{N}}_{1}\left(\text{t}\right)$$
(15)
$$\begin{aligned} & \:{\text{P}}_{{{\text{f}}_{{{\text{before}}}} }} = {\text{Q}}\left( {\frac{\upvarepsilon }{{\sqrt {\sum\nolimits_{{{\text{i}} = 2}}^{{\text{N}}} {\upsigma _{{\text{i}}}^{2} + \upsigma _{1}^{2} } } }}} \right) \\ & \:{\text{P}}_{{{\text{d}}_{{{\text{before}}}} }} = {\text{Q}}\left( {\frac{{\upvarepsilon - \mu _{1} }}{{\sqrt {\sum\nolimits_{{{\text{i}} = 2}}^{{\text{N}}} {\upsigma _{{\text{i}}}^{2} + \upsigma _{1}^{2} } } }}} \right) \\ & \:{\text{P}}_{{{\text{d}}_{{{\text{before}}}} }} = {\text{Q}}\left( {{\text{Q}}^{{ - 1}} \left( {{\text{P}}_{{{\text{f}}_{{{\text{before}}}} }} } \right) - \frac{{\mu _{1} }}{{\sqrt {\sum\nolimits_{{{\text{i}} = 2}}^{{\text{N}}} {\upsigma _{{\text{i}}}^{2} + \upsigma _{1}^{2} } } }}} \right) \\ \end{aligned}$$
(16)

After completing the noising reduction algorithm, the probability of no detecting imaging GNSS signal \(\:{\text{H}}_{0}\) is expressed in Eq. (17), and then the expression after noising reduction \(\:{\text{H}}_{1}\)is shown in Eq. (18). Assuming mean = 0 and variance\(\:\text{v}\text{a}\text{r}={{\upsigma\:}}_{1}^{2}\), the false alarm probability threshold \(\:{\text{P}}_{\text{f}}\) is expressed in Eq. (19), The probability of detecting the imaging GNSS signal is \(\:{\text{P}}_{\text{d}\text{a}\text{f}\text{t}\text{e}\text{r}}\) shown in Eq. (20), and the relationship between \(\:{\text{P}}_{\text{d}}\) and \(\:{\text{P}}_{\text{f}}\) is shown in Eq. (21).

$$\:{\text{H}}_{{0}_{\text{a}\text{f}\text{t}\text{e}\text{r}}}=\text{n}\left(\text{t}\right)\text{P}{\text{N}}_{1}\left(\text{t}\right)$$
(17)
$$\:{\text{H}}_{{1}_{\text{a}\text{f}\text{t}\text{e}\text{r}}}={\text{A}}_{1}\text{cos}{{\upomega\:}}_{1}\text{t}+\text{n}\left(\text{t}\right)\text{P}{\text{N}}_{1}\left(\text{t}\right)$$
(18)
$$\:{\text{P}}_{{\text{f}}_{\text{a}\text{f}\text{t}\text{e}\text{r}}}=\text{Q}\left(\frac{{\upepsilon\:}}{{{\upsigma\:}}_{1}}\right)$$
(19)
$$\:{\text{P}}_{{\text{d}}_{\text{a}\text{f}\text{t}\text{e}\text{r}}}=\text{Q}\left(\frac{{\upepsilon\:}-{{\upmu\:}}_{1}}{{{\upsigma\:}}_{1}}\right)$$
(20)
$$\:{\text{P}}_{{\text{d}}_{\text{a}\text{f}\text{t}\text{e}\text{r}}}=\text{Q}\left({\text{Q}}^{-1}\left({\text{P}}_{{\text{f}}_{\text{a}\text{f}\text{t}\text{e}\text{r}}}\right)-\frac{{{\upmu\:}}_{1}}{{{\upsigma\:}}_{1}}\right)$$
(21)

Assume \({\text{P}}_{{{\text{f}}_{{{\text{before}}}} }} = {\text{P}}_{{{\text{f}}_{{{\text{after}}}} }} = {\text{P}}_{{\text{f}}}^{0} ,\) then \({\text{P}}_{{{\text{d}}_{{{\text{before}}}} }} = {\text{Q}}\left( {{\text{Q}}^{{ - 1}} \left( {{\text{P}}_{{\text{f}}}^{0} } \right) - \frac{{\mu _{1} }}{{\sqrt {\sum\nolimits_{{{\text{i}} = 2}}^{{\text{N}}} {\sigma _{{\text{i}}}^{2} + \sigma _{1}^{2} } } }}} \right),\)\(\:{\text{P}}_{{\text{d}}_{\text{a}\text{f}\text{t}\text{e}\text{r}}}=\text{Q}\left({\text{Q}}^{-1}\left({\text{P}}_{\text{f}}^{0}\right)-\frac{{{\upmu\:}}_{1}}{{{\upsigma\:}}_{1}}\right)\).

As the function \(\:{\text{Q(}} \cdot {\text{)}}\)is decreasing function, when\(\:{\text{P}}_{\text{f}}\) is fixed, \(\:\frac{{{\upmu\:}}_{1}}{\sqrt{{\sum\:}_{\text{i}=2}^{\text{N}}{{\upsigma\:}}_{\text{i}}^{2}+{{\upsigma\:}}_{1}^{2}}}<\frac{{{\upmu\:}}_{1}}{{{\upsigma\:}}_{1}}\), then \(\:{\text{P}}_{{\text{f}}_{{1}_{\text{a}\text{f}\text{t}\text{e}\text{r}}}}>{\text{P}}_{{\text{f}}_{{1}_{\text{b}\text{e}\text{f}\text{o}\text{r}\text{e}}}}\). So the probability of detecting targets after noise reduction is higher.

According to Eqs. 16 and 21, the relationship between the false alarm probability threshold Pf and the probability Pd of detecting imaging GNSS signals before improving the algorithm is shown in Fig. 3. It can be seen that the probability of detecting imaging GNSS signals after algorithm improvement is higher than before improvement.

Fig. 3
figure 3

The relationship between the false alarm probability threshold Pf and the probability Pd of detecting imaging GNSS signals.

Full size image

Testing and analysis

The experiment simulates the motion of the satellite, the measured object is stationary which moves relative to the satellite. In real detection scenarios, it is generally assumed that the satellite is stationary and the detection target moves. In both situations, the actual object detection is the doppler frequency shift caused by the relative motion between the satellite and the detection target. The simulation is include Beidou signal and GPS signal.

Beidou signal simulation

The specific parameters of the simulated satellite signal are shown in Table 1. Since the simulated Beidou B2 signal is divided into I channel and Q channel demodulation and noise reduction is performed on the two signals, so the RDM diagram of the two signals can be obtained.

Table 1 Analog satellite parameters.
Full size table

According to the above scheme, MATLAB is used to simulate the signals of the I branch and the Q branch of the Beidou-2 moving satellite. Figure 4(a) is the B2 satellite signal before noise reduction. Blue represents the I branch, and red represents the Q branch. Figure 4(b) is the B2 satellite signal after two noise reduction cycles, and it is concluded that the signal noise is significantly reduced after the cycle.

Fig. 4
figure 4

Simulation results of the RDM noise reduction algorithm. (a) B2 signal before noise reduction, (b) B2 signal after noise reduction.

Full size image

The obtained B2 signal is subjected to moving target detection. Figure 5 is RDM spectrum which is generated from B2 signal. Figure 5(a) is the RDM spectrum generated before noise reduction. There is a blur in the doppler domain at 2000 Hz and 3000 Hz. The doppler shift straight line. The three-dimensional doppler image is shown in Fig. 5(b), the amplitude is relatively narrow. Figure 6(a) is the RDM spectrum generated by noise reduced signal for moving target detection. The doppler spectrum of the I branch and the Q branch is very clear. The 3D doppler image is shown in Fig. 6(b), and the signal amplitude is greatly improved.

Fig. 5
figure 5

RDM graph by Beidou B2 original signal. (a) Original RDM graph, (b) original 3D RDM graph.

Full size image
Fig. 6
figure 6

RDM map by Beidou B2 signal after noise reduction. (a) RDM graph after noise reduction, (b) original 3D RDM graph.

Full size image

GPS signal simulation

The GPS simulation parameters are shown in Table 2, and the simulation is basically consistent with the basic parameters of the Beidou signal.

Table 2 GPS analog satellite parameter.
Full size table

The signal results before and after the noise reduction of the GPS I and Q signals are shown in Fig. 7. It can be seen that the algorithm is also significantly reduced after the cycle for GPS signal denoising.

Fig. 7
figure 7

Simulation results of the RDM noise reduction algorithm. (a) GPS signal before noise reduction, (b) GPS signal after noise reduction.

Full size image

The obtained GPS signal is subjected to moving target detection and the RDM spectrum is generated for analysis. The original signal and generated RDM of the denoised signal as shown in Figs. 8 and 9 respectively.

Fig. 8
figure 8

RDM map generated by GPS signal. (a) Original RDM, (b) Original 3D RDM.

Full size image
Fig. 9
figure 9

RDM generated by GPS signal after noise reduction. (a) Original RDM, (b) 3D RDM.

Full size image

Analysis of imaging results

The RDM imaging estimated by image contrast or image entropy to analyze effect. Image entropy is calculated as follows. Assuming that P(E) is the probability of occurrence of an I(E) event, in the RDM diagram, P(E) is the probability of detecting the occurrence of a target I(E) event. Then, the relationship between I(E) and P(E) is shown in Eq. (12). If P(E) = 1, it means that there is required information which is the target is detected. When P(E) = 0, it means that the required information does not occur, that is, the target is not detected. Suppose that each discrete point in the RDM graph is; then, the probability associated with it is. The information entropy of the image can be expressed as Eq. (13).

$$\:\text{I}\left(\text{E}\right)=\text{l}\text{o}\text{g}\frac{1}{\text{P}\left(\text{E}\right)}=-\text{l}\text{o}\text{g}\text{P}\left(\text{E}\right)$$
(12)
$$\:\text{H}\left(\text{x}\right)=-\sum\:_{\text{i}=1}^{\text{n}}\text{P}\left({\text{e}}_{\text{i}}\right)\times\:\text{l}\text{o}\text{g}\text{P}\left({\text{e}}_{\text{i}}\right)$$
(13)

From Eq. (12) and Eq. (13), it can be obtain that the less information detected in the image, the smaller value of H(x). In addition, the more information the image contains, and the more likely the target is to be detected. Since the image is composed of three degrees of red (Red), green (Green), and blue (Blue), information entropy of the image can be analyzed by calculating the three colors separately. The calculated information entropy of the Beidou signal and the GPS signal RDM map are shown in Tables 3 and 4, respectively. The image information entropy decreased by 71.69% and 63.23%, respectively. The noise reduction effect of the Beidou signal is better than that of GPS.

Table 3 Analysis of RDM information entropy in BD signal.
Full size table
Table 4 Analysis of RDM information entropy in GPS signal.
Full size table

Comparative analysis of carrier phase compensation algorithms

Based on simulation data, a 35dB background noise is simulated for satellites 3 and 4. Using the carrier phase compensation method described in reference 12, the demodulated signal is divided into 5 sub matrices along the time axis, and each matrix is compressed in the distance direction to obtain 5 compressed distance maps. The azimuth grids in the 5 maps are aligned, and then the 5 maps are merged and compressed in the azimuth direction to generate RDM maps. The RDM spectrum obtained from simulation is shown in Fig. 10.

Fig. 10
figure 10

RDM spectrum after carrier phase compensation.

Full size image

Compared with the RDM generated by the original signal in Fig. 8, the signal in Fig. 10 was not enhanced. Instead, the signal noise was amplified due to accumulation. The information entropy of the RDM image after motion compensation is shown in Table 5. The information entropy of the image after motion compensation not only did not decrease, but also doubled, which is the result of noise accumulation. Therefore, carrier phase compensation is not suitable for noise cancellation environments caused by cross-correlation in GNSS signals, but only for situations where the carrier frequency moves irregularly during imaging. This method may introduce more environmental noise in GNSS reflected signal imaging.

Table 5 Comparison of image entropy of motion compensation methods under 35 dB noise environment.
Full size table

Conclusion

In this paper, a GNSS passive radar moving target noise reduction algorithm is studied. After simulation, it is concluded that the algorithm can reduce the RDM image entropy. In the GNSS passive radar moving target detection model, the relative motion of the satellite and the detected target is simulated by simulating the satellite motion, the doppler frequency shift in the signal is detected, and the motion state is calculated. The main theory of the noise reduction algorithm is to use successively deducting the noise term in GNSS signals to perform cyclic noise reduction and apply it to GNSS radar moving target detection. After looping the algorithm three times, the simulation results show that the RDM image entropy decline rate of moving targets is greater than 50%. Since the current research on GNSS passive radar mainly focuses on static targets, this paper studies the improvement of the detection accuracy of GNSS passive radar dynamic targets. The results show that the detection range of moving targets is significantly enhanced under weak signals. It should be noted that the results of this paper are based on simulation, and the measured signals are problematic and challenging, such as receiving multiple satellites at the same time, satellites and detection targets, and the angle of the receiving antenna. In the future, the team will continue to carry out actual measurements in this direction. GNSS signals verify the feasibility of this algorithm.