Introduction

Partial Differential Equations (PDEs) have a crucial role in mathematics and its numerous applications, as demonstrated by the scientific revolution sparked by Isaac Newton’s calculus. In particular, Nonlinear PDEs (NPDEs) have been used to model many important physical phenomena including Maxwell equation in electromagnetism1, Schrödinger equation in quantum mechanics2, Navier–Stokes, Euler and Kadomstev-Petviashvili equations in fluid mechanics3,4,5, Eikonal equation and Maxwell–Bloch equations in optics6,7, Vlasov equation in plasmas8, Ginzburg–Landau equation in superconductivity9, Lamé and von Karman equations in elasticity10,11, FitzHugh-Nagumo equation in neuroscience12, Black-Scholes equation in finance13, Kolmogorov–Petrovsky-Piskounov in chemical reactions14, Korteweg-de Vries (KdV)equation and modified KdV equation15,16, stochastic KdV equation17 and many more18,19,20. The problem is that, although their derivation as physical models such as classical, quantum, and relativistic etc. are generally well-established, the majority of the resulting PDEs are infamously challenging to solve, and only a select few can be considered fully understood. Many times, the creation of so-called sophisticated numerical approximation schemes–a significant and ongoing field in and of itself–is the only way to compute and comprehend their solutions21,22,23. The analytical and numerical approaches to the subject are closely related since one cannot advance much on their numerical aspects without having a thorough understanding of the underlying analytical features.

Since soliton theories offers significant new insights into the nuances of nonlinear models, accurate solutions of NPDEs—particularly the computing of travelling wave and soliton solutions—are crucial to the research and application of soliton theory in mathematical physics and engineering. Many useful techniques have been created to get soliton solutions for comprehending how these nonlinear models physically operate, which will aid engineers and various other professionals as well as assist them learn more regarding physical issues and their potential uses. Using symbolic computer programmes like Matlab, Maple, Mathematica, and others that simplify difficult algebraic computations, there has been a growing interest in offering accurate soliton solutions for NPDEs in recent years. Several analytical techniques to find novel soliton solutions may be discovered in the literature, including Sine-Gordon method24, Riccati-Bernoulli Sub-ODE method25, Khater method26, \((G'/G)\) -expansion method27,28,29,30, sub-equation method31, exp-function method32, Sardar sub-equation method33, Poincaré–Lighthill–Kuo method34, Extended Direct Algebraic Method (EDAM)35,36,37,38,39,40, Hirota’s bilinear method41, Kudryashov method42, generalized exponential rational function method43,44,45, generalized Riccati equation mapping method46, improved F-expansion approach47, extended modified auxiliary equation mapping method48, Kumar-Malik method49 among others.

The goal of the current study is to present RMESEM and the Hamiltonian system in order to get soliton solutions for the MZKE discrete nonlinear transmission line problem. The formation of weakly nonlinear ion-acoustic waves inside plasma with hot isothermal electrons as well as cold ions in the midst of a uniform magnetic field in the x-direction is one of the many phenomena that this model sheds light on50,51,52. It is possible to utilise this particular model to explain a wide range of technological, mechanical, and physical processes. As an example system for investigating nonlinear excitations, electrical transmission lines, as seen in Figure 1, exhibit nonlinear behaviour within nonlinear media.

Fig. 1
figure 1

Representation of nonlinear electrical transmission line.

Full size image

Mathematical modelling of MZKE

The nonlinear electrical transmission line’s construction relies on either periodic loading of the var-actors or the arrangement of inductors and var-actors in a one-dimensional lattice. This model consists of a dispersive transmission line and a nonlinear network with several nonlinear LC couplings. As seen in Fig. 1, each line in the shunt branch has a nonlinear capacitor with capacitance \(C(\phi _p,q)\) and a conductor L. At each node, there are many dispersive lines that are identical and connected by capacitance \(C_s\). Duan developed the MZKE by applying the Kirchhoff law to the model. The discrete nonlinear transmission is represented mathematically in fractional form as follows53:

$$\begin{aligned} \frac{\partial ^{2} R_{q,p}}{\partial S^{2}}= \frac{\partial ^{2}}{\partial S^{2}}(\phi _{q,p-1}+\phi _{q,p+1}-2\phi _{q,p})C_s+\frac{1}{L}(\phi _{q,p-1}+\phi _{q,p+1}-2\phi _{q,p}). \end{aligned}$$
(1)

The voltage is represented by \(\phi _{q,p}\), a function of S, and the nonlinear charge may be computed as follows:

$$\begin{aligned} R_{p,q}=(\frac{\beta _2\phi ^3_{p,q}}{3}+\frac{\beta _1\phi ^2_{p,q}}{2}+\phi _{p,q})C_0, \end{aligned}$$
(2)

where the unknown invariables \(\beta _1\) and \(\beta _2\) are. Adding (2) to (1) results in:

$$\begin{aligned} \begin{aligned}&C_0\frac{\partial ^{2} }{\partial S^{2}}(\frac{\beta _2 \phi ^3_{p,q}}{3}+\frac{\beta _1 \phi ^2_{p,q}}{2}+\phi _{p,q})= \frac{\partial ^{2}}{\partial S^{2}}(\phi _{p-1,q}+\phi _{p+1,q}-2\phi _{p,q})C_s+\frac{1}{L}(\phi _{p-1,q}+\phi _{p+1,q}-2\phi _{p,q}), \end{aligned} \end{aligned}$$
(3)

replacing \(\phi _{p,q}(S)=\phi (S,p,q)\) yields

$$\begin{aligned} C_0\frac{\partial ^{2} }{\partial S^{2}}(\frac{\beta _2 \phi ^3}{3}+\frac{\beta _1 \phi ^2}{2}+\phi )=C_s\frac{\partial ^{4} (\frac{1}{12}\frac{\partial ^{2}\phi }{\partial q^{2}}+\phi )}{\partial q^{2} \partial S^{2}}+\frac{1}{L}\frac{\partial ^{2}(\frac{1}{12}\frac{\partial ^{2}\phi }{\partial p^{2}}+\phi )}{\partial p^{2}}. \end{aligned}$$
(4)

Reductive perturbation theory allows for the reduction of (4) to the subsequent model:

$$\begin{aligned} \psi _t+f_1 \psi \psi _x+q_1 \psi ^2 \psi _x+d \psi _{xxx}+g \psi _{xyy}=0, \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned}&t=\sqrt{\gamma }S, \quad x=\sqrt{\gamma }(p-v_s S), \quad y= q\sqrt{\gamma },d=\frac{1}{24 v_s L \beta \beta _1}, \quad g=\frac{\beta _1}{288 L^2C^2_0 v_s}, \\&v^2_s=\frac{1}{L C_0}, \quad \phi (S,p,q)=\gamma \psi (t,x,y), \quad f_1= - \beta _1 v_s, \quad q_1=q=-\beta _2 v_s.\\ \end{aligned} \end{aligned}$$
(6)

Before this study, several previous studies used various methods to address the targeted MZKE. For instance, Yu et al. used a Duffing-type equation as simplest auxiliary equation to study exact traveling wave solutions of the Zakharov-Kuznetsov Equation (ZKE), MZKE and their generalized forms using a version of the simplest equation method54. In another study, Ray and Sahoo constructed some analytical exact solutions of fractional ZKE and MZKE in Jumarie’ modified Riemann-Liouville sense by using fractional sub-equation method55. Raut et al. in56 investigated the generalized forms of ZKE and MZKE in the presence of external periodic forcing term together with damping. An array of approximate analytical solutions such as rare effective soliton, positive amplitude soliton, kink type soliton, periodic rational soliton, etc. is obtained by employing the direct assumption technique. Finally, the modified (G’/G)-expansion method has been applied by Islam et al. to seek novel computational results for MZKE in electrical engineering57. Nevertheless, the generation of solitary and twinning kink soliton solutions has not been examined and assessed in the context of the desired model utilizing RMESEM. This claim draws attention to a significant void in the corpus of existing literature. By providing a comprehensive model analysis and describing the recommended RMESEM methodology, our study closes this gap. We introduce RMESEM, which is a unique and useful method among the many analytical approaches. This approach is a modified version of the Modified Simple Equation Method (MSEM)58, which combines the well-known Riccati Nonlinear Ordinary Differential Equation (NODE) with MESEM. RMESEM effectively handles MZKE by converting it into more manageable NODE. For the resulting NODE, a closed form solution using Riccati-NODE is expected, which reduces the NODE into a set of algebraic equations. New families of soliton solutions for the desired MZKE are produced by using Maple to solve the resulting system. These solutions take the form of exponential, rational, hyperbolic, trigonometric, and rational-hyperbolic functions. Three-dimensional, contour, and two-dimensional graphs are used to graphically depict the wave behavior of various soliton solutions. The profiles of kink solitons, such as bell-shaped, lump-like, twinning, and perturbed kinks, are notably displayed by the discovered solitons, according to these graphs. By offering valuable insights into the dynamics and behavior of the MZKE, the acquired results advance our knowledge of the model and its possible applications in related fields.

The other sections of the paper are organised as follows: In “The description of RMESEM”, the RMESEM’s research approach is briefly explained. “Establishing kink soliton solutions for MZKE” presents the developed kink soliton solutions. In “Discussion and graphs”, we present the propagating dynamics of a few kink solitons visually and discuss them in great detail. We conclude our investigation in “Conclusion”.

The description of RMESEM

The literature has established a wide range of analytical methods to study soliton occurrences in nonlinear models59,60,61,62,63. In this part, we describe the operation mechanism of the improved RMESEM. Examining the ensuing general NPDE:

$$\begin{aligned} R( {\psi }, {\psi }_t, {\psi }_{w_1}, {\psi }_{w_2}, {\psi } {\psi }_{w_1}, \ldots )=0, \end{aligned}$$
(7)

where \({\psi }={\psi }(t,w_1,w_2,w_3,\ldots ,w_r)\).

The following steps will be taken in order to solve Eq. (7):

  1. 1.

    The variable-form wave transformation \({\psi }(t,w_1,w_2,w_3,\dots ,w_r)={\Psi }(\varsigma )\) is first carried out. There are several ways to represent \(\varsigma\). In this approach, Eq. (7) is modified to obtain the following NODE:

    $$\begin{aligned} Q({\Psi },{\Psi }'{\Psi },{\Psi }',\dots )=0, \end{aligned}$$
    (8)

    where \({\Psi }'=\frac{d {\Psi }}{d\varsigma }\). On occasion, the NODE may be made to comply with the homogeneous balance requirement by using integrating Eq. (8).

  2. 2.

    The solution of the extended Riccati-NODE is then used to propose the series-based solution for the NODE in (8):

    $$\begin{aligned} {\Psi }(\varsigma )=\sum _{{m}=0}^{{\kappa }}\omega _{m} \left( \frac{\zeta '(\varsigma )}{\zeta (\varsigma )}\right) ^{m}+ \sum _{{{m}}=0}^{{\kappa }-1}\delta _{{m}} \left( \frac{\zeta '(\varsigma )}{\zeta (\varsigma )}\right) ^{{m}} \cdot \left( \frac{1}{\zeta (\varsigma )} \right) . \end{aligned}$$
    (9)

    Here, the solution to the resultant extended Riccati-NODE is denoted by \(\zeta (\varsigma )\), and the unknown constants that need to be found later are represented by the variables \(\omega _{m} ({m}=0,...,{\kappa })\) and \(\delta _{{m}} ({{m}}=0,...,{\kappa }-1)\).

    $$\begin{aligned} \zeta '(\varsigma )={\lambda }+{\mu } \zeta (\varsigma )+{\nu }(\zeta (\varsigma ))^2, \end{aligned}$$
    (10)

    where \({\lambda },{\mu }\) and \({\nu }\) are constants.

  3. 3.

    The positive integer \({\kappa }\) needed in Eq. (9) may be obtained by homogeneously balancing the highest-order derivative and the biggest nonlinear component in Eq. (8).

  4. 4.

    Then, all the components of \(\zeta (\varsigma )\) are combined into an equal ordering when (9) is integrated into (8) or the equation that emerges from the integration of (8). When this process is used, an expression in terms of \(\zeta (\varsigma )\) is generated. By setting the coefficients in this equation to zero, we obtain an algebraic system of equations defining the variables \(\omega _{m} ({m}=0,...,{\kappa })\) and \(\delta _{{m}} ({{m}}=0,...,{\kappa }-1)\) with other related parameters.

  5. 5.

    Using Maple, an analytical assessment of a set of nonlinear algebraic equations is carried out.

  6. 6.

    Analytical soliton solutions for (7) are then produced by computing and entering the unknown values together with \(\zeta (\varsigma )\) (the Eq. (10) answers) in Eq. (9). Using the generic solution of (10), we may get several families of soliton solutions, which are displayed as follows:

Table 1 The family constraint(s) of \(\zeta (\varsigma )\) and \(\bigg (\frac{\zeta '(\varsigma )}{\zeta (\varsigma )}\bigg )\).
Full size table

Where \({w_1}, {w_2} \in \textrm{R}\), \({S} ={\mu }^2-4{\nu } {\lambda }\) and \(\wp =\cosh \left( \frac{1}{4}\,\sqrt{{S}}\varsigma \right) \sinh \left( \frac{1}{4}\,\sqrt{{S}}\varsigma \right)\). The table 1, family constraint(s) of \(\zeta (\varsigma )\) and \(\bigg (\frac{\zeta '(\varsigma )}{\zeta (\varsigma )}\bigg )\).

Establishing kink soliton solutions for MZKE

This section focuses on using RMESEM to explore the soliton solution for the model that is provided and given in (5). The wave transformation that we begin with is as follows:

$$\begin{aligned} \psi (t,x,y)= \Psi (\varsigma ), \quad where \quad \varsigma =\rho x+\varrho y+\sigma t, \end{aligned}$$
(11)

which turn (5) into a NODE; if the acquired ODE is integrated, the following is achieved:

$$\begin{aligned} 6 \sigma \Psi + 3 \rho f_1 \Psi ^2+2 \rho q_1 \Psi ^3+6 \rho (g (\varrho )^2+ d (\rho )^2) \Psi ''+ C=0, \end{aligned}$$
(12)

where the constant of integration is C. After applying homogeneous balance to \(\Psi ^3\) and \(\Psi ''\) present in (12), we obtain \(\kappa =1\), which is the balance number \(\kappa\) present in (9). Closed form solution for (12) proposes the following when \(\kappa =1\) is entered in (9):

$$\begin{aligned} \Psi (\varsigma )=\sum _{{m}=0}^{{1}}\omega _{m} \left( \frac{\zeta '(\varsigma )}{\zeta (\varsigma )}\right) ^{m}+ \delta _{{0}} \left( \frac{1}{\zeta (\varsigma )} \right) . \end{aligned}$$
(13)

An expression in \(\zeta (\varsigma )\) can be obtained by inserting (13) into (12) and gathering all words with the same powers of \(\zeta (\varsigma )\). An equation system of nonlinear equations is produced by equating the coefficients to zero. After using Maple to solve the resulting problem, we obtain the following three sets of solutions:

Case 1:

$$\begin{aligned} \begin{aligned}&\omega _{{0}}=\omega _{{0}},\omega _{{1}}=0,\delta _{{0}}=\delta _{{0}}, \rho =-{\frac{C{\lambda }^{2}}{ \left( -2\,\omega _{{0}}\lambda +\delta _{ {0}}\mu \right) k_{{1}} \left( \omega _{{0}}\delta _{{0}}\mu -\nu \,{ \delta _{{0}}}^{2}-{\omega _{{0}}}^{2}\lambda \right) }},\varrho = \varrho ,\\&\sigma =-\frac{1}{6}\,{\frac{C \left( 6\,{\omega _{{0}}}^{2}{\lambda }^ {2}-6\,\omega _{{0}}\lambda \,\delta _{{0}}\mu +2\,\nu \,\lambda \,{\delta _{ {0}}}^{2}+{\mu }^{2}{\delta _{{0}}}^{2} \right) }{ \left( -2\,\omega _{{0 }}\lambda +\delta _{{0}}\mu \right) \left( \omega _{{0}}\delta _{{0}}\mu - \nu \,{\delta _{{0}}}^{2}-{\omega _{{0}}}^{2}\lambda \right) }},f_{{1}}={\frac{ \left( -2\,\omega _{{0}}\lambda +\delta _{{0}}\mu \right) k_{{1}}}{\lambda }},\\&d=-\frac{1}{6}\,{ \frac{ \left( 6\,{\lambda }^{2}g{\varrho }^{2}+k_{{1}}{\delta _{{0}}}^{ 2} \right) \left( -2\,\omega _{{0}}\lambda +\delta _{{0}}\mu \right) ^{2 }{k_{{1}}}^{2} \left( \omega _{{0}}\delta _{{0}}\mu -\nu \,{\delta _{{0}}}^ {2}-{\omega _{{0}}}^{2}\lambda \right) ^{2}}{{\lambda }^{6}{C}^{2}}},g=g. \end{aligned} \end{aligned}$$
(14)

Case 2:

$$\begin{aligned} \begin{aligned}&\omega _{{0}}=\omega _{{0}},\omega _{{1}}=\omega _{{1}},\delta _{{0}}=0, \rho =-{\frac{C}{k_{{1}}\omega _{{0}} \left( -4\,{\omega _{{1}}}^{2} \lambda \,\nu +2\,{\omega _{{0}}}^{2}+{\omega _{{1}}}^{2}{\mu }^{2}+3\, \omega _{{0}}\omega _{{1}}\mu \right) }},\varrho =\varrho ,\\&\sigma =-\frac{1}{6}\, {\frac{ \left( {\omega _{{1}}}^{2}{\mu }^{2}+6\,\omega _{{0}}\omega _{{1} }\mu -4\,{\omega _{{1}}}^{2}\lambda \,\nu +6\,{\omega _{{0}}}^{2} \right) C }{\omega _{{0}} \left( -4\,{\omega _{{1}}}^{2}\lambda \,\nu +2\,{\omega _{{0 }}}^{2}+{\omega _{{1}}}^{2}{\mu }^{2}+3\,\omega _{{0}}\omega _{{1}}\mu \right) }},f_{{1}}=-k_{{1}}\omega _{{1}}\mu -2\,k_{{1}}\omega _{{0}},\\&d=-\frac{1}{6}\,{\frac{ \left( k_{{1}}{\omega _{{1}}}^{2}+6\,g{ \varrho }^{2} \right) {k_{{1}}}^{2}{\omega _{{0}}}^{2} \left( -4\,{ \omega _{{1}}}^{2}\lambda \,\nu +2\,{\omega _{{0}}}^{2}+{\omega _{{1}}}^{2} {\mu }^{2}+3\,\omega _{{0}}\omega _{{1}}\mu \right) ^{2}}{{C}^{2}}},g=g. \end{aligned} \end{aligned}$$
(15)

Case 3:

$$\begin{aligned} \begin{aligned}&\omega _{{0}}=\omega _{{0}},\omega _{{1}}=\omega _{{1}},\delta _{{0}}=- \omega _{{1}}\lambda ,\rho =-{\frac{C}{k_{{1}} \left( \omega _{{1}}\mu +2 \,\omega _{{0}} \right) \left( \omega _{{0}}\omega _{{1}}\mu +{\omega _{{1 }}}^{2}\lambda \,\nu +{\omega _{{0}}}^{2} \right) }},\varrho =\varrho ,\\&\sigma =-\frac{1}{6}\,{\frac{ \left( {\omega _{{1}}}^{2}{\mu }^{2}+6\,\omega _{{0 }}\omega _{{1}}\mu +6\,{\omega _{{0}}}^{2}+2\,{\omega _{{1}}}^{2}\lambda \, \nu \right) C}{ \left( \omega _{{1}}\mu +2\,\omega _{{0}} \right) \left( \omega _{{0}}\omega _{{1}}\mu +{\omega _{{1}}}^{2}\lambda \,\nu +{ \omega _{{0}}}^{2} \right) }},f_{{1}}=-k_{{1}}\omega _{{1}}\mu -2\,k_{{1}}\omega _{{0}},\\&d=-\frac{1}{6}\,{\frac{ \left( k_{{1}}{\omega _{{ 1}}}^{2}+6\,g{\varrho }^{2} \right) {k_{{1}}}^{2} \left( \omega _{{1}} \mu +2\,\omega _{{0}} \right) ^{2} \left( \omega _{{0}}\omega _{{1}}\mu +{ \omega _{{1}}}^{2}\lambda \,\nu +{\omega _{{0}}}^{2} \right) ^{2}}{{C}^{2} }},g=g. \end{aligned} \end{aligned}$$
(16)

Taking Case 1, we obtain the subsequent sets of kink soliton solutions for MZKE given in (5) through the use of (11), (13), and the equivalent solution of (10):

Family 1.1: When \({S}<0 \quad \nu \ne 0\),

$$\begin{aligned} & \begin{aligned} \psi _{1,1}(x,y,t)= \omega _{{0}}+\delta _{{0}} \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}+\frac{1}{2}\,{\frac{\sqrt{-S}\tan \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) }{\nu }} \right) ^{-1}, \end{aligned} \end{aligned}$$
(17)
$$\begin{aligned} & \begin{aligned} \psi _{1,2}(x,y,t)= \omega _{{0}}+\delta _{{0}} \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}-\frac{1}{2}\,{\frac{\sqrt{-S}\cot \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) }{\nu }} \right) ^{-1}, \end{aligned} \end{aligned}$$
(18)
$$\begin{aligned} & \begin{aligned} \psi _{1,3}(x,y,t)= \omega _{{0}}+\delta _{{0}} \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}+\frac{1}{2}\,{\frac{\sqrt{-S} \left( \tan \left( \sqrt{-S}\varsigma \right) +\sec \left( \sqrt{-S}\varsigma \right) \right) }{\nu }} \right) ^{-1}, \end{aligned} \end{aligned}$$
(19)

and

$$\begin{aligned} \begin{aligned} \psi _{1,4}(x,y,t)= \omega _{{0}}+\delta _{{0}} \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}+\frac{1}{2}\,{\frac{\sqrt{-S} \left( \tan \left( \sqrt{-S}\varsigma \right) -\sec \left( \sqrt{-S}\varsigma \right) \right) }{\nu }} \right) ^{-1}. \end{aligned} \end{aligned}$$
(20)

Family 1.2: When \({S}>0 \quad \nu \ne 0\),

$$\begin{aligned} & \begin{aligned} \psi _{1,5}(x,y,t)= \omega _{{0}}+\delta _{{0}} \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}-\frac{1}{2}\,{\frac{\sqrt{S}\tanh \left( \frac{1}{2}\,\sqrt{S}\varsigma \right) }{\nu }} \right) ^{-1}, \end{aligned} \end{aligned}$$
(21)
$$\begin{aligned} & \begin{aligned} \psi _{1,6}(x,y,t)= \omega _{{0}}+\delta _{{0}} \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}-\frac{1}{2}\,{\frac{\sqrt{S} \left( \tanh \left( \sqrt{S}\varsigma \right) +i{ sech } \left( \sqrt{S}\varsigma \right) \right) }{\nu }} \right) ^{-1}, \end{aligned} \end{aligned}$$
(22)
$$\begin{aligned} & \begin{aligned} \psi _{1,7}(x,y,t)= \omega _{{0}}+\delta _{{0}} \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}-\frac{1}{2}\,{\frac{\sqrt{S} \left( \tanh \left( \sqrt{S}\varsigma \right) -i{ sech } \left( \sqrt{S}\varsigma \right) \right) }{\nu }} \right) ^{-1}, \end{aligned} \end{aligned}$$
(23)

and

$$\begin{aligned} \begin{aligned} \psi _{1,8}(x,y,t)= \omega _{{0}}+\delta _{{0}} \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}-\frac{1}{4}\,{\frac{\sqrt{S} \left( \tanh \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) -\coth \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) \right) }{\nu }} \right) ^{-1}. \end{aligned} \end{aligned}$$
(24)

Family 1.3: When \({S}=0, \quad \mu \ne 0\),

$$\begin{aligned} \begin{aligned} \psi _{1,9}(x,y,t)= \omega _{{0}}-\frac{1}{2}\,{\frac{\delta _{{0}}{\mu }^{2}\varsigma }{\lambda \, \left( \mu \,\varsigma +2 \right) }}. \end{aligned} \end{aligned}$$
(25)

Family 1.4: When \({S}=0\), in case when \(\mu =\nu =0\),

$$\begin{aligned} \begin{aligned} \psi _{1,10}(x,y,t)= \omega _{{0}}+{\frac{\delta _{{0}}}{\lambda \,\varsigma }}. \end{aligned} \end{aligned}$$
(26)

Family 1.6: When \(\mu =\chi\), \(\lambda =n\chi (n\ne 0)\) and \(\nu =0\),

$$\begin{aligned} \begin{aligned} \psi _{1,12}(x,y,t)= {\frac{\omega _{{0}}{\textrm{e}^{\chi \,\varsigma }}-\omega _{{0}}n+\delta _ {{0}}}{{\textrm{e}^{\chi \,\varsigma }}-n}}. \end{aligned} \end{aligned}$$
(27)

In above families of solutions,

$$\varsigma ={\frac{-C{\lambda }^{2} x}{ \left( -2\,\omega _{{0}}\lambda +\delta _{ {0}}\mu \right) k_{{1}} \left( \omega _{{0}}\delta _{{0}}\mu -\nu \,{ \delta _{{0}}}^{2}-{\omega _{{0}}}^{2}\lambda \right) }} +\varrho y-\frac{1}{6}\,{\frac{C \left( 6\,{\omega _{{0}}}^{2}{\lambda }^ {2}-6\,\omega _{{0}}\lambda \,\delta _{{0}}\mu +2\,\nu \,\lambda \,{\delta _{ {0}}}^{2}+{\mu }^{2}{\delta _{{0}}}^{2} \right) t }{ \left( -2\,\omega _{{0 }}\lambda +\delta _{{0}}\mu \right) \left( \omega _{{0}}\delta _{{0}}\mu - \nu \,{\delta _{{0}}}^{2}-{\omega _{{0}}}^{2}\lambda \right) }}.$$

Taking Case 2, we obtain the subsequent sets of kink soliton solutions for MZKE given in (5) through the use of (11), (13), and the equivalent solution of (10):

Family 2.1: When \({S}<0 \quad \nu \ne 0\),

$$\begin{aligned} & \begin{aligned} \psi _{2,1}(x,y,t)= \omega _{{0}}-\frac{1}{2}\,{\frac{\omega _{{1}}S \left( 1+ \left( \tan \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) \right) ^{2} \right) }{-\mu +\sqrt{- S}\tan \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) }}, \end{aligned} \end{aligned}$$
(28)
$$\begin{aligned} & \begin{aligned} \psi _{2,2}(x,y,t)= \omega _{{0}}+\frac{1}{2}\,{\frac{\omega _{{1}}S \left( 1+ \left( \cot \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) \right) ^{2} \right) }{\mu +\sqrt{-S }\cot \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) }}, \end{aligned} \end{aligned}$$
(29)
$$\begin{aligned} & \begin{aligned} \psi _{2,3}(x,y,t)= \omega _{{0}}-{\frac{\omega _{{1}}S \left( 1+\sin \left( \sqrt{-S} \varsigma \right) \right) }{\cos \left( \sqrt{-S}\varsigma \right) \left( -\mu \,\cos \left( \sqrt{-S}\varsigma \right) + \sqrt{-S}\sin \left( \sqrt{-S}\varsigma \right) +\sqrt{-S} \right) }}, \end{aligned} \end{aligned}$$
(30)

and

$$\begin{aligned} \begin{aligned} \psi _{2,4}(x,y,t)= \omega _{{0}}+{\frac{\omega _{{1}}S \left( \sin \left( \sqrt{-S} \varsigma \right) -1 \right) }{\cos \left( \sqrt{-S}\varsigma \right) \left( -\mu \,\cos \left( \sqrt{-S}\varsigma \right) + \sqrt{-S}\sin \left( \sqrt{-S}\varsigma \right) -\sqrt{-S} \right) }}. \end{aligned} \end{aligned}$$
(31)

Family 2.2: When \({S}>0 \quad \nu \ne 0\),

$$\begin{aligned} & \begin{aligned} \psi _{2,5}(x,y,t)= \omega _{{0}}-\frac{1}{2}\,{\frac{\omega _{{1}}S \left( -1+ \left( \tanh \left( \frac{1}{2}\,\sqrt{S}\varsigma \right) \right) ^{2} \right) }{\mu + \sqrt{S}\tanh \left( \frac{1}{2}\,\sqrt{S}\varsigma \right) }}, \end{aligned} \end{aligned}$$
(32)
$$\begin{aligned} & \begin{aligned} \psi _{2,6}(x,y,t)= \omega _{{0}}-{\frac{\omega _{{1}}S \left( -1+i\sinh \left( \sqrt{S} \varsigma \right) \right) }{\cosh \left( \sqrt{S}\varsigma \right) \left( \mu \,\cosh \left( \sqrt{S}\varsigma \right) +\sqrt{S}\sinh \left( \sqrt{S}\varsigma \right) +i\sqrt{S} \right) }}, \end{aligned} \end{aligned}$$
(33)
$$\begin{aligned} & \begin{aligned} \psi _{2,7}(x,y,t)= \omega _{{0}}-{\frac{\omega _{{1}}S \left( 1+i\sinh \left( \sqrt{S} \varsigma \right) \right) }{\cosh \left( \sqrt{S}\varsigma \right) \left( -\mu \,\cosh \left( \sqrt{S}\varsigma \right) - \sqrt{S}\sinh \left( \sqrt{S}\varsigma \right) +i\sqrt{S} \right) }}, \end{aligned} \end{aligned}$$
(34)

and

$$\begin{aligned} \begin{aligned} \psi _{2,8}(x,y,t)= \omega _{{0}}-\frac{1}{4}\,{\frac{\omega _{{1}}S \left( 2\, \left( \cosh \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) \right) ^{2}-1 \right) }{ \cosh \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) \sinh \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) \left( -2\,\mu \,\cosh \left( \frac{1}{4}\,\sqrt{S} \varsigma \right) \sinh \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) + \sqrt{S} \right) }}. \end{aligned} \end{aligned}$$
(35)

Family 2.3: When \({S}=0, \quad \mu \ne 0\),

$$\begin{aligned} \begin{aligned} \psi _{2,9}(x,y,t)= \omega _{{0}}-2\,{\frac{\omega _{{1}}}{\varsigma \, \left( \mu \, \varsigma +2 \right) }}. \end{aligned} \end{aligned}$$
(36)

Family 2.4: When \({S}=0\), in case when \(\mu =\nu =0\),

$$\begin{aligned} \begin{aligned} \psi _{2,10}(x,y,t)= \omega _{{0}}+{\frac{\omega _{{1}}}{\varsigma }}. \end{aligned} \end{aligned}$$
(37)

Family 2.5: When \({S}=0\), in case when \(\mu =\lambda =0\),

$$\begin{aligned} \begin{aligned} \psi _{2,11}(x,y,t)= \omega _{{0}}-{\frac{\omega _{{1}}}{\varsigma }}. \end{aligned} \end{aligned}$$
(38)

Family 2.6: When \(\mu =\chi\), \(\lambda =n\chi (n\ne 0)\) and \(\nu =0\),

$$\begin{aligned} \begin{aligned} \psi _{2,12}(x,y,t)= \omega _{{0}}+{\frac{\omega _{{1}}\chi \,{\textrm{e}^{\chi \,\varsigma }}}{{ \textrm{e}^{\chi \,\varsigma }}-n}}. \end{aligned} \end{aligned}$$
(39)

Family 2.7: When \(\mu =\chi\), \(\nu =n\chi (n\ne 0)\) and \(\lambda =0\),

$$\begin{aligned} \begin{aligned} \psi _{2,13}(x,y,t)= \omega _{{0}}-{\frac{\omega _{{1}}\chi }{-1+n{\textrm{e}^{\chi \,\varsigma } }}}. \end{aligned} \end{aligned}$$
(40)

Family 2.8: When \(\lambda =0\), \(\nu \ne 0\) and \(\mu \ne 0\),

$$\begin{aligned} \begin{aligned} \psi _{2,14}(x,y,t)= \omega _{{0}}+{\frac{\omega _{{1}}\mu \, \left( \sinh \left( \mu \, \varsigma \right) -\cosh \left( \mu \,\varsigma \right) \right) }{- \cosh \left( \mu \,\varsigma \right) +\sinh \left( \mu \,\varsigma \right) -w_{{2}}}}, \end{aligned} \end{aligned}$$
(41)

and

$$\begin{aligned} \begin{aligned} \psi _{2,15}(x,y,t)= \omega _{{0}}+{\frac{\omega _{{1}}\mu \,w_{{2}}}{\cosh \left( \mu \, \varsigma \right) +\sinh \left( \mu \,\varsigma \right) +w_{{2}}}}. \end{aligned} \end{aligned}$$
(42)

In above families of solutions,

$$\varsigma ={\frac{-Cx}{k_{{1}}\omega _{{0}} \left( -4\,{\omega _{{1}}}^{2} \lambda \,\nu +2\,{\omega _{{0}}}^{2}+{\omega _{{1}}}^{2}{\mu }^{2}+3\, \omega _{{0}}\omega _{{1}}\mu \right) }}+\varrho y-\frac{1}{6}\, {\frac{ \left( {\omega _{{1}}}^{2}{\mu }^{2}+6\,\omega _{{0}}\omega _{{1} }\mu -4\,{\omega _{{1}}}^{2}\lambda \,\nu +6\,{\omega _{{0}}}^{2} \right) C t }{\omega _{{0}} \left( -4\,{\omega _{{1}}}^{2}\lambda \,\nu +2\,{\omega _{{0 }}}^{2}+{\omega _{{1}}}^{2}{\mu }^{2}+3\,\omega _{{0}}\omega _{{1}}\mu \right) }}.$$

Taking Case 3, we obtain the subsequent sets of kink soliton solutions for MZKE given in (5) through the use of (11), (13), and the equivalent solution of (10):

Family 3.1: When \({S}<0 \quad \nu \ne 0\),

$$\begin{aligned} & \begin{aligned} \psi _{3,1}(x,y,t)= \omega _{{0}}-\frac{1}{2}\,{\frac{\omega _{{1}}S \left( 1+ \left( \tan \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) \right) ^{2} \right) }{-\mu +\sqrt{- S}\tan \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) }}-\omega _{{1}}\lambda \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}+\frac{1}{2}\,{\frac{\sqrt{-S}\tan \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) }{\nu }} \right) ^{-1}, \end{aligned} \end{aligned}$$
(43)
$$\begin{aligned} & \begin{aligned} \psi _{3,2}(x,y,t)= \omega _{{0}}+\frac{1}{2}\,{\frac{\omega _{{1}}S \left( 1+ \left( \cot \left( \frac{1}{2}\, \sqrt{-S}\varsigma \right) \right) ^{2} \right) }{\mu +\sqrt{-S }\cot \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) }}-\omega _{{1}}\lambda \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}-\frac{1}{2}\,{\frac{\sqrt{-S}\cot \left( \frac{1}{2}\,\sqrt{-S}\varsigma \right) }{\nu }} \right) ^{-1}, \end{aligned} \end{aligned}$$
(44)
$$\begin{aligned} & \begin{aligned} \psi _{3,3}(x,y,t)=&-{\frac{\omega _{{1}}S \left( 1+\sin \left( \sqrt{-S} \varsigma \right) \right) }{\cos \left( \sqrt{-S}\varsigma \right) \left( -\mu \,\cos \left( \sqrt{-S}\varsigma \right) + \sqrt{-S}\sin \left( \sqrt{-S}\varsigma \right) +\sqrt{-S} \right) }}\\&-\omega _{{1}}\lambda \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}+\frac{1}{2}\,{ \frac{\sqrt{-S} \left( \tan \left( \sqrt{-S}\varsigma \right) + \sec \left( \sqrt{-S}\varsigma \right) \right) }{\nu }} \right) ^{-1 }+\omega _{{0}}, \end{aligned} \end{aligned}$$
(45)

and

$$\begin{aligned} \begin{aligned} \psi _{3,4}(x,y,t)=&{\frac{\omega _{{1}}S \left( \sin \left( \sqrt{-S} \varsigma \right) -1 \right) }{\cos \left( \sqrt{-S}\varsigma \right) \left( -\mu \,\cos \left( \sqrt{-S}\varsigma \right) + \sqrt{-S}\sin \left( \sqrt{-S}\varsigma \right) -\sqrt{-S} \right) }}\\&-\omega _{{1}}\lambda \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}+\frac{1}{2}\,{ \frac{\sqrt{-S} \left( \tan \left( \sqrt{-S}\varsigma \right) - \sec \left( \sqrt{-S}\varsigma \right) \right) }{\nu }} \right) ^{-1 } +\omega _{{0}}. \end{aligned} \end{aligned}$$
(46)

Family 3.2: When \({S}>0 \quad \nu \ne 0\),

$$\begin{aligned} & \begin{aligned} \psi _{3,5}(x,y,t)= \omega _{{0}}-\frac{1}{2}\,{\frac{\omega _{{1}}S \left( -1+ \left( \tanh \left( \frac{1}{2}\,\sqrt{S}\varsigma \right) \right) ^{2} \right) }{\mu + \sqrt{S}\tanh \left( \frac{1}{2}\,\sqrt{S}\varsigma \right) }}-\omega _{{1}} \lambda \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}-\frac{1}{2}\,{\frac{\sqrt{S}\tanh \left( \frac{1}{2}\,\sqrt{S}\varsigma \right) }{\nu }} \right) ^{-1}, \end{aligned} \end{aligned}$$
(47)
$$\begin{aligned} & \begin{aligned} \psi _{3,6}(x,y,t)=&-{\frac{\omega _{{1}}S \left( -1+i\sinh \left( \sqrt{S} \varsigma \right) \right) }{\cosh \left( \sqrt{S}\varsigma \right) \left( \mu \,\cosh \left( \sqrt{S}\varsigma \right) +\sqrt{S}\sinh \left( \sqrt{S}\varsigma \right) +i\sqrt{S} \right) }}\\&-\omega _{{1}}\lambda \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}-\frac{1}{2}\,{\frac{ \sqrt{S} \left( \tanh \left( \sqrt{S}\varsigma \right) +i{ sech} \left( \sqrt{S}\varsigma \right) \right) }{\nu }} \right) ^{-1} +\omega _{{0}}, \end{aligned} \end{aligned}$$
(48)
$$\begin{aligned} & \begin{aligned} \psi _{3,7}(x,y,t)=&-{\frac{\omega _{{1}}S \left( 1+i\sinh \left( \sqrt{S} \varsigma \right) \right) }{\cosh \left( \sqrt{S}\varsigma \right) \left( -\mu \,\cosh \left( \sqrt{S}\varsigma \right) - \sqrt{S}\sinh \left( \sqrt{S}\varsigma \right) +i\sqrt{S} \right) }}\\&-\omega _{{1}}\lambda \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}-\frac{1}{2}\,{\frac{ \sqrt{S} \left( \tanh \left( \sqrt{S}\varsigma \right) -i{ sech} \left( \sqrt{S}\varsigma \right) \right) }{\nu }} \right) ^{-1}+\omega _{{0}}, \end{aligned} \end{aligned}$$
(49)

and

$$\begin{aligned} \begin{aligned} \psi _{3,8}(x,y,t)=&-\frac{1}{4}\,{\frac{\omega _{{1}}S \left( 2\, \left( \cosh \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) \right) ^{2}-1 \right) }{ \cosh \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) \sinh \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) \left( -2\,\mu \,\cosh \left( \frac{1}{4}\,\sqrt{S} \varsigma \right) \sinh \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) + \sqrt{S} \right) }}\\&-\omega _{{1}}\lambda \left( -\frac{1}{2}\,{\frac{\mu }{\nu }}-\frac{1}{4}\,{\frac{\sqrt{S} \left( \tanh \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) -\coth \left( \frac{1}{4}\,\sqrt{S}\varsigma \right) \right) }{\nu }} \right) ^{-1}+\omega _{{0}}. \end{aligned} \end{aligned}$$
(50)

Family 3.3: When \({S}=0, \quad \mu \ne 0\),

$$\begin{aligned} \begin{aligned} \psi _{3,9}(x,y,t)= \omega _{{0}}-2\,{\frac{\omega _{{1}}}{\varsigma \, \left( \mu \, \varsigma +2 \right) }}+\frac{1}{2}\,{\frac{\omega _{{1}}{\mu }^{2}\varsigma }{ \mu \,\varsigma +2}}. \end{aligned} \end{aligned}$$
(51)

Family 3.4: When \({S}=0\), in case when \(\mu =\lambda =0\),

$$\begin{aligned} \begin{aligned} \psi _{3,10}(x,y,t)= {\frac{\omega _{{0}}\varsigma -\omega _{{1}}}{\varsigma }}. \end{aligned} \end{aligned}$$
(52)

Family 3.5: When \(\mu =\chi\), \(\nu =n\chi (n\ne 0)\) and \(\lambda =0\),

$$\begin{aligned} \begin{aligned} \psi _{3,11}(x,y,t)= {\frac{-\omega _{{0}}+\omega _{{0}}n{\textrm{e}^{\chi \,\varsigma }}-\omega _{{1}}\chi }{-1+n{\textrm{e}^{\chi \,\varsigma }}}}. \end{aligned} \end{aligned}$$
(53)

Family 3.6: When \(\lambda =0\), \(\nu \ne 0\) and \(\mu \ne 0\),

$$\begin{aligned} \begin{aligned} \psi _{3,12}(x,y,t)= {\frac{-\omega _{{0}}\cosh \left( \mu \,\varsigma \right) +\omega _{{0} }\sinh \left( \mu \,\varsigma \right) -\omega _{{0}}w_{{2}}+\omega _{{1} }\mu \,\sinh \left( \mu \,\varsigma \right) -\omega _{{1}}\mu \,\cosh \left( \mu \,\varsigma \right) }{-\cosh \left( \mu \,\varsigma \right) +\sinh \left( \mu \,\varsigma \right) -w_{{2}}}}, \end{aligned} \end{aligned}$$
(54)

and

$$\begin{aligned} \begin{aligned} \psi _{3,13}(x,y,t)= {\frac{\omega _{{0}}\sinh \left( \mu \,\varsigma \right) +\omega _{{0}} \cosh \left( \mu \,\varsigma \right) +\omega _{{0}}w_{{2}}+\omega _{{1}} \mu \,w_{{2}}}{\sinh \left( \mu \,\varsigma \right) +\cosh \left( \mu \, \varsigma \right) +w_{{2}}}}. \end{aligned} \end{aligned}$$
(55)

In above families of solutions,

$$\varsigma ={\frac{-Cx}{k_{{1}} \left( \omega _{{1}}\mu +2 \,\omega _{{0}} \right) \left( \omega _{{0}}\omega _{{1}}\mu +{\omega _{{1 }}}^{2}\lambda \,\nu +{\omega _{{0}}}^{2} \right) }} +\varrho y-\frac{1}{6}\,{\frac{ \left( {\omega _{{1}}}^{2}{\mu }^{2}+6\,\omega _{{0 }}\omega _{{1}}\mu +6\,{\omega _{{0}}}^{2}+2\,{\omega _{{1}}}^{2}\lambda \, \nu \right) C t}{ \left( \omega _{{1}}\mu +2\,\omega _{{0}} \right) \left( \omega _{{0}}\omega _{{1}}\mu +{\omega _{{1}}}^{2}\lambda \,\nu +{ \omega _{{0}}}^{2} \right) }}.$$

Discussion and graphs

The RMESEM method was successfully applied in the study, which resulted in the creation of novel families of soliton solutions for the MZKE. The results of the study provide important insights into the behavior of the MZKE and also help us better understand the dynamics of the model. The results also provide resources for further research and analysis and demonstrate how RMESEM may be used to solve challenging NPDEs. The relation between different soliton types, propagation patterns, and interactions is visually shown using a combination of 2-D, 3-D, and contour plots. This graphical analysis highlights the significance of our findings and demonstrates the effectiveness of the RMESEM approach in interpreting complex nonlinear systems. The results of this investigation are groundbreaking since this method’s application to the MZKE is new in the literature. Because RMESEM is a straightforward algebraic ansatz and does not necessitate intricate processes like linearization, perturbation, and other transformation techniques–which are occasionally required in other methods–we specifically picked it. Because of RMESEM’s ease of use and efficiency, we may obtain precise closed-form answers without the hassles of more complex techniques. One of the main features of RMESEM is its capacity to provide a large number of solution families, including exponential, rational, hyperbolic, and trigonometric functions. By exposing a wide variety of wave properties that other approaches might miss or be unable to capture, this variation makes it possible to conduct a more thorough investigation of the model. Unlike more traditional approaches, RMESEM provides a range of solution forms, enabling a more thorough and in-depth comprehension of the dynamics present in the model being studied. However, it should be noted that if the highest derivative terms and the largest nonlinear component do not balance homogeneously, the proposed method is ineffective. In this case, soliton creation is impossible since the approach cannot balance the nonlinearity with dispersion. Notwithstanding this drawback, the current study indicates that the approach is precise and trustworthy for dealing with nonlinear issues across a variety of scientific fields.

Kink solitons, which are present in the solutions, are prominently exhibited by the discovered solitons. These features, which are essential to the physical fields that the MZKE describes, include bell-shaped, lump-like, twinning, and perturbed kinks. A solitary kink happens when a single, independent wave maintains its shape while moving; this is a common occurrence in signal transmission, when signal integrity is crucial. A lump-like kink is a localized bump-like protrusion used to mimic discrete energy packets in fiber optic or nonlinear transmission lines. It is a confined disruption in the medium of transmission. A bell-like kink wave is one that gently moves between one eschatological condition to a different one, much like a curve that is bell-shaped. These waves may be very useful in explaining the slow change in electrostatic field strength as well as plasma concentration. Kinks that have minor changes or disruptions, known as perturb kinks, are commonly used to simulate the implications of outside factors or flaws in the substrate, such as fluctuations in electronic circuits. The interaction involving coupled perturbations in plasma systems or linked nonlinear synthesisers is represented by twinning kinks, which are two closely connected kinks traveling alongside each other. Regarding the balance, propagation, and control of waves in electronics-related domains, each of these soliton helps us better understand the complex behaviors and relationships in structures as described by MZKE. Below are several graphs that are shown and discussed:

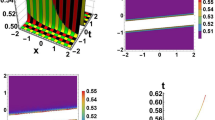
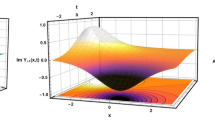
Figure 2, the 3D, contour and 2D (when \(y=10\)) graphs for the solitary kink soliton solution \(\psi _{1, 5 }\) stated in (21), are plotted for \(\lambda := 4, \mu := 5, \nu := 1, \varrho := 0.2E^{-2}, C:= 0.1E^{-2}, t:= 0, \omega _{0}:= 1, \delta _{0}:= 2, k_{1}:= 1.5\). Fig. 3, the 3D, contour and 2D (when \(y= 0\)) graphs for the perturbed lump-type kink soliton solution \(\psi _{1, 8 }\) stated in (24), are plotted for \(\lambda := 8, \mu := 10, \nu := 2, \varrho := 0.20E^{-1}, C:= 1, t:= 1, \omega _{0}:= 4, \delta _{0}:= 3, k_{1}:= 1\). Fig. 4, the 3D, contour and 2D (when \(x= 1\)) graphs for the lump-type kink soliton solution \(\psi _{1, 9 }\) stated in (25), are plotted for \(\lambda := 1, \mu := 4, \nu := 4, \varrho := 0.50E^{-1}, C:= 0.5, t:= 5, \omega _{0}:= 0.5, \delta _{0}:= 5, k_{1}:= 2\). Fig. 5, the 3D, contour and 2D (when \(y=0\)) graphs for the twinning kink soliton solution \(\psi _{2, 4 }\) stated in (31), are plotted for \(\lambda := 1, \mu := 0, \nu := 1, \varrho := 0.75E^{-1}, C:= 0.15, t:= 10, \omega _{0}:= 0.5E^{-1}, \omega _{1}:= 1, k_{1}:= 3\). Fig. 6, the 3D, contour and 2D (when \(x= 100\)) graphs for the bell-shaped kink soliton solution \(\psi _{2, 5 }\) stated in (32), are plotted for \(\lambda := 2, \mu := 5, \nu := 2, \varrho := 0.3E^{-1}, C:= 0.7E^{-2}, t:= 20, \omega _{0}:= 0.1, \omega _{1}:= 1, k_{1}:= 5\). Fig. 7, the 3D, contour and 2D (when \(x= 1\)) graphs for the twinning kink soliton solution \(\psi _{2, 8 }\) stated in (35), are plotted for \(\lambda := 3, \mu := 13, \nu := 12, \varrho := 0.6E^{-1}, C:= 0.51E^{-2}, t:= 30, \omega _{0}:= 1, \omega _{1}:= 5, k_{1}:= 10\). Fig. 8, the 3D, contour and 2D (when \(x= 100\)) graphs for the solitary kink soliton solution \(\psi _{2, 14 }\) stated in (41), are plotted for \(\lambda := 0, \mu := 1, \nu := 2, \varrho := 0.8E^{-2}, C:= 0.24E^{-2}, t:= 25, \omega _{0}:= 3, \omega _{1}:= 2, k_{1}:= 1, w_{2}:= 6\). Fig.9, the 3D, contour and 2D (when \(x=1000\)) graphs for the multiple kink soliton solution \(\psi _{3, 3 }\) stated in (45), are plotted for \(\lambda := 1, \mu := 1, \nu := 1, \varrho := 0.45E^{-2}, C:= 0.27E^{-2}, t:= 3, \omega _{0}:= 1, \omega _{1}:= 5, k_{1}:= 10\). This graph also shows axial perturbation. Fig. 10, the 3D, contour and 2D (when \(x=10\)) graphs for the solitary kink soliton solution \(\psi _{3, 5 }\) stated in (47), are plotted for \(\lambda := 8, \mu := 10, \nu := 2, \varrho := 1, C:= 2, t:= 5, \omega _{0}:= 10, \omega _{1}:= 5, k_{1}:= 20\). Fig. 11, the 3D, contour and 2D (when \(x=100\)) graphs for the perturbed lump-type kink soliton solution \(\psi _{3, 11 }\) stated in (53), are plotted for \(\lambda := 0, \mu := 5,\) \(\nu := 15, \varrho := 0.1,\) \(C:= 0.35, t:= 100, \omega _{0}:= 4,\) \(\omega _{1}:= 2, k_{1}:= 12,\) \(\tau := 5, n:= 3\).

Fig. 2
figure 2

The 3D, contour and 2D (when y = 10) graphs for the solitary kink soliton solution \(\psi _{1, 5 }\) stated in (21), are plotted for \(\lambda := 4, \mu := 5, \nu := 1, \varrho := 0.2E^{-2},\) \(C:= 0.1E^{-2}, t:= 0, \omega _{0}:= 1, \delta _{0}:= 2, k_{1}:= 1.5\).

Full size image
Fig. 3
figure 3

The 3D, contour and 2D (when y = 10) graphs for the perturbed lump-type kink soliton solution \(\psi _{1, 8 }\) stated in (24), are plotted for \(\lambda := 8, \mu := 10, \nu := 2, \varrho := 0.20E^{-1},\) \(C:= 1, t:= 1, \omega _{0}:= 4, \delta _{0}:= 3, k_{1}:= 1\).

Full size image
Fig. 4
figure 4

The 3D, contour and 2D (when x = 1) graphs for the lump-type kink soliton solution \(\psi _{1, 9 }\) stated in (25), are plotted for \(\lambda := 1, \mu := 4, \nu := 4, \varrho := 0.50E^{-1},\) \(C:= 0.5, t:= 5, \omega _{0}:= 0.5, \delta _{0}:= 5, k_{1}:= 2\).

Full size image
Fig. 5
figure 5

The 3D, contour and 2D (when y = 0) graphs for the twinning kink soliton solution \(\psi _{2, 4 }\) stated in (31), are plotted for \(\lambda := 1, \mu := 0, \nu := 1, \varrho := 0.75E^{-1},\) \(C:= 0.15, t:= 10, \omega _{0}:= 0.5E^{-1}, \omega _{1}:= 1, k_{1}:= 3\).

Full size image
Fig. 6
figure 6

The 3D, contour and 2D (when x = 100) graphs for the bell-shaped kink soliton solution \(\psi _{2, 5 }\) stated in (32), are plotted for \(\lambda := 2, \mu := 5, \nu := 2, \varrho := 0.3E^{-1},\) \(C:= 0.7E^{-2}, t:= 20, \omega _{0}:= 0.1, \omega _{1}:= 1, k_{1}:= 5\).

Full size image
Fig. 7
figure 7

The 3D, contour and 2D (when x = 1) graphs for the twinning kink soliton solution \(\psi _{2, 8 }\) stated in (35), are plotted for \(\lambda := 3, \mu := 13, \nu := 12, \varrho := 0.6E^{-1},\) \(C:= 0.51E^{-2}, t:= 30, \omega _{0}:= 1, \omega _{1}:= 5, k_{1}:= 10\).

Full size image
Fig. 8
figure 8

The 3D, contour and 2D (when x = 100) graphs for the solitary kink soliton solution \(\psi _{2, 14 }\) stated in (41), are plotted for \(\lambda := 0, \mu := 1, \nu := 2, \varrho := 0.8E^{-2},\) \(C:= 0.24E^{-2}, t:= 25, \omega _{0}:= 3, \omega _{1}:= 2, k_{1}:= 1, w_{2}:= 6\).

Full size image
Fig. 9
figure 9

The 3D, contour and 2D (when x = 1000) graphs for the multiple kink soliton solution \(\psi _{3, 3 }\) stated in (45), are plotted for \(\lambda := 1, \mu := 1, \nu := 1, \varrho := 0.45E^{-2},\) \(C:= 0.27E^{-2}, t:= 3, \omega _{0}:= 1, \omega _{1}:= 5, k_{1}:= 10\). This graph also shows axial perturbation.

Full size image
Fig. 10
figure 10

The 3D, contour and 2D (when x = 10) graphs for the solitary kink soliton solution \(\psi _{3, 5 }\) stated in (47), are plotted for \(\lambda := 8, \mu := 10, \nu := 2, \varrho := 1,\) \(C:= 2, t:= 5, \omega _{0}:= 10, \omega _{1}:= 5, k_{1}:= 20\).

Full size image
Fig. 11
figure 11

The 3D, contour and 2D (when x = 100) graphs for the perturbed lump-type kink soliton solution \(\psi _{3, 11 }\) stated in (53), are plotted for \(\lambda := 0, \mu := 5, \nu := 15, \varrho := 0.1, C:= 0.35,\) \(t:= 100, \omega _{0}:= 4, \omega _{1}:= 2, k_{1}:= 12, \tau := 5, n:= 3\).

Full size image

Conclusion

This study generated and analysed soliton solutions for the MZKE using the RMESEM, which was helpful in capturing the fundamental physical processes of the model by incorporating exponential, rational, rational hyperbolic, trigonometric, and hyperbolic functions. By giving arbitrary values to the involved free parameters, the behaviour of these solutions was graphically analysed using three-dimensional, contour, and two-dimensional graphs. This revealed that the discovered solitons significantly exhibited the profiles of kink solitons, such as bell-shaped, lump-like, solitary, twinning, and perturbed kinks. Overall, by showcasing the RMESEM’s effectiveness in managing difficult mathematical models and its potential uses in the domains of science and engineering, this research significantly advances our understanding of the MZKE system. The data presented in this publication will be very informative for researchers who are interested in investigating the dynamics of the MZKE and related phenomena. While the RMESEM has contributed significantly to our understanding of soliton dynamics and their relationship to the models under investigation, it is important to acknowledge the limitations of this method, particularly when the nonlinear term and greatest derivative are not balanced evenly. Notwithstanding this limitation, the present investigation demonstrates that the methodology employed in this work is extremely dependable, productive and transferable for nonlinear problems in a variety of natural science domains.