Anomaly detection in double-entry bookkeeping data by federated learning system with non-model sharing approach

Abstract

Anomaly detection is crucial in financial auditing, yet effective detection often requires large volumes of data from multiple organizations. However, confidentiality concerns hinder data sharing among audit firms. Existing journal entry anomaly detectors built on model-sharing federated learning (FL) mitigate data transfer but still demand multiple parameter-exchange rounds with external servers, forcing devices holding confidential data onto networks. We propose a new framework based on data collaboration (DC) analysis, a non-model-sharing FL technique that enables anomaly detection without requiring confidential data to be directly connected to external networks. Our method first encodes journal entry data via dimensionality reduction to obtain secure intermediate representations, then transforms them into collaboration representations for building an autoencoder. Notably, the approach does not require raw data to be exposed or devices to connect to external networks, and the process needs only one round of communication. We evaluated the framework on synthetic and real journal entry datasets from eight organizations. Experiments show the DC-based approach not only surpasses models trained locally but also outperforms model-sharing FL methods such as FedAvg and FedProx, especially under non-i.i.d. conditions reflecting practical audits. This work demonstrates how organizational knowledge can be integrated while preserving confidentiality, advancing practical intelligent auditing systems.

Introduction

In recent years, research on anomaly detection in the financial and accounting domains has progressed rapidly. The anomalies (frauds) under investigation are broadly categorized into external fraud (e.g., credit card fraud, insurance claim fraud, and loan fraud) and internal fraud (e.g., financial statement fraud and money laundering)¹. Among internal fraud studies, those focusing on financial statement manipulation have been identified as a particularly important research theme¹, and several studies have been published (e.g.,^2,3).

As part of audit standards, journal entry data—recorded according to the rules of double-entry bookkeeping—play a pivotal role in financial statement audits⁴. Traditional auditing relies heavily on manual procedures⁵; however, the large volume of journal entries makes it impractical for auditors to inspect every entry manually. Consequently, computer-assisted audit techniques (CAAT) are often employed to extract and analyze these data digitally, screening suspicious transactions via a procedure known as “Journal Entry Testing.” However, as these techniques typically rely on static rules, they often exhibit high false-positive rates⁶. In recent years, numerous anomaly detection methods based on machine learning and deep learning (DL) have been proposed (e.g.,^7,8,9,10,11).

Such models require ample data volume to achieve high accuracy. Additionally, auditing firms accumulate industry-specific expertise by auditing multiple clients within the same sector, thereby improving both audit efficiency and quality¹². In fact, Boersma et al. (2023)¹³ emphasized the importance of benchmarking against peers in the same industry and proposed an approach to identify comparable firms within an industry. These considerations suggest that integrating journal entry data obtained from several companies within the same industry could enable the development of more sophisticated anomaly detection methods. However, accounting data are highly confidential, making companies and auditing firms unwilling to share them directly. Consequently, approaches that preserve client data confidentiality while simultaneously consolidating knowledge across multiple organizations should be developed¹⁴.

To perform anomaly detection on such distributed confidential data while preserving confidentiality, federated learning (FL)¹⁵ has been increasingly adopted. For example, in credit card fraud-detection, models that combine optimization algorithms with FL¹⁶ and models that integrate graph neural networks (GNN) with FL¹⁷ have been proposed. In the auditing domain, to the best of our knowledge, only Schreyer et al. (2022)¹⁸ have applied FL to anomaly detection in journal entry data. They introduced a method that uses Federated Averaging (FedAvg)¹⁵ to detect anomalies in journal entries, presenting a method to construct industry-specific detection models across multiple organizations without sharing confidential data.

In these studies, FL operates by training models on each organization’s client data and sharing model parameters to form an aggregated model. By design, this requires multiple rounds of communication and implicitly assumes that endpoints holding confidential data remain continuously connected to external networks during training. However, for highly sensitive financial data, it is generally recommended to manage systems in air-gapped environments isolated from the internet¹⁹. Although journal entries are not personal information in themselves, they constitute business-confidential information that demands rigorous protection. Consequently, communication overhead and the requirement of persistent connectivity—assumptions intrinsic to FL such as FedAvg and FedProx²¹—can become practical obstacles to deploying anomaly detection models in real-world audit settings.

As an alternative under these constraints, Data Collaboration (DC) analysis has been proposed²⁰. DC analysis enables aggregated model construction without sharing raw data or model parameters by exchanging only intermediate representations obtained via dimensionality reduction. It is therefore a distinct approach from conventional FL —such as FedAvg and FedProx—which relies on sharing model parameters across clients. To situate DC and conventional FL within a common perspective, Imakura et al. (2021)²³ classify privacy-preserving analysis of distributed data into two frameworks: a model-sharing FL framework (conventional FL that shares model parameters across clients) and a non-model-sharing framework (DC, which exchanges only dimension-reduced intermediate representations). Importantly, DC analysis requires just a single round of communication to exchange these representations, and this transfer can be performed offline offline—either by physically transferring the intermediate representations via removable media or by first moving them to a network-connected staging machine and then transmitting them, allowing model construction without connecting confidential systems to external networks. Accordingly, the model can be constructed while keeping the confidential data in an air-gapped environment. DC has been studied as a model-non-sharing approach across multiple domains—including causal inference²⁴, clustering²⁵, and healthcare applications²⁶—with comparisons against model-sharing FL reported in the literature^24,27,28,29.

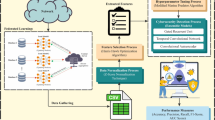
Despite this growing body of work, DC has not been systematically applied to or evaluated in the auditing context. In this study, we propose a novel FL-based anomaly detection method for journal entry data—grounded in data collaboration (DC) analysis. This approach leverages distributed confidential data without requiring direct internet connectivity to raw data (Fig. 1). Moreover, the entire learning process needs only a single round of communication, promising a significant reduction in communication overhead compared with model share-type FL methods. In summary, our study introduces an anomaly-detection framework that explicitly addresses two long-standing obstacles of model-sharing FL (e.g., FedAvg and FedProx)—the requirement of persistent external connectivity and high communication cost—by constructing models based on DC analysis.

Fig. 1

Overview of our proposed method and comparison with existing model-sharing federated learning. (a) Existing anomaly-detection framework for distributed journal-entry data based on model-sharing FL (adapted from¹⁸), which constructs an aggregated model without directly sharing raw data. (b) Our DC-based framework, which, in addition to not sharing raw data, exchanges only dimension-reduced intermediate representations, completes training in a single communication round, and allows model construction without connecting raw data to external networks.

When integrating and analyzing journal entry data owned by different audit firms—or by separate divisions within the same firm—the types of accounts used and the scale of transaction amounts often differ substantially across entities. These distributional differences reflect the diversity of business operations and transaction characteristics among audited companies; such heterogeneity is commonly referred to as non-i.i.d. (non-independent and identically distributed) in the FL literature, where it can lead to performance degradation and unstable training³⁰. By contrast, i.i.d. (independent and identically distributed) describes the ideal scenario in which all entities share the same data distribution. In this study, the effectiveness and robustness of the proposed method are assessed under both i.i.d. and non-i.i.d. conditions to mimic real-world deployment environments.

The novelty of this study lies in the first application of DC analysis to unsupervised learning and in proposing a journal entry anomaly-detection framework that enables model training without directly connecting confidential data to external networks while requiring only a single round of communication. Furthermore, additional innovation is demonstrated by employing journal entry data distributed across real organizations and comparative evaluations are conducted with existing FL methods in experiments that reflect actual distribution scenarios. By targeting the financial auditing domain, this research aims for practical application through the design and evaluation of an intelligent system capable of secure and high-precision anomaly detection in distributed environments. Our main contributions are as follows:

• We propose an anomaly detection framework based on data collaboration analysis, a non-model share-type FL approach. This framework enables collaborative model training in a single communication round—without connecting devices holding raw data to any external network—making it suitable for highly confidential journal entry data.

• Experiments using both synthetic and real data demonstrate that the proposed method outperforms models constructed by a single organization.

• We design experimental evaluations that reflect real-world non-i.i.d. conditions by using journal entry data distributed across multiple organizations. Our results show that the proposed method maintains high detection performance even under such heterogeneous settings. In particular, for local anomalies—which are relatively hard to detect and carry high fraud risk—our approach consistently outperforms existing model share-type FL methods.

Experiment settings

Datasets

We used two types of datasets: a synthetically generated simple dataset and a real-world journal entry dataset obtained from eight organizations. For both datasets, we generated two types of anomalies—global anomalies and local anomalies—following Schreyer et al. (2022)¹⁸. Note that, in this paper, the terms “global anomaly” and “local anomaly” are used based on the definitions in Breunig et al. (2000)³¹ and differ from the notions of “global model” and “local data” in the FL or DC analysis context. A global anomaly refers to a sample that contains extreme values when viewed against the entire dataset; it can be regarded as detecting outliers in individual attributes³². These anomalies often correspond to unintentional errors, are relatively easy to detect, and carry a high probability of being mistakes¹⁸. By contrast, a local anomaly refers to a sample whose combination of attribute values is abnormal compared with its local neighborhood or density; it corresponds to detecting anomalies at the level of combinations of multiple attributes³². These anomalies may indicate intentional deviations, are relatively difficult to discover, and carry a high fraud risk¹⁸.

The synthetic dataset comprises three variables, (a, b, c). Variables a and b are categorical and take values from the set {0,1,2}, whereas c is a continuous variable, with values ranging in [0,1] (Fig. 2). In the synthetic dataset, global anomalies occur when c is significantly larger or smaller than that in normal data (i.e., below 0.1 or above 0.9), whereas local anomalies involve either abnormal (a, b) combinations or anomalous (a, b, c) combinations. The training set consists of 1600 normal samples, and the test set comprises 200 samples containing both normal and anomalous cases. We injected anomalies into the test set at rates of 25% (25 global and 25 local anomalies), 10% (10 global and 10 local), and 5% (5 global and 5 local) to evaluate the effectiveness of the proposed method.

Fig. 2

Distribution of synthetic data.

For the i.i.d. setting, we randomly partitioned the 1,600 training samples into eight organizations, assigning 200 samples to each. In the non-i.i.d. setting, following Laridi et al. (2024)³³, we applied K-means clustering to the normal data and allocated each cluster to one of the eight organizations, thereby creating heterogeneous data distributions across organizations (Fig. 3).

Fig. 3

Distribution of synthetic data across clients after K-means-based non-i.i.d. setting.

The real journal entry dataset consists of multiple years of records from eight clinics in Japan. These data were provided by our collaborative research partners for research purposes and constitute confidential data from eight actual clinics. The dataset includes daily transaction records from 2016 to 2022, maintained according to double-entry bookkeeping rules. Basic descriptive statistics for the data are shown in Table 1. The features used in this study are the debit account, credit account, and transaction amount. Entries from 2016 through 2021 were used for model training, and the 2,737 entries from Clinic A in 2022 were used for testing. Since this dataset contains only normal entries, we generated synthetic anomalies and inserted them into the test set following Schreyer et al. (2022)¹⁸. The anomalous data comprise two types—global anomalies and local anomalies—mirroring the synthetic dataset. Global anomalies are defined as entries with transaction amounts that are extremely relative to the rest of the dataset; specifically, we multiply the amounts of the six largest entries in the normal data by factors of three to five. Local anomalies are generated in two ways: the first involves entries with anomalous account-pair combinations (for example, a debit account of Depreciation Expense and a credit account of Cash, a combination not seen in standard accounting practice), and the second involves altering the amounts of journal entries corresponding to regularly recurring transactions (such as rent or executive compensation). Details of the anomaly generation procedures are provided in the Supplementary materials.

Table 1 Numbers of accounts and statistics of transaction amounts.

In the i.i.d. setting for journal entry data, we first aggregate all entries obtained from the eight clinics and then randomly partition them into eight subsets, each treated as a separate organization. Thus, every organization holds data that are homogeneously and randomly sampled. In the non-i.i.d. setting, each clinic retains its original data distribution, conducting experiments in a manner closer to actual operations. In other words, we train while preserving differences in data volume and account type frequencies across organizations to evaluate performance under conditions reflective of real-world deployment. The number of samples held by each organization in both settings is shown in Table 2.

Table 2 Number of samples per client for synthetic data and real journal entry data under i.i.d. and non-i.i.d. settings.

Metrics

In financial auditing, the goal of anomaly detection is twofold—to identify every anomalous journal entry (thereby maximizing recall) and to avoid excessive false alerts (thus minimizing false positives)⁶. To balance these competing requirements, the average precision (AP), derived from the precision-recall (PR) curve, is well suited as an evaluation metric. In this study, following Schreyer et al. (2022)¹⁸, we treat the reconstruction error from an autoencoder as an anomaly score, generate a PR curve by varying the error threshold, and calculate the area under this curve. Consequently, utilizing this metric, we comprehensively assess the ability of our approach to enhance recall while minimizing false positives. Additional evaluation metrics are reported in Section S3 of the Supplementary Materials.

Baselines

In this study, we compared the proposed method against the following four models:

• Individual Analysis (IA)

  A method that builds an anomaly detection model using only the data from a single organization. When training samples are insufficient, the model may be undertrained.

• Centralized Analysis (CA)

  A method that aggregates each organization’s raw data and trains a model on the combined dataset. Although this approach theoretically achieves the highest performance, it requires direct sharing of confidential data and is therefore impractical for real-world deployment.

• FedAvg

  A representative model-sharing FL method, originally introduced by McMahan et al. (2017)¹⁵ and adopted by Schreyer et al. (2022)¹⁸. In FedAvg, each organization trains a local model on its own data and shares only the model parameters with a central server, which aggregates them to form an updated global model. This process is repeated for multiple communication rounds.

• FedProx

  An extension of FedAvg designed for non-i.i.d. distributed data²¹. FedProx adds a proximal term to each client’s local optimization to mitigate instability caused by data heterogeneity, thereby promoting more stable convergence.

We evaluate the effectiveness of the proposed DC-based method by demonstrating that it outperforms IA and by comparing it with existing methods (FedAvg and FedProx) as well as the ideal but impractical CA.

The following experimental parameters were used: a batch size of 32 and a learning rate of 0.001. For IA, CA, and DC, we set the number of epochs to 200. For FedAvg and FedProx, following Bogdanova et al. (2020)²⁷, we used 20 epochs per client and 10 aggregation rounds so that the total training effort matched that of IA/CA/DC. For IA, CA, FedAvg, and FedProx, the input to the autoencoder consisted of journal entry data that had been one‐hot encoded and normalized. Accordingly, the output‐layer activation functions and loss functions were chosen based on variable type: categorical variables use softmax activation and binary cross‐entropy loss, whereas continuous variables use linear activation and MSE loss. The total autoencoder loss is the sum of these component losses. All the experiments were implemented in Python via Keras and conducted on a machine equipped with a 13th Gen Intel® Core™ i7-13700KF CPU, an NVIDIA GeForce RTX 4060 laptop GPU, and 16 GB of RAM.

Results and discussion

In experiments using both synthetic and real journal entry data, each setup was repeated 10 times with random initialization of the autoencoder parameters, and the mean performance was evaluated. AP_all measures the overall detection performance across both anomaly types, whereas AP_global and AP_local assess the detection performance for global anomalies and local anomalies, respectively. The parameter λ denotes the number of participating organizations: for λ = 4, data from four of the eight organizations are used, and for λ = 8, data from all eight organizations are used.

Synthetic data

Tables 3 and 4 report comparisons of AP_all in the synthetic-data experiments. For the choice of dimensionality-reduction functions in DC analysis, random projection (RP) consistently achieved the highest AP under the i.i.d. setting (Table 3), whereas under non-i.i.d. conditions principal component analysis (PCA) tended to yield the best overall performance (Table 4). Locality preserving projection (LPP) and autoencoder (AE) generally exhibited lower detection performance than PCA and RP. A plausible explanation is that LPP, designed to preserve local structure, may overemphasize relationships among neighboring points in highly sparse, high-dimensional spaces, thereby failing to preserve the global structure of the original data and reducing accuracy²⁶. For AE, because the encoder uses ReLU as the activation function to produce the latent representation, the mapping is nonlinear, which may have been misaligned with our construction of the functions $g_{i}$. Taken together, these results suggest that, within the proposed anomaly-detection framework, constructing the intermediate representations with PCA or RP is more likely to deliver stable and higher detection performance.

Table 3 AP_all comparison of all models on synthetic data under the i.i.d. setting. Values without parentheses represent the means, whereas those within parentheses indicate the standard deviation. Excluding CA, the best scores are shown in bold, and the second-best scores are underlined.

Table 4 AP_all comparison of all models on synthetic data under the non-i.i.d. setting. The presentation style is consistent with that of Table 3.

We next compare the proposed method with the other methods. First, compared with IA, DC (PCA) and DC (RP) outperformed IA on all the metrics (AP_all, AP_global, and AP_local) under both i.i.d. and non-i.i.d. settings. This finding indicates that safely integrating data distributed across multiple organizations can yield a more effective anomaly detection model than training on a single organization’s data alone. Under the i.i.d. setting, DC (PCA/RP) also outperformed FedAvg and FedProx in many scenarios. In particular, for AP_all, although FedAvg and FedProx exhibited marked performance degradation when the anomaly rate decreased from 25 to 5%, the decrease in performance for DC (PCA/RP) was relatively modest. This suggests that our method remains effective even under the highly imbalanced conditions that are typical in auditing practices, where the proportion of anomalies is small. Figure 4 presents a comparison of AP for each anomaly type (global and local). For readability, Fig. 4 visualizes only DC with PCA and RP; results for the other dimensionality-reduction methods (LPP and AE), as well as detailed numerical values, are provided in the Supplementary Materials. For global anomalies, DC (PCA/RP) achieved AP very close to that of CA, which assumes the ideal scenario of fully centralized data. For local anomalies, DC (PCA/RP) outperformed FedAvg and FedProx in most cases and maintained performance close to that of CA.

Fig. 4

Comparison of AP_global and AP_local on synthetic data under the i.i.d. setting.

In the non-i.i.d. setting, AP_all tended to decrease overall compared with the i.i.d. setting, with FedAvg exhibiting a particularly large drop in performance. Although FedProx achieved higher AP_all than FedAvg did, DC (PCA/RP) outperformed FedProx under many configurations. Considering each anomaly type separately (Fig. 5), for global anomaly detection, DC (PCA/RP) analysis continued to maintain AP comparable to that of CA and demonstrated robust performance even under non-i.i.d. conditions. On the other hand, local anomaly detection proved more challenging overall, and AP decreased for all methods; however, DC (PCA/RP) analysis outperformed FedAvg and FedProx and retained the performance closest to that of CA. The Supplementary Materials include detailed tables of AP_global and AP_local means and standard deviations. These results indicate that the proposed method delivers superior anomaly detection performance compared with existing approaches across numerous conditions in both i.i.d. and non-i.i.d. settings and is particularly effective in the non-i.i.d. environments typical of real-world deployment. For the additional evaluation metrics (ROC-AUC, F1 score, recall, and FPR), DC (PCA) and DC (RP) likewise achieved generally favorable results compared with the other methods. Full details are provided in the Supplementary Materials.

Fig. 5

Comparison of AP_global and AP_local on synthetic data under the non-i.i.d. setting.

Real journal entry data

Building on the findings from the synthetic-data experiments, we compared PCA and RP as dimensionality-reduction functions on the real dataset. The experimental results on the real journal-entry data are summarized in Tables 5 and 6. Under the i.i.d. setting (Table 5), DC (PCA) exceeded IA on all three metrics— AP_all, AP_global, and AP_local —for both client counts, and, among methods other than CA (which is impractical due to confidentiality constraints), it achieved the second-best performance on AP_all and AP_local. By contrast, DC (RP) attained the best result for AP_global (= 1.000), but for AP_all and AP_local it fell short of IA in many conditions. Overall, in the i.i.d. setting, FedAvg yielded the best AP_all/AP_local, DC (RP) yielded the best AP_global, and DC (PCA) consistently ranked second on AP_all/AP_local.

Table 5 AP comparison of all models on journal entry data under the i.i.d. setting. The presentation style is consistent with that of Table 3.

Table 6 AP comparison of all models on journal entry data under the non-i.i.d. setting. The presentation style is consistent with that of Table 3.

Under the non-i.i.d. setting (Table 6), DC (PCA/RP) consistently outperformed IA. This indicates that—even with real journal-entry data reflecting practical operating conditions—our method can jointly learn from multiple organizations and produce a more effective model than one trained on a single organization’s data. Among the comparison methods excluding CA, DC (PCA/RP) most often achieved the best overall scores. Specifically, for AP_all, DC (PCA) was best with 4 clients, and DC (RP) was best with 8 clients; for AP_local, DC (PCA) (4 clients) and DC (RP) (8 clients) were best. For AP_global, while FedProx achieved the best result (= 1.000), DC (PCA/RP) attained comparable levels (0.993–1.000). For the additional evaluation metrics, DC (PCA) and DC (RP) likewise achieved generally favorable results compared with the other methods. Full details are provided in the Supplementary Materials.

From these results, in many cases, the proposed method outperforms IA and demonstrates superior anomaly detection performance compared with the existing methods FedAvg and FedProx. In particular, its efficacy under the non-i.i.d. setting—which closely resembles real-world operations—is remarkable; especially for local anomalies, which are relatively difficult to detect and carry high fraud risk, our method consistently achieves higher detection performance than the baselines do. We hypothesize two complementary reasons for the superior performance of DC analysis under non-i.i.d. conditions. First, DC analysis differs from FL in how the model is formed. In FL, each client updates its model to fit its own local data; when client updates reflect heterogeneous distributions, the aggregated update can become unstable or suboptimal. Although FedProx alleviates this issue, it cannot fully eliminate it. In contrast, DC analysis converts samples into a shared collaboration space first and then trains a single model on that space, thereby avoiding cross-client update inconsistency. In our experiments, this benefit outweighed the potential drawback of information loss due to dimensionality reduction. Second, DC analysis and FL differ in the granularity and amount of information used at aggregation. FL aggregates model parameters, whereas DC analysis effectively aggregates sample-level representations. The latter can preserve more task-relevant variation across clients, which may explain the observed accuracy gains under distribution shift. Further theoretical analysis to substantiate these hypotheses is left for future work.

These findings suggest that the proposed approach is effective in actual auditing scenarios where multiple organizations maintain distinct data distributions. However, the detection performance for local anomalies still shows a substantial gap compared with CA. We speculate that this degradation in performance could stem from the intermediate representations generated in our approach; as the data obtained via one-hot encoding of journal entries are highly sparse, the subsequent dimensionality reduction may not preserve sufficient information for generating an effective collaboration representation, ultimately reducing detection accuracy.

Conclusion

In this paper, we have proposed a framework that integrates journal entry data distributed across multiple organizations to construct an anomaly detection model with only a single communication round without requiring devices holding raw data to connect to the internet. Our method is based on DC analysis and builds an aggregated model by integrating only intermediate representations derived from each organization’s data. The novelties of this study include (1) the first application of DC analysis to unsupervised journal entry anomaly detection, achieving model construction in a single communication round without directly connecting confidential data to external networks, and (2) the use of real journal entry data provided by multiple organizations to conduct comparative evaluations against existing FL methods under non-i.i.d. settings. Experiments on both synthetic and real data demonstrated that the proposed method consistently outperforms models trained on a single organization’s data and, under most conditions, exceeds the performance of FedAvg and FedProx. Our framework addresses the critical confidentiality challenges of AI deployment in auditing and holds promise for advancing practical AI applications in this domain.

Several challenges remain. First, further analysis of confidentiality protection is an important task. In this study, no noise was added to the shared intermediate representations, and our privacy discussion is grounded in the structural properties of DC analysis (i.e., non-model-sharing and single-round communication). Building on prior work that applies differential privacy (DP) to dimension-reduced intermediate representations³⁴, enhancing the anomaly-detection methodology constitutes a promising direction for future research. In parallel, it is necessary to conduct quantitative evaluations—following, for example, Asif et al. (2024)³⁵—against attacks such as attribute inference, partial reconstruction, and reverse inference combined with external knowledge bases. Furthermore, for highly sparse data arising from one-hot encoding, as in journal entries, the extent to which PCA and other dimensionality-reduction techniques provide protection should be systematically examined. Second, validation using real-world anomalies remains. Although we followed Schreyer et al. (2022)¹⁸ in generating synthetic anomaly data, future work should evaluate the detection of actual fraudulent or misposted journal entries. Finally, journal entry records include additional information such as transaction dates, data-entry personnel, and journal descriptions that were not used in this study. The incorporation of these supplementary attributes is expected to enable the development of more practical and comprehensive anomaly detection methods for journal entry data.

Methods

Data collaboration analysis

Data collaboration analysis (DC analysis), proposed by Imakura and Sakurai (2020)²⁰, is a non–model share-type distributed data analysis method. Similar to FedAvg and FedProx, DC analysis comprises clients that hold local data and an analyst (server) that constructs the aggregated model. In this method, confidentiality is preserved by converting distributed raw data into intermediate representations before aggregation rather than sharing the data directly. An intermediate representation is obtained by applying a dimensionality-reduction function—such as principal component analysis (PCA)³⁶ or locality preserving projection (LPP)³⁷—which each organization may choose independently. Because the dimensionality-reduction functions are never shared, no organization can infer another’s raw data without access to its specific function. Once the intermediate representations are aggregated at the analyst, they are transformed back into a collaboration representation, enabling integrated analysis.

From here, we outline the fundamentals of DC analysis. Note that DC analysis can enable collaboration not only among organizations that are horizontally partitioned (i.e., samples distributed across organizations) but also among those that are vertically partitioned (i.e., features distributed across organizations). In this paper, however, we focus exclusively on sample-direction (horizontal) collaboration. Let $c$ denote the number of collaborating organizations, and $X_{i} \in {\mathbb{R}}^{{n_{i} \times m}} \left( {0 < i \le c} \right)$ denote the raw data owned by the $i$-th organization. We also define $X^{anc} \in {\mathbb{R}}^{r \times m}$ as the anchor data, where $m$ denotes the dimension of the features and $r$ denotes the sample size. Anchor data are shared among all organizations and used to create the transformation function $g_{i}$, which converts intermediate representations into collaboration representations. The simplest form of anchor data can be a random matrix; however, it can also be generated from public data or basic statistics via methods such as random sampling, low-rank approximations, or synthetic minority oversampling techniques^23,38.

The DC analysis algorithm proceeds as follows. Each organization creates its own intermediate representation function $f_{i}$. The intermediate representation of $\tilde{X}$ is expressed as

$$\begin{array}{*{20}l} {\widetilde{{X_{i} }} = f_{i} \left( X \right) \in {\mathbb{R}}^{{n_{i} \times \tilde{m}_{i} }} ,\left( {0 < \tilde{m}_{i} < m} \right)} \\ \end{array}$$

(1)

where $0 < \tilde{m}_{i} < m$ denotes the dimensions of the intermediate representation. Using the same function $f_{i}$, each organization performs dimensionality reduction on the anchor data:

$$\begin{array}{*{20}l} {\tilde{X}_{i}^{anc} = f_{i} \left( {X^{anc} } \right) \in {\mathbb{R}}^{{r \times \tilde{m}_{i} }} } \\ \end{array}$$

(2)

Subsequently, $\tilde{X}_{i}$ and $\tilde{X}_{i}^{anc}$ are shared with the analyst to create a collaboration representation.

Before constructing the collaboration representation from intermediate representations, we first give an intuition. Each organization’s intermediate representation is expressed in its own local coordinate system, so even for identical source data the vectors generally do not align. Naively concatenating them therefore fails to support meaningful joint analysis. The remedy is to map all intermediate representations into a common coordinate system. Concretely, if we can construct a shared coordinate system $Z$ and function $g_{i}$ such that $g_{i} \left( {\tilde{X}_{i}^{anc} } \right) \simeq Z$ for the anchor data, then each client’s space can be aligned to $Z$ and integrated. The singular value decomposition (SVD) is employed to derive $Z$; Imakura et al. (2020)²⁰ showed that $Z$ can be approximated using SVD. The details are described below.

The goal is to determine the mapping functions $g_{i}$ such that the transformed representations are aligned across organizations, i.e., $g_{i} \left( {\tilde{X}_{i}^{anc} } \right) \simeq g_{j} \left( {\tilde{X}_{j}^{anc} } \right), i \ne j.$ Assuming that the mapping function $g_{i}$ from intermediate representations to collaboration representations is a linear transformation,

$$\begin{array}{*{20}l} {\hat{X}_{i} = g_{i} \left( {\tilde{X}_{i} } \right) = \tilde{X}_{i} G_{i} ,\hat{X}_{i}^{anc} = g_{i} \left( {\tilde{X}_{i}^{anc} } \right) = \tilde{X}_{i}^{anc} G_{i} } \\ \end{array}$$

(3)

These transformations can be determined by solving a least-squares problem using SVD²⁰. The transformation matrix $G_{i}$ is obtained by solving

$$\begin{array}{*{20}l} {\mathop {\min }\limits_{{G_{1} , \ldots ,G_{c} ,Z}} \mathop \sum \limits_{i = 1}^{c} \left\| Z - \tilde{X}^{anc} {G_i} \right\|_F} \\ \end{array}$$

(4)

This problem is difficult to solve directly. However, an approximate solution can be derived using SVD as (5).

$$\begin{array}{*{20}l} {\left[ {\tilde{X}_{1}^{anc} , \tilde{X}_{2}^{anc} , \ldots , \tilde{X}_{c}^{anc} } \right] = \left[ {U_{1} , U_{2} } \right]\left[ {\begin{array}{*{20}l} {{\Sigma }_{1} } & O \\ O & {{\Sigma }_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {V_{1}^{T} } \\ {V_{2}^{T} } \\ \end{array} } \right] \simeq U_{1} {\Sigma }_{1} V_{1}^{T} } \\ \end{array}$$

(5)

The target matrix is set as $Z = U_{1}$. Then, the transformation matrix, $G_{i}$, is obtained as

$$\begin{array}{*{20}l} {G_{i} = \left( {\tilde{X}_{i}^{anc} } \right)^{\dag } U_{1} C} \\ \end{array}$$

(6)

Here, † denotes the Moore–Penrose pseudoinverse, and $\cdot_{F}$ denotes the Frobenius norm. Moreover, ${\Sigma }_{1} \in {\mathbb{R}}^{{\hat{m} \times \hat{m}}}$ is a diagonal matrix, $U_{1}$ and $V_{1}$ are orthogonal matrices, and $C \in {\mathbb{R}}^{{\hat{m} \times \hat{m}}}$ is an invertible matrix. Through these steps, the analyst obtains the collaboration representation

$$\begin{array}{*{20}l} {\hat{X} = \left[ {\hat{X}_{1}^{T} ,\hat{X}_{2}^{T} , \ldots , \hat{X}_{c}^{T} } \right]^{T} \in {\mathbb{R}}^{{n \times \hat{m}}} } \\ \end{array}$$

(7)

This collaboration representation can then be used for classification tasks, predictive modeling, or other forms of analysis.

The privacy characteristics under DC analysis are as follows. Imakura et al. (2021)³⁹ show that, under (1) non-disclosure of locally chosen dimensionality-reduction functions and (2) single-round (non-iterative) sharing, exact recovery of the original data is infeasible for an analyst acting alone and even when collusion involves up to c − 2 participants (where c denotes the number of participating organizations). Furthermore, even if some dimensionality-reduction functions were leaked, a lower bound on reconstruction error due to dimensionality reduction prevents perfect inversion. In addition to protection stemming from dimensionality reduction, a framework has been proposed that adds noise to the shared intermediate representations to satisfy (ε, δ)-differential privacy (DP)³⁴, and empirical studies indicate that combining dimensionality reduction with noise reduces the success rate of re-identification attacks⁴⁰.

Autoencoder

In this study, an autoencoder is adopted as the anomaly detection model^6,18,32. An autoencoder consists of two networks, an encoder and a decoder, that jointly learn to compress input data into a latent space and then reconstruct it back into the original space.

Using an autoencoder for anomaly detection typically involves two steps. First, the autoencoder is trained solely on normal data. Then, when new data containing potential anomalies are subsequently input into the trained autoencoder, the reconstruction error between the output and input is calculated. Samples exhibiting large reconstruction errors are considered to be deviations from the learned representation of normal data and are thus flagged as potential anomalies.

The autoencoder’s layer architecture is tailored to each of the two datasets described below. For experiments on synthetic data, we employ an autoencoder with the following architecture: [input layer, 6, 4, 2, 4, 6, output layer]. For experiments on real journal entry data, following Schreyer et al. (2022)¹⁸, we use an autoencoder with the following architecture: [input layer, 128, 64, 32, 16, 8, 4, 8, 16, 32, 64, 128, output layer].

Proposed method

In this section, we describe our proposed anomaly detection method for journal entry data using DC analysis. Notably, our approach does not require devices holding raw data to connect to any external network, and it requires only a single communication round to integrate data. Our proposed method consists of four steps.

Creation of intermediate representations

First, each organization uses its historical, audited normal journal entry data to generate intermediate representations via a dimensionality reduction function $f$ and shares these representations with the analyst. Because the intermediate representations alone do not permit exact reconstruction of the raw data, confidentiality is preserved³⁹.

In this study, we adopt four types of dimensionality reduction functions: PCA, random projection (RP) [41], LPP, and autoencoder (AE). PCA is a linear method that finds orthogonal directions maximizing data variance; RP maps data to a lower-dimensional space using a random matrix and approximately preserves pairwise distances; LPP is a graph-based linear embedding that preserves local neighborhood structure; and AE is a learned nonlinear encoder–decoder where the encoder provides the low-dimensional representation.

We first preprocess the journal entry data via one-hot encoding of categorical variables and normalization of continuous variables, and then apply the corresponding dimensionality reduction method to obtain reduced-dimensional representations. The same mapping is also applied to the anchor data. Specifically, we set the target dimensionality $\tilde{m}_{i} = m - 1$, and the anchor data consist of a random matrix with values uniformly sampled from 0 to 1. For AE, we train a single-hidden-layer autoencoder with latent dimension $m - 1$, and use the encoder part to perform dimensionality reduction. While the target dimensionality is fixed at $m - 1$ in this study, a systematic ablation over alternative reduction methods and varying target dimensions is left for future work.

Construction of collaboration representations

The analyst uses the intermediate representations of the anchor data collected from each organization to construct $G_{i}$ according to Eq. (6). Next, $G_{i}$ is employed to generate the collaboration representation $\hat{X}_{i}$ as defined in Eq. (3). Finally, these are integrated via Eq. (7) to train the autoencoder.

Autoencoder training

The analyst trains the autoencoder using the integrated representation $\hat{X}$. Rectified linear unit (ReLU) activations are applied to all the hidden layers, and identity activation is used for the output layer. The mean squared error (MSE) loss function is employed. By minimizing the MSE, the model parameters are updated to accurately reconstruct normal patterns—yielding low reconstruction errors—while producing higher reconstruction errors for unseen or anomalous patterns.

Anomaly detection on test data

Finally, we perform anomaly detection on test data that may contain anomalous samples using the trained autoencoder. The analyst sends $G_{i}$ and the trained autoencoder to each organization. Given test data $Y_{i}$, each organization applies the same dimensionality reduction function used on the training data $X_{i}$ to produce $\tilde{Y}_{i}$. Subsequently, $\hat{Y}_{i}$ is generated using $G_{i}$ and input into the trained autoencoder for anomaly detection. Any journal entry with a high degree of reconstruction error is examined further by auditors, if necessary. The pseudocode for the proposed method is provided in the “Proposed Method” Algorithm.