Introduction

Zinc oxide (ZnO) stands as a highly valuable material in modern materials research. Its attractive features include a wide band gap, strong exciton binding energy, and good chemical stability. Researchers widely use ZnO in devices like UV lasers, solar cells, and gas sensors. However, for newer technologies such as spintronics which use the electron’s spin instead of its charge pure ZnO often falls short. It usually shows very weak magnetism at room temperature1,2,3,4.

Recent research has demonstrated that forming nanocomposites with transition metal oxides represents an effective strategy for enhancing and modifying ZnO’s performance characteristics. For instance, studies have shown that dual-doping approaches can simultaneously tailor ferromagnetic and dielectric properties in ZnO nanoparticles for spintronic applications5,6. Similarly, the incorporation of specific transition metals has been shown to modify charge transport mechanisms and enhance room-temperature ferromagnetic interactions in ZnO nanostructures7,8.

For excellent performance in optoelectronics, magnetic data storage, spintronics, magnetic.

For excellent performance in optoelectronics, magnetic data storage, spintronics, magnetic actuators, and solar cells, one-dimensional nanoparticles (NPs) with a high surface-to-volume ratio, more oxygen vacancies (OV), and quantum size confinement have been recommended9,10 To be eligible for such devices, metal-oxide nanocomposites (MONCs) of multiphase must have one, two, or three dimensions smaller than 100 nm. When combined with certain other oxides of 3d-transition metals (TMs), ZnO may need to be precisely adjusted to form unique characteristics of nanocomposite materials, including high OV, big surface area, and strong conductivity, which ultimately adjust their qualities11,12.

Additionally, the integration of ZnO with other metal oxides to form heterostructures represents an effective approach for tailoring material properties beyond the intrinsic limits of single-phase systems. In such nanocomposites, the resulting heterojunction interfaces play a key role in modulating charge carrier dynamics, often leading to superior performance in functional devices. Recent studies on ZnO-based heterostructures highlight their potential in diverse fields, including optoelectronics, catalysis, and energy storage. For instance, the establishment of a p-n junction at the ZnO/CuO interface has been shown to enhance charge separation, making it highly relevant for photovoltaic and sensing applications13,14. Similarly, interfaces in n-n systems like ZnO/Fe₂O₃ can create complex charge transport pathways beneficial for gas sensing and advanced electronics15,16.

On the other hand, with a resistivity of 9.5 Ω.cm at RT, non-stoichiometry of ZnO can lower their energy gap (Eg) to 3.2 eV1,17,18. For spintronic devices, ZnO typically exhibits diamagnetic or poor ferromagnetic behavior at RT (RTFM), which is inconvenient for spintronic devices19. However, interstitial defects and OV are primarily responsible for creating magnetic polarons through the exchange magnetic interaction between OV and the spin of unpaired electrons20,21 However, in the case of TM-doped ZnO, RTFM was created via the exchange interaction between conductive Zn electrons and local d-spin-polarized electrons of 3D transition metals (TMs)22,23. However, the ionic size, valence state, doping content, and magnetic moment of TMs have a major impact on the proper selection of TMs to ZnO24,25 Sadly, the RTFM in doped ZnO has been obtained with a limit concentration of TMs (Co, Mn, Fe, and Ni) that is less than 0.25; nevertheless, the RTFM is destroyed by the super-exchange interaction above 0.25 due to few secondary26,27.

Since inherent defects in ZnO are responsible for the visible photoluminescence (PL) emissions, it can offer a profound understanding of crystallographic flaws, OV, and dangling bonds. The near band edge (NBE) of charge carriers is indicated by the PL band emission in the blue ultraviolet (UV) region, which frequently narrows in a wide band gap (Eg) materials28. For instance, ZnO is perfect for use in cathode-luminescence displays (CLDs) and white light-emitting diodes (LEDs) because of its excellent PL centers resulting from its multicolor emissions29. For this reason, ZnO’s PL is typically characterized by broad-band and strong UV emissions30. Furthermore, faults can produce a variety of colored emissions throughout the visible spectrum31,32 In any event, as the particle size of MONCs approaches the Bohr radius of the excitons, they usually show significant PL intensity due to their enhanced surface-to-volume ratio33.

According to the calculations, the energy needed for defect production has significantly decreased, resulting in mutual interactions that are less expensive in terms of energy28,34. For instance, both pure and TM-doped NPs showed the red28,29. The induced matrix lattice expansion caused by resonant energy transfer between nanomaterials and TMs is the explanation for this behavior29. On the other hand, a generated Ov peak in the core causes a blue shift in the NPs core-shell. Due to the constriction of core-shell development, this may also be described in terms of ascribed strain faults in comparison to the higher strain35,36. However, more information is needed to compare the impact of two distinct groups of TMs added to ZnO as NCs on the PL (two magnetic and one nonmagnetic).

The presence of several valence states for the host lattice of ZnO suggests polar-ionic conduction because of the electrons’ hopping process from lower to higher valence levels37,38. This di-electricity mechanism, described by complicated dielectric parameters against the frequency range up to 10 GHz, is primarily caused by internal faults39,40,41,42,43. High dielectric constant materials are widely known to have drawn particular interest in integrated microwave circuits and mobile phones44,45,46. On the other hand, low dielectric constant materials could be used in nonlinear optical and high-frequency antenna devices47,48,49,50.

Maxwell-Wagner interfacial49,50. The Cole-Cole plots show that conductivity mostly occurs across the grain border and does not contribute through the grains because grain boundary resistance is more common than grain boundary resistance51,52 According to the correlated barrier hopping (CBH) mode, conduction happens via a bi-polaron hopping process in which two electrons concurrently cross the potential barrier between charged defect states53. As a result, single polaron hopping is the main mechanism, and the barrier height is associated with their separation.

Achieving the desired characteristics may necessitate doping ZnO with transition metals (TMs), as this can enable the adjustment of properties such as dielectric constants (ε), dielectric loss (tan δ), and AC conductivity (σac). For example, ε\ and σac of ZnO are significantly decreased by Fe, V, and Mn dopants53,54,55. In contrast, σac increases against frequency (f), and the complex impedance analysis suggests the dominance of grain resistance. The exchange interactions between Zn and TMs are explained by Maxwell-Wagner interfacial polarization and Koops’s phenomenological theory, which explain this behavior. Additionally, the frequency-dependent AC conductivity of NCs follows Jonscher’s power law describing the hopping mechanism of non-Debye relaxation56. In contrast, the increment of σac observed for some of NCs is further required for the efficiency of solar cells46.

CuO is a monoclinic p-type of (1.4–1.65 eV) narrowed indirect Eg, and usually exhibited paramagnetic behavior at RT. It has a low electrical resistivity of 19 (Ω.cm), and therefore, it has been investigated in some advanced electronic devices. It is found that adding Cu to the ZnO host lattice improves its properties57,58. In contrast, Mn3O4 is a tetragonal n-type material with Eg of 2.1 eV and a magnetic moment of 4.9 µB, exhibiting weak paramagnetic behavior. It has an electrical resistivity of 107 Ω·cm at RT in its stoichiometric form. Mn3O4 is not expected to be a source of ferromagnetic domains, but it may be suitable for other applications59,60. On the other hand, α-Fe2O3 is a promising cubic n-type semiconductor due to its wide Eg of 2.2 eV, high chemical stability, and ferromagnetic behavior with a magnetic moment of 3.56 µB. Although α-Fe2O3 is an insulator with an electrical resistivity of 1014 Ω·cm at RT in its stoichiometric form, this resistivity can be reduced by doping with TMs61,62.

These results demonstrated that ZnO’s PL, dielectric medium, and RTFM characteristics remain unclear and require further study, particularly when doped or composited with TMs. The PL, dielectric, and magnetic characteristics of ZnO/M NCs with M = CuO, Fe2O3, and Mn3O4 have been examined with this goal in mind, and the results have been compared with those obtained for ZnO NPs. Although the dielectric and RTFM behaviors of ZnO-NPs are improved when composited with M, the PL intensity is decreased. The composites are to be in the order of ZnO/Mn3O4, ZnO/Fe2O3, ZnO/CuO and ZnO for PL behavior, but the vice is true for dielectric and magnetic behaviors. The correlation behavior between them actually reflects the different and unusual effects of impurities on different properties, which highlights the present investigation.

Experimental details

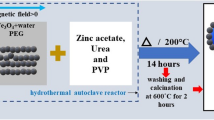
ZnO/M NCs with M = CuO, Fe2O3, and Mn3O4 have been produced utilizing ZnCl2, MnCl2, FeCl3, and NaOH in a hydrothermal process. 20 mL of double-stage distilled water were used to dissolve one mole of each chloride and one mole of NaOH, which were then agitated for 10 min at RT. Using magnetic stirring, NaOH was added to the solutions dropwise and stirred for 60 min, and then they were put in a Teflon container, which was then heated to 453 K for 12 h in a stainless-steel autoclave. Following heating, the items underwent a 3-min, 10,000-rpm intermediate centrifugation before being cleaned with distilled water and acetone. After being cleaned, the composites were crushed, dried for 5 h at 353 K in an oven, and then annealed at 673 K in a furnace. To analyze the nanocrystals (NCs) for phase purity, structural morphology, and elemental composition, an X-ray diffractometer (Philips PW-1700, Netherlands), FEI Quanta 250 scanning electron microscope (SEM), and energy dispersive X-ray (EDX) spectroscopy were employed. The XRD data were further refined using the Rietveld method to extract detailed structural parameters. Photoluminescence (PL) measurements at 320 nm were conducted using a Jasco FP-6500 spectrofluorometer equipped with a 150-watt xenon arc lamp as the excitation source. Broadband dielectric spectroscopy (BDS) was used to obtain dielectric measurements with a high-resolution Alpha analyzer equipped with an active sample head (Novo Control GmbH), covering the frequency range from 0.10 to 20 MHz. The pellets were placed between two parallel gold-coated stainless-steel electrodes, each 20 mm in diameter. Fused silica fibers with a diameter of 50 mm served as spacers. Magnetization measurements were performed using a Lakeshore 7400 vibrating sample magnetometer (VSM), with the magnetic field applied up to 17,300 Oe.

Results and discussions

Structural analysis

The NPs and NCs are arranged to be ZnO, ZnO/CuO, ZnO/Fe2O3, and ZnO/Mn3O4, respectively. The XRD pattern shown in Fig. 1 approved a hexagonal structure for ZnO with a change in the structure of the ZnO/M NCs. Besides the ZnO hexagonal structure, CuO, Fe2O3, and Mn3O4 could be respectively formed in tetragonal, monoclinic, and rhombohedral12. To get a more detailed picture of our crystal structures, we performed Rietveld refinement on the XRD patterns. The refinement plots, which show the measured data, the calculated pattern, and the difference between them, are given in Fig. 1. A good fit is achieved because the difference line (residual) is flat and featureless. For all our samples the residuals are mostly flat, indicating that the structural phases are a strong match for the measured data. The Rietveld refinement gave us a clear look at what’s inside our samples. The Rietveld refinement results in Table 1 confirm we successfully made the composites we intended. Pure ZnO refined nicely, with an R-factor of 7.7. This tells us the crystal structure is a good match for the standard hexagonal ZnO pattern. For the ZnO/CuO composite, the refinement worked even better, giving us our lowest R-factor of 5.8. This is a strong sign that both the hexagonal ZnO and monoclinic CuO phase are present and that our model fits the real data very well. You can see this in the lattice parameters; the a and c values for ZnO in this composite (a = 3.2498 Å, c = 5.2057 Å) are almost identical to pure ZnO, showing that the ZnO structure stayed intact. The ZnO/Mn₃O₄ nanocomposite, the refinement picked up not just ZnO but also a ZnMn₂O₄ phase. The R-factor is a bit higher here at 8.9, which makes sense because fitting two interacting phases is trickier. The fact that it worked confirms we have a nanocomposite, not just a simple mixture. The ZnO lattice in this sample (a = 3.2483 Å, c = 5.2047 Å) shrank just a tiny bit, which could mean some manganese ions squeezed into the ZnO structure. The ZnO/Fe₂O₃ sample was the most challenging. It has the highest R-factor (17) and Chi² (8.3), which points to a more complex structure. The refinement shows that instead of simple Fe₂O₃, a cubic Zn/Fe oxide phase (Fe₀.₇Zn₀.₃) formed alongside ZnO. This new.

Table 1 The crystal structure parameters obtained from the Rietveld refinement method of the XRD data of the nanocomposites.
Full size table
Fig. 1
figure 1

Top: The XRD pattern of (a) ZnO NPs and (b) ZnO/CuO, (c) ZnO/Fe2O3, and (d) ZnO/Mn3O4 NCs. The symbols in the figure are Z: ZnO, Cu: CuO, Fe: Fe2O3, Mn: Mn3O4, and ZnMn: ZnMn2 + 3O 412. Below: the Rietveld Refinement of the XRD data of the nanocomposites.

Full size image

phase, and the bigger change in the ZnO’s lattice parameters (especially the much shorter c-axis at 4.8078 Å), suggests a strong reaction happened between ZnO and Fe₂O₃ during synthesis. This significant structural change is likely the main reason the refinement was harder to fit perfectly.

The crystallite size D is calculated by Scherrer equation (\(\:D=\frac{0.9\lambda\:}{B{cos}\theta\:}\)) based on the three peaks observed for ZnO at (2\(\:\theta\:\) = 31.75o, 34.41o, 36.24o), ZnO/CuO at (31.91o, 34.58o, 36.40o), ZnO/Mn3O4 at (31.73o, 34, 39o, 36.28o) and ZnO/Fe2O3 at (31.72o, 34.36o, 36.21o). The values of \(\:D\) shown in Table 1 are 25.14, 23.49, 25.56, and 26.31 nm for ZnO, and NCs. The \(\:D\:\)is increased by the addition of CuO, Mn3O4 and Fe2O3 to ZnO, respectively. This behavior could be due to the variation of both shape and size of NPs of ZnO/M NCs. In addition, as shown in Table 2, the EDAX confirmed the presence of the considered ions, such that Cu ion is the lower.

Table 2 Dhkl, particle size (PZ), and w % for ZnO NPs and ZnO/M NCs.
Full size table

ion incorporating Zn (30.03%), which is lower than those of Fe and Mn (68.30 and 46.77%). Interestingly, the wt% of O ions decreased from 28.91% for ZnO to 28.8%, 25.46%, and 4.988% for the composites, indicating that impurity ions help with more OV, especially for Mn. Furthermore, as seen in Fig. 2, the morphology of ZnO, and NCs contains nanoparticles (sheets and spheres) and nanorods. But the ZnO/Fe2O3 NCs consists of only NPs and is nearly free of nanorods12. The particle size (PZnano) of ZnO-NPs was decreased from 118 nm to 98, 87, and 105 nm for the NCs, respectively, whereas the PZrods of nanorods was raised from 283 nm to 522, 699 nm (see Table 2).

Fig. 2
figure 2

The SEM images of for ZnO NPs and ZnO/M NCs.

Full size image

Photoluminescence measurements

Figure 3 displays the ZnO and NCs’ PL intensity against wavelength, and Table 2 lists comparable values. In addition to a lower intensity IR emission peak observed for ZnO and ZnO/CuO NCs, three consecutive visible emissions (violet, blue, and green) were recorded. We were unable to detect a discernible shift in the peaks’ wavelengths that would have placed them nearly in the same location (± 6 nm), although their intensities differed greatly. However, the PL intensity is reduced for NCs, and their respective orders are ZnO/Mn3O4, ZnO/Fe2O3, ZnO/CuO, and ZnO. This suggests that more defects are present in NCs, which consequently reduce the PL intensity. Interestingly, the violet and blue spectra recorded between [(413–419 nm); (3.01–2.96 eV)] and [(456–462 nm); (2.72–2.69 eV)] exhibit strong and distinct emissions, respectively. The observed reduction in photoluminescence (PL) intensity in the nanocomposites can be directly linked to the presence of crystal defects, especially oxygen vacancies. These defect states act as non-radiative recombination centers. This means that instead of releasing energy as light, the excited electrons are captured by these traps and lose their energy through other means, primarily as heat through lattice vibrations (phonons). Essentially, the defects introduce a competing pathway for the excited electrons. As the number of defects increases, more electrons choose this non-radiative path over the light-emitting path. This competition effectively quenches the photoluminescence, leading to the significant decrease in PL intensity we observed in all the ZnO/M nanocomposites. The different metal oxides (CuO, Fe₂O₃, Mn₃O₄) likely introduce varying types and densities of these defects, which is why the exact PL behavior, both the intensity drop, and the specific spectral shifts differs between the samples. While collective data from photoluminescence, dielectric, and magnetic measurements strongly suggest the presence of defect states, direct chemical analysis via techniques like X-ray photoelectron spectroscopy (XPS) would be required in future work to unambiguously identify the specific nature and density of these defects.

Fig. 3
figure 3

PL intensity against wavelength for ZnO NPs and ZnO/M NCs.

Full size image

The blue emission in ZnO is greater than that of the violet in ZnO/Fe2O3 and ZnO/Mn3O4 NCs since (IB/IV) > 1, which implies a blue shift, but it became violet for ZnO/CuO NCs because (IB/IV) < 1. The energy of violet is between 2.96 and 3.01 eV, which is similar to ZnO, ZnO/CuO and ZnO/Mn3O4 NCs (2.64–3.13 eV), but it is higher than that of ZnO/Fe2O3 (2 eV), such that the Eg has been decreased for NCs12. It is primarily associated with the recombination of (e-h) pairs from localized levels below the CB61,62. The transition of electrons from a shallow donor level of neutral Znni to the highest level of the VB is connected to violet emissions. This suggests that the shallow donor level is situated about 0.19 eV below the CB63. The electrons’ radiative transfer from the shallow Zni donor to the neutral VZn acceptor is due to the centered blue emission64. The third lower peak between [559 and 563 nm] (2.22–2.20 eV) of green emission is attributed to donor-acceptor VZn recombination/or a transition from the CB to oxygen anti-sites due to OV65,66. The observed lowest intensity IR emission peak centered at 823 nm (1.51 eV) is attributed to the excitation of the (3d/4f) lowest energy of the ZnO, similar to TM3+-doped ZnO when excited above Eg, [320 nm (3.88 eV)]67. However, the photoluminescence (PL) of ZnO and its nanocrystals (NCs) can introduce impurities into the bandgap (Eg) of ZnO nanoparticles (NPs), potentially creating multiple impurity levels through multi-ionization processes20,68. The enhanced blue emission for ZnO/Fe2O3 and ZnO/Mn3O4 NCs confirms that Fe and Mn ions are successfully incorporated into ZnO, whereas its lower values for ZnO/CuO NCs may result from a recombination between the electrons in the CB and the holes trapped in the acceptors24,69. We believed that this trend is linked to either valency of Cu2+ as compared to Fe3+ and Mn2+/3+ or the magnetic moments of Fe and Mn ions, rather than the ionic radii of Cu, Fe, and Mn ions, which are close to that of Zn.

Additionally, the band gap energy (Eg) simply can be evaluated from photoluminescence (PL) using the formula Eg = hc/λ = 1241.4/λ (nm). Using the values of λ against the PL peak of UV emission, the values of Eg are 2.94, 2.97, 2.93, and 2.94 for ZnO, ZnO/CuO, ZnO/Fe₂O₃, and ZnO/Mn₃O₄ samples. This behavior indicates that Eg was increased against CuO, but it was nearly unchanged with the addition of Fe₂O₃ or Mn₃O₄.

Dielectric measurements

The real ε′ part of dielectric constant (ε), loss factor (tan δ) and q-factor are given by45,70;

$$\varepsilon ^{\backslash } = \frac{{Cd}}{{\varepsilon _{ \circ } A}};\tan \partial = \frac{{\varepsilon ^{{\backslash \backslash }} }}{{\varepsilon ^{\backslash } }}$$
(1)

C represents the capacitance of the sample, while C₀ is the capacitance of the empty cell (C₀ = ε₀A/d), where ε’’ denotes the imaginary part of the dielectric constant ε According to Fig. 4a, which plots ε′ against frequency (f), ε\ steadily dropped as f rose until it reached 1 MHz, at which point it saturated. However, the higher values of ε’ at lower frequencies indicate interactions between conductivity contributions and interfacial polarization. As the frequency increases, charge carriers tend to aggregate and generate dipolar polarization in response to the applied field, but they are unable to reverse their orientation when the field reverses71. All of the NCs have orders of ZnO/Fe2O3, ZnO/Mn3O4, and ZnO/CuO, and their ε′ values are greater than ZnO NPs due to the difference of electronegativity between ZnO and NCs, which in turn influences the strength of the ionic bonds and subsequently raises the dielectric polarization43,48. Furthermore, for NCs, a decrease in D and PZ may result in an increase in the number of dipoles, raising ε′ values. Based on the behavior of ε′, the NCs are better suited for integrated microwave circuits and telecommunications than ZnO NPs. The sharp drop in ε′ below 10 kHz, however, is mostly explained by a space charge regime that is roughly 20 nm thick72, and the field in such regime is anticipated to facilitate the de-trapping process and support the ε′ toward a very thin insulating layer. ZnO NPs have interfaces with a volume fraction of roughly 1019 interfaces/cm3, which increased space-charge polarization at low f73. Additionally, a large number of dipoles may develop between O and Ov, resulting in a high ε′ value, as obtained74.

The behavior of ε’’ against f is depicted in Fig. 4b, where ε’’ never reaches saturation but drops linearly with increasing f up to 20 MHz. This is ascribed to the contribution of ion hop and conduction loss of ion migration in addition to ionic polarization at low and moderate f75.

The fluctuation of tanδ against f is displayed in Fig. 4c. As f increases to 100 Hz, the tanδ of ZnO NPs is lower than that of ZnO/Mn3O4 NCs, but it is higher than that of ZnO/CuO and ZnO/Fe2O3. However, as f rises above 100 Hz, it falls below that of NCs. While the NCs displayed relaxation peaks (RPs) at 6.11, 0.295, and 0.0027 kHz, respectively, the ZnO NPs showed no RPs. This indicates a stable condition of the nanocrystals (NCs), rendering them unsuitable to replace ZnO, while showing minimal dynamic activity in dielectric conduction between the electrodes. For the ZnO/Fe₂O₃ and ZnO/Mn₃O₄ NCs, the relaxation peak frequency (f) decreases, primarily due to the hopping mechanism responsible for dc conduction. On the other hand, the RPs for ZnO/CuO NCs are typically shifted to high f by the conduction between localized states in the mobility gap, suggesting that the rate of hopping of localized charge carriers is increasing. Furthermore, the wide distribution of RPs for the NCs points to non-Debye-type behavior in the RPs spread76,77.

Fig. 4
figure 4figure 4

(a): The relation between real part of dialectic constant (ε/) and frequency for ZnO NPs and ZnO/M NCs. (b): The dependance of imaginary part of dialectic constant (ε//) on frequency.(c): Dielectric loss (tanδ) against frequency for ZnO NPs and ZnO/M NCs.

Full size image

The total conductivity (σt) is given by [76]

$$\sigma _{t} (\omega ) = \sigma _{{dc}} + \sigma _{{ac}} = \sigma _{{dc}} + B\omega ^{s}$$
(2)

where s is the frequency exponent, B is a constant, and σdc is the dc conductivity. The AC conductivity (σac) is plotted against f in Fig. 5a for NPs and NCs, in which σac steadily rises as f increases up to 20 MHz. The σac for the NCs is higher than that of ZnO NPs and has the same order of ε’. At a critical f, σac follows the relation (σac ∼ ωs), where s ≤ 1.00 for electronic conduction and s < 0.50 for hole conduction78. The values of s shown in Table 3 are obtained from the linear fit between ln σac and ln ω displayed in Fig. 5b. It is seen that s < 0.50 for all NPs and NCs, indicating hole conduction. The usage of NCs in solar cell design is strongly supported by the greater value of the F-factor for the figure of merit provided by\(F = \frac{{\sigma ^{\backslash } }}{{\varepsilon ^{\backslash } }}\)79. All samples’ F-factor variation with f is shown in Fig. 6, which shows a steady rise in the F-factor as the f increased to 20 MHz. Furthermore, the ZnO NPs F-factor rose for NCs, suggesting that all of them are more qualified than ZnO NPs for solar cell, particularly for ZnO/Mn3O4 at low f (< 10 kHz) and ZnO/CuO at f (> 10 kHz).

Table 3 s, frequency exponent, Binning energy and relaxation peaks of ZnO NPs and ZnO/M NCs.
Full size table
Fig. 5
figure 5

(a): The dependance of Ac conductivity on frequency for ZnO NPs and ZnO/M NCs. (b): The linear plot of ln σac against ln ω for ZnO NPs and ZnO/M NCs.

Full size image
Fig. 6
figure 6

F-factor against frequency for ZnO NPs and ZnO/M NCs.

Full size image

Figures 7a&b display the real (M\) and imaginary (M\\) parts of the electric modulus as functions of frequency (f) for the samples. It is observed that M\ increases with increasing frequency for all samples and then reaches a saturation point above 1 MHz, similar to ε′. Compared to pure ZnO, M\ values for the composites are lower below 1 MHz, but beyond this frequency, M\ surpasses that of ZnO. A similar trend is observed for M\\, although with different relaxation peaks (RPs). For example, M\\ shows a RPs at 100 kHz for ZnO and ZnO/Mn3O4, but it shifted to a low f of 32.80 kHz for ZnO/Fe2O3 and to a high f of 1860 kHz for ZnO/CuO. Likewise, Figures. 8a&b illustrate the real (Z\) and imaginary (Z\\) parts of the electric impedance as functions of frequency (f) for the samples. It is evident that at higher frequencies, Z\ values for all samples converge and stabilize, likely due to the dissipation of space charges80.

It is seen that Z\ gradually decreases as f increases and is saturated above 1 MHz. In addition, the Z\ of ZnO increases for ZnO/Fe2O3 composite, but it decreases for the other. A similar trend is observed for Z\\, with relaxation peaks (RPs) appearing at approximately 0.413, 100, (0.0027, 6.111), and 23.40 kHz, respectively. Additionally, Table 4 summarizes the frequencies of these RPs as determined from the curves of tanδ, M\\, and Z\\, indicating that the relaxation peak frequencies can be ranked in the order: M\\, Z\\, and tanδ. While they are arranged relative to samples to be ZnO/CuO, ZnO/Mn3O4, ZnO, and ZnO/Fe2O3.

Table 4 Wavelength, energy and PL intensity for ZnO NP and ZnO/M NCs.
Full size table

Assuming that the low-frequency relaxation process has a simple Debye behavior, one can determine its characteristic relaxation time (t) from the frequency against relaxation peaks (f max) of M\\ against f plot, using the equation t = (2ꙥfmax)⁻¹ or using t = (2ꙥfcross)⁻¹, where fcross is the crossing frequency between the M\, and M\\,, which usually separate between the Debye and non-Debye processes81. However, the non-Debye relaxation is a behavior in dielectric materials that deviates from the ideal Debye model, where a system is assumed to have a single relaxation time and instantly loses all memory of relaxation. However, for simplicity we have used the formal one. It is found that the values of t are 1.59, 0.086, 4.85, and 1.59 µs for the ZnO, ZnO/CuO, ZnO/Fe₂O₃, and ZnO/Mn₃O₄ samples, respectively. However, carrier relaxation is the process by which excited charge carriers (electrons and holes) lose energy and return to a lower energy state through various mechanisms, such as carrier-phonon scattering, carrier-carrier scattering, and recombination. Based on the above, the carrier relaxation time is similar for the ZnO and ZnO/Mn₃O₄, whereas the highest value is for ZnO/Fe₂O₃ and the lowest is for ZnO/CuO. Such difference between the samples can be attributed to the disorder and structural complexities in the material.

Fig. 7
figure 7

(a): The real part of electric modulus (M/) vs. frequency for ZnO NPs and ZnO/M nanocomposites (b): Imaginary part of electric modulus (M//) agianst frequency for ZnO.

Full size image
Fig. 8
figure 8

(a): The dependance of real part of impedance (Z/) on frequency for ZnO NPs and ZnO/M nanocomposites (b) The imaginary part of impedance (Z//) vs. frequency for ZnO NPs and ZnO/M nanocomposites.

Full size image

Figures 9 a&d display the Cole-Cole (Nyquist) plots of Z\\ versus Z\ for all samples. The plots show a spread rather than a perfect semicircle centered on the real axis, characteristic of non-Debye relaxation behavior. This non-Debye response suggests that the relaxation of dipole moments occurs over a distribution of relaxation times82. The figure displays two regions: the grain region at higher frequencies and the grain boundary region at lower frequencies, which are effectively modeled using an equivalent circuit consisting of parallel RC elements. The plots of Fig. 9 a, b & d for ZnO, ZnO/CuO, and ZnO/Mn₃O₄ samples show single semicircular arcs followed by straight lines or arcs with positive slopes at the tail end. The positive slope suggests an increase in conductivity and implies that a limited number of composite ions may be present at the grain boundaries, potentially facilitating transport across the grain boundaries and promoting grain growth83. In contrast, the plot of Fig. 9cfor ZnO/Fe₂O₃ sample exhibits two consecutive semicircles spanning the frequency range, indicating that the selected frequency range is adequate to distinguish between the conductivities of the grains and the grain boundaries. This behavior was effectively modeled using an equivalent circuit consisting of parallel RC elements, confirming the presence of non-Debye relaxation. The radius and diameter of each plot were used to calculate the first and second impedance components, representing grains and their boundaries as Z\(gf), Z\(gbs), Z\\(gf) and Z\\(gbs), respectively, as summarized in Table 5. It is found that the values of Z\(gf) and Z\(gbf) of ZnO were decreased for the composites, and they have the order of ZnO/CuO, ZnO/Fe2O3 ZnO/Mn3O4. A similar trend was obtained for Z\(gbf), but it has the order ZnO/CuO, ZnO/Mn3O4 and ZnO/Fe2O3. However, the values of Z\(gs) and Z\(gbs) of ZnO/Fe2O3 are 9.5 and 185 MΩ, which are more than those of Z\(gf) and Z\(gbf) (0.224 and 6.11 MΩ). The Z\ a function of f is given by48;

$$Z^{\backslash } (\omega ) = \frac{{R_{B} }}{{1 + (\omega C_{{eff}} R_{B} )^{2} }} \to \frac{1}{{Z^{\backslash } }} = \frac{1}{{R_{B} }} + \omega ^{2} C_{{eff}}^{2} R_{B}^{{}}$$
(3)
Table 5 s, Wm, Z\(g), Z\(gb) of the ZnO NPs and ZnO/M nanocomposites.
Full size table

In this equation, RB represents the series resistance, and Ceff denotes the effective capacitance of the parallel equivalent circuit. The intercepts of the linear plot between [1/Z\(ω)] and (ω²) provide the values of RB, while Ceff can be calculated from the slope, as shown in Table 5. The behavior of RB is similar to Z\ for grains and grain boundaries, with values of 5 MΩ, 0.5 MΩ, 14.30 MΩ, and 3.33 MΩ for ZnO and its composites. The values of Ceff are 0.02, 0.283, 0.012, and 0.03 µF, indicating that (Ceff α Z\)84,85. The observed increase in Ceff for ZnO/CuO composites can be attributed to the deformation of micro-capacitors, primarily influenced by factors such as crystallite size (PZ) and porosity introduced by Cu. Interestingly, high-performance lithium-ion batteries typically display low values of RB and Ceff, often characterized by a semicircular shape in the impedance spectrum. This behavior is mainly associated with the oxidation and reduction reactions of lithium ions within the electrode material83. In contrast, a supercapacitor requires a lower RB and a higher Ceff to minimize energy loss associated with the equivalent series resistance86. These findings strongly recommend that the ZnO, ZnO/Fe2O3 and ZnO/Mn3O4 nanocomposites are more suitable for high-power Li- batteries, whereas ZnO/CuO can be used as a supercapacitor, as reported.

Fig. 9
figure 9

(a-d): Cole- Cole plot of the ZnO NPs and ZnO/M nanocomposites.

Full size image

Magnetic measurements

Figures 10 display the room temperature (300 K) magnetic hysteresis loops of the samples, showing ferromagnetic behavior with varying saturation magnetizations (Ms). The field up to 2000 Oe is not sufficient to reach complete magnetic saturation for ZnO/Fe2O3 and ZnO/Mn3O4 composites. The Ms is 0.035 (emu/g) for ZnO, but it is increased to 0.039, 0.050, and 0.058 (emu/g) for the composites, respectively. Similar behavior was approved for coercive field Hc, magnetic moment µ = (WMs/5585), remnant magnetization (Mr), area under the curve, and magnetic anisotropy γ = (HcMs/0.98), which are listed in Table 622,87,88. In contrast, squareness Sq = (Mr/Ms) was decreased sequentially, and it is between 0.09 and 0.127 (< < 0.50) for all samples, indicating magneto-static interaction for the studied samples [89,90. The slight increase in Hc for the composites is evidence of hard magnetization91. According to TMs, Ms is follows the order of Zn, Cu, Fe and Mn. The RTFM behaviors for ZnO and ZnO/CuO samples are mainly originated by Zn interstitial sites and Ov, since Zn and Cu ions are nonmagnetic ions. Fe is a ferromagnetic ion and should be a source of strong ferromagnetic as compared to paramagnetic Mn ions, but it is further not obtained. Therefore, the RTFM behaviors can be explained by the following; Firstly, we expected that the change of valence state of Fe3+/2+ or Mn2+/3+ may be the source of the induced ferromagnetic as a result of decreasing Ov, see Table 2. This corresponds to the rise in compensated spins on the surface of the sample compared to the particle core, particularly as the particle size exceeds the constraints of quantum size confinement91,92. Secondly, the ferromagnetism may be attributed to strong magnetic interactions between Fe (3.36 µB) or Mn (4.9 µB) ions and singly ionized oxygen vacancies (Ov) via double-exchange mechanisms24,93,94. These ions are mediated by an electron trapped at the vacancy as well as F-center exchange interactions, which in turn supporting the RTFM88,95. So, as compared to Cu, Fe and Mn ions are able to tune the RTFM of ZnO-NPs to be qualified for spintronic devices25,26,96. In addition, the origin of room-temperature ferromagnetism (RTFM) is not solely attributable to well-known ferromagnetic impurity phases or clusters; other factors such as interstitial sites, oxygen vacancies (Ov), and valence states also play a significant role alongside magnetic moments.

Table 6 Magnetization parameters for ZnO NPs and ZnO/M nanocomposites.
Full size table
Fig. 10
figure 10

Magnetization (M) against applied field (H).

Full size image

for ZnO-NPs and ZnO/M nanocomposites.

Magnetization at any field M(H) is related to Ms using the following Stoner–Wohlfarth (S–W)97,98;

$$M = M_{s} (1 - \frac{\beta }{{H^{2} }})$$
(4a)

β is related to the field magnetic anisotropy and it is given by;

$$K_{{eef}}^{{}} = M_{s} \sqrt {(\frac{{15\beta }}{4})} H_{a} = (\frac{{2K_{{eff}} }}{{M_{s} }})$$
(4b)

Keff represents the effective magnetic anisotropy, and Ha is the anisotropy field. Keff is influenced by variations in magnetic anisotropy sources, which can either strengthen or weaken magnetic interactions within the nanocomposites. Values of the parameters β and Ms are deduced from the slope of the plot of magnetization (M) versus (1/H²), as shown in Figure 11, enabling the calculation of Keff and Ha, which are listed in Table 6. The Keff value is 26,247.26 emu·Oe/g for the ZnO sample but increases progressively in the composites, reaching a maximum of 306,431.07 emu·Oe/g for Fe₂O₃, indicating that Keff is proportional to Ms. Conversely, Ha is 17,144.26 Oe for the ZnO sample and decreases to a minimum of 4,895.06 Oe for the ZnO/Fe₂O₃ composite, demonstrating that Ha is inversely proportional to Ms. Additionally, the values of Ha and Keff are higher than those of Hc and γ, implying that the nanocomposites exhibit hard magnetic characteristics, which in turn influence the electron-spin interaction mechanism97,98,99.

Fig. 11
figure 11

Magnetization (M) against applied field (1/H2) for ZnO NPs and ZnO/M nanocomposites.

Full size image

The variation in switching field distribution (SFD) across different angles is crucial for single-domain magnetic particles, determining when each particle flips its magnetization state. This aspect is vital for magnetic recording media, as the anisotropic particles need to align in various field directions. To enhance output quality, it’s recommended to reduce the spin-flip distance (SFD) and keep it at a high level. This would lead to an increased number of reversed states of particle magnetization against H due to reduced demagnetization. The switching field distribution (SFD) is computed by96,98,100;

ΔH represents the full width at half maximum (FWHM) of the (dM/dH) versus H curve, as illustrated in Fig. 12a,b,c&d. The formation of a singular peak in the SFD plot indicates a dual exchange interaction, showcasing the magnetic connection between cations and anions due to the delocalization of electrons. It also signifies the energy barrier distribution within the nanocomposite, which is associated with a corresponding particle coercivity distribution, such as the optimal bias current and noise99. As listed in Table 6, the SDF of ZnO was decreased for the composites, indicating that barrier energy is inversely proportional to the magnetization parameters, but it has a similar behavior for Sq. In addition, the Ha values are 100–200 and 1500–2500 times higher than those of Hc and SDF.

Fig. 12
figure 12

(a-d): dM/dH against field of 100 Oe at 300 K for ZnO NPs and ZnO/M nanocomposites.

Full size image

Summarizing the results obtained for the ZnO/M composites as compared to ZnO (i) decreasing the PL intensity and a violet shift for the ZnO/CuO; increasing the values of ε\, σac and F-factor; decreasing the dielectric loss for ZnO/CuO and ZnO/Fe2O3, but it is increased for ZnO/Mn3O4; shifting the RPs to higher f, especially for ZnO/CuO, whereas it is increased for ZnO/Fe2O3 and ZnO/Mn3O4; decreasing the Z\(g) and Z\(gb) (viii) changing the RB and Ceff; increasing the Ms and most of magnetization parameters; decreasing the Sq. The consistency of these points provides a level of assurance regarding the potential of ZnO/M nanocomposites, making them promising candidates for advanced devices.

The investigated properties in the ZnO/M nanocomposites are correlated through a defect-mediated interplay. The incorporation of transition metal oxides (CuO, Fe₂O₃, Mn₃O₄) introduces oxygen vacancies and creates interfaces, which simultaneously enhance electrical conductivity and room-temperature ferromagnetism by promoting charge hopping and double-exchange interactions. However, these same defects act as non-radiative recombination centers, leading to the observed reduction of photoluminescence intensity. This produces an inverse correlation where the superior functional performance in the electrical and magnetic domains is achieved at the expense of optical emission efficiency. The specific characteristics such as the dielectric properties of ZnO/CuO, the complex impedance of ZnO/Fe₂O₃, and the strongest magnetism in ZnO/Mn₃O₄ are further fine-tuned by the unique cation valency, magnetic moment, and resultant phase composition of each composite, demonstrating the possibility of tailoring these materials for targeted advanced applications.

A key finding from Table 7 is the superior performance of our composites. This is clearly seen in the saturation magnetization (Ms): the ZnO/Mn3O4 and ZnO/Fe2O3 composites exhibit Ms values of 0.058 and 0.050 emu/g. These results are significantly higher by more than an order of magnitude than those reported for ion-doped systems like (Gd, Co) co-doped ZnO. The marked enhancement points to a fundamental conclusion: forming a composite with a discrete magnetic phase is a more productive route to strong ferromagnetism than traditional substitutional doping.

Table 7 A comparison of the ZnO nanocomposites from this study with those reported in the literature.
Full size table

The magnetic stability of these composites is further corroborated by their coercivity (Hc). With Hc values of 72.4, 71.2, and 80.4 Oe, the present composites perform comparably to, or even surpass, other magnetic ZnO systems like (Gd, Co) co-doped ZnO. Such performance indicates the presence of well-defined magnetic domains and effective pinning centers within the composite’s microstructure. A critical distinction for these composites, however, lies in their dielectric properties. They exhibit a high dielectric constant, a feature not emphasized in other high-Ms materials like Fe₃O₄@ZnO/C which are tailored for biomedical applications or in the ZnO–ZnFe2O4 nanocomposite, which is also targeted for spintronics. Even when compared to Sn: ZnO nanoparticles, proposed for high-frequency devices, our composites display a superior dielectric response. This concurrent possession of significant magnetization and high dielectric constant is a pivotal combination for multifunctional applications, particularly in spintronics, where the coupling of magnetic and electric properties is fundamental. In conclusion, the composites developed in this work occupy a unique niche. While they do not exhibit the ultra-high magnetization of iron-oxide-based biomaterials, they offer a more compelling synergy of magnetic and dielectric properties than many doped ZnO systems. This specific property profile renders them strong candidates for advanced spintronic and multifunctional device applications.