Disturbance observer based multiloop proportional feedback system for output voltage regulation in three phase AC to DC converters

Abstract

This paper suggests a disturbance observer (DOB)-based offset-free output voltage regulator for the three-phase AC/DC power converters, taking the nonlinearity, parameter, and load uncertainties into account. The proposed multiloop controller is designed in such a way that it feeds back only proportional errors and stabilizes the output voltage and current tracking errors involving the feed-forward compensation terms driven by the DOBs. The DOBs assist the inner and outer loop controllers to ensure the performance recovery and steady-state error rejection properties, which correspond to a major contribution of this article. A three-phase 3-kW AC/DC power converter is used for experimentally verifying the efficacy of the proposed technique.

Introduction

To achieve high output voltage tracking performance, three-phase AC/DC power converters commonly utilize the pulse-width modulation (PWM) technique, which is well-regarded for its effectiveness in feedback control system design. Ensuring the stable and efficient operation of these converters is essential, particularly under varying parameters and load conditions. This requirement is especially critical in industrial applications where precise and reliable power conversion is imperative. Such applications encompass four primary areas: renewable power plants, microgrid systems, and motor drives.^1,2,3,4.

The cascade control strategy is widely employed to regulate the output voltage of three-phase AC/DC power converters. In this framework, the outer loop generates the appropriate d-frame current command for the inner loop, thereby achieving output voltage regulation. Due to their structural simplicity, proportional-integral (PI) controllers are commonly adopted for both control loops^5,6,7. However, the inherent nonlinearities in three-phase AC/DC converter models, along with significant parameter and load variations, introduce uncertain disturbances that can severely degrade feedback performance or even lead to system instability. To address these challenges, various advanced nonlinear control approaches have been developed for the inner-loop current regulation. Methods such as feedback linearization (FL)^8,9, passivity-based control¹⁰, and predictive control¹¹ have shown substantial improvements in disturbance rejection and nonlinear compensation by leveraging accurate system parameters. In particular, model predictive control (MPC) techniques^12,13,14 enhance transient response by minimizing cost function errors through exhaustive search algorithms executed at each sampling interval. Despite these advancements, the effectiveness of these controllers remains heavily dependent on accurate knowledge of converter parameters, raising concerns about their robustness under varying operating conditions and parameter uncertainties. To address this limitation, an adaptive current controller was proposed in¹⁵ to accommodate such uncertainties. However, its ability to guarantee offset-free current convergence in practical settings is unclear, primarily due to the lack of integral action in its tracking error dynamics. More recently, an adaptive control scheme introduced in¹⁶ integrates a self-tuning algorithm within both the inner and outer loops to improve voltage tracking performance. Nevertheless, the complexity of the resulting control structure is significant, as it incorporates integral action, self-tuning mechanisms, and parameter estimation algorithms^17,18,19,20. Alternatively, disturbance observer-based (DOB) voltage controllers, such as those presented in^21,22,23,24, offer a simpler structure by embedding integrators in the tracking error dynamics, though they may require anti-windup strategies to prevent integrator saturation.

A variety of multivariable control methodologies rooted in advanced control theory have been explored in^25,26,27,28. These strategies generally follow a structured process: initially, a positive definite function is formulated to represent the tracking error dynamics; subsequently, a control input is designed to ensure that this function diminishes steadily over time. Although these techniques provide strong theoretical guarantees for system behavior, their success is highly contingent upon precise knowledge of the actual system parameters, which is essential for achieving both closed-loop stability and targeted control performance.

This article systematically and explicitly addresses nonlinearities and model-plant mismatches within the controller design framework. The proposed method adopts a multivariable control structure comprising a proportional-type nonlinear controller and first-order disturbance observers. The primary contribution of this study lies in the rigorous theoretical proof that the proposed algorithm ensures two critical closed-loop properties: (i) recovery of nominal performance and (ii) steady-state disturbance rejection—achieved without relying on integral action in the tracking error dynamics. This represents a significant departure from conventional approaches, such as those in^21,22, which incorporate integrators for error correction. Furthermore, an experimental study using a prototype 3-kW power converter validates the practical merit of the proposed technique by benchmarking it against the feedback linearization (FL) technique.

Nonlinear dynamics of AC/DC power converters

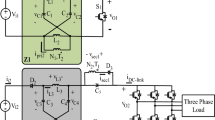
In this section, we briefly introduce the d-q frame dynamics of a three-phase AC/DC power converter aligned to the phase angle $\theta$ of input AC source power (called the d-q transformation). For more comprehensive details, please refer to^25,26. The topology of standard three-phase AC/DC power converter is depicted in Fig. 1 whose dynamics are obtained in this frame:

$$\begin{aligned} L \dot{i}_d(t)= & - R i_d(t) + \omega _r L i_q(t) + e_d(t) - v_d(t), \end{aligned}$$

(1)

$$\begin{aligned} L \dot{i}_q(t)= & - R i_q(t) - \omega _r L i_d(t) + e_q(t) - v_q(t), \forall t \ge 0, \end{aligned}$$

(2)

Fig. 1

Circuit of AC/DC power converter.

The above d-q transformation turns for the original dynamics of the converter into (1) and (2) with the results $e_d(t) = E_m$ and $e_q(t) = 0$, $\forall t \ge 0$, which eliminates the system nonlinearity such that

$$\begin{aligned} p(t)= & \frac{3}{2} \bigg ( e_d(t) i_d(t) + e_q(t) i_q(t) \bigg ) \\= & \frac{3}{2} E_m i_d(t),~\forall t \ge 0, \end{aligned}$$

with $E_m$ denoting the AC source voltage magnitude (in RMS). The nature of input-output power balancing also helps reduce the system nonlinearity by ensuring the relationship for the power p(t):

$$\begin{aligned} p(t) = \frac{3}{2}E_m i_d(t) = v_{dc}(t)i_{dc}(t),~\forall t \ge 0, \end{aligned}$$

(3)

yielding:

$$\begin{aligned} C\dot{v}_{dc}(t)= & i_{dc}(t) - i_L(t) \nonumber \\= & \frac{3E_m}{2 v_{dc}(t)} i_d(t) - i_L(t) \end{aligned}$$

(4)

with the output and load current denoted as $i_{dc}(t)$ and $i_L(t)$, $\forall t \ge 0$.

To address the problems from unmodeled dynamics, parameter uncertainty, and load variations, the dynamical equations are re-written in terms of the nominal converter parameters as

$$\begin{aligned} L_0 \dot{i}_d(t)= & -R_0 i_d(t) + \omega _r L_0 i_q(t) + E_m - v_d(t) + w_{d,o}(t), \end{aligned}$$

(5)

$$\begin{aligned} L_0 \dot{i}_q(t)= & -R_0 i_q(t) - \omega _r L_0 i_d(t) - v_q(t) + w_{q,o}(t), \end{aligned}$$

(6)

$$\begin{aligned} C_0 \dot{v}_{dc}(t)= & \frac{3E_m}{2v_{dc}(t)} i_d(t) + w_{v,o}(t),~\forall t \ge 0. \end{aligned}$$

(7)

with the nominal values $R_0$, $L_0$, and $C_0$, where the time-varying signals $w_{d,o}(t)$, $w_{q,o}(t)$, and $w_{v,o}(t)$ act as the uncertain perturbations from the model-plant mismatches.

Section Output voltage tracking controller design designs a novel output voltage feedback system that guarantees beneficial properties, such as performance recovery and offset-free operation, under the assumptions given by

• 1. The perturbations $w_{d,o}(t)$, $w_{q,o}(t)$, and $w_{v,o}(t)$ are uncertain and time-varying whose changing rate are bounded during the online operations.

• 2. The phase currents in the a-b-c frame are available for feedback, enabling the corresponding d-q frame current to be obtained.

Output voltage tracking controller design

Design objective

Denoting the signals $v_{dc}^*(t)$ as the desired output voltage response driven by the reference $v_{dc,ref}(t)$, the Laplace transforms $V_{dc}^*(s) = \mathscr {L}\{v_{dc}^*(t)\}$ and $V_{dc,ref}(s) = \mathscr {L}\{v_{dc,ref}(t)\}$ define the desired transfer function:

$$\begin{aligned} \frac{V_{dc}^*(s)}{V_{dc,ref}(s)} = \frac{\omega _{vc}}{s + \omega _{vc}},~\forall s \in \mathbb {C}, \end{aligned}$$

(8)

with the bandwidth $\omega _{vc}$ (rad/s, $\frac{\omega _{vc}}{2\pi }$ Hz) as a design parameter. Then, the time domain implementation of the desired system (8) given by

$$\begin{aligned} \dot{v}_{dc}^*(t) = \omega _{vc} (v_{dc,ref}(t) - v_{dc}^*(t)),~\forall t \ge 0, \end{aligned}$$

(9)

constitutes the design objective defined as the exponential convergence

$$\begin{aligned} \lim _{t\rightarrow \infty } v_{dc}(t) = v_{dc}^*(t) \end{aligned}$$

(10)

to assign the desired transfer function (8) to the closed-loop system.

Proposed controller

Outer loop controller

The two systems (4) and (9) and identity $i_d(t) = i_{d,ref}(t) + \tilde{i}_d(t)$ for design variable $i_{d,ref}(t)$ and d-frame current error $\tilde{i}_d(t):= i_{d,ref}(t) - i_d(t)$ yield the system for the output voltage error $\tilde{v}_{dc}^*:= v_{dc}^*(t) - v_{dc}(t)$ given by

$$\begin{aligned} C_0 \dot{\tilde{v}}^*_{dc}(t) = - \frac{3E_m}{2v_{dc}(t)} i_{d,ref}(t) + \frac{3E_m}{2v_{dc}(t)} \tilde{i}_d(t) + w_v(t), \end{aligned}$$

(11)

where $w_v(t):= C_0 \dot{v}^*_{dc}(t) - w_{v,o}(t)$, $\forall t \ge 0$ (to be estimated by the DOB).

The proposed outer loop solution stabilizes the system (11) forming the simple compensated proportional-type control law

$$\begin{aligned} i_{d,ref}(t) = \frac{2v_{dc}(t)}{3E_m}\bigg ( C_0 \lambda _{vc} \tilde{v}^*_{dc}(t) + \hat{w}_v(t) \bigg ),~\forall t \ge 0, \end{aligned}$$

(12)

with a design parameter $\lambda _{vc} > 0$ as the convergence rate of the output voltage error $\tilde{v}_{dc}^*(t)$. Herein, the estimated disturbance $\hat{w}_v(t)$ for $w_v(t)$ acting as the dynamical compensation term satisfies the system (called the DOB):

$$\begin{aligned} \dot{\zeta }_v(t)= & - l_v \zeta _v(t) - l_v^2 C_0 \tilde{v}^*_{dc}(t) + l_v \frac{3E_m}{2 v_{dc}(t)} i_d(t), \end{aligned}$$

(13)

$$\begin{aligned} \hat{w}_v(t)= & \zeta _v(t) + l_v C_0 \tilde{v}^*_{dc}(t),~\forall t \ge 0, \end{aligned}$$

(14)

incorporating $\zeta _v(t)$ and $l_v > 0$ as the state variable and gain, respectively.

Substituting the control law (12) to the system (11) derives the controlled outer loop dynamics given by

$$\begin{aligned} \dot{\tilde{v}}^*_{dc}(t) = - \lambda _{vc}\tilde{v}^*_{dc}(t) + \frac{3E_m}{2C_0 v_{dc}(t)}\tilde{i}_d(t) + \frac{1}{C_0}\tilde{w}_v(t), \end{aligned}$$

(15)

where $\tilde{w}_v(t):= w_v(t) - \hat{w}_v(t)$, $\forall t \ge 0$. Section Closed-loop analysis results presents the feedback system analysis results by further analyzing the controlled system (15).

Inner loop controller

The d-frame current reference given in (12) and q-frame current reference $i_{q,ref}(t) = 0$ define the errors $\tilde{i}_d(t):= i_{d,ref}(t) - i_d(t)$ and $\tilde{i}_q(t):= i_{q,ref}(t) - i_q(t)$ yielding the system from (5) and (6):

$$\begin{aligned} L_0 \dot{\tilde{i}}_x(t) = \phi _{x,0}(t) + v_x(t) + w_x(t) \end{aligned}$$

(16)

where the available functions $\phi _{d,0}(t):= R_0 i_d(t) - \omega _r L_0 i_q(t) - E_m$ and $\phi _{q,0}(t):= R_0 i_q(t) + \omega _r L_0 i_d(t)$ and unavailable perturbations $w_d(t):= L_0 \dot{i}_{d,ref}(t) - w_{d,o}(t)$ and $w_q(t):= L_0 \dot{i}_{q,ref}(t) - w_{q,o}(t)$, $\forall t \ge 0$ (to be estimated by the DOBs).

The proposed inner loop solution stabilizes the system (16) forming the simple compensated proportional-type control law given by

$$\begin{aligned} v_d(t)= & - L_0 \lambda _{cc} \tilde{i}_d(t) - \frac{3L_0 E_m}{2C_0 v_{dc}(t)} \tilde{v}^*_{dc}(t) - \phi _{d,0}(t) - \hat{w}_d(t), \end{aligned}$$

(17)

$$\begin{aligned} v_q(t)= & - L_0 \lambda _{cc} \tilde{i}_q(t) - \phi _{q,0}(t) - \hat{w}_q(t),~\forall t \ge 0, \end{aligned}$$

(18)

including a design parameter $\lambda _{cc} > 0$ as the convergence rates of the current errors $\tilde{i}_d(t)$ and $\tilde{i}_q(t)$. Herein, the estimated disturbances $\hat{w}_d(t)$ and $\hat{w}_q(t)$ for $w_d(t)$ and $w_q(t)$ acting as the dynamical compensation terms satisfy the system (called the DOB):

$$\begin{aligned} \dot{\zeta }_x(t)= & - l_x\zeta _x(t) - l_x^2 L_0 \tilde{i}_x(t) - l_x ( \phi _{x,0}(t) + v_x(t) ), \end{aligned}$$

(19)

$$\begin{aligned} \hat{w}_x(t)= & \zeta _x(t) + l_x L_0 \tilde{i}_x(t),~x=d,q,~\forall t \ge 0, \end{aligned}$$

(20)

incorporating $\zeta _x(t)$ and $l_x > 0$ as the state variable and gain, respectively.

Substituting the control laws (17) and (18) to the system (16) derives the controlled inner loop dynamics given by

$$\begin{aligned} \dot{\tilde{i}}_d(t)= & -\lambda _{cc} \tilde{i}_d(t) - \frac{3 E_m}{2C_0 v_{dc}(t)} \tilde{v}^*_{dc}(t) + \frac{1}{L_0}\tilde{w}_d(t), \end{aligned}$$

(21)

$$\begin{aligned} \dot{\tilde{i}}_q(t)= & -\lambda _{cc}\tilde{i}_q(t) + \frac{1}{L_0}\tilde{w}_q(t), \end{aligned}$$

(22)

where $\tilde{w}_x(t):= w_x(t) - \hat{w}_x(t)$, $x=d,q$, $\forall t \ge 0$. Figure 2 depicts the proposed multi-loop feedback system consisting of (12)-(14) and (17)-(20).

Remark 1

The proposed control laws in (12), (17), and (18) are of a proportional type, incorporating feed-forward compensation terms derived from DOBs. The exclusion of integral actions simplifies the feedback system architecture by eliminating the need for additional anti-windup mechanisms. However, this design choice may reduce the closed-loop robustness to low-frequency disturbances, such as step or pulse-type inputs.

Fig. 2

Proposed DOB-based multi-loop feedback system structure.

Closed-loop analysis results

Lemma 1 gives a property of the feedback system governed by (15), which considerably simplifies the whole feedback system analysis.

Lemma 1

For all $\lambda _{vc} > 0$ and $l_v > 0$, the outer loop control of (12) with the auxiliary system of (9) and DOB of (13) and (14), depicted in Fig. 2, ensures the strict passivity for the system:

$$\begin{aligned} \left[ \begin{array}{cc} \frac{3E_m}{2C_0v_{dc}(t)}\tilde{i}_d(t) \\ \gamma _v \dot{w}_v(t) \end{array}\right] \mapsto \left[ \begin{array}{cc} \tilde{v}^*_{dc}(t) \\ \tilde{w}_v(t) \end{array}\right] , \end{aligned}$$

(23)

for some $\gamma _v > 0$.

Lemma 1 indicates that the output voltage of $v_{dc}(t)$ rapidly converges to its targeted version $v^*_{dc}(t)$ as $\tilde{i}_d(t) \rightarrow 0$, $\dot{w}_v(t) \rightarrow 0$ exponentially. Appendix proves Lemma 1 by showing that

$$\begin{aligned} V_{v_{dc}}(t):= \frac{1}{2}(\tilde{v}^*_{dc}(t))^2 + \frac{\gamma _v}{2}\tilde{w}_v^2(t),~\forall t \ge 0, \end{aligned}$$

(24)

to be:

$$\begin{aligned} \dot{V}_{v_{dc}}(t)\le & - \alpha _{v_{dc}}V_{v_{dc}}(t) + \tilde{v}^*_{dc}(t) \frac{3E_m}{2C_0 v_{dc}(t)}\tilde{i}_d(t) \nonumber \\ & + \gamma _v\tilde{w}_v(t) \dot{w}_v(t),~\forall t \ge 0, \end{aligned}$$

(25)

for some $\alpha _{v_c} > 0$ and $\gamma _v > 0$.

Lemma 2 provides the beneficial results of the closed-loop system (21)-(22), which simplifies the stability analysis of the whole feedback system.

Lemma 2

For all $\lambda _{cc} > 0$, $l_x > 0$, $x=d,q$, the inner loop controls of (17) and (18) with DOB of (19) and (20), depicted in Fig. 2, ensure the strict passivity for the system:

$$\begin{aligned} \left[ \begin{array}{cccc} -\frac{3E_m}{2C_0 v_{dc}(t)}\tilde{v}^*_{dc}(t) \\ 0 \\ \gamma _d \dot{w}_d(t) \\ \gamma _q \dot{w}_q(t) \end{array}\right] \mapsto \left[ \begin{array}{cccc} \tilde{i}_d(t) \\ \tilde{i}_{q}(t) \\ \tilde{w}_d(t) \\ \tilde{w}_q(t) \end{array}\right] , \end{aligned}$$

(26)

for some $\gamma _x > 0$, $x=d,q$.

Lemma 2 establishes that the d–q current tracking errors vanish exponentially whenever $\tilde{v}^*_{dc}(t)$ and $\dot{w}_x(t)$ converge to zero for $x \in {d,q}$. In Appendix, Lemma 2 is proved by asserting the positive-definite function given as

$$\begin{aligned} V_{dq}(t):= \sum _{x=d,q}\frac{1}{2}\tilde{i}^2_x(t) + \sum _{x=d,q}\frac{\gamma _x}{2}\tilde{w}_x^2(t),~\forall t \ge 0, \end{aligned}$$

(27)

to be:

$$\begin{aligned} \dot{V}_{dq}(t)\le & - \alpha _{dq}V_{dq}(t) - \tilde{i}_d(t) \frac{3E_m}{2C_0 v_{dc}(t)}\tilde{v}^*_{dc}(t) \nonumber \\ & + \sum _{x=d,q}\gamma _x \tilde{w}_x(t) \dot{w}_x(t), ~\forall t \ge 0, \end{aligned}$$

(28)

for some constants $\alpha _{dq} > 0$, $\gamma _x > 0$, $x=d,q$.

Remark 2

Lemmas 1 and 2 proves that the corresponding DOBs satisfies

$$\begin{aligned} \dot{\hat{w}}_x (t) = l_x (w_x(t) - \hat{w}_x(t) ),~x=v,d,q,~\forall t \ge 0, \end{aligned}$$

with $\hat{w}_x$ denoting the estimated disturbance of $w_x$, whose transfer function is given by

$$\begin{aligned} \frac{\hat{W}_x(s)}{W_x(s)} = \frac{l_x}{s + l_x},~x=v,d,q,~\forall s \in \mathbb {C}, \end{aligned}$$

(29)

which shows the selection guideline for $l_x > 0$, $x=v,d,q$, as the bandwidth of (29).

Theorem 1 derives the closed-loop property by analyzing the whole closed-loop error dynamics of (15), (21), and (22). The proof of Theorem 1 is given in Appendix.

Theorem 1

Under the same conditions of Lemmas 1and 2, the proposed controls of (12), (17), and (18) with the auxiliary system of (9) and DOBs of (13), (14), (19), and (20), depicted in Fig. 2, guarantee

$$\begin{aligned} |\tilde{v}^*_{dc}(t)| \le \gamma _{cl} e^{-\frac{\alpha _{cl}}{2}t},~\forall |\tilde{w}_x(t)| \ge \underline{w}_x,~\forall t \ge 0, \end{aligned}$$

(30)

for some $\alpha _{cl} > 0$, $\gamma _{cl} > 0$, and $\underline{w}_x > 0$, $x=v,d,q$.

It is important to highlight that the presence of steady-state errors in the closed-loop output voltage control system, when implemented with the proposed algorithm, remains uncertain due to the absence of integral actions in the tracking error dynamics. However, the proposed proportional-type output voltage control method, described in equations (12)–(14) and (17)–(20), guarantees steady-state error rejection without relying on integral actions. This feature simplifies the control algorithm by eliminating the need for anti-windup mechanisms, which represents a practical advantage of the proposed approach. A detailed explanation of this property is provided in Theorem 2, with its proof included in the Appendix.

Theorem 2

The resultant feedback system governed by the proposed controls of (12), (17), and (18) with the auxiliary system of (9) and DOBs of (13), (14), (19), and (20) always gets rid of the steady state errors of the output voltage, i.e,

$$\begin{aligned} v^0_{dc} = v^0_{dc,ref}, \end{aligned}$$

(31)

where $v^0_{dc}$ and $v^0_{dc,ref}$ stand for the steady states of $v_{dc}(t)$ and $v_{dc,ref}(t)$, respectively.

Remark 3

The results presented in this section provide practical guidance for tuning the design parameters of the proposed technique. The recommended tuning procedure is as follows:

• 1. Select the bandwidth $l_x (\ge 30$ rad/s), $x=v,d,q$, based on the first-order transfer function (29) (by Remark 2).

• 2. Select the current error convergence rate $\lambda _{cc} (\ge 2\pi 50)$, considering the desired first-order dynamics $\dot{\tilde{i}}_x^* = -\lambda _{cc}\tilde{i}_x^*$ that approximate the closed-loop error dynamics in (21) and (22) (by Lemma 2).

• 3. Increase the convergence rate $\lambda _{vc} \ge 10$ to observe that $|v_{dc}^* - v_{dc}| \approx 0$ (by Theorem 1).

This sequence yields the final tuned values of the design parameters, as applied in the experimental setup described in Section Experimental results.

Experimental results

Figure 3 shows the hardware platform used to experimentally assess the closed-loop behavior of the proposed method. The system parameters of three-phase power converters were chosen as

$$\begin{aligned} \omega _r = 120\pi ~\text{ rad/s }, ~R = 0.1 \Omega , ~L = 3~mH,~C = 2350 \mu \text{ F }, \end{aligned}$$

(32)

and the nominal values were chosen as

$$\begin{aligned} R_0 = 0.6R_0,~L_0 = 1.4L,~C_0 = 0.8C, \end{aligned}$$

(33)

used for constructing the proposed controller. The AC source voltage magnitude was set to $E_m = 122.47~V$. The digital signal processor (DSP) of TI (Texas Instrument) TMS320F28335 was used to implement the control algorithms, the PWM and control periods were chosen to be 0.1 ms.

Fig. 3

The experimental setup.

The current and output voltage bandwidths were assigned to be $f_{cc} = 150~Hz$ and $f_{vc} = 10~Hz$ so that $\omega _{cc} = 2\pi 150$ rad/s and $\omega _{vc} = 2\pi 10$ rad/s for the implementation of the proposed controller. The DOB gains were adjusted as $l_d = l_q = l_v = 62.8 ~rad/s$, for the transfer functions in (29). Note that, for maximizing the power factor, q-frame current reference was determined as $i_{q,ref} = 0$ (see^26,29). The output voltage convergence parameter of $\lambda _{vc}$ of the proposed algorithm was tuned to be 188.4, and the other design factor of $\lambda _{cc}$ was letting to be the same as the current bandwidth of $\omega _{cc}$ for a fair comparison because the d-q frame current tracking error dynamics of (16) can be approximately written in a low-pass filter $\dot{i}_x(t) = \lambda _{cc} (i_{x,ref}(t) - i_x(t))$, $x=d,q$, $\forall t \ge 0$, for slowly time varying current references $i_{x,ref}(t)$, $x=d,q$.

For a comparison, the FL and multi-loop PI controllers in⁹ and passivity-based controller (PBC) in³⁰ were utilized; (FL controller) $i_{d,ref}(t) = \frac{2v_{dc}(t)}{3E_m}( 2C_0\omega _{vc}\tilde{v}_{dc}(t) + C_0\omega ^2_{vc}\int _0^t \tilde{v}_{dc}(\tau )d\tau )$, $v_d(t) = - L_0\omega _{cc}\tilde{i}_d (t) - R_0 \omega _{cc}\int _{0}^{t}\tilde{i}_d(\tau )$ $d\tau + \omega _r L_0 i_q(t) + E_m$, $v_q(t) = - L_0\omega _{cc}\tilde{i}_q(t) - R_0 \omega _{cc}\int _0^t$ $\tilde{i}_q(\tau )d\tau - \omega _r L_0 i_d(t)$, (multi-loop PI controller) $i_{d,ref}(t) = k_{\text {P,vc}}\tilde{v}_{dc}(t) + k_\text {I,vc}\int _0^t \tilde{v}_{dc}(\tau )d\tau$, $v_d(t) = - k_{\text {P,cc}}\tilde{i}_d (t) -$ $k_{\text {I,cc}}\int _{0}^{t}\tilde{i}_d(\tau ) d\tau$, $v_q(t) = - k_{\text {P,cc}}\tilde{i}_q (t)$ $- k_{\text {I,cc}}\int _{0}^{t}\tilde{i}_q(\tau ) d\tau$, (PBC) $i_{d,ref}(t) = -k_\text {d,vc}v_{dc}(t) + C_0\omega _{vc}\tilde{v}_{dc}(t)$ $+ k_\text {d,vc}\omega _{vc} \int _0^t\tilde{v}_{dc}(\tau )d\tau$, $v_d(t) = -k_\text {d,cc}i_d(t) + L_0\omega _{cc}\tilde{i}_d(t)$ $+ k_\text {d,cc}\omega _{cc}$ $\int _0^t\tilde{i}_d(\tau )d\tau$, and $v_q(t) =$ $-k_\text {d,cc}i_q(t)$ $+ L_0\omega _{cc}\tilde{i}_q(t) +$ $k_\text {d,cc}\omega _{cc}$ $\int _0^t\tilde{i}_q(\tau )d\tau$, where $\tilde{v}_{dc}(t) = v_{dc,ref}(t) - v_{dc}(t)$, $\forall t \ge 0$. The tuning parameters of these baseline controllers were founded to satisfy the desired dynamic behavior given by the closed-loop transfer function $\frac{V_{dc}^*(s)}{V_{dc,ref}(s)} = \frac{\omega _{vc}}{s + \omega _{vc}}$ at $R_L = 300~\Omega$ for the given bandwidths $\omega _{vc} = 2\pi \cdot 10$ and $\omega _{cc} = 2\pi \cdot 150$ rad/s.

Evaluation of tracking performance

This experiment was conducted to evaluate the output voltage tracking performance under three distinct resistive load conditions: $R_L = 80$, 150, 300 $\Omega$. The corresponding output voltage responses, shown in Fig. 4, demonstrate that the proposed control strategy maintains nearly identical voltage behavior across varying load scenarios using fixed control parameters—an outcome not achieved by the PBC, FL, and multi-loop PI techniques. The performance discrepancies observed in the Fig. 4 under other techniques could potentially be mitigated by implementing a gain scheduling mechanism; however, such an approach would increase the computational burden. The associated d-q frame current, control efforts (MI $:= \sqrt{v_d^2 + v_q^2}$), and DOB responses are illustrated in Figs. 5-8.

Fig. 4

Comparison result of output voltage tracking performances for $R_L = 80,150,300\Omega$.

Fig. 5

Comparison result of d-frame current responses under output voltage tracking mode for $R_L = 80,150,300\Omega$.

Fig. 6

Comparison result of q-frame current responses under output voltage tracking mode for $R_L = 80,150,300\Omega$.

Fig. 7

Comparison result of control efforts (MI$=\sqrt{v_d^2+v_q^2}$) under output voltage tracking mode for $R_L = 80,150,300\Omega$.

Fig. 8

DOB responses under $R_L = 80\Omega$.

Evaluation of regulation performance

In the second experimental scenario, the output voltage regulation capabilities were assessed under a sudden load change. The system was initially operating with the output voltage maintained at 300 V under $R_L = 300~\Omega$, which was abruptly reduced to $R_L = 75~\Omega$. As illustrated in the left panel of Fig. 9, the proposed control method significantly enhances voltage regulation by effectively minimizing the undershoot during the transient period. Additionally, as shown in the middle and right panels of Fig. 9, it accelerates the d-q frame current response, thereby contributing to improved dynamic performance of the proposed feedback system.

Fig. 9

Comparison result of output voltage regulation performances and d-q frame current responses under abruptly decreasing load $R_L = 300$ to $75~\Omega$.

Evaluation of performance assignability

Following the same experimental conditions as the first scenario with $R_L = 80~\Omega$, this experiment aimed to investigate how varying the bandwidth, 6, 8, and 10 Hz, affects the output voltage tracking behavior. The results, presented in Fig. 10, validate the performance assignability property established in Theorem 1. These findings confirm that the proposed method enables flexible tuning of the feedback system performance through appropriate selection of the bandwidth.

Fig. 10

Controlled output voltage responses as magnifying bandwidth as 6, 8, 10 Hz.

Evaluation result of feedback system performance

This subsection quantitatively evaluates the performance comparison results described in Sections Evaluation of tracking performance-Evaluation of regulation performance, using the performance index defined as $f_{\text {perf}}:= \sqrt{\int _0^\infty |v_{dc}^* - v_{dc}|^2 + i_d^2 + i_q^2 + \text {MI}^2 dt}$. The comparative outcomes are tabulated in Fig. 11, showing at least an 17$\%$ improvement over the other controllers in all evaluated cases.

Fig. 11

Performance evaluation result.

Evaluation result of computational burden

This subsection investigates the computational burden associated with implementing different feedback control schemes, including the proposed controller, the PBC, and a conventional multi-loop PI controller, as outlined in Section Evaluation result of feedback system performance. A total of 4,000 experiments were conducted using randomly selected position references ranging from 450 to 550 V. As depicted in Fig. 12, the proposed approach required approximately 11$\%$ more computation time than the traditional multi-loop PI controller, mainly because of the presence of DOBs. However, this increase is considered acceptable and reinforces the practicality of the proposed strategy as a viable control alternative.

Fig. 12

Computational burden comparison result

Building on the findings from these experiments, the proposed method consistently ensures reliable closed-loop output voltage tracking and regulation, even when operating modes change, unlike the recent and conventional controllers. As a result, the proposed technique achieves stable and consistent closed-loop performance across a broad spectrum of operating conditions, without the need for an additional gain scheduling mechanism. This practical benefit highlights the effectiveness and robustness of the approach, making it well-suited for real-world industrial applications.

Conclusions

The proposed technique utilizes a multi-loop control structure, eliminating the need for integral action in tracking errors while ensuring performance recovery by integrating a nonlinear DOB with a proportional-type output voltage controller. It has been rigorously demonstrated that this method enhances output voltage tracking and improves closed-loop robustness to load variations, outperforming the traditional feedback linearization approach. However, the technique involves several design parameters, whose optimal values can be determined by solving an optimization problem constrained by linear or bilinear matrix inequalities. Future work will focus on further enhancing robustness through the systematic integration of integrators and disturbance observers.