Introduction

In recent years, fractional calculus has gained significant attention owing to its extensive application in diverse fields, including fluid dynamics1,2,3,4, optical fibers5,6,7,8,9, electromagnetics10,11,12,13,14, mathematical physics15,16,17, and plasma physics18,19. Fractional calculus methodologies] and techniques are now widely utilized in various disciplines of modern science and engineering. Several researchers have explored its potential in modeling and control theory, demonstrating its effectiveness in solving complex problems24,25,26,27,28. Fractional partial differential equations (PDEs) represent a generalized form of nonlinear PDEs that play a fundamental role in investigating nonlinear phenomena in the applied sciences29,30,31,32. These equations have numerous applications in optics, aerodynamics, plasma physics, hydrodynamics, electrochemistry, fluid mechanics, and other scientific and engineering domains.

A particularly significant nonlinear PDE is the Korteweg-de Vries (KdV) equation that describes long-wave motion in shallow water, quantum mechanics, and one-dimensional nonlinear lattices33,34,35,36,37,38. The KdV equation has been extensively used in the modeling of physical phenomena, such as blood pressure wave propagation, tidal waves, long surface waves, wave transmission in shallow water channels, and internal gravity waves in oceanic systems. In addition, a German mathematician investigated the application of the KdV equation to describe wave propagation within electromagnetic fields39,40,41. In physics, water waves play a crucial role in the study of nonlinear dispersive waves and solitons. Notably, researchers such as KdV have extensively analyzed the KdV equation, identifying it as a fundamental model for shallow water waves in streams and oceans, thereby forming the basis for the concept of solitary waves42,43,44.

The importance of fractional PDEs in the applied sciences lies in their ability to provide both exact and numerical solutions. Various advanced analytical techniques have been developed to determine exact solutions, including the simple equation method45, the \(\exp\)-function method46,47, \(\exp (-z(\xi ))\)-expansion method48, the modified simple equation method49, the tri-prong scheme50, the extended mapping method51, the auxiliary equation (NAE) method52, and the modified simple equation method53, among others54,55,56,57.

In this study, the NAE method52 is applied to examine the KdV equation, which is essential for analyzing short waves and shallow water waves in dispersive media. The NAE method is regarded as a generalized framework from which several other methods can be derived under specific conditions, including the functional variable method58 and the first integral method59. The findings of this research hold significant relevance for various practical applications, including wave dynamics, optics, plasma physics, fluid mechanics, and ocean engineering. Soliton and wave solutions play a fundamental role in understanding surface water waves, with applications in coastal engineering, shipbuilding, and wave prediction. Additionally, some of the obtained traveling wave solutions are particularly useful in ocean engineering, addressing phenomena such as ship-induced waves, storm-generated ocean waves, traveling wave propagation, and wave breaking along shorelines.

This paper is organized into six sections. Section 1 introduces the study. Section 2 outlines the definition and key properties of conformable fractional derivatives. The NAE methodology is explained in Section 3. Section 4 describes the application of the proposed approach. A graphical analysis is provided in Section 5, and the final conclusions are presented in Section 6.

Conformal derivative and its properties

Numerous definitions of fractional derivatives have been introduced in the literature, including Caputo and Riemann-Liouville formulations60,61. However, a particularly noteworthy definition, offering both a geometric perspective on fractional derivatives and a complex fractional transformation, was presented by Khalil et al.62 and further investigated by He et al.63. The conformable fractional derivative is designed to extend the classical concept of differentiation to fractional orders while preserving many fundamental properties, such as linearity, product rules, and chain rules. Physically, it can be interpreted as a tool for modeling processes exhibiting memory and hereditary properties with a degree of locality, bridging the gap between integer-order calculus and more complex fractional definitions. This makes it especially suitable for describing anomalous diffusion, viscoelastic behavior, and other phenomena in which non-integer dynamics play a crucial role. In our study, the conformable derivative provides a meaningful framework to capture such intermediate behaviors in the system under investigation, offering both analytical tractability and physical relevance. The concept of conformable fractional derivative, originally proposed by Khalil et al.62, is formulated as follows:

Definition 2.1

Suppose

$$\begin{aligned}g:[0,\infty )\rightarrow \mathbb {R}\end{aligned}$$

be a function. Then conformable derivative of g of \(\alpha 's\) order is defined by

$$\begin{aligned} D^\alpha _t (g(t))=\lim _{\varepsilon \rightarrow 0} \frac{g(t+\varepsilon t^{1-\alpha })-g(t)}{\varepsilon }, \end{aligned}$$
(1)

in which \(t>0\) and \(\sigma _1 \in (0,1]\).

Some properties for conformable derivative are reported as follow:

Theorem 2.1

Suppose if \(0 < \omega \le 1\) and assume g(t) and h(t) are differentiable of \(\omega 's\) order at \(t> 0\), then

1: \(D^\omega _t (t^\beta )=\beta t^{\beta -\omega }\), for all \(\beta \in \mathbb {R}.\)

2: \(D^\omega _t (c)=0\), for all constants.

3: \(D^\omega _t (\phi g(t))=\phi D^\omega _t (g(t))\), where \(\phi\) is constant.

4: \(D^\omega _t (\phi g(t)+\psi h(t))=\phi D^\omega _t(g(t))+\psi D^\omega _t(h(t))\), for all \(\phi ,\psi \in \mathbb {R}.\)

5: \(D^\omega _t(g(t)\times h(t))=h(t)\times D^\omega _t(g(t))+g(t) \times D^\omega _t(h(t)),\)

6: \(D^\omega _t\bigg (\frac{g(t)}{h(t)}\bigg )=\frac{h(t)D^\omega _t (g(t))-g(t)D^\omega _t (h(t))}{h^2(t)}\),

7: \(D^\omega _t g(t)=t^{1-\omega }\frac{dg}{dt}\),

8: \(D^{\omega }_t(g(t)\circ h(t))=t^{1-\omega }h^{\prime }(t)g^{\prime }(h(t)).\)

Methodology of the auxiliary equation method

A general form of a nonlinear PDE can be represented as follows

$$\begin{aligned} P(\mathcal {R},\mathcal {R}_{t},D_t^{\eta }\mathcal {R},\mathcal {R}_{x},D_x^{\eta }\mathcal {R},\mathcal {R}_{xx},\cdots )=0,~~~0< \eta \le 1, \end{aligned}$$
(2)

where \(P\) is a polynomial function involving \(\mathcal {R}\) and its derivatives with respect to the independent variables \(x\) and \(t\).

Step: 1 Consider defining a new dependent \(\psi\) variable as follows

$$\begin{aligned} \mathcal {R}(x,t)=f(\psi ),\qquad \psi =m\frac{x^{\sigma }}{\sigma }\chi -n\frac{t^\omega }{\omega }. \end{aligned}$$
(3)

Substituting Eq. (3) into Eq. (2), the resulting ordinary differential equation (ODE) is obtained as follows

$$\begin{aligned} \mathcal {Q}(f,f^\prime ,f^{\prime \prime },...)=0. \end{aligned}$$
(4)

Step: 2 Consider the solution of Eq. (4) in the following form

$$\begin{aligned} f(\psi )=\sum _{i=0}^{k}b_i\mathcal {L}^{ip(\psi )}, \end{aligned}$$
(5)

while also satisfying the corresponding auxiliary equations.

$$\begin{aligned} p^\prime (\psi )=\frac{1}{\ln (\mathcal {L})}\{\sigma _1 \mathcal {L}^{-p(\psi )} +\sigma _3+\sigma _2 \mathcal {L}^{p(\psi )}\},~~\mathcal {L}>0,~~\mathcal {L}\ne 1, \end{aligned}$$
(6)

where \(b_i\) are constants that will be determined later.

Step: 3 To determine the value of \(k\) in Eq. (5), the balancing procedure is applied, where the highest-order nonlinear term is equated with the highest-order derivative.

Step: 4 By incorporating Eq (5) and Eq (6) into Eq (4), and subsequently gathering the coefficients of various powers of \(\mathcal {L}^{p(\psi )}\) (\(i = 0,1,2,3 \dots\)), we establish a system of algebraic equations by equating all coefficients to zero. The resulting system can be efficiently solved using Maple 2023 software.

Step: 5 The possible forms of solutions for Eq (6) can be determined as follows

Case:1 When \(\sigma ^2_3-\sigma _1\sigma _2<0\) and \(\sigma _2\ne 0\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\tan \bigg (\frac{\sqrt{-(\sigma _3 ^2-\sigma _1\sigma _2)}}{2}\psi \bigg ),\end{aligned}$$
(7)
$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\cot \bigg (\frac{\sqrt{-(\sigma _3 ^2-\sigma _1\sigma _2)}}{2}\psi \bigg ). \end{aligned}$$
(8)

Case:2 When \(\sigma _3^2+\sigma _1\sigma _2>0\) and \(\sigma _2\ne 0\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\tanh \bigg (\frac{\sqrt{(\sigma _3 ^2-\sigma _1\sigma _2)}}{2}\psi \bigg ),\end{aligned}$$
(9)
$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{-\sigma _3}{\sigma _2}-\frac{\sqrt{(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\coth \bigg (\frac{\sqrt{(\sigma _3 ^2-\sigma _1\sigma _2)}}{2}\psi \bigg ). \end{aligned}$$
(10)

Case:3 When \(\sigma _3^2+\sigma _1\sigma _2>0\) and \(\sigma _2\ne 0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\tanh \bigg (\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg ),\end{aligned}$$
(11)
$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\coth \bigg (\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg ). \end{aligned}$$
(12)

Case: 4 When \(\sigma _3^2+\sigma _1\sigma _2<0\), \(\sigma _2\ne 0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\tan \bigg (\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg ),\end{aligned}$$
(13)
$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\cot \bigg (\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg ). \end{aligned}$$
(14)

Case: 5 When \(\sigma _3^2-\sigma _1^2<0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\tan \bigg (\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg ),\end{aligned}$$
(15)
$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\cot \bigg (\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg ). \end{aligned}$$
(16)

Case: 6 When \(\sigma _3^2-\sigma _1^2>0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\tanh \bigg (\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg ),\end{aligned}$$
(17)
$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\coth \bigg (\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg ). \end{aligned}$$
(18)

Case: 7 When \(\sigma _1\sigma _2>0\), \(\sigma _2\ne 0\) and \(\sigma _3=0\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \sqrt{\frac{-\sigma _1}{\sigma _2}}\tanh \bigg (\frac{\sqrt{-\sigma _1\sigma _2}}{2}\psi \bigg ),\end{aligned}$$
(19)
$$\begin{aligned} \mathcal {L}^{p(\psi )}= & \sqrt{\frac{-\sigma _1}{\sigma _2}}\coth \bigg (\frac{\sqrt{-\sigma _1\sigma _2}}{2}\psi \bigg ). \end{aligned}$$
(20)

Case: 8 When \(\sigma _3=0\) and \(\sigma _1=-\sigma _2\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}=\frac{-(1+e^{2\sigma _1\psi })\pm \sqrt{2(1+e^{2\sigma _1\psi })}}{e^{2\sigma _1\psi }-1}. \end{aligned}$$
(21)

Case: 9 When \(\sigma _3^2=\sigma _1\sigma _2\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}=\frac{-\sigma _1(\sigma _3\psi +2)}{\sigma _3^2\psi }. \end{aligned}$$
(22)

Case: 10 When \(\sigma _3=\kappa\), \(\sigma _1=2\kappa\) and \(\sigma _2=0\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}=e^{\psi }-1. \end{aligned}$$
(23)

Case: 11 When \(\sigma _3=\kappa\), \(\sigma _2=2\kappa\) and \(\sigma _1=0\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}=\frac{e^{\psi }}{1-e^{\psi }}. \end{aligned}$$
(24)

Case: 12 When \(2\sigma _3=\sigma _1+\sigma _2\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}=\frac{1+\sigma _1 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}{ 1+\sigma _2 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}. \end{aligned}$$
(25)

Case: 13 When \(-2\sigma _3=\sigma _1+\sigma _2\)

$$\begin{aligned} \mathcal {L}^{p\psi )}=\frac{\sigma _1+\sigma _1 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}{ \sigma _2+\sigma _2 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}. \end{aligned}$$
(26)

Case: 14 When \(\sigma _1=0\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}=\frac{\sigma _3 e^{\sigma _3\psi }}{ 1+\frac{\sigma _2}{2}e^{\sigma _3\psi }}. \end{aligned}$$
(27)

Case: 15 When \(\sigma _1=\sigma _3=\sigma _2\ne 0\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}=\frac{-(\sigma _1\psi +2)}{\sigma _1\psi }. \end{aligned}$$
(28)

Case: 16 When \(\sigma _1=\sigma _2\), \(\sigma _3=0\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}=\tan \bigg (\frac{\sigma _1\psi +c}{2}\bigg ). \end{aligned}$$
(29)

Case: 17 When \(\sigma _2=0\)

$$\begin{aligned} \mathcal {L}^{p(\psi )}=e^{\sigma _3\psi }-\frac{\sigma _1}{2\sigma _3}. \end{aligned}$$
(30)

Step: 6 By substituting all the values of \(\mathcal {L}^{p(\psi )}\) from Step 5 into Eq (5), the corresponding results for Eq (2) are obtained.

Utilization of the proposed methodology

The space-time fractional modified third-order KDV equation64 is expressed as follows

$$\begin{aligned} D_t^{\sigma }\mathcal {R}+\mu \mathcal {R}^2D_x^{\omega }\mathcal {R}+\nu D_x^{3\omega }\mathcal {R}=0, \,\,\,0<\sigma ,\,\,\,\omega \le 1. \end{aligned}$$
(31)

This equation serves as an important mathematical model for describing nonlinear wave propagation phenomena in various physical systems where memory effects and anomalous diffusion are present. Applications include shallow water waves, plasma physics, and nonlinear lattice dynamics, where wave behavior deviates from classical models due to fractional dynamics. The conformable fractional derivative introduces a flexible parameter that captures intermediate dynamics between classical integer-order and more complex fractional-order behaviors, enabling more accurate modeling of wave attenuation and dispersion in complex media. Thus, this study not only contributes to the theoretical understanding of fractional nonlinear wave equations but also has potential implications for improving predictive models in fluid mechanics, optics, and other engineering fields where such wave phenomena are observed. By utilizing Eq (3), Eq (31) can be reformulated into the following ODE.

$$\begin{aligned} -nf'+m\mu f^2f'+m^3\nu f'''=0. \end{aligned}$$
(32)

By performing integration and assuming the constant of integration to be zero, Eq (32) simplifies to

$$\begin{aligned} 3m^3\nu f''-3n f+m\mu f^3=0. \end{aligned}$$
(33)

By applying the balancing principle, we obtain \(n = 1\). Consequently, the solution (5) can be expressed as

$$\begin{aligned} f(\psi )=c_0+c_1\mathcal {L}^{p(\psi )}+b_1\mathcal {L}^{-p(\psi )}. \end{aligned}$$
(34)

Substituting Eq (34) and its derivatives into Eq (33) and equating the coefficients of \(\mathcal {L}^{p(\psi )}\) yield a system of algebraic equations. The solutions to the obtained system are as follows.

Set-1

$$\begin{aligned} \begin{aligned} m&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}},\,\,\, c_0=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}},\,\,\,\\ c_1&=\bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}},\,\,\,b_1=0. \end{aligned} \end{aligned}$$
(35)

Based on Eq (34), the traveling wave solutions of Eq (32) corresponding to the obtained results are given as follows

$$\begin{aligned} f(\psi )=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}}\mathcal {L}^{p(\psi )}. \end{aligned}$$
(36)

By employing the solutions given in Eq (7) through Eq (30), the obtained solutions are as follows.

Family:1 When \(\sigma ^2_3-\sigma _1\sigma _2<0\) and \(\sigma _2\ne 0\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{1}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72 n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}}\bigg (\frac{-\sigma _3}{\sigma _2} +\frac{\sqrt{-(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\\&\tan \bigg (\frac{\sqrt{-(\sigma ^2_3-\sigma _1\sigma _2)}}{2}\psi \bigg )\bigg ), \end{aligned}\end{aligned}$$
(37)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{2}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\\ &\cot \bigg (\frac{\sqrt{-(\sigma _3 ^2-\sigma _1\sigma _2)}}{2}\psi \bigg )\bigg ). \end{aligned} \end{aligned}$$
(38)

Family:2 When \(\sigma _3^2+\sigma _1\sigma _2>0\) and \(\sigma _2\ne 0\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{3}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\\ &\tanh \bigg (\frac{\sqrt{(\sigma _3^2 -\sigma _1\sigma _2)}}{2}\psi \bigg )\bigg ), \end{aligned}\end{aligned}$$
(39)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{4}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{-\sigma _3}{\sigma _2}-\frac{\sqrt{(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\\ &\coth \bigg (\frac{\sqrt{(\sigma _3 ^2-\sigma _1\sigma _2)}}{2}\psi \bigg )\bigg ). \end{aligned} \end{aligned}$$
(40)

Family:3 When \(\sigma _3^2+\sigma _1\sigma _2>0\) and \(\sigma _2\ne 0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{5}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\\ &\tanh \bigg (\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg )\bigg ), \end{aligned} \end{aligned}$$
(41)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{6}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\\ &\coth \bigg (\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg )\bigg ). \end{aligned} \end{aligned}$$
(42)

Family: 4 When \(\sigma _3^2+\sigma _1\sigma _2<0\), \(\sigma _2\ne 0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{7}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\\ &\tan \bigg (\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg )\bigg ), \end{aligned} \end{aligned}$$
(43)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{8}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\\ &\cot \bigg (\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg )\bigg ). \end{aligned} \end{aligned}$$
(44)

Family: 5 When \(\sigma _3^2-\sigma _1^2<0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{9}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\\ &\tan \bigg (\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg )\bigg ), \end{aligned}\end{aligned}$$
(45)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{10}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}}\bigg (\frac{-\sigma _3}{\sigma _2}+ \frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\\ &\cot \bigg (\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg )\bigg ). \end{aligned} \end{aligned}$$
(46)

Family: 6 When \(\sigma _3^2-\sigma _1^2>0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{11}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\\ &\tanh \bigg (\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg )\bigg ), \end{aligned} \end{aligned}$$
(47)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{12}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\\ &\coth \bigg (\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg )\bigg ). \end{aligned} \end{aligned}$$
(48)

Family: 7 When \(\sigma _1\sigma _2>0\), \(\sigma _2\ne 0\) and \(\sigma _3=0\)

$$\begin{aligned} \mathcal {R}_{13}(x,t)= & \frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}}\bigg (\sqrt{\frac{-\sigma _1}{\sigma _2}}\tanh \bigg (\frac{\sqrt{-\sigma _1\sigma _2}}{2}\psi \bigg )\bigg ),\end{aligned}$$
(49)
$$\begin{aligned} \mathcal {R}_{14}(x,t)= & \frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}}\bigg (\sqrt{\frac{-\sigma _1}{\sigma _2}}\coth \bigg (\frac{\sqrt{-\sigma _1\sigma _2}}{2}\psi \bigg )\bigg ). \end{aligned}$$
(50)

Family: 8 When \(\sigma _3=0\) and \(\sigma _1=-\sigma _2\)

$$\begin{aligned} \mathcal {R}_{15}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}}\bigg (\frac{-(1+e^{2\sigma _1\psi }) \pm \sqrt{2(1+e^{2\sigma _1\psi })}}{e^{2\sigma _1\psi }-1}\bigg ). \end{aligned}$$
(51)

Family: 9 When \(\sigma _3^2=\sigma _1\sigma _2\)

$$\begin{aligned} \mathcal {R}_{16}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}} \bigg (\frac{-\sigma _1(\sigma _3\psi +2)}{\sigma _3^2\psi }\bigg ). \end{aligned}$$
(52)

Family: 10 When \(\sigma _3=\kappa\), \(\sigma _1=2\kappa\) and \(\sigma _2=0\)

$$\begin{aligned} \mathcal {R}_{17}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3}\bigg )^{\frac{1}{4}}\bigg (e^{\psi }-1\bigg ). \end{aligned}$$
(53)

Family: 11 When \(\sigma _3=\kappa\), \(\sigma _2=2\kappa\) and \(\sigma _1=0\)

$$\begin{aligned} \mathcal {R}_{18}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}}\bigg (\frac{e^{\psi }}{1-e^{\psi }}\bigg ). \end{aligned}$$
(54)

Family: 12 When \(2\sigma _3=\sigma _1+\sigma _2\)

$$\begin{aligned} \mathcal {R}_{19}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}}\bigg (\frac{1+\sigma _1 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}{ 1+\sigma _2 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}\bigg ). \end{aligned}$$
(55)

Family: 13 When \(-2\sigma _3=\sigma _1+\sigma _2\)

$$\begin{aligned} \mathcal {R}_{20}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}}\bigg (\frac{\sigma _1+\sigma _1 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}{ \sigma _2+\sigma _2 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}\bigg ). \end{aligned}$$
(56)

Family: 14 When \(\sigma _1=0\)

$$\begin{aligned} \mathcal {R}_{21}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{-\mu ^2\sigma _2^2}}+ \bigg (\frac{72n\nu }{-\mu ^2\sigma _2^2}\bigg )^{\frac{1}{4}}\bigg (\frac{\sigma _3 e^{\sigma _3\psi }}{ 1+\frac{\sigma _2}{2}e^{\sigma _3\psi }}\bigg ). \end{aligned}$$
(57)

Family: 15 When \(\sigma _1=\sigma _3=\sigma _2\ne 0\)

$$\begin{aligned} \mathcal {R}_{22}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{3\mu ^2\sigma ^2_1}}+ \bigg (\frac{72n\nu }{3\mu ^2\sigma ^2_1}\bigg )^{\frac{1}{4}}\bigg (\frac{-(\sigma _1\psi +2)}{\sigma _1\psi }\bigg ). \end{aligned}$$
(58)

Family: 16 When \(\sigma _1=\sigma _2\), \(\sigma _3=0\)

$$\begin{aligned} \mathcal {R}_{23}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{-\mu ^2\sigma _1^2}}+ \bigg (\frac{72n\nu }{-\mu ^2\sigma _1^2}\bigg )^{\frac{1}{4}}\tan \bigg (\frac{\sigma _1\psi +c}{2}\bigg ). \end{aligned}$$
(59)

Family: 17 When \(\sigma _2=0\)

$$\begin{aligned} \mathcal {R}_{24}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3}}+ \bigg (\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3}\bigg )^{\frac{1}{4}}\bigg (e^{\sigma _3\psi }-\frac{\sigma _1}{2\sigma _3}\bigg ). \end{aligned}$$
(60)

where \(\psi\) is as defined in (3).

Set-2

$$\begin{aligned} \begin{aligned} m&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}},\,\,\, ~~~~c_0=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}},\,\,\, \\c_1&=0,\,\,\,b_1=2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}}. \end{aligned} \end{aligned}$$
(61)

Now, by substituting the second set into Eq (34), we obtain

$$\begin{aligned} f(\psi )=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}}\mathcal {L}^{-p(\psi )}. \end{aligned}$$
(62)

By employing the solutions given in Eq (7) through Eq (30), the obtained solutions are as follows.

Family:18 When \(\sigma ^2_3-\sigma _1\sigma _2<0\) and \(\sigma _2\ne 0\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{25}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}}\bigg (\frac{-\sigma _3}{\sigma _2} +\frac{\sqrt{-(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\\ &\tan \bigg (\frac{\sqrt{-(\sigma ^2_3-\sigma _1\sigma _2)}}{2}\psi \bigg )\bigg )^{-1}, \end{aligned}\end{aligned}$$
(63)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{26}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\\ &\cot \bigg (\frac{\sqrt{-(\sigma _3 ^2-\sigma _1\sigma _2)}}{2}\psi \bigg )\bigg )^{-1}. \end{aligned} \end{aligned}$$
(64)

Family:19 When \(\sigma _3^2+\sigma _1\sigma _2>0\) and \(\sigma _2\ne 0\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{27}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\\ &\tanh \bigg (\frac{\sqrt{(\sigma _3^2 -\sigma _1\sigma _2)}}{2}\psi \bigg )\bigg )^{-1}, \end{aligned}\end{aligned}$$
(65)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{28}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{-\sigma _3}{\sigma _2}-\frac{\sqrt{(\sigma ^2_3-\sigma _1\sigma _2)}}{\sigma _2}\\ &\coth \bigg (\frac{\sqrt{(\sigma _3 ^2-\sigma _1\sigma _2)}}{2}\psi \bigg )\bigg )^{-1}. \end{aligned} \end{aligned}$$
(66)

Family:20 When \(\sigma _3^2+\sigma _1\sigma _2>0\) and \(\sigma _2\ne 0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{29}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\\ &\tanh \bigg (\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg )\bigg )^{-1}, \end{aligned}\end{aligned}$$
(67)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{30}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\\ &\coth \bigg (\frac{\sqrt{(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg )\bigg )^{-1}. \end{aligned} \end{aligned}$$
(68)

Family: 21 When \(\sigma _3^2+\sigma _1\sigma _2<0\), \(\sigma _2\ne 0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{31}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\\ &\tan \bigg (\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg )\bigg )^{-1}, \end{aligned}\end{aligned}$$
(69)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{32}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{\sigma _2}\\ &\cot \bigg (\frac{\sqrt{-(\sigma _3^2+\sigma _1^2)}}{2}\psi \bigg )\bigg )^{-1}. \end{aligned} \end{aligned}$$
(70)

Family: 22 When \(\sigma _3^2-\sigma _1^2<0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{33}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\\ &\tan \bigg (\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg )\bigg )^{-1}, \end{aligned}\end{aligned}$$
(71)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{34}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\\ &\cot \bigg (\frac{\sqrt{-(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg )\bigg )^{-1}. \end{aligned} \end{aligned}$$
(72)

Family: 23 When \(\sigma _3^2-\sigma _1^2>0\) and \(\sigma _2\ne -\sigma _1\)

$$\begin{aligned} & \begin{aligned} \mathcal {R}_{35}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\\ &\tanh \bigg (\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg )\bigg )^{-1}, \end{aligned} \end{aligned}$$
(73)
$$\begin{aligned} & \begin{aligned} \mathcal {R}_{36}(x,t)&=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{-\sigma _3}{\sigma _2}+\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{\sigma _2}\\ &\coth \bigg (\frac{\sqrt{(\sigma _3^2-\sigma _1^2)}}{2}\psi \bigg )\bigg )^{-1}. \end{aligned} \end{aligned}$$
(74)

Family: 24 When \(\sigma _1\sigma _2>0\), \(\sigma _2\ne 0\) and \(\sigma _3=0\)

$$\begin{aligned} \mathcal {R}_{37}(x,t)= & \frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{-\sigma _2^2}}}\bigg (\sqrt{\frac{-\sigma _1}{\sigma _2}}\tanh \bigg (\frac{\sqrt{-\sigma _1\sigma _2}}{2}\psi \bigg )\bigg )^{-1}, \end{aligned}$$
(75)
$$\begin{aligned} \mathcal {R}_{38}(x,t)= & \frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{-\sigma _2^2}}}\bigg (\sqrt{\frac{-\sigma _1}{\sigma _2}}\coth \bigg (\frac{\sqrt{-\sigma _1\sigma _2}}{2}\psi \bigg )\bigg )^{-1}. \end{aligned}$$
(76)

Family: 25 When \(\sigma _3=0\) and \(\sigma _1=-\sigma _2\)

$$\begin{aligned} \mathcal {R}_{39}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{\mu ^2\sigma _1^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{\sigma _1^2}}} \bigg (\frac{-(1+e^{2\sigma _1\psi })\pm \sqrt{2(1+e^{2\sigma _1\psi })}}{e^{2\sigma _1\psi }-1}\bigg )\bigg )^{-1}. \end{aligned}$$
(77)

Family: 26 When \(\sigma _3^2=\sigma _1\sigma _2\)

$$\begin{aligned} \mathcal {R}_{40}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma ^2_1\sigma _2-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma ^2_1\sigma _2-\sigma _2^2}}}\bigg (\frac{-(\sigma _1\sigma _2\psi +2)}{\sigma _2\psi }\bigg )^{-1}. \end{aligned}$$
(78)

Family: 27 When \(\sigma _3=\kappa\), \(\sigma _1=2\kappa\) and \(\sigma _2=0\)

$$\begin{aligned} \mathcal {R}_{41}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3}}}\bigg (e^{\psi }-1\bigg ). \end{aligned}$$
(79)

Family: 28 When \(\sigma _3=\kappa\), \(\sigma _2=2\kappa\) and \(\sigma _1=0\)

$$\begin{aligned} \mathcal {R}_{42}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{e^{\psi }}{1-e^{\psi }}\bigg )^{-1}. \end{aligned}$$
(80)

Family: 29 When \(2\sigma _3=\sigma _1+\sigma _2\)

$$\begin{aligned} \mathcal {R}_{43}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{1+\sigma _1 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}{ 1+\sigma _2 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}\bigg )^{-1}. \end{aligned}$$
(81)

Family: 30 When \(-2\sigma _3=\sigma _1+\sigma _2\)

$$\begin{aligned} \mathcal {R}_{44}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3-\sigma _2^2}}} \bigg (\frac{\sigma _1+\sigma _1 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}{\sigma _2+\sigma _2 e^{\frac{1}{2}(\sigma _1-\sigma _2)\psi }}\bigg )^{-1}. \end{aligned}$$
(82)

Family: 31 When \(\sigma _1=0\)

$$\begin{aligned} \mathcal {R}_{45}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{-\sigma _2^2}}}\bigg (\frac{\sigma _3 e^{\sigma _3\psi }}{ 1+\frac{\sigma _2}{2}e^{\sigma _3\psi }}\bigg )^{-1}. \end{aligned}$$
(83)

Family: 32 When \(\sigma _1=\sigma _3=\sigma _2\ne 0\)

$$\begin{aligned} \mathcal {R}_{46}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{3\mu ^2\sigma ^2_1}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{3\sigma ^2_1}}} \bigg (\frac{-(\sigma _1\psi +2)}{\sigma _1\psi }\bigg )^{-1}. \end{aligned}$$
(84)

Family: 33 When \(\sigma _1=\sigma _2\), \(\sigma _3=0\)

$$\begin{aligned} \mathcal {R}_{47}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{-\sigma _2^2}}} \bigg (\tan \bigg (\frac{\sigma _1\psi +c}{2}\bigg )\bigg )^{-1}. \end{aligned}$$
(85)

Family: 34 When \(\sigma _2=0\)

$$\begin{aligned} \mathcal {R}_{48}(x,t)=\frac{\mu }{6\nu }\sqrt{\frac{72n\nu }{4\mu ^2\sigma _1\sigma _3-\mu ^2\sigma _2^2}}+ 2\sigma _1\sqrt{-\frac{3\nu \sqrt{2}}{2\mu }\sqrt{\frac{n}{4\sigma _1\sigma _3 -\sigma _2^2}}}\bigg (e^{\sigma _3\psi }-\frac{\sigma _1}{2\sigma _3}\bigg )^{-1}. \end{aligned}$$
(86)

where \(\psi\) is defined in (3).

Physical nature of soliton and other solutions

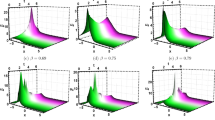
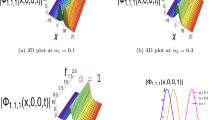
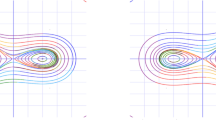
This section presents the physical interpretation of various soliton solutions in three-dimensional (3D), two-dimensional (2D), and contour plots using Mathematica 14.1. The analyzed solutions exhibited diverse structural forms, including dark, bright, mixed bright-dark, combined dark-singular, singular, and periodic singular solitons. These graphical representations were generated using appropriate parameter values that satisfied the conditions for all the considered cases 1-7.

Figures 1 and 2 show the dynamics of singular periodic soliton waves for the values of the fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\) and for the parameters \(\mu =0.01,\nu =0.5,\sigma _1=1.1,\sigma _2=1.2,\sigma _3=0.5,\sigma =0.2, -10\le x \le 10.\)

Figure 3 shows the dynamics of dark soliton wave for the values of the fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\) and for parameters \(\mu =0.01,\nu =0.5,\sigma _1=1.1,\sigma _2=1.2,\sigma _3=0.5,\sigma =0.2, -10\le x \le 10.\)

Figure 4 shows the dynamics of singular soliton wave for the values of the fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\) and for parameters \(\mu =0.01,\nu =0.5,\sigma _1=1.1,\sigma _2=1.2,\sigma _3=0.5,\sigma =0.2, -10\le x \le 10.\)

Figure 5 shows the exponential dynamics of solitary waves for the values of the fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\) and for the parameters \(\mu =0.01,\nu =0.5,\sigma _1=1.1,\sigma _2=1.2,\sigma _3=0.5,\sigma =1, -10\le x \le 10.\)

Figure 6 shows the dynamics of singular solitary waves for the values of the fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\) and for the parameters \(\mu =0.01,\nu =0.5,\sigma _1=1.1,\sigma _2=1.2,\sigma _3=0.5,\sigma =1, -10\le x \le 10.\)

Figure 7 shows the dynamics of singular periodic soliton waves for the values of the fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\) and for the parameters \(\mu =0.01,\nu =0.5,\sigma _1=1.1,\sigma _2=1.2,\sigma _3=0.5,\sigma =1, -10\le x \le 10.\) Similarly, the dynamics of the other solutions can be followed.

Fig. 1
figure 1

Physical dynamics of soliton solution \(|\mathcal {R}_{1}(x,t)|\) of space-time fractional modified KdV Eq (31): (a) Two-dimensional dynamics for the values \(t=0.0,~t=2.0,t=3.0\), (b) Two-dimensional dynamics for the values of fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\), and (c) Three-dimensional dynamics.

Full size image
Fig. 2
figure 2

Physical dynamics of soliton solution \(|\mathcal {R}_{2}(x,t)|\) of space-time fractional modified KdV Eq (31): (a) Two-dimensional dynamics for the values \(t=0.0,~t=2.0,t=3.0\), (b) Two-dimensional dynamics for the values of fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\), and (c) Three-dimensional dynamics.

Full size image
Fig. 3
figure 3

Physical dynamics of soliton solution \(|\mathcal {R}_{3}(x,t)|\) of space-time fractional modified KdV Eq (31): (a) Two-dimensional dynamics for the values \(t=0.0,~t=2.0,t=3.0\), (b) Two-dimensional dynamics for the values of fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\), and (c) Three-dimensional dynamics.

Full size image
Fig. 4
figure 4

Physical dynamics of soliton solution \(|\mathcal {R}_{4}(x,t)|\) of space-time fractional modified KdV Eq (31): (a) Two-dimensional dynamics for the values \(t=0.0,~t=2.0,t=3.0\), (b) Two-dimensional dynamics for the values of fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\), and (c) Three-dimensional dynamics.

Full size image
Fig. 5
figure 5

Physical dynamics of soliton solution \(|\mathcal {R}_{17}(x,t)|\) of space-time fractional modified KdV Eq (31): (a) Two-dimensional dynamics for the values \(t=0.0,~t=2.0,t=3.0\), (b) Two-dimensional dynamics for the values of fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\), and (c) Three-dimensional dynamics.

Full size image
Fig. 6
figure 6

Physical dynamics of soliton solution \(|\mathcal {R}_{18}(x,t)|\) of space-time fractional modified KdV Eq (31): (a) Two-dimensional dynamics for the values \(t=0.0,~t=2.0,t=3.0\), (b) Two-dimensional dynamics for the values of fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\), and (c) Three-dimensional dynamics.

Full size image
Fig. 7
figure 7

Physical dynamics of soliton solution \(|\mathcal {R}_{23}(x,t)|\) of space-time fractional modified KdV Eq (31): (a) Two-dimensional dynamics for the values \(t=0.0,~t=2.0,t=3.0\), (b) Two-dimensional dynamics for the values of fractional parameter \(\omega =0.6,~\omega =0.8,\omega =1.0\), and (c) Three-dimensional dynamics.

Full size image

Conclusions

In summary, this study constructs soliton solutions for the space-time fractional modified third-order KdV Eq. (31) by utilizing the NAE method. The derived solutions encompass trigonometric, rational, polynomial, exponential, and hyperbolic functions that incorporate multiple free parameters. Their validity was confirmed through direct substitution into the original equation. To further analyze the dynamical properties of these solutions, 2D, 3D, and contour plots were presented. In the literature, the authors64 employed two reliable analytical techniques, namely the \((\frac{G'}{G})\)-expansion method and the improved \((\frac{G'}{G})\)-expansion method, to obtain soliton solutions for the KdV Eq. (31). Rehman et al.65 utilized the Sardar sub-equation method to analyze the same model. Nazari66 utilized modified \((G'/G)\)-expansion method to derive singular solutions. A comparative analysis of our findings with those of these studies indicates that our work extends certain classes of soliton solutions for the space-time fractional modified third-order KdV Eq. (31). These findings highlight the efficiency, robustness, and simplicity of the NAE method. One of its major advantages is its applicability to nonlinear partial differential equations, in which most of the obtained solutions satisfy the given model. Furthermore, the method effectively reduces the computational complexity and enhances the efficiency by minimizing lengthy calculations. The comparison is also given by Table 1. In the future, we will be interested in applying machine learning tools67,68,69,70,71 to the same model.

Table 1 Comparison of the current work with recent studies on the space-time fractional modified third-order KdV Eq. (31).
Full size table

The various solution types obtained from nonlinear PDEs20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73 have broad applicability across physical sciences and engineering. Bright solitons are relevant to optical fiber communications and Bose–Einstein condensates, where they describe localized energy packets that maintain their shape over long distances. Dark solitons model intensity dips on a continuous background in nonlinear optics, plasma waves, and shallow water dynamics. Periodic and periodic singular solutions describe wave trains or modulated structures in fluids, plasmas, and photonic crystals. Singular solutions can represent wave breaking, shock formation, or localized energy blow-up in nonlinear media. Combined dark–singular waves are applicable to systems exhibiting mixed localized-depression and singular behavior, such as certain plasma instabilities or nonlinear metamaterials. Exponential-type solutions arise in describing rapidly decaying structures or transition layers in reaction–diffusion systems and quantum field models. Collectively, these diverse wave forms are important for modeling nonlinear propagation phenomena, stability regimes, and energy localization in contexts ranging from nonlinear optics and fluid mechanics to plasma physics and condensed matter systems.