Introduction

With the rapid development of information technology, the internet of things (IoT), and artificial intelligence (AI), the tourism industry is gradually stepping into a new era of “smart tourism”1. Smart tourism not only emphasizes information accessibility and service intelligence but also requires dynamic perception and accurate forecasting of tourist behavior and tourism demand, thereby improving the efficiency of tourism resource allocation and management levels2,3. Especially in the post-pandemic era, tourism demand has shown characteristics of high volatility and spatial heterogeneity, making traditional forecasting methods based on time series or macroeconomic variables face severe challenges in terms of accuracy and adaptability4. On one hand, tourism activities have significant spatial agglomeration and spillover effects, and there are obvious spatial correlations and spatial heterogeneities in tourism demand between different regions5,6. For example, changes in passenger flow in popular scenic spots often have a “siphon” or “radiation” effect on surrounding areas7. Spatial econometric models can effectively identify and quantify these spatial dependencies, enhancing the interpretability of forecasting models for regional interaction mechanisms8. On the other hand, deep learning, as an important method in the current field of AI, has been widely applied to time-series tasks such as traffic flow forecasting and consumer behavior modeling9,10. Its advantage lies in the ability to automatically extract complex nonlinear feature structures, which is particularly suitable for processing high-dimensional, multi-source, and dynamic data11. In the tourism field, deep learning can conduct in-depth modeling of unstructured data such as search indexes, user behavior trajectories, and social media data, thereby better capturing the potential driving factors of tourism demand.

However, in current research on tourism demand forecasting, there are prevalent issues of “insufficient modeling of spatial relationships” and “weak model interpretability”. To address these issues, this paper proposes a methodological framework that integrates spatial econometrics and deep learning. The aim is to combine the advantages of spatial correlation analysis and deep feature learning, constructing a smart tourism demand forecasting model with spatial perception ability, nonlinear forecasting ability, and interpretability. In doing so, it can provide more accurate, dynamic, and interpretable decision support for tourism management departments.

Literature review

With the development of smart tourism, tourism demand forecasting has gradually become a key issue in data-driven governance. Academic research has gradually expanded from traditional statistical models to paths such as deep learning, spatial econometrics, and hybrid modeling, forming a research pattern of multi-dimensional advancement.

Bufalo and Orlando found that the Autoregressive Integrated Moving Average Model (ARIMA) could effectively predict tourist flow in the short term, but the forecasting accuracy decreased significantly under the influence of seasonal fluctuations and sudden events12. Hewapathirana built a model based on support vector regression (SVR) to predict the tourist flow of major tourist cities in China, showing a certain ability of nonlinear modeling, but the spatial dependence characteristics were not incorporated into the model structure13. Ji et al. used the spatial Durbin model (SDM) in their study on the agglomeration effect of domestic tourism. They found that there was a significant spatial spillover effect of tourism demand between cities, and suggested that the tourism policies of neighboring cities should be considered in a coordinated manner14. Chen et al. used the spatial error model (SEM) to analyze the spatial linkage between traffic convenience and tourism attractiveness, emphasizing the role of spatial error terms in improving the explanatory power of the model15. Nguyen-Da et al. introduced the long short-term memory (LSTM) network into tourist flow forecasting, and found that this model could achieve higher accuracy than SVR in multi-time series data scenarios, especially suitable for demand change forecasting during holidays and unconventional events16. Luo et al. constructed a multi-channel Convolutional Neural Network-Long Short-Term Memory (CNN-LSTM) model integrating social media and meteorological data, realizing fine-grained forecasting of Beijing’s tourism demand. This model effectively improved data utilization and dynamic perception capabilities17.

In existing studies, spatial econometric models and deep learning methods are mostly applied independently or combined loosely, often focusing on only one aspect. Although deep learning models can capture complex nonlinear relationships, their spatial dependency structures are usually learned automatically through network topology or adjacency matrices, lacking interpretable spatial terms based on economic significance. In contrast, while spatial econometric models can characterize spatial spillover effects and regional correlations, they struggle to handle multi-dimensional, highly nonlinear time-series data. To address this limitation, this paper proposes a deep forecasting framework that explicitly embeds spatial econometric features: in the model structure, not only are econometric variables such as spatial lag terms and spatial error terms introduced, but these variables are also injected directly into the deep learning forecasting process as prior knowledge with economic and geographical interpretability, forming a dual-channel structure of “explicit spatial econometrics + deep sequence modeling”. Compared with existing hybrid methods, this study differs in the following aspects:

  1. (1)

    Parameters in the model, such as the spatial weight matrix and spatial lag terms, are explicitly estimated using spatial econometric methods, rather than merely learned implicitly through neural networks—this enhances the model’s interpretability and ability to reveal regional mechanisms.

  2. (2)

    In the deep forecasting module, spatial terms are dynamically embedded into the time-series modeling process, enabling the simultaneous modeling of temporal nonlinearity and spatial dependency, instead of the serial processing of “first extracting spatial features and then inputting them into the network”.

  3. (3)

    Through this approach, the model can maintain the high forecasting capability of deep learning while retaining the interpretability of spatial econometric models for policies and regional characteristics, providing a tool that balances high accuracy and interpretability for smart tourism demand forecasting.

Research model

Construction method of spatial econometric model

Commonly used spatial econometric models mainly include three types: spatial autoregressive model (SAR), SEM, and SDM. Among them, SDM is regarded as an extended form of SAR and SEM, and is suitable for most comprehensive modeling scenarios involving spatially lagged dependent variables and explanatory variables11,18.

The SAR model is mainly used to model the spatial correlation between dependent variables, and its basic form is as follows:

$$Y = \rho WY + X\beta + \varepsilon$$
(1)

\(Y\) is the dependent variable of tourism demand. \(W\) is the spatial weight matrix. \(\rho\) is the spatial autoregressive coefficient. \(X\) is the explanatory variable matrix. \(\beta\) is the regression coefficient, and \(\varepsilon\) is the error term. The SEM model is suitable for the case that the error term has spatial autocorrelation, and its form is:

$$Y = X\beta + \xi ,\xi = \lambda W\xi + \varepsilon$$
(2)

In the equation, \(\xi\) is the spatial error coefficient, and the SDM model integrates the above two factors, considering the spatial lag effect of dependent variables and explanatory variables:

$$Y = \rho WY + X\beta + WX\theta + \varepsilon$$
(3)

\(WX\theta\) is the influence of the spatial lag term of the explanatory variable on the dependent variable, which can effectively reflect the interaction of tourism-related factors between regions19,20. Spatial weight matrix is the core of spatial econometric model, which defines the spatial adjacency between regions. Common construction methods are shown in Table 1:

Table 1 Construction of spatial weight matrix.
Full size table

The introduction of spatial econometric models can effectively capture the external effects of tourism demand in the spatial dimension24,25. Especially in popular tourist cities or regional groups, the characteristics of spatial substitution or spatial complementarity in tourists’ behaviors are significant. Spatial econometric modeling not only helps to improve the accuracy of forecasting but also enhances the model’s ability to explain the mechanism of changes in the tourism market. At the same time, the significance test of spatial coefficients can also reveal the direction and intensity of the influence between regions, providing a quantitative basis for formulating regional linkage development strategies.

Design of deep learning forecasting model

In tourism demand forecasting tasks, influencing factors typically exhibit complex characteristics such as non-linearity, multi-temporality, and multi-source heterogeneity. Traditional regression methods struggle to fully explore these intricate relationships, whereas deep learning models possess inherent advantages in time series modeling, non-linear fitting, and high-dimensional data processing, thus gradually becoming one of the core methods in smart tourism research26,27. To better capture the dynamic evolution process of tourism demand, this paper introduces a Recurrent Neural Network (RNN) structure to construct a deep forecasting sub-model, aiming to improve forecasting accuracy and timeliness. The model architecture is shown in Table 2:

Table 2 Model architecture.
Full size table

In the model training, the following types of input features are considered:

  1. (1)

    Historical behavior variables: including historical tourist numbers, scenic spot passenger flow data, etc.

  2. (2)

    Environmental impact variables: such as meteorological information (temperature, rainfall), air quality index, etc.

  3. (3)

    Social public opinion variables: such as Baidu Index, Ctrip popularity, frequency of hot words on Weibo.

  4. (4)

    Time label variables: such as holidays, weekends, statutory schedule adjustments, etc.

  5. (5)

    Spatial correlation variables: spatially lagged dependent variables or spillover effect indicators extracted from spatial econometric models.

All variables need to undergo standardization processing before entering the model to ensure the stability and convergence of network training. During the training process, the mean square error (MSE) is used as the loss function, and the Adam optimizer is adopted for parameter update. The model training uses a sliding window mechanism to construct sample sequences and combines an early stopping mechanism to prevent overfitting. In the parameter tuning process, key attention is paid to optimizing hyperparameters such as time window length, hidden layer dimension, learning rate, and Dropout ratio.

In this paper, the spatial factor is embedded in LSTM, and its propagation path is constructed as follows:

$${\text{x}}_{t} = [x_{t}^{{\left( 1 \right)}} ,x_{t}^{{\left( 2 \right)}} ,...,x_{t}^{{\left( k \right)}} ]^{{ \top }}$$
(4)

\({\text{x}}_{t}\) is the input feature vector at time \(t\). \({x}_{t}^{(k)}\) is the \(k\) th variable, including holidays, environment, historical demand, etc. After introducing the spatial factor, a new input is constructed as follows:

$${\text{x}}_{t}^{*} = {\text{x}}_{t} \oplus {\text{s}}_{t}$$
(5)

\({\text{s}}_{t}\) is a spatial factor vector, which is calculated from the spatial lag term and the error term. To clarify the contribution path of spatial factors in the network, the gradient attribution mechanism is introduced and the target output is defined as the predicted value:

$$\hat{y}_{t} = {\text{MLP}}\left( {h_{t} } \right)$$
(6)

In the equation, \({\widehat{y}}_{t}\) is the predicted value and \({h}_{t}\) is the input target data, and the attribution mechanism is introduced to calculate the influence degree of each variable in the spatial factor on the predicted output:

$${\text{Imp}}\left( {s_{t}^{\left( j \right)} } \right) = \frac{{\partial \hat{y}_{t} }}{{\partial s_{t}^{\left( j \right)} }}$$
(7)

\({s}_{t}^{(j)}\) is \(j\) spatial variables, and \(\text{Imp}\) is the boundary influence. The larger the value, the more sensitive and influential the spatial variable is to the output.

The framework of model fusion and integration

In the task of smart tourism demand forecasting, a single model often struggles to simultaneously account for both the spatial dependence and temporal nonlinear characteristics of data28,29. Spatial econometric models, with strong interpretability, can capture spatial spillover effects between regions. While deep learning models excel at handling complex dynamic nonlinear relationships and are suitable for multi-variable time-series forecasting30,31. To balance forecasting performance and interpretability, this paper constructs an integrated forecasting framework that fuses spatial econometrics and deep learning, enabling in-depth interaction and joint modeling of spatial–temporal features. The core purpose of model fusion is to break the limitation of “separated modeling of space and time” in traditional forecasting methods. Through a cross-model information sharing mechanism, it achieves a more comprehensive portrayal of the evolution mechanism of tourism demand. The spatial lag variables output by spatial econometric models (such as tourist flows in neighboring regions) can serve as important inputs to the deep learning model, enhancing its ability to perceive spatial dependence structures. The residual part of the forecasting results from the deep learning model can be reversely used to update the error terms in the spatial model, improving the stability of local estimation. Through parallel training and feature cross mechanisms, the overall model’s forecasting accuracy and robustness are enhanced.

The integrated framework constructed in this paper adopts a structured integration mechanism of “explicit spatial modeling—deep nonlinear modeling—dynamic feedback update”. It breaks through the traditional shallow fusion mode of “spatial feature concatenation input” and forms a multi-layer linkage mechanism featuring structural coupling, semantic interaction, and coordinated forecasting. The overall framework consists of three functional modules:

  1. (1)

    Module A: Spatial structure modeling subsystem. Based on the SAR/SDM spatial econometric model, it takes the spatial weight matrix and regional macro variables as input, and outputs explicit spatial factors such as spatial lag terms, spatial error terms, and agglomeration indicators. These spatial factors serve as structured input and are independently encoded into spatial vectors and embedded into the subsequent fusion module to maintain the interpretability of regional dependency relationships.

  2. (2)

    Module B: Deep forecasting and fusion subsystem. It receives time-series data (tourist volume, holidays, weather, etc.) and spatial representations extracted by the spatial subsystem. A spatial gating fusion mechanism is designed in the LSTM backbone structure to realize the dynamic regulation of spatial factors on the time modeling process. In each time step, the model adaptively adjusts the influence weight of spatial factors according to the current input state, and constructs a spatial–temporal joint modeling path.

  3. (3)

    Module C: Error feedback and structure update mechanism. By comparing the predicted value of the deep model with the actual value, it extracts residual signals, which are used to reversely correct the spatial error terms and dynamically adjust the spatial adjacency matrix or lag structure parameters. This realizes the coordinated update of the spatial dependency structure and the forecasting model, and enhances the robustness and generalization ability of the model.

To realize information flow and structural coupling among the above-mentioned modules, this paper designs the following interaction mechanisms:

  1. (1)

    The spatial model is trained first and a set of spatial factors is constructed, which serves as input for explicit geographical structure.

  2. (2)

    After embedding encoding, the spatial factors are dynamically fused with time series in the LSTM, rather than being statically concatenated.

  3. (3)

    In joint training, a dual-path loss function is adopted. The spatial path and temporal path share part of the target variables and residual information, enabling the feedback and correction of prediction errors between the two sub-modules.

  4. (4)

    For parameter optimization, a phased parameter tuning strategy is used: first, the deep model is fixed to train the spatial module; then, the spatial module is frozen to fine-tune the deep structure; finally, joint fine-tuning is conducted to achieve convergence.

In summary, the proposed integration framework is reflected in the variable combination at the input layer in terms of fusion mode, and attaches great importance to the interactive modeling of spatial–temporal information inside the structure and the dynamic feedback adjustment mechanism. While maintaining the model’s prediction performance, it significantly improves its interpretability, structural transparency, and ability to model complex tourism behavior patterns.

Experimental design and performance evaluation

Datasets collection

The datasets used in this paper are CityBrain-BJ Tourism Flow Dataset (CB-BJTF), Ctrip Tourism Demand (CTD), and Microsoft Research Asia GeoLife Global Positioning System Trajectory (GeoLife). CB-BJTF records the tourist flow data of multiple key tourist attractions in Beijing at different time periods, combined with various influencing factors such as holidays, weather, and transportation. The data is in a time-series format and has geographical location attributes, making it suitable for spatial–temporal joint modeling. The dataset can be downloaded from https://aistudio.baidu.com/datasetoverview. CTD is a dataset from a Chinese Online Travel Agency (OTA) platform, including search popularity of tourism products, booking quantities, price trends, and user reviews, recorded daily. It is suitable as input variables for deep learning models and can also be used for correlation analysis between social behaviors and tourism demand. The dataset can be downloaded via https://www.kaggle.com/search. GeoLife is a real Global Positioning System (GPS) trajectory dataset provided by Microsoft Research Asia, covering long-term travel trajectories of 182 users. It has rich spatial distribution and movement patterns, and can be used for spatial behavior modeling, cluster analysis, and regional tourism flow forecasting. The dataset can be downloaded from https://www.microsoft.com/en-us/download/details.aspx?id=52367.

Considering the heterogeneity of the three types of data (e.g., source, time granularity, recorded content), this paper uniformly adopts the following three-stage division method for data processing:

  1. (1)

    Training set: Used for model parameter learning, accounting for 70% of the total data;

  2. (2)

    Validation set: Used for model parameter tuning and early stopping judgment, accounting for 15% of the total data;

  3. (3)

    Test set: Used for final performance evaluation and comparative analysis, accounting for 15% of the total data.

In addition, considering that tourism demand has obvious time-series dependency, this paper uses a time-sequential segmentation method to ensure that the training data is earlier than the validation and test data. This avoids future information leakage and enhances the practical application capability of the forecasting model.

Experimental environment and parameters setting

The experimental environment in this paper is shown in Table 3:

Table 3 Experimental environment.
Full size table

In terms of the deep learning sub-model, a two-layer LSTM structure is adopted, with 128 units in each LSTM layer and a time step set to 14 days to capture changes in tourist behavior over the past two weeks. The model input contains multi-variable features, all of which undergo Z-score standardization before input. To avoid overfitting, a Dropout layer is introduced after each LSTM layer with a dropout rate of 0.3. The MSE is used as the loss function, and the Adam optimizer is selected with an initial learning rate of 0.001, which is dynamically adjusted through a learning rate decay strategy during training. In the spatial econometric model, the SDM is used as the basic structure, and the spatial weight matrix adopts a mixed adjacency matrix weighted by inverse distance, which is corrected by combining the intensity of tourist flow between scenic spots. To enhance the model fusion effect, the spatial factors output by the spatial model are directly injected into the LSTM input as static features and kept updated in each training epoch. During the training process, a mini-batch stochastic gradient descent strategy is adopted with a batch size of 64 and a training epoch set to 100. An early stopping mechanism is used to prevent overfitting, which automatically stops training when the validation set loss does not decrease for 10 consecutive epochs. The model training and testing processes are completed in the Ubuntu system environment, and all codes are developed based on the PyTorch framework, ensuring the reproducibility and portability of the model. In addition, the comparison models selected in the experiment are Informer: Efficient transformer for long sequence time-series forecasting (informer) and spatio-temporal graph convolutional network (ST-GCN).

For the Informer model, this paper refers to the structural parameter settings recommended in its original paper and adjusts key parameters through grid search based on the characteristics of actual data—such as input sequence length (seq_len), label length (label_len), hidden dimension (d_model), and number of attention heads (n_heads). Meanwhile, the CosineAnnealing learning rate scheduler and EarlyStopping strategy (with patience = 10) are used. Each set of parameters is tested repeatedly for 5 times, and the average value is finally taken to reduce randomness. For the ST-GCN model, this paper modifies its structure based on open-source implementations to adapt it to the tourism demand forecasting task. Specific modifications include: introducing the spatial adjacency matrix constructed in this paper (which integrates scenic spot geographical distance and traffic connectivity) to replace the original graph structure; adjusting the combined structure of graph convolution and temporal convolution; and optimizing the ReLU activation function and BatchNorm regularization strategy. Similarly, grid search is used to conduct multiple rounds of optimization on hyperparameters such as batch size, learning rate, and dropout. The optimal model configuration is selected on the validation set, and all experiments are also repeated 5 times to ensure stability.

Performance evaluation

Comparison experiment of model performance

In the experiment, the indicators of time and space dimensions of the model are selected, and the comparison results of time dimensions are shown in Fig. 1:

Fig. 1
figure 1figure 1

Comparison results of time dimension (a) MAE (mean absolute error) (b) RMSE (root mean squared error) (c) MAPE (mean absolute percentage error) (d) R2.

Full size image

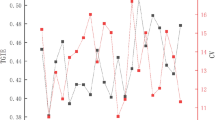
From Fig. 1, in terms of MAE, the proposed optimized model achieves 9.653 on CB-BJTF, 11.234 on CTD, and 7.947 on GeoLife. In terms of RMSE, its results on the three datasets are 12.118, 13.876, and 10.426 respectively, which are significantly better than the Informer model’s 14.006 on GeoLife. In terms of MAPE, the performance of this model on CB-BJTF, CTD, and GeoLife is 14.538%, 16.903%, and 12.664% respectively, all superior to ST-GCN’s 19.758% on CTD. In terms of R2 value, the optimized model reaches 0.924, 0.897, and 0.877 respectively, which is obviously better than Informer’s only 0.872 on the CB-BJTF dataset. The comparison results in the spatial dimension are shown in Fig. 2:

Fig. 2
figure 2figure 2

Comparison results of spatial dimensions (a) Moran’s I of Residuals (b) Spatial R2 (c) MSE (mean spatial error)-geo (d) Coefficient of variation of spatial residuals.

Full size image

The results in Fig. 2 show that the optimized model in this paper achieves lower spatial residual autocorrelation in terms of the Moran’s I index, with values of 0.094 for CB-BJTF, 0.079 for CTD, and 0.061 for GeoLife. In terms of the Spatial R2 index, it reaches 0.868, 0.831, and 0.799 respectively, which is better than ST-GCN’s 0.737 on GeoLife. For the Mean Spatial Error (MSE-Geo), the optimized model yields result of 14.937, 18.117, and 12.368 on the three datasets, outperforming Informer’s 25.392 on CTD data. In terms of the coefficient of variation of spatial residuals, the optimized model also maintains a low level, with values of 0.297, 0.324, and 0.283. In contrast, ST-GCN’s value for this index on CB-BJTF is 0.376.

Analysis of sensitivity of spatial variables

To comprehensively evaluate the impact of various spatial variables on the model’s forecasting performance, this paper adopts the method of item-by-item elimination. Based on the optimized model proposed herein, each spatial variable is removed individually from the CB-BJTF dataset, and the model’s response changes are recorded across 12 performance dimensions. The 4 core spatial variables selected in this paper are as follows:

  1. (1)

    W_Y: tourist flow in neighboring regions (spatial lag term)

  2. (2)

    M_I: Moran’s I index (measuring spatial agglomeration)

  3. (3)

    SP_Avg: average hotel price in surrounding areas (spatial economic variable)

  4. (4)

    Inter_Cnt: on-request data (OD) interaction frequency between regions (spatial interaction behavior)

Table 4 presents a comparison of the performance between the optimized model in its complete state and after the elimination of each of the 4 spatial variables, covering 12 mainstream indicators. For reference, the RMSE and Moran’s I of ST-GCN when W_Y is eliminated are partially listed as a comparison:

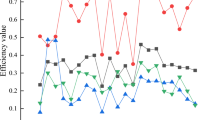
Table 4 Changes of model performance indexes after removing spatial variables.
Full size table

From Table 4, in the complete model, the proposed optimized model shows stable performance in various indicators on the CB-BJTF dataset: MAE is 9.653, RMSE is 12.118, MAPE is 14.538%, R2 is 0.924, Moran’s I is 0.094, Spatial R2 is 0.868, normalized RMSE is 11.423%, residual coefficient of variation is 0.297, SMAPE is 13.841%, forecasting bias (Bias) is 0.019, explained variance is 0.929, and spatial mean square error (MSE-Geo) is 14.937. When the neighboring tourist flow variable (W_Y) is removed, the error indicators of the optimized model generally rise. For example, MAE increases to 12.284, MAPE and NRMSE also increase significantly. Spatial consistency indicators such as Moran’s I rise from 0.094 to 0.238, indicating that the spatial structure is destroyed. Meanwhile, under the same elimination condition, ST-GCN’s RMSE reaches 17.104 and Moran’s I is 0.313, further reflecting the structural advantages of the proposed optimized model. When the Moran’s I index (M_I) is removed, the MAE of the optimized model is 11.018, RMSE rises, and Spatial R2 drops to 0.826, indicating that the model’s ability to model spatial agglomeration is limited. After eliminating the SP_Avg variable, various error indicators rise slightly, but the overall change is not significant, and R2 remains at 0.842, indicating that although this economic variable contributes, its sensitivity is relatively low. When the OD interaction frequency (Inter_Cnt) is removed, the MAE of the optimized model is 10.208, the spatial residual distribution deteriorates slightly, and SMAPE and Bias also increase. It indicates that behavioral spatial variables play an important supplementary role in constructing regional interaction mechanisms.

Robustness analysis

To verify the stability and generalization ability of the proposed “spatial econometrics + LSTM deep forecasting” model under different data divisions, this paper implements stratified fivefold cross-validation on the main CB-BJTF dataset. The specific process is as follows:

  1. (1)

    The data is divided into 5 subsets in chronological order; in each iteration, 4 folds are used as the training set, and the remaining onefold is used as the validation set.

  2. (2)

    After training each fold, key indicators such as R2, Root Mean Square Error (RMSE), and Mean Absolute Error (MAE) are recorded.

  3. (3)

    The average value of all indicators is calculated, and the standard deviation is computed to measure the model’s stability and overfitting risk.

  4. (4)

    Meanwhile, curves of the model’s training loss and validation loss changing with the number of iterations are plotted to analyze whether there is an overfitting trend of “good performance on training set but poor performance on validation set”.

The experimental results are shown in Table 5:

Table 5 Results of fivefold cross-validation.
Full size table

The above results show that the model’s performance fluctuates very slightly across the 5 different validation sets: the standard deviation of R2 is only 0.004, the standard deviation of RMSE is 0.26, and the standard deviation of MAE is only 0.21—indicating good robustness. In addition, all validation losses show an overall downward trend with the number of training epochs, and there is no overfitting phenomenon where the training set is over-fitted while the validation set error increases.

To further verify whether the differences in various prediction indicators between the proposed optimized model and existing comparative models are statistically significant, this paper conducts a significance test on the experimental results of the CB-BJTF dataset. The experimental results are shown in Table 6:

Table 6 Significance test result.
Full size table

The results of the significance test show that the proposed model has significant advantages over Informer and ST-GCN in terms of key performance indicators (RMSE, MAE, MAPE, R2), with all p-values lower than 0.05. This indicates that the improvement in model performance is not accidental, but a statistically significant and robust enhancement. This result further strengthens the credibility and promotion value of the proposed method for smart tourism demand forecasting.

Discussion

In the performance comparison results, from the temporal dimension, the optimized model achieves lower error values and higher goodness of fit across multiple datasets. This indicates its strong responsiveness in handling seasonal fluctuations of tourism demand and abnormal changes during holidays. The model’s advantages in MAE and MAPE are particularly significant, especially in datasets with large geographical spans and frequent demand changes. From the spatial dimension, the optimized model effectively identifies and quantifies the correlation of tourism demand between regions by introducing spatial lag terms and error terms. This makes the spatial distribution of residuals tend to be random and reduced spatial autocorrelation, further enhancing the model’s generalization ability and geographical adaptability. Meanwhile, the improved consistency of spatial fitting reflects the model’s coordinated performance in multi-region and multi-scale forecasting, which helps support regional tourism collaborative governance and optimal resource allocation.

The results of the sensitivity analysis experiment on spatial variables show that different types of spatial variables have significantly varying impacts on model performance. Among them, spatial lag variables play a crucial role in the overall forecasting accuracy and spatial fitting ability of the model. Once removed, they lead to a significant increase in errors and a marked decline in spatial consistency. This indicates that the model is highly dependent on the spatial prior information provided by such variables when identifying the spillover effects of tourism demand between regions. Spatial statistical variables, especially those measuring agglomeration and heterogeneity, are more reflected in the model’s ability to capture hotspots and dense tourist flows. In their absence, the model tends to misjudge local trends or overlook cluster characteristics, resulting in reduced explanatory power and imbalanced forecasting. In contrast, although spatial structure variables and economic behavior variables have a relatively moderate impact on the main indicators, they exhibit obvious compensatory effects in improving model robustness, reducing local biases, and enhancing the interpretation of user behavior characteristics. This reflects the value of micro-interventions based on specific geographical conditions and market behaviors.

Zhou et al. found that combining graph neural networks with attention mechanisms could effectively capture dynamic spatial interactions and temporal dependencies between tourism regions. In the proposed Attention-based Spatio-Temporal Graph Neural Network (AT-STGNN) model, the authors constructed a dynamic graph structure based on user check-in data, used a multi-head attention mechanism to explore the dynamic changes of regional tourism influence, and integrated it with time-series modeling—effectively improving the accuracy of tourism demand forecasting32. The study verified the feasibility of integrating dynamic graph learning and multi-scale temporal modeling, broke through the limitations of traditional static adjacency modeling, and provided a new idea for high-frequency tourism demand modeling. Their research focused on the dynamic evolution of graph structures and tourism behavior perception, while this paper proposes innovations in the interpretability of spatial econometric factors and the error feedback mechanism of deep neural networks. Although both studies integrate spatio-temporal information, this paper emphasizes the explicit modeling of spatial structure factors and a residual feedback loop, making it more suitable for macro tourism forecasting and policy deduction scenarios, and forming a complement in terms of technical boundaries. Yan et al. (2025) found that the Spatio-Temporal Informer based on the Transformer architecture exhibits superior performance in processing long-time-series and strong-period tourism flow data. The study constructed a graph structure between tourist attractions and introduced position embedding into the encoder layer, enabling the model to have spatial perception capabilities33. In tourism forecasting experiments across multiple cities, this model outperformed traditional LSTM and Gated Recurrent Unit (GRU) models in terms of MAE and RMSE indicators, highlighting the potential of the Transformer structure in capturing long-distance dependencies of tourism demand. Their research emphasized the long-sequence modeling capability of the Transformer model, but its spatial modeling was only based on simple position encoding, lacking the modeling and interpretation of structural spatial factors. In contrast, this paper constructs a spatial factor structure based on the spatial econometric model to improve spatial interpretability, and further designs an error feedback mechanism to enhance the model’s adaptability. Therefore, this paper achieves differentiated innovations in the design of spatial interpretability mechanisms and model iterative update paths.

Conclusion

Research contribution

In terms of modeling ideas, innovations in spatial–temporal fusion are achieved. This paper breaks through the problem of separation between time modeling and spatial analysis in traditional tourism demand forecasting. For the first time, this paper introduces econometric variables such as spatial lag terms and spatial agglomeration indicators into the LSTM deep structure, constructing a dynamic forecasting model with spatial perception ability, and improving the model’s adaptability to the regional heterogeneity of tourism behaviors. A systematic method is formed in multi-source data processing and structural embedding. Combining typical tourism datasets such as CB-BJTF, CTD, and GeoLife, this paper constructs a comprehensive input system including multi-dimensional spatial features such as tourist flow, price index, and density. Through the spatial variable injection mechanism, these features are effectively embedded into the deep model structure, realizing complete integration from the data layer to the structural layer. This paper reveals the mechanism of regional structure in forecasting through spatial variable sensitivity experiments. By testing the impact of eliminating key spatial variables on model performance, it clarifies the core status of variables such as spatial lag terms, spatial agglomeration, and regional interaction behaviors in model construction. This paper provides empirical support for regional factor configuration and feature selection in future smart tourism systems.

Future works and research limitations

Despite the progress made in constructing tourism demand forecasting models and spatio-temporal integration methods, this paper still has certain limitations. Currently, this paper uses a static spatial weight matrix constructed based on geographical proximity and administrative boundaries, which fails to fully reflect the real interaction characteristics and dynamic evolution patterns of tourism behaviors among regions. This may lead to insufficient representation of spatial dependence. Especially during holidays, special events, or emergencies, the structure of regional tourism flows often changes abruptly, and the model cannot dynamically perceive and adaptively adjust. Future research could introduce a spatially adaptive weight learning mechanism driven by big behavioral data, such as tourists’ GPS trajectories and social media check-ins. By combining graph neural networks or dynamic adjacency learning frameworks, a more flexible spatial modeling solution that accurately reflects the structure of tourism flows can be constructed. Moreover, although the current model has achieved excellent performance on datasets related to Beijing and its surrounding areas, its generalization ability in other complex urban structures or heterogeneous tourism markets (such as polycentric cities and cross-provincial interaction regions) still needs to be verified. Particularly in scenarios with more complex spatial structures and elastic and diverse tourism behaviors, the model may face issues such as structural adjustment difficulties or unstable training. Therefore, in the future, methods such as multi-regional transfer learning and meta-learning mechanisms can be adopted to enhance the model’s adaptability and robustness in a wider geographical context. Meanwhile, although this paper attempts to reveal the roles of key spatial factors through variable sensitivity analysis, it fails to theoretically explain the internal mechanisms by which spatial factors operate within deep models, and lacks a causal explanation chain for the “space–time-forecasting” path. In subsequent studies, spatial attention mechanisms and interpretable graph learning methods can be further introduced to help understand how spatial factors gradually influence state updates and outputs in multi-layer LSTM, thereby achieving transparent interpretation and traceability of forecasting results.