Stability and parameter sensitivity analysis of hydropower units under full operating conditions based on Pelton turbine refined models

Abstract

This paper investigates the full-condition stability and parameter sensitivity of a Pelton turbine regulation system (PTRS) under high-head hydropower operation. A differentiable, data-driven turbine model based on neural networks is developed to ensure smooth transfer-coefficient extraction across all combinations of head and needle opening. Using Hopf bifurcation analysis, we map the stability domains under multiple operating conditions. Results show that, at a fixed head, the stability-domain area at 25% needle opening is nearly three times that at 65% opening, revealing a significant stability reduction from low to medium openings, with a mild recovery near the rated opening. A system-wide trajectory sensitivity framework is then established to rank the influence of parameters on speed and discharge states. Turbine parameters e_y and e_qy are identified as dominant, followed by the controller integral gain K_i, whereas surge-tank and pipeline parameters have smaller contributions. The sensitivity of the system to the parameters under different operating conditions shows a certain regularity along with the change of the needle opening and the head. This work provides valuable insights into the stability and parameter sensitivity analysis of the PTRS, which can help promote system identification, stability analysis, and optimal control of hydropower plants.

Introduction

Over the past decade, global renewable energy power generation has risen by nearly 8%. Among all renewable energy sources, hydropower remains the dominant contributor, accounting for approximately 72% of global renewable electricity^1,2. Hydropower’s characteristics—renewable, clean, low-cost, and highly regulated—make it a crucial component of the global energy framework, playing a pivotal role in improving energy efficiency and advancing ecological civilization³.

China holds the largest hydropower resources in the world and is developing them rapidly. The country’s 14th Five-Year Plan explicitly outlines the promotion of an energy revolution, the establishment of a clean, low-carbon, safe, and efficient energy system, and the development of a hydropower base along the lower reaches of the Yarlung Zangbo River⁴. Currently, hydropower resources in China’s eastern and central regions, as well as medium- and low-head hydropower resources, have been largely developed. The remaining resources are concentrated in the ecologically fragile, mountainous, and deep-valley areas of southwest China, where high- and ultra-high-head hydropower units offer significant potential for expansion with minimal environmental impact^5,6. However, due to the concentration of hydropower development in mid- and low-altitude regions where resources are more easily accessible, the demand for power station units has primarily been met by Francis, axial-flow, and cross-flow turbines^7,8. This has resulted in a relative lack of research on the stability of regulation systems for Pelton turbine units, which are more commonly used in high- and ultra-high-head hydropower projects⁹.

As the core control unit of hydropower generation, the dynamic characteristics and stability of the turbine regulation system directly affect the reliability of the power system and power quality¹⁰. Therefore, in view of the current research situation and the research content of this paper, the next two aspects of the Pelton turbine model development, stability, and optimized control research are summarized.

The mathematical modeling of Pelton turbines forms the fundamental basis for numerical simulations of hydraulic systems, operational stability assessment, reliability analysis, dynamic characteristic evaluation, and control strategy development. Specifically, Mircea et al. employed experimental identification methods with sinusoidal test signals to determine the frequency response characteristics of Pelton turbines, successfully deriving gain-frequency and phase-frequency characteristics through experimental measurements¹¹. Literature¹² proposed a novel Pelton turbine model incorporating needle valve dynamics and turbine characteristics for water hammer analysis, demonstrating strong agreement between numerical simulations using quasi-steady and unsteady friction models with experimental data. Wang et al. established a dynamic model of Pelton turbines and their governing systems suitable for power grid stability analysis, emphasizing model accuracy and applicability enhancement¹³. Khema et al. developed a turbine regulation system through mathematical parameter calculation for specific hydropower scenarios, ensuring constant rotational speed maintenance under variable loads¹⁴.

System stability serves as the prerequisite for control optimization, while optimized control strategies constitute critical means for improving regulation quality. Current research on stability and optimal control of hydraulic units primarily focuses on stability analysis, nonlinear dynamics, parameter sensitivity studies, and controller design. Pu et al. established mathematical models for Pelton turbines and improved isolated grid analysis models, systematically investigating control parameter stability domains under islanding conditions¹⁵. Song et al. developed mathematical models for governing system analysis, conducting simulation studies on regulation characteristics under both small and large load disturbances in isolated grids¹⁶. Beus et al. addressed nonlinear system dynamics across operational points by developing a model predictive control algorithm featuring linear prediction model parameter adaptation¹⁷. Xu et al. proposed a global sensitivity analysis framework integrating hydraulic (head, flow), mechanical (shaft alignment, bearing stiffness), and electrical (excitation current) parameters, quantitatively evaluating parameter contributions to system stability¹⁸. Randell et al. enhanced frequency regulation characteristics and mitigated traveling wave effects through needle valve control modeling combined with trajectory sensitivity-based parameter optimization¹⁹.

Critical analysis of existing literature reveals three principal limitations: (1) Current Pelton turbine modeling approaches predominantly rely on experimental identification methods or generalized Francis turbine models, with the former lacking real-time applicability and the latter neglecting Pelton-specific structural characteristics, thereby constraining subsequent stability analysis and control optimization. (2) Stability investigations typically concentrate on rated or limited operational conditions with insufficient parameter stability domain precision, hindering a comprehensive understanding of stability mechanisms and controller parameter optimization. (3) Existing sensitivity analyses predominantly examine individual parameter effects on specific subsystems rather than establishing hierarchical relationships between system parameters and operational states.

This study aims to address the issues of quantifying the stability domain under all operating conditions and prioritizing parameter sensitivity in the PTRS. The main objectives and goals of this work are two aspects. The first aspect involves analyzing the stability of the Pelton turbine under all operating conditions. The second aspect involves ranking and analyzing parameter sensitivity in the PTRS. The research results can be applied to guide the optimization of control systems in hydropower stations.

Building upon the preceding research foundation, this study focuses on examining comprehensive operational stability of the PTRS and evaluating state parameter sensitivity through the refined model of the Pelton turbine. The principal academic innovations include: (1) A refined mathematical model of the Pelton turbine based on neural network is established, and the transfer coefficient of the model is calculated accordingly. (2) Systematic stability evaluation employing both analytical methodologies and computational modeling approaches. (3) The stability of the system under full operating conditions of the PTRS and the influencing factors are analyzed. (4) The sensitivity of the main state variables of the PTRS to the system parameters is investigated, and the primary and secondary influence relationships between different parameters between different subsystems are analyzed.

The rest of this paper is organized as follows: In “Mathematical model of PTRS”, the neural network-based Pelton turbine model and other subsystems are mainly introduced, then the transfer coefficients are calculated and the PTRS state space equations are developed. In “Stability analysis under full operating conditions”, the Hopf bifurcation method is first introduced, and then the stability and influence law of the system under full operating conditions are analyzed. In “Parameter sensitivity analysis”, the sensitivity index is first introduced and then the sensitivity of the system state to different parameters and the sensitivity of the operating conditions to different parameters are investigated. The “Discussion” and “Conclusions” contain a discussion, future work and main conclusions, respectively.

Mathematical model of PTRS

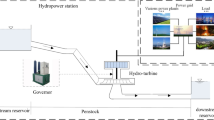
The PTRS constitutes a sophisticated nonlinear system that combines hydraulic, mechanical, and electrical components. The Fig. 1 illustrates its simplified operational diagram. This section primarily presents mathematical representations of critical subsystems including the governor, headrace tunnel, surge tank, servo-system, penstock, Pelton turbine, and generator. Corresponding simulation frameworks have been implemented within the MATLAB/Simulink environment for system analysis.

Fig. 1

Simplified diagram of a hydropower plant.

Neural network-based nonlinear modeling of Pelton turbine

The Pelton turbine represents the core equipment of the PTRS, which is characterized by strong nonlinearity, time-varying, and variable operating conditions. The accuracy of the mathematical model directly affects the simulation accuracy of the research work. Pelton turbines differ greatly from the common Francis turbine in terms of physical design and operating principle, but it is still possible to obtain torque characteristics and discharge characteristics from the hydro-turbine combined characteristic curve. The torque characteristic and discharge characteristic can be expressed as a function of the hydro-turbine needle opening, water head, and speed, respectively, as shown in Eq. (1).

$$\left\{ \begin{gathered} m_{t} = f_{M} (y,h,x) \hfill \\ q_{2} = f_{Q} (y,h,x) \hfill \\ \end{gathered} \right.$$

(1)

Due to the highly nonlinear characteristics of hydro-turbine, there is an absence of a suitable mathematical analytic function with which to express the characteristics. However, it is possible to utilize neural networks^20,21, which possess a strong nonlinear fitting ability, to realize the nonlinear modeling of Pelton turbine.

Firstly, the raw data points of the Pelton turbine are obtained based on the operating parameters and Pelton turbine combined characteristic curve (six needles) of an actual hydropower plant, including needle opening, unit discharge, unit speed, and efficiency. The actual operating parameters of the hydropower plant are shown in Table 1. Then, the efficiency characteristic BP neural network model $\eta = \eta (n_{11} ,Q_{11} )$ is trained, which can be used to calculate the efficiency of the turbine at the operating point where it is located based on the inputs of unit speed and unit discharge. Finally, to ensure effective training, the dataset was divided into training, validation, and test sets, accounting for 70%, 15%, and 15% of the samples, respectively. The Levenberg–Marquardt (LM) algorithm²², which combines the advantages of both gradient descent and Gauss–Newton methods, was employed for training, with a maximum of 1000 iterations. A three-layer neural network structure with one hidden layer was used, containing 10 and 9 neurons in the hidden layer for the torque characteristic surface and the discharge characteristic surface, respectively. The inputs of the models were all the unit speed and needle opening when the turbine was running, and the outputs were the turbine unit torque and unit discharge, respectively. The surfaces of unit torque characteristics and unit discharge characteristics of the turbine are shown in Fig. 2–3.

$$M_{t11} = \frac{30\gamma }{\pi }\frac{{Q_{11} \eta }}{{n_{11} }}$$

(2)

Table 1 The actual operating parameters of the hydropower plant.

Fig. 2

Unit discharge characteristics.

Fig. 3

Unit torque characteristics.

In order to verify the accuracy of the established neural network model, The actual data of Pelton turbine for training neural network and the neural network prediction data are shown in Fig. 4–5. It can be learned that the neural network prediction data and the actual data curve almost coincide with good consistency, which can reflect the trend of the actual data.

Fig. 4

Neural Network Predicted Unit Discharge and Actual Unit Discharge.

Fig. 5

Neural Network Predicted Unit Torque and Actual Unit Torque.

Further in order to facilitate the stability analysis of the system, a linear mathematical model of the Pelton turbine is established by using the method of local linearization at different operating points. Through first-order Taylor expansion of Eq. (1) with higher-order differential terms (second-order and above) neglected, the governing equations for hydro-turbine torque and water discharge rate are derived as follows²³:

$$\begin{array}{*{20}l} {m_{t} = e_{h} h + e_{x} x + e_{y} y} \hfill \\ {q_{2} = e_{qh} h + e_{qx} x + e_{qy} y} \hfill \\ \end{array}$$

(3)

The six transfer coefficients are defined as: $e_{qy} = \frac{{\partial q_{2} }}{\partial y}$, $e_{qx} = \frac{{\partial q_{2} }}{\partial x}$, $e_{qh} = \frac{{\partial q_{2} }}{\partial h}$,$e_{y} = \frac{{\partial m_{t} }}{\partial y}$, $e_{{\text{x}}} = \frac{{\partial m_{t} }}{\partial x}$, $e_{h} = \frac{{\partial m_{t} }}{\partial h}$. Due to the special physical structure of the Pelton turbine, its discharge is only affected by its water head and needle opening, the speed has no effect on the hydro-turbine discharge, i.e. $e_{qx} = \frac{{\partial q_{2} }}{\partial x} = 0$.

The unit parameters are transformed into the actual operating parameters of the unit according to Eq. (4)-(6), thus obtaining the actual needle opening, rotational speed, discharge and torque of the Pelton turbine. Then according to the definition of transfer coefficients, we can find the corresponding partial derivatives of needle opening, speed and water head for the operating point where the turbine is located to the actual torque and discharge according to the established neural network model of unit torque and unit discharge, and thus find the six parameters of the linear model of the Pelton turbine. The resulting transfer coefficients are shown in Fig. 6.

Fig. 6

Pelton turbine transfer coefficients.

$$Q = Q_{11} D^{2} \sqrt H$$

(4)

$$n = \frac{{n_{11} \sqrt H }}{D}$$

(5)

$$M_{t} = \frac{30\gamma }{\pi }\frac{{Q_{11} \eta }}{{n_{11} }}D^{3} H$$

(6)

Other partial mathematical models of PTRS

Headrace tunnel mathematical model: The essence of modeling a diversion system is to use mathematical equations to describe the change in water strike pressure in a pipe caused by a change in the overland flow rate. The equation describing the transient flow process of water in a headrace tunnel is as follows²⁴:

$$T_{w1} \frac{{{\text{d}}q_{1} }}{{ {\text{d}}t}} = - Z_{u} - \frac{{2\alpha_{1} Q_{10}^{2} }}{{H_{0} }}q_{1}$$

(7)

Surge tank mathematical model: for the surge tank, the discharge is conserved. Then, the equation of discharge conservation of surge tank is as follows²⁵:

$$A_{u} \frac{{dZ_{u} }}{dt} = \frac{{Q_{10} }}{{H_{0} }}q_{1} - \frac{{Q_{20} }}{{H_{0} }}q_{2}$$

(8)

Penstock mathematical model: The mathematical equations for the penstock can be obtained by treating it similarly to the headrace tunnel, as shown below²⁶:

$$T_{w2} \frac{{{\text{d}}q_{2} }}{{ {\text{d}}t}} = - Z_{u} - h - \frac{{2\alpha_{2} Q_{20}^{2} }}{{H_{0} }}q_{2}$$

(9)

Generator model: In this paper, a first order model was used for the generator model. The differential equation is described as follows²⁷:

$$T_{a} \frac{{{\text{d}}x}}{{ {\text{d}}t}} = m_{t} - \left( {m_{g} + e_{g} x} \right) \,$$

(10)

Governor model: The governor is mainly composed of controller and the servo-system, and its main function is to generate a control signal based on the measured signal deviation and adjust the needle opening so as to achieve the purpose of regulating the hydro-turbine operation state. In this paper, the governor adopts a frequency control mode with parallel PI control logic. The mathematical equations for the controller and the servo system are presented as follows²⁸:

$$\frac{{{\text{d}}y_{I} }}{{ {\text{d}}t}} = K_{i} u - K_{i} x$$

(11)

$$\frac{{{\text{d}}y}}{{{\text{d}}t}}{ = }\frac{1}{{T_{y} }}(K_{p} u + y_{I} - K_{p} x - y)$$

(12)

To sum up, Eqs. (3) and (7)-(12) are the basic equation of the PTRS. According to the basic equation, the state space equation of the PTRS can be obtained as shown in Eq. (13). The control logic block diagram is shown in the Fig. 7.

$$\left\{ \begin{gathered} \dot{q}_{1} = ( - Z_{u} - \frac{{2\alpha_{1} Q_{10}^{2} }}{{H_{0} }})/T_{w1} \hfill \\ \dot{Z}_{u} = (\frac{{Q_{10} }}{{H_{0} }}q_{1} - \frac{{Q_{20} }}{{H_{0} }}q_{2} )/A_{u} \hfill \\ \dot{q}_{2} = ( - Z_{u} - \frac{{q_{2} }}{{e_{qyh} }} + \frac{{e_{qx} x}}{{e_{qh} }} + \frac{{e_{qy} y}}{{e_{qh} }} - \frac{{2\alpha_{2} Q_{20}^{2} }}{{H_{0} }}q_{2} )/T_{w2} \hfill \\ \dot{y}_{I} = K_{i} u - K_{i} x \hfill \\ \dot{y} = (K_{p} u + y_{I} - K_{p} x - y)/T_{y} \hfill \\ \dot{x} = \left[ {(e_{x} - e_{g} - \frac{{e_{h} e_{qx} }}{{e_{qh} }})x + (e_{y} - \frac{{e_{h} e_{qy} }}{{e_{qh} }})y + \frac{{e_{h} }}{{e_{qh} }}q_{2} - mg} \right]/T_{a} \hfill \\ \end{gathered} \right.$$

(13)

Fig. 7

Bock diagram of the Pelton turbine control logic.

Equation (13) shows that the PTRS contain the state variables $q_{1}$, $Z_{u}$, $q_{2}$, $y_{I}$, $y$ and $x$. The tailwater level is assumed constant during small-signal events. The surge tank free surface is at atmospheric pressure. Initial states satisfy the steady-state equations with x = 0 pu speed deviation and y = y0 (rated needle opening). The hydro-turbine operates under load adjustment conditions, so the $m_{g}$ is an external disturbance to the PTRS. Two typical load adjustment conditions were selected, i.e., load decrease condition and load increase condition. The two conditions correspond to $m_{g} < 0$ and $m_{g} > 0$.

In order to verify the correctness of the linear model, the actual arrangement parameters of a hydropower plant are selected to validate the model, and the key parameters of the hydropower plant are shown in Table 2. The PTRS is simulated using the neural network model and the linear simplified model of the Pelton turbine under increasing and decreasing load conditions, respectively, so as to compare the regulation dynamic process of the system, as shown in Fig. 8.

Table 2 The PTRS parameter values.

Fig. 8

The regulation dynamic process.

As known from the Fig. 8, the simulation results of the dynamic response of the speed output of the simplified linear model and the neural network model are in good agreement. Therefore, the comparison shows that it is reasonable to use the linear model for the stability analysis of different operating conditions.

Stability analysis under full operating conditions

In this section, the full condition stability analysis of the PTRS will be carried out according to the mathematical model established in Chapter 2, Firstly, the stability analysis method and process are introduced, and then the results of the stability analysis are discussed and summarized.

Stability analysis methods

Bifurcation, as a distinctive characteristic of nonlinear systems, exhibits intrinsic connections with stability in PTGS. This study employs Hopf bifurcation theory to investigate PTGS stability, focusing on three critical research objectives: (1) Ascertaining the existence of Hopf bifurcation, which serves as the fundamental prerequisite for bifurcation analysis; (2) Resolving bifurcation orientation by identifying critical thresholds of system parameters; (3) Evaluating bifurcation stability through verification of periodic solutions’ sustainability.

The nonlinear dynamical equation expressed in Eq. (14) is written as follows:

$$\dot{x} = f(x,\mu )$$

(14)

The $x = (q_{1} ,Z_{u} ,q_{2} ,y_{I} ,y,x)^{{\text{T}}}$ is the state vector and the μ is the system bifurcation parameter. Since the system is stable in the initial state, the initial value of the state variable is $(q_{10} ,Z_{u0} ,q_{20} ,y_{I0} ,y_{0} ,x_{0} )^{{\text{T}}} = 0$. The new equilibrium point of the established nonlinear six-dimensional system is found according to $\dot{x} = 0$. The Jacobian matrix associated with the system’s state-space equations is subsequently derived and presented in Eq. (15).

$$J(\mu ) = \left[ {\begin{array}{*{20}c} {\frac{{\partial \dot{q}_{1} }}{{\partial q_{1} }}} & {\frac{{\partial \dot{q}_{1} }}{{\partial Z_{u} }}} & {\frac{{\partial \dot{q}_{1} }}{{\partial q_{2} }}} & {\frac{{\partial \dot{q}_{1} }}{{\partial y_{I} }}} & {\frac{{\partial \dot{q}_{1} }}{\partial y}} & {\frac{{\partial \dot{q}_{1} }}{\partial x}} \\ {\frac{{\partial \dot{Z}_{u} }}{{\partial q_{1} }}} & {\frac{{\partial \dot{Z}_{u} }}{{\partial Z_{u} }}} & {\frac{{\partial \dot{Z}_{u} }}{{\partial q_{2} }}} & {\frac{{\partial \dot{Z}_{u} }}{{\partial y_{I} }}} & {\frac{{\partial \dot{Z}_{u} }}{\partial y}} & {\frac{{\partial \dot{Z}_{u} }}{\partial x}} \\ {\frac{{\partial \dot{q}_{2} }}{{\partial q_{1} }}} & {\frac{{\partial \dot{q}_{2} }}{{\partial Z_{u} }}} & {\frac{{\partial \dot{q}_{2} }}{{\partial q_{2} }}} & {\frac{{\partial \dot{q}_{2} }}{{\partial y_{I} }}} & {\frac{{\partial \dot{q}_{2} }}{\partial y}} & {\frac{{\partial \dot{q}_{2} }}{\partial x}} \\ {\frac{{\partial \dot{y}_{I} }}{{\partial q_{1} }}} & {\frac{{\partial \dot{y}_{I} }}{{\partial Z_{u} }}} & {\frac{{\partial \dot{y}_{I} }}{{\partial q_{2} }}} & {\frac{{\partial \dot{y}_{I} }}{{\partial y_{I} }}} & {\frac{{\partial \dot{y}_{I} }}{\partial y}} & {\frac{{\partial \dot{y}_{I} }}{\partial x}} \\ {\frac{{\partial \dot{y}}}{{\partial q_{1} }}} & {\frac{{\partial \dot{y}}}{{\partial Z_{u} }}} & {\frac{{\partial \dot{y}}}{{\partial q_{2} }}} & {\frac{{\partial \dot{y}}}{{\partial y_{I} }}} & {\frac{{\partial \dot{y}}}{\partial y}} & {\frac{{\partial \dot{y}}}{\partial x}} \\ {\frac{{\partial \dot{x}}}{{\partial q_{1} }}} & {\frac{{\partial \dot{x}}}{{\partial Z_{u} }}} & {\frac{{\partial \dot{x}}}{{\partial q_{2} }}} & {\frac{{\partial \dot{x}}}{{\partial y_{I} }}} & {\frac{{\partial \dot{x}}}{\partial y}} & {\frac{{\partial \dot{x}}}{\partial x}} \\ \end{array} } \right]$$

(15)

The characteristic equation of $J(\mu )$ is $\det \left| {J(\mu ) - \lambda I} \right| = 0$, and the $\det \left| {J(\mu ) - \lambda I} \right| = 0$ is expanded as follows:

$$\lambda^{6} + a_{1} \lambda^{5} + a_{2} \lambda^{4} + a_{3} \lambda^{3} + a_{4} \lambda^{2} + a_{5} \lambda^{1} + a_{6} = 0$$

(16)

The stability criterion of the PTRS at $\mu = \mu_{c}$ is determined through Hopf bifurcation analysis using Eq. (16), where the system transitions to a critically stable regime only when all requisite conditions specified in Eqs. (17)-(22) are concurrently satisfied at this operational state.

$$a_{i} > 0(i = 1,2,3,4)$$

(17)

$$\Delta_{2} = \left| \begin{gathered} a_{1} \, 1 \hfill \\ a_{3} \, a_{2} \hfill \\ \end{gathered} \right| > 0$$

(18)

$$\Delta_{3} = \left| \begin{gathered} a_{1} \, 1 \, 0 \hfill \\ a_{3} \, a_{2} \, a_{1} \hfill \\ 0 \, a_{4} \, a_{3} \hfill \\ \end{gathered} \right| = 0$$

(19)

$$\Delta_{4} = \left| {\begin{array}{*{20}c} {a_{1} } & 1 & 0 & 0 \\ {a_{3} } & {a_{2} } & {a_{1} } & 1 \\ {a_{5} } & {a_{4} } & {a_{3} } & {a_{2} } \\ 0 & {a_{6} } & {a_{5} } & {a_{4} } \\ \end{array} } \right| = 0$$

(20)

$$\Delta_{5} = \left| {\begin{array}{*{20}c} {a_{1} } & 1 & 0 & 0 & 0 \\ {a_{3} } & {a_{2} } & {a_{1} } & 1 & 0 \\ {a_{5} } & {a_{4} } & {a_{3} } & {a_{2} } & {a_{1} } \\ 0 & {a_{6} } & {a_{5} } & {a_{4} } & {a_{3} } \\ 0 & 0 & 0 & {a_{6} } & {a_{5} } \\ \end{array} } \right| = 0$$

(21)

$$\sigma (\mu_{c} ) = {\text{Re}} (\left. {\frac{d\lambda }{{d\mu }}} \right|_{{\mu = \mu_{c} }} ) \ne 0$$

(22)

To be specific, if $\sigma (\mu_{c} ) > 0$, the emerged Hopf bifurcation is supercritical , the PTRS generates the limit cycle on the side of $\mu > \mu_{c}$, and the system is unstable when $\mu > \mu_{c}$; if $\sigma (\mu_{c} ) < 0$, the emerged Hopf bifurcation is subcritical , the PTRS generates the limit cycle on the side of $\mu < \mu_{c}$, and the system is unstable when $\mu < \mu_{c}$.

Stability domain analysis of full operating condition

Based on the stability analysis approach outlined in “Stability analysis methods”, the stability domain of the system is examined under full operating conditions. Here, the governor parameter is considered as the plane, and the trend of its variation is analyzed. This analysis offers valuable insights for selecting control parameters during system operation. The full operating conditions of the system are defined as:

Based on the operational variability of headwater levels and needle opening observed in Pelton turbine systems, distinct operational scenarios are established as follows: For a fixed water head, incremental adjustments of 10% needle opening between 25 and 75% opening ranges are designated as new working condition. Considering the Pelton turbine’s characteristic high-head operation and typical geographical constraints that limit significant headwater fluctuations, new working conditions are defined by 3 m headwater intervals within the 671 m-689 m range for fixed needle opening.

The transfer coefficients for the Pelton turbine are obtained on Fig. 6 based on the operating point at which it is located. The stability domain of the PTRS at 65% rated needle opening and $m_{g} = - 0.1$ with different operating heads is shown in Fig. 9(a). As shown in Fig. 9(a), it can be seen that under the rated needle opening, the stability domain of the PTRS gradually and uniformly decreases as the water head becomes larger.

Fig. 9

Stability domain of PTRS under rated needle opening and water head.

To assess the robustness of the PTRS under a rated water head of 671 m and $m_{g} = - 0.1$ with varying needle openings, the corresponding stability domains are illustrated in Fig. 9(b). As observed in the figure, under rated head conditions, the system’s stability domain initially decreases sharply as the needle opening increases but exhibits a gradual recovery when approaching the rated opening range.

This reveals that the unit’s operational stability diminishes significantly near its rated working conditions, necessitating particular caution in parameter tuning to mitigate destabilization risks during control adjustments.

Further, the area of the stability domain of the system at full operating conditions was calculated and plotted in Fig. 10. Each folded line of Fig. 10(a) represents the area of the stability domain of the system at a fixed water head with different needle openings. Figure 10(b) each folded line represents the area of the system stability domain for different water heads at a fixed needle opening.

Fig. 10

Stability domain under full operating condition.

As can be seen from the Fig. 10, under full operating conditions, the system stability domain area as a whole is similar to the change rule under rated needle opening or rated water head alone. From the perspective of the needle opening: at any water head, the stability domain area of the system decreases sharply and then increases slowly as the needle opening increases. In other words, when the needle opening is increased, the system’s stability initially tends to decline before subsequently recovering. Furthermore, the stability domain area at low needle openings is almost three times larger than that at medium and high needle openings. From a water head perspective, the system’s stability domain area diminishes as the water head increases across all needle opening levels, with the decrease following a roughly linear pattern. Nevertheless, under the same needle opening, the stability domain areas are relatively similar, suggesting that variations in water head have a limited impact on system stability.

The specific mechanism underlying the aforementioned pattern of stable domain changes can be explained as follows: The mechanism is that as the operating conditions of the turbine change, the six transfer coefficients of its model also vary. The stability and area variation patterns result from the combined effects of these six transfer coefficients. As shown in Fig. 6, under identical valve openings but varying head conditions, the relative changes in the six transfer coefficients of the turbine remain relatively small for each operating condition. Conversely, under identical head conditions but varying valve openings, the relative changes in the six transfer coefficients of the turbine become significantly larger for each operating condition. This explains the phenomenon depicted in Fig. 9: in Fig. 9(a), the changes within each stable domain are minimal, whereas in Fig. 9(b), the stable domain exhibit substantial fluctuations, demonstrating the aforementioned pattern.

Parameter sensitivity analysis

This section employs the trajectory sensitivity method and utilizes the mathematical model from Chapter 2 to analyze parameter sensitivity of core system variables under unit load disturbances and parameter perturbations. The study evaluates both the hierarchical influence of parameter variations on system states and the operational condition-dependent responsiveness to parameter adjustments. Through this approach, the prioritization of parameter impacts and the comparative sensitivity across different working conditions are systematically identified.

Sensitivity analysis method and index

Trajectory sensitivity is a method that can quantitatively characterize the extent to which minor alterations in specific parameters or adjustments to particular structures within a system influence specific outputs²⁹. In this paper, a small change is made in a key parameter in each system and the resulting effect on the state of each subsystem is observed. This analysis allows for the identification of parameters with the greatest impact on the system’s state. The subsequent study of a particular subsystem or parameter can then be targeted for further optimization and adjustment.

The trajectory sensitivity of the parameter to the output of the system state is the derivative of the trajectory of the variable with respect to the system parameter, and its expression can be represented by Eq. (23):

$$S_{f} = \frac{\partial z(a,t)}{{\partial a}} = \mathop {\lim }\limits_{\Delta a \to 0} \frac{z(a + \Delta a,t) - z(a - \Delta a,t)}{{2\Delta a}}$$

(23)

$S_{f}$ is the trajectory sensitivity of a state variable of the system to a parameter of the system, which responds to the extent to which a small change in a system parameter corresponding to a given time affects the change in the dynamic trajectory of the system variable. The $a$ is a system parameter such as the discharge inertia time constant. The $z$ is the system state such as the speed.

In order to represent the combined degree of influence of each parameter in the system on a particular system state variable, the average sensitivity of the entire disturbance process can be calculated as a way to represent the average trajectory sensitivity of the parameter to the output of the system state variable, as shown in Eq. (24).

$$S_{a} = \frac{1}{N}\sum\limits_{k = 1}^{N} {\left| {\frac{{\partial z(a,t_{k} )}}{\partial a}} \right|}$$

(24)

where N is the total number of points in the sensitivity trajectory.

Further in order to reflect the sensitivity of the unit operating conditions to the system parameters, the comprehensive sensitivity index $S_{m}$ is defined, which is defined as shown in Eq. (25).

$$S_{m} = \frac{1}{M}\sum\limits_{k = 1}^{M} {\overline{S}_{a}^{k} }$$

(25)

where $\overline{S}_{a}^{k}$ denotes the normalized average sensitivity $S_{a}$ of the kth subsystem to a parameter of the system, The expression for $\overline{S}_{a}^{k}$ is shown in Eq. (26). M is the number of subsystems, C is the number of state of every subsystems.

$$\overline{S}_{a}^{k} = \frac{1}{C}\sum\limits_{i = 1}^{C} {S_{a,i} }$$

(26)

Sensitivity analysis results

According to the operating parameters of the hydropower plant, the basic parameters of the turbine regulation system are shown in Table 2. 12 system parameters are to be analyzed, and 6 system state variables are to be analyzed, which are controller output y_PI, follower system output y, diversion system q₁, surge tank water level Z_u, turbine outputs m_t and q₂, and generator output x. Under rated operating conditions, the average trajectory sensitivity of the proposed system is shown in Table 3.

Table 3 Sensitivity of PTRS state output to system parameters.

Further in order to clearly and intuitively analyses the degree of influence of the parameters on each state of the system, each column of data in Table 3 was normalized to obtain the percentage of sensitivity of each parameter to the state of the system. Taking turbine discharge and headrace tunnel discharge as examples, the influence of parameters on their states is discussed, as shown in Fig. 11.

Fig. 11

The S_a of q₁ and q₂.

As shown in Fig. 11(a), for the discharge of the headrace tunnel, the first parameter that has the greatest influence on its dynamic process is the Pelton turbine parameter, and among all the parameters of the turbine, the change of e_qy and e_y has the greatest influence on its dynamic process; the second control parameter that has the greatest influence on the discharge of the headrace tunnel is the water hammer inertia time constant of the diversion tunnel; and lastly, the K_i parameter of the controller also has a relatively great influence on its dynamic process, higher than the average; the remaining parameters have very little effect on the discharge of the headrace tunnel compared to the above parameters.

Similarly, as shown in Fig. 11(b), for the turbine discharge, the biggest influence on its dynamic process is also the turbine parameters, and among all the parameters of the turbine, it is also the change of e_qy and e_y that has the biggest influence on its dynamic process, which also proves that the discharge of the Pelton turbine regulating system is mainly determined by the change of turbine needle opening; the second parameter that has the biggest influence on the turbine discharge is the K_i parameter of controller; the rest of the other parameters have very little influence on the turbine discharge compared to the above parameters.

To validate the accuracy of the calculated S_a, time-domain simulation verification and trajectory sensitivity calculations were performed using the results of the influence of all system parameters on the state variable q₂ as an example. The simulation results are shown in Fig. 12. As shown in Fig. 12(a)(b)(c), a slight increase in the parameter e_qy will amplify the rate of change in the turbine discharge. Specifically, at any given moment, the change in turbine discharge corresponding to a positive perturbation of e_qy is greater than that corresponding to a negative perturbation. Moreover, the change in turbine discharge is larger under positive perturbations of e_qy. The effect of parameter e_y on the turbine discharge is precisely the opposite of e_qy, though its influence is less significant. The variation in the K_i parameter exerts an even smaller influence on the turbine discharge, affecting its magnitude only within a limited local range. Further analysis of the Fig. 12(d) reveals that the trajectory sensitivity of the three parameters to the turbine discharge follows the order e_qy > e_y > K_i. This aligns with the results from the time-domain simulation and further validates the accuracy of the calculations presented in Table 3. Subsequent conclusions are derived from the data in Table 3, thereby ensuring the accuracy of the subsequent research.

Fig. 12

Dynamic trajectories of states before and after parameter perturbation and trajectory sensitivity.

To investigate the system’s comprehensive sensitivity index, the Fig. 13 presents the comprehensive sensitivity index for different parameters under rated operating conditions. As demonstrated in the figure, the system exhibits primary sensitivity to Pelton turbine parameters e_qy and e_y, followed by controller parameter K_i in secondary importance. Parameters such as T_y and F_u demonstrate relatively low sensitivity levels, with their impact remaining below the system’s average sensitivity threshold. This hierarchy of parameter influence reveals critical relationships between system components and their operational responsiveness.

Fig. 13

The S_m of PTRS under rated operating condition.

To systematically investigate how parameters’ comprehensive sensitivity indexes evolves across operational conditions, this study extends sensitivity analysis to full operating ranges. Considering the numerous parameters involved, the investigation focuses on the top three parameters demonstrating highest comprehensive sensitivity under rated conditions (K_i, e_qy and e_y, ranked by descending sensitivity as previously established). Then take the e_y parameter with the highest comprehensive sensitivity as an example to analyze the change rule of its comprehensive sensitivity with the flexible change of working conditions. The results of comprehensive parameter sensitivity calculation for parameters K_i, e_qy and e_y at full operating conditions are shown in Table 4, 5, 6. In the Table 4, 5, 6, a monochromatic gradient from light to dark is now used to indicate the magnitude of the comprehensive sensitivity S_m darker shades represent higher values and lighter shades represent lower values.

Table 4 Sensitivity of the PTRS to K_i parameters under full operating conditions.

Table 5 Sensitivity of the PTRS to e_qy parameters under full operating conditions.

Table 6 Sensitivity of the PTRS to e_y parameters under full operating conditions.

From Table 6, it can be learned that the sensitivity of the system to the turbine parameter e_y gradually increases with the increase of the needle opening from the perspective of the head, and reaches the maximum when the needle opening reaches 75%; from the perspective of the needle opening, the sensitivity of the system to the turbine parameter e_y gradually decreases. And on the whole, the needle opening is the dominant factor in the sensitivity of the system to e_y. Other parameters can be analyzed in the same way, so we will not repeat them here.

Through the analysis and conclusions drawn in this chapter, it can be further understood that the high sensitivity of e_y and e_qy can be explained from a physical perspective: the former directly regulates the turbine torque, while the latter directly regulates the turbine discharge. An increase in e_y proportionally amplifies the torque gain of the needle valve opening on the mechanical torque. Similarly, e_qy influences flow gain by directly altering the turbine’s discharge, making it the parameter to which the PTRS is most sensitive. In contrast, hydraulic parameters such as T_w1, T_w2, α₁, and α₂ primarily affect dynamic phase characteristics rather than static gain. Regarding the K_i parameter, Chapter 3’s conclusions establish that K_i is the dominant parameter affecting system stability. Thus, increasing K_i accelerates velocity error elimination but simultaneously shifts the dominant pole closer to the imaginary axis, thereby reducing the damping ratio and shrinking the stability domain. This explains why K_i consistently ranks among the most critical control parameters in sensitivity analysis.

Discussion

In recent years, with the adjustment of some national policies, the Pelton turbine hydropower units will usher in a larger application space, but most of the previous studies on Pelton turbine hydropower units are aimed at the three-dimensional design of the units themselves, and the stability analysis of the overall regulation system of the hydropower plant is still slightly insufficient. At the same time, the modern requirements for the control accuracy and safety of hydropower plants are getting higher and higher, so it is becoming more and more necessary to analyze the stability and parameter sensitivity of the regulation system of the Pelton turbine.

The advantages of this study are as follows. Unlike the Francis turbine unit, this paper focuses on the stability and parameter sensitivity of the turbine regulation system for Pelton turbine unit. The mechanism and law of the impact of the operating conditions of the Pelton turbine on its stability are revealed. Based on the trajectory sensitivity index, the primary and secondary influence relations of parameter changes on the system state and the laws of the system’s sensitivity to parameters under different operating conditions are determined. By analyzing the stability domain of the PTRS under full operating conditions, the adjustment range of the system control parameters can be determined according to the minimum stability domain area, which ensures that the system has better stability and dynamic adjustment characteristics under all operating conditions. The result of sensitivity analysis can be used to know the most sensitive key parts and parameters of the system, which is of great significance for the system identification, stability analysis and optimal control of the PTRS. The research results of this paper can provide certain theoretical guidance for the design and operation of hydropower plant.

The current study also has certain limitations, such as not considering the dynamic coupling relationship with the power grid during actual operation, the complex multi-turbines layout structure of hydropower plants, and the various nonlinear of PTRS. Therefore, in the future, this study can be extended in the following aspects.

(1) With the development of the hydropower industry, the layout of hydropower plants has become more and more complex, from the viewpoint of single-stage hydropower plants, the layout of power plants with one tube and two turbines or one tube and multiple turbines is becoming more and more common; from the viewpoint of multi-stage power plants, the hydraulic connection between hydropower plants is becoming more and more close, and each hydropower plant is no longer an ‘island’ between each other. All of the above situations lead to different unit stability and dynamic characteristics of hydropower plants, and bring more challenges between the control of hydropower plants. Therefore, future work is necessary to investigate the stability, transient characteristics and optimal control of hydropower plants units with different topologies.

(2) For Pelton turbines, the nozzle switching mechanism and deflector represent the most significant differences compared to other types of turbines. However, this paper only considers load regulation under small fluctuations, thus excluding the deflector model and nozzle switching scenarios. Future work should establish a transient process model for Pelton turbines that accounts for deflector and nozzle switching scenarios. This will further refine the mathematical model of Pelton turbines and provide support for hydropower plant stability analysis.

Conclusions

This work proposes a unified framework for full-condition stability domain analysis and system-wide parameter sensitivity ranking of Pelton turbine regulation systems (PTRS). A differentiable neural network model enables consistent transfer-coefficient extraction, and Hopf-based mapping reveals how stability domains evolve over head and needle opening. The comprehensive sensitivity index clearly ranks hydraulic and control parameters and can guide robust controller design.

Several conclusions can be drawn from this study:

(1) With the change of operating conditions, the change of its stability domain shows a certain regularity. Under a fixed head, the stability-domain area at 25% needle opening is approximately three times that at 65% needle opening, revealing a pronounced degradation of stability when the needle opening increases from low to medium ranges, followed by a mild recovery near rated needle opening. For a given opening, the stability-domain area decreases nearly linearly with head, but the influence of head is notably smaller than that of needle opening.

(2) The same parameter change affects different states differently, and the same state has different sensitivities to different parameters. The system is most sensitive to the Pelton turbine and controller parameters. The turbine parameters e_y and e_qy are dominant, with normalized indices of 0.37 and 0.21, respectively. The controller integral gain K_i ranks next (0.19), while pipe system and surge-tank parameters play secondary roles.

(3) Changes in the operating conditions of the system will also change the sensitivity of the system to the same parameter, and the trend of the sensitivity shows a certain regularity. Take e_y as an example, the comprehensive sensitivity to e_y increases monotonically with needle opening and decreases slightly with head.