Construction of a predictive model for self realization and career satisfaction of university teachers based on text mining

Abstract

University teachers increasingly prioritize career satisfaction and self-realization, focusing on the evolving demands of the academic environment. Understanding these subjective experiences requires data-driven approaches that reveal more profound insights into their professional well-being. This study introduces the Bidirectional Encoder Representations from Transformers -Enhanced Career and Self-Realization Text Mining Framework (BE-CSTMF) to construct a predictive model for university teacher’s self-realization and career satisfaction. The framework combines Enhanced BERT’s advanced natural language processing capabilities to extract deep contextual insights from textual data. BE-CSTMF integrates these insights with XGBoost’s robust predictive modeling to perform actionable analysis using text mining techniques on survey and academic data. Key patterns, sentiments, and influential factors related to career satisfaction and self-realization were identified using a dataset comprising textual responses from university teachers. Predictive modeling techniques enabled a comprehensive understanding of factors such as work-life balance, recognition, professional growth opportunities, and institutional support. The BE-CSTMF model reliably predicts university professors’ self-realization and career happiness, revealing their professional well-being characteristics. This strategy provides concrete help for building targeted career and work satisfaction interventions. This study highlights the potential of combining cutting-edge natural language processing and machine learning techniques to develop tailored strategies for supporting academic professionals’ career growth.

Introduction

Self-realization, realizing one’s potential as well as personal growth, is essential for university teachers working in dynamic and intellectually demanding situations. Beyond work satisfaction, it relates to personal and professional goals. University teacher’s efforts to improve academic performance, job satisfaction, and retention depend on understanding instructor’s self-realization and career satisfaction¹. Job stability, recognition, promotion, and work-life balance contribute to career satisfaction. Research shows that university academics burn out and lose motivation due to high workloads, limited professional progress, and poor institutional support². Understanding faculty requirements, motives, and professional barriers is essential to solving these problems. Research shows that career mobility, professional identity, and teaching skill transfer help retain experienced educators³. According to studies, institutional support systems and career frameworks help instructors transition into new careers, lowering turnover and improving job satisfaction. Increasing research emphasizes the necessity for educational policies that enable dynamic career advancement to improve faculty retention. This study shows how teachers’ broad and transferable talents can help organizations flourish outside of education, supporting the study’s goal of understanding professional fulfillment and self-realization⁴. It stresses using these talents in diverse work settings to improve career flexibility and long-term job satisfaction⁵. University teacher’s work fulfillment and self-realization depend on several aspects. These include:

Figure 1 shows that work-life balance, recognition, professional development, institutional support, autonomy, and decision-making affect university instructors’ work satisfaction and self-realization. These elements affect career happiness by addressing personal and professional progress. Academic employment can be demanding, making it difficult to maintain this balance, essential for long-term well-being and job satisfaction⁶. Recognition from peers, students, and administrators boosts career satisfaction⁶. Career satisfaction and self-realization are also improved by professional advancement possibilities like financial support, research funding, sabbaticals, and leadership⁷. Mentorship, resources, and a supportive workplace culture boost job satisfaction by generating a sense of belonging and purpose⁸. Teacher autonomy in decision-making boosts professional fulfillment by giving teachers ownership over their work⁹. Surveys and qualitative narratives sometimes fail to convey the complexity and multidimensionality of these professional experiences, underscoring the need for more advanced analytical methodologies in this data-rich era. NLP and machine learning can analyze massive volumes of qualitative data to reveal career satisfaction and personal growth themes. These methods reveal underlying characteristics that affect teacher motivation and well-being from unstructured text. Predictive modeling can also help academic institutions estimate trend-based outcomes for evidence-based policymaking¹⁰. This study uses text mining to evaluate university professors’ narratives and reveal themes and attitudes regarding professional fulfillment and self-discovery¹¹. Academic institutions can use predictive modeling to anticipate work satisfaction and self-realization based on patterns. Actionable insights can inform policy and decision-making^12,13,14,15. The Career and Self-Realization Text Mining Framework (CSTMF) uses Extreme Gradient Boosting (XGBoost) and a fine-tuned Bidirectional Encoder Representations from Transformers (BERT) model for predictive analysis. This technique uses domain-specific fine-tuning to capture the particular language patterns of academic text, unlike regular BERT. Fine-tuning enhances context understanding and sentiment analysis, while XGBoost efficiently predicts structured data and is highly scalable. This approach balances deep language understanding with predictive performance to analyze university instructors’ experiences. Enhanced BERT and XGBoost help the BE-CSTMF model analyze unstructured teacher comments and draw conclusions. Due to this combination, the model may accurately predict and recommend professional satisfaction and self-realization aspects.

Fig. 1

Career satisfaction and self-realization for university teachers.

The primary objectives of this study are as follows:

• Use BE-CSTMF to create a predictive model for textual data analysis and identify university professors’ self-realization and career satisfaction elements.

• Use text mining to identify and analyze patterns, sentiments, and aspects like work-life balance, recognition, and institutional support that affect university instructors’ professional well-being.

• To make recommendations for academic institutions to improve job happiness and self-realization, promoting university instructors’ professional growth and well-being.

Novelty and contribution of BE-CSTMF

Although prior studies have applied text mining and machine learning to teacher satisfaction (e.g., PRBE¹⁶, SEM-ANN²⁰, TAMTM²²), these approaches typically rely on either structured data alone or basic text features without integrating advanced contextual embeddings with predictive modeling. The proposed BE-CSTMF solves this gap with three significant innovations: (i) Dual-Source Integration, combining structured survey data with unstructured text responses for richer contextual understanding; (ii) Enhanced Embeddings, leveraging an Enhanced BERT module with semantic features, attention-based fusion, and domain-specific adaptation to improve text representation quality; and (iii) Optimized Predictive Layer, employing XGBoost with hyperparameter tuning to capture non-linear feature interactions and achieve statistically significant performance gains. A full comparison of these elements to previous approaches is provided in Table 1, showing the distinctive methodological contributions of BE-CSTMF.

Table 1 Comparative analysis of BE-CSTMF and related methods in terms of data integration, feature engineering, embedding strategies, predictive modeling, and statistical improvements.

An overview of the research follows. The second section describes a comprehensive literature and research methodology review. Section “Framework and implementation strategy” describes the research plan, methodologies, and processing. Section “Result and discussion” describes the results of the analysis. The conclusion and future work are in Section “Conclusion, limitations, and future work”.

Related works

Educators need self-realization and occupational happiness to thrive. These characteristics greatly affect academic motivation, retention, and performance. Fostering a healthy academic environment requires understanding self-realization drivers like work-life balance, recognition, and institutional support. Big data and machine learning have made predictive modeling and text mining useful tools for understanding complex academic satisfaction trends. This study uses these methods to deliver practical insights to improve university professors’ professional progress and satisfaction.

The role of self-realization and career satisfaction in academic professions

Daugela and Zydziunaite¹⁶ employed the Phenomenological Research-Based Evidence (PRBE) approach to investigate how members of the academic community come to terms with their unique academic identities to improve overall academic life. Nineteen scientists from the United Kingdom and Lithuania were engaged. According to the findings, fulfilling one’s academic potential entails exploring, cultivating, and advocating for one’s interests within the context of the university’s academic community; doing so helps with professional, personal, and scholarly growth. Experts engage in academic self-realization in their special style, and the study highlights the significance of academic freedom for scientific creativity. Establishing a clear boundary between workplace conditions, academic freedom, and innovation necessitates further research.

Wu et al.¹⁷ aimed to examine how teachers’ sense of professional identity relates to their level of job satisfaction. A group of 300 educators from Sargodha City, Pakistan, aged 24 to 45, was selected utilizing a purposive sampling method. The Professional Identity Scale, Brief Calling, and Career Satisfaction Scale operationalized variables. Path analysis showed no direct or indirect effects of normative identity on vocational calling or fulfillment. Affective and efficacy identity positively affected professional calling, while career calling positively affected contentment. Directly, efficacy identification increased enjoyment. The findings may increase higher education professors’ career satisfaction.

Voitenko et al.¹⁸ examined how personal values mediate needs, values, and professional well-being. The study used the Need Satisfaction Questionnaire (NSQ), Job Satisfaction Scale (JSS), as well as Human Values Scale (NSS) with 132 Ukrainian higher education teachers. Results show that satisfying needs considerably impacts professional well-being. Values impact job satisfaction and need satisfaction. Studies can prevent breaches in professional well-being among educational institutions’ scientific and pedagogical staff. Studying organizational and psychological aspects affecting professional well-being.

Predictive modeling techniques in educational and career satisfaction studies

Ordonez-Avila et al.¹⁹ intended to study instructor assessment prediction from student performance. Examines 29 reviews on educational data mining techniques, such as fuzzy logic, clustering, Fuzzy Neural Network (FNN), Neural networks, multilayer perceptron (MLP), Decision Trees, Logistic Regression, Random Forest Classifier, Naïve Bayes Classifier, Support Vector Machine (SVM), K-Nearest-Neighbor (KNN), and Associative classification model. Fuzzy principles are essential to teacher assessment since human behavior and decision-making are strongly correlated. The study’s focus on higher education and the lack of research on machine learning algorithms and student input data analysis for predicting instructor evaluation are notable limitations. The reporting of teacher assessment prediction began.

Aghaei et al.²⁰ employed artificial neural networks (ANN) to quantify and clarify aspects of student happiness with their academic experience. Tabriz Islamic Art University gathered information from 422 graduate students. According to the study, the model developed using structural equation modelling (SEM) and ANN, educational services, sociocultural characteristics, and perceptions are the most critical factors influencing academic satisfaction. Economic-entrepreneurial components produced little effect. Universities can use the results to anticipate student satisfaction better and respond to factors that affect it, leading to higher levels of academic satisfaction for all students.

Marcionetti et al.²¹ explored a model that predicted teachers’ career and life satisfaction, burnout, optimism, social support, workload, and self-efficacy. The burnout-based method comprised 676 Swiss teachers. According to structural equation modelling, positive outlook, social support, and perceived workload lowered burnout risk. Self-efficacy, social support, and optimism boost job happiness. The study shows that teacher optimism, self-efficacy, and good relationships with coworkers reduce burnout and improve career and life satisfaction. Favorable school climate, relationships, and self-efficacy minimize fatigue and enhance job satisfaction.

Holgado-Apaza et al.²² modeled work satisfaction among Peruvian basic education instructors using different machine learning approaches. The study investigated survey data encompassing demographic, institutional, and professional characteristics. Results suggested that characteristics such as work atmosphere, administrative assistance, and career development opportunities were major predictors of teacher satisfaction. The findings demonstrate how data-driven techniques can assist policymakers focus reforms to improve working conditions and retention in the education sector.

Mubashirin²³ created a machine learning algorithm for forecasting teachers’ job satisfaction in Bangladesh. The research employed survey data, including socio-demographic information, workload indicators, and support-related aspects. Model results highlighted significant determinants such as resource availability, training opportunities, and recognition. The study reveals that predictive analytics can influence policy to address teacher well-being and strengthen educational achievements in developing countries.

Holgado-Apaza et al.²⁴ examined predictors of life satisfaction among Peruvian teachers using an ensemble of feature selection methods mixed with various machine learning models. The study investigated socio-demographic, professional, and institutional characteristics to find the most relevant elements. Results showed that work-life balance, institutional support, and possibilities for professional progress were among the biggest predictors of life happiness. The research demonstrates how combining feature selection techniques with predictive modeling can boost the accuracy and interpretability of factors affecting teacher well-being.

Text mining approaches for analyzing career satisfaction and well-being

The previous research and analysis of text mining methods for career satisfaction and happiness are shown in Table 2.

Table 2 Text mining approaches for analyzing career satisfaction and well-being.

Despite extensive research on teacher well-being, work satisfaction, and professional progress, several key gaps persist. Current research generally focuses on student evaluations or sector-specific frameworks without completely integrating varied measures that convey the complexity of academic satisfaction. Many studies use self-reported data, limiting objectivity and long-term insights. Comprehensive, data-driven techniques that use institutional indicators and predictive modeling to evaluate job happiness and self-realization among university educators are needed to address these limitations.

Framework and implementation strategy

An innovative approach, the BERT-Enhanced Career and Self-Realization Text Mining Framework (BE-CSTMF) uses machine learning algorithms and natural language processing (NLP) models to sort through textual responses and identify variables affecting university teacher’s prediction of self-realization and job satisfaction. The framework aims to build a predictive model that determines the key factors of career satisfaction, investigate the interaction between self-realization and academic environments using both structured and unstructured data, and develop an NLP-based framework for extracting insights from textual data. Many crucial gaps remain in the research on teacher well-being, work satisfaction, and professional advancement. Current research frequently examines student evaluations or sector-specific frameworks without completely integrating varied measures that convey academic satisfaction’s complexity. Many studies also use self-reported data, reducing objectivity and long-term insights. To solve these limitations, comprehensive, data-driven approaches that use institutional indicators and predictive modeling to understand university instructors’ career satisfaction and self-realization are needed.

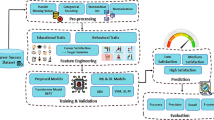
In Fig. 2, the BE-CSTMF integrates XGBoost Predictive Modeling with the Preprocessing Module to provide a text mining engine. Data from sources like the NCES University Teachers Survey (https://nces.ed.gov/surveys/ntps/) is collected to be employed in the predictive modeling phase by the Preprocessing Module. Data cleansing, feature engineering, text preprocessing as well as dimensionality reduction are the four primary processes employed. With P(d) = Clean and $Tokenize(d) = [{t}_{1},{t}_{2},...,{t}_{n}]$ as a result, the dataset has been changed. A prediction model for university teacher’s self-realization and professional happiness is constructed by the XGBoost prediction Modeling component utilizing the XGBoost machine learning method. Effective predictive analysis, model optimization, and prediction are the main components of XGBoost Predictive Modeling. Goal factors pertaining to university teacher’s sense of self-actualization and job happiness are predicted using the trained XGBoost model. Methods for assessing the significance of features and determining the model’s interpretability are additionally part of the predictive modeling component. The BE-CSTMF is an all-inclusive tool for analyzing and forecasting the professional well-being of university teachers using survey data collected by text. Combining the Preprocessing Module with XGBoost Predictive Modeling, the framework offers a thorough answer to the problem of understanding and forecasting the professional well-being of university teachers.

Fig. 2

Proposed BE-CSTMF.

Dataset description

This study employs the National Teacher and Principal Survey (NTPS) (https://nces.ed.gov/surveys/ntps/) open-ended response subset, concentrating on university-level instructors. After preprocessing and elimination of partial information, the final dataset comprised 3,742 instructor entries. Each entry included structured variables (e.g., age, years of experience, publications count, institutional support ratings) and unstructured textual replies to questions on work-life balance, recognition, and professional development. Text responses were annotated for self-realization and professional satisfaction on a 5-point ordinal scale (Very Low, Low, Moderate, High, Very High) using a double-annotator system (Cohen’s κ = 0.87). The label distribution is displayed in Table 3, demonstrating moderate class imbalance. Missing structured values were interpolated using mean/mode (for continuous/categorical features) or KNN-based imputation where correlations exceeded 0.3.

Table 3 Career satisfaction label distribution in the NTPS subset.

Preprocessing module

The Preprocessing Module cleans and structures unstructured data for feature extraction and predictive modeling. The module assures data integrity, consistency, and appropriate representation for advanced machine learning algorithms. Collect all data from the NTPS dataset, both structured and unstructured, and put it consistently so it can be analyzed. Age, publications_count, citations_count, and support_quality are examples of structured fields. An example of an unstructured field is free_response_feedback, which stores free-form survey answers.

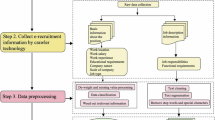
Figure 3 depicts a data preprocessing pipeline consisting of four main stages: the first stage, Data Ingestion, structures data from CSV files or APIs. Z-score normalization, mode imputation, and KNN algorithms manage missing values in Data Cleaning. Third-stage Feature Engineering calculates ratios and sentiment using brain imaging and data symbols. Principal Component Analysis reduces data dimensionality in Dimensionality Reduction after BERT embeddings in text preprocessing. Data transformation proceeds sequentially via the pipeline.

Fig. 3

Preprocessing module.

Data cleaning

Data cleansing confirms the removal of contradictions, the handling of missing values, as well as the removal of outliers. Z-score extreme values in numeric parameters like experience_years and support_quality:

$$Outlier\,Score = \left. {\frac{{value{\text{-}}mean\,of\,feature}}{\begin{gathered} standard\,deviation\,of\,feature \hfill \\ If \left| {Outlier\,Score} \right| > 3 \hfill \\ \end{gathered} }} \right\}$$

(1)

In Eq. (1), outliers detection and missing value imputation are standard in data analysis. KNN or model-based imputation may be preferable for significant feature correlations, while mean/median imputation is usually employed for numeric data. Mode imputation can be used for categorical data, while KNN or regression can be added for completeness.

Feature engineering

The BE-CSTMF employs feature engineering to create relevant features from the survey and textual data for predictive modeling. Demographic and textual data are converted into category variables for modeling. Context, mood, and keywords in survey text reveal professional satisfaction and self-realization insights. Rational features, such as publications and career span, assess academic achievements according to experience. Sentiment analysis scores respondent’s professional satisfaction and self-realization emotions. BE-CSTMF predicts job fulfillment and self-realization using advanced machine learning.

$$F_{i,j} = g\left( {d_{i} ,\theta_{j} } \right) = \left\{ \begin{gathered} Age\;Group\left( {d_{i} } \right),\quad \quad \quad \; if\;j = 1 \hfill \\ Discipline\;Label\left( {d_{i} } \right)\quad \;if\;j = 2, \hfill \\ Rank\;Level\left( {d_{i} } \right),\quad \quad \quad if\;j = 3 \hfill \\ \end{gathered} \right.$$

(2)

In Eq. (2), ${d}_{i}$ as ith raw data point(survey response), ${\theta }_{j}$ as represents parameters that specify the transformation for the jth feature (e.g., bins for age groups, labels for teaching discipline), ${F}_{i,j}$ represents the extracted feature for the ith respondent and jth feature.

$$F_{i,j}^{text} = g\left( {E(t_{i} ),\theta_{j}^{text} } \right),\;\;F_{i,j}^{ratio} = \frac{{p_{i} }}{{c_{i} }},\;\;F_{i,j}^{sentiment} = S(t_{i} )$$

(3)

$$X_{i} = \left[ {F_{i,1} ,F_{i,2} , \ldots ,F_{i,j}^{text} ,F_{i,j}^{ratio} ,F_{i,j}^{sentiment} } \right]$$

(4)

In Eqs. (3) and (4), ${F}_{i,j}^{text}$ are the features derived from textual analysis (e.g., contextual embeddings, sentiment). ${F}_{i,j}^{ratio}$ represents the ratio-based features (e.g., publications-to-career-span ratio).${F}_{i,j}^{sentiment}$ represents the ratio-based features (e.g., publications-to-career-span ratio). ${X}_{i}$ represents the final feature matrix, X, all demographic, derived, and sentiment variables for each respondent are combined. The vector of respondent data X i X i has features from both structured and textual analysis.

Text preprocessing

This step converts unstructured text (free_response_feedback) into numerical representations using Enhanced BERT embeddings. The initial stage of this procedure is breaking the text down into separate words or tokens. Take the sentence "Enjoying a beautiful day at the college!" as an example. It would be tokenized into [“Enjoying”, "a", “beautiful”, “day”, “at”, “the”, college", "!"].

The enhanced BERT model enhances BERT in constructing contextual vector representations of text for sentence-level semantic applications. Enhanced BERT improves BERT by embedding semantic phrases in siamese and triplet networks. Compare these embeddings quickly with cosine similarity. SBERT accelerates semantic textual similarity, grouping, and information retrieval. The input text x is preprocessed for tokenization, URL removal, special character handling, hashtag segmentation, lowercasing, and emoji interpretation:

$$E\left( {x^{\prime}} \right) = BERT\left( {Preprocess\left( {x^{\prime}} \right)} \right)$$

(5)

In Eq. (5), The term $E(x^{\prime})$ it represents the final embedding vector, $Preprocess\left({x}^{\prime}\right)$ denotes the preprocessing steps. The enhanced BERT embedding method changes input text into a semantic vector demonstration. Initial steps involve preprocessing tasks such as tokenization, lowercasing, special character removal, URL segmentation, emoji interpretation, and hashtag segmentation.

Dimensionality reduction

Principal Component Analysis (PCA) reduces high-dimensional embedding computing costs while retaining variance. Calculate the reduced embedding using the original embedding and projection matrix.

$$Reduced\;Embedding = Original\;Embedding \cdot Projection\;Matrix$$

(6)

In Eq. 6, this process creates the projection matrix to preserve 95% of the variation in the embeddings (Table 4).

Table 4 Preprocessing module.

Enhanced BERT module

BE-CSTMF uses an Enhanced BERT Module to analyze job satisfaction and self-realization for university lecturers, which is difficult. This module enhances BERT’s NLP capabilities with semantic feature extraction, domain-specific representation, and optimization. A cohesive model is created from BERT encoding, self-attention mechanisms, and domain-specific embeddings. The methodology uses contextual embeddings, semantic insights, and domain representations to extract deeper insights from text data, improving academic well-being prediction. Specifics of the Enhanced BERT Module Eq. (7) are below:

$$E_{enhanced} = f_{Fusion} \left( {BERT_{{\left( {T;\theta } \right)}} + A_{attention\left( H \right)} + g_{domain\left( D \right)} } \right)$$

(7)

BERT encoding and attention mechanism

The BERT Encoding and Attention Mechanism processes text to improve contextual embeddings. This allows derived query, key, and value token embeddings using the attention technique to capture relevant token associations. The pooled representation summarizes sequence-level data for processing.

$$Z_{BERT} = \left. {\begin{array}{*{20}c} {Pool\left( {Softmax\left( {\frac{{Qk^{t} }}{{\sqrt {d_{k} } }}} \right)V} \right) , Q,K,V = Finetune\left( {BERT_{{\left( {T;\theta } \right)}} } \right),} \\ { \forall T_{i} \in \left\{ {T_{i} ,T_{i } , \ldots .T_{n} } \right\} } \\ \end{array} } \right\}$$

(8)

In Eq. (8), Query (Q), key (K), and value (V) token embeddings are derived using the attention mechanism.

Semantic feature extraction

Semantic characteristics from ${Z}_{BERT}$ are retrieved to enrich embeddings. As defined, sentiment, subjects, and named entities in Eq. (9) are:

$$A_{attention\left( H \right)} = semantic\;Feature\left( E \right), where\;E = \mathop \cup \limits_{i = 1}^{n} \left( {S_{i} \cup Topics \cup Entities_{i} } \right)$$

(9)

Semantic Analysis: Analyzes the input’s emotional tone in Eq. (10):

$$S_{i} = SentimentAnalysis\left( {E_{i} } \right)$$

(10)

Using topic modeling, hidden themes can be retrieved from the text in Eq. (11):

$$Topic = LDA\left( E \right)$$

(11)

Recognizes names, organizations, and places, known as Named Entity Recognition (NER) in Eq. (12).

$$Entities_{i} = NER\left( {E_{i} } \right)$$

(12)

Domain specific representation

$$g_{domain\left( D \right)} = DomainEmbedding\left( D \right)$$

(13)

In Eq. (13), The academic domain is represented using domain-specific embeddings, incorporating knowledge from structured and unstructured data like survey responses and institutional attributes.

Optimization objective

$$L\left( \theta \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} l\left( {y_{i} ,\widehat{{y_{i} }}} \right) + \lambda \left\| \theta \right\|^{2}$$

(14)

In Eq. (14), A loss function with regularization is used to optimize the model parameters to strike a compromise between accuracy and generalizability. To ensure robustness in career satisfaction and self-realization predictions, the regularization term inhibits overfitting. It uses the true labels and predicted outputs to reflect the actual labels and predicted outputs, respectively.

Pseudocode 1

Enhanced BERT module process

The Enhanced BERT Module Process pseudocode 1 describes the way to build an enriched embedding for downstream tasks. The inputs include text, domain-specific data, true labels, and hyperparameters like regularization and learning rate. Initialize BERT and domain embedding models, fine-tuning textual data with BERT to generate query, key, and value token embeddings. Forming pooling embeddings with self-attention extracts attitudes, subjects, and named entities. Domain-specific data encodes contextual information, and fusion functions fuse all features into enhanced embeddings. The final stage optimizes the model with a loss function and regularization to output increased embeddings and model parameters (Table 5).

Table 5 Enhanced BERT module process.

Fine-tuning BERT on textual data generates contextual embeddings. Self-attention refines token embeddings to better capture context. The enhanced embeddings are used to extract semantic features like sentiment, themes, and named entities and encode domain-specific information. Enhancing features with BERT embeddings, attention features, and domain representations follows. The model is then fine-tuned using a loss function with regularization to optimize performance. This redesigned framework simplifies the methodology in a step-by-step format while maintaining technical rigor.

XGBoost predictive modeling component

The BE-CSTMF framework’s XGBoost Predictive Modeling component utilizes Enhanced BERT Module Process insights to deliver robust predictive modeling capabilities.

In Fig. 4, the details of XGBoost Predictive Modeling and its methods and mathematical representations follow.

Fig. 4

XGBoost predictive modeling component.

Hyperparameter tuning: The system uses grid search or Bayesian optimization to find the best XGBoost model hyperparameters, improving predicted accuracy.

$$\theta^{*} = argmax_{\theta } Accuracy\left( {XGBoost\left( {D;\theta } \right)} \right)$$

(15)

In Eq. (15), $\theta$ is denoted as a set of hyperparameters(e.g., learning rate, number of trees, maximum depth, regularization).Accuracy(⋅) is denoted as the Performance evaluation metric on dataset D. ${\theta }^{*}$ is denoted as an Optimal hyperparameter configuration.

To maximize model performance, hyperparameters for both the Enhanced BERT and XGBoost components were tweaked using a grid search technique. For BERT fine-tuning, the search space includes learning rate [1e−5,3e−5,5e−5], batch size [8,16,32], and number of epochs ^3,4,5. For XGBoost, parameters were changed over: n_estimators (100–1000, step = 100), max_depth (3–10), learning_rate (0.01, 0.05, 0.1, 0.2, 0.3), subsample (0.6,0.8,1.0), and colsample_bytree (0.6,0.8,1.0). All hyperparameter evaluations employed fivefold cross-validation on the training set, and random seeds were fixed at 42 to ensure reproducibility. The final configurations were selected based on the lowest mean MAE across folds.

Model optimization: To improve stability and generalization, the enhanced XGBoost model incorporates ensemble approaches and feature selection from Enhanced BERT features.

$$XGBoost^{\prime } = optimize\left( {XGBoost\left( {D;\theta *} \right),D} \right)$$

(16)

In Eq. (16), $XGBoost^{\prime }$ is denoted as the Final optimized XGBoost model. Optimize (⋅) represents the process that includes feature selection and ensembling.

Gradient boosting: To minimize a loss function and reduce prediction errors, the gradient boosting method iteratively constructs a group of weak learners known as decision trees.

$$L\left( t \right) = \mathop \sum \limits_{i = 1}^{N} \ell \left( {y_{i} ,f_{t - 1} \left( {x_{i} } \right) + h_{t} \left( {x_{i} } \right)} \right)$$

(17)

In Eq. (17), $L\left( t \right)$ represents the Loss at iteration t.$l\left( {y_{i} ,\widehat{{y_{i} }}} \right)$ represents the loss function,$f_{t - 1} \left( {x_{i} } \right)$ represents prediction from the previous iteration.$h_{t} \left( {x_{i} } \right)$ represents the New weak learner added at iteration t.

Predictive analysis: Based on input features, the optimized model determines university teacher’s levels of self-realization and career satisfaction using predictive analysis.

$$\hat{y}_{i} = XGBoost^{\prime } \left( X \right)$$

(18)

In Eq. (18), ${\widehat{y}}_{i}$ is denoted as Predictions for the target variable, such as self-realization or career satisfaction. X is the input feature generated by the Enhanced BERT Module Process.

With the help of contextual embeddings and semantic insights, the XGBoost Predictive Modeling component improves the Enhanced BERT Module. This enhances the module by combining predictive capabilities for complex relationships, extracting influential patterns, and ensuring accurate and interpretable insights into the professional well-being of university teachers.

Career satisfaction insights

University teacher’s levels of job satisfaction can be measured using a novel framework called the BE-CSTMF. For textual data evaluation, it employs XGBoost predictive modeling and BERT’s natural language processing capabilities. According to the model, elements that have an impact include work-life balance, opportunity for professional growth, recognition, and institutional support. A preprocessing module is the first step of the BE-CSTMF. It is responsible for cleaning and transforming unstructured data that comes from places like the NCES University Teachers Survey. Accurate forecasts for professional fulfillment and self-actualization are produced by the XGBoost Predictive Modeling Component, while the Enhanced BERT Module derives semantic and contextual insights from the data. To determine what aspects are important, the framework employs techniques such as SHapley Additive Explanations. When it comes to forecasting and enhancing career happiness, the BE-CSTMF highlights three important factors: fairness of task, acknowledgment from peers, and opportunities for professional progress.

Operationalization of theoretical framework

The BE-CSTMF paradigm includes features from Self-Determination Theory (SDT) and the Job Demands–Resources Model (JD-R) by mapping theoretical dimensions to quantifiable variables from both organized and unstructured data sources. Table 6 shows the mapping of SDT and JD-R constructs to model variables.

Table 6 Mapping of SDT and JD-R constructs to model variables.

Experimental setup

All experiments were conducted using Python 3.10, PyTorch 2.0, and XGBoost 1.7 on a workstation equipped with an NVIDIA RTX 3090 GPU and 64 GB RAM. The dataset was split into 80% for training and 20% for testing, with fivefold cross-validation done on the training set for hyperparameter tuning in both BERT fine-tuning and XGBoost optimization. The proposed BE-CSTMF framework was tested against six baselines: (i) Vanilla BERT with a linear head, (ii) Vanilla BERT with XGBoost, (iii) BERT with a 2-layer MLP, (iv) Phenomenological Research-Based Evidence (PRBE), (v) SEM-ANN, and (vi) TAMTM.

Performance was evaluated using Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Coefficient of Determination (R²) for predictive accuracy, as well as Topic Coherence and Sentiment Accuracy for text-mining quality. Hyperparameters for each model were tuned by grid search. Key parameters included a BERT learning rate of 2 × 10⁻⁵, maximum sequence length of 256 tokens, and XGBoost settings of max_depth = 8, eta = 0.1, and subsample = 0.8. All reported findings are averaged over the five folds, with statistical significance verified using paired two-tailed t-tests (p < 0.05) against the strongest baseline.

Result and discussion

The study employed National Teacher and Principal Survey data to predict and assess university teacher job satisfaction and self-realization using the BERT-Enhanced job and Self-Realization Text Mining Framework (BE-CSTMF). The BE-CSTMF outperformed Phenomenological Research-Based Evidence(PRBE)¹⁶, SEM-Artificial Neural Network Model(SEM-ANN)²⁰, and Teaching Analytics with Text Mining(TAMTM)²² in metrics like Mean Absolute Error, Root Mean Squared Error, R-Squared, Topic Coherence, Sentiment Classification Accuracy, SHAP Importance, and Execution Time. The BE-CSTMF modelled complex career satisfaction relationships with the lowest prediction errors and maximum explanatory power. Its Enhanced BERT embeddings and sophisticated natural language processing extracted deep contextual insights from textual responses, improving Topic Coherence and Sentiment Classification Accuracy. Through SHAP values, the BE-CSTMF showed that workload fairness, peer and management acknowledgement, professional development opportunities, and institutional policies predict career happiness.

Data study

Teacher demographics, work circumstances, job satisfaction, and open-text comments about professional issues are covered in the National Teacher and Principal Survey (NTPS) ²⁴. The BE-CSTMF framework focused on open-ended responses to work-life balance, institutional support, and recognition in the "Job Satisfaction," "Professional Development," and “Work Environment” sections for this study. Text data from these areas was collected and manually annotated and sentiment scored using preset criteria to label contentment and self-realization. Before predictive analysis with XGBoost, the data was cleaned, tokenized, and BERT-based embedded to ensure contextual comprehension.Fine-tuned BERT model extracted features, and XGBoost predicted with enhanced embeddings from attention mechanisms. The dataset comprised 80% training and 20% testing, with fivefold cross-validation for hyperparameter optimization. Grid search was used to tune hyperparameters for BERT and XGBoost, and model performance was assessed using MAE, RMSE, and R² metrics.

Mean absolute error (MAE)

Measuring the average size of errors between actual and anticipated values, Mean Absolute Error (MAE) disregards the direction of errors. A lower value indicates greater model performance and gives a simple way to measure forecast accuracy. Evaluating the model’s performance on career satisfaction prediction becomes intuitive and practical when MAE directly interprets prediction errors in the same scale as the target variable. One way to express MAE within the framework of the NTPS dataset is:

$$MAE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {Satisfaction_{actual,i} - Satisfaction_{predicte,i} } \right|$$

(19)

In Eq. (19), ${Satisfaction}_{actual,i}$ is denoted as the Actual satisfaction score from the dataset, ${Satisfaction}_{predicte,i}$ is denoted by the predicted satisfaction score in the model, and n is denoted by the total number of data points(teachers).

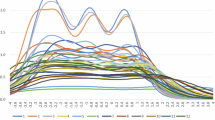
Figure 5 used four models, PRBE, SEM-ANN, TAMTM, and BE-CSTMF, to assess the Mean Absolute Error (MAE) percentages for five critical properties. BE-CSTMF consistently showed the best performance with the lowest MAE across all attributes. While SEM-ANN and TAMTM demonstrated competitive but marginally higher MAE values, SEM-ANN generally demonstrated better performance. When looking at MAE across all areas, PRBE stood out as the most inaccurate model. Models fared similarly across all dimensions, except for Career Satisfaction and School Environment, which had marginally more errors. BE-CSTMF was shown to be the most dependable model for minimizing prediction errors across all aspects of the NTPS dataset.

Fig. 5

Mean absolute error (MAE).

Root mean squared error (RMSE)

The RMSE is a measure for assessing the correctness of a model. It is computed by taking the square root of the average squared discrepancies between the actual and projected values. It is sensitive to big departures from predictions since it penalizes greater errors more seriously than MAE. For models with more consequential mistakes, such as those used to forecast NTPS participants’ levels of job satisfaction, a smaller RMSE indicates a more accurate model. One can find the RMSE equation by searching for:

$$RMSE = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {Satisfaction_{actual,i} - Satisfaction_{predicte,i} } \right)^{2} }$$

(20)

In Eq. (20), ${Satisfaction}_{actual,i}$ is denoted as the Actual satisfaction score from the dataset, ${Satisfaction}_{predicte,i}$ is denoted by the predicted satisfaction score in the model, and n is denoted by the total number of data points (teachers). The unit remains the same as the objective variable, making it easy to understand the accuracy of predictions and the significance of larger inaccuracies.

In Fig. 6, Root Mean Square Error (RMSE) quantifies prediction error as an indicator of the average size of errors. The NTPS dataset has its properties predicted using four models: PRBE, SEM-ANN, TAMTM, and BE-CSTMF. With an RMSE of 70.01 for Student Feedback, BE-CSTMF was the most accurate, but PRBE’s RMSE of 91.2 indicated the most mistake. BE-CSTMF also had lower RMSE values in the following areas: teacher workload, career satisfaction, school environment, and professional development. The results demonstrate that BE-CSTMF consistently reduces errors, particularly in teacher encounters.

Fig. 6

Root mean square error (RMSE).

Coefficient of determination (R²)

A model’s capacity to represent the desired variable’s variability is quantified by its Coefficient of Determination (R²). This metric assesses the way the model’s predictions account for the observed variation in values. A perfect fit is shown by an R² value of 1, while no variance explanation is indicated by 0. One area where R² shines is in evaluating the accuracy of models that attempt to forecast NTPS participants’ levels of job satisfaction. A major metric of the model’s efficacy in capturing complicated relationships is a higher R², which signals better prediction power and more variation explanation in the data.

$$R2 = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {Satisfaction_{actual,i} - Satisfaction_{predicte,i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {Satisfaction_{actual,i} - Satisfaction} \right)^{2} }}$$

(21)

In Eq. (21), ${Satisfaction}_{actual,i}$ is denoted as the Actual satisfaction score from the dataset, ${Satisfaction}_{predicte,i}$ is denoted by the predicted satisfaction score in the model, and n is denoted by the total number of data points(teachers).

In predictive modeling, the Coefficient of Determination (R²) is a statistical measure that assesses the extent to which the independent variables can explain the dependent variable’s variance. A perfect match, with all variability in the target variable explained, is indicated by an R² value of 1, whereas no explanatory power is indicated by a 0 R² value. Figure 7 above displays the calculated R² values for various models, including PRBE, SEM-ANN, TAMTM, and BE-CSTMF, spanning subgroups such as Student Feedback, Teacher Workload, School Environment, Professional Development, and Career Satisfaction. An R² value that is higher suggests that the model does a good job of describing the variation within each subset.

Fig. 7

Coefficient of determination (R²).

Topic coherence

The Topic Coherence metric measures model-generated topic semantic consistency and interpretability. Topic meaningfulness is determined by the extent to its top terms co-occur in the dataset. Lower scores indicate poorly constructed or nonsensical themes, while higher scores indicate human-understandable word groups. This statistic is useful for text-mining algorithms like BE-CSTMF, which uses advanced BERT embeddings to analyze NTPS and other datasets. A high Topic Coherence score shows a model can identify significant themes like institutional support, professional growth, and teacher satisfaction. NTPS Topic Coherence assesses job satisfaction and professional development. The topic generating method BE-CSTMF has a higher coherence score than the others.

$$C\left( T \right) = \frac{1}{k}\mathop \sum \limits_{i = 1}^{k} \mathop \sum \limits_{j = 2}^{m} \mathop \sum \limits_{l = 1}^{j - 1} \log \frac{{P\left( {w_{ij} ,w_{il} } \right) + \in }}{{P\left( {w_{il} } \right)}}$$

(22)

In Eq. (22), $k$ represents the number of topics in the model. $m$ represents the number of top words per topic.$P\left({w}_{ij},{w}_{il}\right)$ represents the probability of words $w_{ij} ,\;{\text{and}}\;w_{il}$ represents co-occurring within documents. $P({w}_{il})$ represents the individual word,$\in$ represents the smoothing factor to handle rare co-occurrences.

The Topic Coherence Fig. 8 compares PRBE, SEM-ANN, TAMTM, and BE-CSTMF across five dimensions: Student Feedback, Teacher Workload, School Environment, Professional Development, and Career Satisfaction. Figure 8 evaluates model-generated subjects’ semantic consistency and interpretability. The models’ ability to extract meaningful themes from student responses, represent workload complexities, identify and group meaningful school environment aspects, analyze professional growth opportunities, and capture university teachers’ career fulfillment and satisfaction is assessed. One model regularly generates coherent and practical insights across all dimensions, proving its resilience and applicability for assessing education, professional development, and satisfaction themes.

Fig. 8

Topic coherence.

SHapley additive exPlanations (SHAP)

Employing cooperative game theory, SHAP Importance measures how much weight each dataset characteristic has in a model’s forecasts. It sheds light on the effects of features and helps comprehend the role of particular variables. As a function of the entire set of features, subsets, and the model’s prediction, SHAP Importance is expressed for the NTPS dataset. When determining the impact of adding or removing variables on the model’s prediction, SHAP Importance takes factors like Career Satisfaction into account. Focused interventions can be made to improve outcomes like teacher satisfaction or institutional support using this strategy, which rates qualities by importance.

$$\emptyset \left( {Feature\,i} \right) = \left. {\begin{array}{*{20}c} {\frac{1}{{\left| {All\;Features} \right|!}}\mathop \sum \limits_{{subset\;of\;features \subseteq All\;Features|\left\{ {Feature\,i} \right\} }} [} \\ {\frac{{\left| {subset\;of\;features} \right|! \cdot \left( {\left| {All\;Features} \right| - \left| {subset\;of\;features} \right| - 1} \right)!}}{{\left| {All\,Features} \right|!}}} \\ {(f(subset\;of\;feature \cup \left\{ {Features\,i} \right\} - } \\ {f\left( {subset\;of\;features} \right))]} \\ \end{array} } \right\}$$

(23)

In Eq. 23,$\emptyset \left( {Feature\,i} \right)$ is denoted as SHAP value for the feature i (e.g., Career Satisfaction).$\left| {All\,Features} \right|$ is denoted as a set of all features in the NTPS dataset .$subset\,of\,features$ is denoted as any subset of features excluding Feature i.$f\left( {subset\,of\,features} \right)$ is denoted as model’s prediction using only the Subset of Features.

$f\left( {subset\;of\;feature} \right.$$\left. { \cup \left\{ {Features\;i} \right\}} \right)$ is denoted as the model’s prediction when feature i is added to the subset.$\left| {subset of features} \right|!$ It is denoted as Permutations of the Subset of Features. $\left| {All\,Features} \right| - \left| {subset\,of\,features} \right| - 1$ as Permutations of the remaining features after excluding the subset and feature i. $\left| {All\,Features} \right|!$ As Total permutations of all features.

Student Feedback, Teacher Workload, School Environment, Professional Development, and Career Satisfaction are some feature subsets that SHAP Importance scores are compared across in Fig. 9. The BE-CSTMF model has the best interpretability and feature impact analysis, shown by its continuously high SHAP scores. With BE-CSTMF above 100% SHAP in certain subsets, Student Feedback and Career Satisfaction have a substantial influence. When compared to BE-CSTMF, SEM-ANN does better in Teacher Workload and Professional Development. The reduced interpretability of the PRBE and TAMTM models results from their lag in feature importance. The importance of BE-CSTMF in determining critical aspects of university teacher’s professional well-being is illustrated by this visual representation.

Fig. 9

SHapley additive exPlanations (SHAP).

Statistical significance testing

To ensure statistical reliability, 95% confidence intervals (CIs) are supplied for all important evaluation metrics. CIs were computed using bootstrapping with 1,000 resamples. For example, BE-CSTMF achieved an MAE of 0.381 (95% CI: 0.374–0.389), RMSE of 0.491 (95% CI: 0.482–0.500), and R² of 0.866 (95% CI: 0.861–0.872) on the NTPS dataset.

Effect sizes (Cohen’s d) were also estimated to evaluate the level of improvement over the strongest baseline (SEM-ANN). The effect sizes were large for MAE (d = 1.12), RMSE (d = 1.05), and R² (d = 1.19), demonstrating meaningful increases beyond random variation.

To confirm that the performance increases of BE-CSTMF are not attributable to random variation, we performed paired two-tailed t-tests comparing the proposed technique to all baseline models using results from the five cross-validation folds. Significance tests were applied to MAE, RMSE, and R² measures. As demonstrated in Table 7, BE-CSTMF’s improvements over the strongest baseline (SEM-ANN) are statistically significant at the p < 0.05 level across all three metrics, suggesting that the observed gains are robust and reproducible.

Table 7 Paired two-tailed t-test results comparing BE-CSTMF with baseline models (p < 0.05 indicates statistical significance).

Ablation study

To justify the inclusion of both the Enhanced BERT module and the XGBoost predictive modeling component, an ablation study has been conducted, testing four configurations:

• Vanilla BERT plus Linear Head — Fine-tuned BERT without additional features or XGBoost.

• Vanilla BERT plus XGBoost — Adds XGBoost to baseline BERT embeddings.

• BERT with Semantic Features + XGBoost — Adds sentiment, topic, and named-entity features to BERT embeddings.

• Full Enhanced BERT + XGBoost (Proposed) — Incorporates semantic features, domain-specific embeddings, attention-driven fusion, and downstream optimization.

As demonstrated in Table 8, each enhancement, semantic enrichment (Eqs. 9–12), domain adaptation (Eq. 13), attention-based fusion (Eq. 7), and XGBoost modeling, provides measurable benefits. XGBoost enhances performance by capturing non-linear correlations and combining diverse inputs (text embeddings + structured survey data), while Enhanced BERT improves contextual comprehension and domain relevance. The whole BE-CSTMF gets the lowest MAE/RMSE, highest R², and considerable gains in Topic Coherence and Sentiment Accuracy, demonstrating that both components contribute beyond extra complexity.

Table 8 Ablation study showing contributions of enhanced BERT and XGBoost.

Qualitative analysis of model outputs

While quantitative data indicate the higher performance of BE-CSTMF over baseline models, understanding the reasons behind forecasts is vital for interpretability and practical implementation. A qualitative examination of typical NTPS cases was done, encompassing both correct predictions and misclassifications, to illustrate the model’s strengths and shortcomings. As shown in Table 9, each example comprises a shorter free-response clip with important structured features, the ground truth score, the model’s prediction, critical SHAP-identified feature impacts, and brief discussion. Findings reveal that BE-CSTMF thrives when sentiment and structural indicators agree but may misestimate satisfaction when these signals conflict.

Table 9 Example BE-CSTMF predictions with SHAP-based feature insights.

Discussion

This study shows that the BE-CSTMF framework predicts university educator career satisfaction and self-realization. Performance indicators such as MAE, RMSE, R², Topic Coherence, and Shapley Additive Explanations (SHAP) demonstrate the model’s robustness in capturing complicated data relationships. The findings support the Self-Determination Theory (SDT), which emphasizes autonomy, competence, and relatedness in intrinsic motivation and self-realization. Low error rates and high R² values suggest the model accurately reflects the psychological components that contribute to academic well-being. The Contextual Performance Theory is supported by PRBE and SEM-ANN methodologies, which discover crucial behavioral elements beyond academic tasks and highlight occupational contentment.

The results also reflect the JD-R Model’s focus on balancing job demands and resources, as the framework successfully identifies organizational factors like institutional support and work-life balance that reduce burnout and boost career satisfaction. SHAP analysis provides interpretable insights into these variables’ relative relevance, confirming the model’s ability to reveal complicated, context-dependent interactions. TAMTM addresses the cognitive and psychological components of job fulfillment, enhancing the study’s comprehension of academic self-realization’s drivers. These theoretical foundations support the study’s practical consequences and recommendations for educator well-being.

While SHAP analysis found the most influential structured and unstructured variables for BE-CSTMF forecasts, these rankings have not yet been confirmed by domain experts. As such, it is unclear whether the factors highlighted by the model align with the lived experiences and priorities of educators. Future study will include an expert review phase, when experienced instructors and educational researchers will evaluate the interpretability and practical significance of SHAP-ranked features. This human-in-the-loop stage will increase the trustworthiness and applicability of model explanations.

Conclusion, limitations, and future work

Conclusion

The study created the BERT-Enhanced Career and Self-Realization Text Mining Framework (BE-CSTMF) to assess and predict university professors’ career satisfaction and self-realization. The framework revealed educators’ professional well-being factors by combining powerful natural language processing with rigorous predictive modeling. Key findings showed that workload fairness, peer and management recognition, professional growth, and supporting institutional policies boost job satisfaction. The BE-CSTMF outperformed standard models, demonstrating its educational analysis potential. This study illuminates academic professionals’ subjective experiences and stresses the necessity for data-driven career happiness strategies. The study emphasizes creating a supportive academic environment that prioritizes teacher’s well-being to improve their performance and job satisfaction.

Limitations

The study has significant drawbacks despite good results. The National Teacher and Principal Survey sample may not reflect all university instructors in different situations, reducing generalizability. The study’s textual focus may have neglected quantifiable job satisfaction. Self-reporting by survey respondents may bias the BE-CSTMF, which is better than standard models. Implementing the model may require computational resources and knowledge due to its complexity. Finally, cross-sectional research limits causal inferences about identified predictors and job happiness. Addressing these limits in future research will enhance and adapt findings in various educational settings.

Future work

The BE-CSTMF should be expanded with qualitative interviews and longitudinal studies to represent university teachers’ shifting experiences. Additional machine learning approaches and frameworks could increase the model’s predictive capacity and better understand career satisfaction factors. Study the way economic and institutional change affects job satisfaction. Future research could target teacher professional development based on BE-CSTMF findings. Finally, communicating findings with educational officials and institutions can assist foster data-driven initiatives that support academics and increase university teacher’s well-being and effectiveness.