Introduction

Metamaterials and composites have grabbed attention in recent years since they can possess unique properties that don’t exist in nature. Complex permittivity \(\:\left({\epsilon}_{0}{\epsilon\:}^{{\prime}}+i{\epsilon}_{0}\epsilon\:^{{\prime}{\prime}}\right)\) and permeability \(\:\left({{\mu\:}_{0}\mu\:}^{{\prime\:}}+i{\mu\:}_{0}{\mu\:}^{{\prime}{\prime}}\right)\) characterize metamaterials. The ability to manipulate these properties provides an extraordinary opportunity to tailor materials according to specific requirements, enabling a wide range of applications using a single material1. High-k composites with low loss find extensive use in microwave devices2,3,4,5,6, while high-loss and negative susceptibility metamaterials have applications in stealth technology. Furthermore, metamaterials have diverse applications in antenna design7,8, split-ring resonators9, medical imaging10,11, wireless power transfer12,13,14,15, anti-reflection coating16,17, optical devices18,19, and negative refractive index materials20,21,22,23,24.

Effective medium theory (EMT) is a widely adopted approach to analyzing composites’ material properties, enabling fine-tuning \(\:{\epsilon\:}^{{\prime\:}}\) and \(\:{\mu\:}^{{\prime\:}}\). However, its efficacy diminishes when the volume fraction approaches the percolation threshold. For instance, Yao et al. have collected the ten most representative EMT models25, all of which can only handle a small region in volume fraction, and none of those predicted a threshold. Most EMT models are for \(\:{\epsilon\:}^{{\prime\:}}\), and some are for \(\:{\mu\:}^{{\prime\:}}\). Standard EMT models (Maxwell–Garnett, Bruggeman, etc.) for \(\:{\epsilon\:}^{{\prime\:}}\) assume \(\:{\mu\:}^{{\prime\:}}=1\), local-field factors that remain finite, and no dispersion. Consequently, they cannot reproduce the power-law divergences and, therefore, unable to predict the percolation threshold. EMT models for \(\:{\mu\:}^{{\prime\:}}\) can only apply on magnetic materials (Ferrite, Nickle, etc.). It cannot predict the magnetism cause by the tiny eddy current caused by the percolation effect. Also, EMT models fail at \(\:{\epsilon\:}^{{\prime}{\prime}}\) and \(\:{\mu\:}^{{\prime}{\prime}}\).

Percolation theory is then applied to handle EMT’s drawback, which was first introduced in 1957 by Broadbent and Hammersley26. Yet, most investigations in the last seven decades have focused on the dielectric constant \(\:\left({\epsilon\:}^{{\prime\:}}\right)\) and the electrical conductivity \(\:\left(\sigma\:\right)\). No prior work has experimentally confirmed the predicted power-law divergence of negative magnetic susceptibility in a metal-insulator composite at microwave frequency. Roughly speaking, research of \(\:\epsilon\:^{{\prime}{\prime}}\)27 and \(\:{\mu\:}^{{\prime\:}}+i\mu\:^{{\prime}{\prime}}\)27,28,29,30 stagnated after the 1990s due to the lack of profound application. There seems to be no room for further exploration, but the necessity of understanding (ε, µ) still serves scientific interests (etc., refraction index \(\:n(\epsilon\:,\:\mu\:)\) and wave impedance, \(\:Z(\epsilon\:,\:\mu\:)\)). If volume fraction p is far away from the percolation threshold, \(\:{p}_{c}\), it is safe to suppose \(\:\mu\:=1\).

Permeability contribution (in terms of \(\:\mu\:\left(p-{p}_{c}\right)\)) seems inevitable when \(\:p\to\:{p}_{c}\). In this situation, the assumption µ ⋍ 1 should be slightly modified. Su et al. showed that silver-epoxy composite exhibits diamagnetism at a low volume fraction \(\:(\leq10\%)\) while epoxy and silver are both non-magnetism31. Lagar’kov et al. showed that the permeability of a ferromagnetic percolation system also has diamagnetic percolative behavior30. Bowman and Stroud showed that superconductor-metal composites possess diamagnetism and follow the power law29. They also predicted that metal-insulator composites have similar properties. Therefore, magnetism may not be rare in composites, and if permeability is assigned to be 1, then the permittivity could be over- or under-estimated.

Now, in formulae, the behavior of a composite’s dielectric constant can be stated as32,33

$$\:\epsilon\:^{\prime\:}=\left\{\begin{array}{cc}{\epsilon\:}_{d}^{\prime\:}{\left|p-{p}_{c}\right|}^{-s}&\:{\:\:\:p<p}_{c},\:p>{p}_{c}\:\\\:{\:{\epsilon\:}_{d}^{\prime\:}}^{\:\frac{t}{t+s}}{\left(\frac{{\sigma\:}_{m}}{\omega\:}\right)}^{\frac{s}{t+s}}&\:\:\:\:\:p\:\text{n}\text{e}\text{a}\text{r}\:{p}_{c}\:\:\end{array}\right.$$
(1)

\(\:p\) is the volume fraction, \(\:{p}_{c}\) is the percolation threshold; \(\:{\epsilon\:}_{d}^{\prime\:}\) is the dielectric constant of the insulator; \(\:{\sigma\:}_{m}\) is the conductivity of the metal; \(\:s\) and \(\:t\) are the critical exponents. The theoretical value is 0.7 ~ 1.0 for \(\:s\) in 3D, and 1.1 ~ 1.3 in 2D32,33,34,35. Near the threshold, there is a remarkable surge in the dielectric constant, reaching a tremendously significant value. However, this substantial enhancement is confined to a narrow vicinity. Consequently, accurately calculating the volume fraction near the threshold poses a challenging task. The imaginary part also follows the power law27,36

$$\:\epsilon\:^{{\prime}{\prime}}\propto\:\left\{\begin{array}{cc}{\left|p-{p}_{c}\right|}^{-q}&\:{\:\:\:\:\:\:\:p<p}_{c}\:\:\\\:{\left(\frac{{\sigma\:}_{m}}{\omega\:}\right)}^{-k}&\:\:\:\:\:\:\:\:p\:\text{n}\text{e}\text{a}\text{r}\:{p}_{c}\:\:\end{array}\right.$$
(2)

Theoretically, the critical exponent \(\:q\) is about 2.5 ~ 3.1 in 3D and 2.2 ~ 2.6 in 2D. As for \(\:k\), it depends on the frequency. At GHz region, \(\:k\approx\:1\)36.

According to Bowman’s model, long-wavelength electromagnetic waves induce diamagnetic currents in loops formed by metal grains. This diamagnetic effect intensifies with an increase in volume fraction, causing a permeability drop due to the more favorable presence of “bond” electrons. However, as the volume fraction continues to rise, the swift expansion of silver nanoparticle clusters prompts the ‘bond’ electrons to transition back to a ‘free’ state. Consequently, the induced current weakens, leading to an increase in permeability. Then, the “negative magnetic susceptibility” (\(\:-{\chi\:}_{b}\)) follows the power law near the threshold28,29

$$\:1-{\mu\:}^{{\prime\:}}=-{\chi\:}_{b}\propto\:{\left|p-{p}_{c}\right|}^{-u}\:\:\:\:\:\:\:\:\:\:\:p\:\text{c}\text{l}\text{o}\text{s}\text{e}\:\text{t}\text{o}\:{p}_{c}$$
(3)

The critical exponent u for the negative magnetic susceptibility has a theoretical value of 0.11 ~ 0.4129. As for the imaginary part, it reads29,30

$$\:\mu\:^{{\prime}{\prime}}\propto\:{\left|p-{p}_{c}\right|}^{-v}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:p\:\text{c}\text{l}\text{o}\text{s}\text{e}\:\text{t}\text{o}\:{p}_{c}\:$$
(4)

According to the theory, the critical exponent, \(\:v\), is equal to u29.

Experimental

Our sample preparation closely followed the established waveguide method37. Commencing with a WR90 copper waveguide, we immerse it in a copper polishing solution to eliminate surface oxidation. Subsequently, the waveguide underwent immersion in distilled water to eliminate the residual polishing solution. A thorough cleansing process ensued, involving washing with acetone to remove water and organic substances. The final step in the washing process involved an isopropanol bath to eliminate traces of acetone.

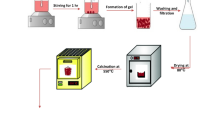
The holder comprised five components: a metal base, two WR90-shaped Teflon plates, and two Teflon plates. Structurally resembling a sandwich, the holder featured the metal base at the bottom, followed by a plate, with the WR90-shaped plates flanking the copper waveguide. Before sealing the waveguide, the composite mixture was introduced. The nano-powder utilized in this study was commercially sourced from US Research Nanomaterials, Inc., boasting a purity exceeding 99.99%, a diameter of 20 nm, and a density of 10.49 g/cm³. The epoxy resin (Epoxy A) combined with the hardener (Epoxy B) has a density of about 1.13 g/cm³. Silver was chosen due to its stability (not easily oxidized), and a relatively lower cost than Au and Pt. The fabrication began by pouring one to three grams of Epoxy A into a flask, then heating it to approximately 65 °C. This temperature adjustment aimed to reduce viscosity, facilitating a more accessible and random distribution of the silver nano-powder. Subsequently, the desired volume fraction of powder was added, and a moderate stirring ensued. Once the mixture had achieved homogeneity, Epoxy B was introduced. The resulting composite was then poured into the Teflon holder, and sealed with the final round plate. The detailed schematic is provided in the supplementary (Fig. SM01).

The holder was placed in a custom-made oven capable of reaching temperatures around 80 °C to expedite curing. A motor inside the oven provides the sample with a moderate rotation during curing, preventing nanoparticle precipitation. While the curing process at room temperature would take about 20 h, elevating the temperature to 70–90 °C allowed the composite to harden within 3 h. However, to ensure the composite is cured, we will turn off the heating and let the composite reset for at least a night (~ 15 h). Upon completion of curing, the composite underwent a polishing phase. The desired outcome was a mirror-like shine for the waveguide and a smooth surface for the composite, devoid of any cavities, pores, or holes to ensure the acquisition of precise results. The thickness is now measured by Mitsutoyo calipers for 10 times to check the uniformity (\(\:\le\:20{\upmu}\text{m}\)). The measurements were conducted using the Keysight PNA-X N5247B, and calibrated by HP X11644A using the calibration wizard. Following the calibration, the two ports were short-connected with a precision thru section to verify system residuals. Across the entire 8.2–12.4 GHz band the measured reflection coefficients were S₁₁, S₂₂ < − 50 dB, while the insertion parameters remained |S₂₁|, |S₁₂| < 0.05 dB. For every targeted volume fraction we fabricated two independent coupons (independent weighing, mixing and curing cycles). Each coupon was inserted into the WR-90 holder and measured twice, after a full thru-reflect-line (TRL) wave-guide calibration. All measurements were carried out under room temperature conditions (around 300 K).

The Fresnel equation reads,

$$r=\frac{{Z}_{0}-Z}{{Z}_{0}+Z}\:\:\:\:\:\:\:\:\:{r\:}^{{\prime\:}}=\frac{Z-{Z}_{0}}{{Z}_{0}+Z}$$
(5)
$$t=\frac{2Z}{{Z}_{0}+Z}\:\:\:\:\:\:\:\:\:{t\:}^{{\prime\:}}=\frac{2{Z}_{0}}{{Z}_{0}+Z}$$

.

where \(\:{Z}_{0}\) is the impedance of vacuum in the waveguide, and \(\:Z\) is the impedance of the composite in the waveguide. The signal measured is the combination of multiple reflections and transmissions, so that the infinite geometric sequence can be written down.

$$\:\left\{\:\:\:\:\begin{array}{c}{S}_{11}=r+\frac{t{r\:}^{{\prime\:}}{t\:}^{{\prime\:}}{e}^{2i\beta\:d}}{1-{r\:}^{{\prime\:}2}{e}^{2i\beta\:d}}\\\:{S}_{21}=\frac{t{t\:}^{{\prime\:}}{e}^{2i\beta\:d}}{1-{r\:}^{{\prime\:}2}{e}^{2i\beta\:d}}\:\:\:\:\:\:\:\:\end{array}\right.$$
(6)

where \(\:\beta\:\) is the wave number of the composite inside the waveguide of the TE01 mode. The acquired data was subjected to analysis through Eqs. (5) and 6. MATLAB (R2021b) was utilized for computation, allowing the retrieval of permittivity and permeability from the S-parameters. The power law \(\:y\left(x\right)=A{\left|x-{p}_{c}\right|}^{-s}\) is fit by MATLAB R2021b (Levenberg–Marquardt) using automatic Jacobian evaluation. Free parameters: amplitude \(\:A\), exponent \(\:s\), and percolation threshold \(\:{p}_{c}\). Initial guesses (\(\:{A}_{0}\), \(\:{s}_{0}\), \(\:{p}_{c0}\)) were taken from the log–log slope and the point of maximum curvature, but convergence proved insensitive to the starting values. All four replicate measurements at a given volume-fraction (two independent coupons × two insertions) showed very similar scatter. Because the variances were essentially uniform over the fitting window, we treated every data point with equal weight.

A breakdown of the dominant uncertainty sources is: (i) VNA magnitude/phase repeatability (Keysight N5247B specification ± 0.05 dB/± 0.3°); (ii) residual flange gap & holder alignment (< 0.02 in |S₁₁|); (iii) sample-thickness tolerance ± 40 μm, propagated through Eq. (6)

Results and discussion

Figure 1 illustrates the frequency dependence for samples with various volume fractions. The results were taken as an average, and the error bar is also given. The result in Fig. 1a shows weak frequency for volume fractions below \(\:25\:\%\), and the frequency dependence becomes visible only when \(\:p>25\:\%\). Figure 1b also has a similar trend when the volume fraction is close to the percolation threshold. We will discuss this issue in detail later.

Figure 2a is the result of \(\:\epsilon\:^{\prime}\) taken at 12.4 GHz (blue triangles) and 8.2 GHz (red squares). It starts from pure epoxy with a dielectric constant of around 3.13.\(\:\epsilon\:^{\prime}\) gradually increases from 3.8 to 8.6 as the volume fraction rises from\(\:\:0\:\%\) to \(\:10\:\%\). Within this range, the silver nanoparticles are isolated and can be treated as a dielectric material, allowing for the application of EMT31. A more pronounced increase occurs at \(\:15\:\%\) to \(\:24\:\%\), and as we further increase the volume fraction, the rate of increment (the slope) surges swiftly and slows down when the volume fraction exceeds \(\:25\:\%\), where the maximum of 496 (8.2 GHz) and 395 (12.4 GHz) were reached.

The fitting results are given in Fig. 2b on a logarithmic scale with the critical exponent, percolation threshold, and the corresponding 95% confidence bound. The percolation thresholds are \(\:26.30\pm\:0.14\:\%\) and \(\:26.36\pm\:0.13\:\%\). From the fitting results, the critical exponents \(\:s\) are \(\:1.2757\pm\:0.1162\) for 12.4 GHz and \(\:1.2989\pm\:0.0278\) for 8.2 GHz. The result is closer to the upper limit in 2D cases. The dimension of a WR90 waveguide is 22.86 mm by 10.16 mm, and the thickness chosen was 2 ~ 3 mm. The shape of the samples resembles a flat slab. This might explain why the critical exponent is higher.

Figure 2a shows \(\:\epsilon\:^{{\prime}{\prime}}\) at 12.4 GHz (green triangles) and 8.2 GHz (orange diamonds). It has a similar trend as \(\:\epsilon\:^{\prime}\). A gradual increase occurs below \(\:10\:\%\). A more pronounced rise was observed from \(\:15\:\%\) to \(\:20\:\%\) and a significant leap at \(\:25\:\%\). Then the increasing rate slows down when raised to 27.04 %, and reaches a maximum value of 688. The fitting results to Eq. (2)a are given in Fig. 2b on a logarithmic scale. The percolation thresholds for the two frequencies are determined to be \(\:26.30\pm\:0.26\:\%\) and \(\:26.36\pm\:0.32\:\%\), which is very close to the result from \(\:\epsilon\:^{\prime}\). The critical exponents \(\:q\) are \(\:2.2611\pm\:0.1162\) and \(\:2.3066\pm\:0.1461\), which are also in the 2D range.

The complex permittivity is frequency dependent near the percolation threshold as predicted in Eq. 1 and verified in Fig. 1. Thus, the fitting result of both \(\:\epsilon\:^{\prime}\) and \(\:\epsilon\:^{\prime\prime}\) to the frequency range of 8.2 GHz ~ 12.4 GHz is exhibited in Fig. 3 with the 95% confidence boundary. The exponents for the volume fraction of \(\:25.01\:\%\) are \(\:0.5680\pm\:0.0181\) (real) and \(\:0.9084\pm\:0.0091\) (imaginary), and for \(\:27.04\:\%\) are \(\:0.5321\pm\:0.0216\) (real) and \(\:0.9843\pm\:0.0073\) (imaginary), which is highly consistent with Eqs. (1) and 2. The theoretical value of the real part’s frequency dependence critical exponent should be between 0 and 133. If we compare the real part of both volume fractions, they have very similar critical exponents, as do the imaginary part. Both results lie in this range. As for the imaginary part, both results are very close to 1, consistent with Ref36. This confirms again that we have reached the percolation threshold since the frequency dependence exponent does not depend on the volume fraction.

Fig. 1
figure 1

The measured permittivity (a) real part and (b) imaginary part, as well as the measured permeability (c) real part and (d) imaginary part versus frequency for various volume fraction of the silver-epoxy nano-composites from \(\:2.00\:\%\) to \(\:27.04\:\%\) with error bar. Those complex permittivity and permeability are extracted from the measured scattering parameters based on Eqs. (5) and (6).

Full size image
Fig. 2
figure 2

(a) The measured real and imaginary permittivity at 8.2 GHz (solid squares and diamonds) and 12.4 GHz (solid triangles) on a logarithmic scale. (b) The fitting result to the percolation theory in Eq. (1a) with a natural log taken to both sides, and the 95% confidence intervals applied.

Full size image

The frequency dependence originates from the accumulated charge carrier. For the real part, at low frequencies, charge carriers accumulate at insulating-conducting interfaces, leading to large polarization effects and high permittivity. On the other hand, these charges cannot follow the field oscillations at higher frequencies, and the effective permittivity decreases38. As for the imaginary part, the trend first decreases and then increases as the frequency increases (from kHz to GHz)38. However, the frequency range in this study is relatively small (8.2 ~ 12.4 GHz), so it only captures the high-frequency behavior. In such high frequency, capacitive effects dominate and decrease as \(\:\epsilon\:^{\prime\prime}\propto\:{\omega\:}^{-1}\). This corresponds to a shift toward dielectric relaxation, where energy dissipation is minimal36.

Fig. 3
figure 3

The measured (solid symbols) and fitting result (solid lines) base on Eq. (1b) and (2b) of the frequency dependence exponent for both the real and imaginary permittivity in \(\:25.01\:\%\) and \(\:27.04\:\%\) with 95% confidence intervals. (\(\:27.04\:\%\) \(\:\epsilon\:^{\prime\prime}\) is in purple diamonds, and \(\:\epsilon\:^{\prime\:}\) in green triangles.\(\:\:25.01\:\%\) \(\:\epsilon\:^{\prime\prime}\) is in blue squares, and \(\:\epsilon\:^{\prime\:}\) in red dots.).

Full size image

The negative magnetic susceptibility results are depicted in Fig. 4a. The difference between the two frequencies is small. At low volume fractions (\(\:<10\:\%\)), the relationship between \(\:-{\chi\:}_{b}\) and volume fraction is quite linear, as in Fig. 4b. Most particles remain isolated within this range, and the cluster size remains small, making the percolation effect less apparent. Instead, the scattering model (or the EMT) under the long-range approximation provides a more suitable explanation.

However, as the volume fraction surpasses \(\:15\:\%\), the impact of percolation becomes dominant. The negative magnetic susceptibility increases slowly from about 0.1 to around 0.2 when the volume fraction is raised from \(\:15\:\%\) to \(\:24\:\%\). Then, it undergoes a remarkable surge of about 0.5 at \(\:25\:\%\), reaching a peak of approximately 0.7 at \(\:27\:\%\).

The fitting curve of the low volume fraction range is given in Fig. 4c. It should follow the relation29,31

$$- \chi _{b} = - N\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {m} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H} _{{inc}} }} = C \cdot p$$
(7)

where \(\:N\) is the number density of the silver nanoparticle. The magnetic dipole to magnetic field relation is \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {m} \sim - 2S^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H} _{{inc}} /P\), where \(\:S\) is the area projected perpendicular to the field, and \(\:P\) is its perimeter.

The relation between the volume fraction and the number density is \(\:{p}_{c}=V\cdot\:N\), where \(\:V\) is the volume of the nanoparticle. For perfect spheres, \(\:C=2{S}^{2}/PV\) is 1.5. However, the measured slopes are \(\:1.2623\pm\:0.2434\)and \(\:1.1322\pm\:0.1104\) for the frequencies of 12.4 and 8.2 GHz, respectively. The obtained slopes suggest that the silver nanoparticles are not ideal spheres. The SEM (scanning electron microscope) image of the nanoparticle is given in the supplementary material (Fig. SM02). Most particles have a geometry close to a sphere, but some are not so rounded. The ellipsoid from the SEM has three axes of approximately 1:1:1.5. We can estimate two extreme scenarios: one is the circle, and the other is the ellipse. These two estimations give us 1 and 0.45; we can take a rough average of 0.7. Since about \(\:70\:\%\:\sim\:80\:\%\) of the particles are in circle with \(\:20\:\%\:\sim\:30\:\%\) in ellipsoid, we then have \(\:C\approx\:1.2600\sim1.3400\), which is slightly higher than the experimental result. This might be due to the fact that most “spheres” are slightly deformed, and as the estimation of an ellipsoid, the factor \(\:C\) would be slightly smaller. Although the model is acceptable for the present analysis, it warrants more rigorous theoretical investigation in future work.

Fig. 4
figure 4

(a) The measured result at 8.2 GHz (solid squares and diamonds) and 12.4 GHz (solid triangles) of the negative susceptibility and imaginary permeability. (b) The fitting result of negative susceptibility in the scattering region. (c) The fitting result of negative susceptibility and imaginary permeability in the percolation region. 95% confidence intervals are all applied to fitted results.

Full size image

For the volume fraction near the threshold case, the fitting results are depicted in Fig. 4c on a logarithmic scale by Eq. 3. The threshold is determined to be \(\:26.23\pm\:0.18\:\%\) and \(\:26.21\pm\:0.06\:\%\), closely aligning with the earlier obtained value. Moreover, the critical exponent \(\:u\) is calculated to be \(\:0.7086\pm\:0.0349\) and \(\:0.7310\pm\:0.0117\), almost twice the value of the 3D theoretical one. However, the theoretical value in 2D is about 0.7729,39, closer to the result. The observed permeability’s power law behavior in this study exhibits strong consistency with the predictions from Bowman and Stroud29.

Figure 4a displays the measured \(\:{\mu\:}^{\prime\prime}\) for two representative frequencies 12.4 and 8.2 GHz. It grew slowly and linearly when the volume fraction was increased from \(\:2\:\%\) to \(\:10\:\%\). Then, the rate of growth paced down between \(\:15\:\%\) and \(\:24\:\%\). As the volume fraction was further increased, the rate of increment surged swiftly to a maximum of 0.22 at \(\:p\:=\:25.01\:\%\) and dropped to around 0.02 when the threshold was exceeded. The fitting result based on Eq. 4 is given in Fig. 4c on a logarithmic scale. The result follows the power law. The threshold is determined to be \(\:26.98\pm\:0.20\:\%\) and\(\:26.17\pm\:0.37\:\%\), which slightly differs from the prior result, but is still in a reasonable region. The critical exponent \(\:v\) is \(\:0.8184\pm\:0.0057\) and \(\:0.7671\pm\:0.0131\), which is highly similar to \(\:u\) in 2D29,39.

All fitted critical exponents (\(\:s\), \(\:q\), \(\:u\), \(\:v\)) are consistent with 2D theoretical value. This might be due to the finite-size crossover effect. Near the percolation threshold, the correlation length \(\:\xi\:\) diverges as \(\:\xi\:\propto\:{\left|p-{p}_{c}\right|}^{-v}\). When \(\:\xi\:\) exceeds the smallest sample dimension (thickness in this study), connectivity along that axis saturates and the system crosses over to an effective 2D universality class32. With \(\:\nu\:\approx\:0.88\) the condition \(\:\xi\:\:>\:T\) is reached for \(\:|p-{p}_{c}|\:\lesssim\:\:0.002\) — well inside the 22 ~ 27 volume fraction window that we fit — so the measured scaling is expected to be 2D.

If we neglect the permeability’s contribution, the result deviates, which is given in supplementary material (Fig. SM03). The real part is still fine, but a problem arises in the imaginary part: frequency dependence only appears near the threshold, and the value should be the highest near the threshold. Nevertheless, the \(\:27.04\:\%\) and \(\:25.01\:\%\) samples intersect with other samples of smaller volume fractions. This implies a frequency-dependent percolation threshold, which has not been reported so far.

The complex permittivity of \(\:{\mu\:}^{{\prime\:}}=1\) to \(\:{\mu\:}^{{\prime\:}}\ne\:1\) was compared, which is illustrated in the supplementary material (Figs. SM04 (a) and (b)). The percolation phenomenon is less obvious, especially in the imaginary part. Also, both \(\:\epsilon\:^{\prime\:}\) and \(\:\epsilon\:^{\prime\prime}\) are smaller than the case \(\:{\mu\:}^{{\prime\:}}\ne\:1\). Finally, we can compare the loss tangent. The loss tangent should also surge near the threshold. The loss tangent is displayed in the supplementary material (Fig. SM04 (c)). Loss tangent surges when we count the permeability’s contribution. Our experimental result suggests that permeability can vary in percolative metal-insulator composites near the percolation threshold. When dealing with a metal-insulator composite system, the effect due to permeability should be taken into account.

Based on percolation theory, we conclude that (a) when the volume fraction approaches the percolation threshold, the permittivity increases while the permeability drops, as predicted. (b) EMT fails near the percolation threshold. (c) In this case, \(\:{\mu\:}^{{\prime\:}}\ne\:1\) near the percolation threshold. For permittivity- and permeability-related quantities, such as \(\:n(\epsilon\:,\:\mu\:)\), it will be necessary to include both \(\:\epsilon\:\) and \(\:\mu\:\) near the percolation threshold. Otherwise, the calculated \(\:n(\epsilon\:,\:\mu\:)\) could deviate.

The percolation theory characterizes composite materials’ behavior near their percolation threshold. All EM properties are power law dependencies. Below the threshold, the composite is in the insulator (dielectric) phase, but there’s a phase transition around the threshold that leads to the conduction phase. While there has been extensive research on the transition from insulator to conductor, percolation theory for permeability hasn’t received as much attention. In detail, the identified percolation threshold is approximately \(\:26.17\:\%\:\sim\:26.98\:\%\), which is relatively high40,41. An EDS (energy dispersive X-ray spectroscopy) mapping of the 25.01% sample is given in three different scales in the supplementary material (Fig. SM05). The mapping coverage is consistent with the volume fraction. The fitted critical exponents indicate that our system is closer to 2D than 3D, which could be attributed to the cross-section-to-thickness ratio32,33.

We also run a simple simulation to check the threshold and the critical exponent \(\:s\), where the model is based on Ref42. (simulation detail is given in caption of Fig. SM06). There is no good model for direct simulation of permittivity, but there’s an alternative. That is by simulating the system of two conductors with the conductivities of relation: \(\:{\sigma\:}_{1}/{\sigma\:}_{2}\ll\:1\). In this case, the total conductivity of the system at the sub-threshold region is \(\:\sigma\:\propto\:{\left|p-{p}_{c}\right|}^{-s}\), which is the same as the real permittivity32,33. The lattice site is set to be 200 × 100 × 20, which is approximately the same geometry as our samples (22.86 mm × 10.16 mm × 2.00 mm). The size chosen is based on accuracy and computation efficiency. The result is given in the supplementary material (Fig. SM06). The simulation was performed 100 times, and the average and the standard deviation is recorded. The result reveals that the percolation threshold is about \(\:26.65\pm\:0.24\:\%\), and the critical exponent is \(\:s=1.1699\pm\:0.0221\), which is consistent with the experimental result. Another system of 74 × 74 × 73 is also performed as a comparison. This size is chosen to be approximately the same lattice sites as 200 × 100 × 20. The percolation threshold is about \(\:20.64\pm\:0.18\:\%\), and the critical exponent is \(\:s=0.8399\pm\:0.0127\). This is consistence with the previous 3D square lattice site percolation problem32,33.

To rule out artefacts. We measured two baseline specimens under identical calibration for an empty waveguide (air) and a coupon of pure epoxy. As shown in the supplementary materials (Fig. SM.07), both controls yield \(\:{\mu\:}^{\prime\:}\approx\:1.00\pm\:0.02\) across 8.2 ~ 12.4 GHz, while the epoxy’s \(\:{{\epsilon\:}}^{{\prime\:}}\approx\:3.1\) and air’s \(\:{\epsilon\:}^{\prime\:}\approx\:1.0\) matches its textbook value. The absence of any negative magnetic susceptibility signature in these reference samples confirms that the pronounced diamagnetism observed in the Ag/Epoxy nanocomposites arises from the percolative network rather than from the measurement setup or background materials (e.g., Copper waveguide).

Conclusion

Our study delivers the first GHz-band experimental proof that a metal–polymer composite can exhibit simultaneous \(\:(\epsilon\:^{\prime\:}\:\gg\:\:1\), \(\:\mu\:^{\prime\:}\:<\:1\)) governed by percolation scaling, and align closely with Bowman and Stroud’s predictions, particularly regarding the power-law behavior of \(\:-{\chi\:}_{b}\), as expressed in Eq. 3. Crucially, the results presented here hold validity across a broad bandwidth (8.2 ~ 12.4 GHz). Although the models have been reported for decades, they have not been widely applied in composite research (judging from the number of citations). Prior studies largely emphasized ε, with fewer quantitative joint\(\:\:{\epsilon\:}-{\mu\:}\) extractions, and simply ignored the magnetic effect. Our study provides solid experimental evidence and validates the predictions on complex permittivity and complex permeability. We anticipate that this work can draw attention to a non-unity permeability in conductor-insulator composites.

Percolative composites, like the one introduced in this study, provide an approach to achieving high-k or low-permeability materials by mixing metal and dielectric components, eliminating the need for complex structural design. This simplicity makes them good candidates for Resistive Random-Access Memory (RRAM) applications, and neuromorphic devices42,43,44. However, a key limitation arises near the percolation threshold, where significant variations in properties (as the simulation result given in Fig. SM06) can lead to low yield and inconsistencies between devices, posing challenges for large-scale manufacturing.