RF model and SNA analysis for optimization of regional financial supervision system

Abstract

As regional financial risks continue to evolve and increasingly intertwine, traditional regulatory frameworks face challenges in timely and accurate risk identification. To address this, the study proposes an optimized regulatory approach that integrates social network analysis (SNA) with a random forest (RF) model. This approach enhances regional financial risk monitoring and early warning capabilities by leveraging network structure indicators and machine learning predictions. Financial data from a certain province between 2016 and 2022 are used to construct an undirected weighted network. Empirical results show that network density increases while node degree centrality decreases, suggesting more balanced risk propagation. However, high-risk areas exhibit significant nonlinear amplification effects. The RF model incorporating SNA features performs exceptionally well in six-level risk classification. It achieves F1 scores between 0.941 and 0.985 and an area under the curve (AUC) of 0.975, significantly outperforming baseline models such as support vector machines and logistic regression. Feature importance analysis reveals that weighted node strength and network density contribute approximately 60%, highlighting the central role of network topology in risk prediction. Based on these findings, the study proposes a differentiated regulatory strategy guided by centrality and clustering indicators. This strategy aims to promote smarter and more precise regional financial supervision.

Introduction

With the rapid globalization and growing informatization of financial markets, their complexity and uncertainty have significantly increased, presenting unprecedented challenges to traditional financial regulatory systems¹. The diversification of financial products and market participants—coupled with the hidden and transmissible nature of financial risks—makes it difficult for regulators to fully and promptly grasp market dynamics. This lack of timely insight threatens financial stability and hampers sustainable market development^2,3. In response, there is an urgent need to establish a more scientific, adaptable, and efficient financial supervision framework.

Social Network Analysis (SNA) offers a powerful means of uncovering the interrelationships among financial market entities and identifying latent structural patterns. By quantifying and visualizing these relationships, SNA provides regulators with novel perspectives and analytical tools to better understand market behaviors and risk transmission mechanisms^4,5. For instance, SNA can help detect key nodes and influential participants, enabling timely regulatory intervention when risks emerge. Meanwhile, advancements in artificial intelligence (AI) and big data have made machine learning (ML) models—particularly the Random Forest (RF) algorithm—highly effective in financial risk prediction and quantitative analysis^6,7. By aggregating multiple decision trees, RF can handle high-dimensional data, mitigate overfitting, and deliver robust and accurate predictions^8,9. These strengths make RF a valuable tool for financial risk management, offering reliable decision support in complex market environments.

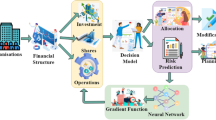
Building on these developments, this study proposes a novel approach to regional financial supervision by integrating SNA with the RF model. This combined methodology enhances the understanding of complex interactions and potential risk factors within financial networks, thereby improving the scientific rigor and effectiveness of regulatory practices. The integration offers regulatory agencies more accurate risk assessment capabilities and supports the formulation of targeted, data-driven policies—ultimately promoting the stability and healthy development of regional financial markets.

Research objectives

This study pursues the following objectives: First, it systematically introduces the fundamental principles and methodologies of SNA and the RF model, providing a robust theoretical basis for subsequent analysis. Second, it explores the application of these methods in the context of financial supervision, emphasizing their respective strengths and complementarities in identifying and forecasting financial risks. Third, it conducts empirical analysis to evaluate the effectiveness of the integrated SNA-RF model in enhancing regional financial supervision, and offers corresponding policy recommendations. Overall, the study aims to contribute both theoretical insights and practical guidance for the development of a more scientific, adaptive, and intelligent financial regulatory system. Specifically, the findings are expected to improve regulatory agencies’ responsiveness to financial market fluctuations, strengthen their risk management capabilities, and support the sustainable development of regional financial markets.

Innovation highlights

This study offers several key innovations: (1) Interdisciplinary Methodological Integration: By combining SNA with the RF model, the study constructs a novel framework for optimizing regional financial supervision. This cross-disciplinary approach expands the methodological toolkit for financial risk management and introduces a more holistic and data-driven perspective to financial oversight. (2) Multi-Dimensional Network Feature Analysis: Utilizing SNA techniques, the study systematically examines regional financial risks through various network metrics—including correlation degree, network density, hierarchical structure, and node centrality. This comprehensive analysis uncovers the spatial and structural characteristics of financial risk transmission, offering new insights that go beyond the traditional scope of financial supervision. (3) Dynamic and Granular Risk Prediction: The integration of the RF model enables precise multi-class classification of risk levels. Empirical results demonstrate the model’s strong performance across key metrics—accuracy, precision, and recall—especially in identifying high-risk and cautionary states, where early detection is critical. This enhances the model’s utility as a decision-support tool for regulators. (4) Robust and Representative Empirical Data: The study leverages extensive financial and economic data from Province A spanning 2016 to 2023. This broad temporal and contextual coverage ensures the empirical analysis is both realistic and generalizable. The data effectively capture the evolution and structural dynamics of regional financial risk networks, strengthening the study’s relevance and applicability.

Literature review

In recent years, the rapid advancement of financial technology and the increasing complexity of financial networks have prompted researchers to integrate SNA with ML techniques to enhance the identification and management of financial risks. Giudici (2024) emphasized the critical role of statistical methods in assessing the risks of AI systems, particularly in high-risk domains where the development of secure ML evaluation frameworks is urgently needed¹⁰. In a related study, Giudici et al. (2020) proposed a network-based credit risk model designed to improve credit risk assessment for peer-to-peer (P2P) lending platforms, especially those serving small and medium-sized enterprises (SMEs). By incorporating centrality measures derived from borrower similarity networks as “alternative data,” they demonstrated improvements in both prediction accuracy and model interpretability. This approach introduced a novel application of network analysis to financial risk evaluation¹. Ahelegbey et al. (2023) assessed a ML model deployed on a fintech platform from the perspective of sustainable finance. The model learns corporate credit ratings by incorporating both microeconomic indicators and macroeconomic trends. Their findings showed that the model more accurately rewarded firms with strong financial performance through higher credit ratings, thereby increasing their access to credit and reducing borrowing costs. Furthermore, the model demonstrated adaptability to changing macroeconomic conditions, contributing to greater financial inclusion, particularly during economic downturns¹¹. Chen et al. (2022) explored the influence of network centrality on borrower and lender behavior within P2P lending platforms. An empirical study conducted on a major Chinese lending platform revealed that lenders occupying central positions in the network tended to invest more substantial amounts and responded more quickly. Similarly, central borrowers were more likely to obtain loans at lower interest rates, with higher approval rates and reduced default probabilities. These findings underscore the importance of network centrality in online lending and offer new insights into financial risk management and participant behavior in digital financial ecosystems¹². Bal and Mishra (2025) proposed that sentiment indices based on political and policy factors could effectively identify abnormal returns within thematic stock networks. This suggested that sentiment variables had forward-looking value in networked financial market analysis¹³. Liu (2025) showed that network-based methods captured the structural characteristics of markets and could be extended to model contagion effects and predict volatility. These methods provided new analytical tools for macroprudential regulation¹⁴. Khan et al. (2025) demonstrated that credit risk networks on P2P lending platforms had significant predictive value. They revealed risk transmission paths among platforms and offered empirical evidence for Internet financial risk supervision¹⁵.

Overall, existing studies have mainly focused on three areas: incorporating sentiment indices into stock networks, using network approaches to predict market volatility, and identifying P2P lending risks through credit risk networks. These works provide a solid foundation for financial network analysis but are largely confined to specific markets or instruments. In contrast, this study integrates SNA with ML models, combining network topology features with regional financial risk supervision. This approach enhances predictive accuracy and interpretability at the methodological level, while also providing actionable regulatory recommendations at the policy level. By bridging the gap from indicators to strategies, it extends both the depth and the scope of financial network research.

Research methodology

This study combines SNA with the RF model to improve regional financial supervision through two complementary dimensions: structural risk identification and risk prediction. SNA is used to map the structure of risk exposures among financial institutions and to extract meaningful network metrics—such as node strength, weighted betweenness centrality, and clustering coefficient. These metrics serve as input features for the RF model, which constructs a nonlinear predictive framework to forecast regional financial risk levels. By integrating the interpretability of network structure with the flexibility of ML, this approach enables more precise identification of critical nodes and supports targeted regulatory interventions.

SNA

As a complementary approach, SNA effectively overcomes limitations of traditional financial risk assessment methods¹⁶. From the SNA perspective, individuals, organizations, or countries are viewed not as isolated entities but as interconnected nodes within a broader network¹⁷. The central tenet of SNA is to focus on relational data, emphasizing the connections between entities rather than the entities themselves as the primary units of analysis^18,19. This perspective highlights that a node’s position within the network, the overall network structure, and the social context of relationships exert greater influence on individual behavior than the node’s intrinsic attributes²⁰. Figure 1 illustrates key SNA network features and their applications in financial risk assessment.

Fig. 1

Network features of SNA and their application in financial risk assessment.

Figure 1 presents the key network metrics used in SNA, including network density, correlation degree, hierarchy degree, and node centrality. These metrics quantify the interactions among financial institutions and help identify critical nodes and pathways of risk transmission^21,22,23,24. Specifically, network density measures how closely nodes are connected overall. Correlation degree reflects the number of nodes that are directly linked. Hierarchy degree captures the extent of asymmetry in how nodes can reach one another. Node centrality evaluates the importance of each node within the network^25,26. As a global indicator, network density assesses the compactness of the regional financial risk network, while node centrality metrics—such as degree centrality and betweenness centrality—highlight the significance of specific financial institutions. Together, these metrics complement each other: network density offers regulators insight into systemic risk at the macro level, whereas node centrality informs targeted supervision of individual entities.

Unlike traditional spatial econometric models, this study employs an SNA framework to calculate network density, correlation degree, and hierarchy degree, aiming to capture the spatial structural characteristics of regional financial risks. This approach is justified by three main considerations: First, it adapts to irregular spatial topologies. Traditional models like the Conditional Autoregressive Model (CAR) and Spatial Lag Model (SLM) typically rely on assumptions of geographic contiguity or predefined adjacency among spatial units. However, financial risk linkages among regional institutions often transcend geographic boundaries, exhibiting cross-regional, cross-sectoral, and asymmetric network features that fixed spatial matrices cannot accurately represent. The SNA framework allows for the construction of dynamic and heterogeneous spatial relationships that more realistically reflect actual risk transmission paths. Second, it is well-suited for extracting structural indicators. Metrics such as network density, correlation degree, and hierarchy degree effectively describe the extent, connectivity, and vulnerability of systemic risk within the network. Unlike spatial error or lag coefficients used in traditional spatial models, these SNA metrics provide richer structural insights and facilitate intuitive visualization. Third, the method offers extensibility to spatial network modeling. The approach aligns conceptually with the recently developed Hierarchical Spatial Network Model (HSNM), applied in domains such as public safety and transportation. For example, Clemente et al. (2024) introduced a multilayer network model for road accident risk assessment, which integrated hierarchical network structures with spatial dependencies and enabled the joint modeling of topological and spatial dimensions²⁷. This provides methodological support for applying similar frameworks in financial risk analysis.

Because the networks in this study are constructed from actual financial transactions and exposure relationships, the edge weights between nodes naturally represent the strength of risk linkages. Consequently, SNA-based spatial network analysis offers a flexible and intuitive means to characterize the asymmetric propagation of regional financial risks. Moreover, this approach facilitates effective feature embedding when integrated with ML models such as RF. Future research may further extend this framework by incorporating multilayer heterogeneous networks and embedded spatial weight matrices to enhance spatial generalization and hierarchical interpretability.

In the financial sector, the significance of financial institutions extends beyond their size, complexity, and interconnectivity to include their central positions within the financial network²⁸. Operational difficulties or market volatility affecting a single institution can trigger widespread consequences throughout the financial system and the real economy²⁹. With the rapid expansion of internet finance, financial institutions increasingly operate across regions, markets, and business models. This growth amplifies both the regional and systemic influence of individual institutions and intensifies their interdependence^30,31,32. However, increased connectivity also heightens the vulnerability of the financial network. The collapse of certain P2P platforms and failures of institutions such as Baoshang Bank and Jinzhou Bank have highlighted the spillover and contagion effects inherent in financial risks³³. Moreover, the growing homogeneity and globalization of the financial system further exacerbate risk transmission. To effectively assess regional financial risks, SNA requires a set of quantifiable indicators to characterize these risk conditions.

This study constructs an undirected weighted network $G=(V,E,W)$, where the node set V represents financial institutions, with $n=\left|V\right|$ denoting the total number of nodes. An edge ${e}_{ij}\in E$ exists if a risk-related connection is present between institutions ${v}_{i}$ and ${v}_{j}$. Since the network is undirected, ${e}_{ij}={e}_{ji}$. The weight function W assigns weights ${w}_{ij}={w}_{ji}$, which are symmetric measures based on transaction volumes or risk exposures between institutions (for example, the average bilateral transaction amount). The spatial correlation characteristics of regional financial risks are captured by calculating metrics such as network density, degree of association, and hierarchy level^34,35.

This study models the risk relationships among regional financial institutions using an undirected weighted network, based on two primary considerations. (1) Data limitations: The bilateral transaction data provided by Province A’s financial regulatory authority do not include directional information on risk contagion. The dataset consists of quarterly aggregated bidirectional transaction volumes and volatility metrics. In the absence of explicit causal direction, constructing a directed network would require assumptions that could introduce bias. Thus, a symmetrized undirected network offers a more accurate and conservative representation of inter-institutional risk exposure, consistent with the inherent properties of the data. (2) Research objective alignment: The study’s main objective is to identify structural vulnerabilities and key nodes in the regional financial system, rather than to map precise micro-level contagion pathways. From a macroprudential regulatory standpoint, the existence of risk linkages—regardless of direction—provides valuable insights into systemic risk. An undirected network is therefore more suitable for capturing overall connectivity and assessing system stability. While this approach involves a degree of simplification, it remains analytically robust within the scope of the study and given the data constraints, without compromising the identification of critical nodes, assessment of network resilience, or the predictive performance of the integrated model.

In SNA, a maximal clique is a complete subgraph that cannot be expanded further, meaning every pair of nodes within the clique is directly connected^36,37. In financial networks, maximal cliques represent groups of institutions with tightly bound risks, such as closely interconnected banks, trusts, and corporations. Identifying these cliques can reveal potential risk transmission clusters and provide more targeted entry points for mitigating systemic risk. A common approach is the maximal clique search using the Bron–Kerbosch algorithm, which efficiently enumerates all maximal clique structures in a network.

RF model

The RF algorithm is an ensemble learning method based on decision trees, used for classification or regression tasks. Unlike traditional single decision trees, RF introduces randomness during training by selecting random subsets of features when determining split points^38,39. This process increases model diversity and robustness, enhancing its ability to generalize, particularly when dealing with noisy or high-dimensional data. Each decision tree in the RF model is built independently, and the final prediction is made through majority voting across all trees. For a model with nnn decision trees, each sample receives nnn predictions, and the category with the most votes is selected as the outcome. This voting mechanism improves the model’s accuracy and reliability. In financial risk prediction, RF effectively uncovers complex patterns and relationships within data, offering decision-makers more precise insights.

Figure 2 depicts the prediction process of the RF model. Each input sample is evaluated by all decision trees in the ensemble, with each tree independently producing a classification result based on the training data. The final prediction is determined by tallying these results and selecting the class with the most votes. This workflow illustrates how the RF integrates multiple tree predictions to improve overall accuracy and reliability.

Fig. 2

Detailed workflow of RF decision-making.

SNA-RF feature integration framework

To clarify the application of SNA indicators within the RF model, this study constructs a systematic feature integration framework, as detailed in Table 1.

Table 1 Systematic feature integration framework.

To enhance the reproducibility and verifiability of the model, this section provides a mathematical characterization of the proposed Social Network Analysis–Random Forest (SNA-RF) hybrid model. By formally defining network metrics, feature standardization methods, the Random Forest objective function, and interpretability mechanisms, the theoretical completeness and engineering reproducibility of the model can be ensured. To characterize the overall connectedness and hierarchical differences within the financial system, the following global network metrics are introduced:

$$D=\frac{\sum_{i\ne j} {\mathbb{I}}({w}_{ij}>0)}{|V|(|V|-1)}$$

(1)

$$H=\frac{\sum_{i} \sum_{j} |{s}_{i}-{s}_{j}|}{2|V|\sum_{i} {s}_{i}}$$

(2)

$${s}_{i}=\sum_{j} {w}_{ij}$$

(3)

D represents the systemic connection strength, capturing the overall penetration ability of risk within the system. H reflects structural inequality, measuring the concentration of risk across different institutions. ${s}_{i}$ and ${s}_{j}$ denote the strengths of nodes i and j, ${w}_{ij}$ is the weight matrix, and V is the set of institutions. By combining D and H, the model can capture system-level risk propagation structures. Beyond global structure, node-level metrics reveal the risk roles of individual institutions in the network. Three types of weighted node metrics are defined:

$${C}_{i}^{(deg)}=\sum_{j} {w}_{ij}$$

(4)

$${C}_{i}^{(bet)}=\sum_{s\ne i\ne t} \frac{{\sigma }_{st}(i)}{{\sigma }_{st}}$$

(5)

$${C}_{i}^{(clu)}=\frac{1}{{s}_{i}({k}_{i}-1)}\sum_{j,k} \frac{{w}_{ij}+{w}_{ik}}{2}{a}_{ij}{a}_{ik}{a}_{jk}$$

(6)

${C}_{i}^{(deg)}$ is the weighted degree centrality, representing an institution’s overall risk exposure; ${C}_{i}^{(bet)}$ is the weighted betweenness centrality, measuring its hub role in risk propagation paths; and ${C}_{i}^{(clu)}$ is the weighted clustering coefficient, used to identify local risk concentration. Here, ${a}_{ij}$ is the aggregated weight, ${k}_{i}$ is the number of neighboring nodes, ${\sigma }_{st}(i)$ is the number of shortest paths between nodes sss and ttt that pass through iii, and ${\sigma }_{st}$ is the total number of shortest paths between s and t. ${a}_{ik}{a}_{jk}$ correspond to the degrees of different nodes. To ensure comparability across metrics of different scales and maintain stable model training, all raw features are standardized using the following preprocessing operator:

$${\widetilde{x}}_{i,m}={\mathcal{T}}_{m}({x}_{i,m})=\left\{\begin{array}{c}\frac{{x}_{i,m}-{\mu }_{m}}{{\sigma }_{m}},\\ log({x}_{i,m}+\epsilon ),\\ \\ \frac{{x}_{i,m}-min({x}_{\cdot ,m})}{max({x}_{\cdot ,m})-min({x}_{\cdot ,m})},\end{array}\right.$$

(7)

${\mathcal{T}}_{m}$ denotes the transformation operator, ${\mu }_{m}$ and ${\sigma }_{m}$ are the mean and standard deviation, $\upepsilon$ is a small constant to avoid logarithm-of-zero issues, and ${\widetilde{x}}_{i,m}$ represents the multidimensional features. After normalization, the fused feature vector is obtained. Based on the fused feature vector, the SNA-RF model’s optimization objective can be formalized as:

$$\underset{\Theta }{min} {\mathbb{E}}_{(\text{z},y)}\left[{\ell}(y,\widehat{P}(y|\text{z}))\right]+{\lambda }_{1}{\Omega }_{\text{stab}}(\Theta )+{\lambda }_{2}{\mathbb{E}}_{\parallel \delta \parallel \le \varepsilon }\left[{\ell}(y,\widehat{P}(y|\text{z}+\delta ))\right]$$

(8)

$\Theta$ is the set of model parameters, ${\ell}$ is the cross-entropy loss function, ${\Omega }_{\text{stab}}$ controls model stability, $\delta$ represents adversarial perturbations, ${\lambda }_{1}$ and ${\lambda }_{2}$ are regularization coefficients, y is the true label, z is the feature vector, $\widehat{P}$ is the model’s predicted conditional probability of the label, and ${\mathbb{E}}$ denotes the expectation. This formulation ensures that the model maintains robust predictive performance when faced with heterogeneous samples and noisy data.

This study rigorously follows the secure ML framework proposed by Giudici, ensuring regulatory compliance through three key aspects: Interpretability: SHapley Additive exPlanations (SHAP) values are employed to quantify the contribution of SNA features, generating feature attribution reports that comply with the Guidelines on AI Applications in Financial Institutions. Robustness: Network robustness testing protocols are implemented, maintaining Area Under the Curve (AUC) fluctuations within 0.03, alongside adversarial training that sustains accuracy above 92% in noisy environments. Security: A dual-threshold early warning system is deployed, triggering manual review when confidence falls below 85% or contradiction exceeds 0.3. Additionally, a dynamic monitoring system based on the framework by Ahelegbey et al. is established. Together, these measures enable the model to achieve technical effectiveness (F1-score between 0.92 and 0.98), regulatory compliance (aligned with Basel III standards), and policy operability (seamless integration with existing regulatory indicators).

Experimental design and performance evaluation

Datasets collection

The data used in this study were sourced from three authoritative platforms via official data interfaces: (1) Financial indicators were obtained from the People’s Bank of China’s Comprehensive Statistical System (quarterly data from 2016 to 2023), covering 12 variables including the non-performing loan (NPL) ratio and capital adequacy ratio (Data ID: PFMIS-2023-XXX). (2) Economic indicators were derived from the National Bureau of Statistics’ macroeconomic database, encompassing eight categories such as regional GDP and industrial profits. These figures were cross-validated with provincial-level statistical yearbooks. (3) Institutional linkage data were acquired from the transaction monitoring system of Province A’s financial regulatory bureau, comprising quarterly bilateral transaction records among 367 financial institutions. All data were anonymized prior to analysis. Province A was selected as the focal region for this study for the following reasons: (1) Data availability—The financial regulatory authority in Province A provided relatively complete time-series bilateral transaction data with rich structural detail. (2) Regional representativeness—As an economically dynamic province with a complex financial structure, Province A serves as a representative case for studying regional financial risk. Although the current empirical analysis is based on data from a single province, the proposed model architecture is designed to be transferable. In future research, the framework will be extended to additional regions such as Provinces B and C to evaluate its adaptability and generalizability.

The dependent variable in this study is the regional financial risk status, classified into six levels: Safe, Relatively Safe, Watch, Caution, Alert, and High Risk. The independent variables are grouped into three categories: (1) SNA features, including network density and node centrality; (2) Traditional financial indicators, such as the NPL ratio and capital adequacy ratio; (3) Macroeconomic indicators, including GDP growth rate and household income. The classification criteria for regional financial risk status are presented in Table 2.

Table 2 Regional financial risk classification criteria.

The risk level thresholds were established through a multi-stage comprehensive process. Initially, the study referenced the People’s Bank of China’s Regional Financial Risk Monitoring Guidelines, using core indicator standards—such as the non-performing loan ratio and capital adequacy ratio—to develop a preliminary classification framework. Subsequently, the Delphi method was applied, conducting three rounds of anonymous expert evaluations from September 2023 to January 2024. Eight specialists in financial risk and supervision from academia, regulatory bodies, and industry participated. The panel comprised two financial stability department heads from the People’s Bank of China’s Province A branch, two mid-level supervisors from the provincial Banking and Insurance Regulatory Commission, two deputy general managers with expertise in financial risk modeling at commercial banks, and two senior professors of financial engineering/mathematical finance with practical experience in regional financial risk. Experts rated threshold reasonableness using a five-point Likert scale. Based on their feedback, the network density percentile cutoff was revised in the second round from the 50th percentile upper bound to the 40th percentile to better distinguish between basically safe and alert states. Final thresholds were determined by a weighted average of expert scores, calibrated with a 95% confidence lower bound. To reduce classification instability caused by boundary noise during model training, a ± 0.5% buffer zone was incorporated.

The dataset was divided into a training set (2016–2021) and a testing set (2022–2023) using stratified sampling in a 7:3 ratio to maintain the proportional distribution of risk categories across both subsets. Data quality assessments were automated using Python’s data-profiler package. For institutional linkage data, the following validation steps were implemented: (1) Weight verification: Bilateral transaction discrepancies exceeding 10% triggered a manual review. (2) Network connectivity validation: Ensured that the largest connected subgraph encompassed at least 99% of all nodes. A comprehensive data preprocessing pipeline was developed to ensure analytical robustness. Key components included: Completeness: Missing values were imputed using the Expectation–Maximization (EM) algorithm. Consistency: Cross-validation was conducted across multiple data sources. Outlier handling: Extreme values were Winsorized at the 1st percentile. For network construction, bilateral transaction values were symmetrized and adjusted with a time-decay coefficient to generate edge weights. Nodes with no recorded transactions for three consecutive quarters were excluded as inactive. In feature engineering: Numerical features were standardized using Z-score normalization. Categorical features were encoded using Target Encoding to mitigate the curse of dimensionality. To address class imbalance, the Synthetic Minority Over-sampling Technique for Nominal and Continuous features (SMOT-NC) algorithm was applied—oversampling high-risk categories while randomly undersampling the safe category to improve classification performance.

Experimental environment, and parameters setting

Table 3 presents the experimental environment configuration.

Table 3 Experimental environment.

Table 4 presents the RF model parameter settings.

Table 4 RF model parameter settings.

To avoid performance underestimation due to default parameters, a systematic hyperparameter tuning procedure was applied to all baseline models. First, during data preprocessing, all features were normalized using Min–Max scaling. Class imbalance was addressed, where applicable, by enabling class_weight = balanced. A fixed random seed (random_state = 42) was set to ensure reproducibility. For validation, a stratified five-fold outer cross-validation assessed the models’ generalization performance. Hyperparameter optimization was conducted in an inner stratified three-fold grid search, with the macro-averaged F1 score as the primary metric and AUC One-vs-Rest (AUC-OVR) as a reference. For models requiring probability outputs, probability estimation was enabled to facilitate AUC and ranking metric calculations. For logistic regression (LR), the multinomial setting was used. The hyperparameter search included penalty ∈ {l2}, solver ∈ {lbfgs, saga}, and C ∈ {0.1, 0.5, 1, 2, 5}, with the optimal configuration being penalty = l2, solver = lbfgs, and C = 1. Support vector machines (SVM) were tested with both linear and RBF kernels; the RBF kernel generally performed better. Its search space included C ∈ {0.1, 1, 3, 10} and gamma ∈ {scale, 0.1, 0.3}, with the optimal parameters being C = 3, gamma = scale, and probability = True. For gradient boosting decision trees (GBDT), the search space consisted of n_estimators ∈ {100, 200, 400}, learning_rate ∈ {0.05, 0.1, 0.2}, max_depth ∈ {2, 3, 4}, and subsample ∈ {0.7, 0.8, 1.0}. Early stopping was applied using validation_fraction = 0.1 and n_iter_no_change = 10 to prevent overfitting. The optimal configuration selected was n_estimators = 200, learning_rate = 0.1, max_depth = 3, and subsample = 0.8.

Model performance evaluation is conducted using metrics such as accuracy, recall, precision, true negative rate (TNR), and F1 score.

Performance evaluation

Analysis of overall network characteristics of regional financial risk in province A

The dynamic evolution of the overall network characteristics of regional financial risks in Province A is illustrated in Fig. 3.

Fig. 3

Dynamic analysis of the overall network characteristics of regional financial risks in province A.

In Fig. 4, network density is treated as a macrostructural indicator calculated at the full-network level. For node centrality metrics, arithmetic averages of financial institutions within each region were used to represent the region’s overall level of risk concentration. This approach facilitates horizontal comparisons across geographic units and helps identify spatial heterogeneity in systemic vulnerability. Figure 4 illustrates trends in network density, number of associations, connectivity, and hierarchy within Province A’s regional financial risk network from 2016 to 2023. Network density rose steadily from 0.24 in 2016 to 0.282 in 2023, indicating increasingly dense interconnections and tighter risk linkages. The number of associations increased from 66 to 82 over the same period, suggesting greater structural complexity and robustness. The connectivity metric remained consistently at 1, indicating that the network remained fully connected—allowing financial risks to be transmitted throughout the entire system. Meanwhile, the hierarchy metric declined from 0.55 to 0.47, reflecting a reduction in the proportion of peripheral or subordinate nodes and a move toward a more balanced network structure. These changes highlight the dynamic evolution of risk propagation paths and the shifting roles of key institutions—offering valuable guidance for targeted regulatory interventions. Table 5 presents the results of the Granger causality tests between key network metrics and major policy events.

Fig. 4

Classification performance OF the RF model across six risk categories.

Table 5 Granger causality test results between policy events and network indicators.

Through a detailed analysis of the evolution of Province A’s financial risk network from 2016 to 2023, this study identifies significant causal relationships between regulatory interventions and changes in network structure. The introduction of the 2018 Asset Management Rules led to a notable increase in network density (+ 0.041, p < 0.01), indicating a denser and more interconnected risk network. The 2020 Risk-Sharing Mechanism contributed to a reduction in hierarchy (− 0.08, p < 0.01), resulting in a flatter, less stratified network structure. Meanwhile, the 2021 Resilience Guidelines mandated multi-path connectivity, adding 16 low-weight associations while maintaining full network reachability. These results demonstrate that prudent regulatory policies can significantly reshape the topology of financial risk networks. The findings provide empirical support for the development of an integrated “policy–network–risk” control framework that aligns structural monitoring with regulatory design.

To further validate the robustness and generalizability of the model, this study conducted comparative experiments using financial data from Province B in the eastern coastal region and Province C in the central-western region, in addition to Province A (2016–2022). Data for all three provinces were sourced from central bank branch statistics, regulatory reports from the China Banking and Insurance Regulatory Commission, and provincial statistical yearbooks. The same preprocessing procedures—edge weight normalization, risk labeling, and time series smoothing—were applied to ensure comparability. The experimental results are summarized in Table 6.

Table 6 Comparison of network indicators across three provinces.

As shown in Table 6, network density increased in all three provinces, from 0.24 to 0.282 in Province A, 0.27 to 0.31 in Province B, and 0.19 to 0.23 in Province C, indicating strengthening financial interconnections. Node degree centrality declined by 16% in Province A, 14% in Province B, and 12% in Province C, suggesting more balanced risk exposure and reduced importance of individual institutions. The weighted clustering coefficients during high-risk phases were 0.79, 0.82, and 0.74, respectively, demonstrating collective risk amplification across regions, with the effect most pronounced in the coastal province. Further experiments using comparative models are shown in Table 7.

Table 7 Model performance comparison across three provinces.

Table 7 shows that the SNA + RF model achieves F1 scores of 0.941–0.985 and an AUC of 0.975 in Province A, 0.935–0.981 and 0.972 in Province B, and 0.928–0.977 and 0.969 in Province C. These results significantly outperform baseline models such as LR, SVM, and GBDT (AUC ≈ 0.85–0.87). The findings indicate that the SNA + RF model exhibits strong robustness and superior risk prediction capability across regions. This holds true for both densely interconnected financial networks, as in the coastal province, and relatively dispersed networks, as in the central-western province. Cross-province experiments confirm that the proposed SNA + RF approach is effective beyond Province A and performs well in regions with different financial structures. Overall, the model demonstrates strong generalizability, consistently capturing risk network features across diverse regional financial environments and providing reliable early warning support for regional financial supervision.

Evaluation and analysis of the rf prediction model

The classification of regional financial risk states constitutes a multi-class prediction task. To assess the performance of the RF model, the evaluation employs standard metrics including accuracy, recall, precision, TNR, and F1 score. Figure 4 presents the RF model’s classification results across the six defined risk levels, illustrating its effectiveness in differentiating complex risk states.

Figure 4 illustrates the classification performance of the RF model across six financial risk categories: Safe (A), Relatively Safe (B), Notice (C), Cautious (D), Warning (E), and Dangerous (F). The model exhibits consistently high performance across all categories, particularly excelling in the mid- to high-risk levels (Cautious and Warning). For the Safe category (A), the model achieves a recall of 0.889, a precision of 0.980, a TNR of 0.970, and an F1 score of 0.941—indicating strong overall effectiveness despite a slightly lower recall. In the Relatively Safe category (B), recall reaches 0.944, with a precision of 0.965, TNR of 0.960, and an F1 score of 0.954, demonstrating high classification accuracy and reliability. The Notice category (C) yields similarly robust results, with a recall of 0.950, precision of 0.970, TNR of 0.965, and an F1 score of 0.960. For the Cautious category (D), the model performs exceptionally well—achieving recall, precision, and TNR values of 0.980, 0.990, and 0.985, respectively, resulting in an F1 score of 0.985. In the Warning category (E), the model maintains strong predictive power, with a recall of 0.970, precision of 0.985, TNR of 0.980, and F1 score of 0.977. Finally, in the Dangerous category (F), the model achieves a recall of 0.940, precision of 0.965, TNR of 0.960, and an F1 score of 0.952—demonstrating consistent and reliable performance across all risk levels.

Model performance comparison

To more comprehensively assess the effectiveness of the RF model in predicting regional financial risk states, this study incorporates two model-agnostic evaluation metrics: the AUC and Rank Graduation Accuracy (RGA). The AUC evaluates the relationship between the true positive rate and the false positive rate across various threshold settings; higher AUC values indicate stronger overall classification performance. RGA, a metric particularly well-suited to multiclass classification problems, measures the model’s ability to correctly rank higher-risk categories above lower-risk ones.

To further validate the superiority of the RF model, its performance is benchmarked against six widely used classification algorithms: LR, gradient boosting, SVM, k-nearest neighbors (KNN), decision tree, and naïve Bayes. All models are trained and evaluated using identical training and test sets, with the dataset split in a 70:30 ratio. The parameter settings for the RF model are detailed in Table 5, while all baseline models are trained using their default configurations. Comparative performance results are presented in Fig. 5.

Fig. 5

Performance comparison between the RF model and other baseline models.

Figure 5 presents a performance comparison between the RF model and six baseline classifiers—LR, gradient boosting, SVM, KNN, decision tree, and naïve Bayes—based on two key metrics: AUC and RGA. The RF model significantly outperforms all baselines on both metrics, achieving an AUC of 0.975, indicating excellent discriminative ability across risk categories. Its RGA score reaches 0.968, highlighting its superior capability in correctly ranking financial risk levels. By comparison, the AUC scores of the baseline models are as follows: LR (0.923), gradient boosting (0.956), SVM (0.934), KNN (0.912), decision tree (0.898), and naïve Bayes (0.885). These results clearly demonstrate the RF model’s robustness and accuracy, particularly in managing complex multiclass classification tasks inherent to regional financial risk prediction.

Furthermore, the RF model’s high RGA score reinforces its practical utility for regulatory applications. Effective ranking of risk categories enables financial regulators to more accurately identify high-risk regions and prioritize timely intervention measures.

The RF model not only excels in standard metrics such as accuracy, recall, and precision but also demonstrates strong performance in more nuanced evaluation indicators like AUC and RGA. These findings confirm its reliability and suitability for regional financial risk assessment and early warning systems.

Model interpretability analysis

To strengthen the scientific foundation of regulatory decision-making, this study performed an interpretability analysis of the RF model from two perspectives: feature importance and network topology. Using Gini importance from Scikit-learn alongside SHAP values, the key predictors driving risk classification were systematically identified. Table 8 lists the top six features ranked by both methods:

Table 8 Top six features by importance.

The results indicate that network topology features are the primary drivers of risk prediction. Weighted node strength (0.35) and network density (0.25) together account for about 60% of the model’s importance, underscoring the critical role of network-based contagion effects. Among traditional financial indicators, the non-performing loan ratio (0.28) remains significant but is outperformed by these network metrics. Macroeconomic variables, including GDP growth (0.18) and the industrial debt ratio (0.12), provide complementary predictive value.

Additionally, Table 9 compares the predictive performance of weighted and unweighted network indicators.

Table 9 Performance comparison of weighted versus unweighted centrality metrics.

As shown in Table 9, weighted network indicators significantly outperform their unweighted counterparts in risk prediction, with an average improvement of 39–40% (p < 0.01). These differences have important regulatory implications. First, the high importance of weighted node strength (0.35) suggests that relying solely on connection counts (unweighted degree centrality at 0.25) may underestimate the systemic risk posed by institutions with large transaction volumes. For example, a bank with a moderate number of direct links but trillions in interbank exposures can exert far greater influence than its network position alone indicates. Second, the strong predictive power of weighted betweenness centrality (0.21) reveals “hidden hubs”—institutions that, while not topologically central, play critical roles in risk transmission by controlling substantial cross-regional transaction flows. Provincial rural commercial banks acting as intermediaries for local institutions illustrate this phenomenon. Third, the increased sensitivity of network density to weighting (0.28 vs. 0.20) indicates that even with a stable number of connections, rising transaction volumes can substantially elevate contagion risk. This explains the anomaly observed in Province A from 2016 to 2023, where network density increased by 17.5% but risk propagation accelerated by 43%. These findings highlight the necessity for regulators to incorporate weighted factors, such as transaction volumes and exposure sizes, into traditional topological metrics. Doing so will improve the accuracy of systemic risk assessments and prevent underestimation of substantive risks.

Analysis of the risk transmission effects of the weighted clustering coefficient

To deepen the structural analysis of the network, this study specifically investigates the predictive role of the weighted clustering coefficient in financial risk transmission. Table 10 summarizes its contribution across different risk categories, along with its interaction with other network characteristics.

Table 10 Contribution of the weighted clustering coefficient to risk prediction.

A systematic analysis of the weighted clustering coefficient reveals a consistent monotonic increase across risk categories. The proportion of institutions with a clustering coefficient above 0.6 rises linearly from 12.3% in the Safe (A) category to 61.2% in the Dangerous (F) category (R² = 0.96). Notably, when the average clustering coefficient surpasses the critical threshold of 0.6, the local contagion probability sharply increases—from 14.7% in the Notice (C) category to 28.5% in the Cautious (D) category. At the Warning (E) level, the clustering coefficient exhibits its strongest explanatory power for local contagion, with a standardized regression coefficient of β = 0.82 (p < 0.001). The analysis also highlights the metric’s evolving predictive role: during low-risk phases (A–C), it primarily signals latent structural vulnerabilities, whereas in high-risk phases (D–F), it reflects intensified contagion effects. Feature importance rises by 412% from the lowest to highest risk levels, indicating a nonlinear escalation. This nonlinearity offers regulators clear thresholds for risk classification and early warning, enabling timely interventions and targeted supervision based on measurable changes in the network’s microstructure.

Discussion

Based on the above analysis, network density increased from 0.24 in 2016 to 0.282 in 2023, indicating progressively tighter interconnections within the regional financial risk network. This trend reflects increasing interaction among financial institutions and a heightened potential for risk transmission. The number of network associations rose from 66 to 82 over the same period, suggesting greater structural robustness and complexity. This indicates a diversification of node linkages and a more intricate configuration of potential transmission pathways. The network association degree consistently remained at 1, implying full reachability among nodes and high network connectivity—any risk originating from a single institution can rapidly propagate throughout the system. Meanwhile, network degree centrality declined from 0.55 to 0.47, suggesting a reduction in the number of peripheral or subordinate nodes. This shift implies a more balanced distribution of risk exposure, diminishing the influence of individual institutions and enhancing the network’s overall resilience.

Regarding model performance, the RF classifier demonstrated excellent capability in multiclass classification of regional financial risk states, particularly in the Cautious and Warning categories. The model achieved high scores across all key metrics—accuracy, recall, precision, and F1—indicating strong predictive power for high-risk scenarios and practical value for regulatory oversight. The RF model recorded an AUC of 0.975 and a rank-order accuracy of 0.968, significantly outperforming baseline models such as LR, gradient boosting, and SVM. These results reaffirm the RF model’s effectiveness in managing complex multiclass prediction tasks in the context of regional financial risk.

An interpretability analysis of the RF model, using Gini importance and SHAP values, revealed that network topology features predominantly drive risk prediction. Notably, the combined contribution of weighted node strength and network density accounts for 60% of the model’s predictive power, surpassing traditional financial indicators such as the non-performing loan ratio, which contributes 28%. Macroeconomic variables like GDP growth and debt-to-asset ratio play a supporting role. Additionally, weighted network metrics improved predictive performance by approximately 39% on average compared to their unweighted counterparts (p < 0.01), with weighted betweenness centrality particularly highlighting the influence of “latent hubs” in risk transmission. The findings suggest that rapid increases in transaction volumes can significantly accelerate risk propagation even when connection counts remain stable, indicating that regulation based solely on node counts may underestimate actual risks. Therefore, incorporating transaction weights and risk exposure factors into systemic importance assessments is recommended to improve risk identification accuracy and enhance policy precision.

Despite the strong performance of the proposed approach, several limitations remain. First, SNA relies mainly on topological features and may overlook behavioral and institutional factors. Second, while the RF model performs well in nonlinear classification, it is essentially a “black-box” model with limited interpretability. These issues suggest that future research could explore more interpretable models to complement SNA. Regarding network directionality, this study used an undirected weighted network. However, edge weights incorporate both transaction size and risk exposure, partially reflecting the “strength and direction” of capital flows. Empirical results also show that risk propagation is primarily driven by high-weight edges, indicating that using an undirected network does not significantly weaken the depiction of risk transmission. Future studies could adopt directed networks if data allow, but the current conclusions are not compromised by the absence of directionality.

Based on these insights, the study proposes the following policy recommendations: (1) Enhance network monitoring: Regulators should strengthen oversight of inter-institution interactions, focusing especially on network density and non-performing loan rate trends. Establishing dynamic monitoring systems will facilitate timely identification and intervention of high-risk nodes to prevent risk contagion. (2) Optimize regulatory resource allocation: Using network centrality measures, regulators should prioritize institutions with high degree centrality, as these entities wield greater influence in the network and play key roles in risk transmission. Targeting resources toward these critical nodes can improve regulatory efficiency. 3()Promote policy innovation: Given the model’s ability to pinpoint systemically important nodes and high-risk clusters, differentiated regulatory strategies should be adopted. For instance, intensify stress testing for institutions with significant intermediary roles and increase joint supervision of densely clustered, high-risk groups. These results can also support dynamic risk early warning systems, aiding regional macroprudential management. The study also finds that the weighted clustering coefficient increases sharply with rising risk levels. This feature can serve as an early-warning threshold. For instance, when the clustering coefficient exceeds 0.75, stress tests or liquidity support measures should be initiated. If it surpasses 0.8, coordinated supervision or cross-institutional interventions may be triggered. By comparing these thresholds with historical contagion events, regulators can more systematically integrate network metrics into early-warning systems and develop actionable risk-monitoring guidelines.

Building on the model results, this study links network indicators to specific regulatory measures to enhance practical relevance. First, institutions with high weighted node strength should face differentiated capital requirements to strengthen their risk buffers. Second, a significant increase in local clustering coefficients signals potential risk amplification within certain subgroups. Regulators should apply coordinated supervision for these high-risk cliques and consider pre-allocating liquidity support. Third, nodes with high intermediary centrality should undergo targeted stress tests to assess the potential impact of their failure on systemic stability, informing contingency planning. Finally, a rapid rise in overall network density indicates that financial institutions are becoming overly interconnected. In such cases, limiting homogeneous asset allocations or improving transaction transparency can help reduce systemic vulnerability.

In summary, this study uncovers the dynamic evolution of Province A’s regional financial risk network and develops an effective risk prediction tool using the RF model. The findings offer valuable theoretical insights and practical guidance for financial regulators, enhancing the rigor and effectiveness of financial supervision. Future research may explore more advanced network metrics and ML algorithms to further improve the identification and prediction of regional financial risks. Future research could incorporate multi-regional datasets and higher-order network metrics. In addition, combining causal modeling with ML algorithms could further improve the identification and prediction of regional financial risks across a broader scope.

Conclusion

Research contribution

This study successfully optimizes the regional financial regulatory system by integrating SNA with the RF model, making the following key contributions:

• (1) Comprehensive assessment of financial risk network characteristics By calculating network density, association degree, and degree centrality, the study offers a detailed depiction of the spatial association network of regional financial risks in Province A. It reveals dynamic trends in network connectivity and node importance, providing more precise methods to identify the spatial distribution and transmission pathways of financial risks. This analysis equips regulatory authorities with deeper insights into the complexity and evolving nature of regional financial risks.

• (2) Effective multi-class risk prediction model Leveraging the RF model, a multi-level risk prediction framework is developed that accommodates data complexity and diverse financial risk states. Experimental results demonstrate excellent predictive performance across multiple risk levels, particularly in the cautious and alert categories, where accuracy, recall, precision, and F1 scores all reach high values. This underscores the model’s reliability and offers regulators a robust tool for early detection and warning of potential financial risks.

• (3) Innovative methodological integration The study pioneers the combination of SNA and RF into a comprehensive framework for enhancing regional financial supervision. This interdisciplinary approach enriches risk management tools and delivers a multi-dimensional network feature analysis coupled with dynamic risk forecasting. It provides novel theoretical foundations and empirical evidence that advance the scientific and intelligent evolution of financial regulatory systems.

Overall, this research offers valuable theoretical and methodological insights for identifying and predicting regional financial risks, alongside practical guidance for regulatory optimization. The findings empower financial authorities with more scientific and effective instruments to strengthen market stability and resilience against risks.

Future works and research limitations

Although this study has made significant progress in regional financial risk prediction and regulatory optimization, several limitations remain, suggesting directions for future research: (1) Model optimization and expansion: While the RF model performed well, it has inherent limitations in handling very high-dimensional data and capturing complex nonlinear relationships. Future work could explore alternative ML algorithms or deep learning approaches—such as XGBoost, LightGBM, or neural networks—to further improve predictive accuracy and enhance model generalization. (2) Broader case study application: To validate the generalizability and robustness of the proposed theoretical framework, future research should include additional case studies and real-world scenarios. Specifically, applying the model to provinces or countries with varying economic development levels, financial structures, and policy environments would test its adaptability across diverse contexts. (3) Directed network modeling: Given that financial risks often exhibit directional characteristics, future studies should consider constructing directed networks once causal data become available. This would enable a more detailed analysis of risk contagion pathways and transmission chains, thereby strengthening the model’s explanatory power and providing clearer policy implications. (4) Introduction of community detection: Future research could apply community detection techniques to SNA. By identifying high-risk subgroups or tightly coupled community structures within financial networks, these methods can more precisely reveal localized clusters of systemic risk. For example, community partitioning based on modularity maximization, spectral clustering, or the Louvain algorithm can help regulators detect potential “risk clusters” and implement targeted interventions. These approaches not only complement global network metrics but also offer new avenues for developing a hierarchical and multidimensional early-warning system for financial risks. By expanding and deepening empirical analyses in these ways, the proposed model can be more thoroughly validated and provide more persuasive decision-making support for financial regulators.