Introduction

Antennas with a cosecant-squared radiation pattern are widely employed in radar, satellite communication, airborne surveillance, and guidance systems1. This antenna features elevation-plane gain that varies with the elevation angle. Several techniques have been developed to synthesize this pattern using different antenna structures2,3,4,5. Design approaches for achieving shaped radiation patterns have evolved through several key stages. Early implementations utilized parabolic reflectors and reflectarray systems, which demonstrated excellent performance for beam-forming applications across wide frequency ranges4,5,6,7,8. Reflectarray technology specifically enabled precise beam shaping through customized patch elements on planar surfaces, offering manufacturing advantages over traditional reflector systems by using standard PCB fabrication methods without requiring specialized tooling. However, these systems share a common architectural constraint: they require precise spatial separation between the feed element and the main radiating structure to achieve proper phase distribution. This configuration inherently results in significant volume requirements and complex mechanical integration. To address these limitations, research efforts shifted toward fully integrated planar architectures. Later developments explored implementations using microstrip transmission lines and substrate-integrated waveguide (SIW) technologies9,10,11,12,13,14,15,16. present a series-fed patch array antenna with a cosecant fourth power pattern. It achieves an bandwith of 5% in the frequency range of 23.8–25 GHz. Most contemporary designs employ series-fed network configurations to minimize architectural complexity and substrate-related losses. While effective for many applications, this feeding approach imposes fundamental bandwidth constraints due to its distributed nature. The resulting bandwidth limitations present significant challenges for modern wideband communication systems and advanced radar applications. Additionally, energy dissipation within dielectric materials continues to constrain achievable efficiency levels in these integrated designs. In this paper, a wideband planar antenna is presented that, in addition to its low weight and low profile height, is well-suited for use in radar systems operating under motion due to its flat geometry. The antenna also features a monopulse pattern in the elevation plane, which enhances angle estimation accuracy. Figure 1 illustrates the geometric relationship between a radar and an airborne target.

Fig. 1
figure 1

Geometry of the radar and target with cosecant-squared radiation pattern.

Full size image

In radar systems, the received power(\({P}_{r}\)) from a target is expressed by Eq. (1):

$$P_{r} = \frac{{P_{t} G^{2} \lambda^{2} \sigma }}{{4\pi^{3} R^{4} }}$$
(1)

where \({P}_{t}\) is the transmitted power, \(G\) is the antenna gain, \(\uplambda\) is the wavelength, \(\upsigma\) is the radar cross section (RCS) of the target, and \(\text{R}\) is the target’s distance from the radar. If the target maintains a fixed altitude \(\text{h}\), the range becomes \(R=h\cdot csc(\theta )\). Assuming constant \(\upsigma\) and \({P}_{t}\), the radar equation reveals that if the antenna gain varies as \({csc}^{2}(\theta )\), the received power remains constant regardless of range. The synthesized cosecant-squared pattern inherently mitigates multipath effects, enhancing performance in complex environments. Since radar detection is based on received signal strength, such a pattern ensures consistent detection performance across various ranges. In recent years, advanced optimization algorithms such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Improved Weighting Strategies (IWS) have been used to design such patterns17,18,19,20,21. The target specifications for the proposed design are summarized in Table 1.

Table 1 Final antenna specifications.
Full size table

Design of a monopulse antenna with a cosecant-squared radiation pattern

The proposed monopulse array antenna with a cosecant-squared radiation pattern consists of a 2 × 8 microstrip element array excited through modified proximity coupling. The antenna operates over a frequency range of 3.5–5.5 GHz. To enhance the gain of both individual elements and the overall array, a secondary ground plane is positioned behind the array at a distance of λ⁄4 (at the center frequency). Given the wide operational bandwidth, metallic walls are placed between the radiating elements to reduce mutual coupling, and a novel structural layout is introduced to support this improvement. A genetic algorithm (GA) is employed to optimize the excitation amplitude and phase of each element to synthesize the desired cosecant-squared pattern, achieving a sidelobe level of – 20 dB. An asymmetric 1-to-8 power divider is used to implement the required amplitude distribution. For accurate phase control, a new set of Schiffman phase shifters is designed, offering stable phase behavior across the operating bandwidth. These 7 phase shifters also share a common reference line to ensure phase consistency throughout the array. Finally, the two asymmetric 1-to-8 power dividers are connected through a rectangular 180-degree hybrid coupler to generate the sum (Σ) and difference (Δ) channels required for monopulse operation. The detailed design and implementation of each component are presented in the following subsections.

Radiating element design

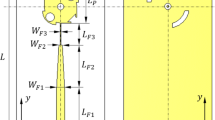
The radiating element is implemented as a microstrip patch antenna with a modified proximity-coupled feed. To achieve slant polarization, the feed slot is oriented at a 45-degree angle, eliminating the need to tilt the patch or the entire antenna structure. In this configuration, the ground plane along with the feed slot acts as an impedance transformer. To enhance the bandwidth, the feed aperture on the ground plane is shaped as shown in Fig. 2, and the end of the 50-Ω microstrip line is modified accordingly. Both substrate layers are made of Rogers 4003 material with a thickness of 0.813 mm. Rogers RO4003C was selected due to its relatively low loss tangent, stable dielectric constant in the C-band, and cost effectiveness. The parameter values used in the design are listed in Table 2. The initial dimensions of the radiating patch are taken from reference21.

$$a = \frac{F}{{\sqrt {\left\{ {1 + \frac{2h}{{\pi \varepsilon_{r} F}}\left[ {\ln \left( {\frac{\pi F}{{2h}}} \right) + 1.7726} \right]} \right\}} }}$$
(2)
$$F = \frac{{8.791*10^{9} }}{{f_{r} \sqrt {\varepsilon_{r} } }}$$
(3)
Fig. 2
figure 2

View of the radiating element.

Full size image
Table 2 Radiating element parameters (dimensions in mm).
Full size table

In the above equations, \({f}_{r}\) denotes the resonant frequency, \(h\) is the substrate thickness, and \({\varepsilon }_{r}\) is the relative dielectric constant. The gap between the radiating patch and the feed line (denoted as \({H}_{1}\)) effectively forms a back cavity for the antenna. This cavity increases the overall height of the antenna stack, which in turn improves the antenna’s bandwidth. The length of the slanted slot on the ground plane is approximately half a wavelength (λ/2) at the center frequency. According to the results shown in Fig. 3, the simulated reflection coefficient (S11) of the radiating element remains below – 10 dB from 3.8 GHz to 4.5 GHz, and the gain reaches 7.2 dBi at 4.6 GHz. The simulated radiation patterns of the element at 4.7 GHz are illustrated in Fig. 4, showing both co-polarization and cross-polarization components. The reason for selecting this antenna is that, although it is a microstrip antenna, it offers a relatively wide bandwidth of approximately 34%. Additionally, it provides higher gain compared to typical microstrip antennas, which usually have a gain around 5 dB. The feeding network is located in the layer beneath the ground plane, which prevents undesired radiation and interference in the antenna’s radiation pattern.

Fig. 3
figure 3

Simulated active reflection coefficients and gain of the radiating element.

Full size image
Fig. 4
figure 4

Simulated radiation patterns of the radiating element at 4.6 GHz.

Full size image

Array design

Array geometry and mutual coupling mitigation

The radiating elements are arranged in a 2 × 8 array configuration. To achieve maximum gain, the optimal spacing between adjacent elements is set to approximately 0.6 λ at the center frequency, which corresponds to 39 mm. Due to the antenna’s wide operational bandwidth, this spacing becomes relatively small at the lower end of the band, leading to increased mutual coupling between adjacent elements. This poses challenges in maintaining the desired radiation characteristics and requires a more complex design approach. To address this issue, particularly at lower frequencies, a method for reducing mutual coupling between elements is essential. As mentioned earlier, each radiating element is mounted on a metallic wall structure. Therefore, the mutual coupling between two adjacent elements is simulated both with and without the presence of the metallic wall. The corresponding results are presented in Fig. 5.

Fig. 5
figure 5

Mutual coupling between adjacent elements with and without metallic wall.

Full size image

As shown in Fig. 5, the use of metallic walls reduce mutual coupling by ~ 10 dB across the entire operating frequency range. Mutual coupling not only disturbs the impedance matching of the elements but also alters the amplitude and phase distribution of the far-field radiation. Therefore, to increase synthesis accuracy, the effect of mutual coupling on the far-field pattern must be taken into account. The final dimensions of the array are 312 × 72 mm.

Optimization strategy

Using a multi-objective genetic algorithm (MOGA) in HFSS [High Frequency Structure Simulator, version 2015 URL: https://www.ansys.com/products/electronics/ansys-hfss], the amplitude and phase excitations of the array elements are optimized to achieve a cosecant-squared radiation pattern with a sidelobe level of − 20 dB. To perform this optimization, an objective function is defined, where the amplitude and phase values of the radiating elements serve as the decision variables. A total of 15 parameters are considered in the optimization process: 8 amplitude values and 7 phase values. The amplitude is allowed to vary in the range of 0.2 to 1, while the phase can range from 0° to 360°. The lower bound of 0.2 for amplitude is chosen to avoid implementation challenges in the feed network due to excessively narrow transmission lines. Figure 6 shows the objective function used to synthesize the cosecant-squared radiation pattern. The function is defined in four distinct angular regions. Based on the specifications listed in Table 1, the angular range over which the radiation pattern is expected to follow the ideal cosecant-squared form is approximately 45°. For simplicity, all pattern levels are normalized to a peak value of 0 dB. The following sections present the relevant equations for each part of the design.

$$\begin{gathered} - 180^{ \circ } < \theta < \theta_{1} :Gain(\theta ) \le - SLL \hfill \\ \to Out_{1} = \max (Gain(\theta )) - SLL \hfill \\ \end{gathered}$$
(4)
$$\begin{gathered} \theta_{1} < \theta < \theta_{2} : - 1dB \le Gain(\theta ) \le 0dB \hfill \\ \to Out_{2} = \max ( - 1dB - Gain(\theta )) \hfill \\ \end{gathered}$$
(5)
$$\begin{gathered} \theta_{2} < \theta < \theta_{3} :Gain(\theta ) \cong csc^{2} (\theta )dB \hfill \\ \to Out_{3} = \left| {Gain(\theta ) - csc^{2} (\theta )} \right| \hfill \\ \end{gathered}$$
(6)
$$\begin{gathered} \theta_{3} < \theta < 180^{ \circ } :Gain(\theta ) \le SLL \hfill \\ \to Out_{4} = \max (Gain(\theta )) - SLL \hfill \\ \end{gathered}$$
(7)
Fig. 6
figure 6

The objective function used in the optimization process.

Full size image

Finally, by assigning a weighting factor to each angular region, the influence of that region in the optimization process can be increased. In the following equation, \({w}_{i}\) (for i = 1,…,4) represents the weighting coefficients assigned to each angular interval during the optimization.

$$Out_{Total} = \sum\limits_{i = 1}^{4} {w_{i} Out_{i} = } w_{1} Out_{1} + ..... + w_{4} Out_{4}$$
(8)

These weighting coefficients are selected based on the required accuracy of the optimization. Since the focus here is on achieving a cosecant-squared radiation pattern and suppressing sidelobe levels, the weights are chosen as w3 = 2, w4 = w1 = 1, and w2 = 0.5. Ultimately, the optimization results can be obtained using HFSS’s built-in optimization module with only a single full-wave simulation. The optimized amplitude and phase excitations for each radiating element are listed in Table 3. These values are then applied to the corresponding elements in the HFSS model.

Table 3 Amplitude and phase values obtained from the genetic algorithm.
Full size table

Final configuration

The final array structure without the feed network is shown in Fig. 7. The eight elements are spaced 39 mm apart along the elevation axis, while the two rows are separated by 35 mm along the azimuth axis. The resulting cosecant-squared radiation pattern, using the excitations derived from the genetic algorithm, is illustrated in Fig. 8.

Fig. 7
figure 7

Array of radiating elements with dimensions 2 × 8 and excitation parameters in Table 3.

Full size image
Fig. 8
figure 8

Radiation patterns of the antenna array shown in Fig. 7 at a frequency of 4.6 GHz.

Full size image

The feed network consists of three main parts. The first part includes an asymmetric 1-to-8 power divider, which is designed to achieve a sidelobe level of − 20 dB by providing the desired amplitude distribution across the array elements. In the second stage, seven fixed Schiffman phase shifters (along with a common reference line) are designed to provide the specific phase values required by each radiating element, thereby enabling the formation of the desired cosecant-squared radiation pattern. Finally, a 180-degree hybrid coupler is used in the third part to combine the outputs of each row of the array. This completes the monopulse antenna configuration with a cosecant-squared radiation pattern for elevation coverage.

Asymmetric 1-to-8 power divider

The power divider is composed of seven asymmetric 1-to-2 dividers, each designed to provide unequal amplitude distribution with identical phase. Quarter-wavelength (λg/4) impedance transformers are used for matching. To achieve the required asymmetric power distribution, each arm of the dividers is implemented with transmission lines of different widths22. The quarter-wavelength line length in the feed network is set to 10 mm. The overall dimensions of the feed network are 22 mm × 300 mm. A schematic view of the designed feed network structure is shown in Fig. 9. As can be observed, the transmission line widths vary along the network, resulting in different power levels delivered to each antenna element. These power levels are chosen according to the amplitude values listed in Table 3. The simulation results, obtained after several stages of optimization, are presented in Fig. 10. The input impedance matching of the feed network is shown by the red curve, with a return loss better than − 15 dB across the operating band.

Fig. 9
figure 9

Schematic view of the asymmetric 1-to-8 feed network.

Full size image
Fig. 10
figure 10

Simulated S parameter(amplitude) of the asymmetric power divider network.

Full size image

The delivered power levels to each antenna element are also shown and demonstrate excellent agreement with the values in Table 3. However, due to the wide bandwidth of the antenna, a deviation of less than 5% from the ideal amplitudes obtained by the genetic algorithm is observed.

Fixed Schiffman phase shifter

To achieve the desired cosecant-squared radiation pattern, each radiating element must be excited with a specific phase as defined in Table 3. A critical consideration in this design is the wide operational bandwidth of the antenna. In some previous studies, this phase adjustment has been implemented using simple physical length differences23,24. However, when operating over a broad frequency range, the phase shift introduced by a fixed length varies significantly across the band, resulting in distortion of the desired radiation pattern. In this work, fixed Schiffman phase shifters25 are employed to provide the required phase offsets. A key distinction of the proposed design lies in two constraints:

  1. 1.

    All seven phase shifters have the same limited space due to the compact arrangement of the radiating elements. This refers to the seven relative phase shifts calculated by taking one element as a reference.

  2. 2.

    A common reference line must be used for all phase shifters to ensure consistent phase alignment.

Figure 11 shows the simulated target phase difference. The maximum deviation in phase, relative to the values listed in Table 3, is approximately ± 10° across the operating frequency band. In the phase shifter design process, the eighth element is considered as a reference and the transmission line length corresponding to each phase shift is calculated according to the phase difference values in Table 3. A layout view of the seven fixed phase shifters with a common reference line is shown in Fig. 12.

Fig. 11
figure 11

Simulated S parameter(phase) of the fixed Schiffman phase shifter.

Full size image
Fig. 12
figure 12

Layout of the seven fixed phase shifters with a common reference line..

Full size image

180-degree hybrid coupler

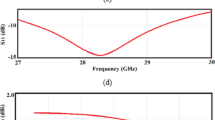
The monopulse comparator network is responsible for generating the sum (Σ) and difference (Δ) radiation patterns. For precise tracking performance, the antenna system must exhibit a deep null in the difference ports and high isolation between the sum and difference ports. To meet these requirements, a two-section rectangular hybrid ring coupler is used. This structure offers the desired characteristics along with a wide operational bandwidth typically around 35%26,27. As illustrated in Fig. 13, the hybrid consists of six quarter-wavelength lines and two half-wavelength lines. The impedance values for each section are obtained using even- and odd-mode analysis and optimized using the ADS software’s[Advanced Design System (ADS), version 2021 URL: https://www.keysight.com/us/en/products/software/pathwave-design-software/pathwave-advanced-design-system.html] built-in optimization tools. The final impedance values are: Z1 = 65.5 \(\Omega\), Z2 = 72.3 \(\Omega\), Z3 = 40.5 \(\Omega\), Z4 = 55 \(\Omega\), Z5 = 79.5 \(\Omega\). The final layout of the hybrid coupler has dimensions of 25 mm × 25 mm. The simulation results of the hybrid ring are presented in Fig. 14. The hybrid operates over a bandwidth of 3.5–5.5 GHz, maintaining a return loss better than − 14 dB across the target frequency range. The isolation between the two input ports exceeds 32 dB. Moreover, the amplitude imbalance between the two output ports remains below 0.3 dB, and the maximum phase error is less than 2.5° across the entire operating band.

Fig. 13
figure 13

(a) Schematic diagram of the hybrid ring; (b) Layout of the 180-degree hybrid coupler.

Full size image
Fig. 14
figure 14

Scattering parameters (S-parameters) of the 180-degree hybrid coupler.

Full size image

Simulation of the final feed network

The final feed network is composed of the asymmetric power divider, the fixed phase shifters, and the 180-degree hybrid coupler. To better illustrate the performance, the simulated amplitude and phase values at three frequencies corresponding to the lower, center, and upper bounds of the operational bandwidth—are presented in Table 4. A layout view of the final feed network is shown in Fig. 15. As previously described, the antenna consists of two rows, each containing eight radiating elements. In order to compare the simulated amplitudes with those listed in Table 3, the values in Table 4 are adjusted by + 3 dB. Comparison of the results in Tables 3 and 4 reveals that the phase deviations are minimal and that the target values are well maintained. The amplitude values show slight discrepancies, which are attributed to the full-wave simulation accounting for dielectric and conductor losses.

Table 4 Simulated amplitude and phase values for the final feed network.
Full size table
Fig. 15
figure 15

Layout of the final feed network.

Full size image

Simulation of the final monopulse antenna with a cosecant-squared radiation pattern

By connecting the feed network to the radiating elements, the final antenna structure is completed. The complete configuration is illustrated in Fig. 16. The eight elements are spaced 39 mm apart along the elevation axis, while the two rows are separated by 35 mm along the azimuth axis.

Fig. 16
figure 16

Final structure of the monopulse antenna with a cosecant-squared radiation pattern.

Full size image

Based on the arrangement of the two rows of radiating arrays, port 1 of the 180-degree hybrid (see Fig. 13) corresponds to the sum (Σ) radiation pattern. First, the antenna’s scattering parameters are shown in Fig. 17. For both the sum and difference inputs, the return loss remains better than − 10 dB over the frequency range of 3.8–5.4 GHz, corresponding to a 34% bandwidth. The isolation between the two inputs is better than 26 dB across the same frequency range. The radiation patterns of the antenna at three key frequencies are presented in Fig. 18. At 4.6 GHz, the antenna achieves a gain of 13.9 dBi. The beamwidth is 23° in the elevation plane and 54° in the azimuth plane. The sidelobe level is approximately − 17 dB, and the null depth reaches − 37 dB. The antenna exhibits excellent conformity to the ideal cosecant-squared pattern within the angular range of 0° to 45°. The 3D radiation pattern of the antenna for the sum and difference patterns is shown in the Fig. 19 for better visualization.

Fig. 17
figure 17

Simulated bandwidth and isolation between the input ports of the antenna.

Full size image
Fig. 18
figure 18

Sum and difference radiation patterns at three frequencies: (a) 3.9 GHz, (b) 4.6 GHz, and (c) 5.1 GHz.

Full size image
Fig. 19
figure 19

The 3D radiation pattern of the antenna at 4.6 GHz: (a) Sum, (b) Difference.

Full size image

Fabrication and measurement

The antenna is composed of four separate parts that are assembled using screws. As shown in Fig. 20, the structure includes two microstrip boards: one containing the feed network and the other containing the radiating patches.

Fig. 20
figure 20

Photographs of the fabricated antenna.

Full size image

The radiating patches are mounted on the top side of the cross-shaped structure, while the feed network is positioned on the bottom side. The scattering parameters of the antenna were first measured using an Agilent E8364B vector network analyzer. By comparing the simulation results in Fig. 17 with the measured data in Fig. 21, it can be concluded that the fabricated antenna demonstrates a good level of agreement and build quality. The differences between the simulation and measurement results are primarily attributed to fabrication and assembly tolerances. For example, according to the manufacturer, the PCB fabrication tolerance can reach up to 0.1 mm in the worst case. In addition, to accommodate screw mounting, the holes are typically designed with an extra clearance of about 0.1 mm. Moreover, the CNC machining accuracy is reported to be around 0.15 mm. These mechanical tolerances may collectively contribute to the discrepancies observed between simulated and measured results. Nevertheless, the measured performance shows reasonably good agreement with the simulated data. The antenna exhibits a − 8.6 dB bandwidth of approximately 34%, and the isolation between the input ports is better than − 24 dB. Subsequently, the antenna’s radiation patterns were measured in an anechoic chamber at three frequencies: 3.9 GHz, 4.6 GHz, and 5.1 GHz. At 4.6 GHz, the measured gain is 13.05 dBi, with a null depth of − 24 dB. The beamwidth is 26° in the elevation plane and 51° in the azimuth plane, and the maximum sidelobe level is approximately − 13 dB. By comparing the results of the fabricated antenna (Fig. 22) with the simulated results (Fig. 18), it is evident that there is a good level of agreement between the fabricated prototype and the simulation. The slight discrepancies observed can be attributed to manufacturing and assembly tolerances, as previously mentioned. The fabrication errors are mainly related to the CNC machining, PCB manufacturing, and assembly process, which in the worst case are estimated to be around 0.3–0.4 mm. Radiation pattern measurements have been performed with a minimum angular resolution of 0.8 degrees. For a more detailed comparison, the measured performance metrics are summarized in Table 5.

Fig. 21
figure 21

Measured bandwidth and isolation between input ports of the fabricated antenna.

Full size image
Fig. 22
figure 22figure 22

Measured radiation patterns of the fabricated antenna at 3.8 GHz, 4.6 GHz, and 5.3 GHz.

Full size image
Table 5 Final results of the monopulse array antenna with a cosecant-squared radiation pattern.
Full size table

The simulated and measured radiation patterns of the antenna at 4.6 GHz are compared in Fig. 23. The average measurement error with simulation is less than 0.9 dB across the target angular region (less than 26 degrees). Table 6, provides a detailed comparison between the proposed antenna and several recently reported designs exhibiting cosecant-squared (CSC2) radiation patterns. Most existing antennas adopt microstrip or SIW-based series-fed structures, which inherently limited bandwidth. In contrast, the proposed antenna utilizes a wideband parallel-feed network integrated with broadband phase shifters, which not only enhances beam control precision but also substantially extends the overall antenna bandwidth. Furthermore, a multi-objective genetic algorithm (MOGA) was employed to simultaneously optimize multiple performance goals, such as sidelobe suppression, pattern shaping. Notably, the antenna supports monopulse operation, making it suitable for high-resolution tracking and radar applications.

Fig. 23
figure 23

Comparison of simulated and measured results for the cosecant-squared radiation pattern at 4.6 GHz.

Full size image
Table 6 Comparison of proposed antenna with recently reported literature’s.
Full size table

Conclusion

This study presented the design, synthesis, and fabrication of a wideband slant-polarized monopulse array antenna with a cosecant-squared radiation pattern, optimized for precise target detection and tracking applications. The proposed antenna is based on a 2 × 8 microstrip element array with modified proximity-coupled feeding. To enhance performance, several advanced techniques were employed: metallic walls were inserted to reduce mutual coupling, a second ground plane was added to increase gain, and a genetic algorithm was used to optimize amplitude and phase excitations considering coupling effects. Asymmetric amplitude weights were applied to suppress sidelobes, and fixed Schiffman phase shifters with a common reference line were designed to maintain phase integrity. A rectangular 180-degree hybrid coupler was integrated to enable monopulse functionality in the azimuth plane, ensuring precise angular resolution. Simulation and measurement results showed good agreement, validating the robustness of the design. The fabricated antenna exhibits a bandwidth of approximately 34%, with an isolation better than − 24 dB between the input ports. At 4.6 GHz, the measured gain is 13.05 dBi, with a null depth of − 24 dB. The beamwidth is 26° in the elevation plane and 51° in the azimuth plane, and the maximum sidelobe level is approximately − 13 dB. The radiation pattern closely followed the desired cosecant-squared shape, demonstrating the antenna’s suitability for advanced radar and surveillance systems. For future work, further miniaturization and extension to higher frequency bands will be considered.