Influence of coriolis force and nanoparticle aggregation on entropy generation and thermal conductivity in dusty nanofluid flow: a numerical investigation

Abstract

The present research introduces a novel framework for analyzing dusty nanofluid flow within a rotating frame, emphasizing the combined influence of nanoparticle aggregation, viscous dissipation, radiation, porous medium effects, and Coriolis force. The study’s novelty lies in integrating these coupled mechanisms with entropy generation analysis to provide a unified thermofluid model. This model offers fresh insights into how radiation-rotation coupling, aggregation, and porous resistance reshape momentum and thermal transport in dusty nanofluid systems. The governing partial differential equations are transformed into nonlinear ordinary differential equations using similarity variables and solved numerically via MATLAB’s bvp4c solver. Validation is established by comparing the results with published studies for limiting cases. The findings indicate that while aggregation reduces velocity, it increases the Nusselt number and temperature. Coriolis forces increase transverse flow and thicken the thermal layer, while radiation increases temperature and heat transfer but diminishes the axial flow. Aggregation lowers the Nusselt and Bejan numbers by about 20% and 15%, respectively. These results provide practical insights for the design of thermal management and nuclear cooling systems, rotating thermal-fluid systems such as filtration processes, aerosol technology, rotating energy devices, and environmental engineering applications.

Introduction

Dusty fluid flow occurs when solid dust particles are distributed throughout a fluid medium. During fluidization process, chemical reactions facilitate the formation of raindrops by interacting with the dusty air and dispersing tiny particles in the fluid. This phenomenon has numerous uses, including paint spraying, nuclear reactor cooling systems, biomedical technologies, and precise guiding systems. Saffman¹ established the concept of dusty fluids and developed constitutive equations using Stokes’ law of drag. His research found that including dust particles in a fluid enhances the thermal transfer rate. Ezzat et al.² investigated the free-convective heat transfer in a dusty fluid flow caused by a vertical plate in a permeable medium with an applied magnetic field. Dey and Chutia³ analyzed bioconvective dusty nanofluid flow over a vertically extended flat surface. Sharif et al.⁴ conducted numerical research on trihybrid Ellis dusty nanofluid flow through an expanding Riga plate. Examining dusty flow mechanisms helps understanding thermodynamic losses, such as entropy formation, in these systems.

Entropy generation, a fundamental thermodynamic term, quantifies irreversibility and disorder in energy transfer. Entropy generation minimization is crucial in solar energy, electronics, and heat exchangers. Bejan^5,6,7 developed the concept of entropy optimization for mass and heat transfer phenomena. Kumar et al.⁸ examined entropy generation in hybrid nanofluids inside porous medium with viscous dissipation, Joule heating, and radiation, while Agrawal and Kaswan⁹ looked at how entropy is generated in nanofluids. Khan et al.¹⁰ investigated nanofluid flow across a curved, stretchy sheet, including heat and mass transfer and entropy generation. Kumar et al.^11,12 employed Darcy–Forchheimer models to look at entropy production, convective heat, and mass transfer in nanofluids. Yusuf et al.¹³ studied entropy generation to evaluate thermodynamic efficiency of nanofluid-assisted enhanced oil recovery. This thermodynamic viewpoint inherently applies to nanofluid research, in which nanoparticle dispersion significantly affects entropy and heat transfer¹⁴.

Choi and Eastman¹⁵ developed the concept of distributing nanoparticles into base fluids to improve thermal conductivity. Incorporation of nanoparticles into base fluids increases heat transfer performance and has many applications^16,17. Darvesh et al.¹⁸ conducted a computational analysis of mixed convective flow of a variable-viscosity Cross nanofluid over a dynamic permeable surface, considering thermal radiation and an inclined magnetic field. Abbas et al.¹⁹ investigated the Buongiorno model for incompressible, time-independent Sutterby fluid flow on a nonlinear stretching cylinder. Shah et al.²⁰ explored how ternary hybrid nanofluids influence blood velocity and heat transfer in stenosed arteries. Recent work on nanofluids may be found in^21,22,23. The efficiency of these nanofluids is contingent upon particle interaction events, including aggregation and clustering.

Studying nanoparticle aggregation is critical because it directly influences the performance and usefulness of nanofluids in various advanced applications. Controlled aggregation improves heat transport, stability, and material characteristics, but excessive clustering causes sedimentation and inefficiency. In biological applications, it determines biodistribution and safety, whereas in material production, it affects uniformity and performance. Aggregation can be tailored for various applications by modifying the surface or adding stabilizers. Experimental studies^25,26 show that nanoparticle aggregation considerably improves the heat transfer properties of nanofluids. Wang et al.²⁷ found that particle clustering significantly improves thermal conductivity of nanofluids. The Coriolis force makes these interactions between particles and fluids much more complicated, affecting both the stability of the flow and the way heat moves through it.

The analysis of fluid flow in rotating systems is crucial across numerous engineering and industrial applications. The Coriolis force fundamentally influences the dynamics. This force is a pivotal factor in systems like vacuum pumps and motors prompting academics to comprehend their underlying science better. The studies by Liu et al.²⁸ on friction stir welding and by Ali et al.³⁰ on Maxwell fluid within a cylinder inherently involve Coriolis-driven flow modifications. Similarly, the impact of this force was explicitly examined by Bilal and Ramzan²⁹ within porous media. Mishra and Mondal³¹ studied a spinning nanofluid under Coriolis and Lorentz forces on a vertically moving plate.

Novelty and significance of the study

The existing literature shows that three-dimensional radiative dusty nanofluid flow within a Darcy–Forchheimer porous medium remains largely unexplored. prior research has primarily concentrated on either nanofluid or dusty fluid in isolation, neglecting the synergistic effects that occur when particle dynamics, radiation, and porous resistance operate simultaneously under rotational motion. The research gap is identified in Table 1. The gap is addressed in this work by formulating a rotating dusty nanofluid model that accounts for thermal radiation, viscous dissipation, nanoparticle aggregation, and Coriolis forces. Both homogeneous and aggregation-based nanoparticle models are utilized to capture realistic behavior. Furthermore, This study extends beyond conventional models by incorporating entropy generation, thereby linking heat transmission behavior with energy efficiency and irreversibility. The novelty of this work lies in:

• Developing a comprehensive framework for three-dimensional rotating dusty nanofluid flow through a Darcy–Forchheimer porous medium.

• Studying the role of the Coriolis force, viscous dissipation, and nonlinear radiation in dusty fluid flow.

• Examining the interactive roles of nanoparticle aggregation and porous resistance on thermal and momentum transport.

• Performing entropy generation analysis to measure irreversibility and assess energy efficiency in thermal-fluid systems.

• Emphasizing the importance of effective nanofluid properties through the Tiwari-Das model to better represent the physical response of nanoparticle suspensions.

This study is important because it looks at these coupled mechanisms, which give us a better idea of how dusty nanofluids move in rotating industrial and environmental systems. The findings have immediate ramifications for the enhancement of engineering processes, including rotating heat exchangers, filtration and cooling apparatus, and aerosol-based systems, where dust accumulation, nanoparticle aggregation, and rotation dictate system efficacy. This study fills a gap in the research and helps make energy use more efficient, cut down on entropy generation, and better control heat and momentum management in porous rotating systems.

Table 1 Identified research gaps and novelty of the present study.

Research objectives

The purpose of this article is to address the following research questions:

• How does nanoparticle aggregation affect effective heat transfer?

• How does Coriolis force impact the thermal and momentum profiles for both fluid and dust phases, with and without nanoparticle aggregation?

• What effects do rotation and porosity have on the motion of the nanofluid in axial and transverse directions?

• How is the temperature of dusty nanofluid affected by the porosity, Forchheimer number, and radiation parameter?

• How can entropy production be optimized?

Flow analysis and mathematical modeling

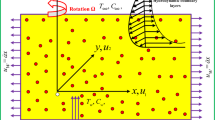
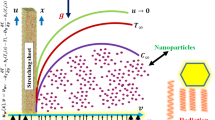
This study investigates the steady, three-dimensional flow of dusty radiative rotating nanofluid induced by a stretching sheet in a porous medium. The work focuses on minimizing entropy generation in dusty nanofluid flow. Adding TiO₂ nanoparticles to water greatly increases its ability to conduct heat and transfer heat through convection, making it a very efficient nanofluid. This enhanced fluid is crucial for solar energy collectors and microelectronics thermal management, where rapid heat dissipation and efficient energy transport are required. Table 2 presents the thermophysical characteristics of base fluid (water) and nanoparticle (TiO₂).

The following physical assumptions are considered for the flow problem:

• The flow inside the porous media is described using the Darcy–Forchheimer model.

• Radiation and viscous dissipation effects are incorporated.

• The surface lies in the $\check{x}\check{y}$-plane of a Cartesian coordinate system, with fluid occupying the region $\check{z} \ge 0$.

• The surface has constant angular velocity $\Omega$.

• The stretching velocity of surface is expressed as $\check{v}_{1w} = b\check{x}$.

• Dust particles are taken as equally sized spheres.

• The density of dust and nanoparticles is considered constant throughout the flow field.

• Figure 1 geometrically illustrates the flow configuration.

Fig. 1

Flow configuration.

Based on the above physical assumptions, the governing system is derived. The following presents a complete statement of the boundary layer problem to ensure mathematical clarity.

Governing system

The conservation of mass, momentum, and energy for steady nanofluid flow is governed by the following system of coupled and nonlinear equations^38,39,41:

$$\begin{aligned}&\frac{\partial \check{v}_1}{\partial \check{x}}+\frac{\partial \check{v}_2}{\partial \check{y}}+\frac{\partial \check{v}_3}{\partial \check{z}}=0, \end{aligned}$$

(1)

$$\begin{aligned}&\check{v}_1\frac{\partial \check{v}_1}{\partial \check{x}}+\check{v}_2\frac{\partial \check{v}_1}{\partial \check{y}}+\check{v}_3\frac{\partial \check{v}_1}{\partial \check{z}}-2 \Omega \check{v}_2=\nu _{nf} \frac{\partial ^2 \check{v}_1}{\partial \check{z}^2}-\frac{\nu _{nf}}{K_{0}}\check{v}_1+\frac{KN}{\rho _{nf}}(\check{v}_{1p}-\check{v}_1)-F^*\check{v}_1^2, \end{aligned}$$

(2)

$$\begin{aligned}&\check{v}_1\frac{\partial \check{v}_2}{\partial \check{x}}+\check{v}_2\frac{\partial \check{v}_2}{\partial \check{y}}+\check{v}_3\frac{\partial \check{v}_2}{\partial \check{z}}+2 \Omega \check{v}_1=\nu _{nf} \frac{\partial ^2\check{v}_2}{\partial \check{z}^2}-\frac{\nu _{nf}}{K_{0}}\check{v}_2+\frac{KN}{\rho _{nf}}(\check{v}_{2p}-\check{v}_2)-F^*\check{v}_2^2, \end{aligned}$$

(3)

$$\begin{aligned}&\left. \begin{array}{rr} \check{v}_1\frac{\partial \check{T}}{\partial \check{x}}+\check{v}_2\frac{\partial \check{T}}{\partial \check{y}}+\check{v}_3\frac{\partial \check{T}}{\partial \check{z}}=& \frac{k_{nf}}{(\rho c_p)}_{nf}\frac{\partial ^2 \check{T}}{\partial \check{z}^2}+\frac{\nu _{nf}}{(c_p)}_{nf} \left[ \left( \frac{\partial \check{v}_1}{\partial \check{z}} \right) ^2+\left( \frac{\partial \check{v}_2}{\partial \check{z}} \right) ^2\right] \\ & -\frac{1}{(\rho c_p)}_{nf}\frac{\partial Q_r^*}{\partial \check{z}}-\frac{\rho _p(c_p)_f}{(\rho c_p)_{nf}\tau _{T}}(\check{T}-\check{T}_{p}) \end{array}\right\} , \end{aligned}$$

(4)

for the dust-phase flow

$$\begin{aligned}&\frac{\partial \check{v}_{1p}}{\partial \check{x}}+\frac{\partial \check{v}_{2p}}{\partial \check{y}}+\frac{\partial \check{v}_{3p}}{\partial \check{z}}=0, \end{aligned}$$

(5)

$$\begin{aligned}&\check{v}_{1p}\frac{\partial \check{v}_{1p}}{\partial \check{x}}+\check{v}_{2p}\frac{\partial \check{v}_{1p}}{\partial \check{y}}+\check{v}_{3p}\frac{\partial \check{v}_{1p}}{\partial \check{z}}=2 \Omega \check{v}_{2p}+\frac{K}{m}(\check{v}_1-\check{v}_{1p}), \end{aligned}$$

(6)

$$\begin{aligned}&\check{v}_{1p}\frac{\partial \check{v}_{2p}}{\partial \check{x}}+\check{v}_{2p}\frac{\partial \check{v}_{2p}}{\partial \check{y}}+\check{v}_{3p}\frac{\partial \check{v}_{2p}}{\partial \check{z}}+2 \Omega \check{v}_{1p}=\frac{K}{m}(\check{v}_2-\check{v}_{2p}), \end{aligned}$$

(7)

$$\begin{aligned}&\check{v}_{1p}\frac{\partial \check{T}_p}{\partial \check{x}}+\check{v}_{2p}\frac{\partial \check{T}_p}{\partial \check{y}}+\check{v}_{3p}\frac{\partial \check{T}_p}{\partial \check{z}}=\frac{c_p}{c_m \tau _t}(\check{T}-\check{T}_p), \end{aligned}$$

(8)

where $(\check{v}_1, \check{v}_2, \check{v}_3)$ and $(\check{v}_{1p}, \check{v}_{2p}, \check{v}_{3p})$ represent the components of fluid and dust phase velocities, respectively, along the $(\check{x}, \check{y}, \check{z})$ directions. The fluid temperature is represented as $\check{T}$, while $\check{T_{p}}$ corresponds to the temperature of the dust phase. The terms $\nu _{nf}$, $k_{nf}$, $\rho _{nf}$, and $(c_p)_{nf}$ indicate the kinematic viscosity, thermal conductivity, density, and heat capacity of the nanofluid, respectively. The angular velocity vector is $\Omega = [0, 0, \Omega ]$. $F^* = \frac{C_b}{\check{x}\sqrt{K_0}}$ denotes the non-uniform inertia coefficient due to porous medium, $K_0$ represents permeability of the porous medium, and $C_b$ stands for drag coefficient.

Table 2 Thermophysical characteristics of base fluid (H₂O) and nanoparticles (TiO₂)^42,43,44.

In high-temperature fluid systems, where transfer of energy occurs via conduction, convection, and electromagnetic emission, thermal radiation is crucial to the energy transfer process. To account for this mechanism, the radiative heat flux $Q_r^*$ is introduced in energy equation. It denotes the net energy transfer rate resulting from thermal radiation. The Rosseland estimation is executed to model this heat flux⁴⁵, expressed as $Q_r^*=-\frac{4\alpha _1^*}{3m^*}\frac{\partial \check{T}^4}{\partial \check{z}},$ where the Stefan-Boltzmann constant is $\alpha _1^*$, while $m^*$ is the coefficient of mean absorption. The nonlinear term $\check{T}^4$ is expanded about ambient temperature $\check{T}_\infty$ using a Taylor series, assuming small temperature variations, as

$$\check{T}^4=4\check{T}_\infty ^3\check{T}-3\check{T}_\infty ^4.$$

Substituting this approximation yields the linearized form of the radiative heat flux⁴⁶:

$$\begin{aligned} Q_r^*=-\frac{4\alpha _1^*}{3m^*}\frac{\partial \check{T}^4}{\partial \check{z}}=-\frac{16\alpha _1^*\check{T}_\infty ^3}{3m^*}\frac{\partial \check{T}}{\partial \check{z}}. \end{aligned}$$

(9)

The intermediate steps are presented in the Appendix. This formulation shows how radiation increases the dusty nanofluid’s effective thermal conductivity, affecting heat transfer. This kind of analysis is very important for making systems that work at high temperatures, like solar collectors, nuclear cooling channels, and rotating energy devices, where radiative heat transfer is the main way heat moves.

Using Eq. (9) in Eq. (4), we get

$$\begin{aligned} \left. \begin{array}{rr} \check{v}_1\frac{\partial \check{T}}{\partial \check{x}}+\check{v}_2\frac{\partial \check{T}}{\partial \check{y}}+\check{v}_3\frac{\partial \check{T}}{\partial \check{z}}=\frac{k_{nf}}{(\rho c_p)}_{nf}\frac{\partial ^2 \check{T}}{\partial \check{z}^2}+\frac{\nu _{nf}}{(c_p)}_{nf} \left[ \left( \frac{\partial \check{v}_1}{\partial \check{z}} \right) ^2+\left( \frac{\partial \check{v}_2}{\partial \check{z}} \right) ^2\right] \\ +\frac{1}{(\rho c_p)}_{nf}\frac{\partial }{\partial \check{z}}\left( \frac{16\alpha _1^*\check{T}_\infty ^3}{3m^*}\frac{\partial \check{T}}{\partial \check{z}}\right) -\frac{\rho _p(c_p)_f}{(\rho c_p)_{nf}\tau _{T}}(\check{T}-\check{T}_{p}) \end{array}.\right\} \end{aligned}$$

(10)

Boundary conditions

The associated boundary conditions are^33,47:

$$\begin{aligned} {\left\{ \begin{array}{ll} \check{v}_1=\check{v}_{1w} = b\check{x}, ~~\check{v}_2 = 0, ~~\check{v}_3 = 0, ~~\check{T} = \check{T}_w,~~ \text {as}~~ \check{z} = 0,\\ \check{v}_1 \rightarrow 0,~ \check{v}_{1p} \rightarrow 0,~ \check{v}_2 \rightarrow 0,~\check{v}_{2p} \rightarrow 0,~ \check{v}_{3p} \rightarrow \check{v}_3,~ \check{T} \rightarrow \check{T}_\infty ,\check{T}_p \rightarrow \check{T}_\infty , ~ \text {as } ~ \check{z} \rightarrow \infty , \end{array}\right. } \end{aligned}$$

(11)

here, $\check{T}_w$ is wall temperature, and $\check{T}_\infty$ represents ambient temperature.

Thermophysical properties

Experiments and theory suggest that nanofluids may demonstrate superior thermal conductivity compared to the base fluid. Enhancement occurs due to Brownian motion, interfacial effects, and significantly, nanoparticle aggregation, which create conductive networks that augment effective conductivity. In this study, we employ established mixture and aggregate models to simulate effective thermophysical properties, clearly delineating the underlying assumptions and their respective ranges of validity (Table 3).

The thermophysical properties of the nanofluid, considering nanoparticle aggregation, are defined as follows^48,49:

Table 3 Thermophysical properties with and without the presence of nanoparticle aggregation.

The thermal properties associated with nanoparticle aggregation (represented by the subscript ’agg’) are:

$$\begin{aligned} \rho _{agg}&= \rho _f(1 - \phi _{int}) +\rho _s \phi _{int},\\ \phi _{int}&=\left( \frac{R_{agg}}{R_p}\right) ^{3-D},\\ \phi _{agg}&= \frac{\phi }{\phi _{int}}, \\ k_{agg}&= \frac{k_f}{4} \left[ \frac{k_s}{k_f}(3\phi _{int} - 1) +\left( 3(1-\phi _{int})-1\right) +\left( \frac{k_s}{k_f}(3\phi _{int} - 1) +\left( 3(1-\phi _{int})-1\right) ^2+8\frac{k_s}{k_f}\right) ^{0.5}\right] ,\\ (\rho c_p)_{agg}&= (\rho c_p)_f(1 - \phi _{int}) + (\rho c_p)_s\phi _{int}. \end{aligned}$$

where $\phi _m$, $\phi$, $\phi _{int}$, and $\phi _{agg}$ denote the maximum particle packing fraction, nanoparticle volume fraction, nanoparticle volume fraction within the aggregate, and effective particle volume fraction of aggregates, respectively. According to fractal theory, $R_{agg}$ and $R_p$ represent the radii of aggregates and primary nanoparticles, respectively. The ratio $\frac{R_{agg}}{R_p}$ is assumed to be 3.34 and the value of $\phi _m$ is 0.605. D is the fractal index, typically 1.8 for spherical particles^50,51 and the value of $\phi$ is 0.03.

Transformations

To streamline the coupled nonlinear PDEs that dictate boundary-layer motion, suitable similarity transformations are employed. These transformations diminish the dimensional complexity of the problem by transforming the system into a series of ordinary differential equations that preserve the fundamental physical attributes of the flow. Such transformations facilitate efficient numerical calculations and enhance understanding of the impacts of governing parameters. Similarity transformations are expressed as follows^41,52

$$\begin{aligned} : {\left\{ \begin{array}{ll} \eta =\check{z}\left( \frac{b}{\nu _f}\right) ^{0.5},~~ \check{v}_1=b\check{x}F'(\eta ),~\check{v}_{1p}=b\check{x}F_p(\eta ),~\check{v}_2=b\check{x}G(\eta ),~(\check{T}_w-\check{T}_\infty )\theta (\eta )=\check{T}-\check{T}_\infty ,\\ ~(\check{T}_w-\check{T}_\infty )\theta _p(\eta )=\check{T}_p-\check{T}_\infty , \check{v}_{2p}=b\check{x}G_p(\eta ),~~ \check{v}_3=-\sqrt{b\nu _f}F(\eta ),~~~~\check{v}_{3p}=-\sqrt{b\nu _f}F_p(\eta ). \end{array}\right. } \end{aligned}$$

(12)

Dimensionless system

Application of transformations given in (12) satisfies Eqs. (1) and (5) automatically and all other governing equations are transformed as:

$$\begin{aligned}&\frac{\chi _1}{\chi _2}(F'''-K_pF')+2\Gamma _rG-(1+F_r)F'^2+FF''-\frac{\Gamma _v\beta _v}{\chi _2}(F'-F'_p)=0, \end{aligned}$$

(13)

$$\begin{aligned}&\frac{\chi _1}{\chi _2}(G''-K_pG)-2\Gamma _rF-F_rG^2+FG'-F'G-\frac{\Gamma _v\beta _v}{\chi _2}(G-G_p)=0, \end{aligned}$$

(14)

$$\begin{aligned}&\frac{1}{\chi _4 P_r}\left( \chi _3 +Rd\right) \theta ''+F\theta '-\frac{\gamma _t\beta _t}{\chi _4}(\theta -\theta _p)+\frac{\chi _1}{\chi _4}E_c\left( F''^2+G'^2\right) =0, \end{aligned}$$

(15)

$$\begin{aligned}&F_pF_p''-F_p'^2+2\Gamma _rG_p+\beta _v(F'-F_p')=0, \end{aligned}$$

(16)

$$\begin{aligned}&F_pG'_p-G_pF_p'-2\Gamma _rF_p'+\beta _v(G-G_p)=0, \end{aligned}$$

(17)

$$\begin{aligned}&F_p\theta _p'-\beta _t\gamma _t(\theta _p-\theta )=0. \end{aligned}$$

(18)

The transformed boundary conditions are:

$$\begin{aligned} {\left\{ \begin{array}{ll} G= 0,~~ F=0, ~~F'= 1, ~~ \theta = 1,~~ \text {for} ~~ \eta = 0\\ F_p' \rightarrow 0,~ F'\rightarrow 0, ~ G\rightarrow 0, ~~ \theta _p '\rightarrow 0, G_p\rightarrow 0, ~ F_p= F\rightarrow 0, ~ \text {for} ~ \eta \rightarrow \infty . \end{array}\right. } \end{aligned}$$

(19)

To address the altered thermophysical characteristics of the nanofluid due to nanoparticle aggregation, various dimensionless factors are proposed. The terms $\chi _1=\frac{\mu _{nf}}{\mu _f}$, $\chi _2=\frac{\rho _{nf}}{\rho _f}$, $\chi _3=\frac{k_{nf}}{k_f}$, and $\chi _4=\frac{(\rho c_p)_{nf}}{(\rho c_p)_f}$ represent the nanofluid-base fluid viscosity, density, thermal conductivity, and heat capacity ratios. These parameters show how nanoparticle incorporation affects momentum and heat transfer. The dimensionless parameters involved in above equations are: the porosity parameter $K_p$, rotation parameter $\Gamma _r$, Forchheimer number $F_r$, radiation parameter Rd, Prandtl number $P_r$, Eckert number $E_c$, and dusty fluid parameters ($\gamma _t, \beta _t, \beta _v, \Gamma _v$). The dimensionless parameters are defined as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} P_r=\frac{(\mu c_p)_f}{k_f},~\Gamma _r=\frac{ \Omega }{b},~ F_r=K_0^{-0.5}C_b,~~K_p=\frac{\nu _f}{bK_0},\\ \Gamma _v=\frac{mN}{\rho _f},~~~~~ \gamma _t=\frac{c_p}{c_m},~~~~~~~~~\beta _v=\frac{K}{bm},\\ \beta _t=\frac{1}{b\tau _t},~~~Rd=\frac{16\alpha _1^*\check{T}_\infty ^3}{3k_fm^*},~~~E_c=\frac{\check{v}_{1w}^2}{\left( \check{T}_w-\check{T}_\infty \right) (c_p)_f}. \end{array}\right. } \end{aligned}$$

(20)

Their dimensionless nature is demonstrated in the Appendix.

Engineering quantities

Skin friction coefficient $C_{f_x}$ and local Nusselt number $N_{u_x}$ are defined as^39,40:

$$\begin{aligned} C_{f_x}=\frac{\check{\tau }_w^x}{\check{v}_1^2 \rho _f}, \quad N_{u_x} = \frac{\check{x} \check{Q}_w}{k_f(\check{T}_w - \check{T}_\infty )}, \end{aligned}$$

(21)

where $\check{\tau }_w^x$ is shear stress at wall and $\check{Q}_w$ denotes heat flux at wall.

$$\begin{aligned} \check{\tau }_w^x=\left. \mu _{nf} \frac{\partial \check{v}_1}{\partial \check{z}} \right| _{\check{z}=0},\quad \check{Q}_w=-\left. \frac{k_f}{k_{nf}} \frac{\partial \check{T}}{\partial \check{z}} \right| _{\check{z}=0}+\left. \frac{4\alpha _1^*}{3m^*}\frac{\partial \check{T}^4}{\partial \check{z}} \right| _{\check{z}=0}. \end{aligned}$$

(22)

Using Eqs. (12) and (22), Eq. (21) takes the form:

$$\begin{aligned} Cf_x {Re}_x^{0.5}=\chi _1F''(0), \quad Nu_x {Re}_x^{-0.5}=-\left( \chi _3+\frac{4}{3}Rd\right) \theta '(0). \end{aligned}$$

(23)

Local Reynolds number is given by $\sqrt{Re_x}=\frac{\check{x}\sqrt{b}}{\sqrt{\nu _f}}$.

Entropy analysis

A dusty nanofluid system generates entropy due to the irreversible effects of drag and interphase momentum exchange as well as the intricate interaction between the fluid and dust particle phases. Given the strong relationship between the production of entropy and energy dissipation, the basic goal of thermodynamic optimization is to minimize entropy generation. It is possible to measure irreversibilities in dusty flows and to account for the energy loss due to dust-fluid coupling and porous resistance by undertaking an entropy evaluation. Measuring entropy production helps identify inefficiencies that may cause system problems. This approach is analogous to detecting operational or process mechanism defects, and once recognized, system efficiency can be greatly improved.

Maximizing thermodynamic efficiency while limiting entropy formation is still a major goal in many industrial and technological domains. The depletion of global energy supplies has emphasized the need to optimize the processes of energy generation, transformation, and application, driving the advancement of sustainable technologies that prioritize efficiency⁵³. The dimensional form of entropy generation rate $E_{gen}$ is given by^35,53,54:

$$\begin{aligned} E_{gen} = \underbrace{\frac{k_{nf}}{\check{T}_\infty ^2}\left[ 1+\frac{16\alpha _1^*\check{T}_\infty ^3}{3m^*k_f }\right] \left( \frac{\partial \check{T}}{\partial \check{z}}\right) ^2}_{\text {irreversibility of heat transfer}} + \underbrace{\frac{\mu _{nf}}{\check{T}_\infty }\left[ \left( \frac{\partial \check{v}_1}{\partial \check{z}}\right) ^2+\left( \frac{\partial \check{v}_2}{\partial \check{z}} \right) ^2\right] }_{\text {irreversibility of fluid friction}} + \underbrace{\frac{\mu _{nf} }{\check{T}_\infty K_0}\left( \check{v}_1^2+\check{v}_2^2\right) }_{\text {irreversibility of porous medium}}. \end{aligned}$$

(24)

Equation (24) reveals three main sources of entropy generation in dusty nanofluid: heat transfer due to temperature gradient, viscous dissipation resulting from interphase drag between dust and fluid particles, and flow resistance within the porous medium. The volumetric entropy generation rate Ns, defined as the ratio of $E_{gen}$ to $E_0$, where $E_0=\left( \frac{\check{T}_w-\check{T}_\infty }{\check{T}_\infty }\right) ^2\frac{bk_{f}}{\nu _f}$^53,54, represents the characteristic entropy generation. By using transformations (12), Eq. (24) becomes

$$\begin{aligned} Ns=\frac{E_{gen}}{E_0}=\chi _3\left( 1+Rd\right) \theta '^2+\chi _1Br\delta \left( F''^2+G'^2\right) +\chi _1Br\delta K_p\left( F'^2+G^2\right) . \end{aligned}$$

(25)

The detailed derivation of Eq. (24) and the reduction of Eq. (25) is given in the Appendix. Above, the dimensionless temperature difference parameter $\left( \delta =\frac{\check{T}_\infty }{\check{T}_w-\check{T}_\infty }\right)$ illustrates the temperature gradient over the boundary layer by comparing the ambient temperature to the surface temperature differential. It is a measure of the system’s non-isothermality, which controls the rate of heat transfer from the surface to the fluid around it. The Brinkman number $\left( Br=\frac{\check{v}_{1w}^2\mu _f}{\Delta \check{T}k_f}\right)$ shows the ratio of heat transfer due to viscous dissipation to heat transfer due to conduction. It measures how much of the overall energy loss is attributable to viscous heating as a result of friction between fluid particles and between phases. In dusty nanofluids, higher Br values signify increased viscous effects due to particle drag, thereby intensifying local entropy generation.

Quantifying the various entropy-generating components in a dusty nanofluid helps evaluate how dust particles alter energy dissipation within the boundary layer. The Bejan number defined mathematically as^7,55, is an important dimensionless number for this assessment.

$$\begin{aligned} Be=\frac{\text {Heat transfer entropy generation}}{\text {Total entropy generation}}, \end{aligned}$$

(26)

non-dimensionalized form is as follows:

$$\begin{aligned} Be=\frac{\chi _3\left( 1+Rd\right) \theta '^2}{Ns}. \end{aligned}$$

(27)

Methodology

The resulting system of ordinary differential equations is highly nonlinear, making it difficult to acquire accurate analytical solutions. Therefore, robust numerical approaches are required to solve the system. To address this, the numerical solution for the nonlinear ODEs (13–18) subject to the boundary conditions (19) is obtained using the advanced boundary value problem solver bvp4c in MATLAB. This solver employs a collocation method with adaptive mesh refinement. The problem-solving flowchart is depicted in Fig. 2. The original boundary value problem (BVP) is systematically converted into an initial value problem (IVP) to make the numerical technique easier to apply. This transformation entails meticulously selecting and incorporating specific variables to ensure the procedure’s efficacy. Error control and adaptive mesh refinement are included in the computational process and are gradually improved based on the computations’ residuals⁵⁶. The boundary layer region is determined for every set of parameter values, allowing for a thorough examination of the system’s behavior. With a tolerance level of $10^{-6}$, the numerical scheme converges, demonstrating the accuracy and dependability of the bvp4c solver.

Fig. 2

Problem-solving flowchart for the present work.

The new variables are:

$$\begin{array}{cccc} F = \hat{y}_1, & F' = \hat{y}_2, & F'' = \hat{y}_3, & G = \hat{y}_4, \\ G' = \hat{y}_5, & \theta = \hat{y}_6, & \theta ' = \hat{y}_7, & F_p = \hat{y}_8,\\ F_p = \hat{y}_9, & G_p = \hat{y}_{10}, & \theta _p = \hat{y}_{11}. \end{array}$$

The system of first-order ODEs is

$$\begin{aligned} \hat{y}_1'= & \hat{y}_2, \end{aligned}$$

(28)

$$\begin{aligned} \hat{y}_2'= & \hat{y}_3, \end{aligned}$$

(29)

$$\begin{aligned} \hat{y}_3'= & K_p \hat{y}_2 - \frac{2\Gamma _r \hat{y}_4 \chi _2}{\chi _1} + \frac{(1+F_r)\hat{y}_2^2 \chi _2}{\chi _1} - \frac{\hat{y}_1 \hat{y}_3 \chi _2}{\chi _1} + \frac{\Gamma _v \beta _v \chi _2}{\chi _1}(\hat{y}_2 - \hat{y}_9), \end{aligned}$$

(30)

$$\begin{aligned} \hat{y}_4'= & \hat{y}_5, \end{aligned}$$

(31)

$$\begin{aligned} \hat{y}_5'= & K_p \hat{y}_4 + \frac{2\Gamma _r \hat{y}_2 \chi _2}{\chi _1} + \frac{F_r \hat{y}_4^2 \chi _2}{\chi _1} - \frac{\hat{y}_1 \hat{y}_5 \chi _2}{\chi _1} + \frac{\hat{y}_2 \hat{y}_4 \chi _2}{\chi _1} + \frac{\Gamma _v \beta _v (\hat{y}_4 - \hat{y}_{10})}{\chi _1}, \end{aligned}$$

(32)

$$\begin{aligned} \hat{y}_6'= & \hat{y}_7, \end{aligned}$$

(33)

$$\begin{aligned} \hat{y}_7'= \frac{- \chi _4 P_r \hat{y}_1 \hat{y}_7 + \gamma _t P_r \beta _t (\hat{y}_6 - \hat{y}_{11}) - \chi _1 P_r E_c \left( \hat{y}_3^2 + \hat{y}_5^2 \right) }{\chi _3 +Rd}, \end{aligned}$$

(34)

$$\begin{aligned} \hat{y}_8'= & \hat{y}_9, \end{aligned}$$

(35)

$$\begin{aligned} \hat{y}_9'= & \frac{\hat{y}_9^2-2\Gamma _r\hat{y}_{10} - \beta _v (\hat{y}_2 - \hat{y}_9)}{\hat{y}_8}, \end{aligned}$$

(36)

$$\begin{aligned} \hat{y}_{10}'= & \frac{\hat{y}_9\hat{y}_{10} +2\Gamma _r\hat{y}_{9}- \beta _v (\hat{y}_4 - \hat{y}_{10})}{\hat{y}_8}, \end{aligned}$$

(37)

$$\begin{aligned} \hat{y}_{11}'= & \frac{\beta _t \gamma _t (\hat{y}_{11} - \hat{y}_6)}{\hat{y}_8}. \end{aligned}$$

(38)

Transformed initial conditions are:

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{y}_1(0) = 0,~~~~~~\hat{y}_4(0) = 0,~~~~~~\hat{y}_2(0) = 1,~~~~~~~~\hat{y}_6(0) = 1,\\ \hat{y}_9(\infty ) \rightarrow 0,~\hat{y}_2(\infty ) \rightarrow 0,~\hat{y}_4(\infty ) \rightarrow 0,\hat{y}_{11}(\infty ) \rightarrow 0,\hat{y}_{10}(\infty ) \rightarrow 0,\hat{y}_8(\infty ) = \hat{y}_1(\infty ) \rightarrow 0. \end{array}\right. } \end{aligned}$$

(39)

The computational domain was truncated at a suitable finite value of $\eta _{\infty } = 12$, which was determined numerically to adequately represent the asymptotic boundary conditions. The solver’s convergence was governed by relative and absolute tolerance settings of $10^{-3}$ and $10^{-6}$, respectively, ensuring that the maximum absolute residuals of the differential equations and boundary conditions satisfied the criterion $\max |\text {Residuals}| < \max (\text {AbsTol}, \text {RelTol} \times |\text {Solution}|)$. Mesh selection and error control were automatically handled by the algorithm based on the residual monitoring of the continuous solution. Different mesh sizes are shown by the relative error in Fig. 3. As the mesh is refined, the error goes down, reaching a minimum of 0.0002493 at a mesh size of 300. This shows that the chosen mesh achieves the best possible numerical accuracy and computational efficiency for this study.

Fig. 3

Relative error for different mesh sizes.

Results and discussion

This section emphasizes interpreting the physical features of the embedded variables on velocity profiles ($F'(\eta )$, $F_p(\eta )$, $G(\eta )$ and $G_p(\eta )$), temperature profiles ($\theta (\eta )$ and $\theta _p(\eta )$), entropy generation ($Ns$), and Bejan number ($Be$), demonstrating the significance of nanoparticle aggregation. The findings are explained in detail via the graphic illustrations, clearly showing the observed trends. For limited cases, Tables 4 and 5 compare the skin friction and local Nusselt number with Rashid et al.⁴⁷. These findings align with reported studies.

The default values of parameters and their ranges are selected based on their physical significance to encompass a broad spectrum of flow behaviors. The default values of physical parameters are: $P_r=6.2$, $E_c=0.1$, $\beta _v=0.2$, $\beta _t=0.1$, $\Gamma _v=0.2$, and $\gamma _t=0.2$. The porosity parameter ($K_p = 0.3{-}2.7$) shows the transition of highly dense medium to significantly permeable. This shows the influence on the degree of fluid penetration through the porous structure. The rotation parameter ($\Gamma _r = 0.5{-}2.5$) shows varying Coriolis effects, ranging from weak to strong rotational motion relevant to geophysical and industrial uses. The Forchheimer number ($F_r = 1{-}6$) measures the change from Darcy to non-Darcy regimes and includes inertial effects that are important at higher flow velocities. The radiation parameter ($Rd = 1{-}3$) corresponds to weak-to-moderate radiative heat transfer, ensuring thermal effects remain within practical operational limits. These ranges of parameters collectively ensure that both theoretical and realistic physical conditions are adequately represented in the analysis.

Table 4 Comparison of skin friction with Rashid et al.⁴⁷ via $\Gamma _r$, $K_p$, and $F_r$, while neglecting other parameters.

Table 5 Comparison of Nusselt number with Rashid et al.⁴⁷ via $K_p$, $\Gamma _r$, and $P_r$, while neglecting other parameters.

Velocity profiles

Figures 4, 5, and 6 demonstrate the influence of embedded parameters on axial and transverse velocities in both fluid and dust phases. Figure 4 illustrates the impact of rotation parameter $\Gamma _r$ on axial velocities $(F'(\eta ), F_p(\eta ))$ and transverse velocities $(G(\eta ), G_p(\eta ))$ for both phases. $\Gamma _r$ quantifies the rotational intensity acting through the Coriolis force, which redistributes momentum between velocity components. As $\Gamma _r$ increases, the Coriolis force attenuates the axial flow while amplifying the transverse velocity, directing part of flow energy toward the perpendicular direction to maintain momentum balance. The maximum axial velocity occurs at $\Gamma _r = 0$, indicating pure stretching-driven flow. Physically, as $\Gamma _r$ grows, the rotational influence dominates over the stretching rate, hindering fluid mobility along the $x$-direction and thereby thinning the boundary layer. Figure 4b also confirms that $\Gamma _r$ promotes flow in the negative y-direction. At low $\Gamma _r$, flow follows the exponential decay pattern $-\eta \exp (-\eta )$, while oscillatory behavior emerges at larger $\Gamma _r$ due to intensified Coriolis effects. Similar results are found by Lou et al.³⁸. Figure 5 explains the variation in velocities caused by porosity parameter $K_p$. As $K_p$ increases, the axial velocities of both phases decrease due to enhanced drag and viscous resistance introduced by the porous medium. Higher porosity signifies more flow resistance, which not only lower axial motion but also diminishes the transverse velocities. Figure 6 portrays the influence of Forchheimer number $F_r$ on $F'(\eta )$, $F_p(\eta )$, $G(\eta )$ and $G_p(\eta )$. The Forchheimer number represents nonlinear inertial resistance in a porous medium. Both axial and transverse velocities decrease as $F_r$ increases, suggesting that inertial drag increases the total resistance to motion by supplementing viscous friction. Rehman et al.⁵⁷ yielded analogous results for Figs. 5 and 6. Furthermore, Figs. 4, 5, and 6 show that when compared to the homogeneous nanoparticle model, the model that takes nanoparticle aggregation into account shows a discernible decrease in both velocity components. The aggregation raises the fluid’s effective viscosity that slows down the axial and transverse fluid velocities by increasing flow resistance. In rotating filtration and cooling systems, where regulating the Coriolis-induced flow redistribution and porous drag aids in preserving the intended flow uniformity and efficiency, these velocity trends are extremely significant.

Fig. 4

Variation in velocity profiles against $\Gamma _r$.

Fig. 5

Variation in velocity profiles against $K_p$.

Fig. 6

Variation in velocity profiles against $F_r$.

Temperature profiles

The effects of different parameters on the temperature profiles $\theta (\eta )$ and $\theta _p(\eta )$ are shown in Figs. 7 and 8. Figure 7 shows that the temperature of both phases increases with the rotation parameter $\Gamma _r$. Enhanced rotation promotes heat exchange between the fluid and particles by strengthening shear interactions and energy dissipation. As a result, the system’s total thermal energy rises as $\Gamma _r$. The findings of Lou et al.³⁸ echo this pattern for the rotation parameter. Higher porosity parameter $K_p$ intensifies temperature because of increased viscous dissipation and frictional heating within the porous medium. Higher thermal fields are produced for both phases as a result of the increased resistance. Rehman et al.⁵⁷ also observed similar trends in their study. Figure 8a reveals a similar trend for the Forchheimer number $F_r$. The nonlinear flow resistance due to inertial effects results in increased energy dissipation as heat, hence elevating $\theta (\eta )$ and $\theta _p(\eta )$, supported by Rehman et al.⁵⁷. Figure 8b indicates that the radiation parameter Rd substantially increases both $\theta (\eta )$ and $\theta _p(\eta )$. Since $Rd=\frac{16\alpha _1^*\check{T}_\infty ^3}{3k_fm^*}$, higher values of Rd reduce the mean absorption coefficient, enhancing radiative heat transfer and thus raising thermal energy in the boundary layer. This result mirrors the findings of Bhatti et al.⁵⁸. Additionally, Figs. 7 and 8 show that the temperature profiles of the model accounting for nanoparticle aggregation are marginally elevated compared to those of the homogeneous model, since aggregation amplifies interparticle interactions, hence enhancing the thermal conduction and storage capacity of the nanofluid^59,60. Such temperature behavior is critical for designing rotational heat exchangers and electronic cooling equipment, since regulating radiative and viscous heating effects provides thermal stability and performance reliability.

Fig. 7

Variation in temperature profiles against $\Gamma _r$ and $K_p$.

Fig. 8

Variation in temperature profiles against $F_r$ and Rd.

Entropy generation and Bejan number

Figure 9 shows that increasing rotation and porosity parameters increase the entropy generation rate Ns, whereas the Bejan number Be exhibits an inverse response. The increase in entropy generation due to rotation results from enhanced Coriolis and centrifugal forces, which disrupt the orderly fluid motion and create more pronounced velocity gradients. These gradients enhance viscous dissipation, resulting in increased energy loss and thermodynamic irreversibility in both the fluid and dust phases. Concurrent with increased porosity, internal friction and interphase drag are amplified, resulting in enhanced mechanical energy conversion into heat via microscale interactions between dust particles and the fluid matrix. As a result, the system becomes increasingly dissipative, raising Ns. The Bejan number, representing a heat loss ratio to total entropy creation, declines with rising porosity and rotation parameters. It in place of Tt signifies that the viscous effects prevail over thermal irreversibility as flow resistance escalates.

The impact of the Forchheimer number on Ns and Be is highlighted in Fig. 10a. Near the boundary layer, an increase in $F_r$ strengthens inertial resistance and accelerates momentum diffusion, thereby increasing entropy formation through viscous dissipation. Away from the wall, the effect of inertia diminishes, resulting in a progressive decrease in energy dissipation and entropy generation. The reduction in Be with increased $F_r$ indicates a transition from thermal to viscous entropy production, affirming that inertial drag amplifies mechanical irreversibility within the porous structure.

The influence of radiation parameter Rd on entropy and Bejan number is presented in Fig. 10b. As radiative heat transport strengthens, more energy is absorbed and re-emitted within the boundary layer, augmenting thermal gradients and promoting higher thermal entropy generation. This improvement happens because radiation makes fluid particles exchange energy more quickly, which speeds up thermal diffusion and irreversible heat transfer. But too much radiation can change the temperature distribution in the area, which can make conduction-dominated heat transfer near the wall less effective. Entropy production increases with radiation amplification because energy scatters more. It can lower conduction-driven entropy in some locations, causing the boundary layer’s irreversibility to be unevenly distributed. These observed trends are in line with those of Hayat et al.⁶¹.

Furthermore, the presence of nanoparticle aggregation amplifies entropy generation while lowering the Bejan number. Aggregated particles enhance effective viscosity and thermal coupling, hence amplifying both viscous and heating dissipation rates. Consequently, entropy generation increases due to intensified particle–fluid interactions and resistance to motion, while the decrease in Be indicates that viscous factors increasingly dictate the overall irreversibility of the system. Comprehending the roles of rotation, porosity, and radiation in entropy formation is essential for the design of energy-efficient porous systems, where the reduction of viscous irreversibility is crucial for enhanced thermal control.

Fig. 9

Variation in Ns and Be against $\Gamma _r$ and $K_p$.

Fig. 10

Variation in Ns and Be against $F_r$ and Rd.

Skin friction coefficient and the Nusselt number

The variations of the skin friction $Cf_x {Re}_x^{0.5}$ and local Nusselt number $Nu_x {Re}_x^{-0.5}$ are depicted in Fig. 11. The local Nusselt number characterizes the heat transfer rate, while skin friction coefficient quantifies the surface shear stress. As observed in Fig. 11a, increasing the Forchheimer’s number and rotation parameter results in a more negative skin friction coefficient, signifying enhanced opposing shear at the wall. This trend results from increased inertial and resistive forces that amplify near-wall momentum retardation in the porous medium. Non-aggregated nanoparticles, due to their uniform dispersion, promote smoother momentum transfer with the base fluid, resulting in a comparatively less negative wall shear than their aggregated counterparts. As seen in Fig. 11b, non-aggregated nanoparticles exhibit superior heat transfer performance compared to aggregated ones owing to their uniform dispersion and larger effective surface area, which promote enhanced thermal conduction. Ali et al.⁴⁹ validate these findings. It shows that preventing clustering of nanoparticles markedly increases the Nusselt number despite the absence of aggregation-induced microchannels often thought to aid heat convection. This improved thermal response of non-aggregated model highlights the crucial role of nanoparticle stability in achieving efficient energy transport in rotating nanofluid systems. Conversely, increasing $F_r$ and $\Gamma _r$ reduces the Nusselt number by intensifying flow resistance and disturbing the thermal boundary layer, thereby weakening convective heat transport. These findings emphasize the necessity of preserving nanoparticle dispersion and reducing flow resistance in practical applications such as nuclear cooling systems and high-speed rotating machinery, where the increase of heat transfer directly influences operational safety and efficiency.

Fig. 11

Variation in $Cf_x {Re}_x^{0.5}$ and $Nu_x {Re}_x^{-0.5}$ against $F_r$ and $\Gamma _r$.

Conclusion

This study examined the nonlinear radiative flow and entropy generation in a rotating dusty nanofluid system, incorporating the combined effects of nanoparticle aggregation, Coriolis effects, Darcy–Forchheimer drag, and viscous dissipation. The governing PDEs were reduced to nonlinear ODEs via similarity transformations and solved using MATLAB’s built-in bvp4c. Main findings drawn from this study are

• Nanoparticle aggregation reduces both axial and transverse velocities due to increased drag. However, it enhances temperature distribution and thermal conductivity, which can be useful in high-temperature applications like compact cooling systems and rotating thermal exchangers.

• Aggregation reduces the Nusselt number nearly 20% in the aggregated case as compared to non-aggregated one, indicating reduced heat transfer efficiency due to clusters.

• The Bejan number decreases by about 15% in the aggregated case relative to non-aggregated case, indicating diminished entropy generation.

• Stronger Coriolis effects suppress flow mobility but thicken the thermal boundary layer. It signifies that rotational intensity helps in flow regulation and heat dispersion in rotating filtration and energy systems.

• Radiation intensifies temperature and entropy generation, elevating the Bejan number, which shows its significance in high-temperature rotating configurations.

• Increasing porosity and Forchheimer number increase thermal boundary layer and entropy generation while lowering momentum and Bejan number. These characteristics are valuable in designing energy-efficient porous rotating systems with controlled permeability and inertial resistance.

Limitations and future research directions

The current model exclusively accounts for steady, laminar, and incompressible flow, whereas real-world systems often exhibit unstable or turbulent conditions that influence flow and heat transfer. Linear drag and energy exchange variables model the dust-fluid interaction without including interparticle collisions or dust-dust interactions, which could affect dispersion in dense or strongly rotating regimes. The magnetic field is assumed to be uniform and perpendicular to the flow; however, actual configurations typically exhibit nonuniform or inclined fields. The presumption of homogeneous aggregate size overlooks polydispersity that alters viscosity and conductivity. The numerical method appears dependable; nonetheless, experimental confirmation would enhance its expected reliability.

Future research may expand the current model to encompass unsteady or transient regimes. The framework can be expanded to elucidate intricate rheological phenomena in hybrid or tri-hybrid dusty nanofluids. Hall currents, nonuniform magnetic fields, and electromagnetohydrodynamic interactions would enhance physical realism. Incorporation of variable particle sizes and thermal nonequilibrium between dust and fluid is feasible. Experimental validation and sophisticated computational techniques, such as finite element method, could enhance precision. The research of entropy formation must include heat generation, chemical processes, and other irreversibilities to enhance the understanding of thermodynamic performance.