Introduction

Climate change and rising urbanisation have intensified the risks of urban waterlogging, highlighting the necessity for enhanced urban resilience (systems) to mitigate these hazards effectively1,2. Resilient systems are inherently sophisticated, with current understanding emphasising only their emergent characteristics and the interplay between micro- and macro-level characteristics3. This perspective aims to grasp the practical implications of the emergence and the holistic nature of building resilient systems, underlining their significance in disaster management. Research on this topic has established that resilient systems display scale effects and cascade attributes, with variations in spatial scales influencing the geographic scope and precision of the analysis4,5. How scales are defined and the precision of analysed units can greatly influence our understanding of the functioning of resilient systems6. Therefore, deepening the knowledge of resilient systems is crucial for formulating more effective urban disaster risk management strategies.

The theory of adaptive cycling, proposed by ecologist Holling, plays a pivotal role in examining the complexity and dynamic shifts in resilience. This framework elucidates the essence of resilience theory’s sustainable development and sets forth the theoretical objective of achieving cross-scale dynamic interactive cycles and systemic innovative breakthroughs7. With this goal in mind, waterlogging disaster prevention and resilience research has accumulated considerable empirical evidence regarding scale effects. These studies primarily focus on boosting waterlogging resilience directly via adjustments in the urban built environment8,9 and indirectly by managing extreme climate phenomena such as heat and rain islands10. It includes an investigation of both the general and spatially heterogeneous features of waterlogging disaster risks and resilience at individual scales11. In addition, it involves comparative studies on the impact of causative factors on disaster adaptation across various scales4.

A majority of studies on waterlogging resilience tend to focus on a single scale, analysing specific characteristics or patterns based on the selected research object and context. However, given the intricacy of waterlogging resilience systems, their overall behaviour cannot be fully grasped via the single-scale analysis alone. Instead, it is crucial to consider resilience across multiple scales to capture a more inclusive understanding of the system’s dynamics12. From a multiscale perspective, common approaches include examining how single spatial elements affect disaster resilience across multiple scales13, assessing how several spatial elements affect disaster resilience at a single scale14,15, and comparing the similarities or differences in impact mechanisms across different scales16. A research paradigm encompassing three levels, namely macro, meso and micro, has emerged. The macro-scale generally refers to the broader region comprising the city or a watershed shaped by hydrological characteristics. The mesoscale focusses on divisions such as cities, neighbourhoods or communities. Moreover, the micro-scale concentrates on smaller units such as land parcels, building blocks or engineered facilities to minimise waterlogging risks. Based on this foundation, the scale transition in the local district management as a spatial governance strategy has become increasingly varied in practical applications. This flexibility enables cities to regulate their capacity to adapt to waterlogging disasters, effectively managing the dynamics between the expansion and contraction of spatial and administrative powers17. From the systems theory perspective, analysing spatial laws’ commensurability and ergodicity across multiple scales must first address the primary challenge of identifying the critical scales at which these laws remain consistent18. However, the selection of scales in single-scale and multiscale studies tends to be more determined by the availability of data or administrative boundaries than by the evolving patterns of resilient systems. It also raises another tricky issue: Do the indicators used to assess waterlogging resilience levels correspond with the scale structure of the resilient system? Addressing this issue underscores a considerable challenge in aligning empirical research with theoretical constructs in resilience studies.

Furthermore, multiscale resilience often exhibits mutual feedback effects across scales19. It is manifested explicitly in that resilience features at various scales are not isolated but are distinguished by cross-scale and multi-system coupling20. Scholar D. Peters has developed a theoretical framework for cross-scale interactions, which is instrumental in understanding and predicting the non-linear dynamic mechanisms of disaster processes across scales21. Accordingly, numerous scholars have investigated waterlogging resilience and evolutionary features across various scales, applying their findings to climate change response and disaster recovery efforts. For example, their research has delved into dynamic feedback loops22,23, causal inference24, spatial and temporal dynamics predictions25, and cascading effects within the disaster chain of waterlogging resilience systems26. These studies underscore the challenges posed by spatial scale suspension in planning discourse (i.e. highlighting spatial scale transitions) and the ensuing cascading effects within waterlogging resilience systems.

As the systemic nature of waterlogging resilience systems becomes increasingly understood, some scholars have recognised that the features determining resilience to waterlogging are spatially non-stationary. They propose that urban resilience to waterlogging hazards operates via similar mechanisms across different scales but with varying degrees of influence5,27. The transmission of resilience effects from fine to larger spatial scales can occur rapidly (amplifying the response) or slowly (buffering the response), depending on the spatial configuration, connectivity and mobility within and between units21. The above conclusions indicate that accurately identifying the scale structure and operational dynamics of waterlogging resilience systems and managing waterlogging disasters can enhance urban resilience and raise disaster adaptation efficiency. However, existing studies focus on refining scale nesting theory and critiquing single-scale and multiscale research limitations. Much of the research also underlines the scale effects within individual resilience systems (e.g. ecological resilience)19,28. In contrast, there is a paucity of in-depth analysis regarding the aspects of scale nesting and threshold effects across multiple scales, particularly within the context of urban disaster resilience.

Given the above analysis, this study seeks to address three crucial scientific questions: (1) Do the critical scales at which substantial improvements in urban waterlogging resilience occur correspond with urban management scales? (2) Are the key indicators influencing the effectiveness of waterlogging disaster adaptation consistent across these scales? (3) Are these indicators’ non-linear relationships and threshold effects on disaster adaptation consistent across different scales? The researchers selected Xiamen Island (XMI) in Fujian Province, China, as a case study. By applying urban multi-source data fusion techniques, network percolation models and machine learning methods, this paper aims to address these questions. The findings present a detailed understanding of the emergence and integrated nature of a complex waterlogging resilience system, offering valuable insights to enhance urban resilience and upgrade disaster adaptation efficiency.

Compared to existing research, this study makes several major innovative contributions: First, we conceptualize a novel integration of adaptive cycle theory with the phenomenon of spatial scale suspension, allowing us to systematically assess whether the critical thresholds of waterlogging resilience transitions correspond with existing scales of urban governance. By uncovering the latent connections between spatial governance scales and the emergent properties of resilience systems, our findings highlight the inherent nonlinearities and threshold effects that structure system behavior, thereby providing both a new theoretical lens and empirical evidence to advance understanding of cross-scale dynamics in urban resilience. Second, we integrate percolation network modeling with interpretable machine learning to establish a robust framework for identifying the scale architecture of localized waterlogging resilience systems, thereby moving beyond conventional approaches constrained by static scale delineations and linear assumptions. Beyond improving the precision and rigor of scale structure identification, this framework offers high-density cities a transferable reference for dynamic regulation that transcends administrative boundaries, thereby charting new pathways to strengthen adaptive capacity in the face of urban disaster risks.

Data and methods

This study investigates the scale effects of an urban waterlogging resilience system and the hierarchical impacts of individual resilience indicators from the perspective of multiscale spatial differentiation. Figure 1 outlines the research approach of this study. (1) The core indicators of the urban waterlogging resilience system were extracted using the theoretical framework offered by the ‘Pressure-State-Response (P-S-R)’ model. These indicators are then quantified and spatialised using ArcGIS tools. After establishing the spatial scale of the smallest unit, the entropy weighting method is applied to comprehensively assess the waterlogging resilience level of the study region. (2) A network percolation model is employed to determine the critical scales corresponding to the emergent patterns of the area’s waterlogging resilience system. (3) The gradient-boosting decision tree (GBDT) algorithm is applied to examine the non-linear relationships between resilience indicators and the effectiveness of waterlogging disaster adaptation across different scales and identify threshold effects.

Note: The satellite imagery used as the base layers in Figures 1–4 was sourced from the Landsat-8 Operational Land Imager (OLI) dataset provided by the United States Geological Survey (USGS; https://earthexplorer.usgs.gov). Specifically, the imagery corresponds to the Landsat-8 OLI scene (Scene ID: LC08_L1TP_119043_20210215_20210301_02_T1), acquired on February 15, 2021. All imagery preprocessing, spatial analysis, and map visualizations were conducted using ArcGIS 10.8.

Fig. 1
figure 1

Research framework.

Full size image

Study area

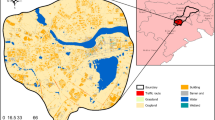
Xiamen Island (XMI) is located in the southeastern coastal region of China (24°24’ N–24°34’ N, 118°04’ E–118°16’ E) and serves as one of the core areas of Xiamen, Fujian Province. As of 2023, XMI had a resident population of approximately 2,067,000, with an urbanisation rate nearing 100%. Although XMI comprises only 6% of Xiamen’s land region, it accommodates about 39% of the city’s population, making it a highly urbanised and densely populated urban island (Fig. 2).

Fig. 2
figure 2

Study area.

Full size image

Because of its unique geographic location and monsoon climate, XMI frequently experiences short-term extreme rainfall events. The island’s high level of urbanisation, dense building concentration and extensive hardened surfaces hinder rapid rainwater infiltration, placing immense pressure on the drainage system. It often leads to poor drainage and rainwater backups. Consequently, XMI has repeatedly faced severe waterlogging events, highlighting its vulnerability and the urgent need to increase the efficiency of its resilience system.

Data sources

Multi-source urban geo-big data were used to comprehensively characterise the waterlogging resilience of XMI and its adaptive responses to waterlogging hazards. The primary data sources include land use, elevation, building, road and municipal facility quality data (Table 1). In addition, statistics on waterlogging events were incorporated to assess the adaptive effects of these hazards. This information, primarily derived from the records of significant rainstorms in 2022, was collected from local government agencies such as the Transportation Bureau, Water Bureau and Disaster Emergency Management Bureau. These records cover disasters that impacted residents’ daily lives and production activities.

Public opinion information on waterlogging events in XMI was also gathered to supplement the official data using web crawler technology. Using data from 1 January 2022 to 31 December 2022, information about rainstorm events on XMI was collected using web scraping Weibo posts and applying text mining techniques. Keywords such as ‘heavy rain’, ‘waterlogged’ and ‘flooded’ were used to identify relevant posts. The collected texts were then filtered, de-duplicated and analysed to extract adequate spatial location information related to the waterlogging events. Wang et al. provided a detailed account of the data acquisition and processing methods used in this study5.

Table 1 Data sources.
Full size table

Methods

Evaluation of waterlogging resilience levels based on the entropy weight method

The P-S-R theoretical model effectively illustrates the interactions between waterlogging disasters and resilience mechanisms29,30. The P-S-R framework was translated into six subsystems specific to the study area by reviewing and synthesising existing research: natural and geographical conditions, land cover conditions, microclimate conditions, road confluence conditions, and municipal infrastructure conditions. This analysis identified a comprehensive waterlogging resilience indicator system comprising 20 secondary indicators (Table 2).

Table 2 Urban waterlogging resilience evaluation index system and selection criteria.
Full size table

The fundamental statistical unit used to measure the level of waterlogging resilience was specified and designated as the minimum scale unit of the XMI waterlogging resilience multiscale structure. Considering the systematic synergy of urban elements in disaster resilience performance, this study preliminarily applied the neighbourhood unit scale (approximately 300 m × 300 m) specified in the Urban Residential Area Planning and Design Standards (GB50180-2018) as the minimum spatial scale. This scale encompasses multiple types of waterlogging resilience elements, somewhat reflecting the localised and independent operation of the resilience system. It aligns with common scale standards for urban spatial management in China. Based on this phenomenon, a homogeneous grid covering the study area quantified and spatialised the features of each element using tools such as ArcGIS, Fragstats and SDNA, and the quantitative results of each resilience indicator with this grid scale were spatially correlated to construct a spatial dataset of the waterlogging resilience components for XMI (Fig. 3).

Fig. 3
figure 3

Quantification and spatialisation of XMI waterlogging resilience indicators.

Full size image

Finally, the entropy weight method was employed to objectively determine the weight of each indicator, providing a comprehensive evaluation of the waterlogging resilience level of XMI. Rooted in information theory, this method quantifies the uncertainty of indicator distributions through entropy, assigning higher weights to indicators with greater discriminative power. By deriving weights directly from data, it minimizes human bias and ensures objectivity and consistency41. The calculation process is detailed as follows:

Standardise each indicator:

$$\:{r}_{ij}=\frac{{x}_{j}-{x}_{min}}{{x}_{max}-{x}_{min}}$$
(1)

where \(\:{x}_{j}\)is the actual value of indicator j, \(\:{x}_{min}\) and \(\:{x}_{max}\) are the minimum and maximum values of the indicator, respectively.

Calculate the entropy weight of each indicator:

$$\:{p}_{ij}=\frac{{r}_{ij}}{\sum\:_{i=1}^{m}{r}_{ij}}$$
(2)
$$\:{e}_{j}=-k\sum\:_{i=1}^{m}{p}_{ij}\text{ln}{p}_{ij}$$
(3)
$$\:{w}_{i}=\frac{(1-{e}_{j})}{\sum\:_{j=1}^{n}\left(1-{e}_{j}\right)}=\frac{{d}_{j}}{\sum\:_{j=1}^{n}{d}_{j}}$$
(4)

where \(\:{p}_{ij}\) is the proportion of each indicator; \(\:{e}_{j}\) is the information entropy of each indicator; \(\:{w}_{i}\) is the entropy weight of each indicator; \(\:m\) is the sample size; k is a constant, usually \(\:k=1/\text{ln}\left(m\right)\); and \(\:{d}_{j}\) is the differentiation degree of the information entropy.

Identification of key scales for waterlogging resilience based on network percolation model

Network percolation models are valuable tools for determining emergent patterns and critical scales of connectivity within complicated systems. They are particularly effective in delineating scale boundaries and revealing the nested structures characterising these systems42. This study conceptualised the waterlogging resilience system as a convoluted network of numerous interdependent resilience units. Using a network percolation model, this paper predicted the critical scale nodes where resilience-level shifts occur due to the connectivity and interdependence of these fundamental units.

First, the critical parameters for network percolation modelling were pre-processed using ArcGIS. The fundamental unit used in Sect. 2.3.1 to evaluate waterlogging resilience served as the foundation for developing a multiscale nested structure. A two-layer topological network layer, R(V, E), incorporating resilience attributes, was constructed using ArcGIS spatial analysis tools. In this network, V represents the connection of waterlogging resilience attributes based on the centre of mass for each sampling point (node-set). In contrast, E represents the distance-based connections derived from the Thiessen polygon, creating a comprehensive network of linkages (edge-set). From a spatial scale perspective, the weight value (WE) used to assess the strength of linkages is determined by the nearest distance, enabling the formation of clusters of systematically connected sites.

Next, the network percolation model was built and run to identify the critical scale nodes based on the model’s output. The graph structure was created using the NetworkX library in a Python environment, where the set of nodes and edges containing resilience attributes were added. Through an iterative process, the nodes were traversed and gradually removed according to the resilience level’s linkage threshold. It allowed the researchers to calculate changes in the connectivity and robustness of the waterlogging resilience system and the variations in the scale of the largest connected cluster. The key scales, where significant shifts in the XMI waterlogging resilience level occur, were filtered out by analysing the fluctuations in the threshold of the largest connected cluster.

Differentiation of waterlogging resilience indicators based on the GBDT model

After refining the scale framework of the waterlogging resilience system, the GBDT algorithm was applied to evaluate the performance of key resilience indicators across different scales. The GBDT model, a machine learning algorithm known for its ability to iteratively improve predictions by combining multiple decision trees, was selected for its proven effectiveness in undertaking high-precision regression and classification tasks43,44. The GBDT model excels at dealing with multi-source data and waterlogging resilience systems distinguished by high complexity and uncertainty due to its robustness against outliers and ability to accurately assess the feature significance, making it an optimal tool for analysing such systems45. A complete mathematical and technical description of the GBDT model can be found in46 and 47.

This study used ArcGIS to create homogeneous grid data layers for each critical scale, covering the entire study area based on the scale structure of the XMI waterlogging resilience system identified by the network percolation model. The indicators for evaluating waterlogging resilience were associated with the grid data at these critical scales, serving as the input datasets for the GBDT model. Given the challenges in directly representing the aggregation effects or neighbourhood impacts of waterlogging events using point data, the kernel density estimation (KDE) tool in ArcGIS was used to capture the spatial distribution characteristics of these events. The KDE calculation results were used as the model’s output dataset by constructing a smooth surface. The calculation formula is expressed as follows:

$$\:f\left(x\right)=\frac{1}{nh}\sum\:_{i=1}^{n}K\left(\frac{x-{x}_{i}}{h}\right)$$
(5)

(i = 1,2,…,n).

where\(\:f\left(x\right)\) is the estimated density value at location x; n is the total number of points for the waterlogging event; h is the bandwidth of the kernel function; K is the kernel function; and \(\:{x}_{i}\)is the point location for each waterlogging event.

The input and output datasets were standardised, and the three-sigma rule was applied to remove outliers, retaining only samples where each column’s data fell within the range of its mean ± 3 standard deviations. The dataset was then randomly split into an 80% training set and a 20% testing set, with a fixed random seed (random_state = 42) to ensure reproducibility.

Python was used to load the GBDT model from the Sklearn library. It was fine-tuned using GridSearchCV. The mean squared error (MSE) was selected as the loss function for its robustness against outliers. Key parameters were optimised: the number of trees ranged from 100 to 1000, the learning rate from 0.01 to 0.1, and the maximum tree depth was set at 3, 5 and 7. The optimal parameter combination was determined via grid search and used to train the model, which was then validated with the testing dataset. The model’s performance was evaluated by calculating the MSE and the coefficient of determination (R²).

Finally, according to the GBDT model’s results, the waterlogging resilience indicators were assigned to different scales according to their importance levels. Simultaneously, the non-linear relationship curves between these indicators and the disaster adaptation effects at each scale were generated. These outputs offer insights into the performance of each indicator across various scales.

Results

Characteristics of waterlogging resilience levels in XMI

According to the significant terrain fluctuations in the southern and central parts of XMI, the ‘stress resilience’ dominated by natural and geographical conditions presents a clear spatial distribution pattern, with higher values in the south and lower values in the north. This pattern demonstrates a pronounced polarisation, with most areas displaying either high or low resilience. In contrast, regions with medium resilience levels are comparatively scarce (Fig. 4a). In contrast, the distribution of ‘state resilience’ adheres to a different pattern: higher in the centre and lower towards the edges (Fig. 4b). Resilience in the Huli district is relatively weak, especially in the northern region, where key transportation hubs such as the airport, passenger terminals, rail transit stations and the round-island interchanges are concentrated. The impervious surface coverage in these areas is significantly higher than in other land uses. Moreover, the land use structure is uniform, increasing the risk of waterlogging caused by heavy rainfall48. Potential roadway waterlogging in this region could also disrupt the entire city’s logistics network during extreme rainfall49. Apart from the concentrated green spaces and water bodies, the ‘response resilience’ follows a pattern of ‘point concentration with diminishing circles’. High resilience values are primarily found in recently developed middle- and high-end residential areas and university campuses (Fig. 4c). In XMI, the ageing of municipal facilities and inadequate management are major contributors to the low level of ‘response resilience’. Despite being in a highly urbanised stage of development with an almost complete infrastructure system, the drainage network frequently requires rainwater and sewage mixing. This issue manifests in several ways. First, due to the design and construction practices of their time, older communities often use combined sewer systems, leading to the persistent mixing of rainwater and sewage. Second, even in areas where rainwater and sewage have been separated, the absence of a proper back-end collection network results in continued combined flows. Finally, drainage systems lack more supervision and enforcement in some regions, leading to widespread mixed and misconnected pipelines. These poorly regulated areas struggle to respond effectively to extreme rainfall, and localised issues can significantly undermine the overall efficiency of the drainage system.

The distribution of waterlogging resilience levels in XMI reveals significant spatial heterogeneity (Fig. 4 d). The Siming district generally exhibits high resilience, with resilience values demonstrating a pronounced clustering pattern. In contrast, the Huli district has relatively low resilience, particularly in its peripheral areas. A comparison of the spatial distribution of waterlogging events indicates a correlation between resilience levels and the effectiveness of adaptation to waterlogging hazards (Fig. 4e). Regions with higher resilience tend to experience lower disaster exposure risks. Therefore, assessing waterlogging resilience levels effectively reflects XMI’s adaptive capacity to such disasters.

Fig. 4
figure 4

Characteristics of waterlogging resilience levels in XMI.

Full size image

Identification of critical scales based on emergent characteristics of waterlogging resilience

An analysis of the network percolation model’s global and local efficiency outputs reveals that both efficiencies follow similar trends with removing nodes, indicating a clear linkage between international and local resilience efficiency. In particular, the overall performance of the entire resilience system collapses when the local resilience network nears failure (Fig. 5a and b). As the number of removed resilience units approaches 50, efficiency values begin to fluctuate sharply, signalling a substantial structural change in the network and the formation of transient efficient connections between the remaining nodes. With further node removal, efficiency values drop dramatically to near zero. It highlights the varying impact that different numbers and sizes of resilience units have on the network’s structural efficiency. When more than 50 units are removed, the creation of independent clusters becomes more pronounced, making the scale structure of the resilient system more explicit.

The linear fluctuations in Fig. 5c illustrate the dynamics of the largest independent cluster’s size within the network as nodes are progressively removed, highlighting the evolution of the system’s robustness under different node removal scenarios. The findings indicate that during the initial phase of node removal, the size of the largest independent cluster gradually shrinks from the entire study area to approximately 30.33 km² (comprising 337 basic units). This sharp decline suggests that the XMI waterlogging resilience system is susceptible to node removal in the early stages, where the failure of units leads to the rapid fragmentation of the largest cluster into smaller ones, largely reducing the network’s overall robustness.

Between the removal of 200–1000 nodes, the curve depicts a continuous linear decline, but the trend flattens with minor localised fluctuations. During this phase, eliminating additional nodes exerts a relatively small impact on overall robustness as the network structure of the waterlogging resilience system gradually adapts to the disruptions caused by node failures. However, as the number of removed nodes approaches 1000, the curve experiences a sharp decline, with the size of the largest independent cluster rapidly shrinking from about 15.21 km² (169 basic units) to nearly 5.04 km² (56 basic units). It indicates that node failures at this stage significantly impact the network’s robustness. When more than 1500 nodes are removed, the maximum cluster size approaches zero, signalling that the network has nearly lost all connectivity and is on the verge of disintegration.

In summary, the analysis of the size variation in the largest independent clusters within the XMI waterlogging resilience system has identified three critical scales: 5.04 km², 15.21 km² and 30.33 km² (Fig. 5c). These scales capture the emergent patterns and multiscale structural characteristics of the XMI waterlogging resilience system.

Fig. 5
figure 5

Efficiency changes and scale variations in the waterlogging resilience system.

Full size image

Main indicators causing shifts in waterlogging resilience levels at different scales

Using the three critical scales of the XMI waterlogging resilience system, the area was divided into three datasets consisting of homogeneous grid cells with sizes of 5.04 km², 15.21 km² and 30.33 km², respectively. Subsequently, the GBDT model was applied to assess whether the effectiveness of each resilience indicator in enhancing adaptive performance varied across these different scales.

The calculation results reveal that MNs are crucial across multiple scales (Fig. 6). That finding aligns with existing research, which shows that the mixing and misconnection of rainwater and sewage in high-density urban areas are common issues. The interaction of mixed flows at these connection points alters the velocity and pressure within the drainage system, making MNs a significant factor in the stability of the waterlogging resilience system in such environments5. This study further demonstrates that this impact persists across four key scales, including the primary scale. However, as the scale increases, system scale effects and more complex hydrologic-terrain interactions make the impact of localised stormwater-sewer mixing nodes on the overall drainage system diminished by other, more macroscopic factors50.

AI_IM exhibits consistent characteristics across different scales. Although its effect is slightly lower at the primary scale, it is more substantial at other scales, highlighting the direct and robust correlation between impervious surface connectivity and waterlogging risks. Continuous impervious surfaces, such as urban roads, rooftops and parking lots, significantly increase surface runoff, decreasing natural rainwater infiltration and groundwater recharge. This results in rapid surface water accumulation during heavy rainfall, which is channelled into the urban drainage system. The concentrated runoff often exceeds the system’s design capacity, increasing the load and risk of blockages, which directly contributes to waterlogging events51. As the scale increases, the influence of AI_IM on waterlogging resilience extends beyond the drainage system, encompassing broader factors such as watershed management, urban water systems, drainage infrastructure, green spaces, climate resilience and the urban heat island effect. These elements indirectly impact the city’s capacity to manage waterlogging and contribute to overall environmental quality52,53.

Apart from the two critical indicators, MNs and AI_IM, the importance of other indicators differs considerably across scales. At the primary scale, the influence of these indicators is more evenly distributed, indicating a more intricate and diverse relationship between factors and adaptive capacity at smaller scales. Green spaces mitigate surface runoff and facilitate rainwater infiltration in smaller units than larger scales. Notably, the ecological land patch morphology indicator, represented by PD_GR (0.36), holds significantly greater importance than impervious surface morphology and coverage.

The influence of some indicators diminishes with the increase in scale size. In contrast, crucial indicators that drive waterlogging resilience become more prominent. For instance, in addition to MNs and AI_IM, the importance of FAR increases at the mesoscale (5 km² and 15 km²). At this scale, the spatial patterns of buildings and clusters play a more important role in shaping urban microclimates, significantly impacting resilience to waterlogging. Higher development intensity reduces surface water infiltration and affects rainwater accumulation and discharge patterns by altering local wind and thermal fields54.

In contrast, at the macro-scale (30 km²), broader structural indicators such as RD (0.31) and SLP (0.07) emerge as critical. These factors affect water flow paths, velocities and pooling points on a larger scale. At this level, structural features exert more direct and widespread control over hydrological processes than localised factors at the micro-scale50.

Fig. 6
figure 6

Distribution of importance of key indicators at different scales.

Full size image

Non-linear patterns of key indicators in exhibiting resilience performance at different scales

The partial dependence plot (PDP) generated from the GBDT model illustrates the non-linear relationship between each waterlogging resilience indicator and the effectiveness of waterlogging disaster adaptation across various scales. The calculations reveal that the non-linear relationships vary depending on the scale (Fig. 7). For example, at the primary scale (r² = 0.45) and the 5 km² scale (r² = 0.65), which both demonstrate high r² values, some indicators exhibit similar non-linear trends across these scales. In particular, indicators like SLP and MNs show a comparable phased upward trend in their influence on adaptation to waterlogging hazards at both the primary and 5 km² scales. Moreover, the adaptive effect of waterlogging hazards increases rapidly when SLPs and MNs are low and then gradually levels off as these indicators continue to rise. This pattern indicates that topographic conditions and the quality of municipal facilities are highly dependent on and sensitive to adapting to waterlogging hazards across different scales. Indicators such as PD_GR and CO_GR display a different trend. Initially, changes in these indicators have minimal impact on the adaptive effect, reflected in a relatively stable phase. However, as the indicator values increase, there is a sudden and significant rise in adaptive effects, rapidly reaching high levels. This non-linear pattern suggests that the distribution of green patches positively affects waterlogging mitigation once a specific density and aggregation are reached, particularly at larger scales (e.g. 5 km²), where scale effects amplify this impact. These findings highlight a hierarchical threshold effect of the SLP, MNs, PD_GR and CO_GR indicators on the system’s adaptive performance to waterlogging.

Fig. 7
figure 7

Non-linear relationships between key indicators and the effects of adaptation to waterlogging at different scales.

Full size image

In contrast, the effect of FAR follows a relatively linear trend, with increases in FAR showing a consistent positive correlation with the adaptive effect. These findings suggest that efficient building density allocation and development intensity adjustments have a sustained positive impact on optimising urban drainage capacity and reducing waterlogging risk across all scales. Conversely, DPL exhibits a steadily declining trend, where the adaptive effect gradually weakens with the increase in the length of defective pipelines. This trend indicates that the integrity of the drainage network directly affects urban adaptation to waterlogging across different scales. The presence of faulty pipes reduces the system’s drainage efficiency, thereby increasing the risk of waterlogging.

However, it is essential to note that some indicators display opposite patterns at different scales, primarily IM, PD_IM and SCD, representing impervious surface coverage and spatial configurations. These indicators reflect variations in the impact of hardened ground cover and urban spatial patterns on waterlogging resilience. In particular, both IM and PD_IM exhibit significant adverse effects at the primary scale, with the adaptive effect decreasing rapidly with the increase in these indicators. These outcomes suggest that the expansion of impervious surfaces directly disrupts natural infiltration and drainage at more minor scales, strongly inhibiting adaptation to waterlogging. Similarly, SCD also exhibits negative effects at small scales, likely due to increased spatial congestion, further restricting drainage efficiency and heightening the risk of localised waterlogging. However, at the 5 km² scale, the impact of IM is less pronounced, displaying a more gradual downward trend, suggesting that at larger scales, the localised negative effects of impervious surfaces are partially offset by broader factors, such as the overall configuration of drainage infrastructure. The impact of PD_IM follows a more complicated pattern: It initially decreases slightly, suggesting that the early increase in impervious surfaces negatively impacts adaptation. However, the adaptive effect improves as the indicator value continues to rise. This phenomenon may be because, beyond a certain threshold, the connectivity of impervious surfaces facilitates centralised and rapid drainage on a macro-scale, enhancing overall drainage efficiency. In addition, the influence of SCD diminishes at larger scales, suggesting that spatial crowding density’s direct impact on waterlogging adaptation becomes diluted or overshadowed by dominant structural factors at these scales.

Discussion

Implications for adaptive policy optimisation

Urban space exhibits significant scale-structured characteristics50,55, and multiscale transmission analysis has become essential for understanding and planning urban spaces. It is also a critical link in achieving efficient coordination between the urban spatial management system and the waterlogging resilience construction system. The interaction across scales and the synergistic advantages of multiscale collaboration largely determine the efficiency of urban disaster responses56,57. In the case study of XMI, the scale transitions of the waterlogging resilience system exhibit phased features, and the scale nodes where system stability undergoes abrupt changes do not align with current administrative divisions or traditional urban management scales. Therefore, it is imperative to emphasise transcending administrative boundaries to achieve multiscale integration and connectivity in urban resilience building. To overcome this challenge, the XMI region should establish a multi-level resilience planning and management unit system tailored to the area’s specific emergent characteristics of waterlogging resilience, namely the ‘5 km²–15 km²–30 km²’ three-tier resilience planning and management units. This hierarchical system can effectively complement the grid management model of traditional block units (administrative management units), facilitating the coordination and integration of disaster adaptation capacities across different scales, thereby enhancing overall urban resilience.

Furthermore, the impact of various waterlogging resilience indicators on disaster adaptability shows significant scale dependence across different levels. To tackle this issue, it is essential to create a differentiated indicator management system and dynamic management mechanisms tailored to the specific importance of each resilience indicator at different scales and their non-linear relationships with adaptation performance. This outcome ensures that management strategies are precisely aligned with the needs of each scale, improving the effectiveness of waterlogging resilience efforts. For instance, at the micro-scale, sub-district offices, community committees, and municipal facility departments should lead resilience management by adjusting infrastructure standards, strengthening oversight of rain–sewage mixing nodes, prioritizing upgrades in high-value MNs zones, optimizing the spatial configuration of green spaces, and ensuring the routine maintenance of drainage systems. At the meso- and macro-scales, urban planning, housing, and water authorities must collaborate to manage the connectivity of impervious surfaces, regulate building density and development intensity, and foster systemic adaptability through the coordinated use of macro-structural elements, including transport networks and topographic conditions, thereby enhancing efficiency through scale effects. Building on these efforts, a matrix-style governance framework that integrates horizontal collaboration with vertical differentiation is essential to embed resilience-oriented strategies into existing administrative structures in a coherent and adaptive manner.

The compatibility between resilience indicators and the emergent characteristics of resilience systems should also be considered crucial in policy formulation. Resilience indicators can be optimised based on the operational order of the system at different scales. For instance, equipping efficient drainage systems and adaptive infrastructure should be prioritised in high-density areas. Increasing the density and integrity of green and open spaces in lower-density areas to create effective stormwater management buffer zones is essential. It is worth noting that the study results emphasise that the relationships between various indicators and waterlogging disaster adaptability are more diverse and complex at the micro-scale than at the macro-scale. Therefore, in smaller-scale resilience governance, precise goal setting and strict control standards are critical to ensuring that governance measures can effectively enhance the overall adaptability of resilience systems in complex environments.

Moreover, the analytical framework presented in this research for examining the scale structure and variations in waterlogging resilience systems has broad applicability. With the growing adoption of the ‘X-minute’ urban planning model, the influx of big data, and the transformative influence of machine learning technologies, multiscale and cross-scale governance is becoming a crucial component of urban management strategies58,59. By utilising this framework, alongside big data resources and the built environment characteristics of the target area, precise scale deconstruction and identification of urban resilience systems—particularly waterlogging resilience—can be achieved. This outcome enables the fine-tuning of crucial indicators at each scale and ensures the seamless integration of scale structures into urban management systems. The approach not only maximises the potential of urban resilience systems but also offers significant research value and wide-ranging application prospects.

Limitations and future research directions

Integrating multi-source data fusion and machine learning has improved the interpretability of relationships between variables, addressing the limitations of conventional geospatial models, which often struggle to establish clear linear connections60. However, differences in data samples across scale levels present challenges. As the scale increases and sample sizes decrease, the robustness of models at macro scales may be compromised61. This study focusses on urban islands characterised by relatively isolated locations and limited spatial scope, which poses additional challenges for systematic analysis. As the scale expands, the reduced sample size at larger scales impacts the uniformity and robustness of results.

To ensure the reliability of the conclusions, this study directs its attention on meso- and micro-scale analyses when exploring threshold effects of resilience indicators. Because urban spaces exhibit nested scale characteristics, future research could broaden the scope—such as examining resilience systems at city, city cluster or regional scales—to increase sample sizes across different scales. This result would enhance the accuracy of macro-scale analyses and provide a more comprehensive understanding of the emergent characteristics of waterlogging resilience systems.

Conclusion

Recognising the virtuous cycle of waterlogging resilience across different scales is crucial for improving urban adaptability to waterlogging disasters and strengthening the scientific foundation of waterlogging disaster management. This research integrated multi-source urban data, network percolation models and machine learning technologies to develop a comprehensive analytical framework for identifying the scale structure of urban waterlogging resilience systems. The framework was empirically tested using the XMI region as a case study. The findings reveal that the vital scale nodes corresponding to the emergent patterns of the XMI waterlogging resilience system are 5 km², 15 km² and 30 km², which do not align with conventional administrative boundaries. In addition, the impact mechanisms of various waterlogging resilience indicators on disaster adaptation performance exhibit significant scale dependence and threshold effects. Indicators like MNs and AI_IM are highly influential across multiple scales, but their importance diminishes as macro-level factors become more prominent at larger scales. FAR’s impact on adaptive performance increases notably at the mesoscale, whereas structural indicators such as RD and SLP dominate at the macro-scale. Thus, managing waterlogging resilience indicators should consider their varying performance at different scales while applying differentiated and dynamic management strategies accordingly.

This study expanded on the concept of the nested cyclical system within evolving resilience theory, deepening our understanding of the scale effects of waterlogging resilience and offering critical theoretical support for constructing a coherent understanding of the complex system structure of resilience from macro to micro levels. By optimising resilience system management across different scales, this research provides novel insights and methods for addressing the challenges posed by complex urban environments. Applying this framework strengthens a city’s capacity to handle extreme weather events and offers practical guidance and policy recommendations for future resilient city development.