Introduction

Screw pump oil recovery is an important lifting method characterized by a simple system structure, relatively few components, and strong adaptability to high-viscosity and high gas–liquid ratio wells, offering significant advantages in heavy oil extraction1,2. Heavy oil reservoirs are typically developed using thermal recovery methods. However, in conventional screw pumps, the stator is made of rubber and the rotor is metallic3. Under thermal recovery conditions, these materials are prone to aging, rubber swelling, and wear4,5,6. To withstand the high-temperature conditions of thermal recovery, all-metal screw pumps have been developed. These pumps employ a clearance-fit design, with both the rotor and stator made of metal, offering advantages such as high-temperature resistance and long service life7,8,9,10. However, because the fit clearance is not adjustable, they cannot accommodate the wide range of fluid viscosities encountered in heavy oil thermal recovery wells11,12. Therefore, based on the conventional all-metal screw pump, a novel all-metal conical screw pump has been developed. In this design, both the rotor and stator are configured with a conical helical structure, allowing the rotor–stator clearance to be adjusted in real time according to the viscosity of the oil during heavy oil production, thereby optimizing the pump’s operational performance.

In recent years, extensive research has been conducted on all-metal screw pumps. Olivet et al.13 investigated the working characteristics of screw pumps with different clearance values through laboratory experiments; however, because the pump structure they examined differs substantially from that of screw pumps used in China, their results are not fully representative of the working characteristics of Chinese all-metal screw pumps. Zheng et al.14, based on laboratory experiments, analyzed the effect of rotor speed on the lifting performance of all-metal screw pumps, but did not take the influence of clearance values into account. Li et al.15 and Zhong et al.16 conducted simulation studies on the structural and operational parameters of all-metal screw pumps and recommended operating parameters for heavy oil production, but did not consider the combined effects of clearance and rotor speed. Zheng et al.17 simplified the transverse and longitudinal clearances of all-metal screw pumps as rectangular and analyzed the effect of clearance on pump leakage, but did not consider the adaptability of the clearance to fluids with different viscosities.

The clearance in conventional all-metal screw pumps is fixed, whereas in all-metal conical screw pumps, the rotor–stator fit clearance can be adjusted by modifying the rotor position. Based on outdoor tests, this study conducts further numerical simulations, analyzing the all-metal conical screw pump by varying the rotor–stator clearance and rotor speed under fluids of different viscosities. The results demonstrate that this pump system can efficiently lift fluids of varying viscosities and is well suited for heavy oil thermal recovery wells.

System components of all-metal conical screw pumps

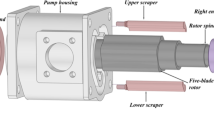
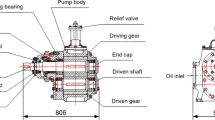
The all-metal conical screw pump system is shown in Fig. 1. The all-metal conical screw pump oil recovery system primarily comprises four assemblies: the all-metal conical screw pump, the well protection assembly, the surface rotary lifting assembly, and the limiter assembly. The all-metal screw pump serves as the core of the system, with both the rotor and stator designed in a conical form. A schematic of the clearance is shown in Fig. 2. During system operation, the rotor–stator clearance can be changed in real time by lifting and lowering the rotor through the surface rotary lifting assembly, thereby ensuring efficient lifting of oils with different viscosities during heavy oil thermal recovery. The well protection assembly contains a sealing device to seal the wellhead, which can ensure the sealing safety of steam injection during hot recovery. The surface rotary lifting assembly can adjust the position of the rotor and change the rotor–stator clearance by the lifting mechanism. The limiter assembly is located at the upper part of the pump, securing the rotor–stator alignment during operation and preventing problems such as eccentric wear or pump sticking.

Fig. 1
figure 1

All-metal conical screw pump system.

Full size image
Fig. 2
figure 2

Schematic diagram of the rotor–stator clearance.

Full size image

The stator-rotor fit clearance εp is calculated as:

$${\varepsilon _p}=\frac{{{d_{out}} - {d_{in}}}}{{2L}}{L_x}$$
(1)

The energy efficiency η and volumetric efficiency ηv of the pump for different operating conditions are further calculated by checking the values of flow, pressure, speed and torque, which are calculated as:

$$\eta =\frac{{{P_s}}}{{{P_z}}} \times 100\%$$
(2)
$${\eta _v}=\frac{Q}{{{Q_t}}} \times 100\%$$
(3)

Among them:\({P_s}=\frac{{Q\Delta p}}{{86.4}}\), \({P_z}=\frac{{\pi nM}}{{30000}}\), \({Q_t}=1440nAT\), \(A=4e{d_{in}} - 8e\varepsilon - \pi \left( {\varepsilon {d_{in}} - {\varepsilon ^2}} \right)\)

Where: Lx is the rotor lifting length, mm; L is the total length of the screw pump, mm; din is the diameter of the inlet end of the rotor, mm; dout is the diameter of the outlet end, mm; Ps is the hydraulic power, kW; Pz is the shaft power of the screw pump, kW; Q is the actual displacement of the screw pump, m3/d; Qt is the theoretical flow rate of the screw pump, m3/d; Δp is the pressure difference between the inlet and outlet of the screw pump, MPa; M is the torque, N·m; n is the rotational speed, r/min; T is the stator lead, m; e is the eccentricity of the screw pump, m.

Modeling and outdoor simulation test

Screw pump flow model and meshing

Modeled with reference to the conical screw pump model GLB208-24E, the main structural parameters of the screw pump are as follows: screw pump total length L = 4800 mm, stator lead T = 192 mm, eccentricity e = 6 mm, the rotor inlet end diameter d in = 49 mm, the rotor outlet end diameter d out = 61 mm. By adjusting the rotor position, the rotor–stator clearance changes synchronously and remains consistent. Moreover, the pressure increase along the single screw is distributed linearly. To simplify the model, the pump is represented as having a uniform diameter and a length equal to one-tenth of the total pump length. In this study, the continuous clearance between the stator and rotor, together with the cavity, is treated as the fluid domain for analysis. The flow channel model is shown in Fig. 3.

Fig. 3
figure 3

Model flow channel diagram.

Full size image

The fluid simulation is conducted based on the finite volume method, and mesh generation plays a critical role. The complex surface geometry of the model makes it difficult to ensure mesh quality during the initial mesh generation, especially given the large number of elements. Furthermore, the simulation involves moving boundaries caused by the planetary motion of the rotor, which complicates dynamic mesh updating when the mesh is both large and of poor quality. To ensure that the mesh meets accuracy requirements while maintaining computational efficiency, Pumplinx software is employed for the simulation. In Pumplinx, a Cartesian grid is used to generate a structured clearance mesh, with local refinement applied at the minimum clearance regions to ensure mesh quality. The final grid model contains 6,233,871 nodes and 1,329,840 elements. The grid model is shown in Fig. 4.

Fig. 4
figure 4

Grid model.

Full size image

Verification of grid independence

Mesh-independence verification is a crucial step in numerical simulation, as the mesh density directly affects the calculation results. The simulation conditions were set as follows: fluid viscosity of 0.1 Pa·s, screw pump rotor speed of 100 r/min, inlet–outlet pressure difference of 5 MPa, clearance of 0.1 mm, eccentricity of 6 mm, and stator lead of 192 mm. Six mesh sizes (770,400; 1,120,050; 1,329,840; 1,609,560; 2,049,420; 2,518,650) were used to simulate the screw pump flow for mesh-independence verification. The simulation results are shown in Fig. 5. It can be seen that the mesh density has little effect on the calculated screw pump flow. In this study, a mesh with 1,329,840 elements was chosen for subsequent calculations and analyses.

Fig. 5
figure 5

Verification of grid-independence.

Full size image

Boundary conditions and numerical solution methodology

The boundary conditions for the numerical simulations in this study were set to match those of the field pump tests. The working medium was oil with a density of 800 kg/m³. The inlet boundary condition was defined as a pressure inlet with a value of 0.1 MPa, corresponding to one-tenth of the actual value, while the outlet boundary condition was defined as a pressure outlet, determined according to the specified pressure-drop conditions. The selected Pumplinx calculation templates included Progressive, Turbulence, Cavitation, and Streamline. Under rotor rotation, the centrifugal and inertial forces of the medium inside the single-screw pump’s sealed chambers are significant, and the flow in the stator–rotor clearance region exhibits high Reynolds number characteristics. Therefore, the Standard k–ε turbulence model was employed for the simulations, with the turbulent kinetic energy k and the turbulent dissipation rate ε calculated as follows18:

$$\frac{{\partial ({\rho _f}k)}}{{\partial t}}+\frac{{\partial ({\rho _f}k{u_j})}}{{\partial {x_j}}}=\frac{\partial }{{\partial {x_i}}}({\alpha _k}{\mu _e}\frac{{\partial k}}{{\partial {x_j}}}]+{G_k}+{G_P} - {\rho _f}\varepsilon$$
(4)
$$\frac{{\partial ({\rho _f}\varepsilon )}}{{\partial t}}+\frac{{\partial ({\rho _f}\varepsilon {u_j})}}{{\partial {x_j}}}=\frac{\partial }{{\partial _{3}^{x}1}}({\alpha _\varepsilon }{\mu _e}\frac{{\partial \varepsilon }}{{\partial {x_j}}})+C_{{1\varepsilon }}^{*}\frac{{{G_k}\varepsilon }}{k} - {C_{2\varepsilon }}\frac{{{\rho _f}{\varepsilon ^2}}}{k}$$
(5)

Among them:\({G_k}={u_t}(\frac{{\partial {u_i}}}{{\partial {x_j}}}+\frac{{\partial {u_j}}}{{\partial {x_i}}})\frac{{\partial {u_i}}}{{\partial {x_j}}}\), \({G_P}= - \sum\limits_{s} {\sum\limits_{i} {\frac{{{n_s}{m_s}}}{{{\tau _{rs}}}}[2(k - {C_s}\sqrt[k]{{k{k_s}}})]} }\),\(C_{k}^{*}={C_1}\varepsilon - \frac{{\zeta (1 - \frac{\zeta }{{\zeta {}_{0}}})}}{{1 - \lambda {\zeta ^3}}}\), \(\zeta ={(2{E_{ij}}{E_{ji}})^{\frac{1}{2}}}\frac{k}{\varepsilon }\), \({E_{ij}}=\frac{1}{2}(\frac{{\partial {u_i}}}{{\alpha {x_j}}}+\frac{{\partial {u_j}}}{{\partial {x_i}}})\)

Where: Gk is the turbulent kinetic energy production term due to the mean velocity gradient; Gp is the additional production term for the multiphase flow; ns is the number of solid particles; ms is the mass of solid particles; ks is the turbulent kinetic energy of solids; αk = αε = 1.39;C1ε=1.42༛C2ε=1.68༛ζ0 = 4.377༛λ = 0.012.

The solver was configured for unsteady numerical calculations. One full rotation of the rotor was divided into 180 time steps, corresponding to a 2° rotation per time step. The results from the fourth rotation of the rotor were selected for analysis. The solver residuals met the default convergence criteria for transient calculations in Pumplinx, ensuring sufficient computational accuracy.

Test equipment setup

To validate the accuracy of the model, an outdoor screw pump test was conducted. To approximate field conditions, a 20 m deep test well was constructed, in which the screw pump was driven by a main motor. The fluid was lifted to the surface through the tubing and then recirculated into the test well via the annulus using a flowmeter, pressure gauge, and pressure-regulating valve. Rotor speed, flow rate, pressure, current, and voltage were all adjustable and recorded through the control system. The experimental setup and procedure are illustrated in Fig. 6. During the test, the wellhead pressure was set to 5 MPa using the pressure-regulating valve, and the rotor speed was maintained at 100 r/min. Considering that heavy oil testing is difficult to operate and involves significant safety risks and costs, and given that the primary purpose of the outdoor test was to ensure that the numerical model could reasonably reflect pump performance, water was selected as the test fluid.

During the test, the fluid in the tubing was drained to reduce the starting torque, thereby ensuring that the sucker rod torque at the wellhead was within a safe range before the motor was started. The rotor speed was set to 100 r/min. By adjusting the wellhead pressure and flow rate using the pressure-regulating valve, the pressure, flow rate, and torque were recorded. The stator–rotor clearance and rotor speed were then varied, and the above measurements were repeated.

Fig. 6
figure 6

Outdoor experimental setup and test flow diagram.

Full size image

Comparison between experimental and simulation results

The comparison between experimental and numerical results is shown in Fig. 7. As can be seen, the variations in flow rate and energy efficiency obtained from the experiments are consistent with those from the simulations. A comparison of flow rate and energy efficiency data under the same clearance and rotor speed conditions shows that the average errors between the simulated and experimental results are 3.46% and 4.64% for flow rate, and 2.77% and 3.62% for energy efficiency, respectively. These errors fall within a reasonable range, thereby validating the accuracy of the screw pump model.

Fig. 7
figure 7

Screw pump model validation.

Full size image

Screw pump simulation results analysis

Effect of stator-rotor fit clearance on the operating characteristics of the screw pump

The all-metal tapered screw pump can adjust the clearance value according to the viscosity of the fluid. To investigate the effect of clearance on pump performance, simulations were conducted under the same single-stage pressure drop while keeping the stator pitch, eccentricity, and rotor speed constant. Fluid viscosities of 0.01 Pa·s, 0.05 Pa·s, 0.1 Pa·s, 0.3 Pa·s, and 0.5 Pa·s were selected. Based on engineering practice, fluids with viscosities below 0.1 Pa·s are classified as low-viscosity, those between 0.1 Pa·s and 0.3 Pa·s as medium-viscosity, and those above 0.3 Pa·s as high-viscosity. The clearance was varied within the range of 0.03–0.8 mm, and the influence of clearance on the lifting performance of the screw pump under different viscosities was analyzed through numerical simulations. The results are shown in Fig. 8.

As shown in Fig. 8, the rotor–stator clearance has a significant influence on the flow rate, energy efficiency, torque, and volumetric efficiency of the all-metal tapered screw pump. For low-viscosity fluids, the relatively small viscous resistance results in a rapid increase in both axial and radial leakage, leading to a sharp decline in effective displacement. When the clearance exceeds 0.2 mm, almost all of the pump flow is lost, indicating that the transport performance of low-viscosity fluids is highly dependent on the sealing effect of the clearance. For medium- to high-viscosity fluids, the poor mobility slows the growth rate of leakage with increasing clearance, thereby mitigating the decline in displacement. As illustrated in Fig. 8b, the energy efficiency of the pump decreases monotonically with increasing clearance when conveying low-viscosity fluids; in contrast, when transporting medium- to high-viscosity fluids, the efficiency first increases and then decreases as the clearance enlarges. Excessively small clearances cause strong frictional losses along the chamber wall, resulting in higher torque and reduced operating efficiency. However, further enlargement of the clearance increases leakage, which ultimately lowers efficiency. Therefore, in engineering practice, the clearance should be reasonably selected according to fluid viscosity to ensure that the pump operates at optimal efficiency. As shown in Fig. 8c, the pump torque decreases with increasing clearance, and the reduction trend is more pronounced for high-viscosity fluids than for low-viscosity fluids. Volumetric efficiency directly reflects the proportion of leakage, and the critical clearance ranges vary with fluid viscosity. As illustrated in Fig. 8d, when the clearance is less than 0.1 mm, the volumetric efficiency of low-viscosity fluids remains above 75%; when the clearance is less than 0.2 mm, the volumetric efficiency of medium-viscosity fluids remains above 63%; and when the clearance is less than 0.4 mm, the volumetric efficiency of high-viscosity fluids remains above 62%.

Fig. 8
figure 8

Effect of clearance value.

Full size image

The primary distinction between the all-metal tapered screw pump and conventional all-metal screw pumps is its ability to adjust the stator–rotor clearance in real time according to the fluid viscosity. To ensure both high efficiency and safe operation, the recommended clearance values are as follows: 0.03–0.16 mm for fluids with viscosities below 0.1 Pa·s; 0.1–0.2 mm for viscosities between 0.1 Pa·s and 0.3 Pa·s; and greater than 0.2 mm for viscosities above 0.3 Pa·s. Within these recommended clearance ranges, the pump can maintain high energy and volumetric efficiencies, while the resulting power and torque remain within safe operational limits.

Effect of rotor speed on the operating characteristics of the screw pump

Rotor speed is one of the primary means of regulating production in field operations. To examine its effect on pump performance, simulations were carried out under the same single-stage pressure drop while keeping the stator pitch and eccentricity constant. A clearance value of 0.1 mm was adopted, and the rotor speed was varied in the range of 80–300 r/min. The influence of rotor speed on the lifting performance of the screw pump under different viscosities was then analyzed by numerical simulation. The results are shown in Fig. 9.

As shown in Fig. 9a, the displacement of the screw pump increases approximately linearly with rotor speed. When the fluid viscosity exceeds 0.05 Pa·s, the displacements under different viscosities become relatively close, indicating that once viscosity is greater than 0.05 Pa·s, the lifting performance of the screw pump is mainly determined by its structural characteristics rather than fluid viscosity. As illustrated in Fig. 9b, torque increases with rotor speed, and the higher the viscosity, the faster the torque rises, whereas the torque of low-viscosity fluids remains nearly unchanged with increasing speed. This is because the poor mobility of high-viscosity fluids requires the pump to deliver greater power to overcome resistance. As shown in Fig. 9c, the energy efficiency of the pump exhibits different trends under various viscosities as rotor speed increases. For fluids with a viscosity of 0.01 Pa·s, energy efficiency improves significantly with speed, rising from 55.84% to 81.43%. For fluids with a viscosity of 0.05 Pa·s, efficiency still increases with speed, but the growth rate gradually diminishes, suggesting that the maximum efficiency of the pump is being approached. In contrast, under medium- and high-viscosity conditions, energy efficiency decreases as speed increases. For low-viscosity fluids, raising rotor speed effectively reduces leakage and increases displacement, while torque remains nearly constant, resulting in a marked improvement in efficiency. However, for medium- to high-viscosity fluids, higher speeds intensify frictional resistance between the fluid and the chamber wall, leading to rapid energy losses and, ultimately, lower efficiency. The effect of rotor speed on volumetric efficiency also varies with viscosity. As shown in Fig. 9d, for low-viscosity fluids, increasing rotor speed markedly improves volumetric efficiency; for medium-viscosity fluids, volumetric efficiency increases more modestly with speed, indicating a weaker influence of speed; and for high-viscosity fluids, volumetric efficiency remains almost unchanged with increasing speed.

Fig. 9
figure 9

Effect of rotor speed.

Full size image

When handling low-viscosity fluids, increasing the rotor speed has a relatively small impact on torque, and an appropriate increase in speed can significantly improve both the pump’s energy efficiency and volumetric efficiency. Therefore, during thermal recovery of heavy oil, the lifting performance of the pump can be enhanced by increasing the rotor speed. In contrast, for medium- to high-viscosity fluids, the pump’s energy efficiency decreases with increasing rotor speed, and the improvement in volumetric efficiency approaches saturation. Consequently, during cold heavy oil recovery, the rotor speed should be reduced or the stator–rotor clearance increased to enhance the pump’s operational efficiency.

Effect of clearance–speed coupling on the operating characteristics of the screw pump

To further verify the adaptability of the all-metal tapered screw pump to fluids with different viscosities, simulations were conducted to analyze the influence of rotor speed on pump energy efficiency under clearance values of 0.2 mm and 0.3 mm, as shown in Fig. 10.

Fig. 10
figure 10

Effect of clearance–speed coupling.

Full size image

From Fig. 10, it can be observed that when the fluid viscosity and clearance value are not well matched, increasing the rotor speed leads to a decline in both energy efficiency and volumetric efficiency. Therefore, at higher fluid viscosities, increasing the clearance value enables the energy efficiency and volumetric efficiency of the screw pump to improve with rising rotor speed. Coordinated optimization of stator–rotor clearance and rotor speed is thus required to achieve efficient lifting performance across fluids of different viscosities.

Conclusion

  1. (1)

    This study systematically analyzes the operating characteristics of the all-metal tapered screw pump under fluids of different viscosities by combining field experiments with numerical simulations, and further recommends appropriate operating parameters for heavy oil reservoirs under various lifting conditions.

  2. (2)

    The all-metal screw pump adopts a stator–rotor clearance-matching design, where different clearance values are suitable for lifting fluids of different viscosities. The results concerning the influence of stator–rotor clearance and rotor speed on pump energy efficiency indicate that the efficiency does not monotonically decrease with increasing clearance. When the stator–rotor clearance is small and the working medium is of high viscosity, the energy efficiency of the screw pump first increases and then decreases with increasing clearance. In addition, for high-viscosity fluids under small clearances, the energy efficiency decreases as the rotor speed increases.

  3. (3)

    In thermal recovery operations, the all-metal tapered screw pump controls production primarily by adjusting the rotor position to vary the stator–rotor clearance and by modifying the rotor speed. When the fluid viscosity is below 0.1 Pa·s, the clearance should be maintained at 0.03–0.16 mm, and a higher rotor speed is preferable. Under these conditions, leakage can be effectively reduced, volumetric efficiency improved, pump displacement increased, and energy efficiency maintained at lower torque. For fluid viscosities between 0.1 Pa·s and 0.3 Pa·s, the recommended clearance is 0.1–0.2 mm, with rotor speeds of 80–120 r/min. When the viscosity exceeds 0.5 Pa·s, the clearance should be greater than 0.2 mm and the rotor speed reduced to prevent excessive load that may compromise safe operation.

  4. (4)

    The all-metal tapered screw pump effectively overcomes the limitations of conventional screw pumps in terms of poor thermal resistance and the inability of ordinary all-metal screw pumps to adapt to variations in fluid viscosity, thereby enabling efficient lifting of fluids with a wide range of viscosities.