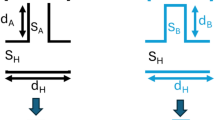Introduction

The study of acoustic wave propagation in phononic crystals (PnCs) has attracted significant attention due to their unique ability to generate phononic band gaps (PnBGs), frequency ranges where sound waves are completely blocked1. Band gaps are formed by the spatial periodicity of the structure based on Bragg conditions2,3 or by local resonance mechanisms in the system4,5. These PnCs offer a wide range of technical applications, including selective acoustic filters, wave reflection, wave guiding, acoustic cloaking, and demultiplexing systems6,7,8,9,10. Waveguide or acoustic duct systems composed of periodic arrangements of different materials or geometries are also capable of creating acoustic band gaps (ABGs), where wave propagation is prohibited due to total reflection within the structure11,12,13. Several waveguide systems have been used in periodic structures to exploit ABGs, such as expansion chambers, closed, open and Helmholtz resonators14,15,16,17,18,19.

While periodic structures have been the cornerstone of phononic crystal research, their performance is fundamentally constrained by the strict symmetry of their unit cells. A key limitation is the emergence of bandgaps only at specific frequency ranges, with a limited ability to tailor wave propagation at different frequencies or create wide, robust bandgaps without significant structural compromise. Furthermore, their response is highly sensitive to the incident angle of acoustic waves, which can limit their effectiveness in practical, multi-directional noise environments. In contrast, quasi-periodic structures, which possess long-range order without translational symmetry, offer a promising alternative. Research has suggested that such structures can exhibit more complex bandgap phenomena, including the formation of complete bandgaps at lower frequencies and a higher degree of design flexibility for targeting specific acoustic properties. It is this potential to overcome the inherent limitations of periodic systems that motivates the present study.

In fact, quasi-periodic structures characterized by the absence of a periodic shifting order are attracting growing scientific interest, offering significant ABGs in well-defined frequency intervals. The design of these quasi-periodic systems is presented by intermediaries between periodic and random structures arranged in a disorderly fashion according to controllable mathematical rules20,21,22. Quasi-periodic acoustic structures are analogous to photonic quasi-crystals, which have provided essential applications in electromagnetic and optics23,24,25,26. There are several quasi-periodic sequences defined by recursive relations, such as Thue-Morse, Cantor, Fibonacci, Double Period, Rudin-Shapiro, etc27,28,29,30,31. In particular, quasi-periodic structures offer an effective solution for creating wide band gaps at low frequencies and generating a large number of resonance peaks, compared with periodic or defect structures32,33. Recently, exciting research has been carried out into the physical properties of quasi-periodic acoustic structures34,35. However, quasi-periodic waveguide structures remain limited to date.

Almawgani et al. have developed a biosensor based on a periodic PnCs structure and quasi-periodic Fibonacci PnCs. Their results showed that the quasi-periodic structure presented a wide PnBGs and high sensitivity compared with periodic PnCs. They also showed that several resonance peaks appeared in the transmission spectra of the quasi-periodic structure36. Chen has constructed a certain type of heterostructure using a combination of 1D periodic PnCs and quasi-periodic Fibonacci or Thue-Morse PnCs. The results demonstrate a new approach to achieving broadband omnidirectional acoustic reflection that can be applied to the design of acoustic mirrors37. Garus and Sochacki used Thue-Morse’s quasi-periodic layer distribution and Severin’s aperiodic multilayer to examine the effects of the incident angle on mechanical waves. Using the transfer matrix method, they demonstrated the existence of broad reflectance bands for the different models examined. Variation in layer geometry resulted in an irregular shift of transmission peaks towards lower frequencies38.

This research focuses on the development of a Generalized Thue-Morse (GTM(m,n)) quasi-periodic structure by examining the properties of acoustic resonators. The proposed structure is composed of two distinct acoustic blocks arranged in a non-periodic pattern following GTM(m, n) sequences, which are varied by adjusting the repetition parameters “m” and “n”. The first block incorporates a series of open/closed resonators connected in parallel along a central waveguide. The following references present a periodic and defective study of this structure in the field of acoustics39,40. The second block studied in this work consists of a closed resonator connected to a main guide15,41. Our aim is to study the acoustic properties of these two blocks in an original way, using GTM(m,n) sequences. We have used the transfer matrix and finite element methods to determine the acoustic transmittance. The results obtained in this study show significant exploitation of controllable ABGs in specific frequency ranges. Quasi-periodic GTM(m, n) structures provide several ABGs with different frequency positions. The variation of the system geometry strongly influences the width of the ABGs, and more specifically by the increase in the ratio between the cross-section of the closed resonator and that of the main waveguide (\(\:{S}_{C}/{S}_{1})\) (see Fig. 1 below). There are also regions of greater forbidden frequencies in stable positions, invariant to increasing \(\:{S}_{C}/{S}_{1}\). The generation of these ABGs is physically due to the local resonance mechanism performed individually by each acoustic resonator making up the system. These results show the importance of using these GTM(m,n) sequences, which are considered good candidates for the exploitation and control of ABGs. GTM(m, n) sequences are a handy application for selective acoustic filters capable of effective noise reduction. On the other hand, the increase in the number of GTM(m, n) iterations from the second generation onwards leads to the existence of localized states corresponding to symmetrical resonance peaks appearing in ABGs. The emergence of these transmission peaks primarily results from constructive interference between resonant modes generated by both periodic and generalized Thue-Morse (GTM) structural arrangements. The quasi-periodicity of our system is considered the optimal choice for tuning resonance peaks in ABGs with maximum and very fine transmittances. These resonance peaks are capable of extracting multiple high-quality transmission channels. Consequently, these results open up a much-needed avenue of research in the field of acoustics, particularly for the fabrication of large ABGs and transmission peaks for quasi-periodic waveguide structures.

Fig. 1
figure 1

Schematic representation of a closed/open resonator (A) and a closed resonator (B) connected in series. The geometrical parameters are:\(\:\:{d}_{1}=0.1\:m\), \(\:{d}_{C}={d}_{O}=0.06\:m\), \(\:{S}_{O}/{S}_{1}=0.9\), with \(\:{S}_{C}/{S}_{1}\) variable in three different values

Full size image

The principal novelty of this work lies in the application of a Thue-Morse quasi-crystal structure with lateral resonators to acoustic gas sensing and multiplexing. This specific configuration is engineered to exploit complex wave localization phenomena, which results in an unprecedented sensitivity that is over three times higher than the best-performing sensors reported in the current literature.

Theoretical model

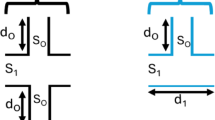
The geometric structures studied in this article are divided into two blocks organized according to the different generations of GTM. Figure 1 shows a detailed representation of block (A), consisting of parallel open/closed resonators, and block (B) consisting of lateral closed resonators. The geometrical configuration of our system indicates that the main duct length and cross-section of each block are \(\:{d}_{1}\) and \(\:{S}_{1}\), respectively. The closed resonators of blocks (A) and (B) have the same length \(\:{d}_{c}\) and cross-section\(\:{\:S}_{c}\), and the open resonators of blocks (A) have length \(\:{d}_{O}\)=\(\:{d}_{c}\) and cross-section\(\:\:{S}_{O}\). The main duct and resonators that make up our system are filled with air which has an acoustic speed of 340 m/s and a density of 1.2\(\:\:\text{k}\text{g}/{m}^{3}\).

In this work, transmittance spectra are established based on the TMM and FEM16,28,42. According to the proposed model, the matrix for (A) is determined by the following matrix Eqs39,40.

$$\:{T}_{A}={T}_{G}{*T}_{OC}*{T}_{G}=\left(\begin{array}{cc}{T}_{11}&\:{T}_{12}\\\:{T}_{21}\:&\:{T}_{22}\:\end{array}\right)$$
(1)

\(\:{T}_{G}\) and \(\:{T}_{OC}\) are, respectively, the transfer matrix (TM) of the main duct and the open/closed parallel resonators. \(\:{T}_{11}\), \(\:{T}_{12}\), \(\:{T}_{21}\), and \(\:{T}_{22}\) are the TM elements of the block (A).

with:

$$\:{T}_{G}=\left(\begin{array}{cc}{cos}\left(k{d}_{1}/2\right)&\:{{jz}}_{1}{sin}\left(k{d}_{1}/2\right)\\\:{{jy}}_{1}{sin}\left(k{d}_{1}/2\right)\:&\:{cos}\left(k{d}_{1}/2\right)\end{array}\right)$$
(2)

where \(\:{z}_{1}=\frac{1}{{y}_{1}}=\frac{\rho\:c}{{s}_{1}},\)

$$\:{T}_{CO}=\left(\begin{array}{cc}1&\:0\\\:{{Y}_{\text{O}}+Y}_{\text{C}}&\:1\:\end{array}\right)$$
(3)

where:

$$\:{Y}_{\text{O}}=-j{y}_{O}\text{c}\text{o}\text{t}\left(k{d}_{O}\right)$$
(4)
$$\:{Y}_{\text{C}}=j{y}_{C}\text{t}\text{a}\text{n}\left(k{d}_{C}\right)$$
(5)

\(\:{Y}_{\text{O}}\) is the acoustic admittance of the open resonator of length \(\:{d}_{O}\) and impedance \(\:{z}_{O}=1/{y}_{O}=\rho\:c/{s}_{O}\) with \(\:j=\sqrt{-1}\). At the same time, \(\:{Y}_{\text{C}}\) represents the admittance of the closed resonator of length \(\:{d}_{C}\) and impedance\(\:\:{z}_{C}=1/{y}_{C}=\rho\:c/{s}_{C}\). \(\:k\) is the acoustic wave vector.

On the other hand, the TM theory for block (B) is also given by:

$$\:{T}_{B}={T}_{G}{*T}_{C}{*T}_{G}=\left(\begin{array}{cc}{T}_{11}^{{\prime\:}}&\:{T}_{12}^{{\prime\:}}\\\:{T}_{21}^{{\prime\:}}\:&\:{T}_{22}^{{\prime\:}}\:\end{array}\right)$$
(6)

The TM of the closed resonator connected to the main conduit (\(\:{T}_{C}\)) is calculated by15,41.

$$\:{T}_{C}=\left(\begin{array}{cc}1&\:0\\\:{Y}_{\text{C}}&\:1\:\end{array}\right)$$
(7)

After traversing the (AB) structure (parallel open/closed resonators in a main duct and closed resonator serial) at normal incidence, the acoustic wave transmittance \(\:T\left(\%\right)\) is calculated as follows14,17:

$$\:T\left(\%\right)=100\text{*}{\left|\frac{2}{{T}_{1}+{T}_{2}/{z}_{1}+{T}_{3}/{y}_{1}+{T}_{4}}\right|}^{2}$$
(8)

where:

$$\:{T}_{AB}={T}_{A}*{T}_{B}=\left(\begin{array}{cc}{T}_{1}&\:{T}_{2}\\\:{T}_{3}\:&\:{T}_{4}\:\end{array}\right)$$
(9)

where \(\:{T}_{AB}\) is the final TM of an acoustic structure composed of blocks (A) and (B) grafted in serial.

Table 1 Dimensions and parameters of COMSOL model
Full size table

To corroborate the analytical findings derived from the TMM, a full-wave numerical simulation was conducted using the FEM within the COMSOL Multiphysics software environment43. A 2D symmetric model of the proposed Thue-Morse sensor structure was constructed, and the Pressure Acoustics module was employed to solve the governing wave equation. Perfectly Matched Layers (PMLs) were applied at the domain boundaries to absorb outgoing waves and simulate an open, non-reflecting environment. The simulated transmission spectrum was obtained by calculating the ratio of the transmitted to incident acoustic power. The close agreement between the resonant frequencies and transmission profiles predicted by the TMM and those computed via FEM validates the accuracy of our theoretical model. It confirms the physical viability of the proposed sensor design. The geometrical and acoustic parameters used for the FEM model in COMSOL Multiphysics are detailed in Table 1.

Results

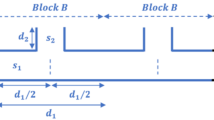
This section presents a numerical analysis of acoustic transmittance spectra in one-dimensional quasi-periodic phononic crystals (1D-PnCs) across multiple generations of Generalized Thue-Morse (GTM) sequences. Our objective is to study the variation of cross-section ratios (\(\:{S}_{C}/{S}_{1}\)) in three different values to analyze the behavior of ABGs and resonance peaks by increasing GTM(m,n) generations. The GTM sequence rules corresponding to blocks A and B are constructed as follows: \(\:\text{A}\to\:{\text{A}}^{m}{\text{B}}^{n}\) and \(\:\text{B}\to\:{\text{B}}^{m}{\text{A}}^{n}\), where m and n are positive integers representing the number of block repetitions28. The GTM sequence follows a recursive generation rule defined as: \(\:{T}_{q+1}={T}_{q}^{m}{\stackrel{-}{T}}_{q}^{n}\), with \(\:{T}_{0}=A\)27,44. Here, the number of GTM generations is increased up to the third sequence, and the parameters m and n are adjusted/modified from 1 to 3 as shown in Table 2 below. The quasi-periodic structures studied in this research are respectively GTM(1,1), GTM(2,1), GTM(3,1), GTM(1,2) and GTM(1,3).

Table 2 Representation of the different GTMS(m, n)
Full size table

GTM(1,1)

This section presents the results of the first 1D quasi-periodic structure built using the GTM sequence. Here, the parameters \(\:m=n=1\) indicate the repetition of the blocks forming the whole of the GTM(1,1) acoustic structure.

Figure 2(a-c) shows transmittance spectra for \(\:1{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{4}\:\)with different cross-section ratios\(\:\:{S}_{C}/{S}_{1}\), where (a)\(\:\:{S}_{C}/{S}_{1}=0.3\), (b)\(\:{\:S}_{C}/{S}_{1}=0.6\), and (c)\(\:\:{S}_{C}/{S}_{1}=0.9\). Parameter \(\:{S}_{C}/{S}_{1}\:\)is the ratio of the cross-sectional area between the closed resonators and the main conduit. The results clearly show the creation of an ABG at the center of the frequency ranges, with a progressive widening of its width as the \(\:{S}_{C}/{S}_{1}\:\)cross-section ratio increases from 0.3 to 0.9. More specifically, the width of the central ABG shown in Fig. 2a at \(\:{S}_{C}/{S}_{1}=0.3\) lies in the frequency range between 4147.48 Hz and 4353.69 Hz. The ABG width increases in Fig. 2b when \(\:{S}_{C}/{S}_{1}=0.6\), which covers the frequency range between 4070.89 Hz and 4430.29 Hz. Whereas Fig. 2c shows a considerable widening of this ABG towards 4017.87 Hz and 4489.19 Hz when the \(\:{S}_{C}/{S}_{1}\) cross-section ratio is increased to 0.9. This demonstrates the ability of the section ratio to control the width of the ABG width in our periodic structure \(\:1{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{4}=ABABABAB\). These results are in agreement with reference42, which confirms the effect of the cross-sections of a periodic waveguide system on ABG broadening. We have also observed the creation of other ABGs in different positions symmetrical to the central ABG.

Fig. 2
figure 2

Transmittance of \(\:1{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{4}\) at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

Furthermore, we have shown that increasing\(\:\:{S}_{C}/{S}_{1\:}\)leads to an increase in the number of ABGs, and more specifically, from 3 to 5 ABGs in Fig. 2a-c. The appearance of these ABGs is due to the mechanism of local resonance4,45,46, where each resonator individually blocks the propagation of acoustic waves. This results in multiple blocking in the system (T = 0%), capable of generating large ABGs at certain frequencies. These results show the significant contribution of your\(\:\:1{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{4}\:\)structure to controlling the behavior of the ABG and therefore to improving acoustic attenuation performance. The transmittance spectra obtained from the FEM and TMM models show excellent agreement in resonant frequencies and ABGs, with minor deviations in transmittance magnitude. These slight differences are attributed to the more comprehensive accounting at the solid-fluid boundaries within the FEM simulation, effects which the idealized TMM does not fully capture.

Figure 3 below illustrates the variation of transmittance by setting the number of iterations to the second generation \(\:2{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{2}\). Moreover, we increased the cross-section ratio \(\:{S}_{C}/{S}_{1}\:\)in three values, namely (Fig. 3a) \(\:{S}_{C}/{S}_{1}=0.3\), (Fig. 3b) \(\:{S}_{C}/{S}_{1}=0.6\), and (Fig. 3c) \(\:{S}_{C}/{S}_{1}=0.9\). We have shown that when \(\:{S}_{C}/{S}_{1}\:\)increases from 0.3 (Fig. 3a) to 0.9 (Fig. 3c), the frequency range of the central ABG increases from 4147.48 to 4347.81 Hz to 4011.99–4489.19 Hz. We also observed the appearance of two wider ABGs in Fig. 3a, situated in the frequency ranges 2551.81–3135.96 Hz and 5361.94–5954.94 Hz. The position and width of these ABGs remain almost stable in Fig. 3b and c, invariant with increasing section ratio \(\:{S}_{C}/{S}_{1}\). This acoustic characteristic arises from the aperiodic spatial arrangement of blocks A and B, governed by sequence \(\:2{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{2}\). In addition, transmittance spectra show the creation of resonance peaks located in the first and third ABGs. These peaks appear narrow and symmetrical with respect to the central frequency \(\:4250\) Hz. Precisely, Fig. 3a shows the generation of two resonance peaks situated at 3070.63 Hz and 5429.37 Hz, respectively, with a very high transmittance. In Fig. 3b, these peaks show a slight symmetrical shift towards low and high frequencies, at positions 3066.3 Hz and 5433.7 Hz, respectively, with the maximum transmittance T ≌100%. The observed transmission peaks within the ABGs emerge from resonant mode coupling between the underlying periodic lattice and the superimposed quasi-periodic arrangement generated by the \(\:\:2{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{2}\) sequence. Figures 4(a-c) exhibit a qualitative behavior similar to that observed in Figures 3(a-c), characterized by a comparable lineshape and number of resonant features. The key distinction lies in the systematic shift in the spectral positions of these resonance peaks.

Fig. 3
figure 3

Transmittance of \(\:2{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{2}\) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

GTM(2,1)

This section deals with the study of a GTM(2,1) structure. Figure 4(a-c) shows transmittance spectra as a function of frequency for different cross-section ratios (\(\:{S}_{C}/{S}_{1}\)). Here, we set the sequential order of the GTM to\(\:\:1{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{4}\), while increasing the parameter m so that\(\:\:m=2>n=1\). The block structure of this sequence is repeated over four periods in the\(\:{\:\left(\text{A}\text{A}\text{B}\right)}^{4}\). As shown in Fig. 4a, three ABGs appear in the transmittance spectrum, positioned in different frequency ranges. The second ABG appears in the center within the frequency region between 4153.38 Hz and 4353.7 Hz with a bandwidth of 200.32 Hz. Figure 4c clearly shows that an increase in \(\:{S}_{C}/{S}_{1}\:\)leads to a considerable widening of the central ABG width. In this case where\(\:\:{S}_{C}/{S}_{1}=0.9\), the width of this ABG extends to 471.33 Hz, from 4153.38 Hz to 4353.7 Hz spectral band. By way of comparison, the widths of the central ABG here are virtually identical to the same widths of the central ABG in Fig. 5a, corresponding to\(\:\:1{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{4}\), demonstrating the insensitivity of the central ABG to changes in the number of parameters m. In contrast, it only depends on the increase in \(\:{S}_{C}/{S}_{1}\). Furthermore, in Fig. 4a, the first and third ABGs appear with significant widths of 589.17 Hz and 595.16 Hz, corresponding to intervals from 2433.03 Hz to 30333.2 Hz, and from 5478.98 Hz to 6074.04 Hz, respectively. It is well shown that the positions and widths of these ABGs remain almost stable in all figures that are insensitive to increasing ratio\(\:{\:S}_{C}/{S}_{1}\). The stability of the ABGs at fixed positions for all three cross-section ratios is due to the robust quasi-periodicity of our structure. This feature is essential for applications such as selective acoustic filters and noise reduction in stable frequency ranges.

Fig. 4
figure 4

Transmittance of 3GTM(1,1) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image
Fig. 5
figure 5

Transmittance of \(\:1{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{4}\) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

In Fig. 6(a-c), we have increased the GTM generation order to \(\:2{GTM\left(\text{2,1}\right)}^{2}\) corresponding to the quasi-periodic structure\(\:\:(\text{A}\text{A}\text{B}\text{A}\text{A}\text{B}\text{B}\text{A}\text{A}{)}^{2}\). The effect of varying the \(\:{S}_{C}/{S}_{1}\:\)on acoustic transmittance properties is clearly illustrated in Fig. 6(a-c). The results show several ABGs with different positions. Physically, the unique distribution of blocks A and B in this sequence \(\:2{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{2}\) gives rise to new ABGs in specific frequency ranges. The width of the central ABG shown in Fig. 6a over the interval from 4147.48 Hz to 1353.7 Hz depends strongly on the variation of the \(\:{S}_{C}/{S}_{1}\:\)ratio. The central ABG is wider as the \(\:{S}_{C}/{S}_{1}\:\)increases. This confirms the essential property of \(\:{S}_{C}/{S}_{1}\:\)to control the behavior of the central ABG, whatever the order of GTM generation. On the other hand, several resonance peaks appear in various ABGs with different acoustic transmittance maxima. The existence of the resonance peaks is due to the non-periodic distribution of blocks A and B across the\(\:\:2{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{2}\). Based on these results, \(\:2{GTM\left(\text{2,1}\right)}^{2}\:\)serves as the best candidate to control and broaden ABG and generate many resonance peaks with high transmittance.

Fig. 6
figure 6

Transmittance of \(\:2{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{2}\) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

Figure 7 shows the transmittance for 3GTM(2,1) with different \(\:{S}_{C}/{S}_{1}\:\)values. This structure contains a large number of blocks A and B, totaling 32 blocks (see Table 2). The effect of this increase on the behavior of the transmittance spectrum is clearly shown by the numerical results obtained. As illustrated in Fig. 7a, the structure exhibits five distinct forbidden frequency bands. These bands of wave attenuation occur sequentially: the first from 2383.64 Hz to 3038.6 Hz, the second from 3405.9 Hz to 3525.4 Hz, the third from 4149.37 Hz to 4352.94 Hz, the fourth from 4981.36 Hz to 5091.99 Hz, and the fifth from 5463.71 Hz to 6109.83 Hz. The appearance of these numerous ABGs is due to the structural quasi-periodicity of 3GTM(2,1), which is achieved through the local resonance mechanism of the open and closed resonators that make up the structure. Similarly, the width of the ABGs is increased by modifying the \(\:{S}_{C}/{S}_{1}\:\)ratio, and particularly the third ABG. Besides, by increasing the \(\:{S}_{C}/{S}_{1}\:\)ratio, a progressive decrease in the transmittance of resonance peaks appearing in a symmetric manner in the first and last ABGs is observed. These results are essential in acoustics for the development of new narrow-transmission filters with tunable amplitudes. In addition, the non-periodic arrangement of blocks A and B, thanks to this 3GTM(2,1), results in considerable transmittance perturbation in the pass band regions. This disturbance confirms the results obtained earlier in Fig. 5, which also show a significant modulation of transmittance in these bands. This confirms that acoustic transmittance in the pass bands is dependent on the unique rule of the third GTM sequence.

Fig. 7
figure 7

Transmittance of 3GTM(2,1) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

GTM(3,1)

In the following case, the parameter m is raised to exponent 3 and the parameter n is fixed to exponent 1, where \(\:{T}_{1}=\text{A}\text{A}\text{A}\text{B}\) represents the first generalized Thue-Morse sequence corresponding to 1GTM(3,1).

In Fig. 8, the transmittance of \(\:1{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{4}={\left(\text{A}\text{A}\text{A}\text{B}\right)}^{4}\:\)is studied by increasing the cross-section ratio \(\:{\:S}_{C}/{S}_{1}\:\)in three values, namely: \(\:{\:S}_{C}/{S}_{1}=0.3\:\)for Fig. 8a, \(\:{\:S}_{C}/{S}_{1}=0.6\)(Fig. 8b), and \(\:{\:S}_{C}/{S}_{1}=0.9\:\)for Fig. 8c. Several ABGs with different positions and widths are observed. These ABGs correspond to regions of zero transmittance, where acoustic waves are totally reflected (T = 0%). The gradual increase in \(\:{\:S}_{C}/{S}_{1}\:\)leads to geometric changes in the structure, resulting in variations in the width and position of the ABGs. This result shows the potential of \(\:{\left(\text{A}\text{A}\text{A}\text{B}\right)}^{4}\) structure for advanced acoustic applications, such as selective filtering and noise control of sound waves. Furthermore, transmittance peaks (resonance peaks) are observed in ABGs where acoustic waves propagate efficiently in the structure. More precisely, a very narrow resonance peak appears in the first and last ABG at frequencies of 2672.3 Hz and 5827.7 Hz, respectively, with the same transmittance. When \(\:{\:S}_{C}/{S}_{1}\:\)increases, the peak located in the first ABG clearly moves towards high frequencies, symmetrically with the peak found in the last ABG, which moves towards low frequencies. This result is typical of these quasi-periodic GTM structures, which demonstrate the ability to create and control resonance peaks in ABGs.

Fig. 8
figure 8

Transmittance of \(\:1{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{4}\) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

In what follows, we study the evolution of the transmittance spectrum by increasing the sequence order up to\(\:\:2{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{2}\), corresponding to the quasi-periodic distribution\(\:\:{\left(\text{A}\text{A}\text{A}\text{B}\text{A}\text{A}\text{A}\text{B}\text{A}\text{A}\text{A}\text{B}\text{B}\text{A}\text{A}\text{A}\right)}^{2}\). Figure 9(a-c) shows acoustic transmittance as a function of frequency for different values of the \(\:{S}_{C}/{S}_{1}\:\)ratio. We can clearly see the influence of increasing \(\:{S}_{C}/{S}_{1}\:\)on the width of the central ABG. Indeed, the width of this ABG extends from 208 Hz to 469.1 Hz between Fig. 9a (\(\:{S}_{C}/{S}_{1}=0.3\)) and Fig. 9c (\(\:{S}_{C}/{S}_{1}=0.9\)). This shows that increasing \(\:{S}_{C}/{S}_{1}\:\)is a good technique for extending the central ABG in this quasi-periodic structure to control low-frequency noise. We have also shown the formation of several ABGs with different widths. The appearance of these new ABGs is essentially due to the aperiodic distribution of blocks A and B in the structure. These results reflect the importance of the \(\:2{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{2}\:\)sequence in the creation of a large number of ABGs. On the other hand, Fig. 9(a-c) shows the presence of resonance peaks in several ABGs. These peaks appeared in different frequency positions with very high transmittance. These results are useful for the design of filters with narrow transmittance.

Fig. 9
figure 9

Transmittance of \(\:2{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{2}\) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

The acoustic transmittance results for the third generation (3GTM(3,1)) are shown in Fig. 10 (a-b) with different values of \(\:{S}_{C}/{S}_{1}.\) The 3GTM(3,1) sequence, with an exponent \(\:m=3\), shows a significant increase in the number of A and B blocks (64 blocks), forming a unique quasi-periodic arrangement (see Table 2 above). Figure 10 shows the creation of several ABGs in different frequency positions with significant widths. Increasing \(\:{S}_{C}/{S}_{1}\) has a clear impact on the behaviour of these ABGs. Specifically, ABGs become wider and deeper when \(\:{S}_{C}/{S}_{1}\) increases. This shows the influence of the geometry (\(\:{S}_{C}/{S}_{1}\)) on the acoustic filtration properties in quasi-periodic systems. In addition, we have shown that increasing \(\:{S}_{C}/{S}_{1}\) leads to a significant disruption of the pass bands. As \(\:{S}_{C}/{S}_{1}\) increases, the width of these pass bands becomes narrower and deeper, as shown in Fig. 10b and c. These properties result in considerable internal reflections that prevent acoustic waves from being transmitted in specific frequency regions. Finally, these results demonstrate the effect of the cross-section ratio and distribution of the 3GTM(3,1) structure on the development of acoustic filters, essential in various applications in the acoustics field.

Fig. 10
figure 10

Transmittance of 3GTM(3,1) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

GTM(1,2)

In this section, we examine the acoustic wave propagation of a GTM(1,2) quasi-periodic structure, varying the exponent parameters m and n such that \(\:m=1\) and \(\:n=2\). In this case, the increase in parameter n forms a greater number of \(\:B\) blocks (laterally closed resonators) than \(\:A\) blocks (parallel open/closed resonators).

Figure 11(a-c) shows the transmittance of\(\:{\:1\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{4}={\left(\text{A}\text{B}\text{B}\right)}^{4}\). The cross-section ratio varies in three different values, namely for (a)\(\:{\:S}_{C}/{S}_{1}=0.3\), for (b)\(\:{\:S}_{C}/{S}_{1}=0.6\), and (c)\(\:\:{S}_{C}/{S}_{1}=0.9\). The results obtained show the ability of this periodic structure (\(\:\text{A}\text{B}\text{B}\text{A}\text{B}\text{B}\text{A}\text{B}\text{B}\text{A}\text{B}\text{B}\)) to create wide ABGs, which are affected by the geometry of the \(\:{\:S}_{C}/{S}_{1}\:\)cross-section ratio. In Fig. 11a, where\(\:{\:S}_{C}/{S}_{1}=0.3\), the central ABG is located between the frequency range 4144.94–4357.36 Hz with a width equal to 212.42 Hz. When the ratio\(\:{\:S}_{C}/{S}_{1}\:\) increases from 0.3 to 0.6, the width of this band widens to 367.31 Hz, as shown in Fig. 11b. Increasing \(\:{\:S}_{C}/{S}_{1}\:\)to 0.9 considerably increases the width of this central ABG, reaching 482.39 Hz in Fig. 11c. This clearly indicates the role of geometry in ABG tunability, and in particular in our resonators structure. We can also observe the generation of two very broad ABGs that are delimited between the frequency intervals 2551.8–3118.25 Hz and 5379.62–5946.07 Hz in Fig. 11a. These ABGs remain virtually stable, maintaining their width as the \(\:{\:S}_{C}/{S}_{1}\:\)parameter increases. The width insensitivity of ABGs generates robust reflective properties that are important for noise reduction. These results are particularly significant for the design of selective filters requiring stable and robust acoustic reflection in appropriate frequency ranges.

Fig. 11
figure 11

Transmittance of \(\:1{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{4}\) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

Figure 12 shows the effect of varying the \(\:{S}_{C}/{S}_{1}\:\)cross-section ratio on acoustic transmittance by fixing the quasi-periodic structure in the second GTM sequence (\(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\)). The quasi-periodic structure of blocks A and B is distributed as \(\:(\text{A}\text{B}\text{B}\text{B}\text{B}\text{A}\text{B}\text{B}\text{A}{)}^{2}\) (see Table 2). Block disorder in this non-periodic system allows the presence of three ABGs. Clearly, the \(\:2{\text{G}\text{T}\text{M}(1,2)}^{2}\:\)results in a significant widening of the first and last ABG compared to the one in Fig. 11 corresponding to the \(\:1{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{4}\). This increase results from the highly chaotic iteration of the \(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\:\)sequences and the presence of a large number of blocks compared to \(\:{1\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{4}\). Figure 12(a-b) also confirms the effect of the \(\:{S}_{C}/{S}_{1}\) ratio in controlling the width of the ABG, which is located in the center of our frequency spectrum. Furthermore, increasing the order of generation to \(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\:\)enables resonance peaks with high acoustic transmittance to be generated in the forbidden frequency ranges. As shown in Fig. 12, there are several narrow resonance peaks located in the first and third ABG. These peaks change position in these ABGs symmetrically with respect to the central position of frequency, gradually as the value of \(\:{S}_{C}/{S}_{1}\:\)increases. In detail on Fig. 12a, three resonance peaks appeared at positions and transmittance 2748.57 Hz (T = 99.871%), 2994.98 Hz (T = 99.99%), and 3087.08 Hz (T = 99.99%), respectively, moving from low to high frequencies within the first ABG delimited between 2538.53 Hz and 3180.21 Hz. The third ABG also features three resonance peaks located symmetrically at positions 5412.92 Hz, 5505.02 Hz, and 5751.43 Hz, with transmission rates of 99.99%, 99.99% and 99.87%, respectively. This shows the significant performance of this \(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\), which symmetrically creates several resonance peaks with maximum transmittances, unlike that of a perfect or defective periodic structure. These results can be used for a variety of applications, such as filtering and guiding multiple high transmission within ABGs.

Fig. 12
figure 12

Transmittance of \(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

The transmittance of 3GTM(1,2) quasi-periodicity structure is clearly illustrated in Fig. 13(a-c) with different values of the \(\:{S}_{C}/{S}_{1}\:\)cross-section ratio. According to the precise non-periodic arrangement and number of blocks (9 A-blocks and 18 B-blocks) of this 3GTM(1,2), several ABGs are formed with zero transmittances (T = 0%) and localized resonance peaks (of high transmittance) within the ABGs. The existence of these ABGs results, in our case, from local resonance mechanisms throughout the structure. In addition, we note that the first and third ABGs have meaningful widths. These two ABGs, as shown in Fig. 13a, have significant widths of 663.82 Hz and 663.81 Hz, respectively. This shows the effect of this exact quasi-periodic structure using 3GTM(1,2) on the behavior of the ABGs. The resonant peaks observed in Fig. 13 exhibit highly localized transmission frequencies, demonstrating how the quasi-periodic structure selectively confines acoustic waves to discrete spectral regions within the ABGs. These properties enable a wide range of applications, including the design of acoustic transmission filters in ABGs. What’s more, the modulation of passbands’ depths and widths, induced by variations in geometric parameters (\(\:{S}_{C}/{S}_{1}\)), is of great importance in adapting our structures to specific needs, such as vibration attenuation and improving the performance of internal reflections that disturb acoustic transmittance.

Fig. 13
figure 13

Transmittance of 3GTM(1,2) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

GTM(1,3)

In this final section, we analyze the behavior of ABGs using the GTM(1,3) structure. Figure 14(a-c) shows the transmittance of \(\:1{\text{G}\text{T}\text{M}\left(\text{1,3}\right)}^{4}={\left(ABBB\right)}^{4}\). The aim is to study the effect of varying \(\:{S}_{C}/{S}_{1}\:\)on ABG properties for three values: 0.3 (Fig. 14a), 0.6 (Fig. 14b), 0.9 (Fig. 14c). Our analysis reveals that progressive increases in the repetition parameter n systematically generate multiple ABGs, each exhibiting distinct spectral positions and bandwidth characteristics. There are exactly seven ABGs placed at different frequencies, as shown in Fig. 14(a-c). This significant increase in the number of ABGs is essentially due to the increase in B blocks and the unique distribution of our \(\:ABBBABBBABABB\) periodic structure. In this study, we also confirmed the effect of \(\:{S}_{C}/{S}_{1}\:\)on the extension of the central ABG. From Fig. 14a and c, we can see a clear broadening of this central band from 212.43 Hz to 477.96 Hz. All these features reflect the essential importance of this structure, particularly the increase in parameter n, which increases and controls the ABGs. These results are very significant for the trapping of acoustic wave propagation in several low-frequency intervals.

Fig. 14
figure 14

Transmittance of \(\:1{\text{G}\text{T}\text{M}\left(\text{1,3}\right)}^{4}\) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\:\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

The variation in acoustic transmittance as a function of frequency for\(\:\:2{\text{G}\text{T}\text{M}\left(\text{1,3}\right)}^{2}\) is shown in Fig. 15 (a-b) for three increasing values of \(\:{S}_{C}/{S}_{1}\). In this case, there are 8 blocks of A and 24 blocks of B arranged quasi-periodically according to the second GTM sequence, revealing interesting acoustic phenomena. Increasing \(\:{S}_{C}/{S}_{1}\) leads to changes in the local geometric and acoustic characteristics, which have a considerable effect on the acoustic transmission factor. This leads to the creation of several ABGs of significant widths, as shown in Fig. 15(a-c). These bands are generated by the local resonance phenomenon resulting from multiple acoustic wave reflections in successive blocks. These bands are linked to the quasi-periodicity of the Thue-Morse structure. Moreover, the numerous peaks observed in ABGs are due to the presence of local resonance modes. The origin of these resonance modes lies in the geometrical properties of our structure. By increasing the sequence order, the quasi-periodic distribution of the structure favors the creation of new resonance modes. It modifies the natural frequencies, leading to the generation of a large number of transmittance peaks. Figure 15 clearly shows the appearance of numerous resonance peaks in the first and third wide ABGs. These peaks are important in applications such as acoustic transmission filtering, wave localization, and control.

Fig. 15
figure 15

Transmittance of \(\:2{\text{G}\text{T}\text{M}\left(\text{1,3}\right)}^{2}\) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

This study investigates the transmittance of third GTM generation sequence. Figure 16(a-c) presents the frequency-dependent transmittance spectra for the 3GTM(1,3) configuration, analyzed across three distinct cross-sectional area ratios (\(\:{S}_{C}/{S}_{1}\)). Figure 16a shows the appearance of three ABGs, with a significant width of the first and third equal ABGs 801.02 Hz and 809.85 Hz. The increase in \(\:{S}_{C}/{S}_{1}\) leads to the extension of the central ABG. This guarantees the property of this parameter (\(\:{S}_{C}/{S}_{1}\)) on the width of the central ABG in all the GTM structures studied in this work. Simultaneously, several resonance peaks appear in different ABGs. These peaks are strongly due to the geometric and physical variations of the quasi-periodic structure of this 3GTM(1,3). On the other hand, transmittance in the pass bands shows significant variations in terms of oscillation and stability. As the \(\:{S}_{C}/{S}_{1}\) ratio increases, the pass bands appear narrower and deeper, indicating an increase in the effects of acoustic localization and wave reflections in the structure.

Fig. 16
figure 16

Transmittance of 3GTM(1,3) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\)

Full size image

In this section, the potential of the first-order generalized Thue-Morse (1GTM) structure as an acoustic multiplexer is demonstrated. As evidenced in Figs. 17(a-c), the sequence \(\:{1\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{N}\) exhibits a direct relationship between the repetition parameter N and the number of sharp resonant peaks within the band gap. This relationship is quantified by:

$$\:Number\:of\:Resonant\:Peaks\:=\:N\:-\:1$$
(10)
Fig. 17
figure 17figure 17

Transmittance of \(\:{1\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{N}\) structure at (a) \(\:{S}_{C}/{S}_{1}=0.3\), (b) \(\:{S}_{C}/{S}_{1}=0.6\), and (c) \(\:{S}_{C}/{S}_{1}=0.9\) as a multiplexer (air sample)

Full size image

Simultaneously, the spectral position of these peaks is highly tunable via the cross-sectional ratio (\(\:{S}_{C}/{S}_{1}\)). An increase in this ratio systematically shifts the entire multiplexed signal spectrum towards lower frequencies. This independent control over the number and frequency of high-transmittance channels establishes the foundation for a versatile acoustic multiplexing device.

The sensing capabilities of the \(\:3\text{G}\text{T}\text{M}\left(\text{1,1}\right)\) sequence were evaluated by characterizing its acoustic response to various gas samples (Fig. 18), each with distinct properties, specifically density (\(\:\rho\:\)) and sound velocity (\(\:c\)). The results, summarized in Table 3, confirm that the sensor’s operational principle is based on the shift of the resonant transmission peak, which is directly correlated with the acoustic environment within the crystal’s pores. This dependence of the resonant frequency on the gas medium fundamentally underpins the sensing mechanism.

Fig. 18
figure 18

Transmittance of \(\:3\text{G}\text{T}\text{M}\left(\text{1,1}\right)\) structure at \(\:{S}_{C}/{S}_{1}=0.3\) for different gas samples as a hazardous greenhouse gas sensor

Full size image

A clear trend is observed where the resonant frequency (\(f\)) exhibits a direct proportionality to the sound velocity (\(c\)) of the gas. For instance, a transition from.

\(\:S{O}_{2}\) (\(\:c\:=\:201\) m/s) to Air (\(\:c\:=\:340\) m/s) results in a significant frequency shift from 3447 Hz to 5830 Hz. This consistent relationship demonstrates that the 3GTM(1,1) structure effectively transduces changes in the acoustic property of the medium into a measurable electrical signal via the resonant frequency. The sensitivity (\(\:S=\frac{\varDelta\:f}{\varDelta\:c}\)), which quantifies this frequency shift per unit change in sound velocity, remains remarkably stable at approximately 17.15 Hz·s/m across most gases, indicating a robust and predictable sensor response.

Further analysis of the sensing performance reveals excellent resolution characteristics. The quality factor (\(\:Q=\frac{f}{FWHM}\)), a measure of the sharpness of the resonance, is consistently high for all tested gases, with values around 6270 (\(\:FWHM\) is the bandwidth). This indicates a narrow resonance linewidth, which is crucial for precise frequency discrimination. The Figure of Merit (\(\:FoM=\frac{S}{FWHM}\)), defined as the ratio of sensitivity to the FWHM of the peak, decreases for gases with higher sound velocity. This is attributed to a concomitant increase in FWHM, which slightly broadens the resonance. Despite this, the sensor achieves an exceptionally low calculated Limit of Detection (\(\:LoD=\frac{f}{20\:S\:Q}\)) for sound velocity, on the order of 0.002–0.003 m/s. This ultra-low LoD underscores the potential of the 3GTM(1,1) sensor for high-resolution gas discrimination and detection applications, capable of identifying gases based on minute differences in their acoustic properties.

Table 3 Different gases, acoustic properties, and sensing parameters
Full size table

A comparative analysis with recent literature underscores the significant performance enhancement achieved by the proposed 3GTM(1,1) sensor structure. As summarized in Table 4, the sensitivity (S) of our design, utilizing Thue-Morse lateral resonators, is calculated to be approximately 17.2 Hz·s/m. This value substantially exceeds the sensitivities reported in recent state-of-the-art acoustic gas sensors, which typically range from 0.5 to 5.8 Hz·s/m for various configurations, including periodic tubes, open and closed resonators, and Helmholtz resonator arrays47,48,49,50,51,52,53,54,55. Specifically, our sensor demonstrates a sensitivity more than three times greater than the highest previously reported values and an order of magnitude improvement over many other designs. This remarkable enhancement in sensitivity can be attributed to the unique quasi-periodic arrangement of the Thue-Morse sequence, which is known to create highly localized and sensitive resonant states compared to conventional periodic structures. The superior sensitivity of our device confirms its potential for detecting minute changes in gas composition with a high degree of precision, positioning it as a leading candidate for next-generation acoustic gas sensing applications.

Table 4 Comparison study
Full size table

Conclusion

This study has systematically examined how quasi-periodic Thue-Morse sequences (GTM(m, n)) influence wave propagation in one-dimensional acoustic waveguide structures, revealing distinct spectral modifications compared to periodic counterparts. The designed structure consists of two blocks: one with open/closed resonators parallel to a main air duct, and the other with closed resonators connected in series. Acoustic transmittances were determined theoretically using the TMM and FEM. Our numerical results demonstrate that the GTM structures enable the creation of several ABGs, accompanied by the appearance of resonant peaks within these ABGs. We have shown that the central band gap width increases with the cross-section ratio parameter (\(\:{S}_{C}/{S}_{1})\). Furthermore, transmittance spectra show the appearance of several resonance peaks with high transmittance reaching 99.9% in different frequency positions. Modifying the sequence order and parameters of GTM (m,n) also has an influence on the number of resonance peaks generated. In particular, we have proven the generation of a high number of resonance peaks in the case of GTMS (2,1), GTMS (1,2) and GTMS (1,3) with maximum transmission rates. As a result, we have tuned these transmittance peaks in the ABGs without inserting any defects in the structure. This demonstrates the effectiveness of our quasi-periodic acoustic structure in controlling ABGs and resonance peaks in transmittance spectra. These results are useful for optimal noise reduction in low-frequency regions and for the design of narrow-band transmission filters and multiplexers. Besides, we have developed and characterized a highly sensitive gas sensor employing a Thue-Morse sequence of lateral resonators. The proposed structure sets a new benchmark for acoustic-based sensing, achieving a record sensitivity that underscores the superior potential of advanced quasi-periodic designs over conventional periodic architectures for high-precision detection applications.