Machine learning based optimization of fly ash content for improving geopolymer concrete compressive strength

Abstract

The increasing demand for sustainable construction materials has intensified interest in fly ash-based geopolymer concrete (FA-GC) as an alternative to traditional concrete. This study aims to predict the compressive strength (CS) of FA-GC and optimize its mix design for maximum performance. Several artificial intelligence (AI) models—Tabular Prior-Data Fitted Network (TabPFN), Histogram-based Gradient Boosting (HistGBoost), M5Prime, and Automatic Feature Interaction Learning (AutoInt)—were applied to predict CS, with hyperparameters tuned via Optuna. Data were split into 75% training and 25% testing. TabPFN achieved the highest accuracy during training (R² = 0.981) and testing, with the lowest RMSE (4.02) and sMAPE (8.20%). Uncertainty analysis also showed TabPFN had the lowest CI (0.697) and R-Factor (2.730), indicating superior stability and predictive reliability compared to other models. For mix design optimization, four metaheuristic algorithms—Harris Hawks Optimization (HHO), Grey Wolf Optimization (GWO), Lyrebird Optimization Algorithm (LOA), and Polar Bear Algorithm (PBA)—were employed. HHO yielded the highest CS at 61.56 MPa, outperforming the others. Sensitivity analysis using SHAP values revealed that Al₂O₃ (%) and SiO₂ (%) most strongly enhanced CS, followed by Coarse aggregate (kg/m³). Partial dependence plots confirmed these trends, while Fine aggregate (kg/m³) and Duration (hr) had less influence. This study highlights that combining advanced AI models with metaheuristic optimization, sensitivity analysis, and uncertainty evaluation can significantly improve the prediction, stability, and mix design of FA-GC, paving the way for more efficient and sustainable geopolymer concrete solutions.

Introduction

The emerging environmental problems and the necessity for green building materials have prompted the development of alternative binders to Portland cement¹. Using green concrete contributes significantly to environmental protection and sustainability^2,3. Fly ash-based geopolymer concrete (FA-GC) has been recognized as an environmentally friendly green material owing to its improved mechanical performance, low carbon emissions, and utilization of industrial waste products^4,5,6. In recent years, FA-GC has attracted significant attention as a sustainable and environmentally friendly alternative to ordinary Portland cement (OPC) concrete⁷. Shi et al.⁸ systematically quantified and compared the environmental impact of fly ash geopolymer concrete and OPC under different strength grades using life cycle assessment (LCA). Their results indicated that the CO₂ emissions of geopolymer concrete can be reduced by up to 62.7%, demonstrating that FA-GC effectively mitigates environmental deterioration without compromising compressive strength. Similarly, Chan et al.⁹ compared the CO₂ emissions associated with producing one tonne of fly ash-based geopolymer cement and OPC. Their study revealed that geopolymer cement results in a carbon footprint of 36.5%, significantly lower than the 63.5% associated with OPC production. These findings highlight the potential of FA-GC as a greener construction material capable of reducing global warming impacts and promoting sustainable development. One of the brightest solutions to develop sustainable cementitious materials is the use of technology in alkali activation, making it possible to replace Ordinary Portland Cement (OPC) completely¹⁰. In contrast to conventional OPC production, based on extensive high-temperature calcination and large-scale energy consumption, alkali-activated binders (AABs) are produced by refraining from such intensive processes. Geopolymers, the principal group of AABs, are three-dimensional aluminosilicate framework inorganic polymers that result from the activation of industrial waste products—e.g., (FA)—using alkaline solutions e.g., sodium hydroxide (NaOH) or sodium silicate (Na₂SiO₃)^11,12,13,14. The materials display excellent mechanical strength and durability in the long term due primarily to their special chemical structure. Moreover, the incorporation of industrial residues as the dominant binding phase presents significant environmental advantages in comparison with traditional OPC systems¹⁵.

However, the complexity of geopolymerization and many variables that influence it render accurate prediction of the compressive strength (CS) of FA-GC rather difficult¹⁶. Over the last few years, machine learning techniques and metaheuristic optimization algorithms have garnered huge interest because of their high capacity to describe intricate nonlinear relationships^17,18. Therefore, accurate prediction of the CS of FA-GC becomes crucial in order to provide secure performance in structural construction^5,19. As the geopolymerization process entails intricate interactions and property variability of raw materials, precise prediction simplifies minimal experimental expenses and time-consuming trial-and-error methods. Moreover, mix design optimization is needed to generate mechanical property requirements with minimum material consumption and environmental impact²⁰. Therefore, combination of advanced prediction models with optimized mix proportion not only enhances the performance of material but also makes the construction practices sustainable and cost-effective.

Given the critical role of accurate strength prediction and mix design optimization, several studies have explored various modeling techniques and optimization algorithms for FA-GC. For example, Peng and Unluer²¹ employed three different machine learning techniques—backpropagation neural networks, support vector machines, and extreme learning machines—to predict the 28-day CS of FA-GC. Their study highlighted differences in prediction accuracy among these models and identified key mix parameters influencing strength development. Such approaches demonstrate the potential of machine learning to enhance prediction reliability and reduce the need for extensive laboratory testing in geopolymer concrete research. However, despite promising results, their study was limited to the integration of optimization algorithms for mix design, which could further improve prediction accuracy and practical applicability. Also, Emarah²² focused on developing predictive models for the 28-day CS of FA-GC using advanced machine learning techniques, including artificial neural networks (ANNs), deep neural networks (DNNs), and deep residual networks (ResNet). By analyzing a comprehensive dataset of 860 samples with multiple influential input parameters—ranging from material proportions to curing conditions—the study demonstrated that the ResNet model outperformed others in accuracy. Sensitivity analysis further revealed that curing temperature, alkaline liquid-to-binder ratio, and Na₂SiO₃ content significantly impact strength prediction. This research highlights the capability of deep learning models to improve the credibility of CS predictions for sustainable concrete mixtures. However, deep learning methodologies are typically data extensive and computationally intensive, limiting their use in the case of scarce data availability or resource-constrained settings. In addition, Ahmad et al.²³ employed supervised machine learning methods to predict the CS of FA-GC. They applied decision tree algorithms along with ensemble techniques such as bagging and boosting regressors to enhance prediction accuracy. Their approach incorporated performance metrics like the coefficient of determination and error indices to validate the models, demonstrating the effectiveness of ensemble models in capturing the complex behavior of geopolymer concrete. Moreover, Shi et al.²⁴ developed a comprehensive predictive framework for estimating the CS of FA-GC by applying advanced soft computing techniques. Their study introduced LSTM networks, enhanced through optimization by a marine predator algorithm, to model the nonlinear relationships between mix components and CS. Utilizing a data set built from prior work, they considered a very large number of input parameters, including chemical composition, aggregate proportions, and curing conditions. Comparison to multiple machine learning models demonstrated the high accuracy of the optimized LSTM approach, highlighting its potential for minimizing the need for large-scale laboratory tests as well as increasing the understanding of the important factors influencing GC performance. Furthermore, Khan et al.²⁵ utilized advanced machine learning techniques to estimate the CS of FA-GC. Their study implemented backpropagation neural networks, random forest regression, and k-nearest neighbors algorithms, incorporating key variables such as chemical composition, mixture ratios, and pre-curing conditions. Through detailed performance evaluation using standard statistical indicators, they identified the backpropagation neural network as the most accurate model. Sensitivity analysis further highlighted the dominant role of coarse aggregate content, silica concentration in FA, and alkali activator levels in influencing strength outcomes. Despite numerous explorations in the prediction of CS in geopolymer concrete, most of the existing research has excessively relied on traditional machine learning approaches, particularly ANN. Although ANN is capable of learning nonlinear relationships, they are often marred by the drawbacks of overfitting, slow convergence, and a lack of generalization capability, especially in dealing with relatively smaller or unbalanced datasets. Also, Shahmansouri et al.²⁶ experimentally investigated the effect of partially replacing GGBS with natural zeolite (NZ) and silica fume (SF) on the compressive strength of GPC. Gene expression programming (GEP) was used to develop predictive models based on 351 specimens from 117 mixtures. The results showed that key factors such as NaOH concentration, NZ, SF, and GGBS content significantly influenced compressive strength, demonstrating the utility of soft-computing techniques for prediction and optimization. Moreover, Shahmansouri et al.²⁷ created a comprehensive database of GGBS-based GPC with 351 specimens from 117 mixtures, considering factors such as specimen age, NaOH concentration, NZ, SF, and GGBS content. GEP was employed to develop simplified mathematical models to predict compressive strength efficiently. Sensitivity analysis confirmed the high accuracy and predictive capability of the proposed models, supporting environmentally beneficial reuse of GGBS. In addition, Shahmansouri et al.²⁸ examined the mechanical properties (compressive, flexural, and tensile strengths) of GGBS-based GPC incorporating NZ and SF with varying NaOH concentrations. Response surface methodology (RSM) was applied to identify optimal mix designs, improving all mechanical properties under specific conditions. The study highlighted that proper substitution of GGBS with NZ and SF, along with appropriate NaOH concentration, enhances overall performance. Also, Shahmansouri et al.²⁹ focused on predicting compressive strength of pozzolanic GPC using an ANN based on 117 specimens from 39 different mixtures. Input variables included NaOH concentration, SF, NZ, GGBS content, and specimen age. The ANN model showed high predictive accuracy and reliability, demonstrating the effectiveness of soft-computing approaches for sustainable geopolymer concrete mix design.

Furthermore, most existing works have focused primarily on strength prediction without addressing the optimization of mix design parameters. There has been comparatively limited attention on employing advanced metaheuristic optimization algorithms to systematically optimize the mix proportions of FA-GC. This creates a significant opportunity to develop more robust and efficient frameworks that not only predict mechanical properties but also provide optimal mix designs, leading to more cost-effective and environmentally sustainable construction solutions.

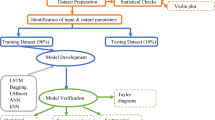
This research has two main objectives: the accurate prediction of CS of FA-GC and the optimization of the concrete mix design. To achieve these objectives, the first step involves predicting CS of FA-GC using advanced artificial intelligence models, followed by the optimization of the mix design to achieve the highest possible CS. In the prediction phase, various AI models, including Tabular Prior-Data Fitted Network (TabPFN), Histogram-based Gradient Boosting (HistGBoost), M5Prime, and Automatic Feature Interaction Learning (AutoInt), are used for simulating and predicting CS under the influence of different parameters. For model optimization and tuning, Optuna is employed to find the best hyperparameters for each model. The dataset is divided into two parts: 75% of the data for model training and 25% for testing. The predictive accuracy of the models is evaluated using the R² (Coefficient of Determination), RMSE (Root Mean Square Error), sMAPE (Symmetric Mean Absolute Percentage Error), WMAPE (Weighted Mean Absolute Percentage Error), and PBIAS (Percent Bias). Additionally, Taylor Diagram and NDA (Normalized Discrepancy Analysis) are used for model comparison and ranking, to identify the best model based on accuracy, stability, and alignment with real-world data. The best-performing prediction model is then used as the primary model for optimizing the FA-GC mix design. In the optimization phase, advanced optimization algorithms such as Harris Hawks Optimization (HHO), Grey Wolf Optimization (GWO), Lyrebird Optimization Algorithm (LOA), and Polar Bear Algorithm (PBA) are employed to determine the optimal composition of the concrete mix components. This research combines Shapley Additive Explanations (SHAP) and Partial Dependence Plots (PDP) sensitivity analyses to identify the parameters influencing the concrete’s performance and evaluates uncertainty using CI and R-Factor to enhance the accuracy of predictions and the stability of the models. These approaches increase prediction accuracy and enable more precise optimization of the FA-GC mix design. The combination of advanced AI models, modern optimization algorithms, and sensitivity and uncertainty analyses in this research represents a truly novel and unique approach. No other study has yet applied this combination of methods for predicting and optimizing the mix design of FA-GC. This approach marks a significant milestone in improving prediction accuracy and optimizing the performance of geopolymer concrete.

Materials and methods

Data collection

For this study, a dataset comprising 110 distinct geopolymer concrete mixtures was collected from eight different sources^{30,31,32,33,34,35,36,37}. The mix designs included components such as FA, fine and coarse aggregates, alkaline activators, water, and chemical additives. The alkaline activators primarily consisted of NaOH and Na₂SiO₃, with both their dosages and molar concentrations taken into consideration. Polycarboxylate superplasticizer (PCE) was commonly used as the chemical admixture in these mixtures. While water content was standardized across all sources to ensure consistency, potential variations in water inclusion methods were not captured due to limited data availability. It is worth noting that in the original studies, some authors combined the alkaline activators with water before mixing with solid materials, while others reported water content separately. To maintain consistency, the total water content was standardized by summing the water present in the alkaline solutions and any additional water added. Table 1 provides a summary of the statistical parameters used in the CS modeling of GC. This table includes the minimum, maximum, median, mean, and standard deviation values for 14 different parameters.

Table 1 Statistical summary of output and input Parameters.

Figure 1 shows the statistical distribution of input and output parameters for the CS modeling. This figure includes the analysis of mean, median, and interquartile range (IQR) for 14 different parameters that influence the mix design and prediction of the FA of GC.

Fig. 1

Statistical distribution of input and output variables for CS modeling, showing mean, median, and IQR to illustrate data spread and central tendency.

Data normalization

To normalize the data, the Z-score method was applied. This is a method of normalizing data to make variables comparable that would otherwise be on different scales. Under this approach, each data point is normalized relative to the mean and standard deviation of the data. The calculation of the Z-score is via the formula:

$$Z=\frac{{X - \mu }}{\sigma }$$

(1)

where X is the data point, µ is the mean of the dataset, and σ is the standard deviation of the dataset. Using this formula, the Z-score of each data point is calculated, representing how many standard deviations the data point is away from the mean. A Z-score greater than 0 indicates that the data point is above the mean, while a Z-score less than 0 indicates it is below the mean. This transformation is useful for comparing data points on a common scale, especially when the original data have different units or ranges. Z-score normalization was applied to standardize the dataset. All data were carefully checked for logical consistency, and no outliers were detected, ensuring reliable model training. Figure 2 shows data distribution both prior to and after normalization. This graph shows how, after applying the formula for Z-score, data are standardized around a mean of zero and a standard deviation of one. Standardization allows variables to be meaningfully compared and improves the performance of machine learning algorithms and statistical tests.

Fig. 2

Data distribution before and after normalization using the Z-score method, showing the effect of scaling on variable ranges.

Figure 3 shows the histograms of normalized data by Z-score normalization and the KDE distribution of all features. The figure clearly reflects how the data has been shifted post-normalization and how they are fitted to a normal distribution through the KDE plots.

Fig. 3

Z-score normalized histograms with KDE curves for each feature, illustrating the data distribution after normalization.

Artificial intelligence models

The use of AI in engineering sciences has gained significant attention in recent years³⁸. To accurately predict the CS of FA-GC, four advanced AI models were employed: Tabular Prior-Data Fitted Network (TabPFN), Histogram-based Gradient Boosting (HistGBoost), M5Prime, and Automatic Feature Interaction Learning (AutoInt). These models were used to simulate and predict CS under the influence of various parameters. The advantage of using these models lies in their high prediction accuracy and their ability to model the complexities of FA-GC data. For hyperparameter tuning and optimization, Optuna was used to identify and fine-tune the best hyperparameters for each model. This process helped the models achieve optimal performance in predicting CS. The data was randomly split into two parts: 75% for model training and 25% for testing and evaluating model performance. The research flowchart is presented in Fig. 4.

Fig. 4

Flowchart of the Research Process.

Tabular Prior-Data fitted network (TabPFN)

TabPFN is Tabular Prior-Data Fitted Network, an artificial intelligence model specifically designed for tabular data, typically existing in a structured form with different types of features (e.g., numerical, categorical, or text). TabPFN uses prior data to improve its performance based on history-driven patterns of data. One of the most outstanding features of TabPFN is its ability to adjust its network architecture autonomously based on the input data, thus making it extremely versatile with different distributions. This model is highly efficient in regression and can handle high-dimensional data. Through the use of both current input information and historical information, it can uncover complex relationships among features and thus is a highly efficient tool for prediction in complex circumstances³⁹.

Histogram-based gradient boosting (HistGBoost)

Histogram-based Gradient Boosting (HistGBoost) is an improved variant of the gradient boosting algorithm with histograms being used in the process to speed up training. In this method, the data is binned into histograms and is utilized for model training. This significantly reduces the computational cost compared to traditional gradient boosting methods, which continue by considering all the interactions of features explicitly. HistGBoost is particularly valuable for large data as it handles huge amounts of data more efficiently by converting continuous features into approximations based on histograms. This method is most suitable for classification and regression problems that require the models to be trained in a short time without compromising on accuracy, especially in real-time applications or extremely large datasets⁴⁰.

M5Prime

M5Prime is an optimized decision tree model for regression problems. It constructs predictive models by partitioning the data into subsets and fitting a regression model on each. One of the selling points of M5Prime is that it provides interpretable and transparent models, and hence it is most useful when the user requires transparency in the model decision-making process. M5Prime is applied very frequently where a simple-to-understand but accurate predictive model is needed. It is especially good at generating linear regression functions that are easy for analysts and engineers to understand, and it is commonly used in applications where the output variable is continuous and needs to be predicted exactly⁴¹.

Automatic feature interaction learning (AutoInt)

Automatic Feature Interaction Learning (AutoInt) is a deep learning model designed specifically to learn and discover automatically feature interactions. Capturing interactions among complex relationships of diverse features in data is one of the most difficult tasks in machine learning. The traditional models do require feature interactions to be manually specified, but AutoInt uses self-attention mechanisms to learn feature interactions automatically while training⁴². This model enables improved prediction by automatically detecting important feature interactions without requiring manual engineering. AutoInt, with the aid of self-attention, can learn sophisticated dynamic feature interactions, improve the precision of prediction, and therefore be a valuable resource for predictive modeling tasks in dealing with high-dimensional data and non-linear variable interactions⁴³.

Model selection rationale and justification

The primary objective of this study was to develop a highly accurate and generalizable predictive model for the CS of FA-GC. This task involves complex feature interactions, nonlinear relationships, and multidimensional dependencies⁴⁴. Accordingly, a set of models with diverse inductive biases and complementary capabilities was selected to better capture the nature of the problem:

• TabPFN is a transformer-based predictor pretrained on hundreds of thousands of classification and regression tasks. It can generalize effectively even with small and noisy datasets and requires minimal hyperparameter tuning, which is particularly valuable in material science applications where data availability is often limited.

• HistGBoost is an optimized gradient boosting model that uses histogram-based binning and stage-wise tree growth, providing faster training and better control over overfitting. It performs robustly on continuous and highly correlated features.

• M5Prime is a model tree approach that combines decision trees with piecewise linear models, offering not only strong predictive accuracy but also local interpretability of linear relationships, which is essential for understanding chemical processes and supporting engineering decisions.

• AutoInt leverages an attention mechanism to automatically discover higher-order feature interactions without the need for manual feature engineering, allowing it to capture complex dependencies that traditional models may overlook.

Widely used algorithms such as SVR, XGBoost, and Random Forest are also well known for their simplicity, stability, and strong performance in various engineering problems^45,46. Nevertheless, the focus of this study was on models that could better capture the complex structure of the data and provide deeper insights into the underlying relationships.

Optimization algorithms for concrete mix design

There were four recent optimization algorithms implemented in this study to optimize the concrete mix design and predict the CS of FA-GC. They include Harris Hawks Optimization (HHO), Grey Wolf Optimization (GWO), Lyrebird Optimization Algorithm (LOA), and Polar Bear Algorithm (PBA). The selection of these algorithms was driven by their distinct capabilities and inherent strength in handling complex optimization problems, particularly those with large, high-dimensional, and non-linear search spaces. These algorithms each have distinct strengths that make them exceedingly adept at exploring diverse solution landscapes and overcoming the challenges that are commonly inherent in optimization problems. Their exploration-exploitation balance strength, flexibility for problem types, and multi-objective and dynamic environment capability are a few of the reasons for their performance. Further, these algorithms have also been well-experimented for real-world optimization problem-solving so that they yield not just theoretically efficient but also practically effective optimal or near-optimal solutions for a wide range of applications.

Harris Hawks optimization (HHO)

Harris Hawks Optimization (HHO) is a novel algorithm inspired by the cooperative hunting behavior of Harris hawks. The algorithm mimics the complex hunting strategies and cooperation among the pack to converge rapidly towards promising regions. One of the most noticeable features of HHO is its ability to smartly search large and complex search spaces. In this algorithm, all of the group members (hunter) follow behaviors like pursuit and attacking of prey. This ability makes HHO specifically suitable for optimization problems with large and complex search spaces. Additionally, by collective intelligence of the group, such as non-random search and selection of different hunting strategies, HHO can discover optimal points in non-linear and multi-objective search spaces⁴⁷.

Grey Wolf optimization (GWO)

Grey Wolf Optimization (GWO) is a nature-inspired optimization algorithm that depends on the social behavior of grey wolves in the wild. Within this algorithm, each wolf in the pack has a specific role to fulfill, e.g., the leader (Alpha), followers (Beta), and the rest of the pack members (Delta and Omega). The algorithm is particularly developed for optimization problems in complex and global search spaces. One of the visible properties of GWO is that it has the ability to balance exploration and exploitation and thus it can perform well in finding global optima. GWO is a popular algorithm since it is easy to implement and has low requirements for parameter tuning. In this study, GWO was employed as an effective optimization method for the prediction of the CS of FA-GC, indicating its capacity to search for optima with high precision in complex, high-dimensional search spaces⁴⁸.

Lyrebird optimization algorithm (LOA)

The Lyrebird Optimization Algorithm (LOA) is a nature-inspired algorithm derived from the natural behavior of the lyrebird, which possesses a remarkable ability to mimic sound and behavior from its environment. LOA emulates the lyrebird’s adaptive behaviors, particularly mimicry, to solve optimization problems. In the algorithm, all individuals (lyrebirds) try to imitate the best solutions found by other individuals, enhancing the collective intelligence of the population. One of the most significant features of LOA is that it can explore big spaces by mimicking the behavior of good agents and adjusting its strategies based on the quality of solutions discovered. LOA is highly appropriate to solve complex, nonlinear, and multi-objective optimization problems since it can balance exploration and exploitation. By adopting several strategies, including imitation and adaptation, LOA can effectively search for optimal solutions in challenging problem spaces. The algorithm has been shown to be highly effective in fields that require high optimization and accuracy performance, such as in machine learning and engineering problems⁴⁹. The algorithm is very effective in searching for optimum points in large, dynamic, and complex search spaces, making it particularly well adapted to this study’s application in optimizing concrete mix design and predicting the CS of FA-GC.

Polar bear algorithm (PBA)

Polar Bear Algorithm (PBA) is a nature-inspired optimization algorithm predicated on the behavior of polar bears. This algorithm is especially effective for optimization problems with large and complex search spaces. Polar bears exhibit behaviors such as cooperation, competition, and exploration of new regions in search for food, which have been incorporated in the PBA. This enables this algorithm to be effective in searching large and complex search spaces. PBA is designed to solve multi-objective and nonlinear optimization issues, especially when exact and fast exploration of vast spaces is required. The algorithm has successfully optimized issues in various areas, including material optimization, engineering design, and other similar disciplines⁵⁰.

Metaheuristic algorithm selection and justification

The correct selection of metaheuristic algorithms plays a critical role in optimization problems, as each algorithm is characterized by specific search mechanisms, strengths, and limitations. An inappropriate choice may lead to issues such as premature convergence to local minima, excessive computational cost, or reduced prediction accuracy. Therefore, employing a diverse set of algorithms that cover different exploration–exploitation behaviors can enhance the robustness and reliability of the results^51,52.

In this study, a set of metaheuristic algorithms with distinct search dynamics was selected to maintain a balance between exploration (global search across the solution space) and exploitation (intensified search in promising regions) and to reduce the risk of stagnation in local minima. The selection criteria and advantages of each algorithm are summarized as follows:

• 1.  Harris Hawks Optimization (HHO)

Inspired by the cooperative hunting strategies of Harris’ hawks, this algorithm provides strong capability to switch dynamically between exploration and exploitation. It has shown competitive and stable performance in continuous optimization and has been successfully applied in various engineering fields.

• 2. Grey Wolf Optimization (GWO)

Based on the leadership hierarchy and hunting mechanism of grey wolves, GWO features a simple structure, fast convergence, and very few hyperparameters. It has been widely used in engineering optimization problems with reliable and consistent performance.

• 3. Lyrebird Optimization Algorithm (LOA)

A more recent algorithm inspired by the behavior of the lyrebird, LOA introduces novel exploration strategies, offering strong ability to search the solution space. Recent studies indicate that LOA can outperform some conventional methods and effectively avoid premature convergence in multimodal problems.

• 4.  Polar Bear Algorithm (PBA)

Developed from the foraging behavior of polar bears on ice, this algorithm benefits from adaptive step mechanisms in the exploration phase. It is particularly effective in high-dimensional spaces where extensive global search is required.

The inclusion of these four algorithms was guided by several comparative advantages over other metaheuristics:

• Coverage of a wide range of exploration–exploitation strategies, enabling diverse search behaviors.

• Moderate computational cost, making multiple independent runs feasible.

• Documented success in structural and material engineering applications, as highlighted in recent literature.

• The possibility of cross-validating optimized parameters by applying multiple algorithms rather than relying on a single optimizer.

Model performance evaluation metrics

In the evaluation of Artificial Intelligence models, the use of various statistical metrics for error estimation is of great importance because these statistical metrics help analyze the performance of models and can reveal the strengths and weaknesses of each model in predicting data and aligning with actual values⁴⁴. These metrics specifically focus on evaluating the deviation of predictions from actual data, assisting in selecting the optimal models based on prediction accuracy. In this study, five key statistical metrics are used to assess the performance of predictive models. These metrics include R², RMSE, sMAPE, WMAPE, and PBIAS⁵³.

$${R^2}=1 - \frac{{\sum\limits_{{i=1}}^{n} {{{({a_i} - {{\hat {a}}_i})}^2}} }}{{\sum\limits_{{i=1}}^{n} {{{({a_i} - \bar {a})}^2}} }}$$

(2)

$${\text{RMSE}}=\sqrt {\frac{1}{n}\sum\limits_{{i=1}}^{n} {{{({a_i} - {{\hat {a}}_i})}^2}} }$$

(3)

$${\text{sMAPE}}=\frac{1}{n}\sum\limits_{{i=1}}^{n} {\frac{{|{a_i} - {{\hat {a}}_i}|}}{{\frac{{|{a_i}|+|{{\hat {a}}_i}|}}{2}}}} \times 100$$

(4)

$${\text{WMAPE}}=\frac{{\sum\limits_{{i=1}}^{n} {{w_i}} |{a_i} - {{\hat {a}}_i}|}}{{\sum\limits_{{i=1}}^{n} {{w_i}} |{a_i}|}}$$

(5)

$${\text{PBIAS}}=\frac{{\sum\limits_{{i=1}}^{n} {({a_i} - {{\hat {a}}_i})} }}{{\sum\limits_{{i=1}}^{n} {{a_i}} }} \times 100$$

(6)

where a_i is the actual values of the data, ${\hat {a}_i}$ is the predictions of the model, $\bar {a}$ is the average value of the data values, n is the number of data, and w_i is the weight assigned to each data for calculation. The optimum value for each of the measures is as below: The optimum value for R² is 1, which would indicate that the model completely explains the variance in the data. The optimum value for RMSE is 0, which is indicating zero difference at all between the predicted and actual values, i.e., the best possible. The optimum value for sMAPE is 0, which indicates the model’s prediction is completely in line with the actuals. For WMAPE, also the best value is 0, i.e., no error between predicted and observed values, but it takes into account the weight given to different data points. Lastly, for PBIAS, the best value is 0, i.e., the model does not have any bias, i.e., does not overestimate or underestimate the observed values.

Comparison and ranking of artificial intelligence models

In this study, two methods, Taylor Diagram and NDA (Normalized Discrepancy Analysis), are employed to compare and rank the AI models used for predicting CS. These methods are selected to assess the accuracy, stability, and model alignment with real-world data, helping identify and rank the best-performing models for CS prediction.

Taylor diagram

The Taylor diagram is a powerful graphical tool for assessing model performance, especially when comparing models that generate numerical predictions. It simultaneously displays three key performance metrics of the models: Standard Deviation, Correlation, and centered RMSE (cRMSE)⁵⁴.

In the Taylor diagram, each model lies on a point of a circular graph. The position of the point indicates the performance of the model according to these three measures. The utility of this tool is to be able to simply find the models with the optimal performance regarding accuracy and proximity to actual data. Tends to be, in general, those models with smaller standard deviations, higher correlations with actual data, and lower values of RMSE that are closer to the middle point of the chart. This is one of the properties that makes the Taylor diagram a useful model comparison instrument, showing model performance in a direct visual format.

NDA (Normalized discrepancy Analysis)

NDA is particularly useful for evaluating models that require high precision in their predictions. In this approach, discrepancies between observed data and model predictions are standardized and then analyzed through a Gaussian distribution (normal distribution). This enables a more precise comparison of models and helps identify which models have the least discrepancies and provide the best alignment with real-world data⁵⁵.

The discrepancies between the observed data and the model predictions are expressed in two forms:

DDR (Discrepancy data Ratio)

This is the unadjusted difference between the forecasted value and the observed data. It is derived by dividing the difference between the observed and the forecasted value by scaling this difference based on data variability.

The DDR gives an indication of how far off the model’s predictions are from the actual observed values. Models with lower DDR values are those that more accurately predict the observed data.

QDDR (Quantified discrepancy data Ratio)

Once the DDR is calculated, the discrepancies are normalized and analyzed through a Gaussian distribution to create QDDR, which is the standardized form of the discrepancy data. QDDR helps quantify the shape and spread of the discrepancy distribution.

The QDDR values represent how well the model fits the observed data by showing how concentrated or spread out the discrepancies are. Models with narrower QDDR curves indicate that their discrepancies are closely clustered around zero, meaning they predict the observed data more accurately⁵⁵. This method uses the Gaussian distribution of discrepancies to visualize and analyze model behavior. Models with more accurate predictions, exhibiting fewer discrepancies from the real data, generate narrower and taller Gaussian curves.

Both Taylor diagrams and NDA were employed to evaluate model performance. Taylor diagrams provide a concise graphical representation of three key statistics—correlation, standard deviation, and cRMSE—enabling rapid visual comparison of model predictions with observed data. In contrast, NDA quantifies the dispersion and bias of model predictions relative to the reference, highlighting systematic deviations that may not be fully captured by Taylor diagrams. Combining these two approaches offers a more comprehensive assessment of model accuracy, consistency, and reliability.

Uncertainty quantification in artificial intelligence models

Uncertainty estimation of artificial intelligence models is extremely critical as these models are widely employed for making accurate and reliable predictions across various fields such as data science and engineering. Estimation of uncertainty minimizes the risks associated with incorrect decision-making. In this study, R-Factor and Confidence Interval (CI) were used to evaluate the uncertainty in the AI models’ prediction of the CS of FA-GC. These two metrics play a crucial role in assessing the stability and reliability of model outputs.

The CI represents the range within which the true value is expected to fall with 95% confidence. To calculate this interval, the bootstrap method was employed, generating 1000 random samples from the model’s outputs, and the 2.5th and 97.5th percentiles were used to define the confidence interval. The number of bootstrap samples was set to 1000, following common practice in uncertainty quantification studies to balance computational cost and stability. Additional tests with 500, 2000, and 5000 samples showed negligible differences (< 1%) in CI and R-Factor values, confirming that 1000 samples provide reliable and stable uncertainty estimates. A narrower CI indicates less uncertainty and greater accuracy of the model⁵⁶. The R-Factor measures the model’s stability by comparing the average width of the confidence interval to the standard deviation of the observed data. Although the CI is scale-dependent, the R-Factor is scale-independent in order to facilitate comparisons among models⁵⁷. Briefly, smaller values of both the R-Factor and CI mean a better model because they have less uncertainty bounds and greater stability compared to the data’s intrinsic variability.

Results

The sensitivity of input features influencing the CS of FA-GC was evaluated using SHAP values, providing a quantitative and interpretable measure of each feature’s impact on model predictions. Figure 5 illustrates this analysis: Panel (a) shows individual SHAP values for each feature, while Panel (b) presents the ranking of feature importance based on cumulative SHAP contributions.

The analysis indicates that Al₂O₃ (%), SiO₂ (%), and Coarse aggregate (kg/m³) have the strongest positive influence on CS, confirming their dominant role in geopolymer chemistry and mix design. Fine aggregate (kg/m³) and Duration (hr) have relatively minor effects, while Temperature (°C) and Water (kg/m³) exhibit moderate impacts, with temperature positively and water negatively affecting CS.

These results highlight the key features to prioritize in FA-GC mix optimization. Increasing alumina and silica content, optimizing coarse aggregate proportion, carefully controlling curing temperature, and limiting excess water can enhance CS, yielding more robust and durable geopolymeric concrete.

Fig. 5

Feature sensitivity analysis using SHAP values: (a) SHAP value distribution for individual features and (b) overall feature importance ranking.

Figure 6 presents a scatter plot matrix showing the relationships between various features and the CS of FA-GC. In this plot, each point represents a sample, comparing different features with CS. By examining this plot, clear patterns of correlation or lack thereof between features and CS can be identified.

Fig. 6

Scatter plot matrix showing the relationships between different features and the compressive strength (CS) of FA-GC.

Based on the results observed in Fig. 6, properties such as FA (kg/m³), SiO₂ (%), and Coarse aggregate (kg/m³) show a good positive correlation with CS. This implies that as these properties increase, the predicted values for CS also increase. These properties definitely follow a trend in the scatter plot with densely packed points, which show strong correlation with CS. On the other hand, features like Fine aggregate (kg/m³) and Duration (hr) appear to have weaker correlations with CS. The points for these features are more dispersed, indicating a less consistent relationship with CS. These observations align with the SHAP analysis, where Fine aggregate (kg/m³) and Duration (hr) were found to have a smaller impact on CS prediction. This scatter plot matrix, in conjunction with SHAP analysis, provides valuable insights into the key features influencing CS prediction and offers guidance for optimizing the mix design of FA-GC for improved performance.

Based on the PDP results shown in Fig. 7, each feature exhibits a distinct influence on the compressive strength (CS) of FA-GC. The main observations are as follows:

• FA (kg/m³): CS increases with FA content up to an optimal level and then plateaus, indicating the importance of maximizing FA proportion carefully.

• SiO₂ (%) and Al₂O₃ (%): Both have consistently positive effects on CS, highlighting their critical role in strengthening geopolymeric bonds.

• Coarse aggregate (kg/m³): Increases CS up to a certain limit, suggesting the need for optimized content.

• Fine aggregate (kg/m³): Exhibits a minor influence compared to coarse aggregate.

• NaOH (kg/m³) and Na₂SiO₃ (kg/m³): Both positively affect CS, with NaOH having a stronger impact due to its activator role.

• Water (kg/m³): Negatively affects CS, as higher water content reduces material strength.

• Temperature (°C): Higher curing temperatures enhance CS through improved geopolymerization.

• Duration (hr): Minimal effect on CS, indicating curing time is less critical in this context.

Overall, SiO₂, Al₂O₃, and coarse aggregate have the greatest influence and should be prioritized in mix optimization, while water and NaOH also play significant roles. Fine aggregate and curing duration have weaker effects. Optimizing these key factors can substantially improve FA-GC performance.

Fig. 7

Partial dependence plots (PDPs) illustrating the influence of key features on the compressive strength (CS) of FA-GC.

To gain deeper insights into the nonlinear influence of each variable on compressive strength and to identify potential threshold effects, one-dimensional Accumulated Local Effects (ALE) analyses were performed for all features used in the machine learning models. Figure 8 illustrate the isolated contribution of individual input parameters while accounting for feature interdependencies.

Fig. 8

Accumulated local effect (ALE) plots of key variables, showing their nonlinear influence on compressive strength.

The ALE curves demonstrate clear nonlinear behaviors and highlight several threshold regions. The AA/FA ratio exhibits two critical zones: an increase in compressive strength begins around 0.47–0.52, while a noticeable negative effect appears beyond 0.58. The content of Al₂O₃ shows a transition from a negative to a positive influence above approximately 16%, indicating that sufficient alumina availability enhances geopolymerization. Similarly, SiO₂ content displays a sharp threshold near 65%, beyond which the effect on strength becomes strongly negative, suggesting silica oversaturation. Aggregates play distinct roles: fine aggregate exhibits an optimal range of 400–505 kg/m³, with strength reduction above 520 kg/m³, while coarse aggregate negatively affects strength when exceeding 1185–1210 kg/m³, implying that excessive aggregate reduces binder continuity. FA shows a significant positive effect above 410 kg/m³, indicating a critical minimum required for optimal geopolymerization. Activator components show pronounced threshold behavior. The Na₂SiO₃ dosage enhances strength above 118–122 kg/m³, while the Na₂SiO₃/NaOH ratio declines sharply beyond ≈ 2.0, suggesting that excessive silicate relative to hydroxide can destabilize the reaction. Both NaOH concentration and alkali molarity (NaOH) present strong nonlinear effects: compressive strength rises significantly when NaOH exceeds ≈ 60 kg/m³ and molarity surpasses ≈ 13–14 M, then plateaus. The PCE content shows a distinct negative shift beyond ≈ 4, indicating overdosing of superplasticizer may hinder geopolymer formation. The water content demonstrates a clear drop in strength when exceeding ≈ 125 kg/m³, underscoring the sensitivity of geopolymerization to water-to-binder ratios. In contrast, curing temperature and curing duration show negligible ALE effects, implying that within the tested range they exert minimal influence compared to chemical composition and mix proportions. These findings confirm that the machine learning models capture complex, nonlinear dependencies and critical thresholds across multiple input variables. Identifying these ranges provides valuable guidance for optimizing mixture design to maximize compressive strength while maintaining material and chemical efficiency.

The hyperparameters of the models, tuned by Optuna, are presented in Table 2. These values were essential in achieving the best performance for each model in predicting the CS of FA-GC during the evaluation.

Table 2 Hyperparameters of the models tuned by optuna for predicting the CS of FA-GC.

Next, the performance of the models AutoInt, M5Prime, HistGBoost, and TabPFN in predicting the CS of FA-GC is examined, and their results are compared. The results obtained from the evaluations help identify the best surrogate model for use in optimizing the mix design of FA-GC. During the training phase, the performance of the models was evaluated based on various metrics. Table 3 presents the evaluation results of the models using different metrics such as R², RMSE, sMAPE, WMAPE, and PBIAS. These results are provided to compare the models’ performance in predicting the CS of FA-GC.

Table 3 Evaluation results of the models during the training Phase.

From the findings outlined in Table 3, a detailed analysis of the performance of the models in forecasting the CS of FA-GC during the training period reveals striking differences in most of the evaluation measures employed, including R², RMSE, sMAPE, WMAPE, and PBIAS. R² measures indicate that TabPFN possesses the largest explanatory power with a value of 0.981 and accounts for 98.1% of the variation in the CS of FA-GC. This shows that TabPFN has the best fit among the models examined. HistGBoost then has an R² of 0.948, demonstrating high predictive validity, although lower than TabPFN’s. AutoInt and M5Prime have lower R² values of 0.913 and 0.901, respectively, which means these models account for less of the variance in the target variable. In RMSE terms, the mean degree of error, TabPFN leads the rest with the least of 1.495, which indicates that its values are closest to true values. HistGBoost has a greater RMSE of 2.439, which indicates greater deviation from true values. AutoInt and M5Prime have greater RMSE of 3.159 and 3.377, respectively, indicating greater discrepancy between their values and observed values. The sMAPE metric, reflecting the accuracy of percentage errors, supports the findings of TabPFN’s superior performance, with the lowest sMAPE of 4.614%. This indicates minimal percentage error in its predictions, making it the most reliable model. HistGBoost follows with a sMAPE of 7.786%, while AutoInt and M5Prime show even higher errors of 9.815% and 10.176%, respectively, pointing to a lower degree of precision. Similarly, in terms of WMAPE, which accounts for the weighted accuracy of predictions, TabPFN leads with a value of 4.493%, further corroborating its overall effectiveness. HistGBoost has a WMAPE of 6.714%, while AutoInt and M5Prime present higher values of 9.161% and 9.982%, respectively, indicating greater weighted errors. Finally, the PBIAS values reveal subtle biases in the predictions. TabPFN exhibits a small positive bias of 0.455%, suggesting a tendency to slightly overestimate the CS. HistGBoost shows no bias with a PBIAS of 0, while AutoInt and M5Prime display negative PBIAS values of −0.269 and 0.043%, respectively, indicating a slight underestimation in their predictions.

Figure 9 provides a comprehensive visual assessment of the predictive performance of the four ML models—TabPFN, HistGBoost, AutoInt, and M5Prime—during the training phase, using three diagnostic plots: (1) the scatter plot of measured versus predicted CS values, (2) the residual plot showing prediction errors across samples, and (3) the KDE plot for comparing the distributions of predicted and actual values.

Fig. 9

Actual vs. predicted values, residuals, and KDE distributions for all models using the training dataset.

Based on the diagnostic plots in Fig. 9, the TabPFN model demonstrates the most accurate and stable predictive performance among the evaluated models. In the scatter plot, its predicted values are very close to the regression line, with nearly all observations falling well within the ± 10% error band. Such accuracy supports the earlier statistical outcomes—namely the model’s greater R² and RMSE values—by confirming strong correlation between predicted and actual CS values.

The residual plot for TabPFN further highlights its robustness, displaying a tight and uniform distribution of errors centered around zero. This pattern reflects minimal bias and indicates homoscedastic behavior, confirming the model’s stability across the entire prediction range. Additionally, the KDE plot reveals an almost perfect overlap between the measured and predicted distributions, suggesting that TabPFN not only achieves pointwise accuracy but also faithfully captures the statistical structure of the data. The HistGBoost model also shows competitive performance, albeit slightly inferior to TabPFN. Its scatter plot reflects a strong linear correlation; however, a broader spread of data points and a few deviations beyond the ± 10% margin suggest a marginal decline in precision. While the residual plot indicates low overall bias, it exhibits larger fluctuations, pointing to less consistent predictive behavior. In the KDE plot, the predicted and measured distributions are closely aligned, though slight discrepancies in the upper tail imply limited generalization under extreme conditions.

In contrast, the AutoInt and M5Prime models exhibit relatively weaker performance. Both models show greater dispersion in their scatter plots, with numerous data points falling outside the ± 10% threshold. Their residual plots present higher variability and non-uniform error patterns, indicative of unstable and less reliable predictions. Also, their KDE plots indicate apparent divergence between the predicted and actual distributions, pointing to their poor capacity to capture the actual data distribution. Generally, the visual diagnostics in Fig. 9 reflect the statistical measures in Table 3. The TabPFN model clearly outperforms its competitors, showing higher accuracy, reliability, and distributional accuracy at training. In testing, the models’ performance was again measured using various metrics.

Table 4 presents the evaluation results of the models based on criteria such as R², RMSE, sMAPE, WMAPE, and PBIAS during the testing phase. These results are provided to further compare the models’ performance in predicting the CS of FA-GC on new data.

Table 4 Evaluation results of the models during the testing Phase.

The performance of the models in the testing stage, as shown by the results in Table 4, reflects considerable variations in some of the most critical indicators like R², RMSE, sMAPE, WMAPE, and PBIAS. All these indicators form a holistic evaluation of the ability of the models to estimate the CS of FA-GC with accuracy and reliability. In R², or the model’s proportion of variance in CS of FA-GC explained, the optimum result is achieved by TabPFN with an R² of 0.916. This means TabPFN explains 91.6% of the variance in the data, indicating a good fit and high prediction precision. HistGBoost, at 0.894 R², follows closely behind, with good predictive power but less explanatory power than TabPFN. AutoInt, at 0.892 R², and M5Prime, with the lowest R² of 0.867, indicate that these models are weaker at understanding underlying variance in the CS of FA-GC, with the poorest fit overall from M5Prime. The RMSE values also support the improved performance of TabPFN, which achieves the lowest RMSE value of 4.02. This implies the model’s predictions are closest to actual values with minimum deviation. HistGBoost (RMSE = 4.522) and AutoInt (RMSE = 4.567) achieve slightly higher errors, with the highest deviation between their predicted and actual values. M5Prime has the highest RMSE of 5.062, which means a higher error in its predictions compared to the other models. On an sMAPE scale, recording percentage prediction error, TabPFN once more has the best performance with an sMAPE of 8.201%. This translates to the lowest percentage error for the model, which is an affirmation of the model’s high accuracy level. M5Prime has a later sMAPE of 11.222%, while AutoInt and HistGBoost lead to higher sMAPE measures of 12.994% and 13.622%, respectively, and illustrate that the models are worse with respect to percentage error. The WMAPE metric, which accounts for the weighted accuracy of predictions, also favors TabPFN with the lowest WMAPE of 9.331%. This demonstrates the model’s strong performance in terms of weighted error. HistGBoost (WMAPE = 12.73%) and AutoInt (WMAPE = 12.909%) show higher weighted errors, while M5Prime (WMAPE = 12.611%) exhibits similar levels of weighted inaccuracy. Finally, the PBIAS values, which indicate the degree of bias in predictions, reveal that TabPFN exhibits the least negative bias with a value of −2.33%, suggesting a slight tendency to underestimate the CS of FA-GC. HistGBoost follows with a PBIAS of −3.195%, while AutoInt and M5Prime show more significant negative biases of −3.986% and − 3.071%, respectively, indicating a greater tendency to underestimate the values.

Figure 10 illustrates the testing-phase prediction performance of four ML models—AutoInt, HistGBoost, M5Prime, and TabPFN—through scatter plots, residual error plots, and KDE distributions comparing predicted and actual CS values.

Fig. 10

Actual vs. predicted values, residuals, and KDE distributions for all models using the testing dataset.

Based on Fig. 10, the TabPFN model once again exhibits the most reliable generalization performance among all evaluated models. On the scatter plot, the predicted values fall very near along the regression line with nearly all points in the ± 10% error range. This visual reliability corroborates the model’s strong statistical performance in the above—most importantly, its high R² (0.916) and low RMSE (4.02)—which indicates high predictive accuracy on novel data. The residual plot also verifies the finding, with a tight and symmetrical scatter of errors around the zero line, which verifies low bias and high stability across the range of predictions. Moreover, the KDE plot provides a virtually perfect overlap between predicted and measured distributions, ensuring that TabPFN is able to accurately capture the pointwise accuracy and also the underlying statistical pattern of the dataset. The HistGBoost model also delivers solid performance, albeit with slightly diminished precision relative to TabPFN. In its scatter plot, most predicted values fall close to the regression line and within the error band, but the overall dispersion is more pronounced. The residual plot indicates modest fluctuations with occasional spikes, suggesting areas of localized error. Although the KDE curves for measured and computed values remain largely similar, minor discrepancies—particularly in the tails—indicate slight limitations in distributional fidelity.

In contrast, the AutoInt and M5Prime models show weaker predictive capabilities in the testing phase. Both models exhibit greater spread in their scatter plots, with a larger number of predictions falling outside the acceptable error margin, suggesting reduced alignment with actual measurements. Their residual plots show more erratic and wider deviations from zero, reflecting less consistent prediction behavior and higher variance. The KDE plots further highlight these limitations, as visible divergences between the predicted and actual distributions—especially in extreme ranges—indicate insufficient ability to replicate the true data characteristics. In conclusion, the visual analyses in Fig. 10 align closely with the quantitative outcomes reported in Table 4, affirming that TabPFN is the most effective model in terms of both predictive accuracy and distributional robustness during the testing phase.

To evaluate and rank the performance of the applied artificial intelligence models in predicting the CS of FA-GC, the Taylor diagram was employed as a robust graphical analysis tool. This diagram simultaneously illustrates three essential metrics—correlation coefficient, standard deviation, and cRMSE—allowing for a comprehensive and visual comparison of model accuracy and consistency. The results for both the training and testing stages are presented in Fig. 11.

Fig. 11

Taylor diagram for comparative evaluation of ai models in training and testing phases.

As indicated in Fig. 11, the TabPFN model also exhibited the highest accuracy with a cRMSE value of 1.50, revealing a high correspondence between its forecast and the actual observed values in the training interval. On the Taylor diagram, this model is positioned closest to the reference point of the measured data, indicating its optimal predictive performance. Following TabPFN, the HistGBoost model achieved a cRMSE of 2.45, performing reasonably well, although with a slightly greater deviation. The AutoInt and M5Prime models showed larger errors, with cRMSE values of 3.18 and 3.40, respectively, placing them behind in terms of training accuracy. During the testing phase, which evaluates the generalization capacity of the models for unseen data, the same tendency is observed. TabPFN was once more the top-performing model with cRMSE = 4.042, placed in a favorable position in the Taylor diagram and proving its stability for datasets. AutoInt and HistGBoost models showed nearly similar results (cRMSE = 4.516 and 4.518, respectively), with moderate accuracy. In contrast, M5Prime produced the highest prediction error with cRMSE = 5.083, which indicates the worst and most unstable performance in testing. In conclusion, based on the Taylor diagram analysis and cRMSE values, the TabPFN model consistently exhibits the best performance across both training and testing phases.

In order to further examine the performance of the models and support the findings obtained from the Taylor diagram, the NDA metric was employed. This statistical approach provides a more detailed assessment of how closely the models’ predictions align with actual values. The NDA results for both the training and testing stages are presented in Fig. 12, offering additional validation of model accuracy and consistency.

Fig. 12

Normalized deviation analysis (NDA) of model predictions during training and testing phases.

In the training phase, the TabPFN model clearly demonstrates the narrowest and tallest QDDR curve, which is symmetrically centered around zero. This distribution indicates minimal variance and high concentration of residuals near zero, affirming the model’s exceptional accuracy and consistency during training. Compared to other models:

• HistGBoost and AutoInt exhibit moderately wide distributions, suggesting a higher spread of errors and lower reliability.

• M5Prime shows the widest and flattest distribution, indicating the largest deviations from actual values and lower predictive confidence.

This confirms that among all models, TabPFN provides the most stable and precise predictions during training, further supporting the results from the Taylor diagram.

In the testing stage, although the QDDR curves for all models are generally wider due to exposure to unseen data, TabPFN continues to maintain the most concentrated distribution around zero. This sustained narrowness underlines the model’s superior generalization capability and robustness in predicting new data points. Meanwhile:

• AutoInt and HistGBoost show comparable but wider distributions, reflecting greater variance and reduced reliability in generalization.

• M5Prime, once again, presents the broadest and flattest curve, confirming its comparatively weak performance under uncertainty.

The NDA results in Fig. 12 validate the findings from the Taylor diagrams by quantitatively demonstrating that the TabPFN model consistently outperforms the other models in both training and testing stages, offering the lowest discrepancy, highest stability, and most reliable predictions.

It is crucial that artificial intelligence models not only have high accuracy but also high reliability. In this regard, to assess the uncertainty of the evaluated models, two metrics, CI and R-Factor, have been used. The results of this evaluation are shown in Fig. 13.

Fig. 13

Evaluation of model uncertainty, showing confidence intervals (CI) and R-factor values for different AI models.

Figure 13 shows that TabPFN is the most excellent model from the uncertainty point of view because it has the lowest CI value of 0.697 and the lowest R-Factor value of 2.730 among all the models under consideration. These results indicate that TabPFN is the most accurate and stable prediction in comparison to the other models. Following TabPFN, the HistGBoost model (CI = 0.704, R-Factor = 2.759) and M5Prime (CI = 0.708, R-Factor = 2.774) have very similar performance, both reducing uncertainty and enhancing the stability of prediction. On the other hand, the AutoInt model with CI = 0.716 and R-Factor = 2.807 shows the highest level of uncertainty and variation in predictions and is therefore less desirable in comparison to the other models. In general, TabPFN, with the highest performance—evinced through the lowest figures for CI and R-Factor—is the most desirable model with greater accuracy and stability of predictions compared to the other models.

To investigate the weaker performance of M5Prime and AutoInt, the following reasons can be noted:

AutoInt

Embedding layers and multi-head interaction blocks introduce many degrees of freedom relative to the sample size, leading to overparameterization and a persistent train–test gap. Performance is sensitive to optimization choices (learning rate, warm-up, regularization, initialization); even with early stopping and multiple seeds, variance remains high and rare regimes are underfit. Under collinearity, attention weights become unstable across near-equivalent inputs, amplifying spurious interactions and reducing identifiability. Predictive uncertainty is less well calibrated in sparsely covered regions of the design space, yielding wider dispersion and less reliable confidence assignments.

M5Prime

As a model tree with piecewise-linear leaves, capacity is limited for non-additive, high-order interactions, producing structured residuals the linear leaves cannot absorb. Greedy splitting under collinearity oscillates among near-equivalent predictors, increasing variance; enlarging the minimum leaf size improves stability but increases bias, sharpening the bias–variance trade-off. Local linearity yields weak extrapolation outside split ranges and creates discontinuities at split boundaries, degrading accuracy and stability when inputs shift slightly or measurement noise moves samples across thresholds.

To further assess the predictive capability and generalizability of the TabPFN model, an external validation was conducted using independent data. External validation serves as an effective approach to evaluate whether a model trained on a specific dataset can reliably predict unseen data from different sources, thereby reducing the risk of overfitting and confirming its practical applicability. For this purpose, additional data were extracted from Nath and Sarker⁵⁸, which are completely independent of the dataset used in the present study. These external data were used to test the TabPFN model’s performance beyond the original dataset, as shown in Table 5. The results of this evaluation are summarized in Fig. 14, where the model demonstrates strong predictive accuracy. On average, the TabPFN model predicted the independent data with an error of 10% across 9 samples, confirming its ability to generalize well to new, unseen data. This external validation complements the internal evaluation and further supports the robustness of the developed model.

Table 5 Dataset used for external validation of TabPFN model.

Fig. 14

Comparison of compressive strength (CS) in external validation data with values predicted by the TabPFN model.

As the TabPFN model is demonstrated to possess both high predictive accuracy and high reliability, it can be trusted for use as a surrogate model in optimization algorithms for concrete mix design. Its superior performance in both the areas of lesser uncertainty and stable prediction results renders it extremely well-suited for guiding the optimization process with high accuracy, resulting in more efficient and reliable mix design solutions.

Table 6 displays the experimental and predicted values of CS for FA-GC.

Table 6 Experimental and predicted values of CS for FA-GC by the assessed artificial intelligence models.

As previously mentioned, this study aimed to develop an optimal mix design for maximizing the CS of FA-GC using four optimization algorithms: HHO, GWO, LOA, and PBA. In this context, the TabPFN model was employed as a surrogate model to predict CS accurately, and the mix design optimization was conducted under two separate scenarios. In the first scenario, the objective was to determine the optimal proportions of two key chemical components—SiO₂ and Al₂O₃—as the primary constituents of FA, to maximize the CS. For this purpose, three existing experimental mix designs were selected. In these designs, 12 out of 14 input variables were fixed based on experimental data, while only SiO₂ and Al₂O₃ were treated as decision variables. The optimization algorithms were then applied to simulate the optimal combination of these two chemical parameters for achieving the highest possible CS. In the second scenario, the goal was to identify a fully optimized mix design by treating all input variables as decision variables.

For the implementation of the optimization algorithms, two main constraints were considered. The first constraint ensured that the decision variables were within an acceptable range. The second constraint required that the sum of the weights of the input parameters divided by their density equals 1. The constraints mentioned can be expressed in the form of Eqs. (7 and 8).

$$L{b_i} \leqslant {W_i} \leqslant U{b_i},i=1,2, \ldots ,n$$

(7)

$$\sum\limits_{{i=1}}^{n} {\frac{{{W_i}}}{{{\rho _i}}}} =1$$

(8)

where ρ_i​ is the density of material i. Table 7 displays the optimized values of SiO₂ and Al₂O₃ for each optimization algorithm. Additionally, the experimental values are included in this table for comparison. The variable notation in the tables of the following text is based on Table 1.

Table 7 Optimization results of mix design in scenario 1.

Table 8 presents the optimization results for FA-GC mix designs in Scenario 2, displaying the values of key parameters for each algorithm (HHA, LOA, GWO, and PBA). Additionally, Fig. 15 compares the CS of FA-GC mixtures optimized by different algorithms across both Scenarios 1 and 2.

Table 8 Optimization results of mix design in scenario 2.

Fig. 15

Comparison of compressive strength (CS) of FA-GC mixtures using different optimization algorithms under Scenarios 1 and 2.

The results show that optimizing the FA-GC mix designs using different algorithms leads to better performance in increasing CS. In Scenario 2, the HHA algorithm achieves the highest CS (61.56 MPa), indicating its superiority over the LOA, GWO, and PBA algorithms. Compared to the experimental values, the Optimized Mix reaches a CS of 61.6 MPa, showing a significant improvement over the initial mixes. These results emphasize that the correct selection of optimization algorithms can have a significant impact on improving the performance of FA-GC mixes, with HHA demonstrating the greatest effectiveness among them.

In addition to predictive accuracy and data efficiency, interpretability is a key criterion in selecting surrogate models for engineering applications. Interpretability refers to the model’s ability to explain the relationships between input variables and its decision-making logic in a way that is understandable to humans. This property is particularly important in industrial contexts, where decision-makers often require not only accurate predictions but also a clear understanding of the factors influencing those predictions.

Following the optimized mix designs, this section critically compares the four optimizers in terms of computational footprint and real-world scalability, and offers practitioner-oriented guidance.

All four methods are population-based. Per-iteration cost scales as:

$${\text{Cost}} \approx {N_{{\text{pop}}}} \times {N_{{\text{iter}}}} \times {C_{{\text{eval}}}}$$

(9)

where C_eval​ is the surrogate call (TabPFN inference in our pipeline). Memory is O(N_pop×D) with D features. Fitness evaluations are embarrassingly parallel across individuals; communication overhead is small.

HHO

Adaptive exploration–exploitation with multiple update regimes. Strong performance on rugged, nonlinear landscapes; good best-found quality under equal budgets. Overhead is moderate due to regime switching; tuning sensitivity is modest. Suitable when solution quality is the priority.

GWO

Parameter-lean and easy to tune. Low setup cost and stable behavior as dimension grows. Convergence can be slightly slower, but wall-clock efficiency and scalability are favorable. Suitable under tight time or resource constraints and for industrial deployment.

LOA

Rapid information sharing yields fast early progress and a balanced exploration–exploitation profile. Similar per-iteration cost to other population methods. Risk of premature convergence under homogeneous imitation; diversity mechanisms (noise, restarts) mitigate this. Useful when quick propagation of good patterns is desired.

PBA

Dynamic population management with aggressive moves can improve evaluation efficiency late in the search and adapt to changing constraints. Slight managerial overhead. Appropriate for scenarios with nonstationary requirements or short evaluation budgets.

Under equal computational budgets in our experiments, HHO achieved the best objective values, GWO was close and stable, and LOA/PBA exhibited advantages in specific regimes consistent with their design trade-offs.

Practitioner guidance

• Quality-first (ample budget, complex landscape): prefer HHO.

• Simplicity and scalability (limited time/resources, easy deployment): prefer GWO.

• Fast early progress and strong information diffusion: consider LOA.

• Dynamic or evolving constraints, short budgets: consider PBA.

In this study, the TabPFN model was selected as the surrogate model due to its superior predictive performance and its ability to learn effectively from limited data. However, because TabPFN is based on a transformer architecture with millions of nonlinear parameters, it is inherently opaque and often regarded as a “black box.” To enhance interpretability, we employed the SHAP method as a post-hoc analysis tool to quantify the contribution of each feature to the model’s predictions.

The SHAP analysis results, reveal the relative importance of different input features in predicting the compressive strength of concrete. According to these results, Al₂O₃, SiO₂, and Coarse aggregate have the most significant impact on the model output. Furthermore, the direction of these effects is consistent with engineering knowledge: for example, increasing cement content strongly enhances compressive strength, whereas increasing the water-to-cement ratio reduces it. These findings demonstrate that, despite its complex structure, the model’s internal logic aligns with known physical and material science principles.

In contrast, simpler models such as M5Prime are inherently interpretable. M5Prime is based on decision tree structures, and its output is expressed as a set of human-readable rules and linear equations. The decision-making path is explicitly defined for each prediction, allowing users to easily trace and understand the reasoning behind the model’s output. Moreover, the simpler structure of M5Prime typically results in higher stability under small data perturbations, and the resulting decision rules can be directly analyzed without the need for additional interpretation tools. A comparison of key interpretability characteristics of TabPFN and M5Prime is presented in Table 9.

Table 9 Comparison of interpretability characteristics between TabPFN and M5Prime surrogate models.

This comparison highlights that the choice of surrogate model ultimately depends on the objectives of the application. If predictive accuracy and data efficiency are the primary goals, TabPFN is a highly powerful candidate. However, if interpretability and explainability are of greater importance, simpler models like M5Prime may be more appropriate. The optimization framework proposed in this study is flexible and can accommodate both types of models—highly accurate or highly interpretable—without requiring modifications to the overall optimization process.

To summarize model performance and uncertainty, Table 10 reports R², RMSE, cRMSE, 95% CI width, and R‑Factor for the train and test phases.

Table 10 Summary comparison of surrogate models on performance and uncertainty.

Meta-learned prior and few-shot generalization

Pretraining supplies a data-driven prior that improves test R² and reduces error on small datasets.

Automatic high-order interactions

Attention captures nonlinear feature interactions without manual feature engineering.

Smooth response surface

The learned mapping yields stable gradients and lower cRMSE, which benefits the optimizer’s inner loop.

Better calibration and tighter uncertainty

Narrower 95% CI and lower R-Factor indicate more reliable predictions.

Robustness to collinearity and noise

Learned inductive biases preserve rank performance across metrics.

Fast inference

After pretraining, per-sample prediction is lightweight, which suits iterative optimization.

Conclusion

This study proposed a comprehensive, data-driven framework to accurately predict and optimize the compressive strength (CS) of fly ash-based geopolymer concrete (FA-GC) using state-of-the-art artificial intelligence (AI) and metaheuristic optimization techniques. By integrating advanced ML algorithms with interpretability tools and uncertainty quantification methods, the research offers a novel, multi-dimensional approach to FA-GC performance enhancement. Among the four evaluated AI models—Tabular Prior-Data Fitted Network (TabPFN), Histogram-based Gradient Boosting (HistGBoost), M5Prime, and Automatic Feature Interaction Learning (AutoInt)—the TabPFN exhibited the highest predictive performance. It achieved an R² of 0.981 in training and 0.916 in testing, along with the lowest RMSE and sMAPE, indicating exceptional accuracy and generalization. Furthermore, TabPFN recorded the lowest uncertainty metrics (CI = 0.697, R-Factor = 2.730), establishing its superiority as both a predictive and stable surrogate model for mix design optimization.

Sensitivity analysis using SHAP and PDP confirmed that Al₂O₃ (%), SiO₂ (%), and Coarse aggregate (kg/m³) had the most significant positive influence on CS. This insight was reinforced by scatter plot matrices and PDP trends, providing robust guidance for targeted feature manipulation in optimization. Using TabPFN as the surrogate model, four metaheuristic algorithms—Harris Hawks Optimization (HHO), Grey Wolf Optimization (GWO), Lyrebird Optimization Algorithm (LOA), and Polar Bear Algorithm (PBA)—were applied to optimize the mix design under realistic constraints. The HHO algorithm emerged as the most effective, achieving a maximum CS of 61.56 MPa in Scenario 2, substantially surpassing experimental baselines and other algorithms.

In summary, this study confirms that the synergy of interpretable AI models, uncertainty quantification, and bio-inspired optimization techniques significantly enhances both the predictive accuracy and mix design efficiency of FA-GC. The proposed framework not only advances the field of intelligent concrete design but also offers a scalable blueprint for future applications in sustainable construction materials.

Feature research

The following directions are suggested for future studies to further validate and expand upon the findings of this research:

• Experimental validation of optimized FA-GC mixes: Based on the optimized designs obtained in this study, samples should be prepared according to the proposed mix variables. Compressive strength tests and other relevant mechanical assessments should be conducted to compare the experimental results with the predicted values from the AI-based optimization. This process will allow evaluation of reproducibility, consistency, and practical applicability of the optimized mix designs.

• Comprehensive environmental assessment (LCA) of FA-GC: A full life cycle assessment of fly ash-based geopolymer concrete is recommended for future studies. This would involve quantifying CO₂ emissions, global warming potential, and other environmental impacts of FA-GC compared to OPC, thereby providing a more robust evaluation of its sustainability benefits.

• Develop a more comprehensive database in which additional variables (such as water quality, microstructural properties, and detailed curing conditions) are systematically included. Such an approach would allow higher-dimensional models to be developed that can capture subtle interactions among a wider range of parameters without compromising prediction accuracy.

• While SiO₂ (%) and Al₂O₃ (%) were included as input variables to represent the chemical composition of fly ash, potential limitations in fly ash availability and access to complete chemical data prevented the inclusion of all relevant characteristics. This limitation is acknowledged and should be addressed in future studies to enhance model generalizability.

• Conduct a detailed analysis of feature interactions while ensuring that generated mix designs remain physically feasible and practically producible.