Novel temperature-based spectral topological indices for QSPR modeling of polyacenes in predicting physicochemical properties

Abstract

Quantitative structure–property relationship (QSPR) studies rely on molecular descriptors that link chemical structure to physicochemical properties. However, the rapid proliferation of topological indices has led to many with limited predictive utility. To address this, we introduce a new class of temperature-based spectral topological indices derived from eigenvalues of temperature-dependent chemical matrices. Using an integrated computational framework, we evaluated 42 such indices on a dataset of 22 lower polycyclic aromatic hydrocarbons (PAHs), targeting normal boiling point and standard enthalpy of formation. Comparative testing revealed that while several Estrada-type indices underperformed, five spectral descriptors achieved exceptional multiple correlations (MCVs$\ge 0.99$). These indices were validated through regression modeling and applied to predict the properties of linear polyacenes, confirming their reliability and robustness. These findings establish temperature-based spectral invariants as powerful and generalizable tools for predictive modeling in cheminformatics.

Introduction

Quantitative structure-property relationship (QSPR) studies¹ form a central tool in theoretical chemistry for predicting physicochemical and thermodynamic properties of molecular systems, especially organic compounds. These models exploit modern computational and mathematical techniques² to establish links between chemical structure and measurable properties. The foundations of QSPR trace back to a seminal work³ by Harold Wiener (1947), where the notion of a path number–defined as the sum of all pairwise distances–was introduced to estimate alkane boiling points, a measure later formalized as the Wiener index of graphs. In current research, structure-based molecular descriptors⁴ provide the essential mathematical framework for QSPR studies. A particularly important class comprises graph-based descriptors, also known as graphical invariants or topological indices⁵, which are among the most extensively examined. These invariants convert hydrogen-suppressed chemical structures (chemical graphs) into non-zero real numbers that capture underlying structural information, where a chemical graph⁶ represents a molecule by assigning vertices to atoms and edges to bonds. Using such descriptors, regression models⁷ are constructed to estimate key physicochemical quantities–such as boiling points and heats of formation⁸–thereby bridging molecular structure and measurable properties.

Graphical indices, depending on the principles underlying their definitions, are classified into several categories, including valency-based descriptors⁹, counting-based descriptors¹⁰, distance-dependent indices¹¹, and spectral descriptors¹². To date, hundreds of such indices have been proposed^4,13, and their number continues to grow rapidly. However, the introduction of new descriptors often lacks well-defined criteria, which has led to a proliferation of measures with limited utility. Notably, many of the less effective descriptors identified in the literature are graph-theoretic in nature. Gutman and Tošović¹⁴ have cautiously remarked that the absence of rigorous standards has allowed this unchecked expansion, resulting in far more descriptors than are scientifically necessary. The readers are referred to applications of degree-based and related indices in benzeneoid systems¹⁵, graphene¹⁶, and Curcumin-conjugated PAMAM dendrimers¹⁷. More applications of graph theory can be found in other areas such as communication networks and IoT^18,19,20,21.

The predictive potential of graph-based descriptors for molecular properties has been explored in several directions. Gutman and Tošović¹⁴ first demonstrated that valency descriptors can successfully capture physicochemical characteristics of isomeric octanes, a canonical class of alkanes. Their findings motivated subsequent studies: Malik et al.²² generalized the approach to polycyclic aromatic hydrocarbons (PAHs), whereas Hayat et al.²³ investigated its utility in predicting quantum-theoretic properties of PAHs. Parallel developments by Hayat et al.^24,25 shifted the focus to distance-based descriptors, establishing their effectiveness in modeling both physicochemical and quantum-theoretic properties of lower PAHs. More recently, the works in^26,27 evaluated eigenvalue-based indices, highlighting their strong correlation with physicochemical parameters as well as the $\pi$-electronic energy of PAHs.

This study introduces eigenvalue-based temperature spectral indices and performs comparative analyses to evaluate their potential in predicting physicochemical properties of PAHs. In line with the work of Gutman and Tošovi’c¹⁴, the normal boiling point ($b_p$) and the standard heat of formation ($\Delta H^o_f$) are selected as the target properties. Following²⁸, the dataset consists of 22 lower PAHs chosen as representative test molecules. Based on multiple correlation values (MCVs), we identify the top five temperature-based spectral indices with MCVs exceeding 0.99. A detailed statistical analysis is then carried out on these five indices. Finally, the applicability of the proposed indices in QSPR modeling is demonstrated through the prediction of physicochemical properties of linear polyacenes.

The remainder of this paper is organized as follows. Section Essential mathematical concepts provides the necessary mathematical preliminaries and introduces the temperature-based spectral topological indices. Section A computational method describes the computational methodology employed for their calculation. The dataset and results of comparative testing are presented in Section Comparative testing. In Section Results and discussion, the five most effective spectral indices–identified according to their multiple correlation values (MCVs)–are examined in detail through statistical analysis and regression modeling. Finally, Section Efficient temperature-based spectral indices in QSPR modeling of polyacenes illustrates the applicability of these indices in QSPR modeling, with particular emphasis on predicting physicochemical properties of linear polyacenes.

Essential mathematical concepts

A graph is a pair $\Phi =(P_\Phi ,L_\Phi )$ comprising a set $P_\Phi$ of point (vertices), and a set $L_\Phi$ of lines (edges). The graph $\Phi$ is finite, if $P_\Phi$ as a set is finite. Moreover, $\Phi$ is simple if $L_\Phi ={P_\Phi \atopwithdelims ()2}$ (every pair of points forms atmost one edge) and $\Phi$ is connected if any two points are connected by a sequence of adjacent points. The graphs in this study are restricted to finite, simple and connected. The degree $\text {deg}_s=|t\in P_\Phi : st\in L_\Phi |$ of $s\in P_\Phi$ is the number of points adjacent to s by a line. A chemical graph is a finite simple connected graph where atoms are represented as points and chemical bonds are represented as lines. The degree of a point corresponds to the valency of the corresponding atom in a chemical graph.

The temperature $\eta _s$ of a point $s\in P_\Phi$, introduced by Fajtlowicz²⁹ in 1988, is defined as:

$$\begin{aligned} \eta _s=\frac{\text {deg}_s}{n-\text {deg}_s}, \end{aligned}$$

(1)

where $n=|P_\Phi |$ is the number of points in $\Phi$. In short, the temperature of a vertex s is the ratio between its degree and co-degree ($n-\text {deg}_s$), where n is the number of vertices. A topological index $T:\Pi \rightarrow \mathbb {R}$ is a map from the set $\Pi$ of chemical graphs to the set of real numbers such that they have application in predictive modeling. A topological index is temperature-eigenvalues-based, if it is defined based on eigenvalues of a temperature-based matrix. In the next subsection, we introduce the associated temperature-based matrices and their spectral indices.

Temperature-based matrices and spectral indices

Importing the defining structures from degree-based indices, Kulli³⁰ introduced a class of temperature-dependent topological indices. A further valued addition was contributed by Gutman³¹ who introduced and studied the temperature version of the classical Sombor degree-based index. Moreover, Kahsay et al.³² (respectively Narayankar et al.³³) put forward the atom-bond connectivity (ABC) temperature index (respectively harmonic temperature index). Hayat et al.²⁸ proposed the reduced reciprocal product-connectivity temperature index and the geometric-arithmetic temperature index. Hayat et al.²⁸ also surveyed and compiled a list of all the temperature indices existing in the literature so far.

Next, we introduce temperature-based matrices and define their respective spectral indices. A temperature-based matrix of an n-vertex chemical graph $\Phi$ is an $n\times n$ real symmetric matrix whose rows and columns are indexed by the vertices of $\Phi$. Mathematically, its st-entry is defined as:

$$(\mathscr {T}(\Phi ))_{st}=\left\{ \begin{array}{ll} \phi (\eta _s,\eta _t), & {st\in E_\Phi ;} \\ 0, & \hbox {otherwise,} \end{array} \right.$$

where $\phi$ is a bivariate symmetric function of temperatures $\eta _s$ and $\eta _t$ of vertices s and t respectively. Based on the function $\phi$, we define different temperature-based graphical matrices given in Table 1.

Table 1 Temperature-based matrices and their corresponding functions.

Assume $P\in \{\mathscr {H}\mathscr {T}_1,\mathscr {H}\mathscr {T}_2,\mathscr {P}\mathscr {T},\mathscr {S}\mathscr {T},\mathscr {R}\mathscr {P}\mathscr {T},\mathscr {R}\mathscr {S}\mathscr {T},\mathscr {F}\mathscr {T},\mathscr {A}\mathscr {G}\mathscr {T}, \mathscr {T}\mathscr {A}\mathscr {B}\mathscr {C},\mathscr {H}\mathscr {T},\mathscr {T}\mathscr {S}\mathscr {O},m\mathscr {T}\mathscr {S}\mathscr {O},\mathscr {R}\mathscr {R}\mathscr {P}\mathscr {T},\mathscr {G}\mathscr {A}\mathscr {T}\}$ is a chemical matrix associated with a temperature graphical index as defined earlier in this section. Since P is real symmetric, employing a standard result in linear algebra gives us that the eigenvalues of P are real and their algebraic and geometric multiplicities coincide. Let $\mu _1\ge \mu _2\ge \ldots ,\mu _{|P_\Phi |}$ be the real eigenvalues of P. Since the trace of P is zero, we obtain that $\mu _1>0$. Moreover, by the Perron-Frobenius theorem in linear algebra, we have that the multiplicity of $\mu _1$ is one. Next, we introduce three standard spectral topological indices associated with a chemical matrix. The spectral radius $\rho (P)$ is defined as:

$$\begin{aligned} \rho (P):=|\mu _1|. \end{aligned}$$

The energy E(P) of the matrix P is defined as the sum of absolute values of the eigenvalues of P.

$$\begin{aligned} E(P):=\sum _{k=1}^{|P_\Phi |}|\mu _k|. \end{aligned}$$

Moreover, the Estrada index $E_I(P)$ of P is defined as the sum of exponential values of the eigenvalues of P. For the associated chemical graph $\Phi$, it is defined as:

$$\begin{aligned} E_I(P):=\sum _{k=1}^{|P_\Phi |}\text {exp}(\mu _k). \end{aligned}$$

These three spectral indices deliver a list of 42 temperature-spectral indices corresponding to the 14 chemical matrices introduced earlier in this section.

Pillai’s Trace is a multivariate test statistic used in MANOVA (Multivariate Analysis of Variance). It is based on the sum of the explained variance components across multiple dependent variables and is considered one of the most robust and powerful tests, especially when assumptions such as homogeneity of covariance matrices are violated. The statistic ranges between 0 and 1, with larger values indicating stronger group differences. Pillai’s Trace is defined for a MANOVA with p dependent variables and a set of independent variables as:

$$V = \textrm{trace}\big (H(H + E)^{-1}\big )$$

where H is the hypothesis sum-of-squares-and-cross-products (SSCP) matrix, and E is the error SSCP matrix.

Let $\lambda _1, \lambda _2, \dots , \lambda _s$ be the eigenvalues of $E^{-1}H$, where $s = \min (p, \text {df}_{\text {effect}})$. Then Pillai’s Trace can be expressed as:

$$V = \sum _{i=1}^{s} \frac{\lambda _i}{1+\lambda _i}.$$

The largest canonical correlation $R_c$ between the independent variables and the set of dependent variables is related to the eigenvalues $\lambda _i$ by:

$$R_c^2 = \frac{\lambda _{\max }}{1 + \lambda _{\max }}.$$

An overall multivariate multiple correlation coefficient can be approximated from Pillai’s Trace as:

$$R_{\text {mult}} = \sqrt{\frac{V}{\min (p, \text {df}_{\text {effect}})}},$$

which represents the proportion of total multivariate variance explained by the independent variables.

Next, we introduce a computer-based computing method for efficiently evaluating the 42 temperature-spectral topological indices introduced earlier in this section.

A computational method

The focus of this section is on outlining a computational approach, implemented with computer assistance, to evaluate the temp-eigenvalue–related topological indices defined in Section Essential mathematical concepts.

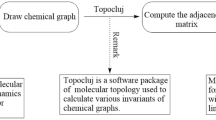
Our computational workflow integrates HyperChem³⁴, TopoCluj³⁵, and MATLAB³⁶ to evaluate the temperature-spectral indices efficiently. HyperChem, a versatile molecular modeling and computational chemistry environment, supports a broad range of tasks such as molecular mechanics, quantum chemistry, molecular dynamics, and visualization. Its capabilities include model construction, three-dimensional visualization, and advanced quantum chemical computations (e.g., Density Functional Theory and Ab-initio methods). In addition, it provides efficient tools for energy minimization within molecular mechanics and for spectral analyses such as UV-Vis, IR, and NMR spectroscopy. TopoCluj, by contrast, is tailored to the computation of molecular topological descriptors derived from matrices and polynomials, which are crucial for analyzing structural and chemical properties in computational chemistry and molecular graph theory. MATLAB (“Matrix Laboratory”), developed by MathWorks, serves as both a high-level programming language and an interactive computational environment, widely employed for algorithm development, data analysis, numerical computation, and visualization.

Next, we present a three-step computational procedure for evaluating the temperature-related spectral indices of a molecular graph $\Phi$:

• Step 1. The molecular structure of $\Phi$ is constructed in three dimensions using the HyperChem drawing module, which outputs a file in the .hin format.

• Step 2. The generated .hin file is processed in TopoCluj to obtain the distance matrix of $\Phi$, and a corresponding .m file is created.

• Step 3. The .m file is executed in MATLAB, where our custom-written code is applied to compute all temperature-related spectral descriptors introduced in Section Essential mathematical concepts.

Figure 1 provides a schematic representation of the proposed step-by-step computational method.

Fig. 1

Step-by-step algorithmic steps of the computing method.

The MATLAB code developed for this work has been made publicly available on GitHub, together with the associated data, and can be accessed via the following link: GitHub repository. Here we refer to^37,38,39 some other novel techniques to compute graphical topological indices.

Comparative testing

This section provides a complete exposition of the data, illustrating its functional application and interpretative implications for advancing structure–property modeling.

The initial stage identifies representative physicochemical properties–normal boiling point ($b_p$) and standard heat of formation ($\Delta H^o_f$)–following Gutman and Tošović¹⁴, as prototypical descriptors of physicochemical behavior. The choice of $b_p$ is warranted by its role in capturing van der Waals and intramolecular interactions, whereas the selection of $\Delta H^o_f$ is justified by its capacity to reflect fundamental thermochemical attributes. Specifically, the normal boiling point of a substance is defined as the temperature at which its vapor pressure equals the atmospheric pressure (1 atmosphere or 101.3 kPa) at sea level, with each compound exhibiting a distinct $b_p$ determined by its molecular properties. Similarly, $\Delta H^o_f$ denotes the enthalpy change associated with the formation of one mole of a compound from its constituent elements in their standard states under standard conditions (298 K and 1 atm), thereby serving as a canonical representation of thermochemical characteristics.

Next, as representative molecules of polycyclic aromatic hydrocarbons (PAHs), we select 22 lower PAHs to serve as the test set. This selection follows earlier investigations by Hayat and Khan⁴⁰ as well as Hayat et al.²⁴. In their comparative analysis, Hayat and Khan employed these 22 lower PAHs to evaluate the effectiveness of eigenvalue-based degree descriptors, whereas Hayat et al.²⁴ utilized the same set to examine the predictive capacity of distance-related graph-theoretic invariants with respect to physicochemical properties of PAHs. The consistently high correlation values obtained for both $b_p$ and $\Delta H^o_f$ across the initial 22 PAHs further substantiate the rationale for their adoption in the present study. Additionally, the sample size of 22 is deemed sufficient to ensure the validity of our statistical inferences. The experimental data for $b_p$ and $\Delta H^o_f$ were obtained from the NIST Standard Reference Database⁴¹ and subsequently cross-validated against the reported values of $\Delta H^o_f$ in Allison and Burgess⁸.

Figure 2 shows two-dimensional representations of the 22 PAHs analyzed in this study. As these illustrations serve merely as two-dimensional representations of the corresponding three-dimensional molecular architectures, the feature of aromaticity has been deliberately omitted. The subsequent step involves the computation of numerical values for the connection-related graphical invariants, as outlined in Section Essential mathematical concepts. To accomplish this, the computational methodology detailed in Section A computational method has been employed. Furthermore, Table 2 reports the experimental values of both $b_p$ and $\Delta H^o_f$ for the 22 lower PAHs under consideration. The application of the proposed method in Section A computational method to the first hyper-temperature spectral radius, energy, Estrada index, and second hyper-temperature spectral radius yields the data presented in Columns 4–7. Although the data corresponding to other spectral invariants are not reported herein, it is pertinent to emphasize that such indices can be computed analogously.

Fig. 2

Two-dimensional graphical schematization of the 22 foundational polycyclic aromatic hydrocarbons (PAHs) identified for use as test molecules.

Table 2 The dataset comprises experimental values of $b_p$ and $\Delta H^o_f$ for 22 lower PAHs, together with their first hyper-temperature spectral radius, energy, Estrada index, and second hyper-temperature spectral radius.

The concluding step of this section involves the employment of the multiple correlation value (MCV) to assess the association between a given spectral index S and the two selected physicochemical properties (PCPs), namely $b_p$ and $\Delta H^o_f$. Specifically, we compute $r:= r(b_p, \Delta H^o_f; S)$, representing the multiple correlation between $X_1 = b_p$, $X_2 = \Delta H^o_f$, and the spectral invariant $Y = S$, based on the dataset provided in Table 2, by means of the Pillai’s Trace method. The computations are performed utilizing the Data Analysis ToolPak of MS Excel. The corresponding multiple correlation values are furnished in Table 3.

Table 3 Multivariate correlations of all temperature–eigenvalue–based topological indices with the test properties $b_p$ and $\Delta H^o_f$ for the 22 foundational PAHs.

In the subsequent section, a comprehensive analysis of the data presented in Table 3 is furnished, highlighting the five most effective eigenvalue-based temperature topological indices for predicting the PCPs of PAHs, while concurrently identifying those indices that warrant no further consideration by researchers.

Results and discussion

This section provides a comprehensive analysis of the molecular line connectivity (MLC) metrics presented in Table 3. An immediately notable and unexpected outcome is that the spectral indices $\rho (\mathscr {H}\mathscr {T}_1)$, $E(\mathscr {H}\mathscr {T}_1)$, $E_I(\mathscr {H}\mathscr {T}_1)$, $\rho (\mathscr {H}\mathscr {T}_2)$, and $E(\mathscr {H}\mathscr {T}_1)$, derived from the classical first and second hyper-temperature matrices $\mathscr {H}\mathscr {T}_i~(i=1,2)$, exhibit markedly poor performance based on their MCVs. Both $\rho (\mathscr {H}\mathscr {T}_2)$ and $E(\mathscr {H}\mathscr {T}_1)$ display MCV values below 0.66, which are considered unsatisfactory for QSPR modeling. Moreover, the MCVs of $\rho (\mathscr {H}\mathscr {T}_1)$, $E(\mathscr {H}\mathscr {T}_1)$, and $E_I(\mathscr {H}\mathscr {T}_1)$ do not exceed 0.87. This outcome is particularly unexpected given that the corresponding temperature indices $HT_1$ and $HT_2$ are among the most extensively studied in the literature. Consequently, these spectral indices are deemed inadequate for applications in structure–property modeling, and their use is strongly discouraged.

Additionally, the MCV for the sum-connectivity temperature Estrada index $E_I(\mathscr {S}\mathscr {T})$ is less than 0.9. While this may be mathematically reasonable, it falls short of the thresholds required for implementation in quantitative structure–property relationship (QSPR) studies. Of particular note, the Estrada index $E_I(\mathscr {P}\mathscr {T})$, associated with the product-connectivity temperature matrix, demonstrates the poorest performance among all 42 temperature-based spectral indices, with an MCV of merely $\rho = 0.3283$.

In addition to the weak predictive ability of indices derived from the hyper-temperature matrices, several other spectral descriptors also demonstrate unsatisfactory performance and thus warrant exclusion from practical QSPR applications. Most notably, the Estrada index associated with the product-connectivity ($E_I(\mathscr {P}\mathscr {T})$) and temperature-atom bond connectivity matrices ($E_I(\mathscr {T}\mathscr {A}\mathscr {B}\mathscr {C})$) exhibit extremely low multiple correlation values (0.3283 and 0.2769, respectively). These values are the poorest among all 42 tested indices, clearly signaling their inability to capture any meaningful structure–property relationship. Similarly, the harmonic Estrada index $E_I(\mathscr {T}\mathscr {H})$ performs poorly with an MCV of only 0.3289, placing it in the same category of ineffective descriptors.

Furthermore, the Estrada indices derived from the sum-connectivity ($E_I(\mathscr {S}\mathscr {T})$) and modified temperature Sombor ($E_I(m\mathscr {T}\mathscr {S}\mathscr {O})$) matrices also fall short of acceptable thresholds, returning MCVs of 0.8499 and 0.4067, respectively. Despite being mathematically well-defined, their low correlation levels indicate a lack of robustness for physicochemical modeling. Together, these results highlight a recurring pattern: while spectral radius and energy indices often achieve strong or even excellent correlations, their Estrada counterparts tend to underperform, with several yielding critically low predictive scores. Consequently, these weak Estrada-based descriptors should be avoided in future QSPR modeling, as their inclusion may dilute statistical reliability and obscure the contributions of stronger indices.

Among the complete set of 42 temperature-spectral indices, five stand out as particularly effective predictors of the selected physicochemical properties. Table 4 lists the five most effective spectral indices. Specifically, the energy of the reciprocal sum-connectivity temperature matrix $E(\mathscr {R}\mathscr {S}\mathscr {T})$, the spectral radius of the sum-connectivity matrix $\rho (\mathscr {S}\mathscr {T})$, and the Estrada index $E_I(\mathscr {R}\mathscr {S}\mathscr {T})$ attain the highest multiple correlation values, all exceeding 0.994. These are closely followed by the Estrada index of the second hyper-temperature matrix $E_I(\mathscr {H}\mathscr {T}_{2})$ and the energy of the reduced reciprocal product-connectivity matrix $E(\mathscr {R}\mathscr {R}\mathscr {P}\mathscr {T})$, with MCVs of 0.9931 and 0.9922, respectively. Such near-unity correlations unequivocally establish the robustness of these indices in capturing structure–property relationships. Their consistently superior performance indicates a high degree of sensitivity to the underlying molecular architecture of PAHs, making them highly reliable descriptors for QSPR modeling. In particular, the recurrent success of sum-connectivity and reciprocal sum-connectivity matrices suggests that connectivity patterns weighted by temperature parameters provide a more refined encoding of molecular information compared to other spectral formulations. These findings strongly endorse the adoption of these top five indices in predictive modeling, as they not only surpass the performance of classical descriptors but also demonstrate the statistical reliability required for practical applications in cheminformatics. Moreover, these results collectively demonstrate that while several Estrada-type indices underperform, energy- and spectral-radius-based descriptors achieve outstanding predictive performance.

Table 4 The five best temp-eigenvalues-based indices.

Subsequently, a comprehensive statistical analysis is undertaken for the five most effective eigenvalues-related spectral graphical invariants. In this stage, suitable multiple linear regression (MLR) models are formulated to establish data-fitting relationships between the physicochemical properties (PCPs) $b_p$ and $\Delta H^o_f$ and the aforementioned top five invariants. Table 5 provides the most appropriate MLR models. In addition, Table 5 provides the computed values of the standard error of estimation s and the coefficient of determination $r^2$ associated with these leading invariants.

Table 5 The rigorously identified, data-fitting multiple linear regression (MLR) models establishing quantitative relationships between the five best temperature-eigenvalues-based graphical invariants and the selected physicochemical properties $b_p$ and $\Delta H^o_f$. Detailed statistics have also been delivered.

Figure 3 depicts the scatter plots illustrating the relationships between the physicochemical properties (PCPs) $b_p$ and $\Delta H^o_f$ and the five most effective temperature-related spectral graphical invariants.

Fig. 3

Scatter plots graphically illustrating the interrelations between the physicochemical properties $b_p$ and $\Delta H^o_f$ and the five preeminent temperature-related spectral topological indices.

Comparison with traditional topological descriptors

Table 6 summarizes the performance of different classes of topological descriptors in predicting physicochemical properties of benzenoid hydrocarbons. Traditional degree-based and distance-based indices, such as the general Randić index and the 2nd ABC index, exhibit strong correlations with correlation values of 0.9634 and 0.9799, respectively. More recent developments, including temperature-based and connection-based descriptors, provide further improvements, with the reduced reciprocal product-connectivity temperature reaching 0.9914. Notably, the newly proposed Reciprocal sum-connectivity temperature energy ($E(\mathscr {R}\mathscr {S}\mathscr {T})$) developed in the current work attains the highest predictive accuracy with a correlation of 0.9969. This highlights the superiority of general temperature-based descriptors and demonstrates the advancement contributed by the present study.

Table 6 Comparison of our work with traditional topological descriptors for predicting physicochemical properties of benzenoid hydrocarbons.

Efficient temperature-based spectral indices in QSPR modeling of polyacenes

Polyacenes are linearly fused benzenoid systems whose extended $\pi$-conjugation governs their electronic and thermal properties. Their extended conjugated $\pi$-electron frameworks engender phenomena such as elevated charge mobility, thereby underscoring their potential utility in the development of organic semiconductors and molecular electronic systems. Furthermore, the geometrical configuration of polyacenes—particularly as the number of fused rings increases—exerts a significant influence on their stability and reactivity, thereby positioning them as valuable paradigms for probing aromaticity and quantum chemical interactions. These distinctive characteristics additionally open promising avenues for the design and advancement of novel optoelectronic devices and photovoltaic materials.

Polyacenes represent an archetypal class of unbranched catacondensed benzenoid systems, defined by the linear fusion of benzene rings wherein each successive ring shares two contiguous carbon atoms with its predecessor. This distinctive structural motif establishes a clear demarcation from branched or more intricate fused aromatic architectures. As the sequence of fused rings extends, the delocalization of $\pi$-electrons correspondingly intensifies, exerting a marked effect on critical electronic properties such as conductivity and aromaticity. The orderly and uninterrupted linear concatenation of benzene units not only engenders characteristic stability patterns but also provides a foundational paradigm for interpreting the structural and electronic behavior of larger aromatic frameworks in organic chemistry.

Within this framework, linear polyacenes are categorized as unbranched catacondensed benzenoid systems (BSs), generated through the sequential linear fusion of m aromatic hexagonal rings. It should be emphasized that the parameter m is constrained to values not less than two, formally expressed as $m \in \mathbb {N}$ with $m \ge 2$. The structural configuration of an m-dimensional polyacene $P_m$ is schematically depicted in Fig. 4.

Fig. 4

An m-dimensional polyacene $P_m$, where $2\le m\in \mathbb {N}$.

Table 7 The five best temperature-based spectral descriptors of polyacene $P_m,~1\le m\le 10.$.

Building upon the preceding detailed examination and statistical analysis, the present section extends the findings to QSPR modeling, wherein a correlation is established between the heat capacity and entropy of the lower linear polyacenes.

By conducting a statistical analysis of the data presented in Table 7, it is observed that the most appropriate data-fitting expressions are linear in form. Moreover, the analysis provides the $95\%$ confidence intervals for both the slope and the intercept associated with these linear relationships.

$$\begin{aligned} b_p&= -227.48_{\pm 64.01} + 34.89_{\pm 4.22} \, E(\mathscr {R}\mathscr {S}\mathscr {T}),~~r=0.991,~r^2=0.982,~s=19.97 \end{aligned}$$

(2)

$$\begin{aligned} \Delta H^{o}_{f}&= -61.31_{\pm 58.08} + 37.97_{\pm 3.82} \, E(\mathscr {R}\mathscr {S}\mathscr {T}),~~r=0.994,~r^2=0.987,~s=18.15. \end{aligned}$$

(3)

The initial ten dimensions $P_{m}$, with $1 \le m \le 10$, of linear polyacenes corresponding to $E(\mathscr {R}\mathscr {S}\mathscr {T})$ are derived through the implementation of the computational framework delineated in Section A computational method. Empirical data for the normal boiling point $b_p$ and the standard heat-of-formation $\Delta H^o_f$, pertaining to the first nine linear polyacenes, are sourced from the authoritative NIST database⁴¹.

Subsequently, a regression analysis is conducted to elucidate the relationship between variations in $b_p$ and $\Delta H^o_f$ with respect to $E(\mathscr {R}\mathscr {S}\mathscr {T})$, construed as a function of the linear dimensions of polyacenes. The findings, illustrated in Fig. 5, demonstrate that the most suitable regression formulations are predominantly linear in character. All statistical evaluations and graphical depictions are derived directly from the dataset presented in Table 8. The consistency between the empirical data and predicted trends further validates the robustness of the proposed indices.

Fig. 5

Linear scatter plot schematizations illustrating the relationships between $b_p$, $\Delta H^o_f$, and the $E(\mathscr {R}\mathscr {S}\mathscr {T})$ index for the ten lower linear polyacenes.

Table 8 Tabulated values of the reciprocal sum-connectivity temperature energy $E(\mathscr {R}\mathscr {S}\mathscr {T})$, normal boiling point $b_p$, and standard enthalpy of formation $\Delta H^o_f$ for the nine lower polyacenes.

Conclusion

Contributions

• We introduced and validated a new class of temperature-based spectral topological indices.

• Developed a computational framework integrating HyperChem, TopoCluj, and MATLAB for efficient descriptor evaluation.

• Conducted comprehensive quality testing of 42 indices on polycyclic aromatic hydrocarbons (PAHs) with respect to boiling points and heats of formation.

• Five indices demonstrated excellent predictive capacity (MCV $\ge 0.99$) for boiling points and enthalpies of formation.

• Validated these indices through regression modeling and applications to linear polyacenes⁴³.

Implications

• Demonstrated that temperature-based spectral invariants provide robust tools for QSPR modeling.

• Established a systematic benchmark for assessing predictive quality of new topological indices.

• Enhanced understanding of structure–property relationships in PAHs.

• Highlighted the utility of spectral descriptors in chemical informatics and materials science⁴⁴.

Limitations

• Analysis focused primarily on PAHs, limiting generalizability across diverse molecular classes⁴⁵.

• The current study might not be applicable for heteroatom-containing compounds and inorganic compounds.

• Some Estrada-type descriptors showed poor performance, reducing their practical value.

Future study

• Study predictive potential of proposed spectral descriptors for other molecular classes such as, isomeric alkanes, inorganic compounds.

• Explore predictive capacity for additional physicochemical and quantum-chemical properties.

• Refine computational algorithms to improve efficiency and accessibility.

• Investigate integration of temperature-based spectral indices with machine learning for property prediction.

• Examine potential applications in drug design, nanomaterials, and environmental chemistry.